基于灵敏度分析的有限元模型修正
合集下载
基于Kriging模型的有限元模型修正方法研究
基于Kriging模型的有限元模型修正方法研究基于Kriging模型的有限元模型修正方法研究摘要：有限元模型是一种常用的结构分析方法，然而，由于模型假设和离散化误差等因素，其结果可能存在一定误差。
本文提出了基于Kriging模型的有限元模型修正方法，通过对已有有限元模型数据进行拟合，进而修正模型中的误差，并对修正效果进行验证。
实验结果表明，基于Kriging模型的有限元模型修正方法能够显著提高有限元模型的精度和稳定性。
关键词：有限元模型；Kriging模型；模型修正；精度；稳定性1. 引言有限元模型是一种常用的结构分析方法，广泛应用于工程领域。
然而，在实际应用过程中，由于对结构复杂性的简化、参数估计误差以及离散化误差等因素的影响，有限元模型的分析结果可能存在一定误差，从而影响工程设计的准确性。
因此，如何对有限元模型进行修正并提高其精度和稳定性成为了一个重要的研究方向。
2. Kriging模型的基本原理Kriging模型是一种基于统计学的插值方法，通过对已有样本数据的拟合，预测未知位置上的数值。
其基本思想是通过已知样本点之间的空间相关性，在未知位置上进行插值，从而得到预测结果。
Kriging模型通过建立样本点之间的半变异函数，从而描述其空间相关性，并通过最小化预测误差来确定未知位置上的数值。
3. 基于Kriging模型的有限元模型修正方法基于Kriging模型的有限元模型修正方法主要包括以下几个步骤：（1）数据采集：首先，需要采集与有限元模型相关的数据，包括原始模型的力学性能、结构几何参数、材料参数等。
（2）数据预处理：对采集到的数据进行预处理，包括数据的筛选、去噪和归一化处理等，以减小数据误差对模型修正的影响。
（3）Kriging模型构建：根据预处理后的数据，构建Kriging模型，包括选择合适的半变异函数、估计其参数，并进行模型的验证。
（4）有限元模型的修正：利用步骤（3）中构建的Kriging模型，对已有的有限元模型进行修正，得到修正后的模型。
基于优化BP神经网络的梁结构有限元模型修正
关． 且通 过整 体结 构 矩 阵修 正 得 到 的结 果 将 改 变 原 有 的结构 矩 阵带状 、 稀疏 特性 而成 为满 秩矩 阵 ， 甚 至 有些 元 素变 为负值 ， 导致 得 到 的结 构矩 阵物 理 意 义 不 明确 ． 其后 ， 众 多研究 人员 根据存 在 的问题 提 出了 他们 的解 决 方 法． Ｋ ａ ｂ ｅ 引入 元 素 相 关 性 的概 念 ，
基 金项 目：国家 自然科学基金 资助项 目（ ５ １ ２ ０ ８ ２ ０ ８ ） ； 广东省交通运输厅科技项 目（ 科技一 ２ ０ １ ２ — ０ ２ — ０ ２ ４ ）
一
方 法大 体可 分为 两 类 ： 整 体 结 构 矩 阵 型修 正 方 法 与 参 数型 修正 方法 ． 整 体 结构 矩 阵 型 修 正方 法 首 先 由 Ｂ ｅ ｒ ｍ ａ ｎ等
提出 ： 以有 限元模 型 的质量 矩 阵 和刚度 矩 阵 的 加 权 范数 最小 化 为 目标 函数 ， 以振 型正 交 性 和 、
验， 验证 了该方 法的 准确性 与 有效性 ．
关键词 ： 梁结构 ； 模型修正 ； 遗传算法 ； Ｂ Ｐ神经网络 中图分类号 ： Ｕ ４ ４ １ ． ３ ｄ ｏ ｉ ： １ ０ ． ３ ９ ６ ９ ／ ｊ ． ｉ ｓ ｓ ｎ ． １ ０ ０ ０ － ５ ６ ５ Ｘ ． ２ ０ １ ３ ． ０ ８ ． Ｏ １ １
华 南 理 工 大 学 学 报 （自 然 科 学 版）
第４ １ 卷 第 ８期
２ ０ １ ３年 ８月
Ｊ ｏｕ ｒ ｎ ａ ｌ ｏｆ Ｓ ｏｕ ｔ ｈ Ｃｈｉ ｎ ａ Ｕｎ ｉ ｖ ｅ ｒ ｓ ｉ ｔ ｙ ｏ ｆ Ｔｅ ｃ ｈｎ ｏ ｌ ｏ ｇ ｙ
Ｖｏ １ ． ４１ Ｎｏ． ８
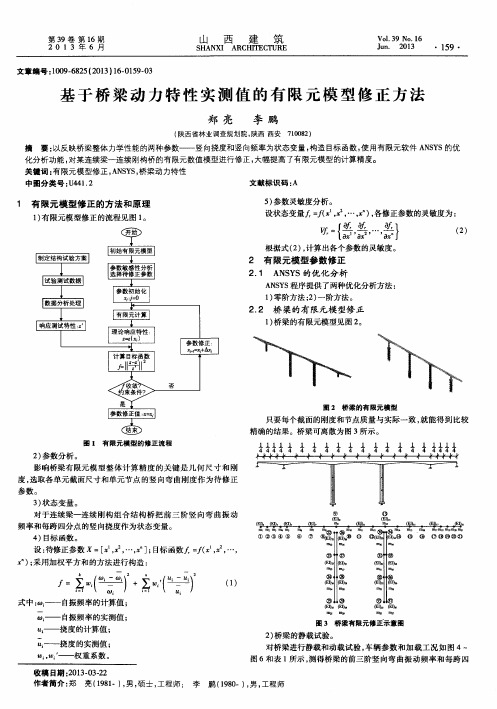
基于桥梁动力特性实测值的有限元模型修正方法
ｒ
ｍ｜ Ｉ ｌ ｌ ‘ ｍｓ ｜ ｌ ｌ ’
０
【 Ｅ Ｉ ） ・ ｍ ｌ ｉ ｆ ｍ １ ７ ￣ｌ ｌ ｍ ｍ
频 率和每跨 四分点 的竖 向挠度作 为状 态变量。
４ ） 目标 函 数 。
① ②③ ④ ⑤
⑥
图 １ 有 限元模型的修正流程
上 上 １ 上 １ 工 １ 上 １ １ 上 Ｊ ＿ Ｊ － Ｊ － 上 Ｊ － 上 上 上 上
４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４
第３ ９卷 第 １ ６期 ２ ０ １ ３ 年 ６ 月
Ｓ ＨＡＮＸＩ ＡＲ ＣＨＩ ＴＥ Ｃ ＴＵ ＲＥ
山 西 建 筑
Ｖｏ１ ． ３ ９ Ｎｏ ． １ ６
Ｊ ｕ ｎ ． ２ ０ １ ３
・１ ５ ９・
文章编号 ： １ ０ ０ ９ － ６ ８ ２ ５ （ ２ ０ １ ３） １ ６ — ０ １ ５ ９ — ０ ３
山 西 建 筑
分 点 的 竖 向挠 度 。
—
凸
前轴
后轴 中轴
十 一 十—— ＝———一 ！ 一 寸 十
一
＼ （ 一 １ ． ８ ４ ６ ） ／ ＋ 上 １ ８ （ ＼ 一 ６ ． ０ １ ７ ） ７ ＋ 。 去 １ ８ （ ＼ 一 １ ． ７ ２ ８ ） ／ ＋ 。 一 １ １ ８ × 一 （ ＼ 一 １ ． ４ ５ ０ ） ／ １ ８ （ ＼ 一 ５ ． １ ７ ２ ） ／ ＋ （ １ ８ ＼ 一 １ ． ５ ０ ４ ） Ｊ ＋ 。 一 １ １ ８ × （ ＼ 一 １ ． ７ ９ １ ） ／ １ ８ （ ＼ 一 ６ ． ０ ４ ０ ） ／ ’ １ ８ （ ＼ 一 １ ． ７ ６ ７ ） Ｊ ＋ 。 一 １ １ ８ × （ ＼ 一 ３ ． ３ ８ １ ） ／ ＋ （ １ ８ ＼ 一 １ ． ２ ９ ０ ） ／ ＋ ’ （ １ ８ ＼ 一 １ ． １ ５ ４ ） 』 ＋ 。 一 １ １ ８ × （ ｌ ＿ ＿ ＝ 石 Ｊ ） ＋ 西 （ ｌ ｗ ＿ ＿ ２ ＝ － Ｏ ． ８ ９ ８ Ｊ Ｉ （ Ｔ ） Ｊ ㈩ ，
ｍ｜ Ｉ ｌ ｌ ‘ ｍｓ ｜ ｌ ｌ ’
０
【 Ｅ Ｉ ） ・ ｍ ｌ ｉ ｆ ｍ １ ７ ￣ｌ ｌ ｍ ｍ
频 率和每跨 四分点 的竖 向挠度作 为状 态变量。
４ ） 目标 函 数 。
① ②③ ④ ⑤
⑥
图 １ 有 限元模型的修正流程
上 上 １ 上 １ 工 １ 上 １ １ 上 Ｊ ＿ Ｊ － Ｊ － 上 Ｊ － 上 上 上 上
４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４ ４
第３ ９卷 第 １ ６期 ２ ０ １ ３ 年 ６ 月
Ｓ ＨＡＮＸＩ ＡＲ ＣＨＩ ＴＥ Ｃ ＴＵ ＲＥ
山 西 建 筑
Ｖｏ１ ． ３ ９ Ｎｏ ． １ ６
Ｊ ｕ ｎ ． ２ ０ １ ３
・１ ５ ９・
文章编号 ： １ ０ ０ ９ － ６ ８ ２ ５ （ ２ ０ １ ３） １ ６ — ０ １ ５ ９ — ０ ３
山 西 建 筑
分 点 的 竖 向挠 度 。
—
凸
前轴
后轴 中轴
十 一 十—— ＝———一 ！ 一 寸 十
一
＼ （ 一 １ ． ８ ４ ６ ） ／ ＋ 上 １ ８ （ ＼ 一 ６ ． ０ １ ７ ） ７ ＋ 。 去 １ ８ （ ＼ 一 １ ． ７ ２ ８ ） ／ ＋ 。 一 １ １ ８ × 一 （ ＼ 一 １ ． ４ ５ ０ ） ／ １ ８ （ ＼ 一 ５ ． １ ７ ２ ） ／ ＋ （ １ ８ ＼ 一 １ ． ５ ０ ４ ） Ｊ ＋ 。 一 １ １ ８ × （ ＼ 一 １ ． ７ ９ １ ） ／ １ ８ （ ＼ 一 ６ ． ０ ４ ０ ） ／ ’ １ ８ （ ＼ 一 １ ． ７ ６ ７ ） Ｊ ＋ 。 一 １ １ ８ × （ ＼ 一 ３ ． ３ ８ １ ） ／ ＋ （ １ ８ ＼ 一 １ ． ２ ９ ０ ） ／ ＋ ’ （ １ ８ ＼ 一 １ ． １ ５ ４ ） 』 ＋ 。 一 １ １ ８ × （ ｌ ＿ ＿ ＝ 石 Ｊ ） ＋ 西 （ ｌ ｗ ＿ ＿ ２ ＝ － Ｏ ． ８ ９ ８ Ｊ Ｉ （ Ｔ ） Ｊ ㈩ ，
结构健康监测课件-第七章-结构有限元模型修正方法
2.确定性修正方法
1）矩阵性有限元模型修正法
=+
=+
摄动法求解，破坏原有的质量、刚度矩阵带状和稀疏特征，失去普遍的物理意义
2）参数性有限元模型修正法 基于结构动力特性或静动力响应来定义目标函数，修正问题转化为优化问题。
3）基于响应面的有限元模型修正法 试验设计，变量的设计空间，拟合结构响应和参数之间的显示函数关系式，构建代理模
Management-Design Approach, Feature Construction, Fault Diagnosis, Prognosis, Gang Niu (auth.), Springer ,2017
4. Structural Health Monitoring- A Machine Learning Perspective,
有限元模型修正流程图
7.2 有限元模型修正方法
1.修正方法分类
模型修正方法分类
按 修 正 对 象
按 测 量 信 息
按
按
按
是
有
整
否
限
体
性
型
性
矩参 阵数 法法
联
静 力
动 力
合 静 动
力
随确 机定 性性 方方 法法
直代 接理 模模 型型 法法
子 结 构 方 法
整 体 方 法
7.2 有限元模型修正方法
型代替有限元模型。依赖大量样本、经验。
4）基于神经网络的有限元模型修正法
7.2 有限元模型修正方法
3.随机性修正方法
( | )= ( ) ( | )
模型参数多时，基于贝叶斯理论的随机有限元模型修正面临计算复杂性，预先假定预测 误差类型，实际上未必。
结构动力模型修正的灵敏度方法研究与探讨
。
、
．
壹
。 …。 ４ ２层 ２６性 台 计 堇 ． ． ＂ ７２９．及‘设’ ‘ 。 ｌ ￣ ｑ ／ 詈 （５载 抗风。究 Ａ ６‘ 特 房－ ３ 研 ）７ … 屋９ ： ９ 风 － 荷 ： ６
初 分析 ［ ］ 河海大 学学报 ，９ ５ Ｊ． １９ ，
４ 结语
中 图分 类 号 ： Ｕ １ ． Ｔ ３ １３ 文献 标 识 码 ： Ａ
１ 概 述
模态应变能法 、 柔度 法 、 灵敏度 分析 法 、 传算 法 、 遗 神经 网络方 法
指标方 法能诊 断结 构的损 伤位 置 ， 要准 确识 别 但 随着现代科学技术的发展 ， 结构损 伤诊 断方法 已从依靠 简单 等 。一般来说 ， 出损伤程度 ， 特别是 多处 损伤 的情况 ， 一般来 说较 为有效 的方 法 的经验 的方法过 渡到依靠 科学 仪器进行 的方 法。在对结 构进行 它 损伤识别 、 监测 与评估方面 的研究 中， 部分 国家正把建设重点转移 是灵敏度分析 法 ， 的基本 做法 是 根据 测试 所得 的结 构振 动参 数， 应用灵敏度分析 法进 行结构参 数 的模型修 正 ， 而根 据修 正 从 到 旧建筑 的鉴定 、 、 维修 改造与加固方面， 相应的投入也越来越多 。
结构 动 力模 型 修 正 的灵 敏度 方 法研 究 与探 讨
李 文雄 陈存 恩
摘 要 ： 对结构动力模 型修 正的灵敏度分析 法作 了介绍 ， 通过对 四层平 面框架 的动力模 型修 正进行研 究， 究表 明， 于 研 对 本箅例的大部 分情况 ， 灵敏度分析法能得 到理 想结果 ， 同时也存在 部分不理 想的情况 ， 但 建议在实际应用 中， 可先使用 灵 敏度 分析 法进行模 型修 正， 再结合其他方法进行检验。 关键词 ： 灵敏度 ， 损伤诊 断， 结构动力模 型修 正
、
．
壹
。 …。 ４ ２层 ２６性 台 计 堇 ． ． ＂ ７２９．及‘设’ ‘ 。 ｌ ￣ ｑ ／ 詈 （５载 抗风。究 Ａ ６‘ 特 房－ ３ 研 ）７ … 屋９ ： ９ 风 － 荷 ： ６
初 分析 ［ ］ 河海大 学学报 ，９ ５ Ｊ． １９ ，
４ 结语
中 图分 类 号 ： Ｕ １ ． Ｔ ３ １３ 文献 标 识 码 ： Ａ
１ 概 述
模态应变能法 、 柔度 法 、 灵敏度 分析 法 、 传算 法 、 遗 神经 网络方 法
指标方 法能诊 断结 构的损 伤位 置 ， 要准 确识 别 但 随着现代科学技术的发展 ， 结构损 伤诊 断方法 已从依靠 简单 等 。一般来说 ， 出损伤程度 ， 特别是 多处 损伤 的情况 ， 一般来 说较 为有效 的方 法 的经验 的方法过 渡到依靠 科学 仪器进行 的方 法。在对结 构进行 它 损伤识别 、 监测 与评估方面 的研究 中， 部分 国家正把建设重点转移 是灵敏度分析 法 ， 的基本 做法 是 根据 测试 所得 的结 构振 动参 数， 应用灵敏度分析 法进 行结构参 数 的模型修 正 ， 而根 据修 正 从 到 旧建筑 的鉴定 、 、 维修 改造与加固方面， 相应的投入也越来越多 。
结构 动 力模 型 修 正 的灵 敏度 方 法研 究 与探 讨
李 文雄 陈存 恩
摘 要 ： 对结构动力模 型修 正的灵敏度分析 法作 了介绍 ， 通过对 四层平 面框架 的动力模 型修 正进行研 究， 究表 明， 于 研 对 本箅例的大部 分情况 ， 灵敏度分析法能得 到理 想结果 ， 同时也存在 部分不理 想的情况 ， 但 建议在实际应用 中， 可先使用 灵 敏度 分析 法进行模 型修 正， 再结合其他方法进行检验。 关键词 ： 灵敏度 ， 损伤诊 断， 结构动力模 型修 正
电气和电子工程用材料科学
O29，O177.922007020132一类两相同部件并联可修系统的稳定性/王定江(浙江工业大学理学院)//浙江工业大学学报.―2006，34（2）.―228～229，236.可修系统是可靠性理论研究的主要内容，可修系统包含串联和并联系统，并联系统是指系统中的多个部件有一个完好系统就能正常工作的一类系统。
该文讨论一类两相同部件并联可修系统的数学模型，应用强连续算子半群证明了系统的非负解的存在唯一性，讨论了系统的稳定性。
图0表0参9O29，O352007020133具有超薄厚度的多孔介质中St okes流的均匀化/赵红星，姚正安(中山大学数学与计算科学学院)//中山大学学报（自然科学版）.―2006，45（3）.―5～8.主要研究了在三维的多孔介质中具有超薄厚度的区域上Stokes流的均匀化。
经过细致地分析，文章最后论证了当流体区域的厚度充分小时，流体的运动状态满足平面流中的“达西定律”。
图0表0参10TB1142007020134小子样条件下基于N or m al-Poi s s on过程的性能可靠性评定/张永强，刘琦，周经伦(国防科技大学信息系统与管理学院)//国防科技大学学报.―2006，28（3）.―128～132.对于高可靠、长寿命产品，基于性能退化数据分析可靠性是一种行之有效的技术途径。
结合航空航天产品性能退化的机理与现场试验小子样的特点，建立了基于Normal-Pois son过程的性能退化模型。
论文在对产品性能退化建模的基础上，结合Bayes方法给出了退化模型参数的估计算法和可靠性推断的公式，最后结合实例说明了方法的有效性。
图0表2参13TB114.32007020135基于G A的可靠性寿命分布参数的极大似然优化估计/方华元，胡昌华，樊红东，丁力(西安第二炮兵工程学院)//上海航天.―2006，23（2）.―50～53.基于极大似然估计法的基本原理和优化理论，建立了可靠性寿命分布参数的极大似然优化估计模型，并采用遗传算法（GA）进行求解。
基于环境激励的预应力混凝土连续梁桥有限元模型修正
Ｋｅ ｙ ｗｏ ｒ ｄ ｓ ： ｍｏ ｄ ｅ ｌ ｕ ｐ ｄ ａ ｔ ｉ ｎ ｇ ； ｓ ｅ ｎ ｓ ｉ ｔ ｉ ｖ ｉ ｔ ｙ ａ ｎ ｌｙ ａ ｓ ｉ ｓ ； ａ ｍｂ ｉ ｅ ｎ ｔ ｖ ｉ ｂ ｒ ａ ｔ ｉ ｏ ｎ； ｉ ｆ ｎ ｉ ｔ ｅ ｅ ｌ ｅ ｍｅ ｎ ｔ ｍｏ ｄ ｅ ｌ Ａｂ ｓ ｔ ｒ ａ ｃ ｔ ： Ｔ ｈ ｅ ｄ ｅ ｖ ｅ ｌ ｏ ｐ ｍｅ ｎ ｔ ｏ ｆ ｔ ｈ ｅ ｍｏ ｄ ｅ ｌ ｕ ｐ ｄ ａ ｔ ｉ ｎ ｇ ｔ ｅ ｃ ｈ ｎ ｏ ｌ ｏ ｙ ｇ ｂ ａ ｓ ｅ ｄ ｏ ｎ ｔ ｈ ｅ ｏ ｐ ｔ ｉ ｍｉ ｚ ａ ｔ ｉ ｏ ｎ ｔ ｈ ｅ ｏ ｒ ｙ ｐ ｒ ｏ ｖ ｉ ｄ ｅ ｓ ａ ｎ ａ ｄ ｖ ａ ｎ ｔ ａ ｇ ｅ ｆ ｏ ｒ ｔ ｈ ｅ ｍｏ ｄ ｅ ｌ ｕ ｐ —
桥二桥为 背景 ， 利用该桥健康监测 系统提供的环境振动测试信息 ， 并基于结构 特征值灵敏度 分析选择 的修 正参数 ，
对该桥进 行结构动 力模 型修正． 修 正后的有限元模型振动 基频 更接近于环 境激励 下的测 量结果 ， 表明大 型通用 软 件提供 的优化 算法可以有效的实施动 力模 型修 正．
ｒ ｉ ｔ ｈ ｍ ｐ ｒ ｏ ｖ ｉ ｄ ｅ ｄ ｂ ｙ ｌ ａ ｒ ｇ ｅ － ｓ ｃ ａ ｌ ｅ ｇ ｅ ｎ ｅ ｒ ｌ ａ ｓ ｏ ｆ ｔ ｗ ａ ｒ ｅ ｃ ａ ｎ ｄ ｏ ｔ ｈ ｅ ｍｏ ｄ ｅ ｌ ｕ ｐ ｄ ａ ｔ ｉ ｎ ｇ ｅ ｆ ｆ ｅ ｃ ｔ ｉ ｖ ｅ ｌ ｙ ．
ｗ ｉ ｔ ｈ ｔ ｈ ｅ ｈ ｅ ｌ ｐ ｏ ｆ ｐ ａ ｒ ａ ｍｅ ｔ ｅ ｒ ｓ ｅ ｎ ｓ ｉ ｔ ｉ ｖ ｉ ｔ ｙ ａ ｎ ａ ｌ ｙ ｓ ｉ ｓ ａ ｎ ｄ ａ ｍｂ ｉ ｅ ｎ ｔ ｖ ｉ ｂ ｒ ａ ｔ ｉ ｏ ｎ ｍｅ ａ ｓ ｕ ｒ ｅ ｍｅ ｎ ｔ ｓ ｏ ｆ ｆ ｅ ｒ ｅ ｄ ｂ ｙ ｔ ｈ ｅ ｈ ｅ ｌｔ ａ ｈ ｍｏ ｎ ｉ ｔ ｏ ｉ ｒ ｎ ｇ ｓ ｙ ｓ ｔ ｅ ｍ．Ｔ ｈ ｅ ｂ ａ ｓ ｉ ｃ
桥二桥为 背景 ， 利用该桥健康监测 系统提供的环境振动测试信息 ， 并基于结构 特征值灵敏度 分析选择 的修 正参数 ，
对该桥进 行结构动 力模 型修正． 修 正后的有限元模型振动 基频 更接近于环 境激励 下的测 量结果 ， 表明大 型通用 软 件提供 的优化 算法可以有效的实施动 力模 型修 正．
ｒ ｉ ｔ ｈ ｍ ｐ ｒ ｏ ｖ ｉ ｄ ｅ ｄ ｂ ｙ ｌ ａ ｒ ｇ ｅ － ｓ ｃ ａ ｌ ｅ ｇ ｅ ｎ ｅ ｒ ｌ ａ ｓ ｏ ｆ ｔ ｗ ａ ｒ ｅ ｃ ａ ｎ ｄ ｏ ｔ ｈ ｅ ｍｏ ｄ ｅ ｌ ｕ ｐ ｄ ａ ｔ ｉ ｎ ｇ ｅ ｆ ｆ ｅ ｃ ｔ ｉ ｖ ｅ ｌ ｙ ．
ｗ ｉ ｔ ｈ ｔ ｈ ｅ ｈ ｅ ｌ ｐ ｏ ｆ ｐ ａ ｒ ａ ｍｅ ｔ ｅ ｒ ｓ ｅ ｎ ｓ ｉ ｔ ｉ ｖ ｉ ｔ ｙ ａ ｎ ａ ｌ ｙ ｓ ｉ ｓ ａ ｎ ｄ ａ ｍｂ ｉ ｅ ｎ ｔ ｖ ｉ ｂ ｒ ａ ｔ ｉ ｏ ｎ ｍｅ ａ ｓ ｕ ｒ ｅ ｍｅ ｎ ｔ ｓ ｏ ｆ ｆ ｅ ｒ ｅ ｄ ｂ ｙ ｔ ｈ ｅ ｈ ｅ ｌｔ ａ ｈ ｍｏ ｎ ｉ ｔ ｏ ｉ ｒ ｎ ｇ ｓ ｙ ｓ ｔ ｅ ｍ．Ｔ ｈ ｅ ｂ ａ ｓ ｉ ｃ
桥梁动力模型修正及破损识别研究综述
◇ 工程科技◇
科技 圈向导
２ ０ １ ３ 年２ ３ 期
桥梁动 力模 型修正及破 损识别研究综述
（ 重庆交通大学
【 摘
要手段 。
魏瑞 营 中国 重庆
４ ０ ０ ０ ７ ４ ）
要】 采用有限元 理论对桥 梁结构进行监 测和评 估， 通过 动力试验进行模型修正 ， 进 而识别损伤 ， 是桥 梁结构健康监测和安全评估 的重
【 关键词 】 有限元 理论 ； 动 力； 模 型修 正； 损伤识 别
０ ． 引 言 大跨桥 梁结构 的健康监测与 安全状态评估 是 目前 国内外的热点 研究领域 ［ １ １ ． 如何根据 采集的数据 和信号反演 出桥梁结构 的工作状态 和健康状况 ． 建立精确 的有限元模 型 ． 识别 出可能的结构损 伤部位及 其损伤程度 ． 并 预测预 报桥梁未来可 能的响应 ． 在此基础上 实现桥梁 安全及 可靠性 评估 ． 是 桥梁结构健康 监测 、 损 伤诊断与安全 评估最核 心和最关键 的问题之一口 桥梁结构的健康监测与评估需要对桥梁进行有 限元 模型修正 ． 即 利用经动载试验结果 （ 频率 、 振型 、 应变 、 位移等 ） 修改理论 有限元模型 的刚度 、 质量 、 边界约束 、 几 何尺寸等参 数 ， 在保证模 型参数 自 身 精度 的前提下 ， 使修正后的有限元模型结果趋于试验值 ； 目标 函数 确定 、 待 修正参数选 择和优化算 法是参数 型有 限元模 型修正的三大关键 问题 经过修正 的有限元模型可 以应用于 以下几个方面 ： ①结构静动力响 应再分析 ； ②某些振 动控制技术 的控制策略制定 ； ③结构的损伤识别 ； ④结构健康监测和安全性评估 ： ⑤结构的优化设计和模 型修改等。 目前结构 动力 学建模 可分为两大类 ： 一类是实 验模 型 ． 此类模 型 好 处是更符合真 实情况 。 但 它仅限于小 型低阶结构 ． 而且实验模态 通 常不完备以及不可忽视的噪声影响 ．对于大型结构成本代价较 高 ： 另 类则是有限元模型 ． 此类模型优点在于成本较低 ． 修改方便 ， 但 它会 带来建模 误差 综合两种建模 方法优点的模型修正技术 随之兴起 ． 成 为当前 结构动力学领域的重要 研究 方向之一
科技 圈向导
２ ０ １ ３ 年２ ３ 期
桥梁动 力模 型修正及破 损识别研究综述
（ 重庆交通大学
【 摘
要手段 。
魏瑞 营 中国 重庆
４ ０ ０ ０ ７ ４ ）
要】 采用有限元 理论对桥 梁结构进行监 测和评 估， 通过 动力试验进行模型修正 ， 进 而识别损伤 ， 是桥 梁结构健康监测和安全评估 的重
【 关键词 】 有限元 理论 ； 动 力； 模 型修 正； 损伤识 别
０ ． 引 言 大跨桥 梁结构 的健康监测与 安全状态评估 是 目前 国内外的热点 研究领域 ［ １ １ ． 如何根据 采集的数据 和信号反演 出桥梁结构 的工作状态 和健康状况 ． 建立精确 的有限元模 型 ． 识别 出可能的结构损 伤部位及 其损伤程度 ． 并 预测预 报桥梁未来可 能的响应 ． 在此基础上 实现桥梁 安全及 可靠性 评估 ． 是 桥梁结构健康 监测 、 损 伤诊断与安全 评估最核 心和最关键 的问题之一口 桥梁结构的健康监测与评估需要对桥梁进行有 限元 模型修正 ． 即 利用经动载试验结果 （ 频率 、 振型 、 应变 、 位移等 ） 修改理论 有限元模型 的刚度 、 质量 、 边界约束 、 几 何尺寸等参 数 ， 在保证模 型参数 自 身 精度 的前提下 ， 使修正后的有限元模型结果趋于试验值 ； 目标 函数 确定 、 待 修正参数选 择和优化算 法是参数 型有 限元模 型修正的三大关键 问题 经过修正 的有限元模型可 以应用于 以下几个方面 ： ①结构静动力响 应再分析 ； ②某些振 动控制技术 的控制策略制定 ； ③结构的损伤识别 ； ④结构健康监测和安全性评估 ： ⑤结构的优化设计和模 型修改等。 目前结构 动力 学建模 可分为两大类 ： 一类是实 验模 型 ． 此类模 型 好 处是更符合真 实情况 。 但 它仅限于小 型低阶结构 ． 而且实验模态 通 常不完备以及不可忽视的噪声影响 ．对于大型结构成本代价较 高 ： 另 类则是有限元模型 ． 此类模型优点在于成本较低 ． 修改方便 ， 但 它会 带来建模 误差 综合两种建模 方法优点的模型修正技术 随之兴起 ． 成 为当前 结构动力学领域的重要 研究 方向之一
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5
Confidential
一、背景介绍—蜂窝夹层板结构组成
具有复杂几何结构的正六边形铝蜂窝夹层板是最为常见的蜂窝板结构形式，其几何结构包括上、下面板， 中间的正六边形蜂窝状夹心以及连接面板和芯层的胶层；
胶层用于连接芯层和面板，厚度较小、质量较轻，不是主要承载部位，因此在蜂窝夹层板分析时可以忽 略胶层的影响。
2.31e-3
3.91e-3 29.28
0.68
s
vs
s
v
s
vs
s
v
v
vv
s
v
s
ov
s
o
v
v
s
s
s
s
v
v
s
s
s
s
s
s
s
s
v
s
v
v
v
s
s
v
s
s
v
s
s
s
s
s
v
s
s
v
s
s
v
s
s
v
s
s
s
s
s
v
v
s
v
o
o
o
Linear
Hz
s
s
vs
s
s
s
vs v
s
v
s
ov o
v
v
s
vv
s
v
s
v
s
v
s
v
s
v
s
v
s
s
s
v
s
v
s
v
s
通过采用MSC.Nastran的灵敏度分析+模型修正技术， 可以提供较好的解决方案，具有现实的工程意义；
4
Confidential
• 图片来源于网络
卫星太阳电池阵帆板（蜂窝板）
一、背景介绍—基于灵敏度分析的精确建模方法
• 一种通过试验矫正计算的迭代逼近式精确建模方法，可获取精确力学特性指标，利于仿真验证。
采用LMS测试系统进行模态试验，将帆板的四角固定于工装
夹具上，工装通过螺栓与振动平台固定连接。在帆板的面板上均
布16个4524-B型加速度传感器，用力锤激励板面中心位置。传感
器端口连接线缆进行信号输出，线缆另一端与采集系统连接，采
集系统输出信号到PC端，进行数据处理。
Honeycomb sandwich panel
航天器的板壳结构中80%-90%是蜂窝夹层板，其有限元 模型的精度会对火箭发射工况下（加速度过载、振动、 冲击和随机噪声等）的环境适应性有着重要的影响;
对于右图所示的卫星来说，由于帆板组件作为外伸的大 型挠性附件，其动力学参数（模态矩阵和耦合系数矩阵 Btran/Brot等）将为卫星在轨姿态的精确控制奠定坚实的 基础。
模态分析
模态试验
• 模态分析：采用具备快速收敛的Lanczos模态提取方法
相关性检验 N
灵敏度分析
模型迭代优化
• 相关性检验：
Y
修正后有限元
模态频率
f
f A fT fA
100%
模型
振型正交性 ViT Vj 0 (i j)
模态判定准则MAC值（Modal Assurance Criterion）
之间相关联程度，采用模态置信度(MAC)来进行评价：
MACEMA,FEA
ETMA
ETMA
FEA
2
EMA FTEA FEA
MAC值总是介于0和1之间，如果矩阵中对角线上的数值 ≥0.8，则说明仿真分析模态与对应的试验模态相关性较好； 同时矩阵中其余位置的数值如果≤0.3，说明不同阶所对应 的模态之间独立性较好，相互之间没有受到彼此的影响。
胶层
依附结构
Structure of honeycomb Z
Structure of
sandwich panel
equivalent panel
d
面板
2h
2h+2d
X
蜂窝
d
6
Confidential
目录
一、背景介绍 二、模态分析FEA与试验EMA 三、模型匹配及相关性检验 四、灵敏度分析及模型修正 五、结论
基于灵敏度分析的有限元模型修正
中国科学院沈阳自动化研究所
11, 09, 2018
目录
一、背景介绍 二、模态分析FEA与试验EMA 三、模型匹配及相关性检验 四、灵敏度分析及模型修正 五、结论
3
Confidential
一、背景介绍—研究目的意义
目前航天器产品中大量使用复合材料，其中蜂窝夹层板 具有较高的比刚度、比强度以及较好的隔热、隔振和耐 冲击等优点，被广泛使用；
10
Confidential
三、模型匹配及相关性检验
频率相关性：模态试验频率ωEMA与仿真分析频率ωFEA 之间的相关程度，用下面的误差百分数来表示： %=(EMA -FEA ) / FEA 一般来说，低频误差≤5%,高频误差≤10%，相关性较好。
振型相关性：模态试验振型ΦEMA与模态分析振型ΦFEA
7
Confidential
二、模态分析FEA与试验EMA
采用MSC.Patran&Nastran建立太阳电池阵帆板 的有限元模型，模型包括：上下面板、蜂窝芯层、 边框、支撑座和压紧套等几部分组成。其中上下面 板、边框和中间蜂窝是壳单元，其余为实体单元， 各部分之间采用胶粘连接；
帆板有限元模型各部分的单元类型和材料属性 详见下表：
Acceleration sensor
PC
LMS signal Frock clamp Vibration table acquisition instrument
9
Confidential
一 阶 振 型
二 阶 振 型
0.81
g/N Amplitude
ss ss ss vs ss ss ss ss ss vv ov vv vv vv ov ov v v s s s v v o
11
Confidential
v
s
v
s
o
s
o
vቤተ መጻሕፍቲ ባይዱ
s
s
v
s
s
v
s
s
v
s
s
v
s
s
v
s
s
s
s
s
v
s
s
v
s
s
s
s
s
s
s
o
o
o
s
30
s
29
s
28
s
27
s
26
s
25
s
24
s
23
s
22
s
21
s
20
s
o
19
s
18
s
17
s
16
s
15
s
14
s
13
s
12
v
11
v
10
o
9
8
7
474.33
稳 态 图
目录
一、背景介绍 二、模态分析FEA与试验EMA 三、模型匹配及相关性检验 四、灵敏度分析及模型修正 五、结论
组件
面板 蜂窝 边框 压紧套 支撑座
单元类型
CQUAD CQUAD CQUAD CTETRA CTETRA
材料
玻璃钢 铝合金 镁合金 钛合金 碳纤维
厚度属性
2mm 0.02mm 0.5mm
— —
8
Confidential
支撑座
上面板 边框
压紧套
蜂窝芯层 下面板 帆板有限元模型爆炸图
前两阶模态振型图
二、模态分析FEA与试验EMA
MACTest , FE
VTTest
VTTest VFE 2 VTest VFTE VFE
• 灵敏度分析：找出对模态敏感的参数变量
i xk
1 2i
uiT
K
xk
i2
M xk
ui
• 模型优化：采用序列二次规划法（NLPQL），全局收敛