求二叉树的高度
第七章和第八章补充练习题(答案)

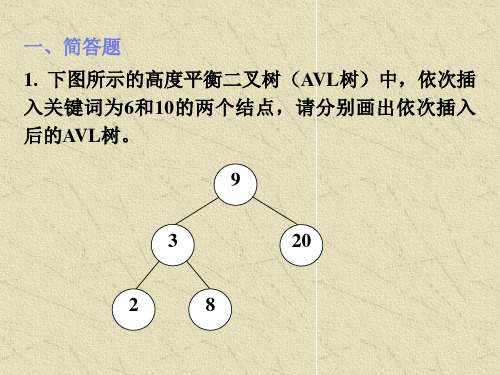
7.3补充练习题及参考答案7.3.1单项选择题1.对于一棵具有n 个结点、度为4的树来说,_____________.A.树的高度最多是n-3B.树的高度最多是是n-4C.第i 层上最多有4(i-1)个结点D.至少在某一层上正好有4个结点答:这样的树中至少有一个结点的度为4,也就是说,至少有一层中有4个或以上的结点,因此树的高度最多是n-3。
本题的答案为A 。
2.度为4、高度为h 的树_____________.A.至少有h+3个结点B.最多有4h -1个结点C.最多有4h 个结点D.至少有h+4个结点答:与上小题分析相同,本题的答案为A 。
3.对于一棵具有n 个结点、度为4的树来说,树的高度至少是_____________.A.)]2([log 4nB.)]13([log 4-nC.)]13([log 4+nD.)]12([log 4+n答:由树的性质4可知,具有n 个结点的m 次树的最小高度为)]1)1(([log +-m n m 。
这里m=4,因此最小高度为)]13([log 4+n 。
本题的答案为C 。
4.在一棵3次树中度为3的结点数为两个,度为2的结点数为一个,度为1的结点数为两个,则度为0的结点数为_____________个。
A.4B.5C.6D.7答:3n =2,2n =1,1n =2,001235n n n n n n +=+++=,n=度之和+1=33n +22n +1n +1=11, 所以65110=-=n 。
本题的答案为C 。
5.若一棵有n 个结点的树,其中所有分支结点的度均为k,该树中的叶子结点个数 是_____________。
A.n(k 一1)/kB.n-kC.(n+1)/kD.(nk 一n+1)/k答:m=k,有k n n n +=0,度之和=n-1=k kn ,k n n k /)1(-=,所以0n =n-k n =n-(n-1)/k=(nk-n+1)/k.本题的答案为D 。
东大14秋学期《数据结构Ⅱ》在线作业1答案

B. 500
C. 254
D.以上答案都不对
?
正确答案:D
19.已知含10个结点的二叉排序树是一棵完全二叉树,则该二叉排序树在等概率情况下查找成功的平均查找长度等于
A. 1.0
B. 2.9
C.
3.4
D.
5.5
?
正确答案:B
20.二叉树中第5层上的结点个数最多为
A. 8
B. 15
C. 16
D. 32
?
正确答案:C
A.各自的头结点
B.各自的尾结点
C.各自的第一个元素结点
D.一个表的头结点,另一个表的尾结点
?
正确答案:B
10.对有18个元素的有序表作二分查找,则查找A[3]的比较序列的下标为
A. 1,2,3
B. 9,5,2,3
C.
9,5,3
D. 9,4,2,3
?
正确答案:D
11.根据数据元素的关键字直接计算出该元素存储地址的存储方法是D.左子源自的高度均小于右子树的高度?
正确答案:B
3.数据结构中所定义的数据元素,是用于表示数据的
A.最小单位
B.最大单位
C.
基本单位
D.
不可分割的单位
?
正确答案:C
4.在有向图G的拓扑序列中,若顶点Vi在顶点Vj之前,则下列情形不可能出现的是
A.
G中有弧<Vi,Vj>
B.
G中有一条从Vi到Vj的路径
C.i
D. i-1
?
正确答案:A
7.下述哪一条是顺序存储结构的优点
A.
存储密度大
B.
插入运算方便
C.
删除运算方便
数据结构第五章参考答案

习题51.填空题(1)已知二叉树中叶子数为50,仅有一个孩子的结点数为30,则总结点数为(___________)。
答案:129(2)3个结点可构成(___________)棵不同形态的二叉树。
答案:5(3)设树的度为5,其中度为1~5的结点数分别为6、5、4、3、2个,则该树共有(___________)个叶子。
答案:31(4)在结点个数为n(n>1)的各棵普通树中,高度最小的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
高度最大的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
答案:2 n-1 1 n 1 n-1(5)深度为k的二叉树,至多有(___________)个结点。
答案:2k-1(6)(7)有n个结点并且其高度为n的二叉树的数目是(___________)。
答案:2n-1(8)设只包含根结点的二叉树的高度为0,则高度为k的二叉树的最大结点数为(___________),最小结点数为(___________)。
答案:2k+1-1 k+1(9)将一棵有100个结点的完全二叉树按层编号,则编号为49的结点为X,其双亲PARENT (X)的编号为()。
答案:24(10)已知一棵完全二叉树中共有768个结点,则该树中共有(___________)个叶子结点。
答案:384(11)(12)已知一棵完全二叉树的第8层有8个结点,则其叶子结点数是(___________)。
答案:68(13)深度为8(根的层次号为1)的满二叉树有(___________)个叶子结点。
答案:128(14)一棵二叉树的前序遍历是FCABED,中序遍历是ACBFED,则后序遍历是(___________)。
答案:ABCDEF(15)某二叉树结点的中序遍历序列为ABCDEFG,后序遍历序列为BDCAFGE,则该二叉树结点的前序遍历序列为(___________),该二叉树对应的树林包括(___________)棵树。
数据库系统l试题库及答案 第6章 树和二叉树

第6章树和二叉树6.1知识点: 树和二叉树的基本概念一、填空题1.高度为h,度为m的树中至少有___________个结点,至多有______________个结点。
2.树的结点是由及若干指向其子树的组成;结点拥有的子树数称为;度为0的结点称为;度不为0的结点成为;树中结点的最大度数称为;树的最大层次称为_____________。
3.对于一棵具有n个结点的树,该树中所有结点的度数之和为___________。
4.如果结点A有3个兄弟结点,而且B是A的双亲,则B的度是___________。
5.二叉树是另一种树形结构,它的特点是。
6.一颗度数为k且有2k-1个结点的二叉树称为。
7.深度为k,且有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时,称之为。
8.一棵深度为6的满二叉树有个分支结点和个叶子。
9.一棵具有257个结点的完全二叉树,它的深度为。
10.设一棵完全二叉树具有1000个结点,则此完全二叉树有个叶子结点,有个度为2的结点,有个结点只有非空左子树,有个结点只有非空右子树。
11.由3个结点可以构成__________种形态的的二叉树,可以构成种形态的树。
12.将含有82个结点的完全二叉树从根结点开始顺序编号,根结点为第1号,其他结点自上向下,同一层自左向右连续编号。
则第40号结点的双亲结点的编号为。
13.一棵高度为5的完全二叉树中,最多包含有____________个结点。
14.一棵具有n个结点的二叉树,若它有n0个叶子结点,则该二叉树上度为1的结点n1=____________。
15.在高度为h(h>=0)的二叉树中至多可以有__________个结点,至少可以有___________个结点。
16.n个结点的二叉树最大高度是____________,最小高度是_______________。
二、选择题1.( )不含任何结点的空树()。
A.是一棵树B.是一棵二叉树C.是一棵树也是一棵二叉树D.既不是树也不是二叉树2.()一棵度为4的树中度为1、2、3、4的结点个数为4、3、2、1,则该树的结点总数为()。
2022-2023学年湘豫名校联考高三上学期10月一轮复习诊断考试(一)数学(文科)试卷(含详解)

C. , D. ,
【答案】B
【解析】
【分析】根据题意和图象求得函数的解析式为 ,利用整体代换法即可求出函数的单调递减区间.【详解】由图象可知, ,
令 ,则 ,即 ,
因为 ,由 ,得 ,
所以 ,由 ,得 ;
又函数图象过点 ,则 ,
得 ,解得 ,
又函数 的最小正周期 满足 ,
即 ,所以 ,当 时, 满足题意,
数学(文科)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合 , , ,则集合 ()
A. B. C. D.
【答案】D
【解析】
【分析】可先求得 ,再求得 ,再求交集即可.
【详解】 ,
,
所以 .
故选:D
2.命题“ , ”的否定是()
A. , B. ,
(2)由 即可求得 的值域.
【小问1详解】
,
.
【小问2详解】
,
, ,
当 ,即 时, 有最小值 ;
当 ,即 时, 有最大值 .
所以函数 在 上的值域为 .
18.已知 的内角A,B,C的对边分别为a,b,c,设 的周长为L,且满足 .
(1)求角C;
(2)若 ,求L的最大值.
【答案】(1)
(2)
【解析】
【分析】(1)利用正弦定理、余弦定理化简已知条件,求得 ,进而求得 .
15.已知函数 图象 一条对称轴为 .若 ,则 的最大______.
16.已知函数 ,函数 有四个不同的零点 , , , ,且 .若 ,则实数a的取值范围是______.
三、解答题:共70分.解答时应写出必要的文字说明、证明过程或演算步骤.
计算机数据结构复习题2
1解、采用遍历方式判断无向图G是否连通。若用深 度优先遍历方法,先给visited[]数组置初值0, 然后从0顶点开始遍历该图。在一次遍历后,若所 有顶点i的visited[i]均为1,则该图是连通的,否 则不连通。
1算法如下: int connect(AGraph *G) { int i,flag=1; for (i=0;i<G->n;i++) visited[i]=0; DFS(G,0); for (i=0;i<G->n;i++) if (visited[i]==0) flag=0; break; } return flag; }
D.(n-1)(m/2 -1)+1 解:根结点至少有一个关键字,其他n-1 个结点至少有(m/2 -1)个关键字,总共包 含.(n-1)(m/2 -1)+1
B. n D.(n-1)(m/2 -1)+1
三、算法设计题
1.假设图G采用邻接表存储,试设计一个算法,判断 无向图G是否连通。若连通则返回1,否则返回0.
5.树形如下:
A
B
C
G
H
D
E
F
I
L
J
K
先根遍历次序:ABCDEFGHIJKL
6.(1) 什么是递归程序? (2) 递归程序的优、缺点是什么? (3) 递归程序在执行时,应借助于什么来 完成? (4) 递归程序的入口语句、出口语句一般 用什么语句实现?
答案:
6.(1)一个函数在结束本函数之前,直接或
}
3.有一种简单的排序算法,叫做计数排序。这种排 序算法对一个待排序的表(用数组表示)进行排序, 并将排序结果存放到另一个新的表中。必须注意的 是,表中所有待排序的关键字互不相同,计数排序算 法针对表中的每个记录,扫描待排序的表一趟,统计 表中有多少个记录的关键字比该记录的关键字小。 假设对某一个记录,统计出数值为c,那么这个记录 在新的有序表中的合适的存放位置即为c。 (1)给出适用于计数排序的数据表定义。 (2)编写实现计数排序的算法。 (3)对于有n个记录的表,比较次数是多少? (4)与直接选择排序相比,这种方法是否更好?为什么?
二叉树结构的特点
二叉树结构的特点二叉树是一种常见的数据结构,它具有以下特点:1. 结构简单:二叉树是一种有序树结构,每个节点最多只有两个子节点,分别称为左子节点和右子节点。
这种结构的简洁性使得二叉树在实际应用中得到广泛使用。
2. 层次性:二叉树具有明显的层次性,即树的每一层都可以通过节点间的父子关系来确定。
根节点是第一层,根节点的子节点是第二层,以此类推。
3. 有序性:在二叉树中,每个节点的左子节点小于它,右子节点大于它。
这种有序性使得二叉树在查找和排序方面具有很高的效率。
4. 高度平衡:二叉树的高度平衡性是指树的左右子树的高度差不超过1。
高度平衡的二叉树可以保证查找、插入和删除操作的平均时间复杂度为O(log n)。
5. 递归性:二叉树的定义是递归的,即每个子树都是二叉树。
这种递归性质使得在二叉树上的操作可以通过递归算法来实现。
6. 存储结构灵活:二叉树的存储结构可以采用顺序存储和链式存储两种方式。
顺序存储是将二叉树的节点按照层次顺序存储在一维数组中,链式存储是通过每个节点的指针来连接各个节点。
在二叉树的基础上,还可以扩展出以下几种特殊的二叉树结构:1. 完全二叉树:完全二叉树是指除了最后一层外,其他层的节点个数都达到最大值,并且最后一层的节点依次从左到右排列。
完全二叉树的特点是高度平衡,可以用数组来存储。
2. 满二叉树:满二叉树是指每个节点都有两个子节点的二叉树,即除了叶子节点外,每个节点都有两个子节点。
满二叉树的特点是节点个数达到最大值,高度平衡。
3. 平衡二叉树:平衡二叉树是指任意节点的左右子树的高度差不超过1的二叉树。
平衡二叉树的特点是高度平衡,可以保证各种操作的时间复杂度较低。
4. 二叉搜索树:二叉搜索树是一种特殊的二叉树,它具有以下性质:对于树中的任意节点,其左子树中的节点值都小于它,右子树中的节点值都大于它。
二叉搜索树的特点是可以高效地进行查找、插入和删除操作。
5. 线索二叉树:线索二叉树是对二叉树的一种扩展,它的特点是在每个节点上增加了指向前驱节点和后继节点的指针。
平衡二叉树平衡因子
平衡二叉树平衡因子
平衡二叉树平衡因子是指该节点的左子树高度减去右子树高度
的绝对值。
平衡因子的取值范围为-1、0、1,若平衡因子的绝对值大于1,则该节点所在的子树不平衡,需要进行旋转操作使其重新平衡。
平衡二叉树的平衡因子是实现平衡的关键,通过平衡因子的计算和调整,可以保证平衡二叉树的高度始终保持在O(log n)的范围内,从而保证了树的查找、插入和删除操作的时间复杂度都能够达到
O(log n)的级别。
平衡因子的计算方法是通过递归遍历左右子树来计算节点的左
右子树高度之差,然后求绝对值。
当平衡因子的绝对值大于1时,需要根据不同情况进行旋转操作,如左旋、右旋、左右旋或右左旋等,以达到平衡二叉树的目的。
总之,平衡二叉树平衡因子是实现平衡的关键,对于平衡二叉树的构建和维护都至关重要。
- 1 -。
名词解释平衡二叉树
名词解释平衡二叉树
平衡二叉树是一种特殊的二叉搜索树,它能够保持左子树和右子树的高度差不超过1,从而保持整棵树的平衡性。
在平衡二叉树中,每个节点都有一个额外的属性,即平衡因子(balance factor),它表示左子树的高度减去右子树的高度。
当平衡因子的绝对值大于1时,就需要对树进行重新平衡操作,以保持树的平衡。
平衡二叉树的特点是,任意节点的左子树和右子树的高度差不超过1。
这意味着在插入或删除节点时,需要对树进行相应的旋转操作来保持平衡。
常用的平衡二叉树包括红黑树、AVL树等。
举个例子,考虑以下二叉树:
5
/ \
3 7
/ \ \
2 4 8
这棵树是平衡二叉树,因为左子树和右子树的高度差不超过1。
但如果我们在树
中插入节点9,那么就会破坏树的平衡:
5
/ \
3 7
/ \ \
2 4 8
\
9
现在右子树的高度比左子树高2,不再平衡。
为了恢复平衡,我们可以对7进行右旋操作,得到以下平衡二叉树:
5
/ \
3 8
/ \ \
2 4 7
\
9
通过旋转操作,我们重新平衡了树,并保持了平衡二叉树的性质。
这样的操作可
以在插入或删除节点时进行,以保持树的平衡。
平衡二叉树的平衡因子
平衡二叉树的平衡因子
平衡二叉树是一种特殊的二叉搜索树,它的左右子树的高度差不超过1,以保证树的平衡性和高效性。
平衡二叉树的平衡因子指的是左子树高度和右子树高度的差值,即:
平衡因子 = 左子树高度 - 右子树高度
当平衡因子为0、1或-1时,树是平衡的;当平衡因子大于1或小于-1时,树就不再平衡,需要通过旋转等操作来重新平衡。
平衡因子的计算可以通过递归的方式来实现:对于每个节点,先递归计算左子树的高度和右子树的高度,再计算平衡因子。
如果平衡因子不满足平衡条件,就需要进行旋转操作。
平衡因子是平衡二叉树中非常重要的概念,它影响着树的平衡性和插入、删除等操作的效率。
因此,在进行平衡二叉树相关的算法设计和实现时,平衡因子的计算和维护是一个必须要考虑的问题。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include
#include
#define MAX 10001
// 树节点
typedef struct node
{
char k;
struct node *lchild;
struct node *rchild;
} Node;
int max(int m, int n)
{
if (m > n)
return m;
else
return n;
}// 获取二叉树的高度
int TreeHeight(Node *root)
{
if (root == NULL)
return 0;
else
return 1 + max(TreeHeight(root->lchild),
TreeHeight(root->rchild));
}// 建立二叉树
Node *BuildTree(char *tree)
{
Node *root, *newnode, *stack[MAX];
int i = 0, top = -1, flag = 0;
root = newnode = NULL;
while(tree[i] != '\0')
{
switch(tree[i])
{
case '(':
top ++;
stack[top] = newnode;
flag = 0;
break;
case ')':
top --;
break;
case ',':
flag = 1;
break;
default:
newnode = (Node *)malloc(sizeof(Node));
newnode->k = tree[i];
newnode->lchild = newnode->rchild = NULL;
if (root == NULL)
root = newnode;
else {
if (!flag)
stack[top]->lchild = newnode;
else
stack[top]->rchild = newnode;
}
break;
}
i++;
}
return root;
}// 释放二叉树
void DestroyTree(Node *root)
{
if (root == NULL)
return ;
else {
DestroyTree(root->lchild);
DestroyTree(root->rchild);
free(root);
}
}
int main()
{
char tree[MAX];
Node *root = NULL;
printf("请输入一个二叉树: ");
scanf("%s", tree);
root = BuildTree(tree);
printf("二叉树的深度:%d\n", TreeHeight(root));
DestroyTree(root);
return 0;
}
