统计与概率本章小结
概率论与数理统计 8-2

H 0 : µ ≤ µ 0 = 225, H 1 : µ > 225,
取 α = 0.05, n = 16, x = 241.5, s = 98.725 0.6685 t0.05 (15) = 1.7531 > t = s/ n
故接受 H 0 , 认为元件的平均寿命不 大于 225小时.
n = 15,
x = 10.48, α = 0.05, s = 0.237,
x − µ 0 10.48 − 10.5 t = = t分布表 = 0.327, s/ n 0.237 / 15 查表得 tα / 2 ( n − 1) = t 0.025 (14) = 2.1448 > t = 0.327, 故接受 H 0 , 认为金属棒的平均长度 无显著变化 .
n2 = 10,
y = 79.43, s2 = 2.225,
2
且s
2 w
(10 −1)s + (10 −1)s = = 2.775, 10 + 10 − 2
2 1 2 2
查表可知 t0.05 (18) = 1.7341,
查表8.1知其拒绝域为 查表 知其拒绝域为 t ≤ − tα ( n1 + n2 − 2). x− y = −4.295, 因为 t = 1 1 sw + 10 10
某切割机在正常工作时, 例1 某切割机在正常工作时 切割每段金属棒的 平均长度为10.5cm, 标准差是 标准差是0.15cm, 今从一批产 平均长度为 品中随机的抽取15段进行测量 其结果如下: 段进行测量, 品中随机的抽取 段进行测量 其结果如下 10.4 10.6 10.1 10.4 10.5 10.3 10.3 10.2
根据第六章 第六章§ 定理四 定理四知 当H 0为真时, 根据第六章§2定理四知,
混合式课程《概率论与数理统计》课程建设的心得——以上海应用技术大学为例

Creative Education Studies 创新教育研究, 2021, 9(2), 391-395Published Online April 2021 in Hans. /journal/ceshttps:///10.12677/ces.2021.92061混合式课程《概率论与数理统计》课程建设的心得——以上海应用技术大学为例汪娜上海应用技术大学理学院,上海收稿日期:2021年3月8日;录用日期:2021年4月15日;发布日期:2021年4月22日摘要基于《概率论与数理统计》混合式教学模式,以上海市重点课程项目申请为契机,从课程建设目标、课程建设举措、课程建设特色和成效、持续课程建设计划这4个方面,阐述了混合式课程《概率论与数理统计》课程建设的一些的举措和成果。
关键词概率论与数理统计,混合式教学,课程建设成效The Experience of the MixedCurriculum Constructionof “Probability Theory andMathematical Statistics”—A Case Study of Shanghai Institute ofTechnologyNa WangCollege of Science, Shanghai Institute of Technology, ShanghaiReceived: Mar. 8th, 2021; accepted: Apr. 15th, 2021; published: Apr. 22nd, 2021汪娜Abstract Based on the mixed teaching mode of “probability theory and mathematical statistics”, taking the application of Shanghai’s key curriculum projects as an opportunity, this paper expounds some measures and achievements of the course construction of “probability theory and mathematical statistics” from the four aspects of curriculum construction objectives, curriculum construction measures, curriculum construction characteristics and effects, and sustainable curriculum con-struction plan. KeywordsProbability Theory and Mathematical Statistics, Mixed Teaching, Course Construction Effect Copyright © 2021 by author(s) and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY 4.0). /licenses/by/4.0/1. 课程建设目标随着《概率论与数理统》[1]教学改革的不断深入,传统的教学方法、教学手段已然发生变化。
统计学第3章-概率、概率分布与抽样分布

互斥事件及其概率
(例题分析)
解:由于每一枚硬币出现正面或出现反面的概率 都是1/2,当抛掷的次数逐渐增大时,上面的4个 简单事件中每一事件发生的相对频数 (概率)将近 似等于 1/4 。因为仅当 H1T2 或 T1H2 发生时,才会 恰好有一枚硬币朝上的事件发生,而事件 H1T2 或 T1H2 又为互斥事件,两个事件中一个事件发 生或者另一个事件发生的概率便是 1/2(1/4+1/4) 。 因此,抛掷两枚硬币,恰好有一枚出现正面的概 率等于 H1T2 或 T1H2 发生的概率,也就是两种事 件中每个事件发生的概率之和
解:设 A = 某住户订阅了日报 B = 某个订阅了日报的住户订阅了晚报
依题意有:P(A)=0.75;P(B|A)=0.50
P(AB)=P(A)·P(B|A)=0.75×0.5=0.375
3-31
独立事件与乘法公式
(例题分析)
【例】从一个装有3个红球2个白球的盒子里摸球 (摸出后球不放回),求连续两次摸中红球的概率
3-17
互斥事件的加法规则
(例题分析)
【例】抛掷一颗骰子,并考察其结果。求出其点 数为1点或2点或3点或4点或5点或6点的概率
解:掷一颗骰子出现的点数(1,2,3,4,5,6)共有
6个互斥事件,而且每个事件出现的概率都为1/6 根据互斥事件的加法规则,得
P(1或2或3或4或5或6) P(1) P(2) P(3) P(4) P(5) P(6) 1 1 1 1 1 1 1 6 6 6 6 6 6
合计
从这200个配件中任取一个进行检查,求 (1) 取出的一个为正品的概率 (2) 取出的一个为供应商甲的配件的概率 (3) 取出一个为供应商甲的正品的概率 (4) 已知取出一个为供应商甲的配件,它是正品的概率
人教B版高中数学必修第二册教学课件:第五章5.4统计与概率的应用

员工 项目 子女教育 继续教育 大病医疗 住房贷款利息 住房租金 供养老人
A
B
C
D
E
F
○
○
×
○
×
○
×
×
○
×
○
○
×
×
×
○
×
×
○
○
×
×
○
○
×
×
○
×
×
×
○
○
×
×
×
○
【解题提示】 (1)按比例分配进行分层抽样。 (2)按照字典排序法列举出所有的抽取结果和事件M的所有基本 事件,然后利用基本事件个数计算概率。
6
6
(3)设第1组抽取的2人为A1,A2,第3组抽取的3人为B1,B2,B3,第4组抽取的1人为C,则从这6人
中随机抽取2人有(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C),(A2,B1),(A2,
B2),(A2,B3),(A2,C),(B1,B2),(B1,B3),(B1,C),(B2,B3),(B2,C),(B3,
估算,其p%分位数即为频率分布直方图中使左侧小矩形面积之和等于p%的分点值. ②某校100名学生的数学测试成绩的频率分布直方图如图:
由此可估计其80%分位数.
首先求分数在130以下的学生所占比例为5%+18%+30%+22% =75%.在140以下的学生所占比例为75%+15%=90%.
因此,80%分位数一定位于[130,140)内,
织了一场PK赛,A,B两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者
得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为 2 ,
概率与数理统计第7章 参数估计
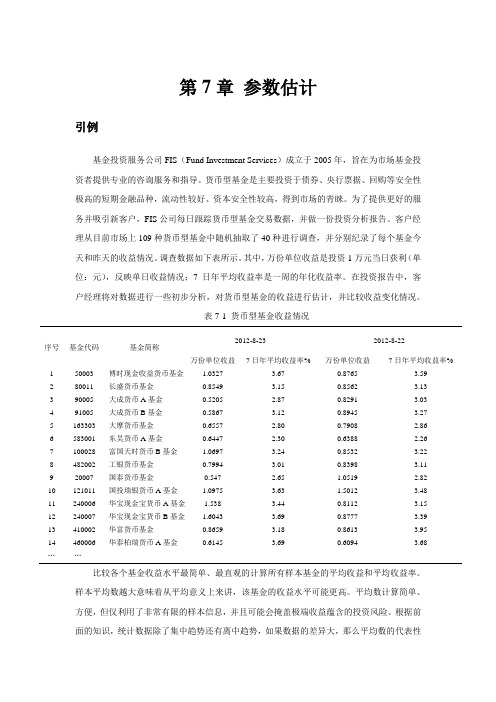
第7章参数估计引例基金投资服务公司FIS(Fund Investment Services)成立于2005年,旨在为市场基金投资者提供专业的咨询服务和指导。
货币型基金是主要投资于债券、央行票据、回购等安全性极高的短期金融品种,流动性较好、资本安全性较高,得到市场的青睐。
为了提供更好的服务并吸引新客户,FIS公司每日跟踪货币型基金交易数据,并做一份投资分析报告。
客户经理从目前市场上109种货币型基金中随机抽取了40种进行调查,并分别纪录了每个基金今天和昨天的收益情况。
调查数据如下表所示。
其中,万份单位收益是投资1万元当日获利(单位:元),反映单日收益情况;7日年平均收益率是一周的年化收益率。
在投资报告中,客户经理将对数据进行一些初步分析,对货币型基金的收益进行估计,并比较收益变化情况。
表7-1 货币型基金收益情况2012-8-23 2012-8-22序号基金代码基金简称万份单位收益7日年平均收益率% 万份单位收益7日年平均收益率%1 50003 博时现金收益货币基金 1.0327 3.67 0.8765 3.592 80011 长盛货币基金0.8549 3.15 0.8562 3.133 90005 大成货币A基金0.5205 2.87 0.8291 3.034 91005 大成货币B基金0.5867 3.12 0.8945 3.275 163303 大摩货币基金0.6557 2.80 0.7908 2.866 583001 东吴货币A基金0.6447 2.30 0.6388 2.267 100028 富国天时货币B基金 1.0697 3.24 0.8532 3.228 482002 工银货币基金0.7994 3.01 0.8398 3.119 20007 国泰货币基金0.547 2.65 1.0519 2.8210 121011 国投瑞银货币A基金 1.0975 3.63 1.5012 3.4811 240006 华宝现金宝货币A基金 1.538 3.44 0.8112 3.1512 240007 华宝现金宝货币B基金 1.6043 3.69 0.8777 3.3913 410002 华富货币基金0.8659 3.18 0.8613 3.9514 460006 华泰柏瑞货币A基金0.6145 3.69 0.6094 3.68……比较各个基金收益水平最简单、最直观的计算所有样本基金的平均收益和平均收益率。
自考04183概率论与数理统计(经管类) 自考核心考点笔记 自考重点资料

《概率论与数理统计(经管类)》柳金甫、王义东主编,武汉大学出版社新版第一章随机事件与概率第二章随机变量及其概率分布第三章多维随机变量及其概率分布第四章随机变量的数字特征第五章大数定律及中心极限定理第六章统计量及其抽样分布第七章参数估计第八章假设检验第九章回归分析前言本课程包括两大部分:第一部分为概率论部分:第一章至第五章,第五章为承前启后章,第二部分为数理统计部分:第六章至第九章。
第一章随机事件与概率本章概述.内容简介本章是概率论的基础部分,所有内容围绕随机事件和概率展开,重点内容包括:随机事件的概念、关系及运算,概率的性质,条件概率与乘法公式,事件的独立性。
本章内容§1.1 随机事件1.随机现象:确定现象:太阳从东方升起,重感冒会发烧等;不确定现象:随机现象:相同条件下掷骰子出现的点数:在装有红、白球的口袋里摸某种球出现的可能性等;其他不确定现象:在某人群中找到的一个人是否漂亮等。
结论:随机现象是不确定现象之一。
2.随机试验和样本空间随机试验举例:E1:抛一枚硬币,观察正面H、反面T出现的情况。
E2:掷一枚骰子,观察出现的点数。
E3:记录110报警台一天接到的报警次数。
E4:在一批灯泡中任意抽取一个,测试它的寿命。
E5:记录某物理量(长度、直径等)的测量误差。
E6:在区间[0,1]上任取一点,记录它的坐标。
随机试验的特点:①试验的可重复性;②全部结果的可知性;③一次试验结果的随机性,满足这些条件的试验称为随机试验,简称试验。
样本空间:试验中出现的每一个不可分的结果,称为一个样本点,记作。
所有样本点的集合称为样本空间,记作。
举例:掷骰子:={1,2,3,4,5,6},=1,2,3,4,5,6;非样本点:“大于2点”,“小于4点”等。
3.随机事件:样本空间的子集,称为随机事件,简称事件,用A,B,C,…表示。
只包含一个样本点的单点子集{}称为基本事件。
必然事件:一定发生的事件,记作不可能事件:永远不能发生的事件,记作4.随机事件的关系和运算由于随机事件是样本空间的子集,所以,随机事件及其运算自然可以用集合的有关运算来处理,并且可以用表示集合的文氏图来直观描述。
第七章 随机变量及其分布(章末小结课件)高二数学(人教A版2019选择性必修第三册)
(2)小红和小明在研究了高尔顿板后,利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图1所示的高尔顿板,付费6元可以玩一次游戏,小球掉入 号球槽得到的奖金为 元,其中 .小明改进了高尔顿板(如图2),首先将小木块减少成5层,然后使小球在下落的过程中与小木块碰撞时,有 的概率向左, 的概率向右滚下,最后掉入编号为1, , , 的球槽内,改进高尔顿板后只需付费4元就可以玩一次游戏,小球掉入 号球槽得到的奖金为 元,其中 .两位同学的高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小红和小明谁的盈利多?请说明理由.
方法总结 求离散型随机变量的均值、方差的步骤: 明确随机变量的取值,以及取每个值的试验结果; 求出随机变量取各个值的概率; 列出分布列; 用期望、方差公式求解; 标准差代入公式 求解.本题渗透了数据分析、数学运算的素养.
题型7 正态分布
例7 某物理量的测量结果服从正态分布 ,则下列结论中不正确的是( ).
方法总结 正态曲线的应用及求解策略:解答此类题目的关键在于将待求的问题向 , , 这三个区间进行转化,然后利用上述区间的概率求出相应的概率.解题过程渗透了直观想象、数学运算以及数据分析的素养.
高尔顿与高尔顿板
一、高尔顿简介
弗朗西斯·高尔顿( , —1911)是英国著名的统计学家、心理学家和遗传学家.他是达尔文的表弟,虽然不像达尔文那样声名显赫,但也不是无名之辈.并且,高尔顿幼年是神童,长大是才子,九十年的人生丰富多彩,是个名副其实的博学家.他涉猎范围广泛,研究水平颇深,纵观科学史,在同辈学者中能望其项背之人寥寥可数.他涉足的领域包括天文、地理、气象、机械、物理、统计、生物、遗传、医学、生理、心理等,还有与社会有关的人类学、民族学、教育学、宗教学,以及优生学、指纹学、照相术、登山术等等.
【5套打包】淄博市初三九年级数学上(人教版)第二十五章概率单元小结(含答案解析)
人教版九年级上册第二十五章《概率初步》单元检测(有答案)(5)一、选择题(每题5分,满分40分) 1.下列事件中,属于随机事件的是( ) A .通常水加热到100C o 时沸腾B .测量孝感某市的最低气温,结果为—150C o C .一个袋中装有5个黑球,从中摸出一个是黑球D .篮球队员在罚球线上投篮一次,未投中 2.已知抛一枚均匀的硬币正面朝上的概率为21,下列说法错误的是( ) A .连续抛一枚均匀硬币2次必有1次正面朝上 B .连续抛一枚均匀硬币10次都可能正面朝上C .大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次D .通过抛一枚均匀硬币确定谁先罚球的比赛规则是公平的3.一个不透明的布袋装有4个只有颜色不同的球,其中2个红色,1个白色,1个黑色,搅匀后从布袋里摸出1个球,摸到红球的概率是( )A .12 B .13 C .14 D .164.某校准备组织师生观看济南全运会球类比赛,在不同时间段里有3场比赛,其中2场是乒乓球比赛,1场是羽毛球比赛,从中任意选看2场,则选看的2场恰好都是乒乓球比赛的概率是( )A .41 B .31 C .21 D .32 5.在一个不透明的袋子里装有2个红球和2个黄球,它们除颜色外都相同.随机从中摸出一球,记下颜色后放回袋中,摇匀后,再随机摸出一球,两次都摸到黄球的概率是( )A .21 B .31 C .41 D .61 6.甲、乙两名同学在一次用频率去估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )A .掷一枚正六面体的骰子,出现1点的概率B .从一个装有2个白球和1个红球的袋子中任取1球,取到红球的概率C .抛一枚硬币,出现正面的概率D .任意写1个整数,它能被2整除的概率7.已知一次函数b kx y +=,k 从—2,3中随机取一个值,b 从1,—1,—2中随机第6题图取一个值,则该一次函数经过二、三、四象限的概率为( )A .31 B .32 C .61 D .65 8.有两把不同的锁和三把钥匙,其中两把钥匙分别能打开其中的一把锁,第三把钥匙不能打开这两把锁.任意取出一把钥匙去开任意一把锁,一次打开锁的概率为( )A .61 B .31C .32D .41备选题:1.班主任王老师将6份奖品分别放在6个完全相同的不透明礼盒中,准备将它们奖给小英等6位获“爱集体标兵”称号的同学.这些奖品中3份是学习文具,2份是科普读物,1份是科技馆通票.小英同学从中随机取一份奖品,恰好取到科普读物的概率是( )A .16B .13C .12D .23 2.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色不同外其它完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是( )A.24 B .18 C .16 D .8 二、填空题(每题5分,满分40分)9.小勇第一次抛一枚质地均匀的硬币时正面向上,他第二次再抛这枚硬币时,正面向上的概率是 .10.从一副扑克牌(去掉大、小王)中任意抽取一张,牌面上数字是“8”的概率是 . 11.在12 的正方形网格格点上放三枚棋子,按图所示的位置已放置了两枚棋子,若第三枚棋子随机放在其他格点上,则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为 .12.已知一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球,若往口袋中再放入x 个白球和y 个黑球,从口袋中随机取出一个白球的概率是41,则y 与x 之间的函数关系式为 .13.口袋内装有大小、质量和材质都相同的红色1号、红色2号、黄色1号、黄色2号、黄色3号的5个小球,从中摸出两球,这两球都是红色的概率是 .14.数学试卷的选择题都是四选一的单项选择题,某同学有两道题不会做,他随便选择了两个答案,请你算一算,他两道选择题都选对的概率是 .15. 如图,正方形ABCD 内接于⊙O ,⊙O 的直径为2分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD 内的概率是 .第题图16. 甲、乙、丙三位好朋友站在一排照合影,甲没有站在中间的概率为 . 备选题:1.在一个不透明的摇奖箱内装有20个形状、大小、质地等完全相同的小球,其中只有5个球标有中奖标志,参与游戏的观众有三次摸球的机会(一次只能摸出一球,且摸出的球不放回),某人前两次摸球均中奖,那么他第三次摸球中奖的概率是______.2.在3 □ 2 □(-2)的两个空格□中,任意填上“+”或“-”,则运算结果为3的概率是 .三、解答题(满分70分)17. (8分)一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色不同外都相同,其中黄球的个数是白球个数的2倍少5个,已知从袋中摸出一个球是红球的概率是103. (1)求袋中红球的个数;(2)求从袋中摸出一个球是白球的概率;(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率. 18. (10分)有两双大小、质地相同、仅有颜色不同的拖鞋(分左右脚,可用A 1、A 2表示一双,用B 1、B 2表示另一双)放置在卧室地板上.若从这四只拖鞋中随即取出两只,利用列表法(树形图或列表格)表示所有可能出现的结果,并写出恰好配成形同颜色的一双拖鞋的概率.19. (10分)小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,他们共做了60次试验,试验结果如下:(1)计算“3点朝上”的频率和“5点朝上”的频率?(2)小颖说:“一次试验中,出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?(3)小颖和小红各投掷一枚骰子,用列表或画树形图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.20. (12分)在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同.甲、乙、两同学玩摸球游戏,游戏规则如下:A BCDO第15题图先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再甲乙同学从中随机摸出一球,记下球号。
概率与数理统计第8章--假设检验与方差分析
第8章假设检验与方差分析【引例】重庆啤酒股份有限公司(以下简称重庆啤酒)于1990年代初斥巨资开始乙肝新药的研发,其股票被视作“生物医药”概念股受到市场热捧。
尤其是2010~2011年的两年间,在上证指数大跌1/3的背景下,重庆啤酒股价却从23元左右飙升最高至元,但公司所研制新药的主要疗效指标的初步统计结果于2011年12月8日披露后,股价连续跌停,12月22日以元报收后停牌。
2012年1月10日重庆啤酒公告详细披露了有关研究结论,复牌后股价又遭遇连续数日下跌,1月19日跌至元。
此公告明确告知:“主要疗效指标方面,意向性治疗人群的安慰剂组与 600μg组,及安慰剂组与εPA-44 900μg组之间,HBeAg/抗HBe 血清转换在统计意义上均无差异”。
通俗地说,用药与不用药(安慰剂组)以及用药多与少(900μg组与600μg 组),都没有明显差异,这意味着该公司研制的乙肝新疫苗无效。
有关数据如表所示:表乙肝新疫苗的应答率注:εP A-44为治疗用(合成肽)乙型肝炎疫苗简称。
上表数据显示,两个用药组的应答率都高于安慰剂组的应答率,但为什么说“在统计意义上均无差异”为什么说这个结论表示乙肝新疫苗无效什么叫“在统计意义上无差异”如何根据样本数据作出统计意义上有无差异的判断解答这些问题就需要本章所要介绍的假设检验。
现实中,人们经常需要利用样本信息来判断有关总体特征的某个命题是真还是伪,或对某个(些)因素的影响效应是否显著作出推断,所以假设检验和方差分析有着广泛的应用。
例如,在生物医学领域,判断某种新药是否比旧药更有效;在工业生产中,根据某批零件抽样检查的信息来判断整批零件的质量是否符合规格要求;在流通领域,鉴别产品颜色是否对销售量有显著影响等等。
这些分析研究都离不开假设检验或方差分析。
假设检验与方差分析的具体方法很多,研究目的和背景条件不同,就需采用不同的方法。
本教材介绍假设检验与方差分析的基本原理和一些基本方法。
概率论与数理统计01 第一节 随机事件及其运算
第一章随机事件及其概率概率论与数理统计是从数量化的角度来研究现实世界中一类不确定现象(随机现象)规律性的一门应用数学学科,20世纪以来,广泛应用于工业、国防、国民经济及工程技术等各个领域. 本章介绍的随机事件与概率是概率论中最基本、最重要的概念之一.第一节随机事件及其运算内容分布图示★随机现象★随机现象的统计规律性★样本空间★随机事件★事件的集合表示★事件的关系与运算★事件的运算规律★例1 ★例2 ★例3★例4 ★例5★内容小结★课堂练习★习题1-1内容要点:一. 随机现象从亚里士多德时代开始,哲学家们就已经认识到随机性在生活中的作用, 但直到20世纪初, 人们才认识到随机现象亦可以通过数量化方法来进行研究. 概率论就是以数量化方法来研究随机现象及其规律性的一门数学学科.而我们已学过的微积分等课程则是研究确定性现象的数学学科.二. 随机现象的统计规律性由于随机现象的结果事先不能预知, 初看似乎毫无规律. 然而人们发现同一随机现象大量重复出现时, 其每种可能的结果出现的频率具有稳定性, 从而表明随机现象也有其固有的规律性. 人们把随机现象在大量重复出现时所表现出的量的规律性称为随机现象的统计规律性. 概率论与数理统计是研究随机现象统计规律性的一门学科.为了对随机现象的统计规律性进行研究,就需要对随机现象进行重复观察, 我们把对随机现象的观察称为随机试验, 并简称为试验,记为E. 例如, 观察某射手对固定目标进行射击; 抛一枚硬币三次,观察出现正面的次数; 记录某市120急救电话一昼夜接到的呼叫次数等均为随机试验.随机试验具有下列特点:1. 可重复性: 试验可以在相同的条件下重复进行;2. 可观察性: 试验结果可观察,所有可能的结果是明确的;3. 不确定性: 每次试验出现的结果事先不能准确预知.三. 样本空间尽管一个随机试验将要出现的结果是不确定的, 但其所有可能结果是明确的, 我们把随机试验的每一种可能的结果称为一个样本点, 记为e (或ω);它们的全体称为样本空间, 记为S (或Ω).基本事件的称谓是相对观察目的而言它们是不可再分解的、最基本的事件,其它事件均可由它们复合而成,一般地,我们称由基本事件复合而成的事件为复合事件.四. 事件的集合表示按定义, 样本空间S 是随机试验的所有可能结果(样本点)的全体, 故样本空间就是所有样本点构成的集合, 每一个样本点是该集合的元素. 一个事件是由具有该事件所要求的特征的那些可能结果所构成的, 所以一个事件对应于S 中具有相应特征的样本点(元素)构成的集合, 它是S 的一个子集. 于是, 任何一个事件都可以用S 的某一子集来表示,常用字母 ,,B A 等表示.五. 事件的关系与运算因为事件是样本空间的一个集合, 故事件之间的关系与运算可按集合之间的关系和运算来处理.六. 事件的运算规律事件间的关系及运算与集合的关系及运算是一致的,为了方便,给出下列对照表:表1.1没有相同的元素与互不相容和事件事件的差集与不发生发生而事件事件的交集与同时发生与事件事件的和集与至少有一个发生与事件事件的相等与相等与事件事件的子集是发生发生导致事件的余集的对立事件子集事件元素基本事件空集不可能事件全集必然事件样本空间集合论概率论记号B A B A AB B A B A B A B A B A AB B A B A B A B A B A B A B A B A B A A A A A ∅=-=⊂∅Ω ω,例题选讲:例1 在管理系学生中任选一名学生, 令事件A 表示选出的是男生, 事件B 表示选出的是三年级学生, 事件C 表示该生是运动员.(1)叙述事件C AB 的意义;(2)在什么条件下C ABC =成立? (3)什么条件下B C ⊂?(4)什么条件下B A =成立?解 (1) C AB 是指当选的学生是三年级男生, 但不是运动员.(2)只有在,AB C ⊂ 即B C A C ⊂⊂,同时成立的条件下才有C ABC =成立, 即只有在全部运动员都是男生, 且全部运动员都有是三年级学生的条件下才有C ABC =.(3) B C ⊂表示全部运动员都是三年级学生, 也就是说, 若当选的学生是运动员, 那么一定是三年级学生, 即在除三年级学生之外其它年级没有运动员当选的条件下才有.B ⊂C(4) B A ⊂表示当选的女生一定是三年级学生, 且A B ⊂表示当选的三年级学生一定是女生. 换句话说, 若选女生, 只能在三年级学生中选举, 同时若选三年级学生只有女生中选举. 在这样的条件下, A B ⊂成立.例2 考察某一位同学在一次数学考试中的成绩, 分别用A , B , C , D , P , F 表示下列各事件(括号中表示成绩所处的范围):]),100,90([优秀--A )),90,80([良好--B )),80,70([中等--C )),70,60([及格--D ]),100,60([通过--P )),60,0([未通过--F 则F D C B A ,,,,是两两不相容事件P 与F 是互为对立事件,即有;F P = D C B A ,,,均为P 的子事件,且有.D C B A P =例3(讲义例1)甲,乙,丙三人各射一次靶,记-A “甲中靶” -B “乙中靶” -C “丙中靶” 则可用上述三个事件的运算来分别表示下列各事件: (1) “甲未中靶”: ;A (2) “甲中靶而乙未中靶”: ;B A (3) “三人中只有丙未中靶”: ;C AB(4) “三人中恰好有一人中靶”: ;C B A C B A C B A (5)“ 三人中至少有一人中靶”: ;C B A(6)“三人中至少有一人未中靶”: ;C B A 或;ABC (7)“三人中恰有兩人中靶”: ;BC A C B A C AB(8)“三人中至少兩人中靶”: ;BC AC AB (9)“三人均未中靶”: ;C B A (10)“三人中至多一人中靶”: ;C B A C B A C B A C B A (11)“三人中至多兩人中靶”: ;ABC 或;C B A注:用其他事件的运算来表示一个事件, 方法往往不惟一,如上例中的(6)和(11)实际上是同一事件,读者应学会用不同方法表达同一事件, 特别在解决具体问题时,往往要根据需要选择一种恰当的表示方法.例4 指出下列各等式命题是否成立, 并说明理由: (1) B B A B A )(=;(2) B A B A =; (3) C AB C B A = ; (4) ∅=))((B A AB . 解(1) 成立.B B A )()()(B B B A =(分配律)S B A )(=.B A =(2) 不成立.若A 发生, 则必有B A 发生, A 发生, 必有A 不发生, 从而B A 不发生, 故BA B A =不成立.(3) 不成立.若C B A 发生, 即C 发生且B A 发生, 即必然有C 发生. 由于C 发生, 故C 必然不发生, 从而C B A 不发生, 故(3)不成立. (4)成立.))((B A AB ))((A B AB =A B B A )(=A A )(∅=A ∅=.∅=例5化簡下列事件:(1) );)((B A B A (2) .B A B A B A 解(1) ))((B A B A )]([)]([B A B B A A =(分配律))()(B B A B B A A A =)()](∅= A B B A A (因A B A ⊂)A B A =.A =(2) B A B A B A B A B A B A B A =B A B A B A B A =(交换律))()(B A B A B A B A =(结合律))()(B B A B A A =.AB A B == (对偶律)课堂练习1. 设当事件A 与B 同时发生时C 也发生, 则 ( ).(A) B A 是C 的子事件; (B);ABC 或;C B A(C) AB 是C 的子事件; (D) C 是AB 的子事件.2. 设事件=A {甲种产品畅销, 乙种产品滞销}, 则A 的对立事件为 ( ).(A) 甲种产品滞销,乙种产品畅销; (B) 甲种产品滞销;(C) 甲、乙两种产品均畅销;(D) 甲种产品滞销或者乙种产品畅销.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 8- T-2 从树状图可以知道所有可能的结果有 16 种, 符合条件的有 4 种, 4 1 P(两人获赠的钢笔型号相同)= = . 16 4
本章总结提升
[ 点评 ] 此题主要考查了利用列表法或树状图法求概率,解 题的关键是会根据题意画出树状图或列出表格求出所有可能的结
果和符合要求的情况,然后利用概率的定义即可解决问题.
码而言,要么中大奖五百万元,要么不中,但是中大奖的概率极
小,不中大奖Βιβλιοθήκη 概率极大,概率不是50%.本章总结提升 ► 类型之四 逻辑分析计算概率
常用画树状图法或列表法把所有等可能的结果一一列举出来 ,利用求概率的公式计算出该事件发生的概率.
本章总结提升
例 4飞飞和欣欣两位同学到某文具专卖店购买文具,恰好赶
本章总结提升
[点评]此题考查了折线统计图,用样本估计总体以及扇形统
计图,弄清题意是解本题的关键.
本章总结提升 ► 类型之三 解释现象:澄清一些日常生活中的错误认识
随机事件发生的概率与试验的先后次序无关,可能性很小的 随机事件,在一次试验中也有可能发生.
本章总结提升
例 3 有人说“福利彩票中,就一个号码而言,要么中大奖
调查的方式有普查和抽样调查两种.普查得到的结论肯定可
靠,但需投入大量的人力、物力;而抽样调查简单易行,它是用
样本估计总体的具体运用,要学会切合实际地选择调查方法.
本章总结提升
例 1
下列调查中,适合用普查方法的是( D )
A.电脑厂要了解一批液晶显示器的使用寿命
B.要了解某市居民的环保意识 C.要了解某市“阳山水蜜桃”的甜度和含水量 D.要了解你校数学教师的年龄状况
本章总结提升
[解析] D
选项A,C中的调查具有破坏性,不易普查;选项
B如果普查,工作量大,人力、物力投入多,而调查出的结果又
没有多大用途,所以不用普查; D选项,因学校数学教师的人数 少,普查起来方便.
本章总结提升 ► 类型之二 统计图的理解及应用
统计图表形象直观,要从统计图表中读出信息及数据,能根 据数据画出统计图表,关键要领会数据与统计图表之间的内在联
上“店庆购物送礼”活动.该文具店设置了A,B,C,D四种型号
的钢笔作为赠品,购物者可随机抽取一支,抽到每种型号钢笔的 可能性相同. (1)飞飞购物后,获赠A型号钢笔的概率是多少? (2) 飞飞和欣欣购物后,两人获赠的钢笔型号相同的概率是 多少?
本章总结提升
[解析] (1)由于文具店设置了A,B,C,D四种型号的钢笔作 为赠品,购物者可随机抽取一支,抽到每种型号钢笔的可能性相
数 学
新课标(SJ) 九年级下册
本章总结提升
本章总结提升 本章知识框架
普查 调查目的 抽样调查 调查对象 抽取样本 样本 科学计算器(或计算机) 现象 决策 相同的 总体 抽签 调查内容和问题 尽可能全面 代表性和广泛性 简单明确
个人观点
估计
n×P(A)
画树状图 列表
本章总结提升
整合拓展创新
► 类型之一 数据的调查方法
割线上,那么重转一次,直到指针指向一个数字为止.
本章总结提升
图8-T-3
本章总结提升
(1)请你通过画树状图的方法求小颖获胜的概率; (2) 你认为该游戏规则是否公平?若游戏规则公平,请说明 理由;若游戏规则不公平,请你帮忙修改一下.
[ 解析 ] 预测游戏规则是否公平 ,要看游戏规则对参与者获 胜的概率是否相等,若相等则公平,若不相等则不公平.
本章总结提升
解: (1)画树状图如图 8-T-4 所示.
图 8- T-4 可见,共有 12 种等可能的情况,其中和小于 10 的有 6 种. 6 1 小颖获胜的概率为 = . 12 2
本章总结提升
(2) 该游戏规则不公平. 由(1)可知,共有 12 种等可能的情况,其和大于 10 的情况 有 3 种, 3 1 1 1 ∴小亮获胜的概率为 = ,显然 ≠ ,故该游戏规则不公 12 4 2 4 平. 游戏规则可修改为:当两个转盘指针所指区域内的数字之和 大于或等于 10 时,小亮获胜;当两个转盘指针所指区域内的数 字之和小于 10 时,小颖获胜.
系,这也是数形结合思想的具体应用.
本章总结提升
例 2
[2013·黔东南州一模 ] 某省有关部门要求各中小学
要把“每天锻炼一小时”写入课表.为了响应这一号召,某校围
绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题, 对在校学生进行了随机抽样调查,从而得到一组数据.如图8-T -1 是根据这组数据绘制的折线统计图和扇形统计图.请结合统 计图回答下列问题:
本章总结提升
图8-T-1
本章总结提升
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调
查人数的百分比是多少?
(3)若该校九年级共有200名学生,图②是根据各年级学生人
数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校
学生中最喜欢跳绳活动的人数约为多少?
五百万元,要么不中五百万元.所以中大奖五百万元的概率是
50%.”你同意这种说法吗?为什么?
[ 解析 ] 就购买彩票而言,仅购一张中大奖五百万元的概率
等于总张数分之一,是极小的,并不是50%.因此购买彩票时要持
有捐赠的心态,切不可为中大奖而狂买彩票.
本章总结提升
解: 不同意.理由:这种说法是不正确的.虽然就一个号
图8-T-5
本章总结提升
[解析] 设A1表示第一个黑球,A2表示第二个黑球,B1表示第 一个白球,B2表示第二个白球,则共有24种可能的结果,利用树
状图表示前三个小球排列的位置,即可得到这些可能结果,如图
8-T-6.
图8-T-6
本章总结提升
解:小华应当乙方.理由:设 A1 表示第一个黑球,A2 表示第 二个黑球,B 1 表示第一个白球, B2 表示第二个白球,则共有 24 种可能的结果(可以利用树状图或表格解释),其中黑白相间排列 8 1 2 的有 8 种.因此,甲方赢的概率为 = ,则乙方赢的概率为 , 24 3 3 故小华应当乙方.
本章总结提升
例 6小明拿着一个罐子来找小华做游戏,罐子里有四个一样
大小的玻璃球,两个黑色,两个白色,小明说:“使劲摇晃罐子
,使罐子中的小球位置打乱,等小球落定后,如果是黑白相间地 排列( 如图8-T-5),就算甲方赢,否则就算乙方赢.”他问小 华要当甲方还是乙方,请你帮小华做决策,并说明理由.
本章总结提升
同,由此即可求出获赠A型号钢笔的概率;(2)首先利用树状图可
以求出所有可能的情况和获赠的钢笔型号相同的情况,然后利用 概率的定义即可解决问题.
本章总结提升
(2)解法1:列表如下:
飞飞
欣欣
A B C D
A A ,A B ,A C ,A D ,A
B A ,B B ,B C ,B D ,B
C A,C B,C C,C D,C
本章总结提升 ► 类型之五 利用概率预测游戏的公平性
判断游戏是否公平,只要正确计算出游戏双方各个事件发生 的概率大小,并比较概率是否相等.
本章总结提升
例 5
如图8-T- 3是两个可以自由转动的转盘,甲转盘被
等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有
相应的数字.小亮和小颖利用它们做游戏,游戏规则是:同时转 动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10 ,小颖获胜;指针所指区域内的数字之和等于 10,为平局;指针 所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分
本章总结提升
[解析] (1)由图①中各项目的人数相加即可求出样本容量;
(2)找出最喜欢篮球的人数 , 除以总人数求出所占的百分比
即可;
(3)由九年级人数与所占的百分比求出总人数 , 乘以跳绳人
数所占的百分比即可求出结果.
本章总结提升
解: (1)根据题意,得 4+8+10 +18+10= 50(人). 则该校对 50 名学生进行了抽样调查; (2) 本次抽样调查中,最喜欢篮球活动的有 18 人,占被调查 18 人数的百分比是 ×100%=36%; 50 (3) 根据题意,得 200÷20%=1000(人) ,则全校学生中最喜 8 欢跳绳活动的人数约为 1000× =160(人). 50
本章总结提升
[点评]修改游戏规则的方式很多,只要修改后的游戏规则符 合题目要求即可.例如游戏规则也可修改为:当两个转盘指针所
指区域内的数字之和为奇数时,小亮获胜;为偶数时,小颖获胜
.
本章总结提升 ► 类型之六 利用概率做决策
通过计算n次试验中,事件A发生的次数的平均值m=n×P(A) 来对现实生活中的一些简单问题做出决策.
D A ,D B ,D C ,D D ,D
本章总结提升
由表格可知:所有可能的结果一共有 16 种,每种结果出现 的可能性相同,其中两人获赠的钢笔型号相同的有 4 种,因此飞 4 1 飞和欣欣购物后,两人获赠的钢笔型号相同的概率是 P = = . 16 4
本章总结提升
解法 2 :依题意画树状图如下:
