六年级上册奥数基础+提高练习-第19讲 面积计算(二) 通用版(含答案)
六年级数学面积公式试题答案及解析

六年级数学面积公式试题答案及解析1.(2分)如图中,DE=EC,平行四边形ABED的面积比三角形BCE的面积大0.6平方分米,那么梯形ABCD的面积是.【答案】1.8平方分米.【解析】因为DE=EC,平行四边形ABED的面积是三角形BCE的面积的2倍,所以根据平行四边形ABED的面积比三角形BCE的面积大0.6平方分米,求出三角形BCE的面积,进而求出梯形的面积.解:0.6×3=1.8(平方分米)答:梯形ABCD的面积是1.8平方分米;故答案为:1.8平方分米.点评:关键是根据题意判断出平行四边形ABED的面积是三角形BCE的面积的2倍,进而解决问题.2.(1分)一个梯形的上底乘高等于6,下底乘高等于9,那么这个梯形的面积是7.5..(判断对错)【答案】正确【解析】利用梯形的面积公式,S=(a+b)×h÷2即可进行求解.解:梯形的面积S=(a+b)×h÷2=(ah+bh)÷2=(6+9)÷2=15÷2=7.5;故答案为:√.点评:此题主要考查梯形的面积公式的灵活应用.3.(2分)如图ABCD是直角梯形,AD=3厘米,BC=12厘米,S1=S2,那么线段EC=厘米.【答案】7.5.【解析】由题意可知:梯形ABED的面积=三角形DEC的面积,可以分别利用梯形和三角形的面积公式进行求解.解:(3+12﹣EC)×AB÷2=EC×AB÷215﹣EC=ECEC=7.5;答:线段EC等于7.5厘米.故答案为:7.5.点评:此题主要考查梯形和三角形的面积公式的灵活应用.4.(3分)图中每个小方格表示1平方厘米,左起第()个图形的面积与其他三个不相等.A.A B.B C.C D.D【答案】C【解析】根据图分别得出A、B、C、D四个图形的面积,然后进行比较即可.解:A图形的面积是3平方厘米;B图形的面积是3平方厘米;C图形的面积是2.5平方厘米;D图形的面积是3平方厘米;所以C图形的面积与其它三个不相等;故选:C.点评:求出四个图形的面积,是解答此题的关键.5.求如图的周长和面积.【答案】解: 3.14×6=18.84(米) 3.14×(6÷2)2=3.14×9=28.26(平方米)答:这个圆的周长是18.84米,面积是28.26平方米【解析】【分析】根据圆的周长公式:C=πd=2πr,圆的面积公式:S=πr2,把数据代入它们的公式进行解答.6.一个圆形游泳池的周长是314米,它的半径是,占地面积是.【答案】50米;7850平方米【解析】略7.边长是10m的正方形中放置一个最大的圆,这个圆的面积是 m2.【答案】78.5【解析】略8.一个周长是25.12米的圆形花坛,它的四周有一条宽2米的小路,求这条小路的面积是多少平方米?【答案】25.12÷3.14÷2=4(米) 4+2=6(米) 3.14×(62-42)=62.8(平方米)【解析】略9.推导圆面积公式时,把一个圆分成若干等份,拼成一个平行四边形,这个平行四边形的周长是()A.B.C.D.【答案】C【解析】略10.一个长方体,长7厘米,宽6厘米,高4厘米,它的底面积是( )平方厘米,表面积是( )平方厘米。
六年级上册奥数第二讲不规则图形面积的计算
第二讲不规则图形面积的计算
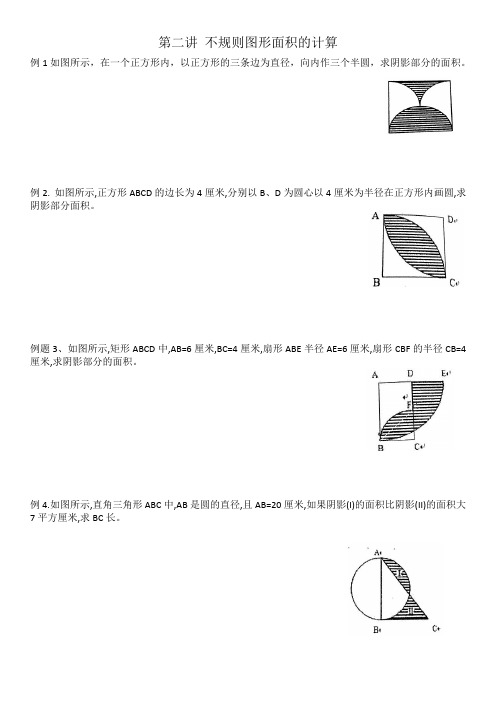
例1如图所示,在一个正方形内,以正方形的三条边为直径,向内作三个半圆,求阴影部分的面积。
例2.如图所示,正方形ABCD的边长为4厘米,分别以B、D为圆心以4厘米为半径在正方形内画圆,求阴影部分面积。
例题3、如图所示,矩形ABCD中,AB=6厘米,BC=4厘米,扇形ABE半径AE=6厘米,扇形CBF的半径CB=4厘米,求阴影部分的面积。
例4.如图所示,直角三角形ABC中,AB是圆的直径,且AB=20厘米,如果阴影(I)的面积比阴影(II)的面积大7平方厘米,求BC长。
同步训练
1.如图所示,大扇形半径是6厘米,小扇形半径是3厘米,求阴影部分的面积。
2.如图所示,三个同心圆的半径分别是2、6、10,求图中阴影部分占大圆面积的百分之几?
3.如下图,正方形ABCD边长为1厘米,依次以A、B、C、D为圆心,以AD、BE、CF、DG为半径画出扇形,求阴影部分的面积。
4.如下图,大圆的直径为4厘米,求阴影部分的面积。
总复习面积问题专题(课件)人教版六年级上册数学(共19张PPT)

AC和AD的中点. 求:三角形DEF的面积。
解:因为点D是BC的中点, SABC 40
所以BD=CD
所以 SACD
SABD
1 2
SABC
1 40 20 2
又因为点E是AC的中点,
A
F
E
所以AE=CE
所以 SADE
SCDE
1 2
SACD
1 20 10 2
B
D
C
【方法总结】在运用等底
因为点F是AD的中点,
解:由题意得:
因为SDABCD=2B12DBD h
h
∟
所以SADC DC h 2BD h 2SABD
1份
2份
二、三角形的面积问题
2.重要结论
导入4:在三角形ABC中,DC=3BD,三角形ABC的高为 h,那么三
角形ABD与三角形ADC的面积具有什么关系呢?
解:由题意得:
SABD BD h
变式 如图,在梯形ABCD中,AC与BD是对角线,其交点O, 求证:三角形AOB与三角形COD面积相等.
解:因为在三角形ABC与三角形DCB中,底都是
BC,高都是AD与BC平行线段的距离,
所以 SABC =SDCB
所以 SABC -SBOC SDCB -SBOC
B
A
D
O
C
即证 SAOB SCOD
因为点D是AB的中点,SAED 30(cm2 )
B
所以AD=BD
所以 SBED SAED 30(cm2 )
D
所以 SABE 2SAED 2 30 60(cm2 )
又因为点E是AC的中点, 所以AE=CE
30
A
E
C
浙教版小学数学六年级上册 第19课时 扇形统计图(二) (II )卷

浙教版小学数学六年级上册第19课时扇形统计图(二)(II )卷姓名:________ 班级:________ 成绩:________小朋友,带上你一段时间的学习成果,一起来做个自我检测吧,相信你一定是最棒的!一、填空题。
(共3题;共6分)1. (1分)要表示各部分同整体之间的关系,需要绘制________统计图.2. (1分)如图是张叔叔每个月工资的安排情况统计图。
(总工资:2500元)(1)上图是________统计图。
(2)________支出最多,________支出最少。
(3)张叔叔基本生活费占________%,________占30%,其他占________%。
(4)张叔叔每个月的基本生活费是________元;每个月用于休闲的费用是________元;每个月用于其他的费用是________元。
(5)休闲费用是基本生活费的________%,储蓄金额比基本生活费少________%。
(6)张叔叔每月开销________元,储蓄________元。
(7)张叔叔想买一台4500元的电脑,他需要________个月的储蓄才能买到。
3. (4分)下面是贝贝家去年各项支出的统计图,其中旅游支出为3000元,请完成下表。
项目饮食服装文化旅游其他合计占总支出的百分比________________________15%________________支出钱数/元________________________3000________________二、选择题。
(共3题;共3分)4. (1分)在一个圆形花坛内种了三种花(如图所示),用下面条形统计图()熊更准确地表示各种花的占地面积。
A .B .C .5. (1分)一种盐水的含盐率是20%,盐与水的比是()。
A . 1:5B . 1 :6C . 1:4D . 1:76. (1分)一个鸡蛋按质量计算,蛋壳、蛋白、蛋黄约占整个鸡蛋的百分比分别为:15%、53%、32%,如果将数据画成统计图,选()统计图较合适。
北师大版小学六年级上册圆的面积(二)10道计算专题训练含答案详情
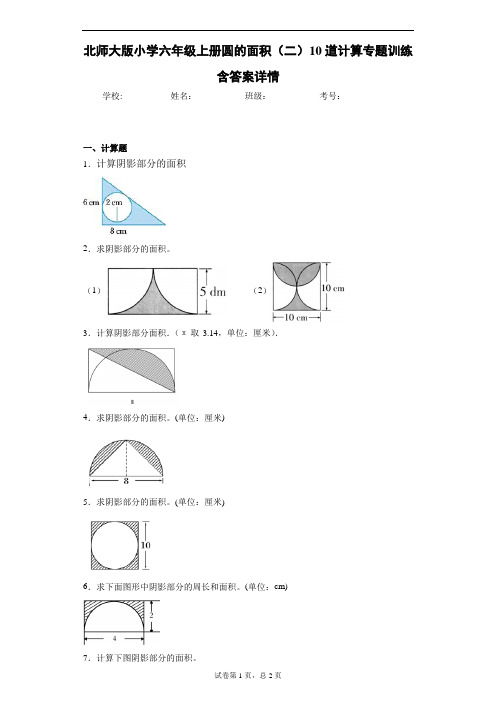
北师大版小学六年级上册圆的面积(二)10道计算专题训练含答案详情学校:___________姓名:___________班级:___________考号:___________一、计算题1.计算阴影部分的面积2.求阴影部分的面积。
(1)(2)3.计算阴影部分面积.(π取3.14,单位:厘米).4.求阴影部分的面积。
(单位:厘米)5.求阴影部分的面积。
(单位:厘米)6.求下面图形中阴影部分的周长和面积。
(单位:cm)7.计算下图阴影部分的面积。
8.求下面图形中阴影部分的面积(单位:厘米)。
9.计算下图阴影部分面积。
10.计算阴影部分的周长和面积。
参考答案1.11.44cm2【解析】【分析】根据图意可知,阴影部分的面积=三角形的面积-空白圆的面积,三角形的面积=底×高÷2,圆的面积:S=πr2,据此列式解答.【详解】解:8×6÷2-3.14×22=48÷2-3.14×4=24-12.56=11.44(cm2)答:阴影部分的面积是11.44cm2.2.(1)10.75dm²;(2)50cm²【解析】【详解】(1)5×2×5-3.14×5²÷2=10.75(dm²)(2)10×10÷2=50(cm²)3.12.56平方厘米【解析】【详解】略4.9.12平方厘米【解析】【详解】1 2×π×(82)2-12×8×82=9.12(平方厘米)5.21.5平方厘米【解析】【详解】102-π×(102)2=21.5(平方厘米)6.14.28cm 1.72cm 2【解析】【详解】周长:3.14×4÷2+4+2×2=14.28(cm)面积:4×2-(4÷2)2×3.14÷2=1.72(cm 2) 7.45.76平方厘米【解析】【详解】12×8-3.14×()282÷=45.76(2cm )8.6.86平方米【解析】【详解】(3+7)×2÷2=10(平方米)(2÷2)2×3.14=3.14(平方米) 10-3.14=6.86(平方米)9.803.84 m 2【解析】【详解】略10.14.28cm 3.44cm 2【解析】【详解】周长:2×4×3.14÷4+4×2=14.28(cm ) 面积:4×4-4×4×3.14÷4=3.44(cm 2)。
北师大版小学六年级上册圆的面积(二)10道计算专题训练含答案详情

北师大版小学六年级上册圆的面积(二)10道计算专题训练含答案详情北师大版小学六年级上册圆的面积(二)10道计算专题训练含答案详情学校:___________姓名:___________班级:___________考号:___________一、计算题1.计算阴影部分的面积2.求阴影部分的面积。
(1)(2)3.计算阴影部分面积.(π取3.14,单位:厘米).4.求阴影部分的面积。
(单位:厘米)5.求阴影部分的面积。
(单位:厘米)6.求下面图形中阴影部分的周长和面积。
(单位:cm)7.计算下图阴影部分的面积。
8.求下面图形中阴影部分的面积(单位:厘米)。
9.计算下图阴影部分面积。
10.计算阴影部分的周长和面积。
参考答案1.11.44cm2【解析】【分析】根据图意可知,阴影部分的面积=三角形的面积-空白圆的面积,三角形的面积=底×高÷2,圆的面积:S=πr2,据此列式解答.【详解】解:8×6÷2-3.14×22=48÷2-3.14×4=24-12.56=11.44(cm2)答:阴影部分的面积是11.44cm2.2.(1)10.75dm2;(2)50cm2【解析】【详解】(1)5×2×5-3.14×52÷2=10.75(dm2)(2)10×10÷2=50(cm2)3.12.56平方厘米【解析】【详解】略4.9.12平方厘米【解析】【详解】×π×()-×8×=9.12(平方厘米)5.21.5平方厘米【解析】【详解】10-π×()=21.5(平方厘米)6.14.28cm1.72cm2【解析】【详解】周长:3.14×4÷2+4+2×2=14.28(cm)面积:4×2-(4÷2)2×3.14÷2=1.72(cm2)7.45.76平方厘米【解析】【详解】12×8-3.14×=45.76()8.6.86平方米【解析】【详解】(3+7)×2÷2=10(平方米)(2÷2)2×3.14=3.14(平方米)10-3.14=6.86(平方米)9.803.84m2【解析】【详解】略10.14.28cm3.44cm2【解析】【详解】周长:2×4×3.14÷4+4×2=14.28(cm)面积:4×4-4×4×3.14÷4=3.44(cm2)本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
圆(圆环的面积)-2024-2025学年六年级上册数学计算大通关(人教版)(答案解析)
专题圆(圆环的面积)答案解析1.计算下面阴影部分图形的面积(单位:厘米)。
【分析】第一题阴影部分的面积=正方形的面积-圆的面积÷4;第二题阴影部分的面积=大圆面积-小圆面积。
【解答】8×8-3.14×8²÷4=64-50.24=13.76(平方厘米)3.14×15²-3.14×10²=706.5-314=392.5(平方厘米)2.求阴影部分的面积(π取3.14)。
【分析】看图可知,阴影部分的面积是圆环面积的一半,圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),求出圆环面积,除以2即可。
【解答】8÷2=4(厘米)4÷2=2(厘米)3.14×(42-22)÷2=3.14×(16-4)÷2=3.14×12÷2=18.84(平方厘米)3.求下面各图中的阴影部分的面积。
(单位:cm)【分析】左图求的是圆环的面积。
根据圆环的面积22r )S π=−(R ,求得大圆和小圆的半径,将数值代入计算即可;右图阴影面积=边长6厘米的正方形面积-半径为3厘米的圆的面积。
根据正方形面积=边长×边长,圆的面积2S r π=×,将数值代入计算即可。
【解答】左图阴影部分面积:8÷2=4(厘米)4÷2=2(厘米)223.14(42)×−=3.14(164)×−=3.1412×=37.68(cm 2)圆环的面积是37.68cm 2。
右图阴影面积:266 3.1462×−×÷()=36 3.149−×=36-28.26=7.74(cm 2)阴影部分面积是7.74cm 2。
4.计算下面各图形中阴影部分的面积。
(单位:cm )【分析】第一个图形,大圆半径=小圆直径,阴影部分的面积=大圆面积-小圆面积,圆的面积=圆周率×半径的平方;第二个图形是个圆环,小圆半径+2=大圆半径,圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),据此列式计算。
小学六年级奥数题100道及答案解析(完整版)
小学六年级奥数题100道及答案解析(完整版)1. 一种商品先提价10%,再降价10%,现价与原价相比()A. 提高了B. 降低了C. 不变D. 无法确定答案:B解析:假设原价为100 元,提价10%后价格为100×(1 + 10%) = 110 元,再降价10%,价格为110×(1 - 10%) = 99 元,所以现价比原价降低了。
2. 一个圆的半径扩大3 倍,它的面积扩大()倍。
A. 3B. 6C. 9D. 27答案:C解析:圆的面积= π×半径²,半径扩大3 倍,面积扩大3²= 9 倍。
3. 甲数的2/3 等于乙数的3/4,甲数()乙数。
A. 大于B. 小于C. 等于D. 无法比较答案:A解析:设甲数×2/3 = 乙数×3/4 = 1,可得甲数= 3/2,乙数= 4/3,3/2 > 4/3,所以甲数大于乙数。
4. 把20 克盐放入200 克水中,盐和盐水的比是()A. 1:10B. 1:11C. 10:1D. 11:1答案:B解析:盐20 克,盐水= 20 + 200 = 220 克,盐和盐水的比是20:220 = 1:115. 一个三角形三个内角的度数比是1:2:3,这个三角形是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定答案:B解析:三个内角分别为180×1/(1 + 2 + 3) = 30°,180×2/(1 + 2 + 3) = 60°,180×3/(1 + 2 + 3) = 90°,是直角三角形。
6. 要反映某地气温变化情况,应绘制()统计图。
A. 条形B. 折线C. 扇形D. 以上都可以答案:B解析:折线统计图能清晰反映数据的变化情况。
7. 一个圆柱和一个圆锥等底等高,它们的体积相差18 立方厘米,圆锥的体积是()立方厘米。
四年级数学奥数讲义+练习-第19讲 应用题(二)(全国通用版,含答案)
奥数已经成为现在孩子学习的加强工具。
一种思维方式的训练,一种让孩子学以致用,举一反三的法宝,一种可以扩宽孩子思维的奥秘兵器。
老师经常对学生们说,养成好的学习品质,拥有好的学习方法比学习知识自己重要得多,它是学好知识的前提。
学习奥数更是如此。
奥数题对学生们的要求是非常严格的,你既要注意到思维有广度有深度,在做题时还要加倍小心。
有些题往往是一字之差,谬之千里。
习惯的养成不是一朝一夕之功。
要养成好的学习习惯,首先,需要学生对这个问题有个正确的认识,有些家长往往错误地认为。
只要是标题问题理解了,出点小错不妨。
这样做的结果,往往助长了学生粗心大意之习气。
而在奥数题中,一点小错,往往是致命的。
学生做题出错了,我们应把它做为一个好的教育学生的契机,引导学生找出错误原因并不停积累,是知识方面的,要牢记。
是习惯方面的,要改正。
相信久而久之,好的习惯必能养成。
第19讲应用题(二)一、知识要点解答复合应用题时一般有如下四个步骤:1.弄清题意,找出已知条件和所求问题;2.分析已知条件和所求问题之间的关系,找出解题的途径;3.拟定解答计划,列出算式,算出得数;4,检验解答方法是否合理,结果是否正确,最后写出答案。
二、精讲精练【例题1】某发电厂有10200吨煤,前10天每天烧煤300吨,后来改进炉灶,每天烧煤240吨。
这堆煤还能烧多少天?【思路导航】条件摘录综合法思路:前10天每天烧煤300吨,可以求出10天烧的吨数;已知煤的总吨数和前10天烧的吨数,可以求出还有多少吨没有烧;根据还剩的吨数和后来每天烧煤240吨,可以求出这堆煤还能烧多少天。
分析法思路:要求还能烧多少天,要知道还有的吨数和后来每天烧的吨数(240吨);要求还有多少吨煤,要知道这堆煤有多少吨(10200吨)和已经烧了多少吨。
要求已经烧了多少吨,要知道已经烧了多少天(10天)和每天烧多少吨(300吨)。
(10200-300×10)÷240=30(天).练习1:1.某电冰箱厂要生产1560台冰箱,已经生产了8天,每天生产120台。
小学数学冀教新版六年级上册圆的面积 练习二
小学数学冀教新版六年级上册
圆的周长和面积圆的面积练习二
知识与技能
1.求下面各圆的面积。
(得数保留两位小数)
2.求下面各图阴影部分的面积。
(单位:厘米)
3.一个石英钟的分针长是8厘米,经过30分钟,这根分针扫过的面积是多少平方厘米?
4.王师傅给一个圆形的井口遮上一块圆形帆布,井口的直径是1.6米,帆布的直径要比井口的直径多0.4米。
这块圆形帆布的面积是多少平方米?
思考与探索
下图中扇形(阴影部分)的面积和圆的面积哪个大? 为什么?
参考答案
知识与技能
1.2.4÷2=1.2分米 3.14×1.2×1.2≈4.52(平方分米)
3.14×5×5=78.5平方厘米
1.6÷2=0.8分米 3.14×0.8×0.8≈
2.01(平方分米)
2.20÷2=10(厘米) 20×20-
3.14×10×10=86(平方厘米)
16÷2=8(厘米) 32×20-3.14×8×8÷2=439.04(平方厘米)
3.3.14×8×8÷2=100.48(平方厘米)
4.(1.6+0.4)÷2=1(米) 3.14×1×1=3.14(平方米)
思考与探索
相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奥数重点常考题 第十九讲 面积计算(二)
基础卷
1、计算下面图形中阴影部分的面积。(单位:cm)
2、三角形ABC是直角三角形,AB是圆的直径,并且AB=20cm,如果阴影I的面积比阴影Ⅱ的
面积大17cm2,那么BC的长度是多少?
3、计算下面图形中阴影部分的面积。(单位:cm)
提高卷
1、计算下面图形中阴影部分的面积。
2、在长方形ABCD中,AB=6cm,BC=4cm,求阴影部分的面积。
3、三角形ABC是等腰直角三角形,直角边AB=2cm,求阴影部分的面积。
4、∠BOA=90°,S=1cm2,求阴影部分的面积。
5、AB=20cm,S1-SⅡ=7cm2,求BC的长。
6、正方形ABCD的面积为16cm2,求阴影部分的面积。
答 案
基 础 卷
