六年级奥数之面积计算(一)
六年级奥数题：平行四边形与组合平行四边形面积
六年级奥数题：平行四边形与组合平行四边形面积问题描述这道题目涉及平行四边形和组合平行四边形的面积计算。
根据给定的信息，我们需要计算出相应的面积值。
问题分析我们知道，平行四边形的面积可以通过底边长和高的乘积来计算。
首先，我们需要检查题目中给出的平行四边形的底边长和高的数值。
对于组合平行四边形，我们需要将其划分为多个简单的几何形状进行计算。
在这道题目中，我们需要划分组合平行四边形为两个三角形，然后计算每个三角形的面积并将其相加。
解题步骤1. 首先，检查题目中给出的平行四边形的底边长和高的数值。
2. 根据底边长和高的数值，使用对应的公式计算平行四边形的面积。
3. 然后，将组合平行四边形划分为两个三角形。
4. 对于每个三角形，使用底边长和高的数值，通过对应公式计算其面积。
5. 将两个三角形的面积相加，得到组合平行四边形的面积。
算法实现以下是一个简单的算法实现示例：def calculate_parallelogram_area(base, height):计算平行四边形的面积area = base * heightreturn area计算组合平行四边形的面积triangle1_area = 0.5 * base1 * height1triangle2_area = 0.5 * base2 * height2示例使用parallelogram_area = calculate_parallelogram_area(5, 4)总结通过对给定问题的分析和解题步骤的实现，我们可以计算出平行四边形和组合平行四边形的面积。
这个算法可以用于解答类似的几何题目，帮助学生更好地理解和应用相关概念。
六年级奥数-面积计算
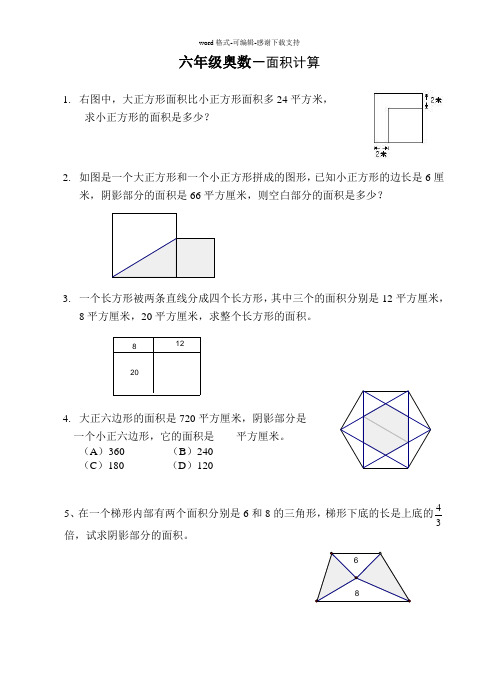
六年级奥数－面积计算1.右图中，大正方形面积比小正方形面积多24平方米，求小正方形的面积是多少？2.如图是一个大正方形和一个小正方形拼成的图形，已知小正方形的边长是6厘米，阴影部分的面积是66平方厘米，则空白部分的面积是多少？3.一个长方形被两条直线分成四个长方形，其中三个的面积分别是12平方厘米，8平方厘米，20平方厘米，求整个长方形的面积。
128204.大正六边形的面积是720平方厘米，阴影部分是一个小正六边形，它的面积是____平方厘米。
（A）360 （B）240（C）180 （D）1204 5、在一个梯形内部有两个面积分别是6和8的三角形，梯形下底的长是上底的3倍，试求阴影部分的面积。
68六年级奥数－面积计算答案1. 解析：设小正方形边长为x 米。
2x+2x+4=24，4x=20，x=5。
5×5=25（平方米）。
2. 解析：先求出大正方形的边长，1062)6666(=÷⨯⨯-厘米，则空白部分面积为7026101010=÷⨯-⨯平方厘米。
3. 解析：708201282012=+++÷⨯平方厘米。
4. 解析：如下图，大正六边形细分成18块，其中阴影部分占6块，所以阴影部分的面积是240618720=⨯÷平方厘米。
5、解析：设上底为3，下底为4，上面三角形的高是6×2÷3=4下面三角形的高是8×2÷4=4则梯形的高是4+4=8，梯形面积是（3+4）×8÷2=28，阴影部分的面积为28－6－8 =14。
六年级奥数1.1表面积与体积
六年级奥数1，1表面积与体积(tǐjī)六年级奥数1，1专题(zhuāntí)简析；小学阶段(jiēduàn)所学的立体图形主要有四种长方体·正方体·圆柱体和圆锥体。
从平面图形(túxíng)到立体图形是认识上的一个飞跃，需要有更高水平的空间想象能力。
因此，要牢固掌握这些几何图形的特征和有关的计算方法，能将公式作适当的变形，养成“数·形”结合(jiéhé)的好习惯，解题时要认真细致观察，合理大胆想象，正确灵活地计算。
在解答立体图形的表面积问题时，要注意以下几点；（1）充分利用正方体六个面的面积都相等，每个面都是正方形的特点。
（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍。
反之，把两个立体图形粘合到一起，减少的表面积等于粘合面积的两倍。
（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来。
若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。
例1，从一个棱长为10里面的正方体上挖去一个长10厘米·宽2厘米·高2厘米的小长方体，剩下部分的表面积是多少？〔思路导航〕这是一道开放题，方法有多种；1)沿一条棱挖，剩下部分的表面积为592平方厘米。
2)在某个面挖，剩下部分的表面积为632平方厘米。
3)挖通某两个对面，剩下部分的表面积为672平方厘米。
练习1，1，把一个长为12分米·宽为6分米·高为9分米的长方体木块锯成两个相同的小长方体木块，这两个小长方体的表面积之和比原来长方体的表面积增加了多少平方米？2，在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后，表面机会发生怎样的变化？例2，把19个棱长为3厘米的正方体重叠起来，拼成一个立体图形(t úx íng)，求这个立体图形的表面积。
〔思路(s īl ù)导航〕要求(y āoqi ú)这个复杂形体的表面积，必须从整体入手，从上·左·前三个方向(f āngxi àng)观察，每个方向上的小正方体各面就组合成了如下图形。
小学六年级奥数- 面积计算
二、精讲精练
【例题5】在图的扇形中，正方形的面积是30平方厘米。求阴影部分的面积。
【思路导航】阴影部分的面积等于扇形的面积减去正方形的面积。可是扇形的 半径未知，又无法求出，所以我们寻求正方形的面积与扇形面积的半径之间的 关系。我们以扇形的半径为边长做一个新的正方形（如图所示），从图中可以 看出，新正方形的面积是30×2＝60平方厘米，即扇形半径的平方等于60。这 样虽然半径未求出，但能求出半径的平方，再把半径的平等直接代入公式计算。 3.14×（30×2）×1/4－30＝17.1（平方厘米） 答：阴影部分的面积是17.1平方厘米。
二、精讲精练
【例题2】如图所示，求图中阴影部分的面积（单位：厘米）。 【思路导航】解法一：先用长方形的面积减去小扇形的面积，得空白 部分（a）的面积，再用大扇形的面积减去空白部分（a）的面积。如 图所示。 3.14×62×1/4－（6×4－3.14×42×1/4）＝16.82（平方厘米） 解法二：把阴影部分看作（1）和（2）两部分如图20－8所示。把大、 小两个扇形面积相加，刚好多计算了空白部分和阴影（1）的面积，即 长方形的面积。
小学奥数 举一反三
(六年级)
第20讲 面积计算 一、知识要点 对于一些比较复杂的组合图形，有时直接分解有一定 的困难，这时，可以通过把其中的部分图形进行平移、翻 折或旋转，化难为易。有些图形可以根据“容斥问题“的 原理来解答。在圆的半径r用小学知识无法求出时，可以把 “r2”整体地代入面积公式求面积。
二、精讲精练
练习4： 1．如图所示，图形中正方形的面积是50平方厘米，分别求出每个图形 中阴影部分的面积。
二、精讲精练
练习4： 2．如图所示，图形中正方形的面积是50平方厘米，分别求出每个图形 中阴影部分的面积。
2019年秋季小学六年级奖学金班奥数培训(5)平面图形的面积二
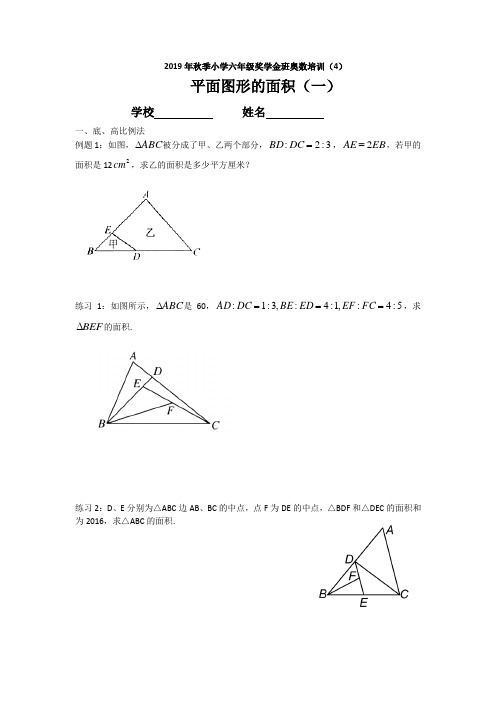
2019年秋季小学六年级奖学金班奥数培训（4）平面图形的面积（一）学校 姓名一、底、高比例法例题1：如图，ABC ∆被分成了甲、乙两个部分，3:2:=DC BD ，EB AE 2=，若甲的面积是122cm ，求乙的面积是多少平方厘米？练习1：如图所示，ABC ∆是60，5:4:,1:4:,3:1:===FC EF ED BE DC AD ，求BEF ∆的面积.练习2：D 、E 分别为△ABC 边AB 、BC 的中点，点F 为DE 的中点，△BDF 和△DEC 的面积和为2016，求△ABC 的面积.二、用字母法（方程法）解题例题11,求阴影部分的面积。
练习1：如图所示，ABC ∆的面积是24平方厘米。
F EC BE ,2=是CD 的中点，求阴影部分的 面积是多少平方厘米.练习2：如图两线段把三角形ABC 分成四块，已知其中3块的面积为5、9、9， 求阴影部分的面积是多少？训练检测1：如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．2：如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．3：如图所示，AE ED =，BD=3CD ，30ABC S ∆=（cm 2）。
求阴影部分的面积。
4：如图所示，BO=3DO ，阴影部分的面积是4平方厘米，那么，梯形ABCD 的面积是多少平方厘米？5：正方形ABCD的边长为24cm，E、F分别是CD、BC的中点，BE与DF交于G。
求阴影部分的面积。
6：如图所示，在三角形ABC中，BD=2DC，AE=2ED，且FC=2016，求AF=？7：如右图，在△ABC中，F是AC的中点，BD=2DC,已知△ABC的面积为36平方厘米。
则阴影部分的面积是多少平方厘米？。
六年级下册数学试题-奥数：第三讲 图形的面积(一)(无答案)全国通用
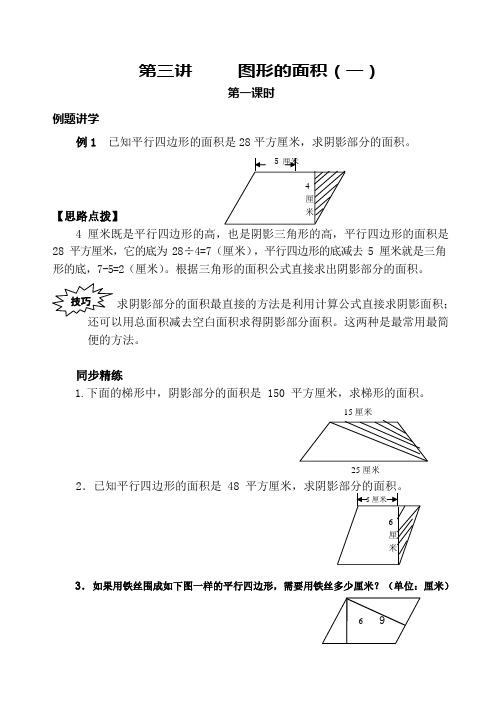
技巧例题讲学第三讲图形的面积（一）第一课时例 1 已知平行四边形的面积是 28 平方厘米，求阴影部分的面积。
【思路点拨】4 厘米既是平行四边形的高，也是阴影三角形的高，平行四边形的面积是 28 平方厘米，它的底为 28÷4=7（厘米），平行四边形的底减去5 厘米就是三角形的底，7-5=2（厘米）。
根据三角形的面积公式直接求出阴影部分的面积。
求阴影部分的面积最直接的方法是利用计算公式直接求阴影面积；还可以用总面积减去空白面积求得阴影部分面积。
这两种是最常用最简便的方法。
同步精练1.下面的梯形中，阴影部分的面积是 150 平方厘米，求梯形的面积。
15 厘米25 厘米2．已知平行四边形的面积是 483．如果用铁丝围成如下图一样的平行四边形，需要用铁丝多少厘米？（单位：厘米）一） 乙甲乙甲例题讲学第三讲图形的面积（第二课时例 2 下图中甲和乙都是正方形，求阴影部分的面积。
（单位：厘米）GACB6E4F【思路点拨】图中的阴影部分是一个三角形，它的三条边的长都不知道，三条边上的高也不知道。
所以，无法用公式计算出它的面积。
仔细观察本题的图，我们可以发现，如果延长 GA 和 FC ，它们会相交（设交点为 H ），这样就得到长方形 GBFH （如下图），它的面积很容易求，而长方形 GBFH 中除阴影部分之外的其他三部分（△AGB 、△BFC 及△AHC ）的面积都能直接求出。
GAH C6E4F同步精练1、求右图中阴影部分的面积。
（单位：厘米）12432、求右图中阴影部分的面积。
（单位：厘米）885例题讲学第三讲图形的面积（一）第三课时例 3 如图所示：，甲三角形的面积比乙三角形的面积大 6 平方厘米，求 CE 的长度。
E【思路点拨】 题目中告诉我们，甲三角形的面积比乙三角形的面积大 6 平方厘米，即甲-乙=6（平方厘米），而甲和乙分别加上四边形 ABCF 后相减的结果还是 6 平方厘米，即：甲-乙=6（平方厘米）5EE（甲+四边形 ABCF ）-（乙+四边形 ABCF ）=6（平方厘米）即：正方形 ABCD- △ABE=6（平方厘米）这就是说正方形 ABCD 的面积比三角形 ABE 的面积大 6 平方厘米。
六年级奥数面积练习题
六年级奥数面积练习题题一：一块正方形的花布边长是3cm，小明用这个花布做了一个正方形桌布，桌布的边长是多少厘米？解答：一个正方形的面积等于边长的平方。
花布的边长为3cm，所以面积为3cm × 3cm = 9cm²。
小明用花布做的桌布也是一个正方形，所以桌布的面积也是9cm²。
根据正方形面积的计算公式，可以得到桌布的边长等于根号下面积，即边长等于√9cm² = 3cm。
题二：一个长方形花坛的长度是6m，宽度是4m，小红在花坛的周边铺上小石子，需要多少个小石子？解答：一个长方形的面积等于长度乘以宽度。
花坛的长度为6m，宽度为4m，所以面积为6m × 4m = 24m²。
小红需要铺满花坛的周边，也就是花坛的周长。
长方形的周长等于两倍的长度加两倍的宽度。
花坛的周长为2 × 6m + 2 × 4m = 12m + 8m = 20m。
小石子的数量要与花坛的周长相等，所以小红需要20个小石子来铺满花坛的周边。
题三：一个直角三角形的两条直角边分别是5cm和12cm，求这个直角三角形的面积。
解答：一个直角三角形的面积等于两条直角边的乘积除以2。
直角三角形的两条直角边分别为5cm和12cm，所以面积为5cm × 12cm ÷ 2 =60cm²。
题四：一个边长为3cm的正方形，围绕它画了一个边长为2cm的边框，求边框的面积。
解答：一个正方形的边框就是在正方形的外部画了一个边长相等的正方形。
原正方形的边长为3cm，边框的边长为2cm，即边框在原正方形的基础上每边扩展1cm。
所以边框的边长为3cm+2cm+2cm=7cm。
边框的面积等于边长的平方，即7cm × 7cm = 49cm²。
题五：一个半径为5cm的圆，求这个圆的面积。
解答：一个圆的面积等于π乘以半径的平方。
圆的半径为5cm，所以面积为π × 5cm × 5cm。
举一反三--六年级奥数面积计算(1)
组合图形的面积(1)
13、图中BO=2DO，阴影部分 的面积是4平方厘米，求梯形 ABCD的面积是多少平方厘米？
14、如图，正方形ABCD的边长 是12厘米，CE=4厘米。求阴影 部分的面积。
组合图形的面积(1)
15、图中三角形ABC的面积是 36平方厘米，AC长8厘米，DE 长3厘米，求阴影部分的面积 （ADFC不是正方形）。 16、有两种自然的放法将正 方形内接于等腰直角三角形。 已知等腰直角三角形的面积 是36平方厘米，两个正方形 的面积分别是多少？
六年奥数——举一反三 面积计算（一）
组合图形的面积(1)
1、已知右面的两个正方形边长 分别为6分米和4分米，求图中阴 影部分的面积。
2、如图，这个长方形的长是9厘 米，宽是8厘米，A和B是宽的中 点，求长方形内阴影部分的面积。
组合图形的面积(1)
3、右图是两个相同的直角三 角形叠在一起，求阴影部分的 面积。（单位：厘米）
4、如图，长方形长18厘米， 宽12厘米，AE、AF两条线段 把长方形面积三等分，求三 角形AEF的面积。
组合图形的面积(1)
5、如图，三角形ABC的面积是 24平方厘米，且DC=2AD，E、 F分别是AF、BC的中点，那么 阴影部分的面积是多少？
6、如图，三角形ABC的面积是 90平方厘米，EF平行于BC， AB=3AE，那么三角形甲、乙、 丙的面积各是多少平方厘米？
组合图形的面积(1)
7、在等腰梯形ABCD中，AD=12 厘米，高DF=10厘米。三角形 CDE的面积是12平方厘米。求梯 形面积。
8、如图，三角形EDF的面积比三 角形ABE的面积大6平方厘米，已 知长方形ABDC的长和宽分别为6 厘米、4厘米，DF的长多少厘米？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
面积计算（一）
1已知如图，三角形ABC的面积为8平方厘米，AE＝ED，BD=
2BC，求阴影部分的面积。
3
2．如图，AE＝ED，BC=3BD，S△ABC＝30平方厘米。
求阴影部分的面积。
3．如图所示，AE=ED，DC＝
1BD，S△ABC＝21平方
3
厘米。
求阴影部分的面积。
4．如图所示，DE＝1/2AE，BD＝2DC，S△EBD＝5平方厘米。
求三角形ABC的面积。
5两条对角线把梯形ABCD分割成四个三角形，如图所示，已知两个三角形的面积，求另两个三角形的面积各是多少？
6．两条对角线把梯形ABCD分割成四个三角形，（如图所示），已知两个三角形的面积，求另两个三角形的面积是多少？
7．已知AO＝1/3OC，求梯形ABCD的面积（如图所示）。
8．已知三角形AOB的面积为15平方厘米，线段OB 的长度为OD的3倍。
求梯形ABCD的面积。
（如图所示）。
9四边形ABCD的对角线BD被E、F两
点三等分，且四边形AECF的面积为15平方
厘米。
求四边形ABCD的面积（如图所示）。
10．四边形ABCD的对角线BD被E、F、G三点四等分，且四边形AECG的面积为15平方厘米。
求四边形ABCD 的面积（如图）。
11．已知四边形ABCD的对角线被E、F、G三点四等分，且阴影部分面积为15平方厘米。
求四边形ABCD的面积（如图所示）。
12．如图所示，求阴影部分的面积（ABCD为正方形）。
13如图所示，BO＝2DO，阴影部分
的面积是4平方厘米。
那么，梯形ABCD
的面积是多少平方厘米？
14．如图所示，阴影部分面积是4平方厘米，OC＝2AO。
求梯形面积。
15．已知OC＝2AO，S△BOC＝14平方厘米。
求梯形的面积（如图所示）。
16．已知S△AOB＝6平方厘米。
OC＝3AO，求梯形的面积（如图所示）。
17如图所示，长方形
ADEF的面积是16，三角形
ADB的面积是3，三角形
ACF的面积是4，求三角形ABC的面积。
18．如图所示，长方形ABCD的面积是20平方厘米，三角形ADF的面积为5平方厘米，三角形ABE的面积为7平方厘米，求三角形AEF的面积。
19．如图所示，长方形ABCD的面积为20平方厘米，S△ABE＝4平方厘米，S△AFD＝6平方厘米，求三角形AEF 的面积。
20．如图所示，长方形ABCD的面积为24平方厘米，三角形ABE、AFD的面积均为4平方厘米，求三角形AEF 的面积。