第四章-受弯构件斜截面受剪承载力计算
受弯构件斜截面承载力计算

第一排弯起钢筋截面面积Asb
Asb≥(V1-Vcs)/(0.8fysinαs)= 472.91mm2 将纵向钢筋中间部位一根弯起(1 25), Asb=490.9mm2>472.91mm2,故满足要求。
【例4.10】钢筋混凝土矩形截面简支梁,两端支承在砖墙 上,净跨度ln=4660mm(图4.41);截面尺寸b×h=250mm ×550mm。该梁承受均布荷载,其中恒荷载标准值 gk=25kN/m(包括自重),荷载分项系数γG=1.2,活荷 载标准值qk=42kN/m,荷载分项系数γQ=1.4;混凝土强 度等级为C20(fc=9.6N/mm2, ft=1.1N/mm2),箍筋采用 HPB235级钢筋(fyv=210N/mm2),按正截面承载力已 配HRB335级钢筋4 25为纵向受力钢筋(fy=300N/mm2)。 试求腹筋数量。 【解】(1) 计算剪力设计值。支座边缘处剪力设计值为 V1=1/2(γGgk+γQqk)ln=206.9kN
对于承受以集中荷载为主的矩形截面独立梁,应改用
V Vcs 0.8 f y Asb Sin s Asv 1.75 ft bh0 1.25 f yv h0 0.8 f y Asb Sin s 1 s
图4.38
抗剪计算模式
(a) 仅配有箍筋;(b) 同时配置箍筋和弯起筋
4.4.3.2 公式适用条件
应按公式(4.38)复核,得 0.25βcfcbh0=223200N>V=200000N 截面尺寸满足要求。 (3) 确定是否需要按计算配置腹筋。 由公式(4.41) 0.7ftbh0=71610N<V=200000N 需进行斜截面受剪承载力计算,按计算配置腹筋。 (4) 箍筋计算。由公式(4.34)得 Asv/s≥(V-0.7ftbh0)/(1.25fyvh0) =1.05mm2/mm
第四章 受弯构件斜截面受剪承载力
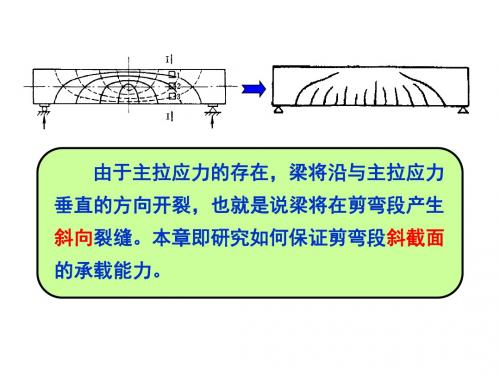
对于均布荷载作用下的简支梁:
l
1 x qlx qx 2 x M l 2 2 ( ) 1 l Vh0 ( ql qx)h 1 2 h0 0 2
跨高比
广义剪跨比
试验表明,对于承受均布荷载的梁,构件跨高比是影响 受剪承载力的主要因素,随着跨高比的增大,受剪承载力 降低。
斜压破坏 一般发生在剪跨比很小或剪跨比虽然 适中,但箍筋配置很多的情况 腹筋未达屈服,梁腹砼即到达抗压 强度发生斜压破坏,承载力取决于砼强 度及截面尺寸,再增加箍筋或弯筋对斜 截面受剪承载力的提高已不起作用。
发生条件
破坏特点
破坏类型
发生条件
无腹筋梁 有腹筋梁
破坏特点
破坏性质
备注
类似于少筋 破坏,设计 时应避免
斜截面破坏应力状态
正截面受弯承载力
KM≤Mu
斜截面受剪承载力KV≤Vu
§4.2 无腹筋梁斜截面的应力状态及破坏形态 无腹筋梁是指不配箍筋和弯起钢筋的梁。 斜裂缝出现后梁内应力状态
剪切破坏时隔离体上的作用力 外力:弯矩、剪力(外荷载 在斜截面AB上引起内力MA 、
VA)
内力:纵向钢筋拉力、砼剪 压面承担剪力与压力 骨料咬合力、纵筋的销栓力 VA
无腹筋梁斜截面受剪破坏形态
剪压破坏 发生条件
剪跨比适中时(一般1≤λ≤3),常发生剪压破 坏
随着荷载增大,先出现垂直裂缝和几根微 细的斜裂缝。荷载增大到一定程度时,其中一 根形成临界斜裂缝。这条裂缝逐渐向斜上方发 展,但仍保留一定受压区而不裂通,剪压区逐 渐减小,直到斜裂缝顶端的混凝土在剪应力和 压应力共同作用下被压碎而破坏。破坏过程比 斜拉破坏缓慢,破坏时的荷载明显高于斜裂缝 出现时的荷载。实质上是残余截面上混凝土的 主压应力超过了混凝土在压力和剪力共同作用 下的抗压强度。
混凝土结构设计原理-第四章斜截面受弯习题讲解学习

第四章小结1、斜截面强度计算是钢筋混凝土结构的一个重要问题。
设计受弯构件时,必须同时解决正截面强度和斜截面强度的计算与构造问题。
2、梁沿斜截面破坏的主要形态有斜压、剪压和斜拉三种。
影响斜截面抗剪强度的主要因素有:剪跨比、混凝土强度、纵向受拉钢筋配筋率和箍筋数量及强度等。
3、斜截面抗剪强度的计算公式是以剪压破坏为基础建立的。
对于斜压和斜拉破坏,一般采用截面限制条件和构造措施予以避免。
斜截面抗剪强度的计算图式、基本计算公式和适用条件,斜截面抗剪设计和复核的方法及步骤。
4、斜截面强度有两个方面:一是斜截面抗剪强度,通过计算配置箍筋或配置箍筋和弯起钢筋来保证,一是斜截面抗弯强度,通过采用一定的构造措施来保证。
第四章 受弯构件斜截面承载力计算一、填空题:1、在钢筋混凝土受弯构件中,( ) 和 ( )称为腹筋或剪力钢筋。
2、影响受弯构件斜截面抗剪力的主要因素( ) 、( ) 、( )和( )。
3、受弯构件斜截面破坏的主要形态( )、( ) 和( )。
桥规抗剪承载力公式是以( )破坏形态的受力特征为基础建立的。
4、梁中箍筋的配箍率公式:( )。
5、纵筋的配筋率越大,受剪承载力越高,这是由于( )和( )。
6、梁式结构受拉主钢筋应有不少于( )根并不少于( )的受拉主钢筋通过支点。
7、支座中心向跨径方向长度在一倍梁高范围内,箍筋间距应不大于( )。
8、控制最小配箍率的目的( ),限制截面最小尺寸的目的( )。
9、影响有腹筋梁斜截面抗剪能力的主要因素有:( )、 ( ) 、 ( )、 ( ) 。
10、钢筋混凝土梁沿斜截面的主要破坏形态有斜压破坏、斜拉破坏和剪压破坏等。
在设计时,对于斜压和斜拉破坏,一般是采用( ) 和 ( ) 予以避免,对于常见的剪压破坏形态,梁的斜截面抗剪能力变化幅度较大,故必须进行斜截面抗剪承载力的计算。
《公路桥规》规定,对于配有腹筋的钢筋混凝土梁斜截面抗剪承载力的计算采用下属半经验半理论的公式:ssb sd sv sv k cu u d A f f f p bh V V θραααγsin )1075.0()6.02()1045.0(3,033210∑⨯++⨯=≤--11、对于已经设计好的等高度钢筋混凝土简支梁进行全梁承载能力校核,就是进一步检查梁沿长度上的截面的( )、 ( )和 ( 是否满足要求。
第四章 斜截面

面积; a s— 弯起钢筋与梁纵轴线的夹角,一般为450,当梁截面超 过800mm时,通常是600;
3 配有箍筋和弯起钢筋梁的斜截面受剪承载力
fy ---弯起钢筋抗拉强度 配有箍筋和弯起钢筋梁的斜截面受剪承载力 1.均布荷载作用下矩形、T形和I形截面的简支梁 Asb----弯起钢筋面积 as---弯起角
我国混凝土结构设计规范中所规定的计算公式就是根据剪
压破坏形态而建立的。考虑了的平衡条件
试验参数及四项基本假设。 1、基本假设
y
0 ,引入一些
(1)剪压破坏时,斜裂缝相交的箍筋和弯起钢筋的拉应 力都达到其屈服强度;
(2)剪压破坏时,不考虑斜裂缝处的骨料咬合力和纵筋 的销栓力;
(3)为计算公式应用简便,仅在计算梁受集中荷载作用 为主的情况下,才考虑剪跨比。 (4)剪压破坏时,斜裂缝所承受的剪力由三部分组成,见 下图:
2、 有腹筋梁的破坏形态
• 斜拉破坏:
配箍率sv很低,或间距S 较大且较大的时候;
• 斜压破坏:
sv很大,或很小(1)斜向压碎,箍筋未屈服;
• 剪压破坏:
配箍和剪跨比适中,破坏时箍筋受拉屈服,剪压区压
碎,斜截面承载力随sv及fyv的增大而增大。
2 有腹筋简支梁的受剪性能
剪跨比(Shear span ratio)
试验表明, 剪跨比越大, 有腹筋梁的 抗剪承载力 越低,如图 所示。对无 腹筋梁来说, 剪跨比越大, 抗剪承载力 也越低,但 当λ≥3 ,剪跨 比的影响不 再明显。
剪跨比对有腹筋梁受剪承载力的影响
混凝土强度
斜截面受剪承载力随混凝土的强度等级的提高而提高。梁
斜压破坏时,受剪承载力取决于混凝土的抗压强度。梁为斜拉
Vsb
受弯构件斜截面受剪承载力计算

梁的斜截面承载力包括斜截面受剪承载力和斜截面受弯承载力。在实
际工程中,斜截面受剪承载力通过计算配置腹筋来保证,而斜截面受弯
承载力则通过构造措施来保证。
有腹筋梁斜截面破坏工程试验
1
剪跨比λ的定义
影响梁斜截面破坏形态有很多因素,其中最主要的两项是剪跨
比λ的大小和配置箍筋的多少
对于承受集中荷载的梁:第一个集中荷载作用点到支座边缘之
距a(剪跨跨长)与截面的有效高度ℎ0 之比称为剪跨比λ,即
λ=a/ℎ0 。
广义剪跨比λ=M/Vℎ0 (如果λ表示剪跨比,集中荷载作用下的
梁某一截面的剪跨比等于该截面的弯矩值与截面的剪力值和有效
高度乘积之比)。
有腹筋梁斜截面破坏工程试验
2
箍筋配筋率
箍筋配箍率是指箍筋截面面积与截面宽度和箍筋间距乘积的比值,
计算公式为:
1 =Βιβλιοθήκη =式中 ——配置在同一截面内箍筋各肢的全部截面面积(2 );
=1 ;
n——同一截面内箍筋肢数;
1 ——单支箍筋的截面面积(2 );
b——矩形截面宽度,T形、I字形截面的腹板宽度(mm);
1.75
≤ =
ℎ0 +
ℎ0
+1
式中 V——梁的剪力设计值(N/2 )
剪跨比λ<1.5时,取λ=1.5;当λ>3时,取λ=3.
谢 谢 观 看
s——箍筋间距;
仅配箍筋时梁的斜截面受剪承载力计算基本公式
对于矩形、T型、I字形截面的一般受弯构件:
≤ = 0.7 ℎ0 +
ℎ0
对承受集中荷载作用为主的独立梁或对集中荷载作用下(包括作用
梁斜截面受剪承载力计算

a h0 2000 530 3.77>3,取 3
1.75 1.75 f t bh0 1.27 200 530 59000N<V=98.5kN 1 3 1
故需按计算配置箍筋
3. 计算箍筋数量
1.75 V f t bh0 3 Asv 98 . 5 10 59000 1 0.356 s f yv h0 210 530
(1)复核截面尺寸
梁的截面尺寸应满足式(4-14)~式(4-15)的要求,否则,应加 大截面尺寸或提高混凝土强度等级。
(2)确定是否需按计算配置箍筋
V 0.7 f t bh0 , 按构造
1.75 V f t bh0 , 按构造 1
(3)确定腹筋数量
Asv V 0.7 f t bh0 s 1.25 f yv h0
【例 4-1】 某办公楼矩形截面简支梁,截面尺寸 250mm×500mm,h0 =465mm,承受均布荷载作用, 以求得支座边缘剪力设计值为 185.85kN , 混凝土为 C25级,箍筋采用HPB235级钢筋,试确定箍筋数量。
【解】查表得fc =11.9N/mm2 ,ft =1.27N/mm2 , fyv=210N/mm2 ,βc =1.0
<V=185.85kN 需按计算配置箍筋。 3. 确定箍筋数量
Asv V 0.7 f t bh0 185.85 103 103346 .25 s 1.25 f yv h0 1.25 210 465
= 0.676mm2 /mm
按构造要求,箍筋直径不宜小于 6mm ,现选用 φ8 双 肢箍筋(Asv1 =50.3mm2 ),则箍筋间距
1.2la或1.2la+h0 20d或h0
水工钢筋混凝土结构习题集2-2
水工钢筋混凝土结构习题集2-2第四章钢筋混凝土受弯构件斜截面承载力计算一、思考题1.钢筋混凝土无腹筋梁斜裂缝发生前后梁内应力状态有何变化其应力重分布表现在哪些方面2.钢筋混凝土无腹筋梁的斜截面受剪破坏的主要形态有哪几种它们的破坏原因和破坏过程有何不同在设计中采用什么措施加以防止3.何谓剪跨比它对无腹筋梁斜截面承载力及斜截面破坏形态有何影响对有腹筋梁的斜截面破坏形态影响怎样4.钢筋混凝土梁的斜截面承载力的计算公式是建立在哪种破坏形态之下的如何避免其他斜截面破坏形态的发生?5.影响无腹筋梁斜截面受剪承载力的主要因素有哪些这些因素对斜截面承载力有什么影响?6.何谓配箍率箍筋在钢筋混凝土受弯构件中的作用是什么?箍筋配箍率有无限制7.梁的斜截面受剪承载力计算公式有什么限制条件?为什么要有这样的限制8.在进行梁的斜截面受剪承载力计算时,其截面位置是怎样确定的9.什么是梁的抵抗弯矩图?它与设计弯矩图是什么关系?抵抗弯矩图是怎样画出的(以伸臂梁为例)10.请解释什么是梁的斜截面受弯承载力在什么情况下才考虑梁的斜截面受弯承载力问题梁的斜截面受弯承栽力是怎样保证的11.纵向受拉钢筋的弯起、截断和锚固应满足哪些要求12.当梁中配有计算所需要的受压钢筋时,其箍筋设置应注意哪些问题为什么13.试述受弯构件斜截面受剪承载力的计算步骤,并写出有关的计算公式。
14.画出图4-1所示钢筋混凝土梁裂缝出现的大致位置和方向。
图4-1二、选择题1.无腹筋梁斜截面受剪破坏形态主要有三种,这三种破坏的性质()。
(A)都属于脆性破坏(B)都属于塑性破坏(C)剪压破坏属于塑性破坏,斜拉和斜压破坏属于脆性破坏(D)剪压和斜压破坏属于塑性破坏,斜拉破坏属于脆性破坏2.无腹筋梁斜截面受剪主要破坏形态有三种。
对同样的构件就其受剪承载力而言()。
(A)斜拉破坏>剪压破坏>斜压破坏(B)斜拉破坏<剪压破坏<斜压破坏(C)斜压破坏>剪压破坏>斜拉破坏(D)剪压破坏=斜压破坏>斜拉破坏3.在进行受弯构件斜截面受剪承载力计算时,对于一般梁(hw/b4.0),若V0.25fcbh0/d,可采取的解决办法有()。
受弯构件斜截面承载力计算—受弯构件的斜截面抗剪承载力
0Vd Vu Vcs Vsb
Vcs a1a2a3(0.45 103 )bh0 (2 0.6p) fcu,k svfsv
Vsb (0.75 103 )fsd Asb sin s
当 hw ≤4.0时,属于一般的梁,应满足
b
当 hw ≥6.0时,属于薄腹梁,应满足
b
V 0.25c fcbh0 V 0.2c fcbh0
当4.0< hw<6.0时,应满足
b
V
0.025(14
hw b
)c
fcbh0
箍筋的构造要求
梁截面高度 h
150<h≤300 300<h≤500 500<h≤800
配有箍筋和弯起钢筋梁的斜截面受剪承载力
V
Vu
acv
ftbh0
f yv
Asv s
h0
0.8 fy Asb
sin as
5.公式的适用范围
(1)公式的上限——截面尺寸限制条件
取斜压破坏作为受剪承载力 的 上限。
hw hw
hw
斜压破坏取决于混凝土的抗
压强度和截面尺寸。
b
防止斜压破坏的截面限制条
sv
sv,min
0.24
ft f yv
抗剪承载能力计算基本公式
抗剪承载力的组成
配有箍筋和弯起钢筋的钢筋混凝土梁,当发生剪压破坏时,其抗剪承载
力 的剪抗能剪力能V力u由Vsv斜和裂弯缝起上钢剪筋压的区抗混剪凝能土力的Vsb抗三剪部能分力所Vc组,成与。斜裂缝相交的箍筋
Vu Vc Vsv Vsb
适用条件:多种荷载作用下,其中集中荷载对支座截面或节 点边缘所产生的剪 力值占总剪力值的75%以上时。
第四章 受弯构件的斜截面承载力
Vu Vc
V u V c V s V sb
第四章 受弯构件的斜截面承载力
第四章 受弯构件的斜截面承载力
桁架模型
适用于有腹筋梁。
把有斜裂缝的RC梁比拟为一个铰接桁架,压区混凝土为上弦杆,受 拉纵筋为下弦杆,腹筋为竖向拉杆,斜裂缝间的混凝土则为斜压杆。
第四章 受弯构件的斜截面承载力
3. 保证斜截面抗剪的措施
1)构造措施
2)配抗剪钢筋
箍筋
双向抗剪
弯起钢筋
单向抗剪
腹筋
工程设计中,应优先选用箍筋,然后再考虑采用弯起钢筋。
第四章 受弯构件的斜截面承载力
腹筋的作用: 箍筋: ①提高斜截面受剪承载力; ②与纵筋绑扎,形成钢筋骨架 便于施工; ③防止纵筋过早压曲,约束核心混凝土。 弯起钢筋: 由纵筋弯起形成 承受较大的剪力。
按桁架模型推导的受剪承载力公式( truss analogy)
Vu
z
f
åA
sv
f yv
Vu
Vu
zcotf
Vu
å
A sv f yv
A sv f yv s
z cot f sv f yv b z cot f
第四章 受弯构件的斜截面承载力
Vu
zcosf
Vu
fc
f
z
åA
sv
取斜拉破坏时的斜裂缝角度作为cot f 的上限,试验结果cotf
=3 左右。因此,当cot f 大于3时,应取等于3,即有,
sv f yv b z V u min 3 sv f yv b z
fc sv f yv
1
第四章 受弯构件的斜截面承载力
第4章 受弯构件的斜截面承载力
条临界斜裂缝,临界斜裂缝扩展,使斜截面剪压区的高度
缩小,导致剪压区混凝土剪压破坏。属脆性破坏。 3) 斜拉破坏 ← λ>3 破坏特征:“一裂就断”。具有很明显的脆性破坏。
(2) 承载力比较
斜压 > 剪压 > 斜拉
(3) 变形能力比较
剪压 > 斜压 > 斜拉
均属脆性破坏类型。
图 4-8 斜截面破坏的F一f曲线
对有腹筋梁来说,只要截面尺寸合适,箍筋配置数量适
当,剪压破坏是最常见的一种破坏形态。
§4.3 简支梁斜截面受剪机理
解释受剪机理的结构模型已有多种,这里讲述三种: 带拉杆的梳形拱模型、拱形桁架模型、桁架模型。
4.3.1
1.梳状结构
带拉杆的梳形拱模型
—— 适用于无腹筋梁 (1)梁的下部:混凝土被斜裂缝和垂直裂缝分割成梳 状齿;纵向受拉钢筋作为拉杆; (2)梁的上部:混凝土作为变截面两铰拱体。
图5-4 斜裂缝 (a)腹剪斜裂缝;(b)弯剪斜裂缝
(1) 腹剪斜裂缝
实线:主拉应力迹线;虚线:主压应力迹线。 在中和轴附近,主拉应力方向大致为450 ,当混凝土 拉裂,沿主压应力迹线产生腹剪斜裂缝。 特点:中间宽两头细,呈枣核形,常见于薄腹梁中。
图 4-3
主应力轨迹线
(2) 弯剪斜裂缝 从主应力迹线图可以看出: 在剪弯区段截面的下边缘,主拉应力还是水平向 的,所以,在这些区段仍可能首先出现一些较短的
式中 a—称为剪跨,最外侧集中力到支座边缘的距离。
λ = (β -β 2)/(1-2β )·L /h0
式中 β L — 计算截面离支座边缘的距离。
(4-5)
剪跨比对梁的斜截面破坏形态和承载力影响极大。
4.2.3 斜截面受剪破坏的三种主要形态
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 19 第4章 受弯构件的斜截面承载力 教学要求: 1深刻理解受弯构件斜截面受剪的三种破坏形态及其防止对策。 2熟练掌握梁的斜截面受剪承载力计算。 3理解梁内纵向钢筋弯起和截断的构造要求。 4知道梁内各种钢筋,包括纵向受力钢筋、纵向构造钢筋、架立筋和箍筋等的构造要求。 4.1 概述 在保证受弯构件正截面受弯承载力的同时,还要保证斜截面承载力,它包括斜截面受剪承载力和斜截面受弯承载力两方面。工程设计中,斜截面受剪承载力是由计算和构造来满足的,斜截面受弯承载力则是通过对纵向钢筋和箍筋的构造要求来保证的。
图4-1 箍筋和弯起钢筋
图4-2 钢筋弯起处劈裂裂缝 工程设计中,应优先选用箍筋,然后再考虑采用弯起钢筋。由于弯起钢筋承受的拉力比较大,且集中,有可能引起弯起处混凝土的劈裂裂缝,见图4-2。因此放置在梁侧边缘的钢筋不宜弯起,梁底层钢筋中的角部钢筋不应弯起,顶层钢筋中的角部钢筋不应弯下。弯起钢筋的弯起角宜取45°或60°
4.2 斜裂缝、剪跨比及斜截面受剪破坏形态 4.2.1 腹剪斜裂缝与弯剪斜裂缝 钢筋混凝土梁在剪力和弯矩共同作用的剪弯区段内,将产生斜裂缝。
主拉应力:2242tp, 2 / 19
主压应力2242cp 主应力的作用方向与构件纵向轴线的夹角a可按下式确定: 2
2tg
图4-3 主应力轨迹线
图4-4 斜裂缝 (a)腹剪斜裂缝;(b)弯剪斜裂缝
这种由竖向裂缝发展而成的斜裂缝,称为弯剪斜裂缝,这种裂缝下宽上细,是最常见的,如图4-4(b)所示。 4.2.2 剪跨比
在图4-5所示的承受集中荷载的简支梁中,最外侧的集中力到临近支座的距离a称为剪跨,剪跨a与梁截面有效高度h0的比值,称为计算截面的剪跨比,简称剪跨比,用λ表示,λ=a/h0。 3 / 19
对于承受集中荷载的简支梁,λ=M/(Vh0)=a/h0,即这时的剪跨比与广义剪跨比相同。 对于承受均布荷载的简支梁,设l为梁的跨度,βl为计算截面离支座的距离,则λ可表达为跨高比l/h0
的函数:
剪跨比λ反映了截面上正应力σ和剪应力τ的相对比值,在一定程度上也反映了截面上弯矩与剪力的相对比值。它对无腹筋梁的斜截面受剪破坏形态有着决定性的影响,对斜截面受剪承载力也有着极为重要的影响。
4.2.3 斜截面受剪破坏的三种主要形态 1 无腹筋梁的斜截面受剪破坏形态
图4-6 主应力迹线分布图 在剪跨比小的图4-6(a)中,在集中力到支座之间有虚线所示的主压应力迹线,即力是按斜向短柱的形式传递的。可见,剪跨比小时,主要是斜向受压而产生斜压破坏。在剪跨比大的图4-6(c)中,集中力与支座之间没有直接的主压应力迹线,故以弯曲传力为主,产生沿主压应力迹线的斜裂缝,并发展为斜拉破坏。试验也表明,无腹筋梁的斜截面受剪破坏形态与剪跨比λ有决定性的关系,主要有斜压破坏、剪压破坏和斜拉破坏三种破坏形态。
图4-7斜截面破坏形态 (a)斜压破坏;(b)剪压破坏; (c)斜拉破坏 4 / 19
(1)斜压破坏(图4-7a) λ<1时,发生斜压破坏。这种破坏多数发生在剪力大而弯矩小的区段,以及梁腹板很薄的T形截面或I形截面梁内。破坏时,混凝土被腹剪斜裂缝分割成若干个斜向短柱而压坏,因此受剪承载力取决于混凝土的抗压强度,是斜截面受剪承载力中最大的。 (2)剪压破坏(图4-7b) 1≤λ≤3时,常发生剪压破坏。其破坏特征通常是,在弯剪区段的受拉区边缘先出现一些竖向裂缝,它们沿竖向延伸一小段长度后,就斜向延伸形成一些斜裂缝,而后又产生一条贯穿的较宽的主要斜裂缝,称为临界斜裂缝,临界斜裂缝出现后迅速延伸,使斜截面剪压区的高度缩小,最后导致剪压区的混凝土破坏,使斜截面丧失承载力。 (3)斜拉破坏(图4-7c) λ>3时,常发生斜拉破坏。其特点是当竖向裂缝一出现,就迅速向受压区斜向伸展,斜截面承载力随之丧失。破坏荷载与出现斜裂缝时的荷载很接近,破坏过程急骤,破坏前梁变形很小,具有很明显的脆性,其斜截面受剪承载力最小。
图4-8 斜截面破坏的F-f曲线 图4-8为三种破坏形态的荷载-挠度(F-f)曲线图。可见,三种破坏形态的斜截面受剪承载力是不同的,斜压破坏时最大,其次为剪压,斜拉最小。它们在达到峰值荷载时,跨中挠度都不大,破坏时荷载都会迅速下降,表明它们都属脆性破坏类型,是工程中应尽量避免的。另外,这三种破坏形态虽然都是属于脆性破坏类型,但脆性程度是不同的。混凝土的极限拉应变值比极限压应变值小得多,所以斜拉破坏最脆,斜压破坏次之。为此,规范规定用构造措施,强制性地来防止斜拉、斜压破坏,而对剪压破坏,因其承载力变化幅度相对较大所以是通过计算来防止的。
2 有腹筋梁的斜截面受剪破坏形态 配置箍筋的有腹筋梁,它的斜截面受剪破坏形态是以无腹筋梁为基础的,也分为斜压破坏、剪压破坏和斜拉破坏三种破坏形态。这时,除了剪跨比对斜截面破坏形态有决定性的影响以外,箍筋的配置数量对破坏形态也有很大的影响。 当λ>3,且箍筋配置数量过少时,斜裂缝一旦出现,与斜裂缝相交的箍筋承受不了原来由混凝土所负担的拉力,箍筋立即屈服而不能限制斜裂缝的开展,与无腹筋梁相似,发生斜拉破坏。如果λ>3,箍筋配置数量适当的话,则可避免斜拉破坏,而转为剪压破坏。这是因为斜裂缝产生后,与斜裂缝相交的箍筋不会立即受拉屈服,箍筋限制了斜裂缝的开展,避免了斜拉破坏。箍筋屈服后,斜裂缝迅速向上发展,使斜裂缝上端剩余截面缩小,使剪压区的混凝土在正应力σ和剪应力τ共同作用下产生剪压破坏。 如果箍筋配置数量过多,箍筋应力增长缓慢,在箍筋尚未屈服时,梁腹混凝土就因抗压能力不足而发生斜压破坏。在薄腹梁中,即使剪跨比较大,也会发生斜压破坏。 所以,对有腹筋梁来说,只要截面尺寸合适,箍筋配置数量适当,使其斜截面受剪破坏成为剪压破坏形态是可能的。 4.3 简支梁斜截面受剪机理 4.3.1 带拉杆的梳形拱模型 5 / 19
带拉杆的梳形拱模型适用于无腹筋梁。 图4-9 梳状结构 图4-10 齿的受力 图4-11 拱体的受力 4.3.2 拱形桁架模型 拱形桁架模型适用于有腹筋梁。
图4-12 拱形桁架模型 4.3.3 桁架模型
图4-13 桁架模型 (a)45°桁架模型;(b)变角桁架模型;(c)变角桁架模型的内力分析 6 / 19
4.4 斜截面受剪承载力的计算 1 剪跨比 随着剪跨比λ的增加,梁的破坏形态按斜压(λ<1)、剪压(1≤λ≤3)和斜拉(λ>3)的顺序演变,其受剪承载力则逐步减弱。当λ>3时,剪跨比的影响将不明显。 2 混凝土强度 斜截面破坏是由混凝土到达极限强度而发生的,故混凝土的强度对梁的受剪承载力影响很大。 3 箍筋的配筋率 梁内箍筋的配筋率是指沿梁长,在箍筋的一个间距范围内,箍筋各肢的全部截面面积与混凝土水平截面面积的比值。
图4-14 箍筋的肢数 (a)单肢箍;(b)双肢箍;(c)四肢箍
图4-15 箍筋的配筋率对梁 受剪承载力的影响 7 / 19
4 纵筋配筋率 纵筋的受剪产生了销栓力,它能限制斜裂缝的伸展,从而使剪压区的高度增大。所以,纵筋的配筋率越大,梁的受剪承载力也就提高。 5 斜截面上的骨料咬合力 斜裂缝处的骨料咬合力对无腹筋梁的斜截面受剪承载力影响较大。 6 截面尺寸和形状 (1)截面尺寸的影响 截面尺寸对无腹筋梁的受剪承载力有较大的影响,尺寸大的构件,破坏时的平均剪应力比尺寸小的构件要低。有试验表明,在其他参数(混凝土强度、纵筋配筋率、剪跨比)保持不变时,梁高扩大4倍,破坏时的平均剪应力可下降25%~30%。 对于有腹筋梁,截面尺寸的影响将减小。 (2)截面形状的影响 这主要是指T形梁,其翼缘大小对受剪承载力有影响。适当增加翼缘宽度,可提高受剪承载力25%,但翼缘过大,增大作用就趋于平缓。另外,加大梁宽也可提高受剪承载力。
4.4.2 斜截面受剪承载力的计算公式 1 基本假设 国内外许多学者曾在分析各种破坏机理的基础上,对钢筋混凝土梁的斜截面受剪承载力给出过不少类型的计算公式,但终因问题的复杂性而不能实际应用。 我国规范目前采用的是半理论半经验的实用计算公式。 对于斜压破坏,通常用控制截面的最小尺寸来防止;对于斜拉破坏,则用满足箍筋的最小配筋率条件及构造要求来防止;对于剪压破坏,因其承载力变化幅度较大,必须通过计算,使 构件满足一定的斜截面受剪承载力,从而防止剪压破坏。 (1) 梁发生剪压破坏时,斜截面所承受的剪力设计值由三部分组成, 见图4-16,即
图4-16 受剪承载力的组成 (2) 梁剪压破坏时,与斜裂缝相交的箍筋和弯起钢筋的拉应力都达到其屈服强度,但要考虑拉应力可能不均匀,特别是靠近剪压区的箍筋有可能达不到屈服强度。 (3) 斜裂缝处的骨料咬合力和纵筋的销栓力,在无腹筋梁中的作用还较显著,两者承受的剪力可达总剪力的50%~90%,但在有腹筋梁中,由于箍筋的存在,虽然使骨料咬合力和销栓力都有一定程度的提高,但它们的抗剪作用已大都被箍筋所代替,试验表明,它们所承受的剪力仅占总剪力的20%左右。另外,
sbscuVVVV
