PUMA560机构的运动学性能分析
基于MATLAB的PUMA机器人运动仿真研究

基于MATLAB的PUMA机器人运动仿真研究摘要:机器人运动学是机器人学的一个重要分支,是实现机器人运动控制的基础。
论文以D-H坐标系理论为基础对PUMA560机器人进行了参数设计,利用MATLAB机器人工具箱,对机器人的正运动学、逆运动学、轨迹规划进行了仿真。
Matlab仿真结果说明了所设计的参数的正确性,能够达到预定的目标。
关键词:机器人PUMA560 D-H坐标系运动学轨迹规划机器人运动学的研究涉及大量的数学运算,计算工作相当繁锁。
因此,采用一些工具软件对其分析可大大提高工作效率,增加研究的灵活性和可操作性。
对机器人进行图形仿真,可以将机器人仿真的结果以图形的形式表示出来,从而直观地显示出机器人的运动情况,得到从数据曲线或数据本身难以分析出来的许多重要信息,还可以从图形上看到机器人在一定控制条件下的运动规律[1]。
论文首先设计了PUMA560机器人的各连杆参数,然后讨论了正、逆运动学算法,轨迹规划问题,最后在MATLAB环境下,运用Robotics Toolbox,编制简单的程序语句,快速完成了机器人得运动学仿真。
设机械手起始位置位于A点,qA=[000000],即表示机器人的各关节都处于零位置处。
机械手在B点和C点相对于基坐标系的位姿可用齐次变换矩阵TB和TC来表示。
图2所示为机械手臂在A点时的三维图形。
可通过matlab编程来给出机器人由A运动到B,转动关节2和转动关节3的角度随时间变换的仿真图,如图3所示。
图4所示为末端关节沿x,y,z方向的运动轨迹。
取仿真时间为2s,采样间隔为0.056s。
从图3可以看出:在所取的仿真时间内,转动关节2由零逐渐变化到1.5708rad;转动关节3由零逐渐变化到-1.5708rad。
图4说明机器人由A运动到B,末端关节沿x,y,z方向位移矢量的变化轨迹,证明机器人可以实现不同方位的姿态。
通过仿真曲线可以观察到机器人从A运动到B时各关节的运动情况,且各关节运动情况均为正常,各连杆没有运动错位的情况,从而验证了所有连杆参数的合理性,且说明了各参数的设计能够实现预定的目标。
第4章 微分运动和雅可比矩阵

2013年7月15日
南京航空航天大学机械电子工程系
10
运动学逆问题
封闭解 1 q1 (nx , n y , nz , , px , p y , pz ) 2 q2 (nx , n y , nz , , px , p y , pz ) q (n , n , n , , p , p , p ) 3 x y z x y z 3 4 q4 (nx , n y , nz , , px , p y , pz ) q (n , n , n , , p , p , p ) 5 x y z x y z 5 6 q6 (nx , n y , nz , , px , p y , pz )
c c s c s 0 c s s s c s s s c c c s 0 c s c s s s s c c s c c 0 0 r11 r12 0 r21 r22 0 r31 r32 1 0 0 r13 0 r23 0 r33 0 0 1
0 nx 0 ny 0 nz 1 0
ox oy oz 0
ax ay az 0
px t111 t112 t113 p y t121 t122 t123 pz t131 t132 t133 1 0 0 0
m113 m123 m133 0
c4 0 3 4T s4 0 s4 0 c4 0
0 0 1 0
0 0 0 1
c2 0 1 2T s2 0
s2 0 c2 0
0 0 1 d2 0 0 0 1
c3 s 2 3 3T 0 0
现在绝大多数的机械手,都满足上面的充 分条件之一,所以封闭式逆解都存在。
机器人学大作业PUMA560工作空间
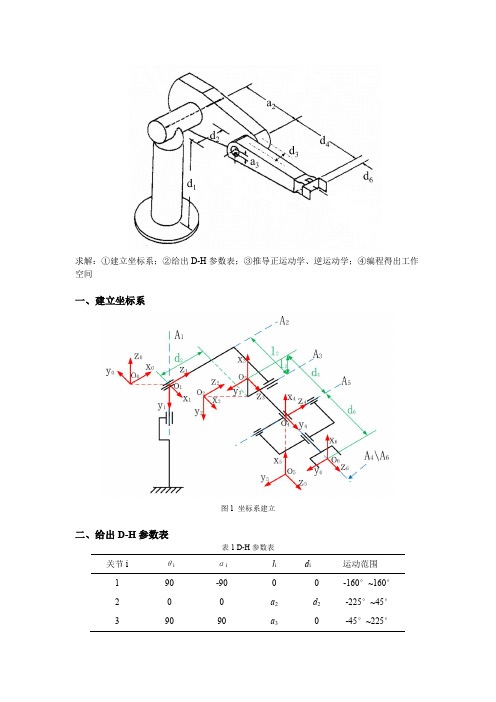
求解:①建立坐标系;②给出D-H参数表;③推导正运动学、逆运动学;④编程得出工作空间一、建立坐标系图1 坐标系建立二、给出D-H参数表表1 D-H参数表关节iθiαi l i d i运动范围190-9000-160°~160°200a2d2-225°~45°39090a30-45°~225°4 0 -90 0 d 4 -110°~170°5 0 90 0 0 -100°~160°6 0d 6-266°~266°三、正运动学推导坐标系O i 与于坐标系O i−1之间的齐次变换矩阵如下:1001i i i i i i i ii i i i i i i i i i i c c s s s l c s c c s c l s T s c d θαθαθθθαθαθθαα--⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦由上式可得:将变换矩阵相乘得到PUMA560机械手变换矩阵:整理得:其中:四、逆运动学推导1.求解θ1设推导得:整理得:12arctan 2(,)arctan 2(,x y p p d θ=-2.求解θ2和θ3整理得:3.求解θ4得到:整理得:14112312323arctan2-,x y x y z s a c a c c c a s c c a s s a θ=+--+()4.求解θ5和θ6可得:整理得:)(555,2arctan c s =θ;),(2arctan 666c s =θ五、逆解编程求解工作空间代码如下:%%逆解求解 a2=431.8; a3=20.32; d2=149.09; d4=433.07; d6=56.25; syms flag; count = 1;for px=-1000:10:1000; for py=-1000:10:1000; for pz=-1000:10:1000;if (px*px + py*py -d2*d2) >= 0theta11 = atan2d(py,px) - atan2d(d2,sqrt(px*px + py*py - d2*d2)); theta12 = atan2d(py,px) - atan2d(d2,-sqrt(px*px + py*py - d2*d2)); if (a3*a3 + d4*d4 - k*k) >=0k = (px^2 + py^2 + pz^2- a2^2 - a3^2 - d2^2 - d4^2)/2/a2; theta31 = atan2d(a3,d4) - atan2d(k, sqrt(a3*a3 + d4*d4 - k*k)); theta32 = atan2d(a3,d4) - atan2d(k, -sqrt(a3*a3 + d4*d4 - k*k)); if -160<theta11&&theta11<160 theta1 = theta11;if -45<theta31&&theta31<225 theta3 = theta31; c1 = cosd(theta1); s1 = sind(theta1); c3 = cosd(theta3); s3 = sind(theta3);up_3 = -(a3 + a2*c3)*pz + (c1*px + s1*py)*(a2*s3 - d4); down_3 = (-d4 + a2*s3)*pz + (c1*px + s1*py)*(a2*c3 + a3); theta23 = atan2d(up_3,down_3);theta2 = theta23 - theta3;flag = 1;endif -45<theta32&&theta32<225theta3 = theta32;c1 = cosd(theta1);s1 = sind(theta1);c3 = cosd(theta3);s3 = sind(theta3);up_3 = -(a3 + a2*c3)*pz + (c1*px + s1*py)*(a2*s3 - d4);down_3 = (-d4 + a2*s3)*pz + (c1*px + s1*py)*(a2*c3 + a3);theta23 = atan2d(up_3,down_3);theta2 = theta23 - theta3;flag = 1;endendif -160<theta12&&theta12<160theta1 = theta12;if -45<theta31&&theta31<225theta3 = theta31;c1 = cosd(theta1);s1 = sind(theta1);c3 = cosd(theta3);s3 = sind(theta3);up_3 = -(a3 + a2*c3)*pz + (c1*px + s1*py)*(a2*s3 - d4);down_3 = (-d4 + a2*s3)*pz + (c1*px + s1*py)*(a2*c3 + a3);theta23 = atan2d(up_3,down_3);theta2 = theta23 - theta3;flag = 1;endif -45<theta32&&theta32<225theta3 = theta32;c1 = cosd(theta1);s1 = sind(theta1);c3 = cosd(theta3);s3 = sind(theta3);up_3 = -(a3 + a2*c3)*pz + (c1*px + s1*py)*(a2*s3 - d4);down_3 = (-d4 + a2*s3)*pz + (c1*px + s1*py)*(a2*c3 + a3);theta23 = atan2d(up_3,down_3);theta2 = theta23 - theta3;flag = 1;endendif flag == 1X(count) = px;Y(count) = py;Z(count) = pz;count = count + 1;endendendendplot3(X,Y,Z,'g.');工作空间求解如下:图2 工作空间图3 工作空间(XOY平面)图4 工作空间(XOZ平面)图5 可达工作空间(YOZ平面)。
机器人学第3章 机器人运动学

(3.46)
如果已知一个表示任意旋转的齐次变换,那么就能够 确定其等价欧拉角。
3.2 机械手运动方程的求解
21
3.2.2 滚、仰、偏变换解
直接从显式方程来求解用滚动、俯仰和偏转表示的变 换方程。 RPY变换各角如下:
atan2(n y , n x ) 180 atan2(n z , cn x sn y ) atan2( sa x ca y , so x co y )
0
T6 0T1 (1 )1T2 (2 )2T3 (3 )3T4 (4 )4T5 (5 )5T6 (6 )
3.1 机器人运动方向的表示
5
3.1.1 运动姿态和方向角
用横滚、俯仰和偏转角表示运动姿态 另一种常用的旋转集合是横滚(roll)、俯仰(pitch) 和偏转(yaw)。
图3.3 用横滚、俯仰和偏转表示机械手运动姿态
3.1 机器人运动方向的表示 6
3.1.1 运动姿态和方向角
对于旋转次序,规定:
1
(3.16)
3.1 机器人运动方向的表示
15
3.1.3 连杆变换矩阵及其乘积
如果机械手与参考坐标系的相对关系是由变换 Z 来 表示的,而且机械手与其端部工具的关系由变换 E 表示,那么此工具端部对参考坐标系的位置和方向 可由变换 X 表示如下:
可求得:
X ZT6 E
T6 Z 1 XE 1
(3.52)
3.2 机械手运动方程的求解
22
3.2.3 球面变换解
把求解滚、仰和偏变换方程的技术用于球面坐标表示 的运动方程。 球面变换的解为:
atan2( p y , p x ), 180 atan2(cp x sp y , p z )
PUMA-560机械手虚拟装配过程中的视觉分析和变换计算的研究

O 引 言
“ 拟 装 配 ” Vr a A sm l) 产 品 数 字 化 定 义 虚 ( iu l s by 是 t e
n l i f f u ifr n a e ,f u ype o r i t r n f r to e e pr po e nd t e f u o r s ndn ayss o o rd fe e tc s s o r t s c o dnae ta s o ma in w r s d a h o r c re po ig o
c l u a i n e e d rv d. a c l to s w r e i e The c re t r b t posto n s u e w e e d rv d f r i e l e t a s mb y. o r c o o ii n a d po t r r e i e nt l g la s mbl v s a n l i ; r n f r c lu a i n; y wo d i a s e t y; i u la ayss t a s o m a c l to PUM A ・ 6 5 0
Ab ta t sr c :An l ssa d e a ain o r d c s e l ef r n ewee u u l o et r u h p y ia mo es ay i n v l t fp o u ta s mb y p r ma c r s al d n h o g h s l d l u o o y c
T AN a — n Xio do g, L U n,ZHAO n I Xi Ya
( ainJa tn nv ri ,S h o o c a ia n iern ,L ann ain 16 2 D l ioo gU ies y c o l fMeh nc l gn eig io ig D l 0 8,C ia a t E a 1 hn )
PUMA560机器人动态性能的工作方式

PUMA560机器人动态性能的工作方式
戴恩光;纪炳炎
【期刊名称】《北京科技大学学报》
【年(卷),期】1994(016)003
【摘要】提出了PUMA560及类似型号机器人不同工作方式对应不同的动态性能优劣程度的问题,并给出了寻找具有良好动态性能工作方式的方法及相应的仿真系统。
【总页数】4页(P294-297)
【作者】戴恩光;纪炳炎
【作者单位】不详;不详
【正文语种】中文
【中图分类】TP242
【相关文献】
1.基于MATLAB的PUMA560机器人运动学仿真 [J], 董慧颖;梁爽
2.基于MATLAB与ADAMS的PUMA560机器人逆运动仿真 [J], 李辉;李开世;黄文权
3.基于Matlab对于PUMA560机器人的运动空间分析研究 [J], 沙漠;邓子龙
4.基于MATLAB的PUMA560机器人运动仿真研究 [J], 臧庆凯;李春贵;闫向磊
5.基于MATLAB的PUMA560机器人正逆解研究 [J], 陈晗;李林升
因版权原因,仅展示原文概要,查看原文内容请购买。
PUMA560型机器人逆运动学问题的解析解

PUMA560型机器人逆运动学问题的解析解
尤波;张永军;毕克新
【期刊名称】《哈尔滨科学技术大学学报》
【年(卷),期】1994(000)004
【摘要】利用PUMA560型机器人的齐次坐标变换矩阵,推导了其逆运动学问题的解析解.与常用的其它方法相比,该方法简单、明了、计算速度快,对PUMA560型机器人的运动规划具有实用价值.
【总页数】5页(P6-10)
【作者】尤波;张永军;毕克新
【作者单位】哈尔滨科学技术大学
【正文语种】中文
【中图分类】TP242
【相关文献】
1.基于MATLAB与ADAMS的PUMA560机器人逆运动仿真 [J], 李辉;李开世;黄文权
2.应用基于运动螺旋的机器人正解映射求解 FANUC机器人的逆运动学问题 [J], 荆学东;浦耿强;王成焘
3.RBF网络在PUMA560机器人运动学逆解中的应用 [J], 李跃息;张文志;林平;李伟娟
4.应用基于运动螺旋的机器人正解映射求解搬运机器人的逆运动学问题 [J], 荆学东;鲁省龙;黄绍民;张宝文
5.基于MATLAB的PUMA560机器人正逆解研究 [J], 陈晗;李林升
因版权原因,仅展示原文概要,查看原文内容请购买。
基于RTW的PUMA560关节控制系统设计

基于RTW的PUMA560关节控制系统设计0 引言PUMA560 机械臂是由原美国Unimation 公司生产的一种工业机器人。
它采用LSI-Ⅱ处理器和VAL-Ⅱ编程语言,属于典型的“专用计算机、专用机器人语言、专用微处理器”的封闭式结构,是一种示教机器人。
PUMA560 有六个自由度,包括6 个可以旋转的关节,分别模仿人的腰部、肩部、肘部和手腕的运动,可以以规定的姿态到达工作范围内的任何一个点。
PUMA560 机械臂包括:机械臂臂体、控制器和示教器三部分[1]。
PUMA560 关节控制系统作为机械臂视觉伺服总系统的下位机,其作用是:MATLAB/RTW 内所设计的关节控制器根据视觉子系统给出的目标位置信息(机械臂各个关节的期望转动角度)计算出各关节控制信号U,U 通过电机驱动电路的伺服放大控制机械臂运动到目标位置。
本文提出的关节控制系统是基于MATLAB/RTW 的位置、速率双闭环系统,该系统具有良好的通用性、可拓展性,为学生进行控制算法研究提供了一个很好的实验平台。
1 MATLAB/RTW 简介本文选择利用计算机内Matlab 环境下的Real-Time Windows Target(RTW)工具箱和研华PCI-1711 数据采集卡来构建PUMA560 机械臂的关节伺服控制系统。
Matlab 是Mathworks公司提供的在控制领域应用最广泛的仿真软件,Simulink 是Matlab 中的可视化图形软件包,RTW 工具箱是Simulink 中的实时目标仿真视窗。
RTW 具有如下几种功能:a) 支持多种目标环境;b) 自动从Simulink 图形模型中生成Ada 语言代码或C 语言代码;c) 可用外部模式,实现在Simulink 图形环境下的半实物仿真并在线监测仿真结果以及修改仿真参数;针对Matlab/Simulink 环境下的RTW 工具箱具备半实物仿真及实时控制的功能,我们构建了一个由计算机、驱动电路以及机械臂组成的控制平台,在Matlab/Simulink 中设计控制器,通过RTW 输入输出窗口以及PCI-1711 数据采集卡实现控制信号的输出以及反馈信号的输入。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3O卷第3期 2006年5月 燕山大学学报 Journal ofYanshan University VO1.3O No.3
May 2006
文章编号:1007—791X(2006)03—0194—04
PUMA560机构的运动学性能分析 刘爽 ,许亚靖 , (1燕山大学电气工程学院,河北秦皇岛066004; 耿清甲 ,黄真
2.燕山大学机械工程学院,河北秦皇岛066004)
摘 要:对串联PUMA560机构的运动学性能进行了分析,分别绘出了速度、加速度的性能图谱,从而为该机 构的尺寸设计提供理论依据。
关键词:影响系数矩阵;PUMA560机构;性能指标 中图分类号:TH113_2 文献标识码:A
0引言 如何提高机器人的运动性能一直是国内外学 者关注的主要问题之一,也是机器人领域的研究热 点。关于机器人操作器的运动性能,各专家提出了 不同的性能指标:1982年Salisbury提出了Jacobian 矩阵条件数的概念;1983年和1985年Yashikawa 引入了“可操作性”概念;1985年Yang定义了机 器人操作器条件数这一概念;1 99 1年Gosselin…在 对机器人的运动进行最优化设计时,定义了全局性 能指标。本文利用郭希娟提出的性能指标呤 对 PI A 560串联机构的运动学及动力学性能进行研 究。
如图1所示PI『MA560机构自由度为6。本文 根据黄真教授提出的影响系数法 ,建立了该机构 的一阶、二阶影响系数矩阵,并根据一阶、二阶影 响系数矩阵及其全域性能指标定义给出该机构的 全域性能指标。由于机构参数的设置是否合理直接 决定机构的性能好坏,本文通过改变机构部分构件 的尺寸,研究其在不同尺寸下的运动全域指标,探 讨机构的性能差异,从而在一组尺寸各不相同的机 构中,选择运动性能较为优良的机构。
1机构描述
系,02,03, ,, 是结构参数, (卢1,2,…,6)是 转角, (卢2,3,…,6)是扭角。该机构输入速度 矢量是六维的。
[∞,1,] 其中09为角速度,1,为线速度。
图1 PUMA560机构 Fig.1 The mechanism ofPUMA560
因为该机构为6自由度机构,只要6个杆件 间的相对转角0。, ,03, ,05,嘶定,该机构 的位形就全部确定了。本文为了简化分析过程,固 定 , , , , ,只令0。以1 rad/s变化,即 如图1所示,PUMA560机构是一个6自由度 的串联开链式机构。D一 y0Z0坐标系是基础坐标 [1 0 0 0 0 0】 (2)
收稿日期:2005—03—31 基金项目:河北省自然科学基金资助项目(No.1042002) 作者简介:刘爽(1978-),男,黑龙江齐齐哈尔人。助教,硕士。主要研究方向为机器人学。
维普资讯 http://www.cqvip.com 第3期 刘爽等PUMA560机构的运动学性能分析 195 在具体分析时,本文采用Denavit-Hartenberg 提出的矩阵方法求解该机构,根据机构的初始参数 o:-431.88 illnl,03=20.32 mm,d,=149.09 miil, d4=433.07 mm,0l=一l15。,0,=55。,03=一68。, = 75。, =一100。,o:40。,o:-95。,0,=105。,0,---90。, 0:--45。,利用影响系数法可求出末端杆运动点的空 间坐标 ,即:
;Py; ]=
2机构的运动学特性 2.1性能指标 本文研究采用的是基于影响系数法的性能指 标b 。当机构的初始参数给定时,按照影响系数法 可求得该机构的一阶影响系数矩阵G和二阶影响 系数矩阵日。这里所得的一阶影响系数矩阵(Jaco- bian矩阵)6伪6x6阵,二阶影响系数矩阵(Hessian 矩阵)日为6 ̄6 ̄6阵。 性能指标定义为影响系数矩阵条件数 , :  ̄v=lla.IIIlG: Ko =lla,IIIl I I蚓lI I (3) (4) (5) 其中, 是一阶影响系数矩阵Jacobian矩阵的前3 行,lla.II为 的Frobenius范数,G:是 的广义逆 矩阵; 是一阶影响系数矩阵Jacobian矩阵的后3 行,日是二阶影响系数矩阵Hessian矩阵,其他的 类似。 2.2全域性能指标分析 机器人的Jacobian矩阵G;I;ⅡHessian矩阵日都 不是常数矩阵,它依赖于机器人的位形,因此如上 定义的条件数 ,.,∈{ , ,日),随着机器人的 位形不同而变化,也就是说在机器人的工作空间内 的不同点的性能指标值是不同的。这样在应用中, 就不便用一个量来度量某一机器人控制精度的好 坏,过去Gosselin 】在工作空间的基础上提出了全 域性能度量指标(Global Conditioning Index),用来 总体评价机器人的性能,即 s 其中,,油机器人的全域性能度量指标;∞为机器 人的可达工作空间。 在此基础上定义了加速度的全域性能度量指 标叩白,叩 。计算这几个指标的时候只要把公式 (6)中的 换成叩白,叩 , 即可。由于l_<Kj<oo,故 1 ,7J>o,因此椭值越大机器人的控制精度越高。 2.3 速度全域性能指标分析 对于本机构利用公式(3)、(4)可以求出尺寸 不同的机构的全域性能指标。现在,改变机构的几 个结构参数值,组成一组机构d,=100-200 miil, a3=5 ̄55 mm( 以10 mill为步长, 以5 mm为 步长变化),其他尺寸不变。这组共有100个机构, 每个机构均取1 00个位形采样点( 在可达空间内 平均取100个位置)。根据式(6)可以相应地计算 出100个,7值。因其角度的等高线为一个平面,在 此未画出。画出其线速度的等高线,如图2所示。
ddmm 图2线速度性能图谱
Fig.2 Atlas ofthe linear velocity performance
一 m 维普资讯 http://www.cqvip.com 燕山大学学报 根据 的值越大,机器人的控制精度越高的原 则可以看出,在图2中de=200mm,a3=55nlnl时机 构 值较大,机器人的控制精度较好。 2.4加速度全域性能指标分析 根据式(5)可以计算该机构的加速度性能,由 于该机构的角速度为一定值,所以其角加速度亦为 平面,在此不再画出。根据式(11)计算出该机 构沿 , 向,即二阶影响系数矩阵的第4层和第 5层矩阵的线加速度图谱,如图3、图4所示。 /mm 图3 方向线加速度图谱 Fig.3 Alms ofthe linear acceleration in direction /mm 图4 Y方向线加速度图谱 Fig.4 Alms ofthe linear acceleration in Y direction 观察图3、图4可以看出在de-100rflrfl,a3=55 rflrfl附近区域内的机构x方向线加速度的指标值较 大,在de--100 rflrfl,a 5 rflrfl附近区域内的机构), 方向线加速度的指标值较大,所以不妨说,在这一 组机构中,de=100I砌,a3=55nlnl附近的时候,机 构 方向线加速度的性能较好,de-100 rflrfl,a 5 rflrfl附近时,机构),方向线加速度的性能较好。
由于该机构在de-100 rflrfl,a3=55 nlnl时 方向 线加速度性能较好,在de=100 nlnl,a 5 nlnl附近 的时 方向线加速度的性能较好,而线速度在 de=100nlnl,a3=55 nlnl时性能指标较大。所以可以 说,对于PIn A560机构运动学性能按照不同的要 求在不同的尺寸各有优缺,可以根据侧重点不同选 取不同的尺寸。
3结论 整体来说,通过上述的讨论可以初步得出对于 该机构来说,de,a3同时增加有助于线速度性能的 提高。在 减少,同时a,增大时 方向线加速度性能 较好;而在de,a,同时减少时 向线加速度性能较 好。
综上所述,通过观察图谱随机构尺寸变化的趋 势,为设计性能优异的机构提供理论依据。本文通 过对串联PI n A560机构研究分析,利用速度和加 速度全域性能指标,对该机构进行了全域性能指标 分析,并依据各个性能指标差异,在众多同类机构 中挑选出性能较优的机构。
参考文献 【l】Steward D A.Platfi'om with 6-DOE Proc【J】_Institution ofMech— anical Engineering,1965,18(1):371—386.
【2】郭希娟.并联机器人机构动力学基础理论研究【D】.秦皇岛: 燕山大学,2002.
【3】黄真,孔令富,方跃法.并联机器人机构学理论及控制【M】.北 京:机械工业出版社,1997.
【4】熊有伦.机器人学【M】.北京:机械工业出版社,1993:65—70. 【5】郭希娟,黄真.并联机器人加速度的性能指标分析[M】.中国 机械工程,2002,12(24):2087—2091.
【6】Gosselin C,Angeles J.A Global Profoi'mance Index for the Kin- ematie Optizafion ofRobotic Manipulators【JL Transactions ofthe ASME。1991。113:220.226.
维普资讯 http://www.cqvip.com
