2011届高考数学 双曲线复习好题精选
新高考数学一轮复习考点知识专题讲解与练习 42 双曲线

新高考数学一轮复习考点知识专题讲解与练习考点知识总结42 双曲线高考 概览高考在本考点的常考题型为选择题、填空题,分值为5分,中、高等难度考纲 研读1.了解双曲线的定义、几何图形和标准方程,知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线) 2.了解双曲线的简单应用 3.理解数形结合的思想一、基础小题1.已知双曲线x 2m 2+16-y 24m -3=1的实轴长为10,则该双曲线的渐近线的斜率为( )A .±54B .±45 C.±53 D .±35 答案 D解析 由m 2+16=52,解得m =3(m =-3舍去).所以a =5,b =3,从而±b a =±35.故选D.2.已知平面内两定点A (-5,0),B (5,0),动点M 满足|MA |-|MB |=6,则点M 的轨迹方程是( )A.x 216-y 29=1 B .x 216-y 29=1(x ≥4) C.x 29-y 216=1 D .x 29-y 216=1(x ≥3) 答案 D解析 由双曲线的定义知,点M 的轨迹是双曲线的右支,故排除A ,C ;又c =5,a =3,∴b 2=c 2-a 2=16.∵焦点在x 轴上,∴轨迹方程为x 29-y 216=1(x ≥3).故选D.3.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为( )A.x 220-y 25=1 B .x 25-y 220=1 C.x 280-y 220=1 D .x 220-y 280=1 答案 A解析 ∵双曲线x 2a 2-y 2b 2=1的焦距为10, ∴c =5=a 2+b 2.①又双曲线的渐近线方程为y =±b a x ,且P (2,1)在渐近线上,∴2ba =1,即a =2b .②由①②,解得a =25,b =5, 则C 的方程为x 220-y 25=1.故选A.4.设双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点为F ,以OF 为直径的圆交双曲线的一条渐近线于另一点A (O 为坐标原点),且|OA |=2|AF |,则双曲线C 的离心率e 为( )A.5 B .52 C.2 D .2 答案 B解析 由题意可得tan ∠AOF =|AF ||OA |=|AF |2|AF |=12,渐近线方程为y =±b a x ,∴b a =12,e 2=c 2a 2=b 2+a 2a 2=a 24+a 2a 2=54,故e =52.故选B.5.已知F 1,F 2为双曲线C :x 2-y 2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1|·|PF 2|等于( )A .2B .4 C.6 D .8 答案 B解析 由双曲线的方程,得a =1,c =2,由双曲线的定义,得||PF 1|-|PF 2||=2.在△PF 1F 2中,由余弦定理,得|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·cos60°=|PF 1|2+|PF 2|2-|PF 1|·|PF 2|=(|PF 1|-|PF 2|)2+|PF 1|·|PF 2|=22+|PF 1|·|PF 2|=(22)2,解得|PF 1|·|PF 2|=4.故选B.6.(多选)已知曲线C 的方程为x 2k 2-2-y 26-k =1,则下列结论正确的是( )A .当k =8时,曲线C 为椭圆,其焦距为4+15B .当k =2时,曲线C 为双曲线,其离心率为3C .对任意实数k ,曲线C 都不可能为焦点在y 轴上的双曲线D .当k =3时,曲线C 为双曲线,其渐近线与圆(x -4)2+y 2=9相切答案 BC解析 对于A ,当k =8时,曲线C 的方程为x 262+y 22=1,该曲线为椭圆,焦距2c =262-2=415,A 错误;对于B ,当k =2时,曲线C 的方程为x 22-y 24=1,该曲线为双曲线,则a =2,c =6,其离心率e =ca =3,B 正确;对于C ,若曲线C 为焦点在y 轴上的双曲线,则⎩⎨⎧6-k <0,k 2-2<0,不等式组无解,故不存在实数k 使得曲线C 为焦点在y 轴上的双曲线,C 正确;对于D ,当k =3时,曲线C 的方程为x 27-y 23=1,该曲线为双曲线,其渐近线方程为y =±217x ,则圆(x -4)2+y 2=9的圆心到渐近线的距离d =|±421|21+49=4310=2305≠3,所以双曲线C 的渐近线与圆(x -4)2+y 2=9不相切,D 错误.故选BC.7.(多选)已知动点P 在双曲线C :x 2-y 23=1上,双曲线C 的左、右焦点分别为F 1,F 2,下列结论正确的是( )A .C 的离心率为2B .C 的渐近线方程为y =±33xC .动点P 到两条渐近线的距离之积为定值D .当动点P 在双曲线C 的左支上时,|PF 1||PF 2|2的最大值为14答案 AC解析 对于双曲线C :x 2-y 23=1,a =1,b =3,c =2,所以双曲线C 的离心率为e =c a =2,渐近线方程为y =±3x ,A 正确,B 错误;设点P 的坐标为(x 0,y 0),则x 20-y 203=1,双曲线C 的两条渐近线方程分别为x -33y =0和x +33y =0,则点P 到两条渐近线的距离之积为⎪⎪⎪⎪⎪⎪x 0-33y 01+⎝ ⎛⎭⎪⎫-332·⎪⎪⎪⎪⎪⎪x 0+33y 01+⎝ ⎛⎭⎪⎫332=⎪⎪⎪⎪⎪⎪x 20-y 20343=34,C 正确;当动点P 在双曲线C 的左支上时,|PF 1|≥c -a =1,|PF 2|=2a +|PF 1|=|PF 1|+2,|PF 1||PF 2|2=|PF 1|(|PF 1|+2)2=|PF 1||PF 1|2+4+4|PF 1|=1|PF 1|+4|PF 1|+4≤12|PF 1|·4|PF 1|+4=18,当且仅当|PF 1|=2时,等号成立,所以|PF 1||PF 2|2的最大值为18,D 错误.故选AC.8.设F 1,F 2分别为双曲线x 216-y 220=1的左、右焦点,点P 在双曲线上,若点P 到焦点F 1的距离为9,则点P 到焦点F 2的距离为________.答案 17解析 解法一:∵实轴长2a =8,半焦距c =6,∴||PF 1|-|PF 2||=8.∵|PF 1|=9,∴|PF 2|=1或|PF 2|=17.又|PF 2|的最小值为c -a =6-4=2,∴|PF 2|=17.解法二:若P 在右支上,则|PF 1|≥a +c =4+6=10>9,∴P 在左支上.∴|PF 2|-|PF 1|=2a =8,∴|PF 2|=9+8=17.9.直线y =k (x +6)(k >0)与双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)及其渐近线从左至右依次交于点A ,B ,C ,D ,双曲线的左、右焦点分别为F 1,F 2,且焦距为4,则△F 2CD 与△F 1AB 的面积之比为________.答案 2解析 由⎩⎪⎨⎪⎧x 2a 2-y2b2=1,y =k (x +6),得⎝ ⎛⎭⎪⎫1a 2-k 2b 2x 2-12k 2xb 2-1-36k 2b 2=0,由⎩⎪⎨⎪⎧x 2a 2-y 2b 2=0,y =k (x +6),得⎝ ⎛⎭⎪⎫1a 2-k 2b 2x 2-12k 2x b 2-36k2b 2=0,由以上两式可知,x A +x D =x B +x C ,故AD ,BC 具有相同的中点,故|AB |=|CD |,又直线y =k (x +6)过定点G (-6,0),如图,过F 1,F 2作直线y =k (x +6)的垂线,垂足分别为N ,M ,由焦距为4可得F 1(-2,0),F 2(2,0),则|GF 2|=2|GF 1|.所以S △F 2CD S △F 1AB=12|CD |·|MF 2|12|AB |·|NF 1|=|GF 2||GF 1|=2.二、高考小题10.(2022·北京高考)双曲线C :x 2a 2-y 2b 2=1过点(2,3),且离心率为2,则该双曲线的标准方程为( )A .x 2-y 23=1 B .x 23-y 2=1C .x 2-3y 23=1D .3x23-y 2=1答案 A解析 ∵e =c a =2,∴c =2a ,b =c 2-a 2=3a ,则双曲线的方程为x 2a 2-y 23a 2=1,将点(2,3)代入双曲线的方程可得2a 2-33a 2=1a 2=1,解得a =1,故b =3,因此,双曲线的方程为x 2-y 23=1.故选A.11.(2022·全国甲卷)已知F 1,F 2是双曲线C 的两个焦点,P 为C 上一点,且∠F 1PF 2=60°,|PF 1|=3|PF 2|,则C 的离心率为( )A.72 B .132 C.7 D .13 答案 A解析 由|PF 1|=3|PF 2|,|PF 1|-|PF 2|=2a ,得|PF 2|=a ,|PF 1|=3a ,在△F 1PF 2中,由余弦定理,得|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|cos ∠F 1PF 2,即(2c )2=(3a )2+a 2-2×3a ×a ×cos60°,得4c 2=7a 2,所以C 的离心率e =c a =72.故选A.12.(2022·天津高考)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点与抛物线y 2=2px (p >0)的焦点重合,抛物线的准线交双曲线于A ,B 两点,交双曲线的渐近线于C ,D 两点,若|CD |=2|AB |.则双曲线的离心率为( )A.2 B . 3 C.2 D .3 答案 A解析 设双曲线x 2a 2-y 2b 2=1(a >0,b >0)与抛物线y 2=2px (p >0)的公共焦点为(c,0),则抛物线y 2=2px (p >0)的准线为x =-c ,令x =-c ,则c 2a 2-y 2b 2=1,解得y =±b 2a ,所以|AB |=2b 2a ,又因为双曲线的渐近线方程为y =±b a x ,所以|CD |=2bc a ,所以2bc a =22b 2a ,即c =2b ,所以a 2=c 2-b 2=12c 2,所以双曲线的离心率e =ca = 2.故选A.13.(2022·浙江高考)已知a ,b ∈R ,ab >0,函数f (x )=ax 2+b (x ∈R ).若f (s -t ),f (s ),f (s +t )成等比数列,则平面上点(s ,t )的轨迹是()A .直线和圆B .直线和椭圆C .直线和双曲线D .直线和抛物线 答案 C解析 因为函数f (x )=ax 2+b ,所以f (s -t )=a (s -t )2+b ,f (s )=as 2+b ,f (s +t )=a (s +t )2+b .因为f (s -t ),f (s ),f (s +t )成等比数列,所以[f (s )]2=f (s -t )f (s +t ),即(as 2+b )2=[a (s -t )2+b ]·[a (s +t )2+b ],化简得-2a 2s 2t 2+a 2t 4+2abt 2=0,得t =0或2as 2-at 2=2b ,即t =0或as 2b -at 22b =1,易知点(s ,t )的轨迹是直线和双曲线.故选C.14.(2022·天津高考)设双曲线C 的方程为x 2a 2-y 2b 2=1(a >0,b >0),过抛物线y 2=4x 的焦点和点(0,b )的直线为l .若C 的一条渐近线与l 平行,另一条渐近线与l 垂直,则双曲线C 的方程为( )A.x 24-y 24=1 B .x 2-y 24=1C.x 24-y 2=1 D .x 2-y 2=1 答案 D解析 由题可知,抛物线的焦点为(1,0),所以直线l 的斜率为-b ,又双曲线的渐近线的方程为y =±b a x ,所以-b =-b a ,-b ×ba =-1.因为a >0,b >0,所以a =1,b =1.故选D.15.(2022·全国Ⅲ卷)设双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,离心率为 5.P 是C 上一点,且F 1P ⊥F 2P .若△PF 1F 2的面积为4,则a =( )A .1B .2 C.4 D .8 答案 A解析 ∵ca =5,∴c =5a ,根据双曲线的定义可得||F 1P |-|F 2P ||=2a ,∵S △PF 1F 2=12|F 1P |·|F 2P |=4,∴|F 1P |·|F 2P |=8.∵F 1P ⊥F 2P ,∴|F 1P |2+|F 2P |2=(2c )2,∴(|F 1P |-|F 2P |)2+2|F 1P |·|F 2P |=4c 2,即(2a )2+2×8=4(5a )2,解得a =1.故选A.16.(2022·全国Ⅱ卷)设O 为坐标原点,直线x =a 与双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线分别交于D ,E 两点,若△ODE 的面积为8,则C 的焦距的最小值为( )A .4B .8 C.16 D .32 答案 B解析 ∵直线x =a 与双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线分别交于D ,E 两点,双曲线的渐近线方程是y =±ba x ,不妨设D 在第一象限,E 在第四象限,联立⎩⎪⎨⎪⎧x =a ,y =b ax ,解得⎩⎨⎧x =a ,y =b .故D (a ,b ).联立⎩⎪⎨⎪⎧x =a ,y =-ba x ,解得⎩⎨⎧x =a ,y =-b .故E (a ,-b ).∴|ED |=2b .∴△ODE 的面积为S △ODE =12a ×2b =ab =8.∵双曲线的焦距为2c =2a 2+b 2≥22ab =216=8,当且仅当a =b =22时取等号,∴C 的焦距的最小值为8.故选B.17.(2022·全国Ⅱ卷)设F 为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P ,Q 两点.若|PQ |=|OF |,则C 的离心率为( )A.2 B . 3 C.2 D . 5 答案 A解析 设双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点F 的坐标为(c,0).由圆的对称性及条件|PQ |=|OF |可知,PQ 是以OF 为直径的圆的直径,且PQ ⊥OF .设垂足为M ,连接OP ,如图,则|OP |=a ,|OM |=|MP |=c 2.由|OM |2+|MP |2=|OP |2得⎝ ⎛⎭⎪⎫c 22+⎝ ⎛⎭⎪⎫c 22=a 2,故c a =2,即e = 2.故选A.18.(2022·全国Ⅲ卷)双曲线C :x 24-y 22=1的右焦点为F ,点P 在C 的一条渐近线上,O 为坐标原点,若|PO |=|PF |,则△PFO 的面积为( )A.324 B .322 C.22 D .3 2 答案 A解析 双曲线x 24-y 22=1的右焦点坐标为(6,0),一条渐近线的方程为y =22x ,不妨设点P 在第一象限,由于|PO |=|PF |,则点P 的横坐标为62,纵坐标为22×62=32,即△PFO 的底边长为6,高为32,所以它的面积为12×6×32=324.故选A.19.(2022·全国Ⅰ卷)已知双曲线C :x 23-y 2=1,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为M ,N .若△OMN 为直角三角形,则|MN |=( )A.32 B .3 C.23 D .4 答案 B解析 因为双曲线的一条渐近线为y =33x ,所以tan ∠FON =33,所以∠FON =30°,∠MON =60°,又因为△OMN 是直角三角形,不妨取∠NMO =90°,则∠ONF =30°,于是|FN |=|OF |=2,|FM |=12|OF |=1,所以|MN |=3.故选B.20.(2022·全国Ⅲ卷)设F 1,F 2是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,O 是坐标原点.过F 2作C 的一条渐近线的垂线,垂足为P .若|PF 1|=6|OP |,则C 的离心率为( )A.5 B .2 C.3 D . 2 答案 C解析 由题可知|PF 2|=b ,|OF 2|=c ,∴|PO |=a .在Rt △POF 2中,cos ∠PF 2O =|PF 2||OF 2|=bc ,∵在△PF 1F 2中,cos ∠PF 2O =|PF 2|2+|F 1F 2|2-|PF 1|22|PF 2||F 1F 2|=b c ,∴b 2+4c 2-(6a )22b ·2c =b c⇒c 2=3a 2,∴e = 3.故选C.21.(2022·天津高考)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线的同一条渐近线的距离分别为d 1和d 2,且d 1+d 2=6,则双曲线的方程为( )A.x 24-y 212=1 B .x 212-y 24=1C.x 23-y 29=1 D .x 29-y 23=1 答案 C解析 解法一:∵双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,∴e 2=1+b 2a 2=4,∴b 2a 2=3,即b 2=3a 2,∴c 2=a 2+b 2=4a 2,由题意可设A (2a,3a ),B (2a ,-3a ),∵b 2a 2=3,∴渐近线方程为y =±3x ,则点A 与点B 到直线3x -y =0的距离分别为d 1=|23a -3a |2=23-32a ,d 2=|23a +3a |2=23+32a ,又d 1+d 2=6,∴23-32a +23+32a =6,解得a =3,∴b 2=9.∴双曲线的方程为x 23-y 29=1.故选C.解法二:如图,设双曲线的右焦点为F (c,0),一条渐近线为y =ba x ,则F 到该渐近线的距离d =|bc |a 2+b2=b ,又d 1+d 2=6,由梯形中位线可知2d =d 1+d 2,即2b =6,b =3,∵双曲线离心率为2,∴e =c 2a 2=a 2+b 2a 2=2,∴a 2=3.∴双曲线的方程为x 23-y 29=1.故选C.22.(2022·新高考Ⅱ卷)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,则该双曲线的渐近线方程为________.答案 y =±3x解析 因为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,所以e =c 2a 2=a 2+b 2a 2=2,所以b 2a 2=3,所以该双曲线的渐近线方程为y =±ba x =±3x .23.(2022·全国乙卷)已知双曲线C :x 2m -y 2=1(m >0)的一条渐近线为3x +my =0,则C 的焦距为________.答案 4解析 双曲线x 2m -y 2=1(m >0)的渐近线为y =±1m x ,即x ±my =0,又双曲线的一条渐近线为3x +my =0,即x +m3y =0,对比两式可得m =3.设双曲线的实半轴长为a ,虚半轴长为b ,半焦距为c ,则有a 2=m =3,b 2=1,所以双曲线的焦距2c =2a 2+b 2=4.24.(2022·北京高考)已知双曲线C :x 26-y 23=1,则C 的右焦点的坐标为________;C 的焦点到其渐近线的距离是________.答案 (3,0)3解析 在双曲线C 中,a =6,b =3,则c =a 2+b 2=3,则双曲线C 的右焦点的坐标为(3,0).双曲线C 的渐近线方程为y =±22x ,即x ±2y =0,所以双曲线C 的焦点到其渐近线的距离为31+2= 3. 25.(2022·全国Ⅰ卷)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1的直线与C 的两条渐近线分别交于A ,B 两点.若F 1A →=AB →,F 1B →·F 2B →=0,则C 的离心率为________.答案 2解析 解法一:由F 1A →=AB →,得A 为F 1B 的中点.又O 为F 1F 2的中点, ∴OA ∥BF 2. 又F 1B →·F 2B →=0, ∴∠F 1BF 2=90°. ∴|OF 2|=|OB |, ∴∠OBF 2=∠OF 2B .又∠F 1OA =∠BOF 2,∠F 1OA =∠OF 2B , ∴∠BOF 2=∠OF 2B =∠OBF 2, ∴△OBF 2为等边三角形. 如图1所示,不妨设B ⎝ ⎛⎭⎪⎫c 2,-32c .∵点B 在直线y =-b a x 上,∴ba =3,∴离心率e =ca = 1+⎝ ⎛⎭⎪⎫b a 2=2. 解法二:∵F 1B →·F 2B →=0,∴∠F 1BF 2=90°.在Rt △F 1BF 2中,O 为F 1F 2的中点,∴|OF 2|=|OB |=c .如图2,作BH ⊥x 轴于H ,由l 1为双曲线的渐近线,可得|BH ||OH |=ba ,且|BH |2+|OH |2=|OB |2=c 2,∴|BH |=b ,|OH |=a ,∴B (a ,-b ),F 2(c,0).又F 1A →=AB →,∴A 为F 1B 的中点.∴OA ∥F 2B ,∴b a =b c -a,∴c =2a ,∴离心率e =c a =2.三、模拟小题26.(2022·广东广州荔湾区高三上调研考试)已知F 1,F 2分别是双曲线C :x 23-y 2=1的左、右焦点,点P 是其一条渐近线上一点,且以线段F 1F 2为直径的圆经过点P ,则点P 的横坐标为( )A .±1B .±2 C.±3 D .±2 答案 C解析 由题设,渐近线为y =±33x ,不妨令P ⎝ ⎛⎭⎪⎫x 0,33x 0,而F 1(-2,0),F 2(2,0),∴F 1P →=⎝ ⎛⎭⎪⎫x 0+2,33x 0,F 2P →=⎝⎛⎭⎪⎫x 0-2,33x 0,又F 1P →·F 2P →=x 20-4+x 203=0,∴x 0=±3.故选C.27.(2022·湖北恩施州高三上第一次教学质量监测)双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左顶点为A ,右焦点为F ,过点A 的直线交双曲线C 于另一点B ,当BF ⊥AF 时满足|AF |>2|BF |,则双曲线离心率e 的取值范围是( )A .1<e <2B .1<e <32 C.32<e <2 D .1<e <3+32 答案 B解析 设双曲线半焦距为c ,因BF ⊥AF ,则由⎩⎪⎨⎪⎧x =c ,x 2a 2-y 2b 2=1,得|BF |=|y |=b 2a ,而|AF |=a +c ,于是得a +c >2·b 2a ,即a +c >2·c 2-a 2a ,整理得a >23c ,从而有e =c a <32,又e >1,所以双曲线离心率e 的取值范围是1<e <32.故选B.28.(2022·湖北黄石高三上调研)P 为双曲线x 2-y 2=1左支上任意一点,EF 为圆C :(x -2)2+y 2=4的任意一条直径,则PE →·PF→的最小值为() A .3 B .4 C.5 D .9 答案 C解析 如图,圆C 的圆心C 为(2,0),半径r =2,PE →·PF →=(PC →+CE →)·(PC →+CF →)=(PC →+CE →)·(PC →-CE →)=|PC →|2-|CE →|2=|PC →|2-4,则当点P 位于双曲线左支的顶点时,|PC →|2-4最小,即PE →·PF →最小.此时PE →·PF→的最小值为(1+2)2-4=5.故选C.29.(2022·重庆实验外国语学校高三上入学考试)如图,O 是坐标原点,P 是双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)右支上的一点,F 是E 的右焦点,延长PO ,PF 分别交E 于Q ,R 两点,已知QF ⊥FR ,且|QF |=2|FR |,则E 的离心率为( )A.174 B .173 C.214 D .213 答案 B解析 如图,令双曲线E 的左焦点为F ′,连接PF ′,QF ′,RF ′,由对称性可知,点O 是线段PQ 的中点,则四边形PFQF ′是平行四边形,而QF ⊥FR ,于是有▱PFQF ′是矩形,设|FR |=m ,则|PF ′|=|FQ |=2m ,|PF |=2m -2a ,|RF ′|=m +2a ,|PR |=3m -2a ,在Rt △F ′PR 中,(2m )2+(3m -2a )2=(m +2a )2,解得m =4a 3或m =0(舍去),从而有|PF ′|=8a 3,|PF |=2a 3,Rt △F ′PF 中,⎝ ⎛⎭⎪⎫8a 32+⎝ ⎛⎭⎪⎫2a 32=4c 2,整理得c 2a 2=179,e =c a =173,所以双曲线E 的离心率为173.故选B.30.(2022·河北沧州第一中学等十五校高三上摸底考试)已知F 1,F 2是双曲线C :x 23-y 2=1的两个焦点,点M 在直线x -y +3=0上,则|MF 1|+|MF 2|的最小值为( )A .213B .6 C.26 D .5 答案 C解析 由双曲线C :x 23-y 2=1可得a 2=3,b 2=1,所以c 2=a 2+b 2=4,可得c =2,所以F 1(-2,0),F 2(2,0),设点F 2(2,0)关于x -y +3=0对称的点为P (m ,n ),由⎩⎪⎨⎪⎧m +22-n 2+3=0,n m -2=-1,可得⎩⎨⎧m =-3,n =5,所以P (-3,5),所以|MF 1|+|MF 2|=|MF 1|+|MP |≥|PF 1|,当且仅当P ,M ,F 1三点共线时等号成立,|PF 1|=[-3-(-2)]2+(5-0)2=26,所以|MF 1|+|MF 2|的最小值为26,故选C.31.(多选)(2022·辽宁朝阳建平县高三上学期第一次联考)双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的焦点在圆O :x 2+y 2=13上,圆O 与双曲线C 的渐近线在第一、二象限分别交于点M ,N ,点E (0,a )满足EO→+EM →+EN →=0(其中O 为坐标原点),则() A .双曲线C 的一条渐近线方程为3x -2y =0 B .双曲线C 的离心率为132 C .|OE→|=1 D .△OMN 的面积为6 答案 ABD解析 如图,设双曲线C 的焦距为2c =213,MN 与y 轴交于点P ,由题可知|OM |=c =13,则P (0,b ),由EO→+EM →+EN →=0得点E 为△OMN 的重心,可得|OE |=23|OP |,即a =23b ,b 2a 2=c 2-a 2a 2=94,a =2,b =3,e 2-1=94,解得e =132.双曲线C 的渐近线方程为3x ±2y =0,|OE →|=2,M 的坐标为(2,3),S△OMN =6.故选ABD.32.(多选)(2022·湖北襄阳五中高三开学考试)已知F 1,F 2分别为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,C 的一条渐近线l 的方程为y =3x ,且F 1到l 的距离为33,点P 为C 在第一象限上的点,点Q 的坐标为(2,0),PQ 为∠F 1PF 2的平分线.则下列结论正确的是( )A .双曲线的方程为x 29-y 227=1 B.|PF 1||PF 2|=2C .|PF 1→+PF 2→|=36 D .点P 到x 轴的距离为3152 答案 ABD解析 ∵F 1(-c,0)到y =3x 距离为33,∴3c2=33,解得c =6,又渐近线方程为y =3x ,则b a =3,结合a 2+b 2=c 2可解得a =3,b =33,则双曲线的方程为x 29-y 227=1,故A 正确;∵PQ 为∠F 1PF 2的平分线,∴S △F 1PQ S △F 2PQ =12×|PF 1|×|PQ |×sin ∠F 1PQ12×|PF 2|×|PQ |×sin ∠F 2PQ =|PF 1||PF 2|,又S △F 1PQ S △F 2PQ =|QF 1||QF 2|=84=2,∴|PF 1||PF 2|=2,故B 正确;由双曲线定义可得|PF 1|-|PF 2|=6,则可得|PF 1|=12,|PF 2|=6,则在△PF 1F 2中,cos ∠F 1PF 2=122+62-1222×12×6=14,则|PF 1→+PF 2→|2=PF 1→2+2PF 1→·PF 2→+PF 2→2=122+2×12×6×14+62=216,则|PF 1→+PF 2→|=66,故C 错误;在△PF 1F 2中,sin ∠F 1PF 2=1-cos 2∠F 1PF 2=154,设点P 到x 轴的距离为d ,则S △PF 1F 2=12×|F 1F 2|×d =12|PF 1|×|PF 2|×sin ∠F 1PF 2,即12×12×d =12×12×6×154,解得d =3152,故D 正确.故选ABD.33.(2022·湖南娄底双峰县第一中学高三上学期入学摸底)双曲线x 2-my 2=m (m >0)的一条渐近线与y =2x 垂直,右焦点为F ,则以原点为圆心,|OF |为半径的圆的面积为________.答案 5π解析 由x 2-my 2=m (m >0)可得x 2m -y 2=1,所以a =m ,b =1,所以渐近线方程为y =±b a x =±1m x ,因为双曲线x 2-my 2=m (m >0)的一条渐近线与y =2x 垂直,所以-1m ×2=-1,可得m =4,所以c =a 2+b 2=m +1=5,所以右焦点为F (5,0),所以|OF |=5,以|OF |为半径的圆的面积为π×(5)2=5π.34.(2022·上饶模拟)已知F 1,F 2分别是双曲线x 2-y 2b 2=1(b >0)的左、右焦点,A 是双曲线上在第一象限内的点,若|AF 2|=2且∠F 1AF 2=45°,延长AF 2交双曲线的右支于点B ,则△F 1AB 的面积为________.答案 4解析 由题意知a =1,由双曲线定义知|AF 1|-|AF 2|=2a =2,|BF 1|-|BF 2|=2a =2,∴|AF 1|=2+|AF 2|=4,|BF 1|=2+|BF 2|.由题意知|AB |=|AF 2|+|BF 2|=2+|BF 2|,∴|AB |=|BF 1|,∴△F 1AB 为等腰三角形, ∵∠F 1AF 2=45°,∴∠ABF 1=90°, ∴△F 1AB 为等腰直角三角形.∴|AB |=|BF 1|=22|AF 1|=22×4=2 2.∴S △F 1AB =12|AB |·|BF 1|=12×22×22=4.一、高考大题1.(2022·新高考Ⅰ卷)在平面直角坐标系xOy 中,已知点F 1(-17,0),F 2(17,0),点M 满足|MF 1|-|MF 2|=2.记M 的轨迹为C .(1)求C 的方程;(2)设点T 在直线x =12上,过T 的两条直线分别交C 于A ,B 两点和P ,Q 两点,且|TA |·|TB |=|TP |·|TQ |,求直线AB 的斜率与直线PQ 的斜率之和.解 (1)因为|MF 1|-|MF 2|=2<|F 1F 2|=217,所以点M 的轨迹C 是以F 1,F 2分别为左、右焦点的双曲线的右支.设双曲线的方程为x 2a 2-y 2b 2=1(a >0,b >0),半焦距为c ,则2a =2,c =17,得a =1,b 2=c 2-a 2=16,所以点M 的轨迹C 的方程为x 2-y 216=1(x ≥1).(2)设T ⎝ ⎛⎭⎪⎫12,t ,由题意可知直线AB ,PQ 的斜率均存在且不为0,设直线AB 的方程为y -t =k 1⎝ ⎛⎭⎪⎫x -12(k 1≠0),直线PQ 的方程为y -t =k 2⎝ ⎛⎭⎪⎫x -12(k 2≠0),由⎩⎪⎨⎪⎧y -t =k 1⎝ ⎛⎭⎪⎫x -12,x 2-y 216=1,得(16-k 21)x 2-2k 1⎝ ⎛⎭⎪⎫t -k 12x -⎝ ⎛⎭⎪⎫t -k 122-16=0. 设A (x A ,y A ),B (x B ,y B ),易知16-k 21≠0,则x A x B =-⎝ ⎛⎭⎪⎫t -k 122-1616-k 21,x A +x B =2k 1⎝ ⎛⎭⎪⎫t -k 1216-k 21, 所以|TA |=1+k 21⎪⎪⎪⎪⎪⎪x A -12=1+k 21⎝ ⎛⎭⎪⎫x A -12, |TB |=1+k 21⎪⎪⎪⎪⎪⎪x B -12=1+k 21⎝ ⎛⎭⎪⎫x B -12, 则|TA |·|TB |=(1+k 21)⎝ ⎛⎭⎪⎫x A -12⎝ ⎛⎭⎪⎫x B -12 =(1+k 21)⎣⎢⎡⎦⎥⎤x A x B -12(x A +x B )+14 =(1+k 21)-⎝ ⎛⎭⎪⎫t -k 122-1616-k 21-12·2k 1⎝ ⎛⎭⎪⎫t -k 1216-k 21+14=(1+k 21)(t 2+12)k 21-16. 同理得|TP |·|TQ |=(1+k 22)(t 2+12)k 22-16. 因为|TA |·|TB |=|TP |·|TQ |,所以(1+k 21)(t 2+12)k 21-16=(1+k 22)(t 2+12)k 22-16, 所以k 22-16+k 21k 22-16k 21=k 21-16+k 21k 22-16k 22,即k 21=k 22,又k 1≠k 2,所以k 1=-k 2,即k 1+k 2=0. 二、模拟大题2.(2022·湖南岳阳第一次模拟)已知双曲线C :x 2a 2-y 2b 2=1的离心率为52,点P (4,3)在C 上.(1)求双曲线C 的方程;(2)设过点(1,0)的直线l 与双曲线C 交于M ,N 两点,问在x 轴上是否存在定点Q ,使得QM →·QN→为常数?若存在,求出点Q 的坐标及此常数的值;若不存在,说明理由. 解(1)由题意,得⎩⎪⎨⎪⎧16a 2-3b 2=1,c a =52,a 2+b 2=c 2,解得a 2=4,b 2=1.∴双曲线C 的方程为x 24-y 2=1.(2)设直线l 的方程为x =my +1,设定点Q (t,0), 联立⎩⎪⎨⎪⎧x24-y 2=1,x =my +1,得(m 2-4)y 2+2my -3=0.∴m 2-4≠0,且Δ=4m 2+12(m 2-4)>0,解得m 2>3且m 2≠4.设M (x 1,y 1),N (x 2,y 2),∴y 1+y 2=-2m m 2-4,y 1y 2=-3m 2-4,∴x 1+x 2=m (y 1+y 2)+2=-2m 2m 2-4+2=-8m 2-4,x 1x 2=(my 1+1)(my 2+1)=m 2y 1y 2+m (y 1+y 2)+1=-3m 2m 2-4-2m 2m 2-4+1=-4m 2+4m 2-4=-4-20m 2-4.∴QM →·QN →=(x 1-t ,y 1)·(x 2-t ,y 2)=(x 1-t )(x 2-t )+y 1y 2=x 1x 2-t (x 1+x 2)+t 2+y 1y 2=-4-20m 2-4+t ·8m 2-4-3m 2-4+t 2=-4+t 2+8t -23m 2-4为常数,与m 无关,∴8t -23=0,即t =238,此时QM →·QN→=27364.∴在x 轴上存在定点Q ⎝ ⎛⎭⎪⎫238,0,使得QM →·QN →为常数27364.3.(2022·广东珠海高三摸底)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点为F (2,0),且经过点T ⎝ ⎛⎭⎪⎫52,12.(1)求双曲线C 的标准方程;(2)已知点A 是C 上一定点,过点B (0,1)的动直线与双曲线C 交于P ,Q 两点,若k AP +k AQ 为定值λ,求点A 的坐标及实数λ的值.解 (1)由题意a 2+b 2=c 2=2.且54a 2-14b 2=1.联立解得a =b =1,所以双曲线C 的标准方程为x 2-y 2=1. (2)设A (m ,n ),过点B 的动直线为:y =tx +1.设P (x 1,y 1),Q (x 2,y 2),联立⎩⎨⎧x 2-y 2=1,y =tx +1得(1-t 2)x 2-2tx -2=0,由1-t 2≠0且Δ>0,解得t 2<2且t 2≠1,所以x 1+x 2=2t1-t 2,x 1x 2=-21-t 2,k AP +k AQ =λ,即y 1-n x 1-m +y 2-n x 2-m =λ,即tx 1+1-n x 1-m +tx 2+1-nx 2-m =λ,化简得(2t -λ)x 1x 2+(-mt +1-n +λm )(x 1+x 2)-2m +2mn -λm 2=0, 所以(2t -λ)-21-t 2+(-mt +1-n +λm )2t 1-t 2-2m +2mn -λm 2=0, 化简得m (λm -2n )t 2+2(λm -n -1)t +2λ-2m +2mn -λm 2=0, 由于上式对无穷多个不同的实数t 都成立, 所以⎩⎪⎨⎪⎧m (λm -2n )=0,λm -n -1=0,2λ-2m +2mn -λm 2=0如果m =0,那么n =-1,此时A (0,-1)不在双曲线C 上,舍去. 因此m ≠0,从而λm =2n =n +1,所以n =1,代入2λ-2m +2mn -λm 2=0, 得2λ=λm 2,解得m =±2,此时A (±2,1)在双曲线C 上. 综上,A (2,1),λ=2或A (-2,1),λ=- 2.4. (2022·广东普通高中高三阶段性质量检测)如图,在平面直角坐标系xOy 中,已知等轴双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)的左顶点为A ,过右焦点F 且垂直于x 轴的直线与E 交于B ,C 两点,若△ABC 的面积为2+1.(1)求双曲线E 的方程;(2)若直线l :y =kx -1与双曲线E 的左、右两支分别交于M ,N 两点,与双曲E 的两条渐近线分别交于P ,Q 两点,求|MN ||PQ |的取值范围.解 (1)因为双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)为等轴双曲线,可得a =b . 设双曲线的焦距为2c ,c >0, 故c 2=a 2+b 2=2a 2,即c =2a . 因为BC 过右焦点F ,且垂直于x 轴,将x B =c =2a 代入双曲线的方程可得|y B |=a ,故|BC |=2a . 又△ABC 的面积为1+2,即12|BC |·|AF |=12×2a ×(a +c )=1+2, 解得a =1.故双曲线E 的方程为x 2-y 2=1.(2)由题意可得直线l :y =kx -1与双曲线的左右两支分别交于M ,N 两点, 联立⎩⎨⎧x 2-y 2=1,y =kx -1,可得(1-k 2)x 2+2kx -2=0,所以1-k 2≠0,Δ=(2k )2-4(1-k 2)(-2)>0,x M x N <0,可得-1<k <1, 且x M +x N =-2k1-k 2,x M x N=-21-k 2, 所以|MN |=(x M -x N )2+(y M -y N )2 =1+k 2|x M -x N |=1+k 2·(x M +x N )2-4x M x N =21+k 2·2-k 21-k 2,联立⎩⎨⎧y =x ,y =kx -1,可得x P =1k -1,同理可得x Q =1k +1, 所以|PQ |=1+k 2|x P -x Q |=1+k 2·⎪⎪⎪⎪⎪⎪1k -1-1k +1=21+k 21-k 2,所以|MN ||PQ |=21+k 2·2-k 221+k2=2-k 2, 其中-1<k <1,所以|MN ||PQ |∈(1,2].。
椭圆双曲线抛物线 高考数学专题复习精细高效梳理(附详解)
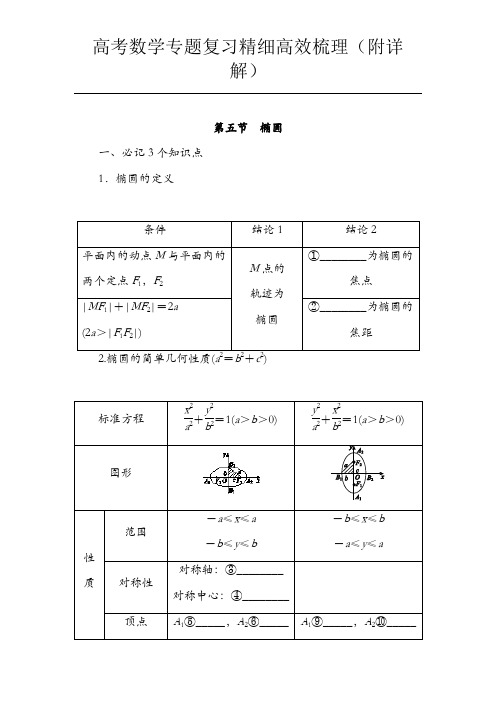
第五节椭圆一、必记3个知识点1.椭圆的定义-a≤x≤a(1)设椭圆x 2a 2+y 2b2=1(a >b >0)上任意一点P (x ,y ),则当x =0时,|OP |有最小值b ,这时,P 在短轴端点处;当x =±a 时,|OP |有最大值a ,这时,P 在长轴端点处.(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a 是斜边长,a 2=b 2+c 2.(3)已知过焦点F 1的弦AB ,则△ABF 2的周长为4a .(4)若P 为椭圆上任一点,F 为其焦点,则a -c ≤|PF |≤a +c .二、必明3个易误点1.椭圆的定义中易忽视2a >|F 1F 2|这一条件,当2a =|F 1F 2|其轨迹为线段F 1F 2,当2a <|F 1F 2|不存在轨迹.2.求椭圆的标准方程时易忽视判断焦点的位置,而直接设方程为x 2a 2+y 2b 2=1(a >b >0). 3.注意椭圆的范围,在设椭圆x 2a 2+y 2b 2=1(a >b >0)上点的坐标为P (x ,y )时,则|x |≤a ,这往往在求与点P 有关的最值问题中特别有用,也是容易被忽略而导致求最值错误的原因.三、技法1. 求椭圆标准方程的2种常用方法(1)直接求出a ,c 来求解e .通过已知条件列方程组,解出a ,c 的值.(2)构造a ,c 的齐次式,解出e .由已知条件得出关于a ,c 的二元齐次方程,然后转化为关于离心率e 的一元二次方程求解.(3)通过取特殊值或特殊位置,求出离心率.提醒:在解关于离心率e 的二次方程时,要注意利用椭圆的离心率e ∈(0,1)进行根的取舍,否则将产生增根.3. 求解最值、取值范围问题的技巧(1)与椭圆几何性质有关的问题要结合图形进行分析,即使画不出图形,思考时也要联想到一个图形.(2)椭圆的范围或最值问题常常涉及一些不等式.例如,-a ≤x ≤a ,-b ≤y ≤b,0<e <1,在求椭圆的相关量的范围时,要注意应用这些不等关系.(3)最值问题,将所求列出表达式,构造基本不等式或利用函数单调性求解.4. 判断直线与椭圆位置关系的四个步骤第一步:确定直线与椭圆的方程.第二步:联立直线方程与椭圆方程.第三步:消元得出关于x (或y )的一元二次方程.第四步:当Δ>0时,直线与椭圆相交;当Δ=0时,直线与椭圆相切;当Δ<0时,直线与椭圆相离.5.直线被椭圆截得的弦长公式设直线与椭圆的交点坐标为A (x 1,y 1),B (x 2,y 2),则|AB |=(1+k 2)[(x 1+x 2)2-4x 1x 2]= ⎝ ⎛⎭⎪⎪⎫1+1k 2[(y 1+y 2)2-4y 1y 2](k 为直线斜率).参考答案①F1,F2②|F1F2| ③x轴,y轴④坐标原点⑤(-a,0) ⑥(a,0) ⑦(0,-b) ⑧(0,b) ⑨(0,-a) ⑩(0,a) ⑪(-b,0) ⑫(b,0) ⑬2a⑭2b⑮2c⑯(0,1) ⑰c2=a2-b2第六节双曲线一、必记3个知识点1.双曲线的定义(1)平面内与两个定点F1、F2(|F1F2|=2c>0)的距离①________________为非零常数2a(2a<2c)的点的轨迹叫做双曲线.这两个定点叫做双曲线的②________,两焦点间的距离叫做③________.(2)集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.(ⅰ)当④________________时,M点的轨迹是双曲线;(ⅱ)当⑤________________时,M点的轨迹是两条射线;(ⅲ)当⑥________________时,M点不存在.2.双曲线的标准方程和几何性质⑧________ x∈R3.双曲线中的4个常用结论(1)双曲线为等轴双曲线⇔双曲线的离心率e=2⇔双曲线的两条渐近线互相垂直.(2)渐近线的斜率与双曲线的焦点位置的关系:当焦点在x轴上时,渐近线斜率为±ba,当焦点在y轴上时,渐近线斜率为±ab.(3)渐近线与离心率.x2 a2-y2b2=1(a>0,b>0)的一条渐近线的斜率为ba=e2-1.(4)若P为双曲线上一点,F为其对应焦点,则|PF|≥c-a.二、必明4个易误点1.双曲线的定义中易忽视2a<|F1F2|这一条件.若2a=|F1F2|,则轨迹是以F1,F2为端点的两条射线,若2a>|F1F2|则轨迹不存在.2.双曲线的标准方程中对a,b的要求只是a>0,b>0,易误认为与椭圆标准方程中a,b的要求相同.若a>b>0,则双曲线的离心率e∈(1,2);若a=b>0,则双曲线的离心率e=2;若0<a<b,则双曲线的离心率e> 2.3.注意区分双曲线中的a,b,c大小关系与椭圆a,b,c关系,在椭圆中a2=b2+c2,而在双曲线中c2=a2+b2.4.易忽视渐近线的斜率与双曲线的焦点位置关系.当焦点在x轴上,渐近线斜率为±b a ,当焦点在y 轴上,渐近线斜率为±a b.三、技法1. 双曲线定义的应用 (1)判定满足某条件的平面内动点的轨迹是否为双曲线,进而根据要求可求出曲线方程;(2)在“焦点三角形”中,常利用正弦定理、余弦定理,经常结合||PF 1|-|PF 2||=2a ,运用平方的方法,建立|PF 1|与|PF 2|的关系.[注意] 在应用双曲线定义时,要注意定义中的条件,搞清所求轨迹是双曲线,还是双曲线的一支,若是双曲线的一支,则需确定是哪一支.2. 求双曲线标准方程的一般方法(1)待定系数法:设出双曲线方程的标准形式,根据已知条件,列出参数a ,b ,c 的方程并求出a ,b ,c 的值.与双曲线x 2a 2-y 2b2=1有相同渐近线时,可设所求双曲线方程为:x 2a 2-y 2b 2=λ(λ≠0). (2)定义法:依定义得出距离之差的等量关系式,求出a 的值,由定点位置确定c 的值.3. 求双曲线离心率或其范围的方法(1)求a ,b ,c 的值,由c 2a 2=a 2+b 2a 2=1+b 2a2直接求e .(2)列出含有a ,b ,c 的齐次方程(或不等式),借助于b 2=c 2-a 2消去b ,然后转化成关于e 的方程(或不等式)求解.4.求双曲线的渐近线方程的方法求双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线的方法是令x 2a 2-y 2b 2=0,即得两渐近线方程为:x a ±y b=0.参考答案①之差的绝对值 ②焦点 ③焦距 ④2a <|F 1F 2| ⑤2a =|F 1F 2| ⑥2a >|F 1F 2|⑦x ≥a 或x ≤-a ⑧y ≥a 或y ≤-a ⑨x 轴,y 轴 ⑩坐标原点 ⑪x 轴,y 轴⑫坐标原点 ⑬(-a,0) ⑭(a,0) ⑮(0,-a ) ⑯(0,a ) ⑰y =±b a x ⑱y =±a bx ⑲c a ⑳ a 2+b 2 ○212a ○222b ○23a 2+b 2第七节抛物线一、必记2个知识点1.抛物线定义、标准方程及几何性质x轴⑤________y轴⑥________设AB 是过抛物线y 2=2px (p >0)的焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则(1)x 1x 2=p 24,y 1y 2=-p 2. (2)弦长|AB |=x 1+x 2+p =2p sin 2α(α为弦AB 的倾斜角). (3)以弦AB 为直径的圆与准线相切.(4)通径:过焦点且垂直于对称轴的弦,长等于2p .二、必明2个易误点1.抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与直线垂直的直线.2.抛物线标准方程中参数p 易忽视,只有p >0,才能证明其几何意义是焦点F 到准线l 的距离,否则无几何意义.三、技法1. 应用抛物线定义的2个关键点(1)由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线上一点P (x ,y )到焦点F 的距离|PF |=|x |+p 2或|PF |=|y |+p 2. 2. 求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法,因为未知数只有p ,所以只需一个条件确定p 值即可.(2)因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量.3.确定及应用抛物线性质的技巧(1)利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化为标准方程.(2)要结合图形分析,灵活运用平面几何的性质以图助解.4. 解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.提醒:涉及弦的中点、斜率时,一般用“点差法”求解.参考答案①相等 ②y 2=-2px (p >0) ③x 2=-2py (p >0) ④x 2=2py (p >0) ⑤x 轴 ⑥y 轴⑦F (-p 2,0) ⑧F (0,-p 2) ⑨F (0,p 2) ⑩e =1 ⑪x =-p 2 ⑫y =-p 2 ⑬-y 0+p 2⑭y 0+p 2⑮y ≤0 ⑯y ≥0。
高考数学一轮复习学案 第50讲 双曲线(解析版)

第50讲 双曲线(解析版)考点内容解读要求 常考题型 1.双曲线的定义掌握双曲线的定义,标准方程,几何性质,离心率,通径,最值。
Ⅰ选择题,填空题,大题 2.双曲线的性质 能利用双曲线的简单性质求双曲线的方程.能用双曲线的简单性质分析解决一些简单的问题.Ⅱ选择题,填空题,大题一、双曲线的简单几何性质双曲线22221x y a b -=(a >0,b >0)的简单几何性质1. 范围22221x x a ax a x a 即或≥≥∴≥≤-双曲线上所有的点都在两条平行直线x=-a 和x=a 的两侧,是无限延伸的。
因此双曲线上点的横坐标满足x ≤-a 或x ≥a . 2.对称性对于双曲线标准方程12222=-b y a x (a >0,b >0),把x 换成-x ,或把y 换成-y ,或把x 、y同时换成-x 、-y ,方程都不变,所以双曲线12222=-by a x (a >0,b >0)是以x 轴、y 轴为对称轴的轴对称图形,且是以原点为对称中心的中心对称图形,这个对称中心称为双曲线的中心。
3.顶点①双曲线与它的对称轴的交点称为双曲线的顶点。
②双曲线12222=-by a x (a >0,b >0)与坐标轴的两个交点即为双曲线的两个顶点,坐标分别为A 1(-a ,0),A 2(a ,0),顶点是双曲线两支上的点中距离最近的点。
③两个顶点间的线段A 1A 2叫作双曲线的实轴;设B 1(0,-b ),B 2(0,b )为y 轴上的两个点,则线段B1B2叫做双曲线的虚轴。
实轴和虚轴的长度分别为|A 1A 2|=2a ,|B 1B 2|=2b 。
a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长。
①双曲线只有两个顶点,而椭圆有四个顶点,不能把双曲线的虚轴与椭圆的短轴混淆。
②双曲线的焦点总在实轴上。
③实轴和虚轴等长的双曲线称为等轴双曲线。
4.离心率①双曲线的焦距与实轴长的比叫做双曲线的离心率,用e 表示,记作aca c e ==22。
高考数学复习考点知识与题型专题讲解52 双曲线

已知双曲线 C
1(a>0,b>0)的左,右焦点分别为 F1,F2,抛物线 y2=2px(p>0)与双曲线 C
有相同的焦点.设 P 为抛物线与双曲线 C 的一个交点,cos∠PF1F2 ,则双曲线 C 的离心率为( )
A. 或
B. 或 3
.C 2 或
.D 2 或 3
集合 = - = , = ,其中 , 为常数且 , P {M|||MF1| |MF2|| 2a} |F1F2| 2c
ac
a>0 c>0.
当 (1) 时, 2a<|F1F2| P 点的轨迹是双曲线;
当 (2) = 时, 2a |F1F2| P 点的轨迹是两条射线;
当 (3) 时, 2a>|F1F2| P 点不存在. 2.双曲线的标准方程和几何性质
由双曲线的定义知:|AF2|﹣|AF1|=2a ①, ﹣ |BF2| |BF1| ②,
又 = = ,① ②得: ﹣ , |AF1|+|BF1| |AB| 8 +
|AF2|+|BF2| |AB|
∴ = ,则 的周长为 , |AF2|+|BF2| 8
△ABF2
16
故选:B.
【再练一题】 已知 、F1 F2 为双曲线 : ﹣ = C x2 y2 1 的左、右焦点,点 P 在 C 上,∠F1PF2=60°,则 P 到 x 轴的距离为( )
故答案为:
1(y≤﹣3).
【再练一题】
已知点 F1(﹣3,0)和 F2(3,0),动点 P 到 、F1 F2 的距离之差为 4,则点 P 的轨迹方程为( )
A.
B.
C.
D.
【解答】解:由题设知点 P 的轨迹方程是焦点在 x 轴正半轴的双曲线的右支,
2011高考数学知识点汇总——椭圆与双曲线高考生必备1

2011 高考数学知识点汇总精编椭圆与双曲线的对偶性质 -- (必背的经典结论)高三数学备课组椭 圆1.点 P 处的切线 PT 均分△ PF 1 F 2 在点 P 处的 外角 .2. PT 均分△ PF 1F 2 在点 P 处的外角,则焦点在直线 PT 上的射影 H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点 .3. 以焦点弦 PQ 为直径的圆必与对应准线 相离 .4.以焦点半径 PF 1 为直径的圆必与以长轴为直径的圆内切 .5. 若 P 0 ( x 0 , y 0 )x2y21x 0 x y 0 y 1.在椭圆b 2上,则过 P 0 的椭圆的切线方程是b2a 2a26. 若 P 0 ( x 0 , y 0 ) x 2 y 21 外 ,则过 Po 作椭圆的两条切线切点为 P 1、P 2,则切点弦 P 1P2 的直线方程在椭圆22是x 0xy 0 yab1.a 2b 213. 若 P 0 ( x 0 x 2 y 2x 2 y 2, y 0 ) 在椭圆22 1内,则过 Po 的弦中点的轨迹方程是a 2b 2a b双曲线1. 点 P 处的切线 PT 均分△ PF 1F 2 在点 P 处的内角 .2. PT 均分△ PF 1F 2 在点 P 处的内角,则焦点在直线 PT 上的射影 H 点的轨迹是以长两个端点 .3. 以焦点弦 PQ 为直径的圆必与对应准线 订交 .4. 以焦点半径 PF 1 为直径的圆必与以实轴为直径的圆相切 .(内切: P 在右支;5. 若 00 0)在双曲线 x 2 y 21( a > 0,b > 0)上,则过 0 的双曲线的切线P (x , ya 2b 2P6. 若 P 0 (x 0, y 0 )x 2 y 2 1( a > 0,b > 0)外 ,则过 Po 作双曲线的在双曲线b 2a 2切点弦 P 1P 2 的直线方程是x 0xy 0 y .a 2b 2 1x2y27.1( a > 0,b > o )的左右焦点分别为F 1 , F 2,点 P 为双曲线双曲线b 2a 2则双曲线的焦点角形的面积为S F 1PF 2b 2co t .27.x 2 y 21 (a > b > 0)的左右焦点分别为F 1, F 2,点 P 为椭圆上任意一点椭圆 22ab角形的面积为 S F PFb 2 tan .1 228.x2y21( a > b > 0)的焦半径公式:椭圆a 2b 2| MF 1 | a ex 0 , | MF 2 | a ex 0 ( F 1 ( c,0) , F 2 (c,0) M (x 0 , y 0 ) ).9.设过椭圆焦点 F 作直线与椭圆订交 P 、Q 两点, A 为椭圆长轴上一个极点,连结点 F 的椭圆准线于 M 、 N 两点,则 MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点 P 、 Q, A 1、 A 2 为椭圆长轴上的极点,和 A 1Q 交于点 N ,则 MF ⊥ NF.F 1PF 2,则椭圆的焦点AP 和 AQ 分别交相应于焦A 1P 和 A 2Q 交于点 M , A 2P8.x 2 y 21( a > 0,b > o )的焦半径公式: ( F 1 ( c,0) , F 2 (c,0)双曲线b 2 a 2当 M (x 0 , y 0 ) 在右支上时, | MF 1 | ex 0 a ,| MF 2 | ex 0 a .当 M (x 0 , y 0 ) 在左支上时, | MF 1 |ex 0 a , | MF 2 | ex 0 a9.设过双曲线焦点 F 作直线与双曲线订交 P 、Q 两点, A 为双曲线长轴上一个极交相应于焦点 F 的双曲线准线于 M 、N 两点,则 MF ⊥ NF.10. 过双曲线一个焦点F 的直线与双曲线交于两点 P 、 Q, A 1、 A 2 为双曲线实轴点 M ,A 2P 和 A 1Q 交于点 N ,则 MF ⊥NF.x 2y 2 1 ( a > 0,b > 0 )的不平行于对称轴的弦,M (11. AB 是双曲线b 2a 2b 2xb 2x11. AB 是椭圆 x 2 y 21M ( x 0 , y 0 ) 为 AB 的中点,则 k OMkABb 2a2b 2的不平行于对称轴的弦,a2 ,即K ABb 2 x 0 。
2011届高考数学第一轮复习精品试题:圆锥曲线

2011届高考数学第一轮复习精品试题:圆锥曲线第2章 圆锥曲线与方程考纲总要求:①了解圆锥曲线的实际背景,了解在刻画现实世界和解决实际问题中的作用. ②掌握椭圆的定义、几何图形、标准方程与简单几何性质.③了解双曲线、抛物线的定义、几何图形和标准方程,知道它们的简单几何性质. ④理解数形结合的思想. ⑤了解圆锥曲线的简单应用. §重难点:建立并掌握椭圆的标准方程,能根据条件求椭圆的标准方程;掌握椭圆的简单几何性质,能运用椭圆的几何性质处理一些简单的实际问题.经典例题:A 、B 为椭圆22a x +22925a y =1上两点,F2为椭圆的右焦点,假如|AF2|+|BF2|=58a ,AB 中点到椭圆左准线的距离为23,求该椭圆方程.当堂练习:1.如下命题是真命题的是〔 〕A .到两定点距离之和为常数的点的轨迹是椭圆B .到定直线c a x 2=和定点F(c ,0)的距离之比为a c的点的轨迹是椭圆C .到定点F(-c ,0)和定直线ca x 2-=的距离之比为a c(a>c>0)的点的轨迹 是左半个椭圆D .到定直线c a x 2=和定点F(c ,0)的距离之比为ca(a>c>0)的点的轨迹是椭圆2.假如椭圆的两焦点为〔-2,0〕和〔2,0〕,且椭圆过点)23,25(-,如此椭圆方程是〔 〕A .14822=+x yB .161022=+x yC .18422=+x yD .161022=+y x 3.假如方程x2+ky2=2表示焦点在y 轴上的椭圆,如此实数k 的取值X 围为〔 〕A .〔0,+∞〕B .〔0,2〕C .〔1,+∞〕D .〔0,1〕4.设定点F1〔0,-3〕、F2〔0,3〕,动点P 满足条件)0(921>+=+a a a PF PF ,如此点P的轨迹是〔 〕A .椭圆B .线段C .不存在D .椭圆或线段 5.椭圆12222=+b y a x 和k b y a x =+2222()0>k 具有〔 〕 A .一样的离心率 B .一样的焦点C .一样的顶点D .一样的长、短轴6.假如椭圆两准线间的距离等于焦距的4倍,如此这个椭圆的离心率为〔 〕 A .41B .22C .42D . 217.P 是椭圆13610022=+y x 上的一点,假如P 到椭圆右准线的距离是217,如此点P 到左焦点的距离〔 〕A .516B .566C .875D .8778.椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是〔 〕A .3B .11C .22D .109.在椭圆13422=+y x 内有一点P 〔1,-1〕,F 为椭圆右焦点,在椭圆上有一点M ,使|MP|+2|MF|的值最小,如此这一最小值是〔 〕A .25B .27C .3D .410.过点M 〔-2,0〕的直线m 与椭圆1222=+y x 交于P1,P2,线段P1P2的中点为P ,设直线m 的斜率为k1〔01≠k 〕,直线OP 的斜率为k2,如此k1k2的值为〔 〕A .2B .-2C .21D .-2111.离心率21=e ,一个焦点是()3,0-F 的椭圆标准方程为 ___________ .12.与椭圆 4 x 2 + 9 y 2 = 36 有一样的焦点,且过点(-3,2)的椭圆方程为_______________.13.()y x P ,是椭圆12514422=+y x 上的点,如此y x +的取值X 围是________________ . 14.椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9,如此椭圆E的离心率等于__________________.15.椭圆的对称轴为坐标轴,离心率32=e ,短轴长为58,求椭圆的方程.16.过椭圆4:),(148:220022=+=+y x O y x P y x C 向圆上一点引两条切线PA 、PB 、A 、B 为切点,如直线AB 与x 轴、y 轴交于M 、N 两点. 〔1〕假如0=⋅PB PA ,求P 点坐标; 〔2〕求直线AB 的方程〔用00,y x 表示〕;〔3〕求△MON 面积的最小值.〔O 为原点〕17.椭圆12222=+b y a x (a >b >)0与直线1=+y x 交于P 、Q 两点,且OQ OP ⊥,其中O 为坐标原点.〔1〕求2211b a+的值; 〔2〕假如椭圆的离心率e 满足33≤e ≤22,求椭圆长轴的取值X 围.18.一条变动的直线L 与椭圆42x +2y 2=1交于P 、Q 两点,M 是L 上的动点,满足关系|MP|·|MQ|=2.假如直线L 在变动过程中始终保持其斜率等于1.求动点M 的轨迹方程,并说明曲线的形状.第2章 圆锥曲线与方程 §重难点:建立并掌握双曲线的标准方程,能根据条件求双曲线的标准方程;掌握双曲线的简单几何性质,能运用双曲线的几何性质处理一些简单的实际问题.经典例题:不论b 取何实数,直线y=kx+b 与双曲线1222=-y x 总有公共点,试某某数k 的取值X 围.当堂练习:1.到两定点()0,31-F 、()0,32F 的距离之差的绝对值等于6的点M 的轨迹 〔 〕 A .椭圆B .线段C .双曲线D .两条射线2.方程11122=-++k y k x 表示双曲线,如此k 的取值X 围是〔 〕A .11<<-kB .0>kC .0≥kD .1>k 或1-<k 3. 双曲线14122222=--+m y m x 的焦距是〔 〕A .4B .22C .8D .与m 有关4.m,n 为两个不相等的非零实数,如此方程mx -y+n=0与nx2+my2=mn 所表示的曲线可A B C D 5. 双曲线的两条准线将实轴三等分,如此它的离心率为〔 〕A .23B .3C .34D . 36.焦点为()6,0,且与双曲线1222=-y x 有一样的渐近线的双曲线方程是〔 〕A .1241222=-y xB .1241222=-x yC .1122422=-x yD .1122422=-y x7.假如a k <<0,双曲线12222=+--k b y k a x 与双曲线12222=-b y a x 有〔 〕A .一样的虚轴B .一样的实轴C .一样的渐近线D . 一样的焦点8.过双曲线191622=-y x 左焦点F1的弦AB 长为6,如此2ABF ∆〔F2为右焦点〕的周长是〔 〕A .28B .22C .14D .129.双曲线方程为1422=-y x ,过P 〔1,0〕的直线L 与双曲线只有一个公共点,如此L 的条数共有 〔 〕A .4条B .3条C .2条D .1条10.给出如下曲线:①4x+2y -1=0;②x2+y2=3;③1222=+y x ④1222=-y x ,其中与直线y=-2x -3有交点的所有曲线是〔 〕 A .①③B .②④C .①②③D .②③④11.双曲线17922=-y x 的右焦点到右准线的距离为__________________________.12.与椭圆1251622=+y x 有一样的焦点,且两准线间的距离为310的双曲线方程为____________.13.直线1+=x y 与双曲线13222=-y x 相交于B A ,两点,如此AB =__________________.14.过点)1,3(-M 且被点M 平分的双曲线1422=-y x 的弦所在直线方程为 .15.求一条渐近线方程是043=+y x ,一个焦点是()0,4的双曲线标准方程,并求此双曲线的离心率.16.双曲线()0222>=-a a y x 的两个焦点分别为21,F F ,P 为双曲线上任意一点,求证:21PF PO PF 、、成等比数列〔O 为坐标原点〕.17.动点P 与双曲线x2-y2=1的两个焦点F1,F2的距离之和为定值,且cos ∠F1PF2的最小值为-13.〔1〕求动点P 的轨迹方程;〔2〕设M(0,-1),假如斜率为k(k ≠0)的直线l 与P 点的轨迹交于不同的两点A 、B ,假如要使|MA|=|MB|,试求k 的取值X 围.18.某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上).第2章 圆锥曲线与方程 §重难点:建立并掌握抛物线的标准方程,能根据条件求抛物线的标准方程;掌握抛物线的简单几何性质,能运用抛物线的几何性质处理一些简单的实际问题.经典例题:如图, 直线y=21x 与抛物线y=81x2-4交于A 、B 两点, 线段AB 的垂直平分线与直线y=-5交于Q 点. 〔1〕求点Q 的坐标;〔2〕当P 为抛物线上位于线段AB 下方〔含A 、B 〕的动点时, 求ΔOPQ 面积的最大值.当堂练习:1.抛物线22x y =的焦点坐标是 〔 〕 A .)0,1(B .)0,41(C .)81,0(D . )41,0(2.抛物线的顶点在原点,焦点在y 轴上,其上的点)3,(-m P 到焦点的距离为5,如此抛物线方程为〔 〕A .y x 82=B .y x 42=C .y x 42-=D .y x 82-=3.抛物线x y 122=截直线12+=x y 所得弦长等于 〔 〕A .15B .152C .215D .154.顶点在原点,坐标轴为对称轴的抛物线过点(-2,3),如此它的方程是 〔 〕A .yx 292-=或x y 342=B .x y 292-=或y x 342= C .y x 342=D .xy 292-= 5.点)0,1(P 到曲线⎩⎨⎧==t y t x 22〔其中参数R t ∈〕上的点的最短距离为〔 〕A .0B .1C .2D .26.抛物线)0(22>=p px y 上有),,(),,(2211y x B y x A ),(33y x C 三点,F 是它的焦点,假如CFBF AF ,, 成等差数列,如此 〔 〕A .321,,x x x 成等差数列B .231,,x x x 成等差数列C .321,,y y y 成等差数列D .231,,y y y 成等差数列7.假如点A 的坐标为〔3,2〕,F 为抛物线x y 22=的焦点,点P 是抛物线上的一动点,如此PF PA + 取得最小值时点P 的坐标是 〔 〕A .〔0,0〕B .〔1,1〕C .〔2,2〕D .)1,21(8.抛物线)0(22>=p px y 的焦点弦AB 的两端点为),(11y x A ,),(22y x B ,如此关系式2121x x y y 的值一定等于 〔 〕A .4pB .-4pC .p2D .-p9.过抛物线)0(2>=a ax y 的焦点F 作一直线交抛物线于P ,Q 两点,假如线段PF 与FQ 的长分别是q p ,,如此qp 11+〔 〕 A .a 2B .a21C .a 4D .a410.假如AB 为抛物线y2=2px (p>0)的动弦,且|AB|=a (a>2p),如此AB 的中点M 到y 轴的最近距离是 〔 〕A .21aB .21pC .21a +21pD .21a -21p11.抛物线x y =2上到其准线和顶点距离相等的点的坐标为 ______________. 12.圆07622=--+x y x ,与抛物线)0(22>=p px y 的准线相切,如此=p ___________. 13.如果过两点)0,(a A 和),0(a B 的直线与抛物线322--=x x y 没有交点,那么实数a 的取值X 围是 .14.对于顶点在原点的抛物线,给出如下条件; 〔1〕焦点在y 轴上; 〔2〕焦点在x 轴上; 〔3〕抛物线上横坐标为1的点到焦点的距离等于6;〔4〕抛物线的通径的长为5; 〔5〕由原点向过焦点的某条直线作垂线,垂足坐标为〔2,1〕.其中适合抛物线y2=10x 的条件是(要求填写适宜条件的序号〕 ______.15.点A 〔2,8〕,B 〔x1,y1〕,C 〔x2,y2〕在抛物线px y 22=上,△ABC 的重心与此抛物线的焦点F 重合〔如图〕〔1〕写出该抛物线的方程和焦点F 的坐标; 〔2〕求线段BC 中点M 的坐标; 〔3〕求BC 所在直线的方程.16.抛物线y=ax2-1上恒有关于直线x+y=0对称的相异两点,求a 的取值X 围.17.抛物线x2=4y 的焦点为F ,过点(0,-1)作直线L 交抛物线A 、B 两点,再以AF 、BF 为邻边作平行四边形FARB ,试求动点R 的轨迹方程.18.抛物线C :2742++=x x y ,过C 上一点M ,且与M 处的切线垂直的直线称为C 在点M 的法线.〔1〕假如C 在点M 的法线的斜率为21-,求点M 的坐标〔x0,y0〕;〔2〕设P 〔-2,a 〕为C 对称轴上的一点,在C 上是否存在点,使得C 在该点的法线通过点P ?假如有,求出这些点,以与C 在这些点的法线方程;假如没有,请说明理由.第2章 圆锥曲线与方程 §1)如果实数y x ,满足等式3)2(22=+-y x ,那么x y的最大值是〔 〕A 、21B 、33C 、23D 、32)假如直线01)1(=+++y x a 与圆0222=-+x y x 相切,如此a 的值为〔 〕 A 、1,1- B 、2,2- C 、1 D 、1-3)椭圆125222=+y ax )5(>a 的两个焦点为1F 、2F ,且8||21=F F ,弦AB 过点1F ,如此△2ABF 的周长为〔 〕〔A 〕10 〔B 〕20 〔C 〕241〔D 〕 4144)椭圆13610022=+y x 上的点P 到它的左准线的距离是10,那么点P 到它的右焦点的距离是〔 〕〔A 〕15 〔B 〕12 〔C 〕10 〔D 〕85)椭圆192522=+y x 的焦点1F 、2F ,P 为椭圆上的一点,21PF PF⊥,如此△21PF F 的面积为〔 〕〔A 〕9 〔B 〕12 〔C 〕10 〔D 〕86)椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是〔 〕〔A 〕3〔B 〕11〔C 〕22〔D 〕107)以坐标轴为对称轴、渐近线互相垂直、两准线间距离为2的双曲线方程是〔 〕〔A 〕222=-y x 〔B 〕222=-x y 〔C 〕422=-y x 或422=-x y 〔D 〕222=-y x 或222=-x y 8)双曲线191622=-y x 右支点上的一点P 到右焦点的距离为2,如此P 点到左准线的距离为〔 〕〔A 〕6 〔B 〕8 〔C 〕10 〔D 〕129)过双曲线822=-y x 的右焦点F2有一条弦PQ ,|PQ|=7,F1是左焦点,那么△F1PQ 的周长为〔 〕〔A 〕28 〔B 〕2814-〔C 〕2814+〔D 〕2810)双曲线虚轴上的一个端点为M,两个焦点为F1、F2,︒=∠12021MF F ,如此双曲线的离心率为〔 〕〔A 〕3〔B 〕26〔C 〕36〔D 〕3311)过抛物线2y ax =(a>0)的焦点F 作一直线交抛物线于P 、Q 两点,假如线段PF 与FQ 的长分别为p 、q ,如此11p q +等于〔 〕〔A 〕2a 〔B 〕12a 〔C 〕4a 〔D 〕4a12) 如果椭圆193622=+y x 的弦被点(4,2)平分,如此这条弦所在的直线方程是〔 〕〔A 〕02=-y x 〔B 〕042=-+y x 〔C 〕01232=-+y x 〔D 〕082=-+y x13)与椭圆22143x y +=具有一样的离心率且过点〔2,14〕离心率35=e ,一条准线为3=x 的椭圆的标准方程是 。
最新-2021届高考数学 专题六第2讲 椭圆、双曲线、抛物线复习课件 理 精品
可得 a2=5b2,c2=a2+b2=6b2,e=ac=
30 5.
(2)联立yx=2-x5-y2c=,5b2, 得 4x2-10cx+35b2=0.
设 A(x1,y1),B(x2,y2),则xx11+x2=x2=3545b2c2.,
①
设O→C=(x3,y3),O→C=λO→A+O→B,
即xy33==λλyx11++yx22., 又 C 为双曲线上一点,即 x32 5 y32 5b2 ,
3.(2011·山东)已知双曲线ax22-by22=1(a>0,b>0)的两条渐近线均 和圆 C:x2+y2-6x+5=0 相切,且双曲线的右焦点为圆 C
的圆心,则该双曲线的方程为
()
A.x52-y42=1 C.x32-y62=1
B .x42-y52=1 D.x62-y32=1
解析 ∵双曲线ax22-by22=1 的渐近线方程为 y=±bax, 圆 C 的标准方程为(x-3)2+y2=4,
又|BC|=2|BF|,所以|BC|=2|BM|.
由 BM∥AQ 得,|AC|=2|AQ|=6,
|CF|=3. ∴|NF|=12|CF|=32. 即 p=32.抛物线方程为 y2=3x. 答案 (1)B (2)y2=3x
二、圆锥曲线的方程及应用 例 2 (2010·天津) 已知椭圆xa22+by22=1(a>b>0)的离心率 e=
=-21(+2-4k82k2)+1+6k4k2(1+4k4k2+1+6k4k2)=4(16(k14++41k52k)22-1)=4
整理得
7k2=2,故
k=±
714.所以
y0=±2
14 5.
综上,y0=±2
2或
y0=±2
14 5.
高考数学十年真题专题解析—双曲线
双曲线年份题号考点考查内容2011理7双曲线直线与双曲线的位置关系,双曲线的几何性质2012理8文10双曲线抛物线与双曲线的几何性质,直线与双曲线的位置关系2013卷1文理4双曲线双曲线的离心率和渐近线2014卷1理4双曲线双曲线的标准方程及其几何性质文4双曲线双曲线的离心率卷2理5双曲线双曲线的标准方程及其几何性质2015卷1文16双曲线双曲线的定义;直线与双曲线的位置关系卷2理11双曲线双曲线的标准方程及其几何性质文15双曲线双曲线的标准方程的求法,双曲线的渐近线2016卷2理11双曲线双曲线的几何性质,双曲线离心率的计算2017卷1理15双曲线双曲线的几何性质,双曲线离心率的求法文5双曲线双曲线标准方程及其几何性质卷2理9圆、双曲线圆的几何性质,双曲线的几何性质,双曲线离心率的计算文5双曲线双曲线的几何性质,双曲线离心率的计算卷3理5双曲线双曲线与椭圆的几何性质,待定系数法求双曲线的方程文14双曲线双曲线的渐近线2018卷1理11双曲线双曲线的几何性质,直线与双曲线的位置关系卷2理5文6双曲线双曲线的几何性质卷3理11双曲线双曲线的几何性质,双曲线离心率的求法文10双曲线双曲线的离心率、渐近线,点到直线距离公式2019卷1理16双曲线双曲线的几何性质,双曲线离心率的求法文10双曲线双曲线的离心率、渐近线卷2理11文12圆、双曲线直线与圆的位置关系,双曲线的几何性质,双曲线离心率的求法卷3理10双曲线双曲线的定义、标准方程及其几何性质文10双曲线双曲线的定义、标准方程及其几何性质2020卷1理15双曲线双曲线的定义、标准方程及其几何性质,双曲线离心率的求法文11双曲线双曲线的定义、标准方程及其几何性质卷2理8文9双曲线双曲线的几何性质,直线与双曲线的位置关系卷3理11双曲线双曲线的定义、标准方程及其几何性质文14双曲线双曲线的渐近线、离心率考点出现频率2021年预测考点92双曲线的定义及标准方程23次考2次命题角度:(1)双曲线的定义及应用;(2)双曲线的标准方程;(3)双曲线的几何性质.核心素养:直观想象、数学运算考点93双曲线的几何性质23次考21次考点94直线与双曲线的位置关系23次考5次考点92双曲线的定义及标准方程1.(2017新课标Ⅲ理)已知双曲线C :22221(0,0)x y a b a b -=>>的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为A .221810x y -=B .22145x y -=C .22154x y -=D .22143x y -=【答案】B 【解析】由题意可得:52b a =,3c =,又222a b c +=,解得24a =,25b =,则C 的方程为2145x y 2-=,故选B .2.(2017天津理)已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,.若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线,则双曲线的方程为A .22144x y -=B .22188x y -=C .22148x y -=D .22184x y -=【答案】B 【解析】设(,0)F c -,双曲线的渐近线方程为b y x a =±,由44PF k c c -==-,由题意有4b c a=,又ca=222c a b =+,得b =,a =B .3.【2017天津文】已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,点A 在双曲线的渐近线上,OAF△是边长为2的等边三角形(O 为原点),则双曲线的方程为()A .221412x y -=B .221124x y -=C .2213x y -=D .2213y x -=【答案】D【解析】由题意可得2222tan 603c c a b ba ⎧⎪=⎪=+⎨⎪⎪=︒=⎩,解得221,3ab ==,故双曲线方程为2213y x -=,故选D .4.(2016天津理)已知双曲线222=1(0)4x y b b->,以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点,四边形的ABCD 的面积为2b ,则双曲线的方程为()A .22443=1y x -B .22344=1y x -C .2224=1x y b-D .2224=11x y -【答案】D 【解析】不妨设A 在第一象限,(,)A x y ,所以2242x y by x ⎧+=⎪⎨=⎪⎩,解得224424x b y b ⎧=⎪+⎪⎨⎪=⎪+⎩,故四边形ABCD 的面积为22232442444bxy b b b b =⨯==+++,解得212b =.故所求的双曲线方程为2224=11x y -,故选D .5.【2016天津文】已知双曲线)0,0(12222>>=-b a b y a x 的焦距为52,且双曲线的一条渐近线与直线02=+y x 垂直,则双曲线的方程为()A .1422=-y x B .1422=-y x C .15320322=-y x D .12035322=-y x 【答案】A【解析】由题意得2215,2,11241b x yc a b a ==⇒==⇒-=,故选A .6.(2015安徽理)下列双曲线中,焦点在y 轴上且渐近线方程为2y x =±的是A .2214y x -=B .2214x y -=C .2214y x -=D .2214x y -=【答案】C 【解析】由题意,选项,A B 的焦点在x 轴,故排除,A B ,C 项的渐近线方程为2204y x -=,即2y x =±,故选C .7.(2014天津理)已知双曲线22221x y a b-=()0,0a b >>的一条渐近线平行于直线l :210y x =+,双曲线的一个焦点在直线l 上,则双曲线的方程为A .221520x y -=B .221205x y -=C .2233125100x y -=D .2233110025x y -=【答案】A 【解析】依题意得22225b a c c a b ìï=ïïï=íïïï=+ïî,所以25a =,220b =,双曲线的方程为221520x y -=.8.(2012湖南文理)已知双曲线C :22x a -22y b =1的焦距为10,点P(2,1)在C 的渐近线上,则C 的方程为A .220x -25y =1B .25x -220y =1C .280x -220y =1D .220x -280y =1【答案】A 【解析】设双曲线C :22x a -22y b=1的半焦距为c ,则210,5c c ==.又 C 的渐近线为b y x a =±,点P(2,1)在C 的渐近线上,12ba∴=,即2a b =.又222c a b =+,a ∴==,∴C 的方程为220x -25y =1.9.(2011山东文理)已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线均和圆C :22x y +-650x +=相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为A .22154x y -=B .22145x y -=C .22136x y -=D .22163x y -=【答案】A 【解析】圆22:(3)4C x y -+=,3,c =而32bc=,则22,5b a ==,故选A .10.(2016北京文)已知双曲线22221x y a b-=(0,0)a b >>的一条渐近线为20x y +=,一个焦点为,则a =_______;b =_____________.【答案】1,2a b ==.【解析】依题意有2c b a⎧=⎪⎨-=-⎪⎩,结合222c a b =+,解得1,2a b ==.11.(2016北京理)双曲线22221(0,0)x y a b a b -=>>的渐近线为正方形OABC 的边,OA OC 所在的直线,点B 为该双曲线的焦点.若正方形OABC 的边长为2,则a =______.2【解析】不妨令B 为双曲线的右焦点,A 在第一象限,则双曲线图象如图,∵OABC 为正方形,2=OA∴==c OB π4∠=AOB ,∵直线OA 是渐近线,方程为=b y x a ,∴tan 1=∠=bAOB a,又∵2228+==a b c ,∴2=a.12.(2015新课标1文)已知双曲线过点)3,4(,且渐近线方程为x y 21±=,则该双曲线的标准方程为.【答案】2214x y -=【解析】∵双曲线的渐近线方程为x y 21±=,故可设双曲线的方程为22(0)4x y λλ-=>,又双曲线过点)3,4(,∴2244λ-=,∴1λ=,故双曲线的方程为2214x y -=.13.(2015北京理)已知双曲线()22210x y a a-=>0y +=,则a =.33【解析】因为双曲线()22210x y a a -=>的一条渐近线为y =,所以1a =,故33a =.14.(2011山东文理)已知双曲线22221(0,0)x y a b a b -=>>和椭圆221169x y +=有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为.【答案】22143x y -=【解析】由题意可知双曲线的焦点(,,即c =心率为274c a =,∴2a =,故23b =,∴双曲线的方程为22143x y -=.考点93双曲线的几何性质15.(2020·新课标Ⅰ文)设12,F F 是双曲线22:13y C x -=的两个焦点,O 为坐标原点,点P 在C 上且||2OP =,则12PF F △的面积为()A .72B .3C .52D .2【答案】B【解析】由已知,不妨设12(2,0),(2,0)F F -,则1,2a c ==,∵121||1||2OP F F ==,∴点P 在以12F F 为直径的圆上,即12F F P 是以P 为直角顶点的直角三角形,故2221212||||||PF PF F F +=,即2212||||16PF PF +=,又12||||22PF PF a -==,∴2124||||PF PF =-=2212||||2PF PF +-12||||162PF PF =-12||||PF PF ,解得12||||6PF PF =,∴12F F P S =△121||||32PF PF =,故选B .16.【2020年高考全国Ⅲ卷理数11】已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点12,F F ,离心率为5.P 是C 上的一点,且P F P F 21⊥.若21F PF ∆的面积为4,则=a ()A .1B .2C .4D .8【答案】A【思路导引】根据双曲线的定义,三角形面积公式,勾股定理,结合离心率公式,即可得出答案.【解析】解法一:ca=c ∴=,根据双曲线的定义可得122PF PF a -=,12121||42PF F PF F S P =⋅=△,即12||8PF PF ⋅=,12F P F P ⊥ ,()22212||2PF PF c ∴+=,()22121224PF PF PF PF c ∴-+⋅=,即22540a a -+=,解得1a =,故选A .解法二:由题意知,双曲线的焦点三角形面积为2tan 221θb S F PF =.∴︒45tan 2b =4,则2=b ,又∵5==ace ,∴1=a .解法三:设n PF m PF ==21,,则421==mn S F PF ,a n m 2=-,5,4222===+ace c n m ,求的1=a .17.【2020年高考浙江卷8】已知点()()()0,0,2,0,2,0O A B -.设点P 满足–2PA PB =,且P 为函数y =图像上的点,则OP =()A.2B.5CD.【答案】D【解析】由条件可知点P 在以,A B 为焦点的双曲线的右支上,并且2,1c a ==,∴23b =,方程为()22103yx x -=>且点P为函数y =上的点,联立方程()22103y x x y ⎧-=>⎪⎨⎪=⎩,解得:2134x =,2274y =,OP ∴==D .18.【2019·全国Ⅰ文】双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线的倾斜角为130°,则C 的离心率为()A .2sin40°B .2cos40°C .1sin50︒D .1cos50︒【答案】D【解析】由已知可得tan130,tan 50b ba a-=︒∴=︒,1cos50 cea∴======︒,故选D.19.【2019年高考全国Ⅱ理】设F为双曲线C:22221(0,0)x y a ba b-=>>的右焦点,O为坐标原点,以OF 为直径的圆与圆222x y a+=交于P,Q两点.若PQ OF=,则C的离心率为A BC.2D【答案】A【解析】设PQ与x轴交于点A,由对称性可知PQ x⊥轴,又||PQ OF c==,||,2cPA PA∴=∴为以OF为直径的圆的半径,∴||2cOA=,,22c cP⎛⎫∴ ⎪⎝⎭,又P点在圆222x y a+=上,22244c c a∴+=,即22222,22c ca ea=∴==.e∴=,故选A.20.【2019年高考全国Ⅲ卷理数】双曲线C:2242x y-=1的右焦点为F,点P在C的一条渐近线上,O为坐标原点,若=PO PF,则△PFO的面积为A .324B .322C .22D .32【答案】A【解析】由222,2,6,a b c a b ===+=6,2P PO PF x =∴=,又P 在C 的一条渐近线上,不妨设为在b y x a =上,则263222P P b y x a =⋅=⨯=,1133262224PFO P S OF y ∴=⋅=⨯⨯=△,故选A .【名师点睛】本题考查以双曲线为载体的三角形面积的求法,渗透了直观想象、逻辑推理和数学运算素养.21.【2019·全国Ⅲ文】已知F 是双曲线C :22145x y -=的一个焦点,点P 在C 上,O 为坐标原点,若=OP OF ,则OPF △的面积为A .32B .52C .72D .92【答案】B【解析】设点()00,P x y ,则2200145x y -=①.又453OP OF ==+=,22009x y ∴+=②.由①②得20259y =,即053y =,0115532232OPF S OF y ∴=⋅=⨯⨯=△,故选B .22.【2019·北京文】已知双曲线2221x y a-=(a>0)的离心率是5,则a=()A 6B .4C .2D .12【答案】D【解析】∵双曲线的离心率c e a ==c =,∴1a=12a =,故选D .23.【2019·浙江卷】渐近线方程为x±y=0的双曲线的离心率是()A .22B .1C .D .2【答案】C【解析】∵双曲线的渐近线方程为0x y ±=,∴a b =,则c ==,∴双曲线的离心率ce a==C .24.(2018全国Ⅱ文理)双曲线22221(0,0)-=>>x y a b a b的离心率为()A .=yB .=yC .2=±y x D .2=±y x 【答案】A【解析】∵c e a ==,∴2222221312b c a e a a-==-=-=,∴b a =b y x a =±,∴渐近线方程为y =,故选A .25.【2018·全国Ⅲ文】已知双曲线2222:1(0,0)x y C a b a b-=>>,则点(4,0)到C 的渐近线的距离为A B .2C .322D .【答案】D【解析】c e a === 1b a ∴=,∴双曲线C 的渐近线方程为0x y ±=,∴点(4,0)到渐近线的距离d ==,故选D .26.【2018高考浙江2】双曲线2213x y -=的焦点坐标是()A .()),0,B .()()20,0,2,-C .((0,,0D .()()0,22,0,-【答案】B【解析】试题分析:根据双曲线方程确定焦点位置,再根据222c a b =+求焦点坐标.试题解析: 双曲线方程为2213x y -=,∴焦点坐标可设为()0,c ±.222,3142c a b c =+=+== ,∴焦点坐标为()20,±,故选B .【名师点睛】由双曲线方程()222210,0x y a b a b-=>>可得焦点坐标为()(,0c c ±=,顶点坐标为()0,a ±,渐近线方程为by x a=±.27.【2018高考全国1理11】已知双曲线13:22=-y x C ,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为,M N .若OMN △为直角三角形,则=MN ()A .23B .3C .32D .4【答案】B【解析】【基本解法1】(直接法)∵双曲线221,(2,0)3x y F -=,∴渐近线方程为33y x =±,倾斜角分别为30,150 ,∴60MON ∠= ,不妨设90MNO ∠= ,∴30,30OMN FON ∠=∠= ,∵2OF =,∴在Rt FON ∆中,3cos3022ON OF =⋅=⨯=,∴在Rt MON ∆中,tan 603MN ON =⋅==.【基本解法2】(直接法)根据题意,可知其渐近线的斜率为()2,0F ,从而得到30FON ∠=︒,∴直线MN 的倾斜角为60︒或120︒,根据双曲线的对称性,设其倾斜角为60︒,可以得出直线MN的方程为)2y x =-,分别与两条渐近线y =和y x =联立,求得(33,,,32M N MN ⎛∴= ⎝⎭,故选B .28.【2018高考天津文理7】已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为()A .221412x y -=B .221124x y -=C .22139x y -=D .22193x y -=【答案】C【解析】设双曲线的右焦点坐标为()()00,F c c >,则A B x x c ==,由22221c y a b -=可得:2b y a =±,不妨设:22,,,b b Ac B c a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,双曲线的一条渐近线方程为:0bx ay -=,据此可得:21bc b d c -==,22bc b d c +==,则12226bc d d b c +===,则23,9b b ==,双曲线的离心率:2c e a ===,据此可得:23a =,则双曲线的方程为22139x y -=,故选C .29.【2017·全国Ⅰ文】已知F 是双曲线C :1322=-y x 的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是(1,3),则△APF 的面积为A .13B .12C .23D .32【答案】D【解析】由2224c a b =+=得2c =,∴(2,0)F ,将2x =代入2213y x -=,得3y =±,∴3||=PF ,又点A 的坐标是(1,3),故△APF 的面积为133(21)22⨯⨯-=,故选D .30.【2017·全国Ⅱ文】若1a >,则双曲线2221x y a-=的离心率的取值范围是()A .)+∞B .2)C .D .(1,2)【答案】C【解析】由题意得222222111c a e a a a+===+,∵1a >,∴21112a <+<,则1e <<C .31.(2017新课标Ⅱ理)若双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线被圆22(2)4x y -+=所截得的弦长为2,则C 的离心率为()A .2B C D .233【答案】A 【解析】双曲线C 的渐近线方程为0bx ay ±=,圆心(2,0)到渐近线的距离为2b d c==,圆心(2,0)到弦的距离也为d ==,所以2b c =,又222c a b =+,所以得2c a =,所以离心率2ce a==,选A .32.(2016全国I 理)已知方程222213x y m n m n-=+-表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是A .(–1,3)B .(–1,3)C .(0,3)D .(0,3)【答案】A 【解析】由题意得22()(3)0m n m n +->,解得223m n m -<<,又由该双曲线两焦点间的距离为4,得M 2234m n m n ++-=,即21m =,所以13n -<<.33.(2016全国II 理)已知1F ,2F 是双曲线E :22221x y a b-=的左、右焦点,点M 在E 上,1MF 与x 轴垂直,211sin 3MF F ∠=,则E 的离心率为()A B .32C D .2【答案】A 【解析】设1(,0)F c -,将x c =-代入双曲线方程,得22221c y a b -=,化简得2by a=±,因为211sin 3MF F ∠=,所以222212112||tan ||222b MF b c a a MF F F F c ac ac-∠=====122224c a e a c e -=-=,所以22102e e --=,所以e =A .34.(2016浙江理)已知椭圆1C :2221x y m +=(1m >)与双曲线2C :2221x y n -=(0n >)的焦点重合,1e ,2e 分别为1C ,2C 的离心率,则A .m n >且121e e >B .m n >且121e e <C .m n <且121e e >D .m n <且121e e <【答案】A 【解析】由题意知2211m n -=+,即222m n =+,222221222221111()2m n n n e e m n n n -+++=⋅=⋅+4242422111122n n n n n n ++==+>++,∴121e e >.故选A .35.(2015湖南文)若双曲线22221x y a b-=的一条渐近线经过点(3,4)-,则此双曲线的离心率为A.3B .54C .43D .53【答案】D 【解析】由已知可得双曲线的渐近线方程为by x a=±,点(3,4)-在渐近线上,∴43b a =,又222a b c +=,∴2222162599c a a a =+=,∴53c e a ==.36.(2015四川文理)过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于,A B 两点,则||AB =A.3B .C .6D .【答案】D 【解析】双曲线2213y x -=的右焦点为(2,0),渐近线方程为y =,将2x =代入y =得y =±,∴||AB =.37.(2015福建理)若双曲线22:1916x y E -=的左、右焦点分别为12,F F ,点P 在双曲线E 上,且13PF =,则2PF 等于()A .11B .9C .5D .3【答案】B 【解析】由双曲线定义得1226PF PF a -==,即236PF -=,解得29PF =,故选B .38.(2015湖北理)将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度,得到离心率为2e 的双曲线2C ,则A .对任意的,a b ,12e e >B .当a b >时,12e e >;当a b <时,12e e <C .对任意的,a b ,12e e <D .当a b >时,12e e <;当a b <时,12e e >【答案】D【解析】由题意1e a ==,2e ==∵()()b b m m b a a a m a a m +--=++,由于0m >,0a >,0b >,所以当a b >时,01b a <<,01b m a m +<<+,b b m a a m +<+,22(()b b m a a m+<+,所以12e e <;当a b <时,1b a >,1b m a m +>+,而b b m a a m +>+,22((b b m a a m+>+,所以12e e >.所以当a b >时,12e e <;当a b <时,12e e >.39.(2015重庆文)设双曲线22221(0,0)x y a b a b-=>>的右焦点是F ,左、右顶点分别是12,A A ,过F 做12A A 的垂线与双曲线交于,BC 两点,若12A B A C ⊥,则双曲线的渐近线的斜率为A .12±B .22C .1±D.【答案】C 【解析】由题意,得12(,0),(,0),(,0)A a A a F c -,将x c =代入双曲线方程,解得2b y a =±.不妨设2(,)b B c a ,2(,)b C c a -,则1222,A BA C b b a a k k c a c a-==+-,根据题意,有221b b a a c a c a -⋅=-+-,整理得1b a=,∴双曲线的渐近线的斜率为1±.40.(2015重庆理)设双曲线22221x y a b-=(0,0a b >>)的右焦点为F ,右顶点为A ,过F 作AF 的垂线与双曲线交于,B C 两点,过,B C 分别作,AC AB 的垂线,两垂线交于点D .若D 到直线BC的距离小于a ,则该双曲线的渐近线斜率的取值范围是A .(1,0)(0,1)-∪B .(,1)(1,)-∞-+∞∪C.∪D.(,1))-∞-+∞∪【答案】A 【解析】由题意22(,0),(,),(,)b b A a B c C c a a -,由双曲线的对称性知D 在x 轴上,设(,0)D x ,由BD AC ⊥得221b b a a c x a c -⋅=---,解得42()b c x a c a -=-,所以42()b c x a a c a c a -=<=+-,所以42222b c a b a <-=221b a ⇒<01b a ⇒<<,而双曲线的渐近性斜率为b a±,所以双曲线的渐近线的斜率取值范围是(1,0)(0,1)- ,故选A .41.(2014新课标1文理)已知F 是双曲线C :223(0)x my m m -=>的一个焦点,则点F 到C 的一条渐近线的距离为AB .3CD .3m【答案】A 【解析】双曲线方程为22133x y m -=,焦点F到一条渐近线的距离为b =,故选A .42.(2014广东文理)若实数k 满足09k <<,则曲线221259x y k -=-与曲线221259x y k -=-的A .焦距相等B .实半轴长相等C .虚半轴长相等D .离心率相等【答案】A 【解析】∵09k <<,∴90,250k k ->->,本题两条曲线都是双曲线,又25(9)(25)9k k +-=-+,∴两双曲线的焦距相等,故选A .43.(2014重庆文理)设21F F ,分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点,双曲线上存在一点P使得,49||||,3||||2121ab PF PF b PF PF =⋅=+则该双曲线的离心率为A .34B .35C .49D .3【答案】B 【解析】由双曲线的定义得12||||||2PF PF a -=,又12||||3PF PF b +=,∴22221212(||||)(||||)94PF PF PF PF b a +--=-,即124||||9PF PF ab =,因此22949b a ab -=,即299()40b b a a --=,则(31b a +)(34ba-)=0,解得41(33b b a a ==-舍去),则双曲线的离心率251()3b e a =+=.44.(2013新课标1文理)已知双曲线C :22221x y a b-=(0,0a b >>)的离心率为52,则C 的渐近线方程为A .14y x =±B .13y x =±C .12y x =±D .y x=±【答案】C 【解析】由题知,52c a =,即54=22c a =222a b a +,∴22b a=14,∴b a =12±,∴C 的渐近线方程为12y x =±,故选C .45.(2013湖北文理)已知04πθ<<,则双曲线22122:1cos sin x y C θθ-=与222222:1sin sin tan y x C θθθ-=的A .实轴长相等B .虚轴长相等C .焦距相等D .离心率相等【答案】D 【解析】双曲线1C 的离心率是11cos e θ=,双曲线2C 的离心率是()222sin 1tan 1sin cos e θθθθ+==,故选D .46.(2012新课标文理)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于A 、B 两点,34||=AB ,则C 的实轴长为()A .2B .22C .4D .8【答案】C 【解析】设222:(0)C x y a a -=>交x y 162=的准线:4l x =-于(4,23)A -(4,23)B --得:222(4)(23)4224a a a =--=⇔=⇔=47.(2012福建文理)已知双曲线22215x y a -=的右焦点为(3,0),则该双曲线的离心率等于A .31414B .324C .32D .43【答案】C 【解析】∵双曲线22215x y a -=的右焦点为(3,0),∴2a +5=9,∴2a =4,∴a =2,∵c =3,∴32c e a ==,故选C .48.(2011安徽文理)双曲线x y 222-=8的实轴长是()A .2B .22C .4D .42【答案】C 【解析】x y 222-=8可变形为22148x y -=,则24a =,2a =,24a =.故选C .49.(2011湖南文理)设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为A .4B .3C .2D .1【答案】C 【解析】由双曲线方程可知渐近线方程为3y x a=±,故可知2a =.50.(2011天津文理)已知双曲线22221(0,0)x y a b a b-=>>的左顶点与抛物线22(0)y px p =>的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为()A .23B .25C .43D .45【答案】B 【解析】双曲线22221(0,0)x y a b a b-=>>的渐近线为by x a =±,由双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1)得22p -=-,即4p =,又∵42pa +=,∴2a =,将(-2,-1)代入by x a=得1b =,∴225c a b =+=,即225c =.51.【2020年高考全国Ⅰ理15】已知F 为双曲线()2222:10,0x y C a b a b-=>>的右焦点,A 为C 的右顶点,B 为C 上的点,且BF 垂直于x 轴.若AB 的斜率为3,则C 的离心率为.【答案】2【思路导引】根据双曲线的几何性质可知,2b BF a=,AF c a =-,即可根据斜率列出等式求解即可.【解析】依题可得,3BFAF =,而2b BF a=,AF c a =-,即23b a c a=-,变形得22233c a ac a -=-,化简可得,2320e e -+=,解得2e =或1e =(舍去).故答案为:2.52.【2020年高考江苏6】在平面直角坐标系xOy 中,若双曲线2221(0)5x y a a -=>的一条渐近线方程为52y x =,则该双曲线的离心率是.【答案】32【解析】由22205x y a -=得渐近线方程为5y x a =±,又0a >,则2a =,2259c a =+=,3c =,得离心率32c e a ==.53.【2020年高考北京卷12】已知双曲线22:163x y C -=,则C 的右焦点的坐标为________;C 的焦点到其渐近线的距离是__________.【答案】(3,0)【解析】∵双曲线22163x y -=,∴26a =,23b =,222639c a b =+=+=,∴3c =,∴右焦点坐标为(3,0),∵双曲线中焦点到渐近线距离为b,∴b =.54.【2019·江苏】在平面直角坐标系xOy 中,若双曲线2221(0)y x b b-=>经过点(3,4),则该双曲线的渐近线方程是▲.【答案】y =【解析】由已知得222431b-=,解得b =b =,∵0b >,∴b =.∵1a =,∴双曲线的渐近线方程为y =.55.【2018·北京文】若双曲线2221(0)4x y a a -=>的离心率为52,则a =________________.【答案】4【解析】在双曲线中c ==,且2c e a ==,∴2a a =,即216a =,∵0a >,∴4a =.56.(2018北京理14)已知椭圆22221(0)x y M a b a b +=>>:,双曲线22221x y N m n-=:.若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点,则椭圆M 的离心率为__________;双曲线N 的离心率为__________.12-;【解析】设椭圆的右焦点为(,0)F c ,双曲线N 的渐近线与椭圆M 在第一象限内的交点为A ,由题意可知(,22c A ,由点A 在椭圆M 上得,22223144c c a b +=,∴22222234b c a c a b +=,222b a c =-,∴22222222()34()a c c a c a a c -+=-,∴4224480a a c c -+=,∴428+40e e -=椭椭,∴24e =±椭,∴1e =椭(舍去)或1e =椭,∴椭圆M 1,∵双曲线的渐近线过点3(,22c A ,渐近线方程为y =,故双曲线的离心率2e ==双.57.【2018高考江苏8】在平面直角坐标系xOy 中,若双曲线()222210,0x y a b a b-=>>的右焦点(),0F c 到一条渐近线的距离为32,则其离心率的值是▲.【答案】2【解析】试题分析:先确定双曲线的焦点到渐近线的距离,再根据条件求离心率.试题解析:∵双曲线的焦点(),0F c 到渐近线by x a=±即0bx ay ±=的距离为bcb c==,2b c ∴=,因此222222311244,,2a c b c c c a c e =-=-===.【名师点睛】双曲线的焦点到渐近线的距离为b ,焦点在渐近线上的射影到坐标原点的距离为a .58.【2018高考上海2】双曲线2214x y -=的渐近线方程为.【答案】2x y =±【解析】由已知得24,1a b ==,渐近线方程为2x y =±.【考点分析】双曲线简单的几何性质,考查运算求解能力59.(2017新课标Ⅰ理)已知双曲线C :22221(0,0)x y a b a b-=>>的右顶点为A ,以A 为圆心,b 为半径做圆A ,圆A 与双曲线C 的一条渐近线交于M 、N 两点.若MAN ∠=60°,则C 的离心率为________.【答案】233【解析】如图所示,AH MN ⊥,AM AN b ==,MAN ∠=60°,所以30HAN ∠= ,又MN 所在直线的方程为by x a=,(,0)A a 到MN的距离AH =在Rt HAN ∆中,有cos HA HAN NA =,所以32=,即2=,因为222c a b =+,得2a c =,所以3c e a ==.60.(2017新课标Ⅲ文)双曲线2221(0)9x y a a -=>的一条渐近线方程为35y x =,则a =.【答案】5【解析】由双曲线的标准方程可得渐近线方程为3y x a=±,结合题意可得5a =.61.(2017山东文理)在平面直角坐标系xOy 中,双曲线22221(00)x y a b a b-=>>,的右支与焦点为F 的抛物线22(0)x py p =>交于A ,B 两点,若||||4||AF BF OF +=,则该双曲线的渐近线方程为.【答案】22y x =±【解析】由抛物线定义可得:||||=4222A B A B p p pAF BF y y y y p ++++=⨯⇒+=,∵22222222221202x y a y pb y a b a bx py⎧-=⎪⇒-+=⎨⎪=⎩,∴222A B pb y y p a a +==⇒=⇒渐近线方程为22y x =±.62.(2017北京文理)若双曲线221y x m-=的离心率为m =_________.【答案】2【解析】∵221,a b m ==,∴11c a ==2m =.63.【2016浙江文】设双曲线x 2–23y=1的左、右焦点分别为F 1,F 2.若点P 在双曲线上,且△F 1PF 2为锐角三角形,则|PF 1|+|PF 2|的取值范围是_______.【答案】(27,8).【解析】由已知得1,3,2a b c ===,则2ce a==,设(,)P x y 是双曲线上任一点,由对称性不妨设P 在双曲线的右支上,则12x <<,121PF x =+,221PF x =-,12F PF ∠为锐角,则2221212PF PF F F +>,即222(21)(21)4x x ++->,解得72x >,∴722x <<,则1247,8)PF PF x +=∈.64.(2016山东文理)已知双曲线E :22221x y a b-=(0,0)a b >>,若矩形ABCD 的四个顶点在E 上,AB ,CD 的中点为E 的两个焦点,且2||3||AB BC =,则E 的离心率是.【答案】2【解析】依题意,不妨设6,4AB AD ==,作出图象如下图所示则2124,2;2532,1,c c a DF DF a ===-=-==故离心率221c a ==65.(2015新课标1文)已知F 是双曲线C :2218y x -=的右焦点,P 是C 左支上一点,(0,66)A ,当APF ∆周长最小时,该三角形的面积为.【答案】C :2218y x -=的右焦点为(3,0)F ,实半轴长1a =,左焦点为(3,0)M -,∵P 在C 的左支上,∴ΔAPF 的周长|||||l AP PF AF =++||||||||PF AF AM PM ++-≥=||||21515232AF AM a ++=++=,当且仅当,,A P M 三点共线且P 在,A M 中间时取等号,此时直线AM的方程为13x =-,与双曲线的方程联立得P的坐标为(2,-,此时,ΔAPF的面积为116622⨯⨯-⨯⨯=.66.(2015山东文)过双曲线()2222:10,0x y C a b a b-=>>的右焦点作一条与其渐近线平行的直线,交C 于点P ,若点P 的横坐标为2a ,则C 的离心率为.【答案】2【解析】设直线方程为()b y x c a =-,由22221()x y a b b y x c a ⎧-=⎪⎪⎨⎪=-⎪⎩,得222a c x c +=,由2222a c a c+=,ce a =,解得2e =+(2e =-舍去).67.(2015山东理)平面直角坐标系xOy 中,双曲线1C :22221x y a b -=(0,0)a b >>的渐近线与抛物线2C :22x py =(0p >)交于,,O A B ,若△OAB 的垂心为2C 的焦点,则1C 的离心率为_______.32【解析】22122:1(0,0)x y C a b a b-=>>的渐近线为by x a =±,则2222(,)pb pb A a a ,2222(,)pb pb B a a -,22:2(0)C x py p =>的焦点(0,)2p F ,则22222AFpb pa a k pb b a-==,即2254b a =,2222294c a b a a +==,32c e a ==.68.(2014山东文理)已知双曲线22221(0,0)x y a b a b-=>>的焦距为2c ,右顶点为A ,抛物线22(0)x py p =>的焦点为F ,若双曲线截抛物线的准线所得线段长为2c ,且||FA c =,则双曲线的渐近线方程为.【答案】y x =±【解析】抛物线的准线2p y =-,与双曲线的方程联立得2222(1)4p x a b =+,根据已知得2222(1)4p a c b +=①,由||AF c =得2224p a c +=②,由①②得22a b =,即a b =,∴所求双曲线的渐近线方程为y x =±.69.(2014浙江文理)设直线30(0)x y m m -+=≠与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A ,B ,若点(,0)P m 满足||||PA PB =,则该双曲线的离心率是.【答案】2【解析】联立直线方程与双曲线渐近线方程b y x a =±可解得交点为(,)33am bmA b a b a--,(,33am bmB b a b a-++,而13ABk =,由||||PA PB =,可得AB 的中点3333(,)22am am bm bmb a b a b a b a -+-+-+与点)0,(m P 连线的斜率为-3,可得224b a =,∴52e =.70.(2014北京文理)设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________;渐近线方程为________.【答案】221312x y -=2y x =±【解析】设与2214y x -=具有相同渐近线的双曲线C 的方程为224y x k -=,将点()2,2代入C 的方程中,得3k =-.∴双曲线的方程为221312x y -=,渐近线方程为2y x =±.71.(2014湖南文理)设F 1,F 2是双曲线C :22221(0,0)x y a b a b-=>>的两个焦点.若在C 上存在一点P ,使PF 1⊥PF 2,且∠PF 1F 2=30°,则C 的离心率为_________.1+【解析】由已知可得,12cos30PF c ==,22sin 30PF c c == ,由双曲线的定义,2c a -=,则1c e a ===.72.(2013辽宁文理)已知F 为双曲线22:1916x y C -=的左焦点,,P Q 为C 上的点,若PQ 的长等于虚轴长的2倍,点(5,0)A 在线段PQ ,则PQF ∆的周长为.【答案】44【解析】由题意得,||||6FP PA -=,||||6FQ QA -=,两式相加,利用双曲线的定义得||||28FP FQ +=,∴PQF ∆的周长为||||||44FP FQ PQ ++=.73.(2013陕西理)双曲线221169x y -=的离心率为.45【解析】所以离心率为45,45162516922222=⇒==⇒=e ac e a b 74.(2012辽宁文理)已知双曲线122=-y x ,点21,F F 为其两个焦点,点P 为双曲线上一点,若21PF PF ⊥,则21PF PF +的值为.【答案】121,22,a c PF PF a ==∴-==22112224PF PF PF PF ∴-+=22212121221212,(2)8,24,()8412,PF PF PF PF c PF PF PF PF PF PF ⊥∴+==∴=∴+=+=∴+= 75.(2012天津文理)已知双曲线)0,0(1:22221>>=-b a by a x C 与双曲线1164:222=-y x C 有相同的渐近线,且1C的右焦点为F ,则a =b =.【答案】1,2【解析】双曲线的116422=-y x 渐近线为x y 2±=,而12222=-b y a x 的渐近线为x a by ±=,∴有2=a b,a b 2=,又双曲线12222=-by a x 的右焦点为)0,5(,∴5=c ,又222b a c +=,即222545a a a =+=,∴2,1,12===b a a .76.(2012江苏文理)在平面直角坐标系xOy 中,若双曲线22214x y m m -=+m 的值为.【答案】2【解析】由题意得m >0,∴a =m ,b =,4,422++=∴+m m c m 由e =5=a c得542=++mm m ,解得m =2.77.(2011北京文理)已知双曲线2221(0)y x b b-=>的一条渐近线的方程为2y x =,则b =.【答案】2【解析】由2221(0)y x b b -=>得渐近线的方程为2220y x b-=,即y bx =±,由一条渐近线的方程为2y x =得2b =.考点94直线与双曲线的位置关系78.(2020·新课标Ⅱ文理8)设O 为坐标原点,直线a x =与双曲线()2222:10,0x y C a b a b-=>>的两条渐近线分别交于,D EODE 的面积为8,则C 的焦距的最小值为()A .4B .8C .16D .32【答案】B【思路导引】∵()2222:10,0x y C a b a b-=>>,可得双曲线的渐近线方程是b y x a =±,与直线x a =联立方程求得D ,E 两点坐标,即可求得||ED ,根据ODE ∆的面积为8,可得ab值,根据2c =结合均值不等式,即可求得答案.【解析】∵2222:1(0,0)x y C a b a b -=>>,∴双曲线的渐近线方程是b y x a=±,直线x a =与双曲线2222:1(0,0)x y C a b a b-=>>的两条渐近线分别交于D ,E 两点,不妨设D 为在第一象限,E 在第四象限,联立x ab y x a =⎧⎪⎨=⎪⎩,解得x a y b =⎧⎨=⎩,故(,)D a b ,联立x ab y x a =⎧⎪⎨=-⎪⎩,解得x a y b =⎧⎨=-⎩,故(,)E a b -,∴||2ED b =,∴ODE ∆面积为:1282ODE S a b ab =⨯==△.双曲线2222:1(0,0)x y C a b a b-=>>,∴其焦距为28c =≥==,当且仅当a b ==取等号,∴C 的焦距的最小值:8,故选B .79.(2020·浙江卷)已知点O(0,0),A(–2,0),B(2,0).设点P 满足|PA|–|PB|=2,且P 为函数y=图像上的点,则|OP|=()A .222B .4105CD.【答案】D【解析】∵||||24PA PB -=<,∴点P 在以,A B 为焦点,实轴长为2,焦距为4的双曲线的右支上,由2,1c a ==可得,222413bc a=-=-=,即双曲线的右支方程为()22103y x x -=>,而点P 还在函数y =由()22103y x x y ⎧⎪⎨->==⎪⎩,解得132332x y ⎧=⎪⎪⎨⎪=⎪⎩,即OP ==80.(2019天津文理)已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为()ABC .2D【答案】D【解析】抛物线24y x =的准线l 的方程为1x =-,双曲线的渐近线方程为by x a=±,则有(1,(1,)b b A B a a ---,∴2b AB a =,24b a =,2b a =,∴c e aa===D .【名师点睛】本题考查抛物线和双曲线的性质以及离心率的求解,解题关键是求出AB 的长度.解答时,只需把4AB OF =用,,a b c 表示出来,即可根据双曲线离心率的定义求得离心率.81.【2018高考全国2理5】双曲线22221(0,0)x y a b a b-=>>,则其渐近线方程为()A.y =B.y =C .22y x =±D .32y x =±【答案】A【解析】试题分析:根据离心率得,a c 关系,进而得,a b 关系,再根据双曲线方程求渐近线方程,得结果.试题解析:222222,12,c b c a b e e a a a a-==∴==-=∴= .∵渐近线方程为,by x a=±∴渐近线方程为y =,故选A .【名师点睛】已知双曲线方程222210,0x y a b a b -=>>求渐近线方程:22220x y by x a b a-=⇒=±.【考点】双曲线的简单几何性质(离心率、渐近线方程)82.【2018高考全国3理11】设12F F ,是双曲线()2222100x y C a b a b-=>>:,的左,右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P.若1PF =,则C 的离心率为()AB .2CD【答案】C【解析】试题分析:由双曲线性质得到2PF b =,PO a =,然后在2Rt POF △和在12Rt PF F △中利用余弦定理可得.试题解析:由题可知22,PF b OF c ==,PO a ∴=.在2Rt POF △中,222cos P O PF bF OF c ∠==,22221212212||||||cos P O 2||||PF F F PF b F PF F F c ∠+-=∴=,222224(6),322b c bc a b c c+-∴=∴=⋅,e ∴=,故选C .【名师点睛】本题主要考查双曲线的相关知识,考查了双曲线的离心率和余弦定理的应用,属于中档题.83.(2018天津文理)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为()A .22139x y -=B .22193x y -=C .221412x y -=D .221124x y -=【答案】A【解析】设双曲线的右焦点坐标为(,0)(0)F c c >,则A B x x c ==,由22221c y a b -=可得2by a=±,不妨设2(,)b A c a ,2(),b B c a -,双曲线的一条渐近线方程为0bx ay -=,据此可得21d ==2bc b c -,222bc b d c +==,则12226bc d d b c +===,则3b =,29b =,双曲线的离心率2c e a ====,据此可得23a =,则双曲线的方程为22139x y -=,故选A .84.(2014天津文)已知双曲线22221x y a b-=()0,0a b >>的一条渐近线平行于直线l :210y x =+,双曲线的一个焦点在直线l 上,则双曲线的方程为A .221520x y -=B .221205x y -=C .2233125100x y -=D .2233110025x y -=【答案】A 【解析】依题意得22225b a c c a b ìï=ïïï=íïïï=+ïî,∴25a =,220b =,双曲线的方程为221520x y -=.85.(2013重庆文理)设双曲线C 的中心为点O ,若有且只有一对相较于点O 、所成的角为060的直线11A B 和22A B ,使1122A B A B =,其中1A 、1B 和2A 、2B 分别是这对直线与双曲线C 的交点,则该双曲线的离心率的取值范围是A.(,2]3B.[,2)3C.(,)3+∞D.[,)3+∞【答案】A 【解析】设双曲线的焦点在x 轴上,则由作图易知双曲线的渐近线的离心率ba必须满足33b a <,∴21(33b a <≤,241()43ba <+≤,既有23<,又双曲线的离心率为。
高考数学真题:双曲线含答案
专题九 解析几何第二十七讲 双曲线2019年1.(2019全国III 理10)双曲线C :2242x y -=1的右焦点为F ,点P 在C 的一条渐进线上,O 为坐标原点,若=PO PF ,则△PFO 的面积为A B C . D .2.(2019江苏7)在平面直角坐标系xOy 中,若双曲线2221(0)y x b b-=>经过点(3,4),则该双曲线的渐近线方程是 .3.(2019全国I 理16)已知双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1,F 2,过F 1的直线与C 的两条渐近线分别交于A ,B 两点.若1F A AB =,120F B F B ⋅=,则C 的离心率为____________.4.(2019年全国II 理11)设F 为双曲线C :22221(0,0)x y a b a b-=>>的右焦点,O 为坐标原点,以OF 为直径的圆与圆222x y a +=交于P ,Q 两点.若PQ OF =,则C 的离心率为ABC .2D 5.(2019浙江2)渐近线方程为x ±y =0的双曲线的离心率是A B .1CD .26.(2019天津理5)已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为C.22010-2018年一、选择题1.(2018浙江)双曲线2213x y -=的焦点坐标是A .(,B .(2,0)-,(2,0)C .(0,,D .(0,2)-,(0,2)2.(2018全国卷Ⅰ)已知双曲线C :2213-=x y ,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为M 、N .若∆OMN 为直角三角形,则||MN =A .32B .3C .D .43.(2018全国卷Ⅱ)双曲线22221(0,0)-=>>x y a b a bA .=yB .=yC .2=±y x D .2=±y x 4.(2018全国卷Ⅲ)设1F ,2F 是双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若1|||PF OP =,则C 的离心率为AB .2CD5.(2018天津)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线同一条渐近线的距离分别为1d 和2d , 且126d d +=,则双曲线的方程为A .221412x y -= B .221124x y -= C .22139x y -= D .22193x y -=6.(2017新课标Ⅱ)若双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线被圆22(2)4x y -+=所截得的弦长为2,则C 的离心率为A .2BCD .37.(2017新课标Ⅲ)已知双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线方程为2y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -=8.(2017天津)已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F .若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线,则双曲线的方程为A .22144x y -=B .22188x y -=C .22148x y -=D .22184x y -= 9.(2016天津)已知双曲线222=1(0)4x y b b->,以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点,四边形的ABCD 的面积为2b ,则双曲线的方程为A .22443=1y x -B .22344=1y x -C .2224=1x y b -D .2224=11x y - 10.(2016年全国I)已知方程222213x y m n m n-=+-表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是A .(–1,3)B .(–1,3)C .(0,3)D .(0,3)11.(2016全国II)已知1F ,2F 是双曲线E :22221x y a b-=的左、右焦点,点M 在E 上,1MF 与x 轴垂直,211sin 3MF F ∠=,则E 的离心率为A B .32C D .2 12.(2015四川)过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于,A B 两点,则AB =A B . C .6 D .13.(2015福建)若双曲线22:1916x y E -= 的左、右焦点分别为12,F F ,点P 在双曲线E 上,且13PF =,则2PF 等于A .11B .9C .5D .314.(2015湖北)将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度,得到离心率为2e 的双曲线2C ,则A .对任意的,a b ,12e e >B .当a b >时,12e e >;当a b <时,12e e <C .对任意的,a b ,12e e <D .当a b >时,12e e <;当a b <时,12e e > 15.(2015安徽)下列双曲线中,焦点在y 轴上且渐近线方程为2y x =±的是A .2214y x -= B .2214x y -= C .2214y x -= D .2214x y -= 16.(2015新课标1)已知00(,)M x y 是双曲线C :2212x y -=上的一点,12,F F 是C 的两个焦点,若120MF MF ⋅<,则0y 的取值范围是A .(B .(C .(,33-D .(33- 17.(2015重庆)设双曲线22221x y a b-=(0,0a b >>)的右焦点为F ,右顶点为A ,过F作AF 的垂线与双曲线交于,B C 两点,过,B C 分别作,AC AB 的垂线,两垂线交于点D .若D 到直线BC 的距离小于a 则该双曲线的渐近线斜率的取值范围是A .(1,0)(0,1)-∪B .(,1)(1,)-∞-+∞∪C .∪D .(,1))-∞-∞∪18.(2014新课标1)已知F 是双曲线C :223(0)x my m m -=>的一个焦点,则点F 到C的一条渐近线的距离为A B .3 C D .3m19.(2014广东)若实数k 满足09k <<,则曲线221259x y k-=-与曲线221259x y k -=-的 A .焦距相等 B .实半轴长相等 C .虚半轴长相等 D .离心率相等20.(2014天津)已知双曲线22221x y a b 0,0a b 的一条渐近线平行于直线l :210y x ,双曲线的一个焦点在直线l 上,则双曲线的方程为 A .221520x y B .221205x yC .2233125100x y D .2233110025x y21.(2014重庆)设21F F ,分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点,双曲线上存在一点P 使得,49||||,3||||2121ab PF PF b PF PF =⋅=+则该双曲线的离心率为 A .34 B .35 C .49D .322.(2013新课标1)已知双曲线C :22221x y a b-=(0,0a b >>C的渐近线方程为A .14y x =± B .13y x =± C .12y x =± D .y x =± 23.(2013湖北)已知04πθ<<,则双曲线1C :22221cos sin x y θθ-=与2C :22sin y θ2221sin tan y θθ-=的 A .实轴长相等 B .虚轴长相等 C .焦距相等 D . 离心率相等 24.(2013重庆)设双曲线C 的中心为点O ,若有且只有一对相较于点O 、所成的角为060的直线11A B 和22A B ,使1122A B A B =,其中1A 、1B 和2A 、2B 分别是这对直线与双曲线C 的交点,则该双曲线的离心率的取值范围是A .(2]3 B .[,2)3 C .()3+∞ D .[)3+∞ 25.(2012福建)已知双曲线22215x y a -=的右焦点为(3,0),则该双曲线的离心率等于A .14B .4 C .32D .4326.(2012湖南)已知双曲线C :22x a -22y b=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C 的方程为A .220x -25y =1B .25x -220y =1C .280x -220y =1 D .220x -280y =1 27.(2011安徽)双曲线x y 222-=8的实轴长是A .2B .C .4D .28.(2011山东)已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线均和圆22:650C x y x +-+=相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为A .22154x y -=B .22145x y -=C .22136x y -=D .22163x y -= 29.(2011湖南)设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为 A .4 B .3 C .2 D .130.(2011天津)已知双曲线22221(0,0)x y a b a b-=>>的左顶点与抛物线22(0)y px p =>的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(2,1)--,则双曲线的焦距为A .B .C .D .31.(2010新课标)已知双曲线E 的中心为原点,(3,0)P 是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为(12,15)N --,则E 的方程式为A .22136x y -= B .22145x y -= C .22163x y -= D .22154x y -= 32.(2010新课标)中心在原点,焦点在x 轴上的双曲线的一条渐近线经过点(4,2)-,则它的离心率为A B C .2 D .233.(2010福建)若点O 和点F 分别为椭圆22143x y +=的中心和左焦点,点P 为椭圆上的任意一点,则OP FP ⋅的最大值为A .2B .3C .6D .8 二、填空题34.(2018上海)双曲线2214x y -=的渐近线方程为 . 35.(2018江苏)在平面直角坐标系xOy 中,若双曲线22221(0,0)x y a b a b-=>>的右焦点(,0)F c 到一条渐近线的距离为2c ,则其离心率的值是 . 36.(2017江苏)在平面直角坐标系xOy 中 ,双曲线2213x y -=的右准线与它的两条渐近线分别交于点P ,Q ,其焦点是1F ,2F ,则四边形12F PF Q 的面积是 .37.(2017新课标Ⅰ)已知双曲线C :22221(0,0)x y a b a b-=>>的右顶点为A ,以A 为圆心,b 为半径做圆A ,圆A 与双曲线C 的一条渐近线交于M 、N 两点.若MAN ∠=60°,则C 的离心率为________.38.(2017山东)在平面直角坐标系xOy 中,双曲线22221(00)x y a b a b-=>>,的右支与焦点为F 的抛物线22(0)x py p =>交于A ,B 两点,若||||4||AF BF OF +=,则该双曲线的渐近线方程为 .39.(2017北京)若双曲线221y x m-=m =_________.40.(2016年北京)双曲线22221(0,0)x y a b a b-=>>的渐近线为正方形OABC 的边,OA OC所在的直线,点B 为该双曲线的焦点.若正方形OABC 的边长为2,则a =______.41.(2016山东)已知双曲线E :22221x y a b-=(0,0)a b >>,若矩形ABCD 的四个顶点在E上,AB ,CD 的中点为E 的两个焦点,且2||3||AB BC =,则E 的离心率是 .42.(2015北京)已知双曲线()22210x y a a-=>0y +=,则a = .43.(2015江苏)在平面直角坐标系xOy 中,P 为双曲线122=-y x 右支上的一个动点.若点P 到直线01=+-y x 的距离大于c 恒成立,则是实数c 的最大值为 .44.(2015山东)平面直角坐标系xOy 中,双曲线1C :22221x y a b-=(0,0)a b >>的渐近线与抛物线2C :22x py =(0p >)交于,,O A B ,若△OAB 的垂心为2C 的焦点,则1C 的离心率为_______.45.(2014山东)已知双曲线22221(0,0)x y a b a b-=>>的焦距为2c ,右顶点为A ,抛物线22(0)x py p =>的焦点为F ,若双曲线截抛物线的准线所得线段长为2c ,且||FA c =,则双曲线的渐近线方程为 .46.(2014浙江)设直线30(0)x y m m -+=≠与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A ,B ,若点(,0)P m 满足||||PA PB =,则该双曲线的离心率是____.47.(2014北京)设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________;渐近线方程为________.48.(2013陕西)双曲线221169x y -=的离心率为 .49.(2014湖南)设F 1,F 2是双曲线C :22221(0,0)x y a b a b-=>>的两个焦点.若在C 上存在一点P ,使PF 1⊥PF 2,且∠PF 1F 2=30°,则C 的离心率为_________.50.(2013辽宁)已知F 为双曲线22:1916x y C -=的左焦点,,P Q 为C 上的点,若PQ 的长等于虚轴长的2倍,点(5,0)A 在线段PQ ,则PQF ∆的周长为 .51.(2012辽宁)已知双曲线122=-y x ,点21,F F 为其两个焦点,点P 为双曲线上一点,若21PF PF ⊥,则21PF PF +的值为 .52.(2012天津)已知双曲线)0,0(1:22221>>=-b a by a x C 与双曲线1164:222=-y x C 有相同的渐近线,且1C 的右焦点为F ,则a = b = .53.(2012江苏)在平面直角坐标系xOy 中,若双曲线22214x y m m -=+则m 的值为 .54.(2011山东)已知双曲线22221(0,0)x y a b a b -=>>和椭圆221169x y +=有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .55.(2011北京)已知双曲线2221(0)y x b b-=>的一条渐近线的方程为2y x =,则b = .三、解答题56.(2014江西)如图,已知双曲线C :2221x y a-=(0a >)的右焦点F ,点B A ,分别在C的两条渐近线上,x AF ⊥轴,BF OB AB ,⊥∥OA (O 为坐标原点).(1)求双曲线C 的方程;(2)过C 上一点)0)((00,0≠y y x P 的直线1:020=-y y axx l 与直线AF 相交于点M ,与直线23=x 相交于点N ,证明:当点P 在C 上移动时,NFMF 恒为定值,并求此定值.57.(2011广东)设圆C 与两圆2222(5)4,(5)4x y x y ++=+=中的一个内切,另一个外切.(1)求C 的圆心轨迹L 的方程; (2)已知点M 3545(,5,0)55F ,且P 为L 上动点,求MP FP -的最大值及此时点P 的坐标.专题九 解析几何第二十七讲 双曲线答案部分2019年1. 解析 双曲线22:142x y C -=的右焦点为6,0)F ,渐近线方程为:22y x =±,不妨设点P 在第一象限,可得2tan POF ∠=63P ,所以PFO △的面积为: 133262=.故选A .2. 解析 因为双曲线2221(0)y x b b-=>经过点(3,4),所以221631b-=,解得22b =,即2b =. 又1a =,所以该双曲线的渐近线方程是2y x =±. 3.解析 如图所示,因为1F A AB =,所以A 为1F B 的中点. 又O 为12F F 的中点,所以212AOBF ,212AO BF =. 因为120F B F B ⋅=,所以1290F BF ∠=︒, 且O 为12F F 的中点,所以12212OB F F OF c ===. 由212AOBF 得2121BOF AOF BF F ∠=∠=∠,所以2OB BF =, 因此2OPF △为等边三角形,260BOF ∠=︒,即渐近线的斜率为3,也即3ba=, 所以2212b e a=+=.4.A 解析:解法一:由题意,把2c x =代入222x y a +=,得2224c PQ a =-,再由PQ OF =,得2224ca c -=,即222a c =,所以222c a=,解得2c e a ==.故选A .解法二:如图所示,由PQ OF =可知PQ 为以OF 为直径圆的另一条直径,所以,22c c P ⎛⎫± ⎪⎝⎭,代入222x y a +=得222a c =, 所以222c a=,解得2c e a ==.故选A .解法三:由PQ OF =可知PQ 为以OF 为直径圆的另一条直径,则1222OP a OF ===,2c e a ==故选A . 5.解析 根据渐进线方程为0x y ±=的双曲线,可得a b =,所以2c a =,则该双曲线的离心率为2ce a==C . 6.解析 因为抛物线24y x =的焦点为F ,准线为l ,所以()1,0F ,准线l 的方程为1x =-.因为与双曲线()222210,0x y a b a b=>>的两条渐近线分别交于点A 和点B ,且4AB OF =(为原点),所以2b AB a =,1OF =,所以24b a=,即2b a =, 所以225c a b a +=,所以双曲线的离心率为5ca==.故选D .2010-2018年1.B 【解析】由题可知双曲线的焦点在x 轴上,因为222314c a b =+=+=,所以2c =,故焦点坐标为(2,0)-,(2,0).故选B .2.B 【解析】因为双曲线2213-=x y 的渐近线方程为33=±y x ,所以60∠=MON .不妨设过点F 的直线与直线3=y 交于点M ,由∆OMN 为直角三角形,不妨设90∠=OMN ,则60∠=MFO ,又直线MN 过点(2,0)F ,所以直线MN 的方程为3(2)=-y x ,由2)⎧=-⎪⎨=⎪⎩y x y x,得32⎧=⎪⎪⎨⎪=⎪⎩x y3(,22M ,所以||==OM所以|||3==MN OM .故选B . 3.A 【解析】解法一由题意知,==ce a,所以=c,所以=b ,所以=b a=±=by x a,故选A .解法二由===c e a,得=ba,所以该双曲线的渐近线方程为=±=by x a.故选A . 4.C 【解析】不妨设一条渐近线的方程为by x a=, 则2F 到by x a =的距离d b ==, 在2Rt F PO ∆中,2||F O c =,所以||PO a =,所以1||PF =,又1||F O c =,所以在1F PO ∆与2Rt F PO ∆中,根据余弦定理得22212)cos cos 2a c aPOF POF ac c+-∠==-∠=-,即2223)0a c +-=,得223a c =.所以ce a==.故选C . 5.C 【解析】通解 因为直线AB 经过双曲线的右焦点,所以不妨取2(,)b A c a,2(,)b B c a -,取双曲线的一条渐近线为直线0bx ay -=,由点到直线的距离公式可得221bc b d c -==,222bc b d c +==, 因为126d d +=,所以226bc b bc b c c-++=,所以26b =,得3b =.因为双曲线22221(0,0)x y a b a b -=>>的离心率为2,所以2ca=,所以2224a b a+=,所以2294a a +=,解得23a =, 所以双曲线的方程为22139x y -=,故选C . 优解 由126d d +=,得双曲线的右焦点到渐近线的距离为3,所以3b =.因为双曲线22221(0,0)x y a b a b -=>>的离心率为2,所以2ca=,所以2224a b a+=,所以2294a a +=,解得23a =, 所以双曲线的方程为22139x y -=,故选C . 6.A 【解析】双曲线C 的渐近线方程为0bx ay ±=,圆心(2,0)到渐近线的距离为2bd c==,圆心(2,0)到弦的距离也为d ==所以2b c =222c a b =+,所以得2c a =,所以离心率2ce a==,选A . 7.B【解析】由题意可得:b a =,3c =,又222a b c +=,解得24a =,25b =, 则C 的方程为2145x y 2-=.选B . 8.B 【解析】设(,0)F c -,双曲线的渐近线方程为b y x a =±,由44PF k c c-==-,由题意有4bc a=,又c a =222c a b =+,得b =,a =.选B .9.D 【解析】不妨设A 在第一象限,(,)A x y ,所以2242x y b y x ⎧+=⎪⎨=⎪⎩,解得x y ⎧=⎪⎪⎨⎪=⎪⎩, 故四边形ABCD的面积为2324424bxy b b ===+,解得212b =.故所求的双曲线方程为2224=11x y -,选D . 10.A 【解析】由题意得22()(3)0m n m n +->,解得223m n m -<<,又由该双曲线两焦点间的距离为4,得M 2234m n m n ++-=,即21m =,所以13n -<<.11.A 【解析】设1(,0)F c -,将x c =-代入双曲线方程,得22221c y a b -=,化简得2by a=±,因为211sin 3MF F ∠=,所以222212112||tan ||222b MF b c a a MF F F F c ac ac -∠=====,12222c a e a c e -=-=210e --=,所以e =A . 12.D 【解析】由双曲线的标准方程2213y x -=得,右焦点(2,0)F ,两条渐近线方程为y =,直线AB :2x =,所以不妨设取(2,A,(2,B -,则||AB =,选D .13.B 【解析】由双曲线定义得1226PF PF a -==,即236PF -=,解得29PF =,故选B .14.D【解析】由题意1e ==2e ==∵()()b b m m b a a a m a a m +--=++,由于0m ,0a ,0b , 所以当a b 时,01b a <<,01b m a m +<<+,b b m a a m +<+,22()()b b m a a m+<+, 所以12e e <;当a b <时,1ba>,1b m a m +>+,而b b m a a m +>+,22()()b b m a a m +>+, 所以12e e >.所以当a b >时,12e e <;当a b <时,12e e >.15.C 【解析】由题意,选项,A B 的焦点在x 轴,故排除,A B ,C 项的渐近线方程为2204y x -=,即2y x =±,故选C . 16.A 【解析】由题意知22a,21b ,所以23c,不妨设1(F,2F ,所以100(,)=--MF x y ,200(3,)=-MF x y ,又∵00(,)M x y 在双曲线上,所以220012x y -=,即220022x y =+,222120003310MF MF x y y ⋅=-+=-<,所以033-<<y ,故选A . 17.A 【解析】 由题意22(,0),(,),(,)b b A a B c C c a a-,由双曲线的对称性知D 在x 轴上,设(,0)D x ,由BD AC ⊥得221b b a a c x a c-⋅=---,解得42()b c x a c a -=-,所以42()b c x a a c a c a -=<=+-,所以42222b c a b a <-=221b a⇒<01b a ⇒<<,而双曲线的渐近性斜率为ba±,所以双曲线的渐近线的斜率取值范围是(1,0)(0,1)-,选A .18.A 【解析】双曲线方程为22133x y m -=,焦点F 到一条渐近线的距离为b =A . 19.A 【解析】∵09k <<,∴90,250k k ->->,本题两条曲线都是双曲线,又25(9)(25)9k k +-=-+,∴两双曲线的焦距相等,选A .20.A 【解析】 依题意得22225ba cc a b ,所以25a,220b ,双曲线的方程为221520x y .21.B 【解析】由双曲线的定义得12||||||2PF PF a -=,又12||||3PF PF b +=,所以22221212(||||)(||||)94PF PF PF PF b a +--=-,即124||||9PF PF ab =,因此22949b a ab -=,即299()40b b aa --=,则(31b a +)(34ba-)=0,解得41(33b b a a ==-舍去),则双曲线的离心率53e ==.22.C 【解析】由题知,2c a =,即54=22c a =222a b a +,∴22b a =14,∴b a =12±,∴C 的渐近线方程为12y x =±,故选C . 23.D 【解析】双曲线1C 的离心率是11cos e θ=,双曲线2C 的离心率是21cos e θ==,故选D . 24.A 【解析】设双曲线的焦点在x 轴上,则由作图易知双曲线的渐近线的离心率ba必须满足3b a <,所以21()33b a <≤,241()43b a<+≤,2<,又双曲线的离心率为c e a ==23e <≤. 25.C 【解析】∵双曲线22215x y a -=的右焦点为(3,0),∴2a +5=9,∴2a =4,∴a =2∵c =3,∴32c e a ==,故选C . 26.A 【解析】设双曲线C :22x a -22y b=1的半焦距为c ,则210,5c c ==.又C 的渐近线为b y x a =±,点P(2,1)在C 的渐近线上,12ba∴=,即2a b =.又222c a b =+,a ∴==,∴C 的方程为220x -25y =1.27.C 【解析】x y 222-=8可变形为22148x y -=,则24a =,2a =,24a =.故选C . 28.A 【解析】圆22:(3)4C x y -+=,3,c =而32bc =,则22,5b a ==,应选A . 29.C 【解析】由双曲线方程可知渐近线方程为3y x a=±,故可知2a =.30.B 【解析】双曲线22221(0,0)x y a b a b -=>>的渐近线为by x a=±,由双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1)得22p-=-,即4p =, 又∵42p a +=,∴2a =,将(-2,-1)代入by x a=得1b =,∴c ==2c =31.B 【解析】由双曲线E 的中心为原点,(3,0)P 是E 的焦点可设双曲线的方程为2222221(9)x y a b a b -=+=,设1122(,),(,)A x y B x y ,即 2222112222221,1x y x y a b a b -=-= 则22121222121212015115312y y x x b b x x a y y a -+-+=⋅=⋅==-+-+,则22225,5,44b b a a ===,故E 的方程式为22145x y -=.应选B . 32.D 【解析】设双曲线的方程为22221(0,0)x y a b a b -=>>,其渐近线为x aby ±=,∵点(4,2)-在渐近线上,所以12b a =,由2e ==. 33.C 【解析】由题意,F (-1,0),设点P 00(,)x y ,则有2200143x y +=, 解得22003(1)4x y =-, 因为00(1,)FP x y =+,00(,)OP x y =,所以2000(1)OP FP x x y ⋅=++=00(1)OP FP x x ⋅=++203(1)4x -=20034x x ++, 此二次函数对应的抛物线的对称轴为02x =-,因为022x -≤≤,所以当02x =时,OP FP ⋅取得最大值222364++=,选C . 34.12y x =±【解析】由题意2a =,1b =,∴12b y x x a =±=±.35.2【解析】不妨设双曲线的一条渐近线方程为b y x a =2b ==,所以222234b c a c =-=,得2c a =,所以双曲线的离心率2ce a==. 36.232a x c ==,渐近线的方程为3y x =±,设3(,22P,则3(,22Q -,1(2,0)F -,2(2,0)F , 所以四边形12F PF Q的面积为1211||||422F F PQ =⨯=. 37.3【解析】如图所示,AH MN ⊥,AM AN b ==,MAN ∠=60°, x所以30HAN ∠=,又MN 所在直线的方程为by x a=, (,0)A a 到MN的距离AH =,在Rt HAN ∆中,有cos HA HAN NA =,所以2==因为222c a b =+a c =,所以c e a ==.38.y x =【解析】设11(,)A x y ,22(,)B x y ,由抛物线的定义有1212||||22p p AF BF y y y y p +=+++=++,而||2p OF =, 所以1242py y p ++=⨯,即12y y p +=,由2222212x y a b x py⎧-=⎪⎨⎪=⎩得2222220a y pb y a b -+=,所以21222pb y y a +=, 所以222pb p a=,即a =,所以渐近性方程为2y x =±. 39.2【解析】221,a b m ==,所以1c a ==,解得2m =. 40.2【解析】不妨令B 为双曲线的右焦点,A 在第一象限,则双曲线图象如图∵OABC 为正方形,2=OA∴==c OB ,π4∠=AOB ∵直线OA 是渐近线,方程为=b y x a ,∴tan 1=∠=bAOB a又∵2228+==a b c ∴2=a41.2【解析】由题意||2BC c =,所以||3AB c =,于是点3(,)2cc 在双曲线E 上,代入方程,得2222914c c a b -=,在由222a b c +=得E 的离心率为2ce a==,应填2. 42.3【解析】因为双曲线()22210x y a a -=>的一条渐近线为y =,所以1a=故3a =. 43.2(,),(1)P x y x ≥,因为直线10x y -+=平行于渐近线0x y -=,所以c 的最大值为直线10x y -+=与渐近线0x y -== 44.32【解析】22122:1(0,0)x y C a b a b -=>>的渐近线为b y x a =±,则2222(,)pb pb A a a ,2222(,)pb pb B a a -,22:2(0)C x py p =>的焦点(0,)2p F , 则22222AFpb pa a k pb b a-==,即2254b a =,2222294c a b a a +==,32c e a ==. 45.y x =±【解析】抛物线的准线2p y =-,与双曲线的方程联立得2222(1)4p x a b =+,根据已知得2222(1)4p a c b+= ①,由||AF c =得2224p a c += ②,由①②得22a b =,即a b =,所以所求双曲线的渐近线方程为y x =±.46.2【解析】联立直线方程与双曲线渐近线方程by x a=±可解得交点为(,)33am bm A b a b a --,(,)33am bm B b a b a -++,而13AB k =,由||||PA PB =,可得AB 的中点3333(,)22am am bm bmb a b a b a b a -+-+-+与点)0,(m P 连线的斜率为-3,可得224b a =,所以e =47.221312x y -= 2y x =±【解析】设与2214y x -=具有相同渐近线的双曲线C 的方程为224y x k -=,将点()2,2代入C 的方程中,得3k =-.∴双曲线的方程为221312x y -=,渐近线方程为2y x =±.48.45【解析】。
高考数学 双曲线总复习测试题
用心 爱心 专心 1 高考数学 双曲线总复习测试题 一、填空题 1. (2010·安徽改编)双曲线方程为x2-2y2=1,则它的右焦点坐标为________. 2. 双曲线2x2-y2+6=0上一点P到一个焦点的距离为4,则它到另一个焦点的距离为________. 3. (2011·江苏扬州中学模拟)如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为________.
4. (2010·苏州市高考信息卷)若双曲线经过点(3,2),且渐近线方程是y=±13x,则这条双曲线的方程是________. 5. 双曲线x29-y216=1的右顶点为A,右焦点为F.过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为________. 6. (2011·南通市第三次调研测试)双曲线x216-y29=1上的点P到点(5, 0)的距离是6,则点P的坐标是________. 7. 设双曲线x2a2-y2b2=1(a>0,b>0)的半焦距为c.已知原点到直线l:bx+ay=ab的距离
等于14c+1,则c的最小值为________. 8. (2011·皖南八校联考)双曲线x2a2-y2b2=1(a>0,b>0)中,F为右焦点,A为左顶点,点B(0,b)且AB⊥BF,则此双曲线的离心率为________. 二、解答题 9. 已知定圆M:(x-2)2+y2=8,动圆P过点N(-2,0),且与定圆M外切,求动圆P的圆心的轨迹方程.
10. 已知双曲线的渐近线方程为y=±43x,并且焦点都在圆x2+y2=100上,求双曲线方程. 用心 爱心 专心 2
11. (2010·山东改编)如图,已知椭圆x2a2+y2b2=1(a>b>0)的离心率为22,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为4(2+1).一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双曲线 题组一 双曲线的定义及标准方程 1.(2010·汕头一模)中心在原点,焦点在x轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为2,则双曲线方程为 ( ) A.x2-y2=1 B.x2-y2=2
C.x2-y2=2 D.x2-y2=12
解析:由题意,设双曲线方程为x2a2-y2a2=1(a>0), 则c=2a,渐近线y=x,∴|2a|2=2,∴a2=2. ∴双曲线方程为x2-y2=2. 答案:B 2.已知双曲线的两个焦点为F1(-10,0)、F2(10,0),M是此双曲线上的一点,且满足1MF·2MF=0,|1MF |·|2MF |=2,则该双曲线的方程是 ( )
A.x29-y2=1 B.x2-y29=1 C.x23-y27=1 D.x27-y23=1 解析:∵1MF·2MF=0,∴1MF⊥2MF,∴MF1⊥MF2, ∴|MF1|2+|MF2|2=40, ∴(|MF1|-|MF2|)2=|MF1|2-2|MF1|·|MF2|+|MF2|2=40-2×2=36, ∴||MF1|-|MF2||=6=2a,a=3, 又c=10,∴b2=c2-a2=1,
∴双曲线方程为x29-y2=1. 答案:A 题组二 双曲线的几何性质
3.(2009·宁夏、海南高考)双曲线x24-y212=1的焦点到渐近线的距离为 ( ) A.23 B.2 C.3 D.1
解析:双曲线x24-y212=1的焦点为(4,0)或(-4,0).渐近线方程为y=3x或y=-3x.由双曲线的对称性可知,任一焦点到任一渐近线的距离相等,d=|43+0|3+1=23. 答案:A 4.(2010·普宁模拟)已知离心率为e的曲线x2a2-y27=1,其右焦点与抛物线y2=16x的焦点重合,则e的值为 ( )
A.34 B.42323 C.43 D.234 解析:抛物线焦点坐标为(4,0),则a2+7=16, ∴a2=9,∴e=ca=43. 答案:C 5.(2009·江西高考)设F1和F2为双曲线x2a2-y2b2=1(a>0,b>0)的两个焦点,若F1,F2,P(0,2b)是正三角形的三个顶点,则双曲线的离心率为 ( ) A.32 B.2 C.52 D.3
解析:|PO||F1O|=tan60°, 2bc=3⇒4b2=3c2⇒4(c2-a2)=3c2⇒c2=4a2⇒c2a2=4⇒e=2:]
答案:B 6.(2010·广州模拟)已知点F是双曲线x2a2-y2b2=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是 ( ) A.(1,+∞) B.(1,2) C.(1,1+2) D.(2,1+2) 解析:如图,要使△ABE为锐角三角形,只需∠AEB为锐角,由双曲线对称性知△ABE为等腰三角形,从而只需满足∠AEF<45°.
又当x=-c时,y=b2a,
∴tan∠AEF=|AF||EF|=b2a(a+c)<1, ∴e2-e-2<0, 又e>1,∴1答案:B 题组三 直线与双曲线的位置关系 7.(2010·西安调研)过点P(4,4)且与双曲线x216-y29=1只有一个交点的直线有 ( ) A.1条 B.2条 C.3条 D.4条 解析:如图所示,满足条件的直线共有3条.
答案:C 8.设双曲线x29-y216=1的右顶点为A,右焦点为F,过点F作平行双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为________. 解析:由题意知,A(3,0),F(5,0),渐近线斜率k=±43,
则直线方程为y=43(x-5),代入x29-y216=1,得x=175, ∴y=-3215,即B(175,-3215), ∴S△AFB=12×2×3215=3215. 答案:3215 题组四 双曲线的综合问题 9.(2010·德州模拟)P为双曲线x2-y215=1右支上一点,M、N分别是圆(x+4)2+y2=4和(x-4)2+y2=1上的点,则|PM|-|PN|的最大值为________. 解析:双曲线的两个焦点为F1(-4,0)、F2(4,0),为两个圆的圆心,半径分别为r1=2,r2=1,|PM|max=|PF1|+2,|PN|min=|PF2|-1,故|PM|-|PN|的最大值为(|PF1|+2)-(|PF2|-1)=|PF1|-|PF2|+3=5. 答案:5 10.(1)已知双曲线关于两坐标轴对称,且与圆x2+y2=10相交于点P(3,-1),若此圆过点P的切线与双曲线的一条渐近线平行,求此双曲线的方程;
(2)已知双曲线的离心率e=52,且与椭圆x213+y23=1有共同的焦点,求该双曲线的 方程. 解:(1)切点为P(3,-1)的圆x2+y2=10的切线方程是3x-y=10. ∵双曲线的一条渐近线与此切线平行,且双曲线关于两坐标轴对称,∴两渐近线方程为3x±y=0. 设所求双曲线方程为9x2-y2=λ(λ≠0). ∵点P(3,-1)在双曲线上,代入上式可得λ=80, ∴所求的双曲线方程为x2809-y280=1.
(2)在椭圆中,焦点坐标为(±10,0), ∴c=10,又e=ca=10a=52,∴a2=8,b2=2. ∴双曲线方程为x28-y22=1. 11.已知双曲线C:x24-y2=1,P是C上的任意点. (1)求证:点P到双曲线C的两条渐近线的距离的乘积是一个常数; (2)设点A的坐标为(3,0),求|PA|的最小值. 解:(1)证明:设P(x1,y1)是双曲线上任意一点, 该双曲线的两条渐近线方程分别是 x-2y=0和x+2y=0,
点P(x1,y1)到两条渐近线的距离分别是|x1-2y1|5和|x1+2y1|5.
它们的乘积是|x1-2y1|5·|x1+2y1|5=221145xy=45. ∴点P到双曲线C的两条渐近线的距离的乘积是一个常数. (2)设P的坐标为(x,y),则
|PA|2=(x-3)2+y2=(x-3)2+x24-1
=54(x-125)2+45. ∵|x|≥2,∴当x=125时,|PA|2的最小值为45, 即|PA|的最小值为255. 12.(文)已知椭圆C1的方程为x24+y2=1,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点. (1)求双曲线C2的方程; (2)若直线l:y=kx+2与双曲线C2恒有两个不同的交点A和B,且OA·OB>2(其中O为原点),求k的取值范围.
解:(1)设双曲线C2的方程为x2a2-y2b2=1, 则a2=4-1=3,c2=4, 由a2+b2=c2,得b2=1,
故C2的方程为x23-y2=1.
(2)将y=kx+2代入x23-y2=1,得 (1-3k2)x2-62kx-9=0. 由直线l与双曲线C2交于不同的两点,得
1-3k2≠0,Δ=(-62k)2+36(1-3k2)=36(1-k2)>0,
∴k2≠13且k2<1. ① 设A(x1,y1),B(x2,y2),则 x 1+x2=62k1-3k2,x1x2=-91-3k2.∴x1x2+y1y2=x1x2+(kx1+2)(kx2+2)
=(k2+1)x1x2+2k(x1+x2)+2=3k2+73k2-1. 又∵OA·OB>2,得x1x2+y1y2>2, ∴3k2+73k2-1>2,
即-3k2+93k2-1>0,解得13<k2<3, ② 由①②得13<k2<1, 故k的取值范围为(-1,-33)∪(33,1). (理)已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(3,0). (1)求双曲线C的方程; (2)若直线:y=kx+m(k≠0,m≠0)与双曲线C交于不同的两点M、N,且线段MN的垂直平分线过点A(0,-1),求实数m的取值范围.
解:(1)设双曲线方程为x2a2-y2b2=1(a>0,b>0). 由已知得a=3,c=2. 又a2+b2=c2,得b2=1.
故双曲线C的方程为x23-y2=1. (2)联立 y=kx+mx23-y2=1整理得 (1-3k2)x2-6kmx-3m2-3=0. ∵直线与双曲线有两个不同的交点,
∴ 1-3k2≠0Δ=12(m2+1-3k2)>0,可得m2>3k2-1且k2≠13. ① 设M(x1,y1),N(x2,y2),MN的中点为B(x0,y0).
则x1+x2=6km1-3k2,x0=x1+x22=3km1-3k2, y 0=kx0+m=m1-3k2. 由题意,AB⊥MN,
∵kAB=m1-3k2+13km1-3k2=-1k(k≠0,m≠0). 整理得3k2=4m+1. ② 将②代入①,得m2-4m>0,∴m<0或m>4.
又3k2=4m+1>0(k≠0),即m>-14.∴m的取值范围是(-14,0)∪(4,+∞).
高二数学 上学期直线的斜率与倾斜角例题(三) [例1]求经过两点P1(2,1)和P2(m,2)(m∈R)的直线l的斜率,并且求出l的倾斜角α及其取值范围. 选题意图:考查倾斜角与斜率之间的关系及斜率公式. 解:(1)当m=2时,x1=x2=2,∴直线l垂直于x轴,因此直线的斜率不存在,倾斜角
α=2
(2)当m≠2时,直线l的斜率k=21m∵m>2时,k>0. ∴α=arctan21m,α∈(0,2), ∵当m<2时,k<0 ∴α=π+arctan21m,α∈(2,π). 说明:利用斜率公式时,应注意斜率公式的应用范围. [例2]若三点A(-2,3),B(3,-2),C(21,m)共线,求m的值. 选题意图:考查利用斜率相等求点的坐标的方法. 解:∵A、B、C三点共线,
