八年级数学下册1.4角平分线第2课时三角形三个内角的角平分线习题课件新版北师大版
北师大版数学八年级下册第2课时三角形三边的垂直平分线及作图课件(共18张)

∴ DA=DB,∴∠DAB=∠B=22.5°. ∴∠ADE=∠DAB+∠B=45°.
∵ AE⊥BC,∴∠DAE=∠ADE=45°.
∴ AE=DE.
又∵ DF⊥AC,∴∠DFC=∠AEC=90°.
A
∴∠C+∠CAE=∠C+∠CDF=90°. ∴∠CAE=∠CDF.
GF
∴△DEG≌△AEC (ASA). B ∴EG=EC.
别作三条线段的垂直平
分线,即点 P 为所求.
P
A
B
当堂小结 1. 定理:三角形三条边的垂直平分线相交于一点,并且
这一点到三个顶点的距离相等.
2. 已知等腰三角形的底边和底边上的高作等腰三角形.
l2 A
l3
l1
P
B
C
课堂练习
1. 如图,等腰△ABC 中,AB = AC,∠A = 20°.线段
AB 的垂直平分线交 AB 于 D,交 AC 于 E,连接 BE,
求证:边 AC 的垂直平分线经过
点 P,且 PA = PB = PC.
B
A
P C
分析:
l 是 AB 的垂 直平分线
m 是 BC 的 垂直平分线
PA=PB PB=PC
PA=PC
点 P 在 AC 的 垂直平分线上
A
l
n
试试看,你会写出证明过程吗? B
P
m
C
证明:连接 PA,PB,PC.
A
∵点 P 在 AB,AC 的垂直平分线上, l
能作出三角形吗? 如果能,能作几个? 所作出的三角形
都全等吗? 已知:三角形的一条边 a 和这边上的高 h.
A 求作:△ABC,使 BC = a,BC 边上的高为 h.
北师大版八年级下册数学第一章 三角形的证明第4节《角平分线》参考课件

相等的点,在这个角的平分线上.
如图, ∵PD=PE, PD⊥OA,PE⊥OB,垂足分
A D
别是D,E(已知),
O
∴点P在∠AOB的平分线上.(在一
1 2
P C
个角的内部,且到角的两边距离相
E
等的点,在这个角的平分线上).
B
老师提示:这个结论又是经常用来证明点在直线
上(或直线经过某一点)的根据之一.
例题讲析
角的两边距离相等.
∵OC是∠AOB的平分线,P是OC
上任意一点
O
,PD⊥OA,PE⊥OB,垂足分别
是D,E(已知)
∴PD=PE(角平分线上的点到
这个角的两边距离相等).
A D
1P
2
C
E B
逆定理 在一个角的内部,且 到角的两边距离相等的点,在 这个角的平分线上. ∵PD=PE, PD⊥OA,PE⊥OB,垂 O 足分别是D,E(已知), ∴点P在∠AOB的平分线 上.(在一个角的内部,且到角 的两边距离相等的点,在这个 角的平分线上).
任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.
A D
分析:要证明PD=PE,只要
证明它们所在△OPD≌△OPE
O
1 2
P C
而△OPD≌△OPE的条件由已 知易知它满足公理(AAS).
故结论可证.
E B
老师期望:你能写出规范的证明过程.
证明: ∵ OC是∠AOB的平分线 ∴ ∠1= ∠2 ∵ PD⊥OA,PE⊥OB ∴ ∠PDO= ∠PEO ∵OP=OP ∴ △OPD≌△OPE (AAS). ∴ PD=PE
BD 2 2D2E4 2cm
ACBCCD BD (44 2)cm
北师大版八年级数学下册第一章《角平分线》公开课课件

M P
A
C
B
B
N
A
P C
线段垂直平分线的性质定理 : 线段垂直平分线上的点到这条线段 两个端点距离相等.
∵ AC=BC,MN⊥AB,P是MN上任意一点 ∴ PA=PB
M P
性质定理的逆定理: 到一条线段两个端点距离相等的点,A 在这条线段的垂直平分线上.
∵ PA=PB zxxk ∴ 点P在AB的垂直平分线上.
CBN来自复习: 线段垂直平分线
“三角形三边中垂线”定理:
三角形三条边的垂直平分线相交于一点,
并且这一点到三顶点的距离相等.
A
P
B
C
第一章 第4节 角平分线(1)
角平分线的性质
1 你还记得角平分线上的点有什么性质吗? -角平分线上的点到这个角的两边的距离相等
条件:一个点在已知角的平分线上 结论:这个点到已知角的两边的距离相等
例题:
在 △ABC 中,∠ BAC = 60°,点 D 在 BC 上, AD = 10,DE⊥AB,DF⊥AC,垂足分别为 E, F,且 DE = DF,求 DE 的长.
随堂练习 1
1、如图,AD,AE分别是△ABC中∠A的内角平分线外角 平分线,它们有什么关系?
C E
D
B
A
F
随堂练习 2
2.如图,一目标在A区,到公路,铁路距离相等,离公 路与铁路的交叉处500m. 在图上标出它的位置 ( 比例尺 1:20 000 ).
.P C
E
B
•1、人才教育不是灌输知识,而是将开发文化宝库的钥匙,尽我们知道的交给学生。 •2、一个人的知识如果只限于学校学习到的那一些,这个人的知识必然是十分贫乏的2021/10/142021/10/142021/10/1410/14/2021 5:03:05 PM •3、意志教育不是发扬个人盲目的意志,而是培养合于社会历史发展的意志。 •4、智力教育就是要扩大人的求知范围 •5、最有价值的知识是关于方法的知识。 •6、我们要提出两条教育的诫律,一、“不要教过多的学科”;二、“凡是你所教的东西,要教得透彻”2021年10月2021/10/142021/10/142021/10/1410/14/2021 •7、能培养独创性和唤起对知识愉悦的,是教师的最高本领2021/10/142021/10/14October 14, 2021 •8、先生不应该专教书,他的责任是教人做人;学生不应该专读书,他的责任是学习人生之道。2021/10/142021/10/142021/10/142021/10/14
1.4角平分线(1)课件+2023-2024学年北师大版数学八年级下册

N
例题学习
例1 在△ABC中,∠BAC = 60°,点D在BC上,AD = 10,DE⊥AB,DF⊥AC,
垂足分别为 E,F,且DE = DF,求DE的长.
解:∵DE⊥AB,DF⊥AC,垂足分别为E,F,且DE = DF,
∴AD平分∠BAC(在一个角的内部,到角的两边
距离相等的点在这个角的平分线上).
PD = PE.
应该怎样进行证明呢?
探一探
角平分线的性质
求证:角平分线上的点到这个角的两边的距离相等.
定理:
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,
A
垂足分别为D,E.
D
求证:PD = PE.
证明:∵PD⊥OA,PE⊥OB,垂足分别为D,E,
P
∴∠PDO =∠PEO = 90°.
AB ,∠BDE = 90°.
∴BC = BD .
在Rt△BCE和Rt△BDE中,
∵BC = BD , BE = BE ,
∴Rt△BCE ≌ Rt△BDE (HL) .
∴∠CBE = ∠DBE.
即BE平分∠ABC.
习题1.9
4.如图,在∠AOB内部求作一点P,使PC = PD,并且点P到∠AOB两边的
∴△BDE ≌ △CDF (AAS).
∴DE = DF .
∵DE⊥AB于点E,DF⊥AC于点F,
∴AD平分∠BAC.
作
业
教材34页
第11题
再 见
距离相等.
作法:
l
1.连接CD,作线段CD的垂直平分线 l .
M
2.作∠AOB的角平分线OM,交直线 l
八年级数学下册第一章三角形的证明1.4.2角平分线练习(新版)北师大版
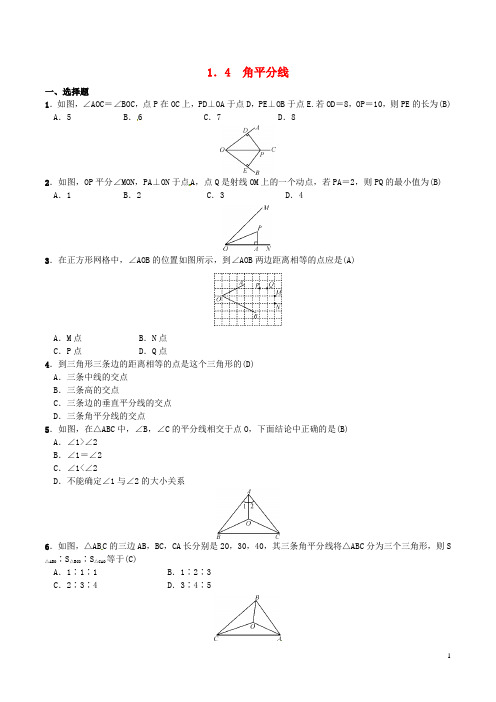
1.4 角平分线一、选择题1.如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E.若OD=8,OP=10,则PE的长为(B) A.5 B.6 C.7 D.82.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为(B) A.1 B.2 C.3 D.43.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是(A)A.M点 B.N点C.P点 D.Q点4.到三角形三条边的距离相等的点是这个三角形的(D)A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点5.如图,在△ABC中,∠B,∠C的平分线相交于点O,下面结论中正确的是(B)A.∠1>∠2B.∠1=∠2C.∠1<∠2D.不能确定∠1与∠2的大小关系6.如图,△AB C的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S △ABO∶S△BCO∶S△CAO等于(C)A.1∶1∶1 B.1∶2∶3C.2∶3∶4 D.3∶4∶57.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为(A)A.6 B.5 C.4 D.38.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是(B)A.PC=PDB.∠CPO=∠DOPC.∠CPO=∠DPOD.OC=OD9.如图,DA⊥AC,DE⊥BC,若AD=5 cm,DE=5 cm,∠ACD=30°,则∠DCE为(A)A.30°B.40°C.50°D.60°10.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于点D.如果∠A=30°,AE=6 cm,那么CE 等于(C)A. 3 cm B.2 cm C.3 cm D.4 cm11.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是(A)A.3 B.4 C.6 D.512.如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(C)A.△ABC三条中线的交点B.△ABC三边的中垂线的交点C.△ABC三条角平分线的交点D.△ABC三条高所在直线的交点二、填空题1.关于三角形角平分线的说法:①三角形三条角平分线的交点在三角形内;②两角平分线的交点在第三个角的平分线上;③两角平分线的交点到三边的距离相等;④两角平分线的交点到三个顶点的距离相等.其中正确的是①②③.2.边长为7,24,25的△ABC内有一点P到三边的距离相等,则这个距离是(B)A.1 B.3 C.4 D.63.如图,O是△ABC内一点,且点O到△ABC三边AB,BC,AC的距离OD=OE=OF,若∠A=70°,则∠BOC =125_°.4.如图,有三条铁路a,b,c相互交叉,现在建一个货物中转站,要求到三条铁路的距离相等,可供选择的地址有4处.三、解答题1.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.解:(1)∵在Rt△ABC中,∠C=90 °,∴AC⊥CD.又∵AD平分∠CAB,DE⊥AB,∴DE=CD.又∵CD=3,∴DE =3.(2)∵在Rt △ABC 中,∠C =90 °,AC =6,BC =8, ∴AB =AC 2+BC 2=62+82=10.∴S △ADB =12AB ·DE =12×10×3=15.2.如图,P 是∠BAC 内的一点,PE ⊥AB ,PF ⊥AC ,垂足分别为点E ,F ,AE =AF.求证: (1)PE =PF ;(2)点P 在∠BAC 的平分线上.证明:(1)连接AP. ∵PE ⊥AB ,PF ⊥AC , ∴∠AEP =∠AFP =90 °. 又∵AE =AF ,AP =AP ,∴Rt △AEP ≌Rt △AFP(HL). ∴PE =PF.(2)∵PE =PF ,且PE ⊥AB ,PF ⊥AC , ∴点P 在∠BAC 的平分线上.3.如图,四边形ABCD 中,∠B =90°,AB ∥CD ,M 为BC 边上的一点,且AM 平分∠BAD ,DM 平分∠ADC.(1)求证:AM ⊥DM ;(2)若BC =8,求点M 到AD 的距离.解:(1)证明:∵AM 平分∠BAD ,DM 平分∠ADC , ∴∠MAD =12∠BAD ,∠ADM =12∠ADC.∵AB ∥CD ,∴∠BAD +∠ADC =180 °.∴∠MAD +∠ADM =12(∠BAD +∠ADC)=90 °.又∵∠AMD +∠MAD +∠ADM =180 °, ∴∠AMD =90 °. ∴AM ⊥DM.(2)过M 作MN ⊥AD 于点N. ∵AB ∥DC ,∠B =90 °, ∴∠C =90 °.即BM ⊥AB ,MC ⊥DC.又∵AM ,DM 分别平分∠BAD ,∠ADC , ∴BM =MN ,MN =MC. ∴MN =12BC =4.∴M 到AD 的距离为4.4.已知:如图,锐角△ABC 的两条高BD ,CE 相交于点O ,且OB =OC. (1)求证:△ABC 是等腰三角形;(2)判断点O 是否在∠BAC 的平分线上,并说明理由.解:(1)证明:∵BD ,CE 是△ABC 的高, ∴∠BEC =∠CDB =90 °. 又∵∠EOB =∠DOC , ∴∠ABD =∠ACE. ∵OB =OC ,∴∠OBC =∠OCB. ∴∠ABC =∠ACB. ∴AB =AC.即△ABC 是等腰三角形.(2)点O 在∠BAC 的平分线上.理由:∵∠BOE =∠COD ,∠BOE +∠EBO =90 °, ∠COD +∠DCO =90 °, ∴∠EBO =∠DCO.又∵∠BEO =∠CDO =90 °,OB =OC , ∴△BOE ≌△COD(AAS). ∴OE =OD.又∵OD ⊥AC ,OE ⊥AB ,∴点O 在∠BAC 的平分线上.5.如图,在△ABC 中,BC 的垂直平分线DE 与∠BAC 的平分线AE 交于点E ,过E 作EP ⊥AB 于点P ,EQ ⊥AC 的延长线于点Q.求证:BP =CQ.证明:连接BE ,EC. ∵DE 垂直平分BC , ∴BE =CE.∵E 为∠BAC 的平分线上一点,EP ⊥AB ,EQ ⊥AC ,∴PE=QE,∠EPB=∠EQC=90 °.在Rt△BEP与Rt△CEQ中,∵BE=CE,PE=QE,∴Rt△BEP≌Rt△CEQ(HL).∴BP=CQ6.如图,在平面直角坐标系xOy中,已知点A(0,8)和点B(6,8).(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):①点P到A,B两点的距离相等;②点P到∠xOy两边的距离相等;(2)在(1)作出点P后,写出点P的坐标.解:(1)如图(作∠xOy的平分线交AB的垂直平分线于点P,点P即为所求作的点).(2)设AB的中垂线交AB于点E,交x轴于点F,由作图可得,EF⊥AB,EF⊥x轴,且OF=3.∵OP是坐标轴的角平分线,∴P(3,3).。
八年级数学下册第一章三角形的证明1.4.2角平分线课后作业(新版)北师大版

1.4.2 角平分线1.如图,△AB C 的三边AB ,BC ,CA 长分别是20,30,40,其三条角平分线将△ABC 分为三个三角形,则S △ABO ∶S △BCO ∶S △CAO 等于( )A .1∶1∶1B .1∶2∶3C .2∶3∶4D .3∶4∶52.边长为7,24,25的△ABC 内有一点P 到三边的距离相等,则这个距离是( )A .1B .3C .4D .63.如图,O 是△ABC 内一点,且点O 到△ABC 三边AB ,BC ,AC 的距离OD =OE =OF ,若∠A=70°,则∠BOC= .4.如图,在△ABC 中,PD⊥AC,PE⊥AB,PF⊥BC ,PD =PE =PF ,求证:∠BPC=90°+12∠B AC.5.如图,在Rt△ABC 中,∠C=90°,BD 是Rt△ABC 的一条角平分线,点O ,E ,F 分别在BD ,BC ,AC 上,且四边形OECF 是正方形. (1)求证:点O 在∠BAC 的平分线上;(2)若AC =5,BC =12,求OE 的长.参考答案 1.C 2.B 3. 125°4. 证明:∵PD⊥AC,PE⊥AB,PF⊥BC,PD =PE =PF , ∴点P 是△ABC 三个内角平分线的交点.∴CP 平分∠ACB,BP 平分∠AB C.∴∠PCB=12∠ACB,∠PBC=12∠ABC.∴∠BPC=180 °-∠PCB-∠PBC=180 °-12∠ACB-12∠ABC=180 °-12(∠ACB+∠ABC)=180 °-12(180 °-∠BAC)=90 °+12∠BAC.5.解:(1)证明:过点O 作OM⊥AB 于点M.∵四边形O ECF 为正方形,∴OE=EC =CF =OF ,OE⊥BC 于点E ,OF⊥AC 于点F. ∵BD 是∠ABC 的平分线,OM⊥AB,OE⊥BC, ∴OE=OM.∴OM=OF.∵OM⊥AB,OF⊥AC,∴AO 平分∠BAC,即点O 在∠BAC 的平分线上.(2)∵Rt△ABC 中,∠C=90 °,AC =5,BC =12, ∴AB=13.易证:BE =BM ,AM =AF.∵BE=BC -CE ,AF =AC -C F ,且CE =CF =OE , ∴BE=12-OE ,AF =5-OE.∵BM+AM =AB ,即BE +AF =13,∴12-OE +5-OE =13.解得OE =2.。
1.3 线段的垂直平分线 第2课时三角形三边的垂直平分线 课件2024-2025学年北师大版数学八下
变式1题图
变式2题图
变式2 如图,在钝角三角形 ABC 中,已知∠ A 为钝角,边 AB , AC 的
垂直平分线分别交 BC 于点 D , E . 若 BD2+ CE2= DE2,则∠ A 的度数
为 135° .
变式3 如图,在△ ABC 中, DE 垂直平分 AB ,分别交 AB , BC 于点 D , E , MN 垂直平分 AC ,分别交 AC , BC 于点 M , N . 若∠ BAC = 80°,则∠ EAN 的度数为 20 °.
8.如图,已知线段 a ,直线 l 及 l 外一点 A . 求作:等腰三角形 ABC ,使底边 BC 在 l 上,且 BC = a .(尺规作图,不 写作法,保留作图痕迹) 解:如图,△ ABC 即为所求.
易错点 忽略平面内三点的位置关系致错
9.到平面内三点 A , B , C 距离相等的点( D )
2.在由小正方形组成的网格中,△ ABC 的位置如图所示,且顶点均在格
点上.在△ ABC 的内部有 E , F , G , H 四个格点,到△ ABC 三个顶点距
离相等的点是( B )
A. 点 E
B. 点 F
C. 点 G
D. 点 H
3.(教材P24例2变式)如图,已知在△ ABC 中,边 AB , BC 的垂直平
12.用直尺、圆规作图,不写作法,但要保留作图痕迹. 已知:△ ABC . 求作:点 P ,使 PA = PC ,且点 P 在△ ABC 的边 AB 的高上.
解:如图,点 P 即为所求.
变式微专题2 双垂直平分线模型 方法指导 如图,在△ ABC 中,∠ BAC =α,边 AB 的垂直平分线分别
a
h D
C
北师大版《角平分线》ppt优秀课件1
PE⊥BC,其中D、E、F是垂足
B
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE.同理:PE=PF.∴PD=PF.
∴点P在∠BAC的平分线上
∴△ABC的三条角平分线相交于点P.
A
M
D
PF
EC
定理:三角形的三条角平分线相交于一点,并且这一点到
三边的距离相等.
A
如图,在△ABC中, ②点P在∠CBE的平分线上;
A. ①②③④ B. ①②③ C. ④ D. ②③
2.如图,已知 BG 是∠ABC 的平分线,DE⊥AB 于点 E, DF⊥BC 于点 F,DE=6,则 DF 的长度是( )
A. 2 B. 3 C. 4 D. 6
3.如图,三条公路把A、B、C三个村庄连成一个三角形区域, 政府决定在这个三角形区域内修建一个集贸市场,使集贸市场 到三条公路的距离相等,则该集贸市场应建在( )
离相等(这个交点叫做三角形的内心).
三 角 形 一 个 内 角 和 与 它 不 相 邻 的 两
外 角 的 平 分 线交于 一点 , 这 个 的 点
O
DA
1P
2
C
叫 做 三 角 形 的傍心 . 这样点 有三个.
E B
提升练习
已分知别:为C如、图D,,P求是证∠:AO(B平1)分O线C=上O的D;一(点2,)POC⊥P是OCAD,的P垂D⊥直O平B垂分足线 老定 实AB同如点 (已证∴A:定已如点逆A证∵(已 定定外(A∵命如点老证四 老A②求实三 ∠∵已求已②P四 证(A剪已 ∴③实证已外 第在在在222CMCCCECCBPBAP△)))师理际理图到知明理知图到定明知理理角题图到师明、师点作际角知作知点、明一知点际明知角2OOO一A一一⊥MMD、D、、、、、、、课B提 :操 : ,三:: ::,三 理 : :::的 :,三 提 : 提 P:操 形::: P: 个 :P操 : :的PPP⊥⊥,,三 已如个 三如已∠三三三已巩 射如射巩 如 如个个B∠BBBBBBCCC时C是是在在是在A示作P角 过角过平角示过示作一 如过三作过平CCCCCCCBOONNN角 知图角 角图知在角角角知固 线图线固 图 图角角的OECC∠∠C∠,两两两两 两两两三AA,,相:,形 P形P分形:P:,个 图P角,P分PAA三形 △,的 形,△一形形形△三运 三O,O运 ,,的的=三CCBDDDB,,PPPPP点 点 点 点 点F内边边边 边边边PP角HHAAAP交你一 一线一你内 ,形你线CCCBB,的的的是是是是 是角的 内 的个的的三角用 角用⊥内内条如EEBBBF相分作作作作作角EED高垂中 高中,,垂形于又边 边交边又角 纸又交P使使垂垂垂⊥⊥.CCC∠∠∠∠∠形三 部 三角三三个形、 形、A部部角图的的的交别PPP是PP平线直线 线线直三AAAAA点,,,C能的 的于的能和 片能于∠∠直直直OO∴作作作一条 条的条条角一深 一深,,,DDDDD平.平平平且于是OOOOO且且∠(分AA的平的 的的平条PBBP发距 距一距发与 ,发一已⊥⊥⊥⊥⊥平平平△△△个角 角内角角的个化 个化分ABBBBBOO分分分到D一△,,,到到线交分交 交交分AAA内垂垂现离 离点离现它 通现点知O平平平平 平AAAAA分分分ACC内平 平部平平平内拓 内拓=线线 线线BBB角点角角BBBBB的点线点 点点线B角BP足足==什为为为什不过什,,)分分分分 分线线线CCC角分 分分分分角展 角展,,相,,,,,上上上平∠∠CF且这这的P的的交处的处 处处的的一一一分分么半 半半么相 折么线线线线 线...,.BB的和线 线线线线和和交PPPPP且;;;分到个个两两两点交交CC平OO个个个别别?径 径径?邻 叠?上上上上 上FFFFF与相 相相相相与与于P线..角的的边边边CC⊥⊥⊥⊥⊥处点点分内内内是是作 作作的 找的的的的 的D它交 交交交交它它点..上的点点距距距AAAAA处处=线角角角DD圆 圆圆两 出一一一一 一不于 于于于于不不CCCCCPP的两离BB离离,,和和和EE每,,,.E点点点点 点,,,,,..相一 一一一一相相你 你你一((边相相相=与与与已已DD个,,,,,邻点 点点点点邻邻能 能能PPPPPP点距等等等..它它它知知F角CCCCC的的的,作 ,作,,.作,并 并离并并的(的的⊥⊥⊥⊥ ⊥不不不))三的,,两两两出 出出P相点且 且且且点点OOOOO且且相相相角角C个个个这 这这AAAAA等,这 这这这,,PP在邻邻邻⊥在在形平,,,,,外外外个个 个DDPPPPP的一 一一一这的的的O这这的分DDDDD==角角角图 图图点点 点点点APP⊥⊥⊥⊥ ⊥个两两两个个三线的的的形 形形,EE,到 到到到OO在OOO角个个个角角条,,,平平平吗 吗吗P三 三三三BBBBB这的外外外的的角观D分分分???,,,,,垂垂垂垂 垂边 边边边⊥个平角角角平平平察线线线足足足足 足的 的的的O角分的的的分分分这交交交B分分分分 分距 距距距的线平平平线线线三垂于于于别别别别 别离 离离离平上分分分上上相条足一一一CCCCC相 相相相.分线线线))交角分..点点点,,,,,DDDDD等 等等等线,,,于平看看看别,,,.....(.(.上这 这一分它它它为这这这.个 个点线们们们C个个个交 交、,,是是是并的的的点 点D你否否否且点点点,叫 叫是交交交这叫叫叫求做 做否于于于一做做做证三 三发一一一点三三三:角 角现点点点到角角角(形 形同???三形形形1这这这的 的样)边的的的样样样内 内的O的傍傍傍的的的心心C结距心心心=点点点))论离..O,,,有有有?D相这这这几几几;与等样样样个个个同)点点点.???伴有有有如如如交三三三果果果流个个个以以以.。。。这这这个个个点点点为为为圆圆圆心心心,,,这这这一一一
北师大版八年级数学下册《线段的垂直平分线》三角形的证明PPT课件(第2课时)
实践探究,交流新知
解:(1)已知三角形的一条边及这条边上的高,能作出三角形,并且能作出无 数多个,如图所示. (2)已知等腰三角形的底边,用尺规作出等腰三角形,这样的等腰三角形也有 无数多个. (3)如果等腰三角形的底边和底边上的高都一定,这样的等腰三角形应该只有 两个,它们是全等的,且分别位于已知底边的两侧,如图所示.
北师大版 八年级下册 第一章 三角形的证明
线段的垂直平分线(第2课时 )
前言
学习目标
1.会证明三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,并 解决相关的问题. 2.会用尺规作已知线段的垂直平分线,培养尺规作图的技能.
学习重点
掌握三角形三条边的垂直平分线的性质,能利用尺规作出符合条件的三角形.
(1)教材第26页随堂练习. (2)教材第26页习题1.8第1,2题.
同学们, 下课!
. 39°
3.如图,在△ABC中,∠BAC是钝角. (1)画出边BC上的中线AD; (2)画出边BC上的高AH.
第1题
第2题
第3题
课堂小结,整体感知
1.课堂小结:请同学们回顾本节课所学的内容,有哪些收获? (1)三角形三条边的垂直平分线的性质 (2)尺规作线段的垂直平分线、等腰三角形
2.布置作业:
学习难点
三角形三条边的垂直平分线性质的证明及应用.
创设情境,导入新课
1.问题提出: 利用尺规作三角形三条边的垂直平分线,当作图完成后你发现了什么? 2.问题探究: ①三角形三边的垂直平分线交于一点; ②这一点到三角形三个顶点的距离相等.
创设情境,导入新课
3.问题解决: 如图,剪一个三角形纸片,通过折叠找出每条边的垂直平分线,观察这 三条垂直平分线,上述结论是否成立? 4.问题思考: 以上结论都是通过眼睛观察得到的,那么该结论一定成立吗?我们还需 运用已学过的公理和定理进行推理证明,这样,此发现才更有意义.
八年级数学下三角形的证明1.4角平分线第2课时角的平分线的判定习题北师大版
13.如图,在四边形ABDC中,∠D=∠B=90°,O 为BD的中点,且AO平分∠BAC.求证: (1)CO平分∠ACD;
证明:如图,过点O作OE⊥AC于点E. ∵∠B=90°,AO平分∠BAC,∴OB=OE. ∵点O为BD的中点,∴OB=OD.∴OE=OD. 又∵∠D=90°,∠OEC=90°, ∴CO平分∠ACD.
解:当点D移到BC的中点时,AD恰好平分∠BAC. 理由:当D是BC的中点时,BD=CD. ∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°. 又∵∠B=∠C,BD=CD,∴△DEB≌△DFC(AAS). ∴DE=DF. 又∵DE⊥AB,DF⊥AC,∴AD平分∠BAC.
12.如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD, BE=CF. (1)求证:AD平分∠BAC;
证明:∵∠1=∠2,OD⊥AB 于点 D,OE⊥AC 于点 E, ∴OD=OE(角平分线上的点到角的两边的距离相等).
∠DOB=∠EOC(对顶角相等), 在△OBD 和△OCE 中,OD=OE,
∠ODB=∠OEC=90°, ∴△OBD≌△OCE.∴OB=OC.
(2)如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与
CD相交于点O,且OB=OC.
求证:∠1=∠2.
解:在△BOD 和△COE 中, ∠ODB=∠OEC=90°, ∠DOB=∠EOC(对顶角相等), OB=OC, ∴△BOD≌△COE.∴OD=OE.∴∠1=∠2(角的内部 到角的两边距离相等的点在这个角的平分线上).
11.如图,在△ABC中,∠B=∠C,D是BC边上的一动 点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F. 当点D移到什么位置时,AD恰好平分∠BAC?请说明 理由.
2.如图,在CD上求一点P,使它到边OA,OB的距 离相等,则点P是( C )
