第3章刚体力学基础
第3章刚体力学

例8 : 一质点的质量为m,位矢为:r =acost i+bsint j (式中a、b、 均为常量); 求质点的角动量及它所受的力矩。
dr 解: a sin ti b cos tj dt L r ( m ) 2 2 mab cos tk mab sin tk
mg
14
例6: 一根质量为m、长为l的均匀细棒AB,可绕一水平光滑 轴o在竖直平面内转动,o轴离A端的距离为 l/3。今使棒从静
止开始由水平位置绕o轴转动,求棒转过角 时的角加速度和
角速度。 解 细棒AB受的重力可集中在质心,故重力的力矩为
M o mg l cos
6
A
o C
1 l 2 1 2 2 I o ml m( ) ml 12 6 9
I V r dm
2
式中r为刚体上的质元dm到转轴的距离。 线状刚体: 面状刚体: 体状刚体:
dm dl dm dS dm dV
Io
o
d
Ic
C
2 (3)平行Biblioteka 定理: Io=Ic+MdM
Ic 通过刚体质心的轴的转动惯量;
M 刚体系统的总质量; d 两平行轴(o,c)间的距离。
动力学规律可以推广应用到刚体。
2
二 . 刚体定轴转动的描述
刚体在作定轴转动时,刚体上所以质点都作圆周运动且角 速度相同,所以用角量描述最为方便。
d , dt
线量与角量的关系:
d dt
r a r a r 2 n
o
r
P
x
刚体作匀速、匀变速定轴转动时,各角参量之间的关系 与质点作匀速、匀变速圆周运动时所满足的关系一样。
刚体和流体

y
角动量的方向: 位矢和动量的矢积方向. 特例: 如果质点绕参考点O作圆周运动
v p
O
L = r p = mv r
注意: 1.角动量与所取的惯性系有关. 2.角动量与参考点O的位置有关.
v r
第三章 刚体力学基础
质点对定轴的角动量
v v v v v L = r × p = r × mv
L = mvr = mr 2ω = Jω
(原点O在棒的左端点)
第三章 刚体力学基础
例题2: 一质量为m, 半径为R的均匀圆盘, 求通过盘中心并与 盘面垂直的轴的转动惯量. 解: dm = σdS = σ 2 π rdr
J = ∫ r dm = 2 πσ ∫ r dr
2
3
J = 2πσ ∫ r dr
3
R
R
r O
dr
πσ R 1 2 = = mR 2 2
v v v 加速度: 合外力矩: M z = ∑ ri × Fi v v v v v M z = ∑ ∆mi ri × aiτ + ∑ ∆mi ri × ain
v第三章v刚体力学基础 v ai = aiτ + ain
v 2 v v v v v 其中: ri × ain = 0 ri × aiτ = ri aiτ sin 90°k = ri β k v v 2 M z = ∑ ∆mi ri β 转动惯量 J v v 转动定律: M z = Jβ
θ ( rad) 角位移: ∆θ , dθ dθ −1 ( rad ⋅ s ) 方向右旋 ω= dt v
第三章 刚体力学基础
线速度与角速度之间的关系
r v v v dv d ω v v dr a= = ×r +ω× dt dt dt v 2 v = β reτ + ω ren
大学物理第三章刚体力学

薄板的正交轴定理:
Jz Jx J y
o x
y
X,Y 轴在薄板面上,Z轴与薄板垂直。
例3、质量m,长为l 的四根均匀细棒, O 组成一正方形框架,绕过其一顶点O 并与框架垂直的轴转动,求转动惯量。 解:由平行轴定理,先求出一根棒 对框架质心C的转动惯量:
C
m, l
1 l 2 1 2 2 J ml m( ) ml 12 2 3
M F2 d F2 r sin
若F位于转动平面内,则上式简化为
M Fd Fr sin
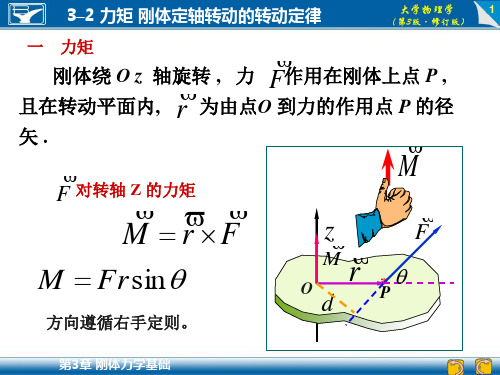
力矩是矢量,在定轴转动中, 力矩的方向沿着转轴,其指向 可按右手螺旋法则确定:右手 四指由矢径r的方向经小于的 角度转向力F方向时,大拇指的 指向就是力矩的方向。根据矢 量的矢积定义,力矩可表示为:
例9 行星运动的开普勒第二运动定律:行星对太阳 的位矢在相等的时间内扫过相等的面积。 解:行星在太阳引力(有心 力)作用下沿椭圆轨道运动, 因而行星在运行过程中,它 对太阳的角动量守恒不变。
L rmvsin 常量
因而掠面速度:
dS dt
r dr sin 2dt
1 rv sin 常量 2
Fi fi Δmi ai
切向的分量式为
Fi sin i f i sin i mi ri
Fi sin i f i sin i mi ri
两边同乘ri,得
Fi ri sin i fi ri sin i mi ri2
上式左边第一项为外力Fi对转轴的力矩,而第二项是 内力fi 对转轴的力矩。对刚体的所有质点都可写出类 似上式的方程,求和得
质点的角动量一质量为m的质点以速度v运动相对于坐标原点o的位置矢量为r定义质点对坐标原点o的角动量为sinrmv282质点的角动量定理质点所受的合外力对某一参考点的力矩等于质点对该点的角动量对时间的变化率角动量定理
第03章(刚体力学)习题答案

内力做功,机械能守恒,动量守恒的条件为合外力为零,转轴不属于系统,转轴与盘之间有
作用力,动量不守恒。
3-2 如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑
O
固定轴 O 旋转,初始状态为静止悬挂.现有一个小球自左方水平打
击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆
与小球这一系统的哪种物理量守恒? 答:在碰撞时,小球重力过转轴,杆的重力也过轴,外力矩为
思考题 32 图
零,所以角动量守恒。因碰撞时转轴与杆之间有作用力,所以动量不守恒。碰撞是非弹性的,
所以机械能也不守恒。
3-3 一圆盘绕过盘心且与盘面垂直的光滑固定轴 O 以角速度w按图示方向转动.若如图
所示的情况那样,将两个大小相等方向相反但不在同一条直线的力
F 沿盘面同时作用到圆盘上,则圆盘的角速度w 如何变化?
解:此过程角动量守恒
Jw0
=
1 3
Jw
Þ
w
=
3w0
3-10 一轴承光滑的定滑轮,质量为 M=2.00 kg,半径为 R=0.100 m,
一根不能伸长的轻绳,一端固定在定滑轮上,另一端系有一质量为 m=5.00
kg 的物体,如图所示.已知定滑轮的转动惯量为 J= 1 MR 2 ,其初角速 2
w 0
R M
解:(1)设在任意时刻定滑轮的角速度为w,物体的速度大小为 v,则有 v=Rw.
则物体与定滑轮的总角动量为: L = Jw + mvR = Jw + mR2w
根据角动量定理,刚体系统所受的合外力矩等于系统角动量对时间的变化率:
M = dL ,该系统所受的合外力矩即物体的重力矩:M=mgR dt
所以: b
刚体力学基础

非专业训练,请勿模仿
例 解 由转动定律得
1 mgl sin J 2 1 2 式中 J ml 3 3g sin 得 2l
角加速度与质量无关,与长 度成反比,竹竿越长越安全。
-------------------------------------------------------------------------------
刚体的一般运动 质心的平动
+
绕质心的转动
-------------------------------------------------------------------------------
二、刚体绕定轴转动定律
F外力 F内力 mi ai
ai :质元绕轴作圆运动
-------------------------------------------------------------------------------
二、定轴转动的角动量守恒定律
质点角动量(相对O点)
定轴转动刚体
L r p r mv
-------------------------------------------------------------------------------
解:
M 1l gdl cos M mgL cos 2 m g1 l cos dl cos mgl M 2 3g cos L 1 22 J 2l M ml L g 3 cos L 2 3g cos d d d d 1 2 l dt cos d d mgL dt 2
2 法向: F cos F cos m r 法向力的作用线过转轴 i i i i. 内力 ,其力矩为零 外力 切向:F外力 sin i F内力 sin i mi ri
力矩 刚体定轴转动的转动定律
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
12
考虑到所有质元到转轴的距离均为R,所以细圆环对 中心轴的转动惯量为
J dJ R dm R
2 m
2
m
dm mR
2
(2)求质量为m,半径为R的圆盘对中心轴的转动惯量
m 如图 dS 2 rdr , , dm dS 2 rdr 2 R
l 2
o
P
d d d d dt d dt d
代入初始条件积分 得
第3章 刚体力学基础
3g d sin d 2l 3g (1 cos ) l
1 2 J x dx ml 0 3
l 2
由此看出,同一均匀细棒,转轴位置不同,转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m,半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动,求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元,其质量 为dm,距离为R, 则该质元对转轴的 转动惯量为
解 (1)转轴通过棒的中心并与棒垂直
m l
dm dx
dJ x 2dm x 2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J dJ
l 2 l 2
1 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时,整个棒对该轴的 转动惯量为
解 (1) M k 2 ,故由转动定律有
k k J 即 J 2 1 k0 0 3 9J
第三章4-5刚体运动方程与转动惯量

对通过空间某一点O的轴线, , , 为转动瞬轴相对于 坐标轴的方向余弦, 则 z
P ( d , m)
x , y , z
(3.5.15)
o x
y
z x y
I I xx 2 I yy 2 I zz 2 2I yz 2I zx 2I xy
2 i i
Jy
m x y m x z m y x m z x m y z
2 i y i i i z i i i i
x
i
i i
y
i
2 i
2 i
i
z
i
i i
i
i
i
J z x mi zi xi y mi zi yi z mi x y
Fx 0, N1 sin 0 f 0 Fy 0, N1 cos 0 N 2 P 0
对A点
Pl cos 0 N1h / sin 0 0 f Pl cos 0 sin 2 0 / h
N 2 P Pl cos 2 0 sin 0 / h
0
例1、一根均匀的棍子、重为P长为2l. 今将其一端置于 粗糙地面上,又以其上的C点,靠在墙上,墙离地面的 高度为h.当棍子与地面的角度为最小值0时, 棍子在 上述位置仍处于平衡状态,求棍与地面的摩擦系数
解: 受力分析知本题是一共 面力系的平衡问题, 取棍子所 在的平面为xy平面, 则 y B C h O N1 l P l N2 A x
叫做惯量张量, 元素叫惯量张量的组元或惯量系数.
利用矩阵乘法,得
I
I xx I yx I zx
I xy I yy I zy
第三章 刚体力学1

1
v v v rvc = 0 v v J = rc × m v c + J ′ → = J ′
上页 下页 返回 结束
角速度 与其本身的叉积。 与其本身的叉积。 ωv
v
dA v v = ω× A dt
例: 单位矢量的微商公式 v v
di v v =ω×i dt
v dj v v dk v v 后面要用! = ω × k 后面要用! = ω× j dt dt
上页 下页 返回 结束
第三章 刚体力学
§3.3 欧勒角
: 静系 o −ξηζ
v v ∆n v v v v v v r → r ′ = r + ∆r = r + ∆n × r
(1)
v v ∆ n′ v v v v r → r ′ = r + ∆n′ × r
v v ∆n v v v v v v v v v r′ → r ′′ = r + ∆n′ × r + ∆n × r + ∆n × (∆n′ × r ) (2) v v 比较(1)、 , 很小时, 比较 、(2),只有 ∆ n 与 ∆ n ′ 很小时,二阶小量忽
v v v M = r ×F
上页 下页 返回 结束
v v v F2 = −F = F 1
PO2 F2 − PO1F1 = O1O2F P v M : 可作用于力偶面上的任一
点,亦称为自由矢量。 亦称为自由矢量。 自由矢量 (3)空间力系求和 ) 为作用在刚体A点上的一 设: A 为作用在刚体 点上的一 个力, 为空间任一点 为空间任一点。 个力,P为空间任一点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章刚体力学基础第3章刚体力学基础一、目的与要求1.确切理解描述刚体平动和定轴转动的基本物理定义及性质,并掌握角量与线量的关系。
2.确切理解和掌握力矩、转动惯量的概念及计算方法,掌握刚体定轴转动的动力学方程,熟练应用刚体定轴转动定律求解刚体定轴转动及与质心联动问题。
3.理解刚体转动动能概念。
掌握力矩的功,刚体的重力势能,刚体的动能定理和机械能守恒定律。
4.确切理解角动量概念,并能对含有定轴转动刚体在内的系统正确应用角动量定理及角动量守恒定律。
5.了解进动现象和基本描述。
二、内容提要1.刚体的基本运动刚体的平动:刚体运动时,在刚体内所作的任一条直线始终保持和自身平行。
其特点为:对刚体上任两点A 和B ,它们的运动轨迹相似,B A v v =,B A a a =。
因此描述刚体的平动时,可用其上任一质点的运动来代表。
刚体的定轴转动:刚体内各质元均作圆周运动,且各圆心在同一条固定不动的直线上。
刚体的平面平行运动:刚体上每一质元均在平行于某一固定平面的平面中。
2.力矩和转动惯量力矩:使刚体产生角加速度的外来作用F r M ?=转动惯量:刚体转动惯性大小的量度∑=ii i r m J 2对于质量连续分布的刚体=Vm r J d 2转动惯量的平行轴定理:2md J J c z += 转动惯量的垂直轴定理:y x z J J J +=3.刚体定轴转动定律:刚体所受的外力对转轴的力矩之代数和等于刚体对该轴的转动惯量与刚体的角加速度的乘积βωJ tJM ==d d M 、β、J 均相对于同一转轴。
4.刚体定轴转动的动能定理力矩的功:?=θd M A转动动能:221ωJ E k = 动能定理:21222121ωωJ J A -=机械能守恒定律:系统(包括刚体)只有保守力作功时,系统的动能(包括转动动能)与势能之和为常量,即=+=P k E E E 常量5.刚体定轴转动的角动量定理及其守恒定律角动量定理:对一固定轴的合外力矩等于刚体对该轴的角动量对时间的变化率,即z z M J t=)(d dω 角动量守恒定律:当0=z M 时,=ωz J 常量。
6.刚体的平面平行运动动能:作平面平行运动的动能等于质心的平动动能与刚体绕过质心的瞬时轴的转动动能之和222121ωc c k J m E +=v 三、例题3-1 一轻绳绕于半径为R 的圆盘边缘,在绳端施以mg F =的拉力,圆盘可绕水平固定光滑轴转动,圆盘质量为M ,圆盘从静止开始转动,试求(1)圆盘的角加速度及转动的角度和时间的关系。
(2)如以质量m 的物体挂在绳端,再计算圆盘的角加速度及转动的角度和时间的关系。
分析本题是刚体绕定轴转动问题,应用转动定律βJ M =即可求出圆盘的角加速度,对转动定律积分可求解)(t ωω=。
解(1)圆盘所受的合外力矩为FR M =对圆盘用转动定律,有ββ)21(2MR J FR ==因而角加速度为MR mgMR FR 222==β (1)由于td d ωβ=,且0=t 时,0=ω,积分(1)式,有t MRm gd 2d ωω 得t MRmg2=ω (2)而td d θω=,且0=t 时,0=θ,积分(2)式,有=tt t MR m gd 2d ωθ 可得转动角度和时间的关系为2t MRmg =θ (2)设T 为绳子的张力,对圆盘,由转动定律有β)21(2MR TR =(4)对物体m ,由牛顿定律,有ma T mg =- (5) 而βR a =(6)联立(4)、(5)、(6)式,即可解得转动角度与时间的关系为MR mgmR MR mgR222122+=+=β(7)由t d d ωβ=,td d θω=,且0=t 时,0=ω,0=θ。
通过对(7)式积分,即可得转动角度与时间的关系为22t mRMR mg+=θ(8)说明本题的第二问是典型的刚体与质点连接的联体问题,可采用隔离研究,对质点用牛顿定律,对刚体用转动定律,并注意与(1)问的区别。
同时,从(7)式可明显看出,这类问题也可将系统看成一个转动惯量为2221mR MR +的刚体,运用转动定律求解。
3-2 长为l ,质量分布不均匀的细杆,其线密度为br a +=λ(a 、b 为常量),细杆可绕轴z 在铅直平面内转动,如图所示,忽略轴z 的摩擦力,将杆从水平位置释放,试求杆转到铅直位置时,杆所具有的角速度ω。
分析这是一个刚体绕定轴转动问题。
当求细杆重力对轴的力矩时,因杆质量不均匀,要先恰当地求出元力矩z M d ,通过积分求z M ,然后采用转动定律θωωωd d d d J t J M ==形式,积分即可求ω。
解设t 时刻杆与垂线间的夹角为θ,由于杆的质量不均匀,求重力对z 轴的力矩时,可在杆上取线元r d ,该线元对z 轴的力矩为θλsin )d (d gr r M z -=对z 轴的总力矩为θλsin )d (0gr r M lz ?-=r r br a g ld sin )(0θ?+-=θsin )32(2l ba gl +-=细杆的质量不均匀,因此其对z 轴的转动惯量为==llz r r m r J 0202)d (d λ+=lr br a r 02d )(434131bl al +=根据转动定律t J M z z d d ω=,有t l bl a l b a gl d d )4131(sin )32(32ωθ?+=+-积分变量替换θωωωd d d d ?=t代入上式化简得ωωθθd )43(d sin )32(l l ba lb a g +=+-初始条件2π=θ时,0=ω,当转到0=θ时,积分上式+=+-ωωωθθ002πd )43(d sin )32(l l b a l b a g 得lbl a gbl a )34()23(4++=ω说明本题有多种解法。
题中给出了用转动定律求解的方法,也可用动能定理,机械能守恒定律求解。
读者可自己考虑。
3-3 一均质细杆,长为l ,质量为M ,可绕通过一端的水平轴O 转动,如图。
一质量为m 的子弹以速度0v 射入细杆,子弹射入点离O 点的距离为4/3l ,试求(1)杆刚开始运动时的角速度及可摆到的最大角度。
(2)求轴上的横向力为零时,子弹射入的位置(即打击中心位置)。
分析子弹射入细杆过程中,子弹、细杆系统角动量守恒;细杆摆动时,机械能守恒,由两守恒定律可求ω及max θ。
子弹射入细杆,细杆轴受力,轴受横向力的冲量应等于子弹、细杆系统动量的改变,横向力0=横N 时,即可求出打击中心位置。
解(1)子弹射入细杆过程极其短暂,此过程中杆的位置还来不及变化,故子弹和细杆这个系统的重力对定轴O 无力矩,轴力当然也无力矩,故这个系统在子弹射入过程中对定轴O 的角动量守恒ω])43(31[43220l m Ml m l +=v (1)射入后子弹与杆共同摆动过程中,系统机械能守恒,取子弹射入处为势能零点 4])43(31[21222l Mg l m Ml ++ω)]cos 1(24[)cos 1(43θθ-++-=ll Mg l mg(2)联立(1)、(2)可解得杆的角速度及可摆到的最大角度分别为lm M m )2716(360+=v ω])2716)(32(541[cos 221maxglm M m M m ++-=-v θ(2)将子弹和细杆视为一个系统,则系统受的外力为Mg ,mg ,横N ,竖N ,如图,设子弹打在距轴x 处,根据动量定理 0d v v v m M m t Nc -+=?横02v m lMmx -+=ωω (3)系统对O 轴角动量守恒,有ωJ xm xm +=v v 0ωω2231Ml m x +=ω)31(22Ml m x +=因而2231Mlm x xm +=v ω (4)将(4)式代入(3)式022031)21(d v v m Ml m x xm ML m x t N -+?+=?横当0=横N 时,则031)21(0220=-+?+v v m Ml m x xm ML m x解此方程得l x 32=此即打击中心的位置。
说明子弹和细杆组成的系统受到外界对细杆转轴的作用力,故系统动量不守恒,这一点需特别注意,但由于该作用力通过转轴,不产生力矩,系统角动量守恒,并且因该力通过转轴,其力矩的功(实际上也就是力的功)为零,系统机械能守恒,综合角动量守恒,机械能守恒求解本题。
另外,打击中心即为使杆在轴处沿打击方向横向力为零时的打击点。
3-4 一质量为m 的子弹,穿过与均匀细杆连接的物体后,速度由v 减至2v,设杆可绕过O 点的固定轴在竖直平面内转动,杆长为l ,杆与物体的质量均为M ,如图,开始时,杆与物体静止于铅垂位置,物体的大小可以忽略不计,子弹与物体作用过程极短,试求,欲使物体与杆可以在竖直平面内完成圆周运动,子弹的速度不能小于多少?分析子弹、物体系统对O 轴角动量守恒,物体绕O 轴转动机械能守恒,物体与杆恰能完成圆周运动的条件是其转到垂直位置时的动能为零,由此求解本题。
解假定子弹穿过物体后,物体与杆的角速度为ω,物体与杆转动过程中,由机械能守恒及物体与杆恰能完成圆周运动的条件,有)2(22)31(21222l l Mg l Mg l Mg Ml Ml ++?=++ω 解得lg29=ω 子弹穿过物体,子弹、杆、物体组成系统对O 轴角动量守恒,因此2)31(22lm Ml Ml l m ?++=v v ω解得223238mglM m Ml ==ωv 所以2232m glM ≥v 说明本题综合运用角动量守恒和机械能守恒求解,其关键在于分析守恒条件,子弹和细杆组成的系统在细杆转轴处受外力作用,但此力力矩为零,因此其力矩的功也为零,因而角动量、机械能守恒。
3-5 如图,有一长度为l ,质量为1m 的均匀细杆静止水平放在摩擦系数为μ的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动,另一质量为2m 水平运动的小滑块从侧面沿垂直于杆的方向与杆的另一端A 相碰撞,并被反向弹回,碰撞时间极短。
已知小滑块与细杆碰撞前后的速率分别为1v 和2v ,求(1)碰撞后杆绕O 轴转动的角速度;(2)碰撞后从杆开始转动到停止转动的过程中所需的时间。
分析滑块与细杆碰撞角动量守恒,由此求细杆转动的ω,此后,细杆受摩擦力矩作用转速逐渐减为零,由摩擦力矩,根据角动量定理即可求出时间t 。
解(1)以杆和滑块为研究系统。
由于碰撞时间极短,杆所受到的摩擦力矩远小于滑块的冲力矩,故可认为合外力矩为零,因此系统的角动量守恒,即ω21221231l m l m l m +-=v v(1)解得lm m 1212)(3v v +=ω(2)碰后杆在转动过程中所受的摩擦力矩为gl m x x l gm x m g M lf 10121d d μμμ-=-=?-=??(2)由角动量定理得ω210310d l m t M tf -=? (3)由式(1)、(2)、(3)联立解得gm m t 12122μv v +=说明本题需注意两点:(1)在处理碰撞问题时,通常因碰撞时间极短,摩擦力矩远小于碰撞产生的冲力矩,角动量守恒;(2)棒各处摩擦力矩不同,首先要写出微元力矩,即mx g d μ-,通过积分求摩擦力矩。
