根据极坐标与参数方程中的路径问题专题训练
专题05 参数方程与极坐标(训练篇B)含详解-用思维导图突破圆锥曲线压轴题

令 得点 由 得
所以
从而直线 的斜率
所以
.
所以 ,所以
综上可知,直线 与直线 平行.
8.自 引直线交抛物线 于 两点,在 上取一点 ,使 三者的倒数成等差数列,求 点的轨迹方程.
解设 : ( 为倾斜角, 为参数)
代入 中得 ①
由题意得 即 ,
解得 或 .②
设Q对应的参数为 ,则 .
所以 的面积的最大值为 .
注: 的范围不能仅有(*)确定,因直线AB还与椭圆 相交,还要得到(**),由两者共同确定 的范围.
解2用椭圆的参数方程.设 , ,则AB中点 .
.
因为M在椭圆内,所以 ,即 ,于是
.
7.已知椭圆 ,过点 且不过点 的直线与椭圆 交于 , 两点,直线 与直线 交于点 .
(1)求椭圆 的离心率;
由于 在 上位于 的同侧,所以 ,
所以 ,由于点Q(x,y)满足
即 ③
由②得 .
将③化为普通方程得
注过定点作二次曲线的割线,运用直线的参数方程,通过参数来表示线段长度,回避了距离公式,显得事半功倍.
(2)若 垂直于 轴,求直线 的斜率;
(3)试判断直线 与直线 的位置关系,并说明理由.
解(1)椭圆 的标准方程为 ,所以 所以椭圆 的离心率
(2)因为 过点 且垂直于 轴,所以可设 直线 的方程为 令 ,得 所以直线 的斜率
(3)当直线 的斜率不存在时,由(2)可知
因为直线 的斜率 所以
当直线 的斜率存在时,设其方程为 .
从而点 到直线 的距离 .
当 时, .
因此,当点 的坐标为 时,曲线 上的点 到直线 的距离的最小值为 .
4.在直角坐标系 中,直线 的参数方程为 为参数, 为倾斜角),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
参数方程 极坐标专项训练

极坐标方程sin所表示的曲线是 化1653cos为直角坐标方程。 化下列极坐标方程为直角坐标方程: (1)20ctg·csc;(2)222cossin
参数方程xeeyeetttt(t为参数)表示的曲线是
为参数)()(为参数)()(cos1sin4cos1cos421681861222yxkkky
kkkx
过点P(2,0)的直线l夹在直线yxyx332和间线段长为2,则l的普通方程是
设Pxy(),是椭圆231222xy上的一个动点,则xy2的最大值 最小值是
已知极坐标系中的两点AB343143,,,则AB 曲线的参数方程为xtytt3210522,则曲线是: A.线段 B.双曲线一支 C.圆弧 D.射线
参数方程xycossinsin2212102 等腰直角三角形ABC,三顶点A、B、C按顺时针方向排列,A是直角,腰长为a,顶点A、B分别在x轴y轴上滑动,求顶点C的轨迹方程(要求把结果写成直角坐标系的普通方程)
已知线段BB=4,直线l垂直平分BB于点O,在属于l并且以O为起点的同一射线上取两点P、P,使OPOP·9。求直线BP与直线BP的交点M的轨迹方程。
课外思考: 1.当,ab均为有理数时,称点(,)Pab为有理点,又设
(1998,0),(0,2000)AB,则直线AB上( ) (A)不存在有理点 (B)仅有一个有理点 (C)仅有两个有理点 (D)有无穷多个有理点 2.过点(1,4)引直线l,使它在两坐标轴上的截距都是正数,且截距和为最小,求直线l的方程. 过双曲线16922yx的左焦点,且被双曲线截得线段长为6的直线有_________条. 椭圆的中心在原点,离心率31e,一条准线方程为x=11,椭圆上有一点M横坐标为-1,M到此准线异侧的焦点F1的距离为_________.
高考极坐标参数方程含答案(经典39题)(1)_看图王

方程. C1 与 C2 公共点的个数和 C 1 与C2 公共点的个数是否相同?说明你的理由.
29.在平面直角坐标系
xoy
中,圆
C
的参数方程为
x
y
4 cos 4 sin
(
为参数),直线
l
(2)求证直线 l 和曲线 C 相交于两点 A 、 B ,并求 | MA | | MB | 的值.
(2, )
6.在极坐标系中,O 为极点,已知圆 C 的圆心为 3 ,半径 r=1,P 在圆 C 上运动。 (I)求圆 C 的极坐标方程;(II)在直角坐标系(与极坐标系取相同的长度单位,且以极点 O 为原点, 以极轴为 x 轴正半轴)中,若 Q 为线段 OP 的中点,求点 Q 轨迹的直角坐标方程。
程是
4 cos
,直线 l
的参数方程是
x
3 y1 2
3 2 t.
t
,
(t
为参数)。求极点在直线 l
上的射影点
P
的
极坐标;若 M 、 N 分别为曲线 C 、直线 l 上的动点,求 MN 的最小值。
x 4 cos
8.平面直角坐标系中,将曲线
y
sin
( 为参数)上的每一点纵坐标不变,横坐标变为原来的
为
t
2
,Q
为
C
2
上的动点,求
PQ
中点
M
到直线
C3
:
2x
y
7
0
(t
为参数)距离的最大值。
第 13页 共 16页
◎
第 14页 共 16页
2023年高考数学真题分训练 极坐标系与参数方程(含答案含解析)

专题34 极坐标系与参数方程2⎩2 2考点 116 平面直角坐标系中的伸缩变换 考点 117 极坐标和直角坐标的互化⎧x = t + 1,⎪x = 4cos 2θ, 1.(2023 全国Ⅱ文理 21)已知曲线C 1 , C 2 的参数方程分别为C 1 : ⎨ (θ为参数),C : ⎪ t ( t 为 ⎩ y = 4sin 2θ⎪ y = t - 1参数).(1) 将C 1 , C 2 的参数方程化为一般方程;⎪ t(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系.设C 1 , C 2 的交点为 P ,求圆心在极轴上,且经过极点和 P 的圆的极坐标方程.(解析)(1)由cos 2 θ+ sin 2 θ= 1得C 1 的一般方程为: x + y = 4 ,⎧x = t + 1 ⎧x 2= t 2 + 1 + 2 ⎪ t ⎪ t 2 C 2 2由⎨ 1 得: ⎨1 ,两式作差可得2 的一般方程为: x - y = 4 . ⎪ y = t - ⎪ y 2 = t 2 + - 2 ⎪ t ⎪ t 2⎧x = 5 ⎧x + y = 4 ⎪ (2)由 得: 2 ,即 P ⎛ 5 , 3 ⎫. ⎨x 2 - y 2= 4 ⎨ ⎪ y = 3 ⎩ 2 ⎪ ⎝ ⎭⎛ 5 ⎫2⎛3 ⎫217设所求圆圆心的直角坐标为(a , 0),其中 a > 0 ,则 a - ⎪ + 0 - ⎪ = a 2 ,解得:a = ,⎝2 ⎭⎝2 ⎭10∴ 17 ∴⎛ 17 ⎫2⎛ 17 ⎫222 2 17 所求圆的半径 r = , 10 所求圆的直角坐标方程为: x - 10 ⎪ + y = 10 ⎪ ,即 x + y = x ,5 ∴所求圆的极坐标方程为ρ= 17cos θ.5⎝ ⎭ ⎝ ⎭103⎩⎪x = 2 - t - t 2, 2.(2023 全国Ⅲ文理 22)在直角坐标系 xOy 中,曲线C 的参数方程为⎪ y = 2 - 3t + t 2( t 为参数且t ≠ 1),C与坐标轴交于 A , B 两点.(1) 求 AB ;(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,求直线 AB 的极坐标方程.(解析)(1)令 x = 0 ,则t 2 + t - 2 = 0 ,解得t = -2 或t =1(舍),则 y = 2 + 6 + 4 = 12 ,即 A (0,12) . 令 y = 0 ,则t 2 - 3t + 2 = 0 ,解得t = 2 或t =1(舍),则 x = 2 - 2 - 4 = -4 ,即 B (-4, 0) .∴ AB == 4 .(2)由(1)可知 k AB =12 - 00 - (-4)= 3 ,则直线 AB 的方程为 y = 3(x + 4) ,即3x - y +12 = 0 .由 x = ρcos θ, y = ρsin θ可得,直线 AB 的极坐标方程为3ρcos θ- ρsin θ+12 = 0 .3.(2023 江苏 22)在极坐标系中,已知点 A (ρ, π) 在直线l : ρcos θ= 2 上,点 B (ρ , π) 在圆C : ρ= 4 sin θ上1 32 6(其中ρ≥ 0 , 0 ≤θ< 2π).(1)求ρ1 , ρ2 的值(2)求出直线l 与圆C 的公共点的极坐标.(解析)(1) Q ρ cos π = 2∴ρ = 4; Q ρ = 4 s inπ2 .131 26 ∴ρ2 = (2) Q ρcos θ= 2, ρ= 4 sin θ∴ 4 sin θcos θ= 2,∴sin 2θ= 1 Q θ∈0, 2π)∴θ= π, 5π,4 4当θ= π时ρ= 2 4;当θ= 5π 时ρ= -2 4 < 0 (舍);即所求交点坐标为当π (2 2, ) . 4 4.(2023 全国 II 文理 22)在极坐标系中,O 为极点,点 M (ρ0 ,θ0 )(ρ0 > 0)在曲线C : ρ= 4 s in θ上,直线 l 过点 A (4, 0) 且与OM 垂直,垂足为 P . (1)当θ = π时,求ρ 及 l 的极坐标方程;3(2)当 M 在 C 上运动且 P 在线段 OM 上时,求 P 点轨迹的极坐标方程.(解析)(1)因为 M (ρ,θ ) 在C 上,当θ = π 时,ρ = 4 s in π= 2 .0 0 0 3 03由已知得| OP |=| OA | cos π= 2 .322333⎢⎥⎢⎥设Q (ρ,θ) 为l 上除P 的任意一点.在Rt △OPQ 中ρcos⎛θ-π ⎫=| OP |= 2 , 3 ⎪ ⎝ ⎭π ⎛ π ⎫经检验,点P (2, ) 在曲线ρcos θ- ⎪ = 2 上. ⎝ ⎭所以,l 的极坐标方程为ρcos ⎛θ- π ⎫= 2 .3 ⎪ ⎝ ⎭(2)设 P (ρ,θ) ,在Rt △OAP 中, | OP |=| OA | cos θ= 4 cos θ,即 ρ= 4 cos θ..因为P 在线段OM 上,且 AP ⊥ OM ,故θ的取值范围是⎡π , π⎤. ⎣ 4 2 ⎦所以,P 点轨迹的极坐标方程为ρ= 4 cos θ,θ∈ ⎡π , π⎤ .⎣4 2 ⎦5.(2023 全国 III 文理 22)如图,在极坐标系 Ox 中, A (2, 0) , B ( 2, π) ,C ( 2, 3π) , D (2, π) ,弧 AB ,4 4 A , A 所在圆的圆心分别是(1, 0) ,π, (1, π) ,曲线 M 是弧 A ,曲线 M 是弧 A ,曲线 M 是BC CD(1, ) 21 AB2 BC3 弧C D .(1) 分别写出 M 1 , M 2 , M 3 的极坐标方程;(2) 曲线 M 由 M 1 , M 2 , M 3 构成,假设点 P 在 M 上,且| OP |= ,求P 的极坐标.(解析)(1)由题设可得,弧 AB , B C ,C D 所在圆的极坐标方程分别为ρ= 2 cos θ,ρ= 2 s in θ,ρ= -2 cos θ,所以 M 的极坐标方程为ρ= 2 cos θ⎛0 θ π ⎫ , M 的极坐标方程为 1 4⎪ 2⎝⎭ρ= 2 sin θ⎛ π θ3π ⎫ , M 的极坐标方程为ρ= -2 cos θ⎛ 3πθ π ⎫ . 4 4 ⎪ 34 ⎪ ⎝ ⎭ ⎝ ⎭(2)设 P (ρ,θ) ,由题设及(1)知3332⎩⎩⎩⎩⎩θ假设0 θπ,则 2 cos θ=,解得θ=π;4 6假设 π θ 3π ,则 2 sin θ= ,解得θ= π 或θ= 2π ; 4 4 3 3 假设 3π θ π ,则-2 cos θ= ,解得θ= 5π .4 ⎛ 综上,P 的极坐标为3, π ⎫ 或⎛3, π ⎫ 或⎛63,2π ⎫ 或⎛3, 5π ⎫ .6⎪ 3⎪ 3 ⎪ 6 ⎪ ⎝⎭ ⎝⎭ ⎝⎭ ⎝ ⎭考点 118 参数方程与一般方程的互化6.(2023 上海 14)已知直线方程3x + 4 y +1 = 0 的一个参数方程可以是()⎧x = 1+ 3t A . ⎨ y = -1+ 4t ⎧x = 1- 4tB . ⎨y = -1- 3t⎧x = 1- 3tC . ⎨y = -1+ 4t ⎧x = 1+ 4t D . ⎨y = -1- 3t(答案)D(解析)A .参数方程可化简为 4x - 3y - 7 = 0 ,故 A 不正确;B .参数方程可化简为3x - 4 y - 7 = 0 ,故B 不正确;C .参数方程可化简为 4x + 3y -1 = 0 ,故 C 不正确;D .参数方程可化简为3x + 4 y +1 = 0 , 故 D 正确.应选 D .7.(2023 全国Ⅲ)选修 4—4:坐标系与参数方程](10 分)在平面直角坐标系 xOy 中, A O 的参数方程为⎧x = cos θ(θ为参数),过点(0, -2) 且倾斜角为α的直线l 与A O 交于 A , B 两点.(1) 求α的取值范围;(2) 求 AB 中点 P 的轨迹的参数方程.⎨ y = sin ,(解析)(1) A O 的直角坐标方程为 x 2 + y 2 = 1. 当α= π时, l 与A O 交于两点.2当α≠ π时,记 tan α= k ,则l 的方程为 y = kx -.l 与A O 交于两点当且仅当< 1 ,解得 k < -1 或2α∈π ππ 3πk > 1,即( , ) 或α∈ ( , ) .4 2 2 4α π 3π 综上,的取值范围是( , ) . 4 4222222⎨(2) l 的参数方程为⎪x = t cos α, (t 为参数, π < α< 3π) . ⎨⎩ y = - + t sin α 4 4 设 A , B , P 对应的参数分别为 t , t , t ,则t =t A + t B,且t , t 满足t 2 - 2 2t sin α+ 1 = 0 .ABPP2A B于是t A + t B= 2 2 sin α, t P =2 sin α.又点 P 的坐标(x , y ) 满足 ⎪x = t P cos α,y = - + t sin α.⎧ ⎪x =2sin 2α, 2 ⎩P π 3π 所以点 P 的轨迹的参数方程是⎨ ⎪ y = - 2 - 2 cos 2α (α为参数, < α< ) . 4 4 ⎪ 2 2考点 119 极坐标方程与参数方程的综合应用8.(2023 北京文理)在极坐标系中,直线ρcos θ+ ρsin θ= a (a > 0) 与圆ρ=2 cos θ相切,则 a =.(答案)1+ (解析)利用 x = ρcos θ, y = ρsin θ,可得直线的方程为 x + y - a = 0 ,圆的方程为(x -1)2 + y 2 = 1 ,所以圆心(1, 0) ,半径 r = 1,由于直线与圆相切,故圆心到直线的距离等于半径,即|1- a |= 1 ,∴ a = 1+ 或1- ,又 a > 0 ,∴ a = 1+ .9.(2023 北京文理)在极坐标系中,点 A 在圆ρ2- 2ρcos θ- 4ρsin θ+ 4 = 0 上,点 P 的坐标为(1, 0) ),则| AP | 的最小值为.(答案)1(解析)圆的一般方程为 x 2 + y 2 - 2x - 4y + 4 = 0 ,即(x -1)2 + ( y - 2)2 = 1 .设圆心为C (1, 2) ,所以| AP |min =| PC | -r = 2 -1 = 1 .10.(2023 天津文理)在极坐标系中,直线4ρcos(θ- π) +1 = 0 与圆ρ= 2 s in θ的公共点的个数为.6(答案)2(解析)直线的一般方程为 2 3x + 2 y +1 = 0 ,圆的一般方程为 x 2 + ( y -1)2= 1 ,因为圆心到直 3线的距离 d = < 1 4,所以有两个交点.11.(2023 北京文理)在极坐标系中,直线ρcos θ- | AB |= .3ρsin θ-1 = 0 与圆ρ= 2 cos θ交于 A , B 两点,则(答案)2(解析)将ρcos θ-3ρsin θ-1 = 0 化为直角坐标方程为 x - 3y -1 = 0 ,将ρ=2cos θ化为直角坐标方程为(x -1)2+ y 2= 1 ,圆心坐标为(1,0),半径 r=1,又(1,0)在直线 x - 3y -1 = 0 上,所以|AB|=2r=2.222234y x ⎩⎩⎩)⎩12.(2023 广东文理)已知直线l 的极坐标方程为 2ρsin(θ- π= 47πA (2 2,) ,则点 Α 到直线l 的距离为 .42 ,点 Α 的极坐标为(答案)(解析)由 2ρsin(θ- 2π ) = 得2ρ´ 4 2 7π(sin θ- cos θ) = ,所以 y - x = 1, 故直线l 的直角坐标方程为 x - y +1 = 0 ,而点 A (2 2, ) 对应的直角坐标为4 A (2,-2) ,所以点 A (2,-2) 到直线l : x - y +1 = 0 的距离为| 2 + 2 +1| = 5 2. 213.(2023 安徽文理)在极坐标系中,圆ρ= 8sin θ上的点到直线θ=是.π(ρ∈ R ) 距离的最大值 3(答案)6(解析)圆ρ= 8sin θ即ρ2= 8ρsin θ,化为直角坐标方程为 x 2+ ( y - 4)2= 16 ,π直线θ=,则tan θ=,化为直角坐标方程为 3x - y = 0 ,圆心(0, 4) 到直线3的距离为| -4 |= 2 ,所以圆上的点到直线距离的最大值为 6.14.(2023 全国Ⅰ文理 21)⎧x = cos k t ,在直角坐标系 xOy 中,曲线C 1 的参数方程为⎨ y = sin k t(t 为参数) .以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,曲线C 2 的极坐标方程为 4ρcos θ-16ρsin θ+ 3 = 0 .(1) 当 k = 1时, C 1 是什么曲线?(2) 当 k = 4 时,求C 1 与C 2 的公共点的直角坐标.(解析)(1)当 k = 1时,曲线C 的参数方程为⎧x = cos t ,( t 为参数),两式平方相加得 x 2 + y 2 = 1 ,1⎨y = sin t∴曲线C 1 表示以坐标原点为圆心,半径为 1 的圆.⎧x = cos 4 t ,(2)当 k = 4 时,曲线C 1 的参数方程为⎨ y = sin 4t ( t 为参数),∴ x ≥ 0, y ≥ 0 ,曲线C 1 的参数方程化为⎧ x = cos 2 t ⎨ y = sin 2t(t 为参数),两式相加得曲线C 1 方程为 + = 1,得 = 1 - ,平方得 5 22x yx 77⎩2y = x - 2 + 1, 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 ,曲线C 2 的极坐标方程为4ρcos θ-16ρsin θ+ 3 = 0 ,曲线C 2 直角坐标方程为4x -16 y + 3 = 0 ,联立C , C 方程⎪ y = x - 2 +1 , ,整理得12 x - 32 + 13 = 0 ,解得 x = 1 或 = 13(舍去),1 2⎨ ⎩4x -16 y + 3 = 02 6 ∴ x = 1 , y = 1 ,∴C ,C 1 1 公共点的直角坐标为( , ) .4 4 1 24 4⎧ 1- t 2 ⎪x =1+ t 215.(2023 全国 1 文理 22)在直角坐标系 xOy 中,曲线 C 的参数方程为⎨ ⎪ y = ⎩ 4t 1+ t 2(t 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线 l 的极坐标方程为 2ρcos θ+ 3ρsin θ+11 = 0 .(1) 求 C 和 l 的直角坐标方程;(2) 求 C 上的点到 l 距离的最小值.1- t 2⎛ y ⎫2⎛ 1- t 2 ⎫24t 2 (解析)(1)因为-1 < ≤ 1 ,且 x 2 + ⎪ = ⎪ + = 1,所以C 的直角坐标方程为2y 2 1+ t 2⎝ 2 ⎭ ⎝1 + t 2 ⎭ (1+ t 2 )2x += 1(x ≠ -1) .4l 的直角坐标方程为 2x + 3y +11 = 0 .⎧x = cos α, (2)由(1)可设C 的参数方程为 (α为参数, -π <α< π ).⎨y = 2sin α4 cos ⎛α- π ⎫ +113 ⎪ C 上的点到l 的距离为 = ⎝ ⎭.当α= - 2π 时, 4 c os ⎛α- π ⎫+11 取得最小值7,故C 上的点到l 距离的最小值为 . 3 3 ⎪ ⎝ ⎭16.(2023 全国Ⅰ文理) 在直角坐标系 xOy 中,曲线C 1 的方程为 y = k |x | + 2 .以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ2+ 2ρcos θ- 3 = 0 . (1) 求C 2 的直角坐标方程;x x x | 2 c os α+ 2 3 sin α+11|7⎨y = 4 s in θ,⎩(2) 假设C 1 与C 2 有且仅有三个公共点,求C 1 的方程.(解析)(1)由 x = ρcos θ, y = ρsin θ得C 2 的直角坐标方程为(x +1)2 + y 2 = 4 .(2)由(1)知C 2 是圆心为 A (-1, 0) ,半径为 2 的圆.由题设知,C 1 是过点 B (0, 2) 且关于 y 轴对称的两条射线.记 y 轴右边的射线为l 1 ,y 轴左边的射线为l 2 .由于 B 在圆C 2 的外面,故C 1 与C 2 有且仅有三个公共点等价于l 1 与C 2 只有一个公共点且l 2 与C 2 有两个公共点,或l 2 与C 2 只有一个公共点且l 1 与C 2 有两个公共点.当l 与C 只有一个公共点时, A 到l 所在直线的距离为 2 ,所以| -k + 2 |= 2 ,故 k = - 4 或 k = 0 .1213经检验,当k = 0 时, l 与C 没有公共点;当 k = - 4时, l 与C 只有一个公共点, l 与C 有两个公共点.1231 2 2 2| k + 2 | 当l 与C 只有一个公共点时, A 到l 所在直线的距离为2 ,所以= 2 ,故 k = 0 或 k = 4 .2 2 23经检验,当k = 0 时, l 与C 没有公共点;当 k = 4时, l 与C 没有公共点.1 2 32 2综上,所求C 的方程为 y = - 4| x | +2 .1317.(2023 全国Ⅱ文理)在直角坐标系 xOy 中,曲线C 的参数方程为⎧x = 2 cos θ,( θ 为参数),直线l 的参数⎩⎧x = 1+ t cos α 方程为⎨ y = 2 + t sin α ( t 为参数).(1) 求C 和l 的直角坐标方程;(2) 假设曲线C 截直线l 所得线段的中点坐标为(1, 2) ,求l 的斜率.x 2 + y 2 =(解析)(1)曲线C 的直角坐标方程为 1. 4 16当cos α≠ 0 时, l 的直角坐标方程为 y = tan α⋅ x + 2 - tan α; 当cos α= 0 时, l 的直角坐标方程为 x = 1 .(2)将l 的参数方程代入C 的直角坐标方程,整理得关于t 的方程(1+ 3cos 2 α)t 2 + 4(2 cos α+ sin α)t - 8 = 0 .①3317⎩⎨ y = 1- ty 因为曲线C 截直线l 所得线段的中点(1, 2) 在C 内,所以①有两个解,设为t 1 , t 2 ,则t 1 + t 2 = 0 .4(2 cos α+ sin α)又由①得t 1 + t 2 = -1+ 3cos 2α,故 2 cos α+ sin α= 0 ,于是直线l 的斜率 k = tan α= -2 .18.(2023 江苏)在极坐标系中,直线l 的方程为ρsin( π-θ) = 2 ,曲线C 的方程为ρ= 4 cos θ,求直线l 被曲6 线C 截得的弦长.(解析)因为曲线C 的极坐标方程为ρ=4 cos θ,所以曲线C 的圆心为(2, 0) ,直径为 4 的圆.因为直线l 的极坐标方程为ρsin( π -θ) = 2 ,则直线l 过 A (4, 0) ,倾斜角为 π,所以 A 为直线l 与圆C 的一6 6 个交点.设另一个交点为 B ,则∠OAB= π ,连结 OB ,因为 OA 为直径,从而∠OBA= π ,所以 AB = 4 c os π= 2 .6 因此,直线l 被曲线C 截得的弦长为 2 .2 6⎧x = 3cos θ19.(2023 全国Ⅰ文理)在直角坐标系 xOy 中,曲线C 的参数方程为⎨ y = sin θ ,(θ为参数),直线l 的参数方程为⎧x = a + 4t( t 为参数).⎩ (1) 假设 a = -1,求C 与l 的交点坐标;(2) 假设C 上的点到l 距离的最大值为 ,求 a .(解析)(1)曲线C 的一般方程为 x 2 + 29= 1.当a = -1时,直线l 的一般方程为 x + 4 y - 3 = 0 .⎧x + 4 y - 3 = 0⎧x = - 21 ⎪ ⎧x = 3 ⎪25 21 24由⎨ x 2 2解得⎨ y = 0 或⎨ ,从而C 与l 的交点坐标为(3, 0) , (- 24 , ) . ⎩ 9+ y = 1 ⎩⎪ y = ⎩ 25 25 25171717171733342⎩(2)直线l 的一般方程为 x + 4 y - a - 4 = 0 ,故C 上的点(3cos θ, sin θ) 到l 的距离为| 3cos θ+ 4 sin θ- a - 4 |d =.当a ≥-4 时, d 的最大值为a + 9.由题设得a + 9= ,所以a = 8 ;当a < -4 时, d 的最大值为 -a + 1 .由题设得 -a + 1= ,所以 a = -16 . 综上, a = 8 或 a = -16 .20.(2023 全国Ⅱ文理)在直角坐标系 xOy 中,以坐标原点为极点, x 轴的正半轴为极轴建立极坐标系,曲线C 1 的极坐标方程为ρcos θ= 4 .(1) M 为曲线C 1 上的动点,点 P 在线段OM 上,且满足| OM | ⋅ | OP |= 16 ,求点 P 的轨迹C 2 的直角坐标方程;π(2) 设点 A 的极坐标为(2, 3) ,点 B 在曲线C 2 上,求∆OAB 面积的最大值. (解析)(1)设 P 的极坐标为(ρ,θ) (ρ> 0) , M 的极坐标为(ρ1 ,θ) (ρ1 > 0) .由椭圆知| OP |= ρ, | OM |= ρ1 =cos θ.由| OM | ⋅ | OP |= 16 得C 2 的极坐标方程ρ= 4 cos θ(ρ> 0) , 因此C 的直角坐标方程为(x - 2)2 + y 2= 4(x ≠ 0) .(2)设点 B 的极坐标为(ρB ,α) (ρB > 0) .由题设知| OA |= 2 , ρB = 4cos α,于是∆OAB 面积1 π π 3S = 2 | OA | ⋅ρB ⋅sin ∠AOB = 4cos α| sin(α- 3 ) | = 2 | sin(2α- 3 ) - | ≤ 2 + . 2 当α= - π时, S 取得最大值 2 + ,所以∆OAB 面积的最大值为 2 + .1221.(2023 全国Ⅲ文理)在直角坐标系 xOy 中,直线l 的参数方程为⎧x = 2 + t( t 为参数),直线l 的参数方⎧x = -2 + m⎪1 ⎨ y = kt 2程为⎨ ⎩ y = m k( m 为参数).设l 1 与l 2 的交点为 P ,当 k 变化时, P 的轨迹为曲线C .(1) 写出C 的一般方程;17175224 5⎨t⎩(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l3 :ρ(cosθ+ sinθ) -交点,求M 的极径.= 0 ,M 为l3与C 的(解析)(1)消去参数t 得l 的一般方程l : y =k (x -2),消去参数m 得l 的一般方程l : y =1 (x+2).11⎧y =k (x-2)22k⎪设P(x, y) ,由题设得⎨⎩y=1 (x+2)k,消去k 得x2-y2=4 (y ≠0),所以C 的一般方程为x2-y2=4 (y ≠0).⎪ρ2(cos2θ-sin2θ)=4(2)C的极坐标方程为ρ2(cos2θ-sin2θ)=4(0<θ<2π,θ≠π),联立⎨得⎩ρ(cosθ+sinθ)-2=0cosθ- sinθ=2 (cosθ+sinθ),故tanθ=-1,从而cos2θ=9,sin2θ=1,代入ρ2(cos2θ-sin2θ)=4得3ρ2=5,所以交点M的极径为.10 10⎧x =-8 +t22.(2023 江苏)在平面坐标系中xOy 中,已知直线l 的参考方程为⎪y = ( t 为参数),曲线C 的参数方⎧x=2s2⎪2程为⎨⎩y=22s( s 为参数).设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值.(解析)直线l 的一般方程为x - 2 y + 8 = 0 .因为点P 在曲线C 上,设P(2s2 , 2 2s) ,从而点P 到直线l 的的距离4 5d == ,当s =时,dmin=5.因此当点P 的坐标为(4, 4) 时,曲线C 上点P 到直线l 的距离取到最小值.5⎧x =a cos t23.(2023 全国I 文理)在直角坐标系xOy 中,曲线C1 的参数方程为⎨y = 1+a sin t(t 为参数,a>0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C2 :ρ= 4 cosθ.(I)说明C1 是哪种曲线,并将C1 的方程化为极坐标方程;(II)直线C3 的极坐标方程为θ=a0 ,其中a0 满足tan a0 =2 ,假设曲线C1 与C2 的公共点都在C3上,求a.22(s -2)2 +4510 10 ⎫2152⎩1123⎩⎨⎩=⎧x = a cos t (解析)(1) ⎨ y = 1 + a sin t( t 均为参数),∴x 2 + ( y - 1)2= a 2 ①∴ C 为以(0 ,1) 为圆心, a 为半径的圆.方程为 x 2 + y 2 - 2 y +1 - a 2 = 0 .∵ x 2 + y 2 = ρ2 ,y = ρsin θ,∴ ρ2- 2ρsin θ+ 1 - a 2 = 0 ,即为C 的极坐标方程.(2) C :ρ= 4cos θ,两边同乘ρ得ρ2 = 4ρcos θ ρ2= x 2 + y 2 ,ρcos θ= x ,∴ x 2 + y 2 = 4x ,即( x - 2)2+ y 2 = 4 ②C 3 :化为一般方程为 y = 2x ,由题意: C 1 和C 2 的公共方程所在直线即为C 3 ,①—②得: 4x - 2 y + 1 - a 2 = 0 ,即为C ,∴1 - a 2 = 0 ,∴ a = 1 .24.(2023 全国 II 文理)在直角坐标系 xOy 中,圆 C 的方程为( x + 6)2+ y 2 = 25 .(I) 以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求 C 的极坐标方程;⎧x = t cos α(II)直线 l 的参数方程是⎨ y = t sin α(t 为参数),l 与 C 交于 A 、B 两点, AB = ,求 l 的斜率.⎧ρ2 = x 2 + y 2 (解析)(Ⅰ)整理圆的方程得 x 2 + y 2 + 12 + 11 = 0 ,由⎪ρcos θ= x ⎪ρsin θ= y 可知圆C 的极坐标方程为ρ2 + 12ρcos θ+ 11 = 0 .(Ⅱ)记直线的斜率为 k ,则直线的方程为 kx - y = 0 ,由垂径定理及点到直线距离公式知:= 36k 2 290 ,整理得 k 2 = 5 ,则 k = ± . 1 + k 4 3 3⎪x =3 cos α25.(2023 全国 III 文理)在直角坐标系 xOy 中,曲线C 1 的参数方程为⎨ ⎩ y = sin α(α为参数),以坐标原点为极点,以 x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为ρsin(θ+ π) = 2.24(Ⅰ)写出C 1 的一般方程和C 2 的直角坐标方程;(Ⅱ)设点 P 在C 1 上,点 Q 在C 2 上,求| PQ |的最小值及此时 P 的直角坐标.x 2 2(解析)(Ⅰ) C 1 的一般方程为 3+ y = 1, C 2 的直角坐标方程为 x + y - 4 = 0 .(Ⅱ)由题意,可设点 P 的直角坐标为( 3 cos α, sin α) ,因为C 2 是直线,所以| PQ | 的最小值,即为 P 到C 2| 3 cos α+sin α- 4 |2222⎨⎩⎪=1⎩的距离d (α) 的最小值, d (α) ==π2 | sin(α+ π ) - 2 | .3 3 1当且仅当α= 2k π+(k ∈ Z ) 时, d (α) 取得最小值,最小值为 6,此时 P 的直角坐标为( , ) . 2 2 ⎧x = 1 + 1t , 26.(2023 江苏)在平面直角坐标系 xOy 中,已知直线l 的参数方程为⎪ ⎪ y = ⎩ 2 3 t , 2(t 为参数) ,椭圆C 的参数⎧x = cos θ,方程为⎨ y = 2sin θ, (θ为参数) ,设直线l 与椭圆C 相交于 A , B 两点,求线段 AB 的长.⎧x = 1+ 1t(解析)椭圆C 的一般方程为 x 2 + y 4 = 1,将直线l 的参数方程⎨ ⎪ y = ⎩2 3 t2 ,代入 x 2 + y 4 = 1,得(1+ 1 t )2 + 3 t )22 = 1,即7t 2 +16t = 0 ,解得t = 0 , t = - 16 ,所以 AB =| t - t | 16 .2 4 1 2 71 2727.(2023 全国Ⅰ文理)在直角坐标系 xOy 中,直线C : x = -2 ,圆C :(x -1)2 + ( y - 2)2= 1 ,以坐标原12点为极点, x 轴的正半轴为极轴建立极坐标系.(Ⅰ)求C 1 , C 2 的极坐标方程;(Ⅱ)假设直线C 3 的极坐标方程为θ=(ρ∈ R ) ,设C 2 与C 3 的交点为 M , N ,求∆C 2MN 的面积.4(解析)(Ⅰ)因为 x = ρcos θ, y = ρsin θ,∴ C 的极坐标方程为ρcos θ= -2 , C 的极坐标方程为ρ2- 2ρcos θ- 4ρsin θ+ 4 = 0 .12(Ⅱ)将θ= π代入ρ2- 2ρcos θ- 4ρsin θ+ 4 = 0 ,得ρ2- 3 2ρ+ 4 = 0 ,解得ρ = 2, ρ = , 4|MN|= ρ - ρ = ,因为C 的半径为 1,则A C MN 的面积 ⨯ 122 ⨯1⨯sin 45o = 1 . 1 2 22 2 2 ⎧x = t cos α,28.(2023 全国Ⅱ文理)在直角坐标系 xOy 中,曲线C 1 : ⎨ y = t sin α, ( t 为参数,t ≠0)其中0 ≤α<π,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2 : ρ= 2 sin θ, C 3 : ρ= 2 3 cos θ. (Ⅰ)求C 2 与C 3 交点的直角坐标;(Ⅱ)假设C 1 与C 2 相交于点 A , C 1 与C 3 相交于点 B ,求| AB | 的最大值.222(π3623)( x -1+ y +1= )()⎨(解析)(Ⅰ)曲线C 的直角坐标方程为 x 2 + y 2 - 2 y = 0 ,曲线C 的直角坐标方程为 x 2 + y 2- 2 3x = 0 .联⎪x 2+ y 2- 2 y = 0,⎧x = 0, ⎧ 3 ⎪x = 2 , 立⎨x 2 + y 2 - 2 3x = 0,解得⎨ y = 0, 或⎨ 3 ⎪ ⎩ ⎪ y = ,⎩ 23所以C 2 与C 1 交点的直角坐标为(0, 0) 和( , ) .2 2(Ⅱ)曲线C 1 的极坐标方程为θ= α(ρ∈ R , ρ≠ 0) ,其中0 ≤α<π. 因此 A 得到极坐标为(2 sin α,α) , B 的极坐标为(2 3 cos α,α) . π5π所以 AB = 2 sin α- 2 3 cos α = 4 s in(α-) ,当α= 时, AB 取得最大值,最大值为 4 . 3 629.(2023 江苏) 已知圆 C 的极坐标方程为ρ2+ 2 2ρsin(θ- π- 4 = 0 ,求圆 C 的半径.4(解析) 以极坐标系的极点为平面直角坐标系的原点O ,以极轴为 x 轴的正半轴,建立直角坐标系 xoy .圆C 的极坐标方程为ρ2 + 2⎛ 2 sin θ- 2cos ⎫4 = 0 ,化简,得ρ2 + 2ρsin θ- 2ρcos θ- 4 = 0 . ρ 22 θ⎪⎪ - ⎝ ⎭则圆C 的直角坐标方程为 x 2 + y 2 - 2x + 2 y - 4 = 0 ,即2 2,所以圆C 的半径为 . ⎧x = 3 + 1 t 30.(2023 陕西文理)在直角坐标系 xOy 中,直线l 的参数方程为⎪2⎪ y = 3 t ⎩ 2 轴正半轴为极轴建立极坐标系,⊙ C 的极坐标方程为ρ= 2 3 sin θ. (Ⅰ)写出⊙ C 的直角坐标方程;( t 为参数).以原点为极点, x(Ⅱ) P 为直线l 上一动点,当 P 到圆心C 的距离最小时,求 P 的直角坐标.(解析)(Ⅰ) 由ρ= 2 3 sin θ, 得ρ2= 2 3ρsin θ,从而有 x 2+y 2= 2 3y , 所以x 2+ (y -3 )2= 3 .(Ⅱ)设P (3 += ,故当t =0 时,| PC |取最小值,此时 P 点的直角坐标为(3, 0) .21t,3t), 又C(0, 3) ,则| PC |=3222 3 ⎪55⎨y = 2 - 2t⎩⎩31.(2023 全国Ⅰ文理)已知曲线C : x 4 + y 29 = 1,直线l : ⎧x = 2 + t ( t 为参数). ⎩(Ⅰ)写出曲线C 的参数方程,直线l 的一般方程;(Ⅱ)过曲线C 上任一点 P 作与l 夹角为30o的直线,交l 于点 A ,求| PA |的最大值与最小值.⎧x = 2 cos θ.(解析)〔I 〕曲线C 的参数方程为⎨ y = 3sin θ. (θ为参数).直线l 的一般方程为2x + y - 6 = 0. ……5 分(Ⅱ)曲线C 上任意一点P(2cos θ.3sin θ)到l 的距离为d =4 cos θ+ 3sin θ- 6 .则 PA =d = sin 30︒ 5sin(θ+α) - 6 , 其中α为锐角,且tan α= 4 . 3当sin (θ+α)=-1时,PA 取得最大值,最大值为22 5 .5当sin(θ+α) = 1时,PA 取得最小值,最小值为2 5 .532.(2023 全国Ⅱ文理)在直角坐标系 xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,半圆 C 的极坐标方程为ρ= 2 cos θ,θ∈ ⎡0,π⎤ .(Ⅰ)求 C 的参数方程;⎣⎢ 2 ⎥⎦(Ⅱ)设点 D 在 C 上,C 在 D 处的切线与直线l : y = 3x + 2 垂直,依据(Ⅰ)中你得到的参数方程,确定 D 的坐标.(解析)(I)C 的一般方程为(x -1)0 ≤ t ≤ x ).2 + y 2⎧x = 1+ cos t , = 1(0 ≤ y ≤ 1) ,可得 C 的参数方程为⎨ y = sin t ,(t 为参数,(Ⅱ)设 D (1+ cos t , sin t ) .由(I)知 C 是以 G(1,0)为圆心,1 为半径的上半圆. π因为 C 在点D 处的切线与 t 垂直,所以直线 GD 与 t 的斜率相同, tan t = 3, t =.32 5523⎩⎩⎩1⎩⎩ππ 3故D 的直角坐标为(1+ cos , s in ) ,即( , ) .3 3 2 233.(2023 全国Ⅰ文理)已知曲线C 的参数方程为⎧x = 4 + 5 cos t( t 为参数),以坐标原点为极点,x 轴的正1 ⎨y = 5 + 5sin t半轴为极轴建立极坐标系,曲线C2 的极坐标方程为ρ= 2 s inθ.(Ⅰ)把C1 的参数方程化为极坐标方程;(Ⅱ)求C1 与C2 交点的极坐标( ρ≥0 ,0 ≤θ≤2π).⎧x = 4 + 5 c os t2 2(解析)将⎨y = 5 + 5sin t消去参数t ,化为一般方程(x - 4) + ( y -5) = 25 ,即C1 :x 2 +y2⎧x =ρcosθ-8x -10 y+16 = 0 ,将⎨y =ρsinθ代入x 2 +y2- 8x -10 y + 16 = 0 得,ρ2 - 8ρcosθ-10ρsinθ+16 = 0 ,∴C 的极坐标方程为ρ2 - 8ρcosθ-10ρsinθ+16 = 0 .⎪x2+y2-8x-10y+16=0(Ⅱ) C 的一般方程为x2 +y2 - 2 y = 0 ,由⎨⎧x =1解得⎨⎧x = 0或⎨,2∴C1 与C2 的交点的极坐标分别为(⎩x2+y2-2y=0π),(2, ) .4 2⎩y =1 ⎩y = 2 34.(2023 全国Ⅱ文理)已知动点P ,Q 都在曲线C与β= 2α( 0 <α< 2π) M 为PQ 的中点.⎧x = 2 c os β:⎨y = 2 s in β(β为参数)上,对应参数分别为β=α(Ⅰ)求M的轨迹的参数方程(Ⅱ)将M 到坐标原点的距离d 表示为α的函数,并推断M 的轨迹是否过坐标原点.(解析)(Ⅰ)由题意有P(2c osα,2sinα),Q(2c os2α,2sin2α),因此M(cosα+cos2α,sinα+sin2α),⎧x = cosα+ cos 2α,M 的轨迹的参数方程为⎨y = sinα+ sin 2α, (0 <α< 2π).(Ⅱ)M 点到坐标原点的距离d ==0 <α< 2π),当α=π时,d = 0 ,故M 的轨迹过坐标原点.2,π3⎩100⎩135.(2023 全国文理)已知曲线C 的参数方程是⎧x = 2 cos ϕϕ为参数),以坐标原点为极点, x 轴的正半轴1⎨y = 3sin ϕ(为极轴建立极坐标系,曲线C 2 的极坐标方程是ρ= 2 .正方形 ABCD 的顶点都在C 2 上,且 A 、 B 、C 、πD 依逆时针次序排列,点 A 的极坐标为(2, ) . 3(Ⅰ)求点 A 、 B 、C 、 D 的直角坐标;(Ⅱ)设 P 为C 上任意一点,求| PA |2 + | PB |2 + | PC |2 + | PD |2 的取值范围.π5π 4π 11π(解析)(1)点 A , B , C , D 的极坐标为(2, ), (2, ), (2, ), (2, ) ,3 6 3 6点 A , B , C , D 的直角坐标为(1, 3),(-⎧x 0 = 2cos ϕ3,1), (-1, - 3),( 3, -1) .(2)设 P (x 0 , y 0 ) ;则⎨ y = 3sin (ϕ为参数) , ⎩ 0ϕt = PA 2+ PB 2+ PC 2+ PD 2= 4x 2 + 4 y 2 +16 = 32 + 20 sin 2ϕ∈32, 52.⎧x = 2 c os α 36.(2011 全国文理)在直角坐标系 xOy 中,曲线C 1 的参数方程为⎨ y = 2 + 2 s in(α为参数),M 是C 上 α的动点, P 点满足OP = 2OM , P 点的轨迹为曲线C 2(Ⅰ)求C 2 的方程(Ⅱ)在以 O 为极点,x 轴的正半轴为极轴的极坐标系中,射线θ= π与C 的异于极点的交点为 A ,与C 的异于极点的交点为 B ,求 AB .31 2(解析)(I)设 P (x , y ) ,则由条件知 M( x , y).由于 M 点在C 上,⎧ x = 2 cos α ⎪ 2 2 2⎧ x = 4 cos α 1⎧ x = 4 cos α 所以⎨ y ,即⎨y = 4 + 4 s in ,从而C 2 的参数方程为⎨y = 4 + 4 s in (α为参数), ⎪ = 2 + 2 s in α ⎩ α ⎩ α⎩ 2(Ⅱ)曲线C 1 的极坐标方程为ρ= 4sin θ,曲线C 2 的极坐标方程为ρ= 8sin θ.射线θ= π与C 的交点 A 的极径为ρ = 4sin π,射线θ= π与C 的交点 B 的极径为ρ = 8sin π.3 1 1 3 32 23所以| AB |=| ρ2 - ρ1 |= 2 .。
新课标极坐标参数方程高考题汇总

极坐标参数方程训练题1、(2014·福建高考理科·T21)已知直线l 的参数方程为2()4x a tt y t =-⎧⎨=-⎩为参数,圆C 的参数方程为4cos 4sin x y θθ=⎧⎨=⎩(θ为参数). (1)求直线l 和圆C 的普通方程; (2)若直线l 与圆C 有公共点,求实数a 的取值范围. 2..(2014·辽宁高考)将圆221x y +=上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.(Ⅰ)写出C 的参数方程; (Ⅱ)设直线:220l x y +-=与C 的交点为12,P P ,以坐标原点为极点,x 轴正半轴为极坐标建立极坐标系,求过线段12P P 的中点且与l 垂直的直线的极坐标方程.3..(2014·新课标全国卷Ⅱ高考·T23) (2014·新课标全国卷Ⅱ高考理科数学·T23)(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,以坐标原点为极点,x 轴为极轴建立极坐标系,半圆C 的极坐标方程为ρ=2cos θ,θ∈0,2π⎡⎤⎢⎥⎣⎦. (1)求C 的参数方程. (2)设点D 在C 上,C 在D 处的切线与直线l:y=3x+2垂直,根据(1)中你得到的参数方程,确定D 的坐标.4.(15年新课标1)在直角坐标系xOy 中,直线1:2C x =-,圆()()222:121C x y -+-=,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.(I )求12,C C 的极坐标方程.(II )若直线3C 的极坐标方程为()πR 4θρ=∈,设23,C C 的交点为,M N ,求2C MN ∆ 的面积.5.(2015新课标(II ))直角坐标系xoy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩(t 为参数,0t ≠),其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线2:2sin C ρθ=,曲线3:23cos C ρθ=.(Ⅰ).求2C 与1C 交点的直角坐标;(Ⅱ).若2C 与1C 相交于点A ,3C 与1C 相交于点B ,求AB的最大值.6.(2013·辽宁高考)在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系。
参数方程与极坐标 专题强化训练

参数方程与极坐标 专题强化训练1. 在直角坐标系xOy 中,曲线1C 的参数方程为1cos (sin x t t y t αα=-+⎧⎨=⎩为参数,[0,))απ∈,在以坐标原点为极轴,x 轴正半轴为极轴的极坐标系中,曲线2C :4cos ρθ=.(1)求2C 的直角坐标方程;(2)若曲线1C 与2C 交于A ,B 两点,且||AB >α的取值范围. 1.【解析】(1)由4cos ρθ=得24cos ρρθ=,…………………………………1分由互化公式,得224x y x +=, …………………………………3分 所以2C 的直角坐标方程为22(2)4x y -+=.…………………………………4分(2)易知直线1C 的斜率存在,设其普通方程为(1)y k x =+,…………………5分 曲线2C 是以(2,0)为圆心,以2为半径的圆,由||AB >32=, ……………………6分32<,解得33k -<<,即tan 33α-<<,………………8分 得06πα≤<,56παπ<<. …………………………………10分2. 在平面直角坐标系xOy 中,曲线C 的参数方程为cos (0sin x a a a y a ββ=+⎧>⎨=⎩,β为参数).以O 为极点,x 轴的正半轴为极轴,建立极坐标系,直线l 的极坐标方程3cos()32πρθ-=. (1)若曲线C 与l 只有一个公共点,求a 的值;(2)A ,B 为曲线C 上的两点,且3AOB π∠=,求AOB ∆的面积最大值.2.【解析】(1)曲线C 时以(,0)a 为圆心,以a 为半径的圆;直线l 的直角坐标方程为30x -=. ……………………………2分 由曲线C 与直线l 只有一个公共点,可得|3|2a a -=,……………………3分 解得3a =-(舍去)或1a =. …………………………………4分(2)曲线C 的极坐标方程为2cos (0)a a ρθ=>,设A 的极角为,B 的极角为3πθ+, …………………………………5分则1||||sin |2cos ||2cos()|2343OAE S OA OB a a πθθθ∆==+⋅⋅2|cos cos()|3πθθ=+, …………………………………7分2111cos 2cos cos()cos sin cos 2322224πθθθθθθθ++=-=-⋅11111(cos 2sin 2)cos(2)2224234πθθθ=-+=++, 所以当6πθ=-时,11cos(2)234πθ++取得最大值34.……………………9分所以AOB ∆的面积最大值是24. …………………………………10分3. 在极坐标系中,点)6A π,)2B π,曲线C : 2cos()(0)3πρθρ=-≥.以极点为坐标原点,极轴为x 轴正半轴建立平面直角坐标系.(1)在直角坐标系中,求点A 、B 的直角坐标及曲线C 的参数方程;(2)设点M 为曲线C 上的动点,求22||||MA MB +的取值范围.3.【解析】(1)由cos x ρθ=,sin y ρθ=,解得3(2A ,B .………2分因为2cos()3πρθ=-,所以212(cos )22ρρθθ=+,即220x y x +--=,即221()(12x y -+-=. ……………………………………4分 所以曲线C的参数方程为1cos 2sin 2x y θθ⎧=+⎪⎪⎨⎪=+⎪⎩(02θπ≤<,θ为参数). ………5分(2)不妨设1(cos ,sin )22M αα++, 则22||||MA MB+22221(cos 1)sin (cos )(sin 22αααα=-++++-4cos 42sin()6πααα=-=-+,………………………………8分 因为sin()[1,1]6πα+∈-,所以42sin()[2,6]6πα-+∈. 所以22||||MA MB +的取值范围是[2,6].…………………………………………10分4. 在直角坐标系xOy 中,以原点O 为极点,x 轴正半轴为极轴建立极坐标系.若曲线C 的极坐标方程为2cos 4sin 0ρθθ-=,P 点的极坐标为(3,)2π,在平面直角坐标系中,直线l 经过点P(1)写出曲线C 的直角坐标方程和直线l 的参数方程;(2)设直线l 与曲线C 相交于 A B ,两点,求11PA PB+的值. 【解析】(1)曲线C 的极坐标方程化为直角坐标方程为24x y =,……………2分P 点的极坐标为:(3,)2P π,化为直角坐标为(0,3)P ……………………………3分 直线l 的参数方程为cos 33sin 3x t y t ππ⎧=⎪⎪⎨⎪=+⎪⎩,即123x t y ⎧=⎪⎪⎨⎪=+⎪⎩ (t 为参数),………………5分(2)将l 的参数方程代入曲线C的直角坐标方程,得21124t =+,整理得:2480t --=, …………………………………6分显然有0∆>,则1248t t =-,12t t +=1212||||||||||48PA PB t t t t ===, …………………………………8分1212||||||||||PA PB t t t t +=+=-==所以11||||||||||||6PA PB PA PB PA PB ++==. …………………………………10分。
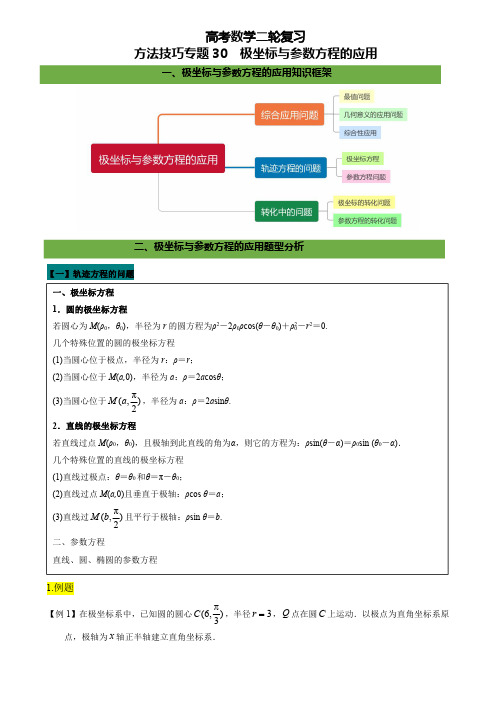
高考数学二轮复习-专题30 极坐标与参数方程的应用(解析版)
又因为 O是圆 C 上的点,所以 POQ PCQ π 。
26
【三】最值、几何意义的综合问题
1.距离最值(点到点、曲线点到线、) 距离的最值: ---用“参数法” (1)曲线上的点到直线距离的最值问题 (2)点与点的最值问题 “参数法”:设点---套公式--三角辅助角 ①设点: 设点的坐标,点的坐标用该点在所在曲线的的参数方程来设 ②套公式:利用点到线的距离公式 ③辅助角:利用三角函数辅助角公式进行化一 2.面积的最值问题 面积最值问题一般转化成弦长问题+点到线的最值问题 3.几何意义及其综合应用:
P(2,
)
在曲线
cos(
)
2
上.
3
3
所以,l的极坐标方程为
cos(
)
2
.
3
(2)设 P(, ) ,在 Rt△OAP 中, | OP || OA | cos 4 cos , 即 4 cos .
因为P在线段OM上,且
AP
OM
,故
的取值范围是 [
,
]
.
42
所以P点轨迹的极坐标方程为
4 cos ,
(1)分别写出 M1 , M 2 , M 3 的极坐标方程;
(2)曲线 M 由 M1 , M 2 , M 3 构成,若点 P 在 M 上,且 | OP | 3 ,求 P 的极坐标.
【解析】(1)由题设可得,弧 AB, BC,CD 所在圆的极坐标方程分别为
2 cos , 2sin , 2 cos .
[ ,
] .[来源:学*科*网]
42
【练习 2】在极坐标系中,已知圆 C 经过点 P (2 2, ) ,圆心为直线ρsin(θ-π)=- 3与极轴的交点,求
极坐标与参数方程训练系列 (2)

极坐标与参数方程训练系列六1.参数方程⎩⎪⎨⎪⎧x =t -1y =t +2(t 为参数)的曲线与坐标轴的交点坐标为( )A .(1,0),(0,-2)B .(0,1),(-1,0)C .(0,-1),(1,0)D .(0,3),(-3,0) 2.若t >0,下列参数方程的曲线不过第二象限的是( )A .⎩⎪⎨⎪⎧ x =-t y =tB .⎩⎪⎨⎪⎧ x =1y =tC .⎩⎪⎨⎪⎧x =t -1y =t 2-1 D .⎩⎪⎨⎪⎧x =1-1t y =t3.已知O 为原点,当θ=-π6时,参数方程⎩⎪⎨⎪⎧x =3cos θy =9sin θ(θ为参数)上的点为A ,则直线OA 的倾斜角为( ) A .π6 B .π3 C .2π3 D .5π64.已知⎩⎪⎨⎪⎧x =2+cos θ,y =sin θ(θ为参数),则(x -5)2+(y +4)2的最大值是( )A .4B .25C .36D .65.已知点()0,0,43,2,2,2O B A ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛--ππ则ABO ∆为( ) A .正△ B .直角△ C .锐角等腰△ D .直角等腰△6.曲线⎩⎪⎨⎪⎧x =3+cos θy =4+sin θ(θ为参数)上的点到坐标轴的最近距离为________.7.在极坐标系中,已知点A ⎝⎛⎭⎫1,34π,B ⎝⎛⎭⎫2,π4,则A 、B 两点间的距离为_______. 8.若直线3x +4y +m =0与圆⎩⎪⎨⎪⎧x =1+cos θ,y =-2+sin θ(θ为参数)相切,则实数m 的值是________.9.设质点沿以原点为圆心,半径为2的圆做匀角速度运动,角速度为π60 rad/s.试以时间t 为参数,建立质点运动轨迹的参数方程.10.已知点P(x,y)是圆x2+y2-6x-4y+12=0上的动点,求(Ⅰ)x2+y2的最值;(Ⅱ)x+y的最值;(Ⅲ)P到直线x+y-1=0距离d的最值.11.圆M的参数方程为x2+y2-4Rx cos α-4Ry sin α+3R2=0(R>0).(Ⅰ)求该圆的圆心坐标以及半径;(Ⅱ)当R固定,α变化时,求圆心M的轨迹.极坐标与参数方程训练系列七1.曲线⎩⎪⎨⎪⎧x =1+cos θy =-2+sin θ的中心坐标为( )A .(-2,1)B .(-1,2)C .(1,-2)D .(1,2)2.直线x -3y +4=0与曲线⎩⎪⎨⎪⎧x =2cos θy =2sin θ(θ为参数)的公共点有( )A .0个B .1个C .2个D .3个3.设曲线C 的参数方程为⎩⎪⎨⎪⎧x =2+3cos θy =-1+3sin θ(θ为参数),直线l 的方程为x -3y +2=0,则曲线C上到直线l 距离为71010的点的个数为( ) A .1 B .2 C .3 D .44.参数方程⎩⎪⎨⎪⎧x =12cos 2t +sin 2 ty =cos t +sin t(t 为参数)表示的曲线是( )A .关于x 轴对称B .关于y 轴对称C .关于原点对称D .关于直线y =x 对称5.动点M 作等速直线运动,它在x 轴和y 轴方向的分速度分别为9和12,运动开始时,点M 位于A (1,1),则点M 的参数方程是________.6.已知F 是曲线⎩⎨⎧x =22cos θy =1+cos 2θ(θ∈R )的焦点,A (1,0),则|AF |的值等于________.7.在平面直角坐标系xOy 中,已知曲线:sin x a C y a⎧=⎪⎨=⎪⎩(a 为参数),在以原点O 为极点,x 轴的非负半轴为极轴建立的极坐标系中,直线l 的极坐标方程为1)4cos(22-=+πθρ.求圆C 的普通方程和直线l 的直角坐标方程;8.曲线⎩⎪⎨⎪⎧x =1+cos θy =sin 2θ(θ为参数)与直线y =a 有两个公共点,求a 的取值范围.9.已知圆的极坐标方程为ρ2-42ρcos ⎝⎛⎭⎫θ-π4+6=0. (1)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程; (2)若点P (x ,y )在该圆上,求x +y 的最大值和最小值.10.已知点P (m ,n )在圆x 2+y 2=2上运动,求点Q (m +n,2mn )的轨迹方程,并判断轨迹极坐标与参数方程训练系列八1.θ取一切实数时,连接A (4sin θ,6cos θ)和B (-4cos θ,6sin θ)两点的线段的中点轨迹是( )A .圆B .椭圆C .直线D .线段 2.参数方程⎩⎨⎧x =⎪⎪⎪⎪cos θ2+sin θ2,y =12(1+sin θ)(0≤θ<2π)表示轨迹( )A .双曲线的一支,过点⎝⎛⎭⎫1,12B .抛物线的一部分,过点⎝⎛⎭⎫1,12 C .双曲线的一支,过点⎝⎛⎭⎫-1,12 D .抛物线的一部分,过点⎝⎛⎭⎫-1,12 3.下列参数方程(t 为参数)与普通方程x 2-y =0表示同一曲线的方程是( )A .⎩⎪⎨⎪⎧ x =|t |y =tB .⎩⎪⎨⎪⎧x =cos ty =cos 2t C .⎩⎪⎨⎪⎧ x =tan ty =1+cos2t 1-cos2t D .⎩⎪⎨⎪⎧x =tan t y =1-cos2t 1+cos2t4.已知过曲线⎩⎪⎨⎪⎧x =3cos θ,y =4sin θ(θ为参数,0≤θ≤π)上一点P ,原点为O ,直线PO 的倾斜角为π4,则P 点坐标是( )A .(3,4)B .⎝⎛⎭⎫322,22 C .(-3,-4) D .⎝⎛⎫125,125 5.曲线θ=2π3与ρ=6sin θ的两个交点之间的距离为( )A .1 B. 3 C .3 3 D .66.圆ρ=4cos θ的圆心到直线tan θ=1的距离为( )A.22B. 2 C .2 D .2 2 7.设椭圆的参数方程为⎩⎪⎨⎪⎧x =a cos θ,y =b sin θ(0≤θ≤π),M (x 1,y 1),N (x 2,y 2)是椭圆上两点.M ,N 对应的参数为θ1,θ2且x 1<x 2,则θ1,θ2大小关系是________.8.已知抛物线y 2=2px (p >0),过顶点的两弦OA ⊥OB ,则分别以OA ,OB 为直径的两圆的另一交点Q 的轨迹是________.9.在极坐标系中,若过点A (4,0)的直线l 与曲线ρ2=4ρcos θ-3有公共点,则直线l 的斜率的取值范围为__________.10.如图所示,已知曲线4x2+9y2=36(x>0,y>0),点A在曲线上移动,点C(6,4),以AC为对角线作矩形ABCD,使AB∥x轴,AD∥y轴,求矩形ABCD的面积最小时点A坐标.11.直线l:3x+2y-6=0与抛物线y2=23x交于A、B两点,求∠AOB的值.极坐标与参数方程训练系列九1.已知直线⎩⎪⎨⎪⎧x =3+4ty =-4+3t (t 为参数),下列命题中错误的是( )A .直线经过点(7,-1)B .直线的斜率为34C .直线不过第二象限D .|t |是定点M 0(3,-4)到该直线上对应点M 的距离2.以t 为参数的方程⎩⎨⎧x =1-12ty =-2+32t 表示( )A .过点(1,-2)且倾斜角为π3的直线B .过点(-1,2)且倾斜角为π3的直线C .过点(1,-2)且倾斜角为2π3的直线D .过点(-1,2)且倾斜角为2π3的直线3.直线⎩⎪⎨⎪⎧x =-1+t sin 10°y =2-t cos 10°(t 为参数)的倾斜角为( )A .10°B .80°C .100°D .170°4.直线⎩⎨⎧x =1+12t ,y =-33+32t (t 为参数)和圆x 2+y 2=16交于A ,B 两点,则AB 的中点坐标为( )A .(3,-3)B .(-3,3)C .(3,-3)D .(4,0)5.若圆的参数方程为⎩⎪⎨⎪⎧ x =-1+2cos θ,y =3+2sin θ(θ为参数),直线的参数方程为⎩⎪⎨⎪⎧x =2t -1,y =6t -1(t 为参数),则直线与圆的位置关系是( )A .过圆心B .相交而不过圆心C .相切D .相离 6.点P (x ,y )在椭圆(x -2)24+(y -1)2=1上,则x +y 的最大值为( )A .3+ 5B .5+ 5C .5D .67.过点P ()-3,0且倾斜角为30°的直线和曲线⎩⎨⎧x =t +1t ,y =t -1t(t 为参数)相交于A ,B 两点,则线段AB 长为________.8.已知直线l 经过点P (1,1),倾斜角α=π6,设l 与曲线⎩⎪⎨⎪⎧x =2cos θ,y =2sin θ(θ为参数)交于两点A ,B ,则点P 到A ,B 两点的距离之积为________.9.已知抛物线C :⎩⎨⎧x =s 2+1s2-2,y =2s -2s(参数为s ),过抛物线C 的焦点F 作倾斜角为α的直线l ,交抛物线C 于A ,B .(Ⅰ)将抛物线化为普通方程,并写出直线l 以t 为参数的参数方程; (Ⅱ)若AF →=3FB →,求倾角α.10.在直角坐标系xOy 中,直线l 的参数方程为⎩⎨⎧x =3-22t ,y =5+22t (t 为参数).在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为ρ=25sin θ.(Ⅰ)求圆C 的直角坐标方程;(Ⅱ)设圆C 与直线l 交于点A ,B .若点P 的坐标为(3,5),求|P A |+|PB |.参数方程单元测试题一、选择题(本大题共12小题,每小题5分,共60分.1.下列点不在直线12x y ⎧=--⎪⎪⎨⎪=+⎪⎩(t 为参数)上的是( )A .(-1,2)B .(2,-1)C .(3,-2)D .(-3,2)2.圆的参数方程为⎩⎪⎨⎪⎧x =4cos θ,y =4sin θ(θ为参数,0≤θ<2π),若Q (-2,23)是圆上一点,则对应的参数θ的值是( )A.π3 B.23π C.43π D.53π3.直线⎩⎪⎨⎪⎧x =3+t ,y =2-2t (t 为参数)的斜率为( ) A .2 B .-2 C.32 D .-324.已知O 为原点,当θ=-π6时,参数方程⎩⎪⎨⎪⎧x =3cos θ,y =9sin θ(θ为参数)上的点为A ,则直线OA 的倾斜角为( ) A.π6 B.π3 C.2π3 D.5π65.已知A (4sin θ,6cos θ),B (-4cos θ,6sin θ),当θ为一切实数时,线段AB 的中点轨迹为( )A .直线B .圆C .椭圆D .双曲线6.椭圆⎩⎪⎨⎪⎧x =3cos θ,y =4sin θ(θ为参数)的离心率是(B.C.D.7.已知圆M :x 2+y 2-2x -4y =10,则圆心M 到直线⎩⎪⎨⎪⎧x =4t +3,y =3t +1(t 为参数)的距离为( )A .1B .2C .3D .48.若直线⎩⎪⎨⎪⎧ x =t cos α,y =t sin α(t 为参数)与圆⎩⎪⎨⎪⎧x =4+2cos φ,y =2sin φ(φ为参数)相切,那么直线的倾斜角为( )A.π6或5π6B.π4或3π4C.π3或2π3 D .-π6或-5π69.若直线y =x -b 与曲线⎩⎪⎨⎪⎧x =2+cos θ,y =sin θθ∈[0,2π)有两个不同的公共点,则实数b 的取值范围是( ) A .(2-2,1) B .[2-2,2+2]C .(-∞,2-2)∪(2+2,+∞)D .(2-2,2+2)10.实数x ,y 满足3x 2+2y 2=6x ,则x 2+y 2的最大值是( )A .2 B .4 C .92D .511.参数方程⎩⎪⎨⎪⎧x =1+sin θy =cos 2⎝⎛⎭⎫π4-θ2(θ为参数,0≤θ<2π)所表示的曲线是( ) A .椭圆的一部分 B .双曲线的一部分C .抛物线的一部分,且过点⎝⎛⎭⎫-1,12D .抛物线的一部分,且过点⎝⎛⎭⎫1,12 12.已知直线l :⎩⎨⎧x =3t ,y =2-t(t 为参数),抛物线C 的方程y 2=2x ,l 与C 交于P 1,P 2,则点A (0,2)到P 1,P 2两点距离之和是( ) A .4+ 3 B .2(2+3) C .4(2+3) D .8+ 3 二、填空题(本大题共4小题,每小题5分,共20分,把正确答案填在题中横线上)13.双曲线⎩⎪⎨⎪⎧x =tan φ,y =sec φ(φ是参数)的渐近线方程为________.14.在极坐标系中,直线过点(1,0)且与直线θ=π3(ρ∈R )垂直,则直线极坐标方程为________.15.在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知射线θ=π4与曲线⎩⎪⎨⎪⎧x =t +1,y =(t -1)2(t 为参数)相交于A ,B 两点,则线段AB 的中点的直角坐标为________. 16.在直角坐标系xOy 中,椭圆C 的参数方程为⎩⎪⎨⎪⎧x =a cos φ,y =b sin φ(φ为参数,a >b >0).在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,直线l 与圆O 的极坐标方程分别为ρsin ⎝⎛⎭⎫θ+π4=22m (m 为非零常数)与ρ=b .若直线l 经过椭圆C 的焦点,且与圆O 相切,则椭圆C 的离心率为________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)已知圆O 的参数方程为⎩⎪⎨⎪⎧x =2cos θy =2sin θ(θ为参数,0≤θ<2π).(Ⅰ)求圆心和半径; (Ⅱ)若圆O 上点M 对应的参数θ=5π3,求点M 的坐标.18.(12分)已知曲线C :⎩⎪⎨⎪⎧x =4cos φ,y =3sin φ(φ为参数). (Ⅰ)将C 的方程化为普通方程;(Ⅱ)若点P (x ,y )是曲线C 上的动点,求2x +y 的取值范围.19.(12分)已知直线l 的参数方程为⎩⎨⎧x =3+12t ,y =2+32t (t 为参数),曲线C 的参数方程为⎩⎪⎨⎪⎧x =4cos θ,y =4sin θ(θ为参数). (Ⅰ)将曲线C 的参数方程化为普通方程;(Ⅱ)若直线l 与曲线C 交于A ,B 两点,求线段AB 的长.20.(12分)已知动点P 、Q 都在曲线C :⎩⎪⎨⎪⎧x =2cos t ,y =2sin t (t 为参数)上,对应参数分别为t =α与t =2α(0<α<2π),M 为PQ 的中点.(Ⅰ)求M 的轨迹的参数方程;(Ⅱ)将M 到坐标原点的距离d 表示为α的函数,并判断M 的轨迹是否过坐标原点.21.(12分)在直角坐标系xOy 中,l 是过定点P (4,2)且倾斜角为α的直线;在极坐标系(以坐标原点O 为极点,以x 轴非负半轴为极轴,取相同单位长度)中,曲线C 的极坐标方程为ρ=4cos θ.(Ⅰ)写出直线l 的参数方程,并将曲线C 的方程化为直角坐标方程;(Ⅱ)若曲线C 与直线相交于不同的两点M ,N ,求|PM |+|PN |的取值范围.22.(12分)在平面直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧ x =cos φy =sin φ(φ为参数),曲线C 2的参数方程为⎩⎪⎨⎪⎧x =a cos φy =b sin φ(a >b >0,φ为参数).在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线l :θ=α与C 1,C 2各有一个交点.当α=0时,这两个交点间的距离为2,当α=π2时,这两个交点重合.(Ⅰ)分别说明C 1,C 2是什么曲线,并求出a 与b 的值;(Ⅱ)设当α=π4时,l 与C 1,C 2的交点分别为A 1,B 1,当α=-π4时,l 与C 1,C 2的交点分别为A 2,B 2,求四边形A 1A 2B 2 B 1的面积.参数方程单元测试题答卷班级、姓名、学号、总分一、选择题13.、14.、15.、16.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据极坐标与参数方程中的路径问题专题
训练
引言
路径问题是极坐标和参数方程中重要的数学应用之一。
通过研
究极坐标和参数方程中的路径问题,我们能够更好地理解曲线的性
质和特点。
本文将介绍一些与路径问题相关的专题训练。
一、极坐标中的路径问题
1. 定义和性质:极坐标表示点的位置和距离,路径问题是研究
极坐标中曲线的轨迹和形状。
曲线可以用极坐标方程或参数方程表示。
通过探索极坐标中的路径问题,我们可以了解极坐标坐标系的
特点和应用。
2. 实例训练:通过给定的极坐标方程或参数方程,求解曲线的
方程、性质以及与其他曲线的关系。
例如,给定极坐标方程r =
2sinθ,求解曲线的方程、对称性以及与其他曲线的交点。
3. 应用举例:路径问题在实际生活中有广泛的应用。
以天体运
动为例,我们可以通过极坐标来描述和预测天体的轨迹和运动规律。
通过在极坐标中研究路径问题,我们可以更好地理解天体运动的本质。
二、参数方程中的路径问题
1. 定义和性质:参数方程表示点的位置和运动轨迹。
路径问题研究参数方程中的曲线轨迹和特性。
参数方程可以用来描述复杂的曲线和图形。
2. 实例训练:通过给定的参数方程,求解曲线在不同参数范围内的形状和特性。
例如,给定参数方程x = 2cos(3t),y = 2sin(3t),求解曲线在参数范围[0,2π]内的形状和长度。
3. 应用举例:参数方程在物理学、工程学和计算机图形学等领域有广泛的应用。
通过研究参数方程中的路径问题,我们可以模拟和描述物理系统、工程结构和计算机生成的图形。
结论
通过对极坐标和参数方程中的路径问题进行专题训练,我们可以深入了解曲线的性质、特点和应用。
路径问题在数学和实际应用
中起着重要的作用,通过专题训练能够提高我们的数学建模能力和问题解决能力。
参考文献
[1] 张三,李四. 极坐标与参数方程中的路径问题研究[J]. 数学学报,2019,40(3):123-135.
[2] 王五,赵六. 极坐标与参数方程的基础教程[M]. 北京:科学出版社,2020.。
