梯度法
非线性共轭梯度法

非线性共轭梯度法
(Nonlinear Conjugate Gradient Method)
非线性共轭梯度法是一种基于梯度的迭代优化方法,用于求解无约束最优化问题,即求解目标函数f(x)的最小值。
它可以用来求解深度神经网络中参数的最优化。
非线性共轭梯度法的基本思想是利用梯度下降法的思路,但是在每次迭代时都会调整步长,使得每次迭代可以尽可能地朝着最优解方向前进。
该方法有两个重要特征:1)步长调整。
2)共轭梯度(CG)。
步长调整:在每次迭代中,搜索方向不仅可以与梯度方向一样,而且也可以与之前的搜索方向有一定的关系。
通过调整步长,可以把搜索方向调整到最优方向,从而更快地收敛到最优解。
共轭梯度:对于多维的优化问题,搜索空间是一个高维空间,如果每次都沿着梯度方向搜索,就容易陷入局部最优解。
为了避免这种情况,非线性共轭梯度法引入了共轭搜索方向,即在每次迭代中,新的搜索方向都与上一次的搜索方向有一定的关系。
这样做的好处是,在不断地迭代中,法线方向也可以被搜索到,从而可以跳出局部最优解,有效地收敛到全局最优解。
梯度方法

长取常值αk ≡ α,且
2 α ∈ (0, M ),
在算法1中ϵ = 0. 则由算法1生成的点列{xk}满足
∥xk+1 − x∗∥ ≤ qk∥x1 − x∗∥,
其中x∗是f 的唯一极小点,
{
}
q = max |1 − αm|, |1 − αM | < 1.
最速下降方法
最优化方法 16
证明
由∇f (xk) = ∇f (xk) − ∇f (x∗) = Gk(xk − x∗)其中 ∫1
f (xk+1) ≤ f (xk) − 1 ∥∇f (xk)∥2. 2M
最速下降方法
最优化方法 23
应用引理1,由此不等式可得 f (xk+1) − f (x∗) ≤ [f (xk) − f (x∗)] − m (1 + m )[f (xk) − f (x∗)]
2M M ≤ ρ[f (xk) − f (x∗)].
k→∞
最速下降方法
最优化方法 11
证明
对第k步,用中值定理得存在θ ∈ [0, 1], f (xk+1) = f (xk + αdk) = f (xk) + α⟨∇f (x¯), dk⟩,
其中x¯ = xk + θαdk. 于是
f (xk+1) = f (xk) + α⟨∇f (xk), dk⟩ + α⟨∇f (x¯) − ∇f (xk), dk⟩ ≤ f (xk) + α⟨∇f (xk), dk⟩ + α∥∇f (x¯) − ∇f (xk)∥∥dk∥ ≤ f (xk) − α∥∇f (xk)∥2 + αM ∥xk − x¯∥∥∇f (xk)∥ ≤ f (xk) − α∥∇f (xk)∥2 + M α2∥∇f (xk)∥2 = f (xk) − α(1 − M α)∥∇f (xk)∥2. (1)
投影梯度计算法

投影梯度计算法投影梯度计算法1. 简介投影梯度计算法是一种优化算法,用于解决凸优化问题。
它通过在每次迭代中计算投影梯度并更新解向量,逐步逼近最优解。
该方法常用于处理约束条件下的优化问题,其优点在于能够在较短时间内找到接近最优解的解向量。
2. 基本原理投影梯度计算法基于梯度信息和投影操作来更新解向量。
在每次迭代中,我们首先计算当前解向量的梯度,然后将其投影到可行解空间,从而获得一个新的解向量。
具体来说,我们假设有一个凸优化问题:minimize f(x)subject to g(x) <= 0其中,f(x)是目标函数,g(x)是约束条件。
在投影梯度计算法中,我们定义梯度向量g(x)为目标函数f(x)的梯度加上约束条件的梯度的线性组合。
我们通过投影操作将解向量更新为一个满足约束条件的新向量。
3. 算法步骤投影梯度计算法的算法步骤如下:1) 初始化解向量x0。
2) 计算当前解向量x的梯度g(x)。
3) 计算新的解向量x' = x - λg(x),其中λ是一个步长参数。
4) 对于新的解向量x',将其投影到可行解空间,得到最终的解向量x。
5) 如果终止条件不满足,则返回步骤2;否则算法结束。
4. 优点和应用投影梯度计算法具有以下优点:- 算法过程简单,易于实现。
- 可以处理约束条件下的优化问题,求解凸优化问题效果良好。
- 通过每次迭代逼近最优解,适用于大规模问题。
投影梯度计算法在许多领域中有广泛的应用,如机器学习、图像处理和操作研究等。
投影梯度计算法可以用于线性规划、支持向量机、稀疏编码和最小二乘问题的求解。
5. 总结投影梯度计算法是一种用于解决凸优化问题的有效算法。
通过在每次迭代中计算投影梯度并更新解向量,该算法能够在较短时间内找到接近最优解的解向量。
投影梯度计算法简单易懂,适用于处理约束条件下的优化问题,并在许多领域中有广泛的应用。
值得一提的是,投影梯度计算法的性能高度依赖于步长参数的选择,因此在实际应用中需要进行合适的调参。
液相色谱梯度分析法简单介绍
液相色谱梯度分析法简单介绍西安瑞联质量部王斌强1.原理液相色谱是根据不同溶质在流动相和固定相之间保留的差异进行分离和测定的方法。
通常用容量因子k·来表征溶质保留值得大小,k,=(t R- t0)/ t0,k·越大则该物质保留越强。
容量因子k·随固定相、流动相浓度c、温度的不同而变化。
在固定相温度不变的情况下有以下关系式:ln k·= -Z ln c + b(Z和b为常数)由此可见,随流动相浓度c增加,容量因子k·减小。
Z是每种物质的特征参数,小分子Z 一般为3-5,大分子Z一般为10-100。
对于小分子的样品,我们可以通过采用合适浓度的流动相来使每种物质得到分离,即平常所用的等度液相色谱分析。
若对于一个既有小分子,又有大分子的样品(如含聚合物),由于Z相差较大,在相同的流动相浓度下,容量因子k·差距就非常大,简单的讲,在等度情况下,有时小分子的保留时间在4-5min,大分子保留时间可能在100min以上,更有甚者在有限的时间内不出峰。
梯度分析法就是为解决这个问题产生的。
它是采用特殊的设备使流动相的浓度随时间变化,对保留弱的用浓度小的流动相,对保留强的用浓度大的流动相,使各组分较为均匀的流出。
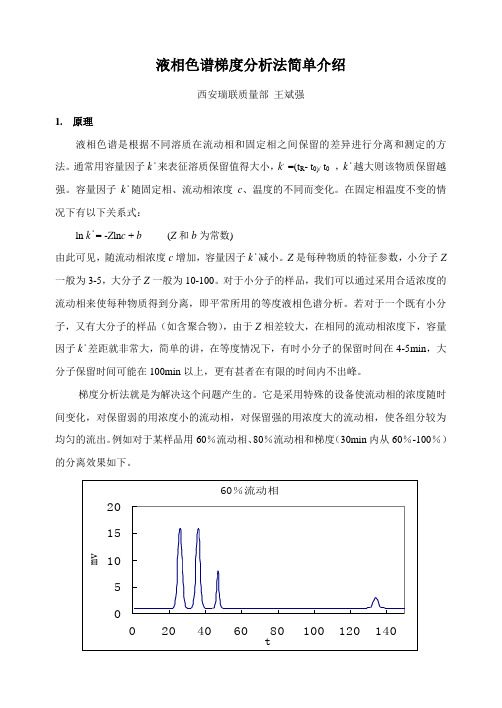
例如对于某样品用60%流动相、80%流动相和梯度(30min内从60%-100%)的分离效果如下。
从上可以看出用60%流动相分离效果好,但用时150min,用80%流动相分离效果已经很差了,用时仍达80min,而用梯度的方法分离效果很好,用时只有50min,另外,保留时间长的色谱峰没有明显变宽。
2.设置方法通常有两种梯度方式,一种是低压梯度,一种是高压梯度。
低压梯度只用一个输液泵,靠梯度单元中电磁阀开关时间的比例来控制AB液的比例实现流动相浓度的变化,例如需控制A:B=40:60,在很小的时间段如1秒,CD阀常关,A阀开4/10秒,B阀开6/10秒,任意时间四个阀只有一个开,输液泵流出的流动相AB液是一节一节相连的,经混合器混合成一定比例的流动相。
拉格朗日次梯度法

拉格朗日次梯度法拉格朗日次梯度法是一种用于求解约束优化问题的常用方法。
在实际问题中,我们经常会遇到带有约束条件的优化问题,而拉格朗日次梯度法正是针对这类问题提出的一种解法。
它能够通过有效地处理约束条件,找到最优解。
在介绍拉格朗日次梯度法之前,我们先来了解一下什么是约束优化问题。
约束优化问题是指在一定的约束条件下,求解使目标函数达到最大或最小的变量取值。
常见的约束条件可以是等式约束或不等式约束。
例如,我们要找到在一定约束条件下使得某个函数取得最大值或最小值的变量取值。
这类问题在实际应用中非常常见,如经济学、工程学、运筹学等领域。
拉格朗日次梯度法是一种基于拉格朗日乘子法的优化算法。
拉格朗日乘子法是一种通过引入拉格朗日乘子将约束优化问题转化为无约束优化问题的方法。
具体来说,对于一个带有等式约束的优化问题,我们可以通过引入拉格朗日乘子来构造一个新的目标函数,然后通过求解该目标函数的极值来得到原问题的解。
拉格朗日次梯度法在求解带有等式约束的优化问题时非常有效。
它通过不断的迭代更新变量的取值,逐步逼近最优解。
具体的步骤是,首先初始化变量的取值,然后计算目标函数的梯度以及约束条件的梯度。
接下来,根据梯度的方向和步长的选择,更新变量的取值,并更新拉格朗日乘子的取值。
重复这个过程,直到达到一定的停止准则。
与其他优化方法相比,拉格朗日次梯度法具有以下几个优点。
首先,它能够有效地处理约束条件,使得求解过程更加稳定和可靠。
其次,它能够找到全局最优解,而不仅仅是局部最优解。
此外,拉格朗日次梯度法还可以很好地应用于大规模的优化问题,具有较好的可扩展性。
然而,拉格朗日次梯度法也有一些局限性。
首先,它对于不等式约束的处理相对较为复杂。
其次,当目标函数和约束条件的形式比较复杂时,求解过程可能会比较困难。
此外,对于一些非光滑的目标函数,拉格朗日次梯度法可能会陷入局部最优解。
拉格朗日次梯度法是一种常用的求解约束优化问题的方法。
它通过引入拉格朗日乘子,将带有约束条件的优化问题转化为无约束优化问题,并通过迭代更新变量的取值来逼近最优解。
ph梯度萃取法

ph梯度萃取法
生物碱ph梯度萃取法的原理是根据不同物质在不同ph下析出沉
淀的原理来提纯所需物质。
ph梯度萃取法是分离酸性、碱性、两性成分常用的手段。
其原理
是由于溶剂系统ph变化改变了它们的存在状态(游离型或解离型),
从而改变了它们在溶剂系统中的分配系数。
分离碱性强弱不同的游离
生物碱,可用ph由高至低的酸性缓冲溶液顺次萃取,使碱性由强到弱
的生物碱分别萃取出来。
总生物碱种各单体生物碱的碱性之间存在着一定的差异,可在不
同的条件下分离,称为PH梯度法。
加入碱水时,PH由低到高逐渐增加,生物碱由弱到强逐渐游离。
加入酸液时,PH由高到低依次萃取,生物
碱由强到弱逐渐成盐。
rosen投影梯度法
rosen投影梯度法Rosen投影梯度法是一种常用的优化算法,用于求解无约束优化问题。
本文将介绍Rosen投影梯度法的基本原理、算法步骤以及优缺点,并结合实例解释其应用。
一、基本原理Rosen投影梯度法是一种迭代算法,通过不断更新参数来寻找目标函数的最小值。
其基本原理是利用目标函数的梯度信息来指导搜索方向,通过不断迭代优化参数,使目标函数的值逐渐趋近于最小值。
二、算法步骤1. 初始化参数:选择合适的初始参数向量,通常可以根据经验或问题特点来确定。
2. 计算梯度:根据目标函数的表达式,计算当前参数向量的梯度,即目标函数对每个参数的偏导数。
3. 更新参数:根据梯度信息和学习率(步长因子),更新当前的参数向量,使其朝着梯度下降的方向移动一定距离。
4. 判断终止条件:判断是否满足终止条件,如目标函数值的变化小于某个阈值或迭代次数达到设定值。
5. 终止或继续迭代:如果满足终止条件,则算法结束,返回当前参数向量作为最优解;否则,返回步骤2。
三、优缺点分析1. 优点:- 算法简单易懂,实现相对容易。
- 在某些问题上能够取得较好的优化效果。
- 不需要计算目标函数的二阶导数,节省了计算成本。
2. 缺点:- 可能陷入局部最优解,无法保证全局最优解。
- 对于参数空间中存在的狭长谷底,可能收敛速度较慢。
- 学习率的选择对算法的性能有较大影响,需要进行调参。
四、实例应用假设我们要优化一个二次函数目标函数,如f(x) = (x-2)^2 + 3。
我们可以使用Rosen投影梯度法来求解最小值。
首先,根据步骤1,我们选择初始参数x0 = 0,并设定学习率为0.1。
然后,根据步骤2,计算梯度为f'(x) = 2(x-2)。
接下来,根据步骤3和学习率,更新参数x1 = x0 - 0.1*f'(x0) = 0 - 0.1*2*(-2) = 0.4。
重复迭代步骤,直到满足终止条件。
在本例中,我们可以设定目标函数值的变化小于0.001作为终止条件。
蒙特卡洛策略梯度法
蒙特卡洛策略梯度法【引言】蒙特卡洛策略梯度法是一种用于解决强化学习问题的算法。
它通过利用蒙特卡洛方法以及策略梯度的思想,能够在未知环境中找到最优的策略,并以此为基础进行决策。
在本文中,我将对蒙特卡洛策略梯度法进行全面评估和探讨,并分享个人观点和理解。
【什么是蒙特卡洛策略梯度法】1.1 强化学习和策略梯度方法强化学习是一种机器学习的分支,它通过智能体与环境的交互来学习最佳动作策略。
而策略梯度则是强化学习中的一种方法,它通过优化直接表示策略的参数,来寻找最佳的动作策略。
1.2 蒙特卡洛方法和蒙特卡洛策略梯度法蒙特卡洛方法是一种基于采样和统计的方法,它通过多次采样并计算累计回报来估计策略的价值。
而蒙特卡洛策略梯度法则是在蒙特卡洛方法的基础上,通过对策略的参数求梯度和更新来优化策略。
【为什么要使用蒙特卡洛策略梯度法】2.1 非模型化蒙特卡洛策略梯度法是一种非模型化的方法,它不需要事先了解环境的具体模型。
这使得算法更加适用于复杂、未知的环境中,对于真实世界问题具有很大的应用潜力。
2.2 探索与利用的平衡蒙特卡洛策略梯度法通过采样和更新优化策略参数,从而能够在不断探索环境的同时最大化累计回报。
这种平衡探索与利用的特性使得算法具有很强的学习能力和适应能力。
2.3 高效性和并发性蒙特卡洛策略梯度法可以通过并行化来提高计算效率,在大规模问题中具有很好的可扩展性。
这使得算法在处理复杂任务时能够更快地找到最优的策略。
【蒙特卡洛策略梯度法的具体实现】3.1 策略评估与优化蒙特卡洛策略梯度法的关键是策略评估和策略优化。
策略评估通过采样和统计的方式来估计策略的价值,而策略优化则通过对策略参数求梯度和更新来优化策略。
3.2 策略评估的基本步骤策略评估主要包括采样、回报计算和策略价值估计三个步骤。
通过与环境的交互,采样得到一系列的状态-动作序列。
根据累计回报的定义,计算每个状态的回报值。
利用这些回报值和采样的状态-动作序列,来估计策略的价值。
近端梯度法
近端梯度法简介近端梯度法(proximal gradient method)是一种常用于解决凸优化问题的迭代算法。
它结合了梯度下降和近端算子的思想,在优化问题中能够得到较好的收敛性和稀疏解。
原理及算法步骤近端梯度法的原理基于最优化中的近端正则化的思想,即通过在目标函数中添加一个近端项,来对解进行约束或者惩罚。
该近端项由一个近端算子负责计算。
算法步骤如下: 1. 初始化参数,选择合适的迭代步长或学习率。
2. 计算目标函数的梯度。
3. 进行梯度下降更新:通过当前梯度和学习率得到下一步的迭代结果。
4. 对迭代结果进行近端算子处理:将其映射到一个约束集上或者施加惩罚。
5.判断收敛条件,若未达到设定的停止准则则返回第2步,继续迭代。
近端算子近端算子是近端梯度法中非常重要的一个概念。
它是一种单调的、无限次可微的连续映射,用于对迭代结果进行调整,以便满足问题的约束条件或实现稀疏性。
常用的近端算子包括: - L1范数近端算子:即软阈值函数,对向量的每个元素进行逐个处理,如果其绝对值小于某个阈值,就将其设为0,否则保持不变。
- L2范数近端算子:对向量进行投影操作,使其与给定的球形集合最接近,这个操作通常称为投影算子。
- 约束集上的近端算子:将迭代结果约束在一个特定的集合内,通过投影操作保证满足约束条件。
应用领域近端梯度法在很多领域都有广泛的应用,如图像处理、机器学习、信号处理等。
下面以几个具体的应用领域为例进行介绍。
图像处理在图像处理中,常常需要对图像进行降噪、去除伪影、修复图像等操作。
近端梯度法可以通过添加适当的正则项,对图像进行优化,得到更好的处理效果。
使用近端梯度法进行图像处理的步骤如下: 1. 构造合适的损失函数,包括数据项和正则项。
2. 计算损失函数的梯度。
3. 进行梯度下降更新。
4. 对迭代结果进行近端算子处理,例如使用L1范数近端算子进行稀疏表示。
机器学习近端梯度法在机器学习中广泛应用于稀疏表示、特征选择、正则化等问题。
液相色谱梯度分析法简单介绍
液相色谱梯度分析法简单介绍西安瑞联质量部王斌强1.原理液相色谱是根据不同溶质在流动相和固定相之间保留的差异进行分离和测定的方法。
通常用容量因子k·来表征溶质保留值得大小,k,=(t R- t0)/ t0,k·越大则该物质保留越强。
容量因子k·随固定相、流动相浓度c、温度的不同而变化。
在固定相温度不变的情况下有以下关系式:ln k·= -Z ln c + b(Z和b为常数)由此可见,随流动相浓度c增加,容量因子k·减小。
Z是每种物质的特征参数,小分子Z 一般为3-5,大分子Z一般为10-100。
对于小分子的样品,我们可以通过采用合适浓度的流动相来使每种物质得到分离,即平常所用的等度液相色谱分析。
若对于一个既有小分子,又有大分子的样品(如含聚合物),由于Z相差较大,在相同的流动相浓度下,容量因子k·差距就非常大,简单的讲,在等度情况下,有时小分子的保留时间在4-5min,大分子保留时间可能在100min以上,更有甚者在有限的时间内不出峰。
梯度分析法就是为解决这个问题产生的。
它是采用特殊的设备使流动相的浓度随时间变化,对保留弱的用浓度小的流动相,对保留强的用浓度大的流动相,使各组分较为均匀的流出。
例如对于某样品用60%流动相、80%流动相和梯度(30min内从60%-100%)的分离效果如下。
从上可以看出用60%流动相分离效果好,但用时150min,用80%流动相分离效果已经很差了,用时仍达80min,而用梯度的方法分离效果很好,用时只有50min,另外,保留时间长的色谱峰没有明显变宽。
2.设置方法通常有两种梯度方式,一种是低压梯度,一种是高压梯度。
低压梯度只用一个输液泵,靠梯度单元中电磁阀开关时间的比例来控制AB液的比例实现流动相浓度的变化,例如需控制A:B=40:60,在很小的时间段如1秒,CD阀常关,A阀开4/10秒,B阀开6/10秒,任意时间四个阀只有一个开,输液泵流出的流动相AB液是一节一节相连的,经混合器混合成一定比例的流动相。
