空间几何体的内切球与外接球问题
空间几何外接球和内切球含详解

A.
B.
C.
D. ⺁
2.已知如图所示的三棱锥 D ABC 的四个顶点均在球 O 的球面上, ABC 和 DBC 所在平面相互垂直, AB 3 , AC 3 , BC CD BD 2 3 ,则球 O 的表面积为 ( )
A . 4
B .12
C .16
D . 36
3.三棱锥 P ABC 的底面是等腰三角形,C 120 ,侧面是等边三角形且与底面 ABC 垂直,AC 2 ,
ᒺ ,若三棱柱的所有顶点都在同一
考向三 棱锥的外接球
类型一:正棱锥型
【例 3-1】已知正四棱锥 P ABCD 的各顶点都在同一球面上,底面正方形的边长为 2 ,若该正四棱锥的
体积为 2,则此球的体积为 ( )
A. 124 3
B. 625 81
C. 500 81
D. 256 9
【套路总结】
【举一反三】
【举一反三】 1. 设直三棱柱 ABC-A1B1C1 的所有顶点都在一个球面上,且球的表面积是 40π,AB=AC=AA1,∠BAC=120°, 则此直三棱柱的高是________.
2.直三棱柱 홨 홨 中,已知 홨 홨, 홨 ᒺ ,홨 ᒺ ⺁, 球面上,则该球的表面积为__________.
B. 20
C. 12
D. 20 3
【套路总结】 侧棱垂直与底面---垂面型
【举一反三】 1.已知几何体的三视图如图所示,则该几何体的外接球的表面积为( )
A. ⺁π
B. ᒺπ
C. π
D. ⺁π
2.已知三棱锥 S-ABC 中, SA 平面 ABC ,且 ACB 30 , AC 2AB 2 3.SA 1 .则该三棱锥
【举一反三】
立体几何中球的内切和外接问题完美版

性质
内切球的球心位于旋转体 的轴线上,且球的半径等 于旋转体半径。
应用
在几何和工程领域中,内 切球常用于研究旋转体的 体积和表面积。
旋转体的外接球
定义
旋转体的外接球是指与旋 转体外侧相切的球。
性质
外接球的球心位于旋转体 外侧,且球的半径等于旋 转体轴线到旋转体外侧的 垂直距离。
应用
在几何ቤተ መጻሕፍቲ ባይዱ工程领域中,外 接球常用于研究旋转体的 空间位置和关系。
立体几何中球的内 切和外接问题完美 版
目 录
• 球与多面体的内切和外接问题 • 球与旋转体的内切和外接问题 • 球与几何体的内切和外接问题实例 • 总结与展望
01
CATALOGUE
球与多面体的内切和外接问题
多面体的内切球
01
02
03
04
多面体的内切球是指与多面 体的所有顶点和面都相切的
球。
内切球半径的求法:设多面体的 每个面为$S_i$,内切球的半径
03
CATALOGUE
球与几何体的内切和外接问题实例
多面体内切球实例
总结词
多面体内切球是指一个球完全内切于一个多面体,且与多面体的每个面都相切 。
详细描述
多面体内切球的问题可以通过几何定理和公式来解决,例如欧拉公式和球内切 定理。例如,一个正方体的内切球就是其中心,半径等于正方体边长的一半。
旋转体外接球实例
外接球的性质:外接球与 多面体的每个顶点都相切 ,且外接球的直径等于多 面体的对角线长度。
外接球的应用:在几何、 物理和工程领域中,外接 球的概念被广泛应用于研 究多面体的性质和计算。
02
CATALOGUE
球与旋转体的内切和外接问题
球专题几何体的外接球与内切球问题(教学课件)——高中数学人教A版(2019)必修第二册

请同学回顾球的表面积与体积公式
(1)设球的半径为 R,则球的表面积 S=4πR 2 .
(2)设球的半径为 R,则球的体积 V= πR 3 .
例题解析
1
球的截面问题
用一个平面去截球,截面一定是圆面.
截面过球心,圆为球的大圆(如地球仪上
的赤道圈);截面不过球心,圆为球的小
圆
例题解析
所以球的表面积
为2,求球的表面积.
解:如图所示,作出轴截面,因为ΔABC为正三角形,
练习巩固
练习巩固
练习3:已知OA为球O的半径,过OA的中点M且垂直于OA的平面截球面
得到圆M.若圆M的面积为3π,则球O的表面积等于
解析:由题意得圆 M 的半径 r=
由勾股定理得 R2=r2+
答案:16π
,解得
,又球心到圆
1
球的截面问题
练习巩固
1
球的截面问题
练习: 过球面上A,B,C三点的截面和球心的距离是球
半径的一半,且AB=BC=CA=2,则球的表面积是多少?
课堂探究
2
球与几何体外接、内切问题
解决与球有关的外接、内切问题的关键
1、确定球心位置
重
要!
2、构造直角三角形,确定球的半径
球与多面体
1、多面体外接球:多面体顶点均在球面上;球心到各顶点距离为R
2、多面体内切球:多面体各面均与球面相切;球心到各面距离为R
球与旋转体
旋转体的外接球与内切球:球心都在旋转轴上
球与旋转体
①长方体或正方体的外接球的球心是其体对角线的中点;
②正三棱柱的外接球的球心是上下底面中心连线的中点.
例题解析
2
八个有趣模型——搞定空间几何体的外接球与内切球(学生版)高考资料高考复习资料中考资料
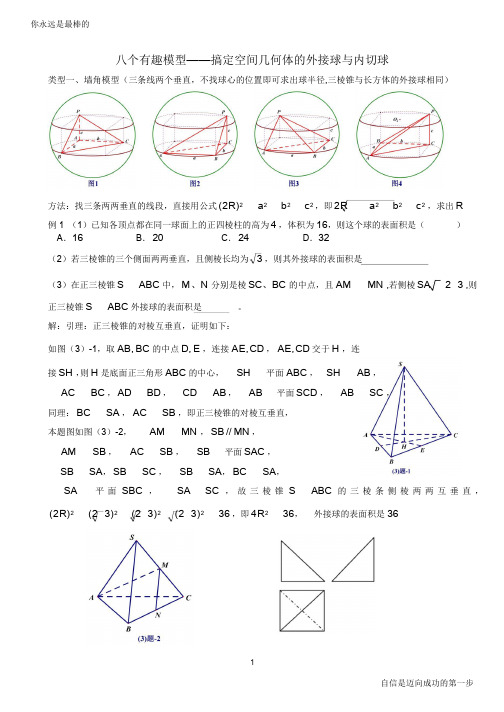
八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径,三棱锥与长方体的外接球相同)方法:找三条两两垂直的线段,直接用公式 (2R)2 a 2 b 2 c 2 ,即 2R a 2 b 2 c 2 ,求出 R例 1 (1)已知各顶点都在同一球面上的正四棱柱的高为 4 ,体积为16,则这个球的表面积是( )A .16B . 20C . 24D .32 (2)若三棱锥的三个侧面两两垂直,且侧棱长均为 3 ,则其外接球的表面积是 (3)在正三棱锥 S ABC 中, M 、N 分别是棱 SC 、BC 的中点,且 AMMN ,若侧棱 SA 2 3 ,则正三棱锥 SABC 外接球的表面积是。
解:引理:正三棱锥的对棱互垂直,证明如下:如图(3)-1,取 AB, BC 的中点 D, E ,连接 AE,CD , AE,CD 交于 H ,连 接 SH ,则 H 是底面正三角形 ABC 的中心,SH 平面 ABC , SH AB , AC BC , AD BD , CDAB , AB 平面 SCD , ABSC ,同理: BC SA , ACSB ,即正三棱锥的对棱互垂直,本题图如图(3)-2,AMMN , SB // MN ,AM SB , AC SB ,SB平面 SAC ,SBSA , SBSC , SB SA , BCSA ,SA 平 面 SBC , SA SC , 故 三 棱 锥 S ABC 的 三 棱 条 侧 棱 两 两 互 垂 直 ,(2R)2(2 3)2(2 3)2(2 3)236 ,即 4R 236,外接球的表面积是361自信是迈向成功的第一步(4)在四面体 S ABC 中, SA 平面ABC , BAC120 ,SA AC 2, AB 1, 则该四面体的外接球的表面积为()10 40A.11B.7C.D.33(5)如果三棱锥的三个侧面两两垂直,它们的面积分别为 6、4、3,那么它的外接球的表面积是(6)已知某几何体的三视图如图上右所示,三视图是腰长为 1 的等腰直角三角形和边长为 1 的正方形, 则该几何体外接球的体积为类型二、垂面模型(一条直线垂直于一个平面)1.题设:如图 5, PA 平面 ABC解题步骤:第一步:将 ABC 画在小圆面上, A 为小圆直径的一个端点,作小圆的直径 AD ,连接 PD ,则 PD 必过球心O ;第二步: O 为ABC 的外心,所以OO平面 ABC ,算出小圆O的半111径O 1Dr (三角形的外接圆直径算法:利用正弦定理,得a sin A bc12 ),OO PAr 1;sin B sinC2第三步:利用勾股定理求三棱锥的外接球半径:① (2R)2 PA 2(2r)22RPA 2(2r)2 ;②2 RR r 2OO212r2OO12自信是迈向成功的第一步你永远是最棒的2.题设:如图 6,7,8,P 的射影是 ABC 的外心 三棱锥 P ABC 的三条侧棱相等三棱锥 P ABC 的底面 ABC 在圆锥的底上,顶点 P 点也是圆锥的顶点解题步骤:第一步:确定球心O 的位置,取 ABC 的外心O ,则1P,O,O 三点共线;1第二步:先算出小圆 O 的半径 AOr1,再算出棱锥的高 PO 1h (也是圆锥的高);1第三步:勾股定理:OA2R 2 (h R)2 r 2 ,解出 R .2O A 2 O O11方法二:小圆直径参与构造大圆。
空间四面体的外接球和内切球问题

空间四面体的外接球和内切球问题
概述
空间四面体的外接球和内切球问题是几何学中的一个重要问题。
外接球是指与四面体的四个顶点都接触的球,内切球则是指与四面
体的每个面都相切的球。
这两个球体在几何学和物理学中都有广泛
的应用。
外接球的存在性和唯一性
对于任意给定的四面体,是否存在一个与之外切的球?答案是
肯定的。
根据几何学原理,四面体的外接球的球心一定位于四个顶
点的垂直平分面的交点上。
而外接球的半径等于球心与任意一个顶
点的距离。
内切球的存在性和唯一性
同样,对于任意给定的四面体,是否存在一个与之内切的球?
答案也是肯定的。
内切球的球心一定位于四个面的角平分线的交点上,而内切球的半径等于球心到四个面的距离的最小值。
解决方法
虽然存在多种方法来计算空间四面体的外接球和内切球,但最
常用的方法是使用线性代数和解析几何的技巧。
通过分析四面体的
顶点坐标和面的方程,可以求解外接球和内切球的半径和球心坐标。
应用领域
空间四面体的外接球和内切球在许多领域都有应用,比如计算
机图形学、物理学和工程学。
在计算机图形学中,外接球和内切球
可以用来优化渲染技术和三维模型的建模。
在物理学中,外接球和
内切球可以用来分析四面体的形状和体积。
在工程学中,外接球和
内切球可以用来优化结构设计和空间布局。
结论
空间四面体的外接球和内切球问题是一个重要且有趣的几何学
问题。
通过使用适当的解决方法和分析工具,我们可以计算出外接
球和内切球的半径和球心坐标,并在实际应用中发挥重要的作用。
【高中数学】空间几何体外接球与内切球问题

8.16作业 空间几何体外接球与内切球问题
1. 已知正四面体棱长为2,分别求该正四面体的外接球与内切球的半径.
2. 已知圆柱的内切球(圆柱的上、下底面及侧面都与球相切)的体积为43
π,求该圆柱的体积.
3. O 内切于该圆锥. (1)求该圆锥的高;
(2)求内切球O 的体积.
4.
5. 在长方体1111ABCD A B C D −中,AB =6,BC =8,16AA =.
(1)求三棱锥1D ABC −的体积;
(2)在三棱柱111ABC A B C −内放一个体积为V 的球,求V 的最大值.
6. 半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体
现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.若二十四等边体的棱长2,
(1)求其体积;
(2)若其各个顶点都在同一个球面上,求该球的表面积.。
空间正方体的外接球和内切球问题
空间正方体的外接球和内切球问题外接球
外接球是一个与正方体相切于所有顶点的球体。
换句话说,外接球的球心与正方体的顶点相重合,并且球体的半径刚好与正方体的边长相等。
由于正方体的六个顶点之间的距离是相等的,所以外接球也是一个等边球体。
外接球的性质有以下几点:
1. 外接球的球心与正方体的中心重合。
2. 外接球的半径等于正方体的边长。
内切球
内切球是一个与正方体的六个面相切的球体。
换句话说,内切球的球心位于正方体的中心,并且球体的半径刚好与正方体的边长的一半相等。
内切球的性质有以下几点:
1. 内切球的球心与正方体的中心重合。
2. 内切球的半径等于正方体的边长的一半。
外接球和内切球的关系如下:
1. 外接球的半径等于内切球半径的两倍。
2. 外接球的球心和内切球的球心重合。
外接球和内切球的问题在几何学和工程学中具有一定的应用价值。
通过研究它们的性质和特点,可以帮助我们更好地理解立体几何和球体的关系。
本文只是简单介绍了空间正方体的外接球和内切球问题,希望能对您有所帮助。
如需深入了解此问题,还需进一步研究和探索。
空间锥体的外接球和内切球问题
空间锥体的外接球和内切球问题问题描述
在三维空间中,我们有一个锥体,其顶点位于原点,底面是一
个正多边形。
我们希望找到这个锥体的外接球和内切球的半径。
解决方法
为了解决这个问题,我们可以采用以下简单的方法:
1. 外接球的半径:外接球的半径等于底面正多边形边长的一半。
这是因为正多边形的顶点位于外接圆上,所以外接圆的半径等于顶
点与中心之间的距离。
2. 内切球的半径:内切球的半径等于底面正多边形边长的二分
之根号3。
这是因为正多边形的中心与内切圆的圆心重合,所以内
切圆的半径等于中心到一条边的距离。
示例
假设我们有一个底面为正六边形的锥体,边长为4个单位。
按照上述方法,我们可以计算出:
- 外接球的半径为2个单位。
- 内切球的半径为2根号3个单位。
总结
通过简单的方法,我们可以求解三维空间中锥体的外接球和内切球的半径。
这个方法适用于任意底面为正多边形的锥体,提供了一种简洁而没有法律复杂性的解决方案。
以上内容为对"空间锥体的外接球和内切球问题"的描述和解决方法。
根据问题的具体情况,可以通过计算公式得出外接球和内切球的半径。
请根据实际需求进行具体计算。
高中数学掌握8大模型解决空间几何的外接球和内切球问题
⾼中数学掌握8⼤模型解决空间⼏何的外接球和内切球问题⼋个有趣模型——搞定空间⼏何体的外接球与内切球正三棱锥 S ABC 外接球的表⾯积是。
36 解:引理:正三棱锥的对棱互垂直。
证明如下:如图( 3)-1 ,取 AB,BC 的中点D,E ,连接 AE,CD ,AE,CD 交于 H ,连接 SH ,则 H 是底⾯正三⾓形 ABC 的中⼼, SH 平⾯ ABC , SH AB ,AC BC , AD BD , CD AB , AB 平⾯ SCD ,AB SC ,同理: BC SA , AC SB ,即正三棱锥的对棱互垂直,本题图如图( 3)-2, AM MN , SB// MN ,AM SB , AC SB , SB 平⾯ SAC , SB SA , SB SC , SB SA , BC SA , SA 平⾯ SBC , SA SC ,故三棱锥 S ABC 的三棱条侧棱两两互相垂直,(2R)2 (2 3)2 (2 3)2 (2 3)2 36,即 4R 2 36,正三棱锥 S ABC 外接球的表⾯积是 36类型⼀、墙⾓模型(三条线两个垂直,不找球⼼的位置即可求出球半径) 图3 图1 图2 ⽅法: a c 2 ,即 2R b 2 找三条两两垂直的线段,直接⽤公式 (2R) PcCa b 2 c 2,求出 R例1 A .1)已知各顶点都在同⼀球⾯上的正四棱柱的⾼为 16 B . 20 C . 24 4,体积为 16,则这个球的表⾯积是(. 322) 若三棱锥的三个侧⾯两垂直,且侧棱长均为 3,则其外接球的表⾯积是解: 1) V a 2h 16,a 2, 4R 2 a 2 a 2h 24 4 16 24 , S 24 ,选 C ;2) 4R 2 3 34 R 2 9 3) 在正三棱锥 S ABC中, M 、N 分别是棱 SC 、BC 的中点,且 AM MN , 若侧棱 SA 2 3 ,则CC4)在四⾯体S ABC 中,SA 平⾯ABC ,BAC 120 ,SA AC 2,AB 1, 则该四⾯体的外接5)6)解析:BC 球的表⾯积为( D )A.11 B.7如果三棱锥的三个侧⾯两两垂直,它们的⾯积分别为已知某⼏何体的三视图如图所⽰,三视图是腰长为何体外接球的体积为4)在ABC中,BC 2 AC22AB2 2AB7 ,ABC 的外接球直径为2rBCsin B AC5)三条侧棱两两⽣直,ab 12bc abcac6) (2R) b2V 4R333382 2 2(2R)2(2r)2SA2403S40设三条侧棱长分别为24,a 3,b2 3,R2 3,43,2,⼀条直线垂直于⼀个平⾯)10C.36、4、40D.33,那么它的外接球的表⾯积是1的等腰直⾓三⾓形和边长为1的正⽅形,则该⼏BC3,选cos12027a,b,c( a,b,c4,c 2,(2R)2R327,R),则b2 29 ,S 4 R2 29 ,类型⼆、垂⾯模型1.题设:如图5,PA 平⾯ABC 解题步骤:第⼀步:将ABC 画在⼩圆⾯上,A 为⼩圆直径的⼀个端点,作⼩圆的直径AD ,连接PD ,则PD 必过球⼼O ;第⼆步:O1为ABC的外⼼,所以OO1 平⾯ABC ,算出⼩圆O1的半O1D r (三⾓形的外接圆直径算法:利⽤正弦定理,得a sin Absin BsincC 2r ),OO1 21PA;第三步:利⽤勾股定理求三棱锥的外接球半径:①2 2 2(2R)2 PA2 (2r)2222R PA2(2r)2;2.题设:如图6,7,8,P的射影是ABC 的外⼼三棱锥P ABC的三条侧棱相等三棱锥P ABC的底⾯ABC 在圆锥的底上,顶点P点也是圆锥的顶点解题步骤:ABC的外⼼O1,则P , O, O1三点共线;第⼆步:先算出⼩圆O1 的半径AO1 r ,再算出棱锥的⾼PO1 h (也是圆锥的⾼);第三步:勾股定理:OA2 O1A2 O1O2 R2 (h R)2 r 2,解出R ⽅法⼆:⼩圆直径参与构造⼤圆。
外接球与内切球问题解题技巧梳理
外接球与内切球问题解题技巧梳理一.外接球8大模型秒杀公式推导r α说明:为底面外接圆的半径,R 为球的半径,l 为两面公共边的长度 为两个面的二面角,h 是空间几何体的高,H 为某一面的高1.墙角模型(1) 使用范围:3组或3条棱两两垂直;或可在长方体中画出该图且各顶点与长方体的顶点重合 (2)推导过程:长方体的体对角线就是外接球的直径(2) 秒杀公式:222222a b c 3a R (a b c R (a 44++==、、为长方体的长宽高)正方体的边长)(4)图示过程(3) 秒杀公式:2.汉堡模型(1)使用范围:有一条侧棱垂直与底面的柱体或椎体 (2)推导过程第一步:取底面的外心O 1,,过外心做高的的平行且长度相等,在该线上中点为球心的位置第二步:根据勾股定理可得222h R r 4=+(3)秒杀公式:222h R r 4=+(4)图示过程3.斗笠模型(1)使用范围:正棱锥或顶点的投影在底面的外心上 (2)推导过程第一步:取底面的外心O 1,,连接顶点与外心,该线为空间几何体的高h 第二步:在h 上取一点作为球心O第三步:根据勾股定理22222r h R (h R)r R 2h+=-+⇔=(3)秒杀公式:22r h R 2h+=(4)图示过程4.折叠模型(1)使用范围:两个全等三角形或等腰三角形拼在一起,或菱形折叠 (2)推导过程第一步:过两个平面取其外心H 1、H 2,分别过两个外心做这两个面的垂线且垂线相交于球心O第二步:计算2222222111OH H E tan=(CE-H E)tan (H r)tan (222ααα==-α为两个平面的二面角) 第三步:22222211OC OH CH (H r)tanr 2α=+=-+ (3)秒杀技巧:2222R (H r)tanr 2α=-+ (4)图示过程5.切瓜模型(1)使用范围:有两个平面互相垂直的棱锥 (2)推导过程:第一步:分别在两个互相垂直的平面上取外心F 、N ,过两个外心做两个垂面的垂线,两条垂线的交点即为球心O ,取BC 的中点为M ,连接FM 、MN 、OF 、ON第二步:22222222212l ONMF OA AN ON AN MF R r r 4∴=+=+∴=+-为矩形由勾股可得(3)秒杀公式:222212l R r r 4=+-(4)图示过程6.麻花模型(1)使用范围:对棱相等的三棱锥(2)推导过程:设3组对棱的长度分别为x 、y 、z,长方体的长宽高分别为a 、b 、c2222222222222x a b x y z y b c R 8z a c ⎧=+⎪++⎪=+⇔=⎨⎪=+⎪⎩(3)秒杀公式:2222x y z R 8++=(4)图示过程7.矩形模型(1)使用范围:棱锥有两个平面为直角三角形且斜边为同一边(2)推导过程:根据球的定义可知一个点到各个顶点的距离相等该点为球心可得,斜边为球的直径(3)秒杀公式:22l R 4=(4)图示过程8.鳄鱼模型(1)使用范围:适用所有的棱锥 (2)推导过程:121212222121221212221122211O O O O O O OO E r (1sin O O E O O =O E O E 2O E O E cos 2 OD O O O D 3OD O O O D∴α∆+-α=+=+第一步:在两个平面上分别找外心、两外心做这两面的垂线相交于球心第二步:四点共圆,正弦定理可得OE=2=)在中,()()第三步:由(1)(2)(3)整理可得 且 过 2221122212112222221211122221212 =OE O E O DO O O EO Dsin O E O E 2O E O E cos O E O D sin O E O E 2O E O E cos =sin -+=-+α+-α=-+α+-α=2211O E O B-+α2122222O E=m O E=n AB=l,m n2mncos lR=+sin4α+-αα第四步:设,,两个面的二面角为由第三步可得(3)秒杀公式:22222m n2mncos lR=+sin4+-αα(4)图示过程二.内切球的半径---等体积法1.推导过程P ABC PAB PAC PBC ABCPAB PAC PBC ABC11111V S h RS RS RS RS 333331=R(S S S S)31=RS33VR=S-∆∆∆∆∆∆∆∆==++++++∴底面表面积几何体表面积以三棱锥P-ABC为例2.秒杀公式:3VR=S几何体表面积3.图示过程技巧1 外接球之墙角模型【例1】已知长方体''''ABCD A B C D -中,''A B =''1B C =,'A B 与平面''ACC A 所成角的正)A .4πB .16πC .163π D .323π 【举一反三】1.棱长为2的正方体的外接球的表面积为( )A .4πB .43π C .12πD .2.球面上有,,,A B C D 四个点,若,,AB AC AD 两两垂直,且4AB AC AD ===,则该球的表面积为( ) A .803πB .32πC .42πD .48π技巧2 外接球之汉堡模型【例2】已知四棱锥A BCDE -中,四边形BCDE 是边长为2的正方形,3AB =且AB ⊥平面BCDE ,则该四棱锥外接球的表面积为( ) A .4π B .174πC .17πD .8π【举一反三】1.各顶点都在一个球面上的正四棱柱(底面是正方形,侧棱垂直于底面)高为2,体积为8,则这个球的表面积是( ) A .16πB .12πC .10πD .8π2.如图,在三棱锥A ﹣BCD 中,BD ⊥平面ADC ,BD =1,AB =2,BC =3,AC A ﹣BCD 外接球的体积为( )A .4πB .3πC .D .3.在长方体1111ABCD A B C D -中,1AB CC ==1BC =,点M 在正方形11CDD C 内,1C M ⊥平面1ACM ,则三棱锥11M ACC -的外接球表面积为( )A .11π2B .7πC .11πD .14π4.(2020·全国高三月考(文))三棱柱111ABC A B C -中,1AA ⊥平面ABC ,AC AB ⊥,1AC =,AB =12AA =,则该三棱柱111ABC A B C -的外接球的体积为( )A .3B .3C .3D .8π技巧3 外接球之斗笠模型【例3】正三棱锥S ABC -中,2SA =,AB = )A .B .4πC .12πD .6π【举一反三】1.已知正三棱锥S ABC -的侧棱长为6,则该正三棱锥外接球的表面积是________. 2.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A .814πB .16πC .9πD .274π技巧4 外接球之折叠模型【例4】在三棱锥A ﹣BCD 中,△ABD 与△CBD 均为边长为2的等边三角形,且二面角A BD C --的平面角为120°,则该三棱锥的外接球的表面积为( ) A .7π B .8πC .163πD .283π【举一反三】 1.已知二面角PAB C 的大小为120°,且90PAB ABC ∠=∠=︒,AB AP =,6AB BC +=.若点P 、A 、B 、C 都在同一个球面上,则该球的表面积的最小值为______.2.如图所示,三棱锥S 一ABC 中,△ABC 与△SBC 都是边长为1的正三角形,二面角A ﹣BC ﹣S 的大小为23π,若S ,A ,B ,C 四点都在球O 的表面上,则球O 的表面积为( )A .73π B .133π C .43π D .3π技巧5 外接球之切瓜模型【例5】已知三棱锥P ABC -中,1PA =,3PB =,AB =CA CB ==面PAB ⊥面ABC ,则此三棱锥的外接球的表面积为( ) A .143πB .283πC .11πD .12π【举一反三】1.已知三棱锥A BCD -中,平面ABD ⊥平面BCD ,且ABD △和BCD △都是边长为2的等边三角形,则该三棱锥的外接球表面积为( ) A .4πB .163πC .8πD .203π技巧6 外接球之麻花模型【例6】在四面体ABCD 中,若AB CD ==2==AC BD ,AD BC ==ABCD 的外接球的表面积为( ) A .2πB .4πC .6πD .8π技巧7 外接球之矩形模型【例7】在四面体ABCD 中,AB =,1DA DB CA CB ====,则四面体ABCD 的外接球的表面积为( ) A .π B .2πC .3πD .4π【举一反三】1.四面体SABC 中,AC BC ⊥,SA ⊥平面ABC ,SA =AC =BC =,则该四面体外接球的表面积为( ) A .323πB .163πC .16πD .32π2.已知四面体ABCD 满足:1AB BC CD DA AC =====,BD =,则四面体ABCD 外接球的表面积为_______.技巧8 内切球半径【例8】正四面体的外接球与内切球的表面积比为( ) A .9: 1 B .27: 1C .3: 1D .不确定【举一反三】1.如图所示,球内切于正方体.如果该正方体的棱长为a ,那么球的体积为( )A .343a πB .3aC 3aD .316a π2.已知直三棱柱ABC -A 1B 1C 1的底面ABC 为等边三角形,若该棱柱存在外接球与内切球,则其外接球与内切球表面积之比为( ) A .25︰1B .1︰25C .1︰5D .5︰13的内切球,则此棱柱的体积是( ).A .3B .354cmC .327cmD .3巩固练习1.直三棱柱111ABC A B C -的所有顶点都在同一球面上,且2AB AC ==,90BAC ∠=︒,1AA =则该球的表面积为( ) A .40πB .32πC .10πD .8π2.在三棱锥P ABC -中,AB AC ==120BAC ∠=,PB PC ==,PA =棱锥的外接球的表面积为( ) A .40πB .20πC .80πD .60π3.已知四棱锥A BCDE -中,AB ⊥平面BCDE ,底面BCDE 是边长为2的正方形,且3AB =,则该四棱锥外接球的表面积为( ) A .4πB .174πC .17πD .8π4.已知点P ,A ,B ,C 在同一个球的球表面上,PA ⊥平面ABC ,AB ⊥AC ,PB BC ,PC =2,则该球的表面积为( ) A .6πB .8πC .12πD .16π5.四面体A BCD -中,AB ⊥底面BCD ,AB BD ==1CB CD ==,则四面体A BCD -的外接球表面积为( ) A .3πB .4πC .6πD .12π6.平行四边形ABCD 中,AB BD ⊥,且2224AB BD +=,沿BD 将四边形折起成平面ABD ⊥平面BDC ,则三棱锥A BCD -外接球的表面积为( )A .2π B .2πC .4πD .16π7.张衡(78年~139年)是中国东汉时期伟大的天文学家、文学家、数学家.他的数学著作有《算罔论》,他曾经得出结论:圆周率的平方除以十六等于八分之五.已知正方体的外接球与内切球上各有一个动点A ,B ,若线段AB 1,利用张衡的结论可得该正方体的外接球的表面积为( )A .30B .C .D .368.已知直三棱柱111ABC A B C -的顶点都在球O 上,且4AB =,16AA =,30ACB ∠=︒,则此直三棱柱的外接球O 的表面积是( ) A .25πB .50πC .100πD .500π39.已知三棱柱111ABC A B C -(侧棱1AA ⊥底面111A B C ,底面111A B C △是正三角形)内接于球O ,1AB 与底面111A B C 所成的角是45°.若正三棱柱111ABC A B C -的体积是3,则球O 的表面积是( ) A .228π c m 3B .256π c m 3C .27π c m 3D .214π c m 310.在四棱锥P ABCD -中,//BC AD ,AD AB ⊥,AB =6AD =,4BC =,PA PB PD ===P BCD -外接球的表面积为( )A .60πB .40πC .100πD .80π11.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( ) A .10B .20πC .24πD .32π12.我国古代数学名著《九章算术》中,将底面是直角三角形的直三棱柱(侧棱垂直于底面的三棱柱)称之为“堑堵”.如图,三棱柱111ABC A B C -为一个“堑堵”,底面ABC 是以AB 为斜边的直角三角形且5AB =,3AC =,点P 在棱1BB 上,且1PC PC ⊥,当1APC 的面积取最小值时,三棱锥P ABC -的外接球表面积为( )A .45π2B C .30π D .45π13.已知正三棱柱111ABC A B C -的体积为54,6AB =,记三棱柱111ABC A B C -的外接球为球1O ,则外接球1O 的表面积是__________.14.在三棱锥P ABC -中,侧棱PA ⊥底面,120,1ABC BAC AB AC ∠===且2,PA BC =则该三棱锥的外接球的体积为__________.15.如图所示,在三棱锥B ACD -中,3ABC ABD DBC π∠=∠=∠=,3AB =,2BC BD ==,则三棱锥B ACD -的外接球的表面积为______.16.鳖臑(bi ē n ào )出自《九章算术·商功》:“斜解立方,得两重堵.斜解壍堵,其一为阳马,一为鳖臑.”鳖臑是我国对四个面均为直角三角形的三棱锥的古称.如图,三棱锥A BCD -是一个鳖臑,其中AB BC ⊥,AB BD ⊥,BC CD ⊥,且4AB BC DC ===,过点B 向AC 引垂线,垂足为E ,过E作CD 的平行线,交AD 于点F ,连接BF .设三棱锥A BCD -的外接球的表面积为1S ,三棱锥A BEF -的外接球的表面积为2S ,则12S S =________.17.若体积为8的正方体的各个顶点均在一球面上,则该球的体积为______.18.在我国古代数学名著《九章算术》中,把两底面为直角三角形的直棱柱称为“堑堵”,已知三棱柱111ABC A B C -是一个“堑堵”,其中12AB BB ==,1BC =,AC =表面积为___.19.在长方体1111ABCD A B C D -中,1AB CC ==1BC =,点M 在正方形11CDD C 内,1C M ⊥平面1ACM ,则三棱锥11M ACC -的外接球表面积为______.20.在四面体S ABC -中,SA ⊥平面ABC ,120BAC ∠=︒,2SA =,BC =球的表面积为________.21.我国古代数学名著《九章算术》中将正四棱锥称为方锥.已知某方锥各棱长均为2,则其内切球的体积为______.22.已知在三棱锥P ABC -中,PA PB ==,23APB ∠=π,6ACB π∠=,则当点C 到平面PAB 的距离最大时,三棱锥P ABC -外接球的表面积为_____.23.三棱锥A BCD -中,60ABC CBD DBA ===∠∠∠,2BC BD ==,面ACD,则此三棱锥外接球的表面积为___.24.在三棱锥P ABC -中,平面PAB 垂直平面ABC,PA PB AB AC ====120BAC ∠=︒,则三棱锥P ABC -外接球的表面积为_________.25在三棱锥D ABC -中,AD ⊥平面ABC ,3AC =,BC =1cos 3BAC ∠=,若三棱锥D ABC-,则此三棱锥的外接球的表面积为______26.设A ,B ,C ,D 为球O 的球面上的四个点,满足2AB AC BC ===,DC BD ==.若四面体ABCD 的表面积为O 的表面积为______.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间几何体的内切球与外接球问题 1.[2016·全国卷Ⅱ] 体积为8的正方体的顶点都在同一球面上,则该球的表面积为( ) A.12π B.323π C.8π D.4π [解析]A 因为正方体的体积为8,所以正方体的体对角线长为23,所以正方体的外接球的半径为3,所以球的表面积为4π·(3)2=12π. 2.[2016·全国卷Ⅲ] 在封闭的直三棱柱ABC - A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )
A.4π B.9π2 C.6π D.32π3 [解析]B 当球与三侧面相切时,设球的半径为r1,∵AB⊥BC,AB=6,BC=8,∴8-r1+6-r1=10,解得r1=2,不合题意;当球与直三棱柱的上、下底面相切时,设球的半径为r2,
则2r2=3,即r2=32.∴球的最大半径为32,故V的最大值为43π×323=92π. 3.[2016·郑州模拟] 在平行四边形ABCD中,∠CBA=120°,AD=4,对角线BD=23,将其沿对角线BD折起,使平面ABD⊥平面BCD,若四面体ABCD的顶点在同一球面上,则该球的体积为________.
答案:2053π;解析:因为∠CBA=120°,所以∠DAB=60°,在三角形ABD中,由余弦定理得(23)2=42+AB2-2×4·AB·cos 60°,解得AB=2,所以AB⊥BD.折起后平面ABD⊥平面BCD,即有AB⊥平面BCD,如图所示,可知A,B,C,D可看作一个长方体中的四个顶点,长方体的体对角线AC就是四面体ABCD外接球的直径,易知AC=22+42=25,
所以球的体积为2053π.
4.[2016·山西右玉一中模拟] 球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,平面SAB⊥平面ABC,则棱锥S-ABC的体积的最大值为( )
A.33 B.3 C.23 D.4 选A;[解析] (1)由于平面SAB⊥平面ABC,所以点S在平面ABC上的射影H落在AB上,根据球的对称性可知,当S在“最高点”,即H为AB的中点时,SH最大,此时棱锥S-ABC的体积最大.
因为△ABC是边长为2的正三角形,所以球的半径r=OC=23CH=23×32×2=233.
在Rt△SHO中,OH=12OC=33, 所以SH=2332-332=1, 故所求体积的最大值为13×34×22×1=33.
5.[2016·赣州模拟] 如图7-38-19所示,设A,B,C,D为球O上四点,AB,AC,AD两两垂直,且AB=AC=3,若AD=R(R为球O的半径),则球O的表面积为( )
图7-38-19 A.π B.2π C.4π D.8π 选D;解析:因为AB,AC,AD两两垂直,所以以AB,AC,AD为棱构建一个长方体,如图所示,则长方体的各顶点均在球面上,AB=AC=3,所以AE=6,AD=R,DE=2R,则有R2+6=(2R)2,解得R=2,所以球的表面积S=4πR2=8π.
6.[2016·安徽皖南八校三联] 如图所示,已知三棱锥A-BCD的四个顶点A,B,C,D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=3,BC=2,CD=5,则球O的表面积为( )
A.12π B.7π C.9π D.8π [解析]A 由AC⊥平面BCD,BC⊥CD知三棱锥A-BCD可以补成以AC,BC,CD为三条棱的长方体,设球O的半径为R,则有(2R)2=AC2+BC2+CD2=3+4+5=12,所以S球=4πR2=12π.
7.[2016·福建泉州质检] 已知A,B,C在球O的球面上,AB=1,BC=2,∠ABC=60°,且点O到平面ABC的距离为2,则球O的表面积为________. 答案:20π [解析] 在△ABC中用余弦定理求得AC=3,据勾股定理得∠BAC为直角,故BC的中点O1即为△ABC所在小圆的圆心,则OO1⊥平面ABC,在直角三角形OO1B中可求得球的半径r=5,则球O的表面积S=4πr2=20π.
8. [2016·河南中原名校一联] 如图K3816所示,ABCD-A1B1C1D1是边长为1的正方体,S-ABCD是高为1的正四棱锥,若点S,A1,B1,C1,D1在同一个球面上,则该球的表面积为( ) 图K3816 A.916π B.2516π C.4916π D.8116π
选D;[解析] 如图所示作辅助线,易知球心O在SG1上,设OG1=x,则OB1=SO=2-x,同时由正方体的性质知B1G1=22,则在Rt△OB1G1中,由勾股定理得OB21=G1B21+
OG21,即(2-x)2=x2+222,解得x=78,所以球的半径R=2-78=98,所以球的表面积S=4πR2=8116π.
9.[2013·课标全国Ⅰ]如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( )
A.500π3 cm3 B.866π3 cm3 C.1 372π3 cm3 D.2 048π3 cm3
解析:设球半径为R,由题可知R,R-2,正方体棱长一半可构成直角三角形,即△OBA为直角三角形,如图. BC=2,BA=4,OB=R-2,OA=R, 由R2=(R-2)2+42,得R=5, 所以球的体积为43π×53=5003π(cm3),故选A项. 答案:A
10.已知正四棱锥的侧棱与底面的边长都为32,则这个四棱锥的外接球的表面积为( ) A.12π B.36π C.72π D.108π 选B;解析:依题意得,该正四棱锥的底面对角线长为32×2=6,高为
322-12×62=3,因此底面中心到各顶点的距离均等于3,所以该四棱锥的外接球的球心为底面正方形的中心,其外接球的半径为3,所以其外接球的表面积等于4π×32=36π. 11.[2014·石家庄质检一]已知球O,过其球面上A、B、C三点作截面,若O点到该截面的距离是球半径的一半,且AB=BC=2,∠B=120°,则球O的表面积为( )
A.64π3 B.8π3 C.4π D.16π9 解析:如图,球心O在截面ABC的射影为△ABC的外接圆的圆心O′.由题意知OO1=R2,OA=R,其中R为球O的半径.在△ABC中,
AC=AB2+BC2-2AB·BC·cos120° = 22+22-2×2×2×-12=23. 设△ABC的外接圆半径为r,则2r=ACsin120°=2332=4,得r=2,即O′A=2.在Rt△OO1A
中,OO21+O1A2=OA2,即R24+4=R2,解得R2=163,故球O的表面积S=4πR2=64π3,故选A. 答案:A 12.[2014·郑州模拟]在三棱锥A-BCD中,AB=CD=6,AC=BD=AD=BC=5,则该三棱锥的外接球的表面积为__________. 解析:依题意得,该三棱锥的三组对棱分别相等,因此可将该三棱锥补形成一个长方体,
设该长方体的长、宽、高分别为a、b、c,且其外接球的半径为R,则 a2+b2=62,b2+c2=52,c2+a2=52,得a2+b2+c2=43,即(2R)2=a2+b2+c2=43,易知R即为该三棱锥的外接球的半径,所以该三棱锥的外接球的表面积为4πR2=43π. 答案:43π 13.[2014·全国卷] 正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A.81π4 B.16π C.9π D.27π4 答案:A; [解析] 如图所示,E为AC与BD的交点.因为正四棱锥的底面边长为2,所以AE=12AC=2.设球心为O,球的半径为R,则OE=4-R,OA=R.又因为△AOE为直角三角形,所以OA2=OE2+AE2,即R2=(4-R)2+2,解得R=94,所以该球的表面积S=4πR2=4π942=81π4.
14.[2016·湖南八校联考] 如图是一个几何体的三视图, 则这个几何体外接球的表面积为( ) A.8π B.16π C.32π D.64π
答案:C; [解析] 该几何体为一个四棱锥,其外接球的球心为底面正方形的中心,所以半径为22,表面积为4π×(22)2=32π.
15.已知四棱锥S -ABCD的所有顶点在同一球面上,底面ABCD是正方形且球心O在此平面内,当四棱锥的体积取得最大值时,其表面积等于16+163,则球O的体积等于( )
A.42π3 B.162π3 C.322π3 D.642π3 答案:D; [解析] 由题意,当此四棱锥的体积取得最大值时,四棱锥为正四棱锥.设球O
的半径为R,则AC=2R,SO=R,∴AB=2R,则有(2R)2+4×12×2R·22R2+R2=16+163,解得R=22,∴球O的体积是43πR3=6423π. 16.[2016·武汉调研] 已知直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=90°,则该球的体积等于________. 答案:43π; [解析] 设该球的球心为O,△ABC所在圆面的圆心为O1,则OO1⊥平面ABC且OO1=1.在△ABC中,因为AB=AC=2,∠BAC=90°,所以△ABC外接圆的
半径r=12BC=12AB2+AC2=2,所以该球的半径R=r2+O1O2=(2)2+12=3,
所以该球的体积V=43πR3=43π.
