人教版2017高中数学(必修一)第一章 1.3 1.3.1 第二课时 函数的最大(小)值PPT课件
合集下载
2017版高中人教A版数学必修1课件:第一章 集合与函数概念1-3-1-2

[练习 1]画出函数 f(x)=-2x,x∈-∞,0,
的图象,
x2+2x-1,x∈[0,+∞
并求出函数的单调区间与函数的最小值.
解:f(x)的图象如图所示.
f(x)的单调递增区间是(-∞,0)和[0,+∞),函数的最小值 为 f(0)=-1.
第十五页,编辑于星期六:三点 二十二分。
类型 2 利用单调性求函数的最值 [要点点击] 函数的最值与单调性的关系 (1)如果函数 y=f(x)在区间(a,b]上是增函数,在区间[b,c) 上是减函数,则函数 y=f(x),x∈(a,c)在 x=b 处有最大值 f(b). (2)如果函数 y=f(x)在区间(a,b]是减函数,在区间[b,c)上 是增函数,则函数 y=f(x),x∈(a,c)在 x=b 处有最小值 f(b). (3)如果函数 y=f(x)在区间[a,b]上是增(减)函数,则在区间 [a,b]的左、右端点处分别取得最小(大)值、最大(小)值.
第十八页,编辑于星期六:三点 二十二分。
∵x1,x2∈[3,5],且 x1<x2, ∴x1-x2<0,x1+2>0,x2+2>0. ∴f(x1)-f(x2)<0,∴f(x1)<f(x2), ∴函数 f(x)=xx- +12在[3,5]上为增函数. (2)由(1)知,当 x=3 时,函数 f(x)取得最小值为 f(3)=25;当 x=5 时,函数 f(x)取得最大值为 f(5)=47.
第三十二页,编辑于星期六:三点 二十二分。
由于 x2>x1>12,所以 x2-x1>0, 且(2x1-1)(2x2-1)>0, 所以 f(x1)-f(x2)>0,即 f(x1)>f(x2), 所以函数 f(x)=2x-3 1在区间12,+∞上是减函数. (2)由(1)知函数 f(x)在[1,5]上是减函数,因此,函数 f(x)= 2x-3 1在区间[1,5]的两个端点上分别取得最大值与最小值,即最 大值为 f(1)=3,最小值为 f(5)=13.
高中数学 第一章 §1.3.1第2课时函数的最大(小)值课件 新人教A版必修1

为 f(b) ,最小值为 f(a) .
(2)若函数 y=f(x)在区间[a,b]上单调递减,则 f(x)的最大值
为 f(a) ,最小值为 f(b) .
第三页,共22页。
研一研·问题(wèntí)探究、课堂更高效
问题情境:同学们,我们班最高的男生是谁?说他最高的根 据是什么?“我们班最高的男生是姚明”对吗?为什么? 答 我们班最高的男生是 A 同学,根据是班内任选一名男生, 都一定比 A 同学矮;不对,因姚明不是我们班的男生.
第十五页,共22页。
研一研·问题探究(tànjiū)、课堂更高效
跟踪训练 3 已知函数 f(x)=x2-2x-3,若 x∈[t,t+2]时,求 函数 f(x)的最值. 解 ∵对称轴 x=1, ①当 1≥t+2 即 t≤-1 时, f(x)max=f(t)=t2-2t-3, f(x)min=f(t+2)=t2+2t-3. ②当t+t2+2≤1<t+2,即-1<t≤0 时, f(x)max=f(t)=t2-2t-3,
第一页,共22页。
填一填·知识要点(yàodiǎn)、记下疑难点
1.函数最大值定义 一般地,设函数 y=f(x)的定义域为 I,如果存在实数 M 满足:(1)对于任意的 x∈I,都有 f(x)≤M .(2)存在 x0∈I, 使得 f(x0)=M .那么,称 M 是函数 y=f(x)的最大值.
第二页,共22页。
填一填·知识要点、记下(jì xià)疑难 点
2.函数最小值定义
一般地,设函数 y=f(x)的定义域为 I,如果存在实数 M,
满足:(1)对于任意 x∈I,都有 f(x)≥M .(2)存在 x0∈I, 使得 f(x0)=M .那么,称 M 是函数 y=f(x)的最小值.
(2)若函数 y=f(x)在区间[a,b]上单调递减,则 f(x)的最大值
为 f(a) ,最小值为 f(b) .
第三页,共22页。
研一研·问题(wèntí)探究、课堂更高效
问题情境:同学们,我们班最高的男生是谁?说他最高的根 据是什么?“我们班最高的男生是姚明”对吗?为什么? 答 我们班最高的男生是 A 同学,根据是班内任选一名男生, 都一定比 A 同学矮;不对,因姚明不是我们班的男生.
第十五页,共22页。
研一研·问题探究(tànjiū)、课堂更高效
跟踪训练 3 已知函数 f(x)=x2-2x-3,若 x∈[t,t+2]时,求 函数 f(x)的最值. 解 ∵对称轴 x=1, ①当 1≥t+2 即 t≤-1 时, f(x)max=f(t)=t2-2t-3, f(x)min=f(t+2)=t2+2t-3. ②当t+t2+2≤1<t+2,即-1<t≤0 时, f(x)max=f(t)=t2-2t-3,
第一页,共22页。
填一填·知识要点(yàodiǎn)、记下疑难点
1.函数最大值定义 一般地,设函数 y=f(x)的定义域为 I,如果存在实数 M 满足:(1)对于任意的 x∈I,都有 f(x)≤M .(2)存在 x0∈I, 使得 f(x0)=M .那么,称 M 是函数 y=f(x)的最大值.
第二页,共22页。
填一填·知识要点、记下(jì xià)疑难 点
2.函数最小值定义
一般地,设函数 y=f(x)的定义域为 I,如果存在实数 M,
满足:(1)对于任意 x∈I,都有 f(x)≥M .(2)存在 x0∈I, 使得 f(x0)=M .那么,称 M 是函数 y=f(x)的最小值.
人教版高中数学必修一第一章1.3.1函数的单调性PPT教学课件

条件 x1,x2,当x1<x2时
都有f(fx(x)< 1)<f(ff((xx)2)
都有f(fx()x_1)_>__f(_x> 2) f
结论 那么就说函数f(x)在区间D上是增 增函数 那么就说函数f(x)在区间D上是减 减函数
人教版高中数学必修一精品课件
图示
思考1:增(减)函数定义中的x1,x2有什么特征?
人教版高中数学必修一精品课件
PART 03
合作探究·攻重难
TO WORK TOGETHER TO FIND OUT WHAT'S GOING ON
[合作探究 · 攻重难 ]
求 函数 的 单调 区 间
例1 求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
1
2x+1,x≥1,
(1)f(x)=-;(2)f(x)=
1
思 考2: 函 数y=在 定 义 域 上 是 减 函 数 吗 ? x
1
1
[提示] 不是 . y=在(- ∞, 0)上递 减, 在(0, +∞ )上也 递减 ,但不 能说y=在(-∞ ,0)∪
x
x
(0,+ ∞)上递 减.
人教版高中数学必修一精品课件
[基础自测] 1.思考辨析 (1)因为f(-1)<f(2),所以函数f(x)在[-1,2]上是增函数.( ) (2)若f(x)为R上的减函数,则f(0)>f(1).( ) (3)若函数f(x)在区间(1,2]和(2,3)上均为增函数,则函数f(x)在区间(1,3)上为增函数.( )
-x2+2x+3,x≥0, (3)因为f(x)=-x2+2|x|+3=-x2-2x+3,x<0. 根据解析式可作出函数的图象如图所示,由图象可知, 函数f(x)的单调区间为(-∞,-1],(-1,0),[0,1),[1,+∞). f(x)在(-∞,-1],[0,1)上是增函数,在(-1,0),[1,+∞)上是减函数.
人教版高中数学必修一1.3.1《单调性与最大(小)值》ppt课件1

⑥ 利用笔记抓住老师的思路。记笔记不仅有利于理解和记忆,而且有利于抓住老师的思路。
2019/8/11
最新中小学教学课件
8
谢谢欣赏!
2019/8/11
最新中小学教学课件
9
自学教材P30-P32 例3、例4、函数的最 值与单调性有怎样的关系?
编后语
老师上课都有一定的思路,抓住老师的思路就能取得良好的学习效果。在上一小节中已经提及听课中要跟随老师的思路,这里再进一步论述听课时如何 抓住老师的思路。
① 根据课堂提问抓住老师的思路。老师在讲课过程中往往会提出一些问题,有的要求回答,有的则是自问自答。一般来说,老师在课堂上提出的问 题都是学习中的关键,若能抓住老师提出的问题深入思考,就可以抓住老师的思路。
函数y = f(x),根据图象说出函数的单调区间,
以及在每一单调区间上,它是增函数还是减
函数?
y
3
2
1
-5 -4 -3 -2 -1 0 1 2 3 4 5
x
-1
-2
例2. 物理字中的波意耳定律P = (k为 k V
正常数)告诉我们,对于一定量的气体,当 其体积V减小时,压强P将增大,试用函数的 单调性证明之。
② 根据自己预习时理解过的逻辑结构抓住老师的思路。老师讲课在多数情况下是根据教材本身的知识结构展开的,若把自己预习时所理解过的知识 逻辑结构与老师的讲解过程进行比较,便可以抓住老师的思路。
③ 根据老师的提示抓住老师的思路。老师在教学中经常有一些提示用语,如“请注意”、“我再重复一遍”、“这个问题的关键是····”等等,这些 用语往往体现了老师的思路。来自:学习方法网
「知识辨析」
辨析1:能否只取两个点(a,f (a) )、
2019/8/11
最新中小学教学课件
8
谢谢欣赏!
2019/8/11
最新中小学教学课件
9
自学教材P30-P32 例3、例4、函数的最 值与单调性有怎样的关系?
编后语
老师上课都有一定的思路,抓住老师的思路就能取得良好的学习效果。在上一小节中已经提及听课中要跟随老师的思路,这里再进一步论述听课时如何 抓住老师的思路。
① 根据课堂提问抓住老师的思路。老师在讲课过程中往往会提出一些问题,有的要求回答,有的则是自问自答。一般来说,老师在课堂上提出的问 题都是学习中的关键,若能抓住老师提出的问题深入思考,就可以抓住老师的思路。
函数y = f(x),根据图象说出函数的单调区间,
以及在每一单调区间上,它是增函数还是减
函数?
y
3
2
1
-5 -4 -3 -2 -1 0 1 2 3 4 5
x
-1
-2
例2. 物理字中的波意耳定律P = (k为 k V
正常数)告诉我们,对于一定量的气体,当 其体积V减小时,压强P将增大,试用函数的 单调性证明之。
② 根据自己预习时理解过的逻辑结构抓住老师的思路。老师讲课在多数情况下是根据教材本身的知识结构展开的,若把自己预习时所理解过的知识 逻辑结构与老师的讲解过程进行比较,便可以抓住老师的思路。
③ 根据老师的提示抓住老师的思路。老师在教学中经常有一些提示用语,如“请注意”、“我再重复一遍”、“这个问题的关键是····”等等,这些 用语往往体现了老师的思路。来自:学习方法网
「知识辨析」
辨析1:能否只取两个点(a,f (a) )、
高中数学第一章集合与函数概念1.3.1.2函数的最大值、最小值课件新人教A版必修1

跟踪训练 3 已知函数 f(x)=3x2-12x+5,当自变量 x 在下列 范围内取值时,求函数的最大值和最小值:
(1)R;(2)[0,3];(3)[-1,1].
解析:f(x)=3x2-12x+5=3(x-2)2-7. (1)当 x∈R 时,f(x)=3(x-2)2-7≥-7,当 x=2 时,等号成立.故 函数 f(x)的最小值为-7,无最大值. (2)函数 f(x)=3(x-2)2-7 的图象如图所示, 由图可知,在[0,3]上,函数 f(x)在 x=0 处取得最 大值,最大值为 5;在 x=2 处取得最小值,最小 值为-7. (3)由图可知,函数 f(x)在[-1,1]上是减函数, 在 x=-1 处取得最大值,最大值为 20;在 x=1 处取得最小值, 最小值为-4.
知识点 函数的最大值与最小值
最大(小)值必须是一个函数值,是值域中的一个元素,如函数 y=x2(x∈R)的最大值是 0,有 f(0)=0.
[小试身手]
1.判断(正确的打“√”,错误的打“×”) (1)任何函数都有最大值或最小值.( × ) (2)函数的最小值一定比最大值小.( × )
2.函数 f(x)=1x在[1,+∞)上( ) A.有最大值无最小值 B.有最小值无最大值 C.有最大值也有最小值 D.无最大值也无最小值
(2)当 0≤a≤1 时,由图②可知, f(x)min=f(a)=-1-a2, f(x)max=f(2)=3-4a.
(3)当 1<a≤2 时,由图③可知,f(x)min=f(a)=-1-a2,f(x)max =f(0)=-1.
(4)当 a>2 时,由图④可知,f(x)min=f(2)=3-4a,f(x)max=f(0) =-1.
解析:函数 f(x)=1x是反比例函数,当 x∈(0,+∞)时,函数图 象下降,所以在[1,+∞)上 f(x)为减函数,f(1)为 f(x)在[1,+∞) 上的最大值,函数在[1,+∞)上没有最小值.故选 A.
人教版2017高中(必修一)数学1.3.1_单调性与最大(小)值(第1课时)ppt课件
x1<x2;
②作差变形:即作差f(x1)-f(x2)(或f(x2)-f(x1)),并 用因式分解、配方、有理化等方法将差式向有利于判 断差的符号的方向变形; ③定号:确定差f(x1)-f(x2)(或f(x2)-f(x1))的符号,
当符号不确定时,可进行分类讨论;
④判断:根据定义得出结论.
探究实践
1 画出反比例函数f(x)= 的图象. x (1)这个函数的定义域I是什么?
如何用函数的解析 式和数学语言进行 描述?
对函数f(x)=x2而言,“函数值在(0,+∞)上随 自变量的增大而增大”,可以这样描述:在区间 (0,+∞)上任取两个实数x1,x2,得到函数值 f(x1)<f(x2). f(x1)=x12,f(x2)=x22,当x1<x2时,有____________ 请同学们用数学语言描述函数f(x)在(-∞,0]上
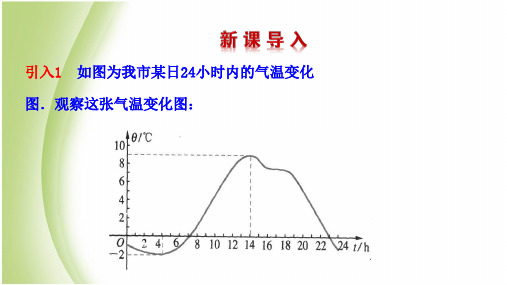
引入1
如图为我市某日24小时内的气温变化
图.观察这张气温变化图:
引入2
德国有一位著名的心理学家艾宾浩斯,对
人类的记忆牢固程度进行了有关研究.他经过测试, 得到了以下一些数据:
时间间 隔 t 记忆量y (百分比) 8-9 1天 刚记忆 20分 60分 完毕 钟后 钟后 小时后 后 100 58.2 44.2 35.8 2天 后 6天 一个 后 月后
增函数或减函数 , 如果函数y=f(x)在区间D上是_______________ 那么就说函数y=f(x)在这一区间具有(严格的)单调
性,区间D叫做y=f(x)的单调区间.
对函数单调性的理解 第一、在中学数学中所说的单调性是指严格的单
调性, 即必须是f(x1)<f(x2) (或f(x1)>f(x2)), 而不能是f(x1)≤f(x2) (或f(x1)≥f(x2));
课件_人教版高中数学必修一函数的单调性与最大值PPT课件_优秀版
1
2
作差
=3( x - x ) 变形 如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上,f(x)是增函数还是减函数
。 画出下列函数的图象,并指出函数的单调
1
2
由x <x ,得 x - x <0 所以,函数f(x)=3x+2在R上是增函数。
例题4
求 函 数f (x) x2 2x 3在 区 间[0,a]上 的 最 大 值 和 最 小. 值
若 f(x)x24x4在 区 [a1间 ,a] 上 的 值 [1,8]求 ,域 a的 为值 。
函数值随着自变量x 的增大而增大
函数值随着自变量x 的增大而减小
引入四:
y x2
x 0 1 -1 2 -2 … y 0 1 -1 8 -8 …
y x3
1)图象在y轴右侧随着x 的增加,y的值在增加
2)图象在y轴左侧随着x 的增加,y的值在减小
函数值随着自变量x 的增大而增大
单调性:
y
y f(x)
判号
即 f(x1)<f(x2)
所以,函数f(x)=3x+2在R上是增函数。
结论
证明单调性:
证明函数 f(x) 为增函数。
2x1在
[
1 2
任意
, ) 上
x1<x证2,明则:f(设x 1 x)1 ,x2f是(x [2) 12 ,2 x 1) 上1 任 意两2 x 彻个2 实底1 数,且 遇到根号
取值 作差
1.已知 f(x)在R上单调递减, (1)比较 f(a2 1)与f(a)的大小; (2)若f(m2) f(3),求 m的取值范 . 围
高中数学人教版A版必修一课件:第一章 《集合与函数概念》 1.3.1 第2课时 函数的最大值、最小值
(1) 解析
作出函数 f(x) 的图象 ( 如图 ) .由图象可知,当 x =±1
时,f(x)取最大值为f(±1)=1.当x=0时,f(x)取最小值f(0)=0,
故f(x)的最大值为1,最小值为0. 答案 1 0
(2)解
任取 2≤x1<x2≤5,
x1 x2 则 f(x1)= ,f(x2)= , x1-1 x2-1 x1-x2 x2 x1 f(x2)-f(x1)= - = , x2-1 x1-1 x2-1x1-1 ∵2≤x1<x2≤5,∴x1-x2<0,x2-1>0,x1-1>0, ∴f(x2)-f(x1)<0,∴f(x2)<f(x1). x ∴f(x)= 在区间[2,5] 上是单调减函数. x-1 2 5 5 ∴f(x)max=f(2)= =2,f(x)min=f(5)= =4. 2-1 5-1
解
(1)设月产量为 x 台,则总成本为 20 000+100x,
1 2 - x +300x-20 0000≤x≤400, 从而 f(x)= 2 60 000-100xx>400. 1 (2)当 0≤x≤400 时,f(x)=-2(x-300)2+25 000; ∴当 x=300 时,f(x)max=25 000, 当 x>400 时,f(x)=60 000-100x 是减函数, f(x)<60 000-100×400<25 000. ∴当 x=300 时 ,f(x)max=25 000. 即每月生产 300 台仪器时利润最大,最大利润为 25 000 元.
规律方法
求解实际问题的四个步骤
(1)读题:分为读懂和深刻理解两个层次,把“问题情景” 译为数学语言,找出问题的主要关系(目标与条件的关系).
(2)建模:把问题中的关系转化成函数关系,建立函数解析
高一数学(人教A版)必修1课件:1-3-1-2函数的最值
(2)图象法求最值的一般步骤是:
[例 1] 如图为函数 y=f(x),x∈[-4,7]的图象,指出它的 最大值、最小值.
[分析] 利用图象法求函数最值,要注意函数的定义 域.函数的最大值、最小值分别是图象的最高点和最低点的 纵坐标.
[解析] 观察函数图象可以知道,图象上位置最高的点是 (3,3),最低的点是(-1.5,-2),所以函数 y=f(x)当 x=3 时取 得最大值即 ymax=3;
【归纳提升】 (1)M 首先是一个函数值,它是值域的一 个元素.如 f(x)=-x2(x∈R)的最大值为 0,有 f(0)=0,注意 对定义②中“存在”一词的理解.
(2)对于定义域内的全部元素,都有 f(x)≤M 成立,“任 意”是说对每一个值都必须满足不等式.
(3)这两条缺一不可,若只有定义中的①,M 不是最大值, 如 f(x)=-x2(x∈R),对任意 x∈R,都有 f(x)≤1 成立,但 1 不是最大值,否则大于零的任意实数都是最大值了;最大值 的核心是不等式 f(x)≤M,故不能只有定义中的②.
(3)函数 y=x2-2x-3 在[-2,0]上的最小值为________, 最大值为________;在[2,3]上的最小值为________,最大值为 ________ ; 在 [ - 1,2] 上 的 最 小 值 为 ________ , 最 大 值 为 ________.
[答案]
(1)-5
(4)评价:对结果进行验证或评估,对错误加以改正,最 后将结果应用于现实,做出解释或预测.
也可认为分成“设元——列式——求解——作答”四个 步骤.
[例 3] 某公司生产一种电子仪器的固定成本为 20000 元,每生产一台仪器需增加投入 100 元,已知总收益满足函 数:
新人教A版高中数学必修一1.3 函数的基本性质 最大(小)值教学参考课件
④ 紧跟老师的推导过程抓住老师的思路。老师在课堂上讲解某一结论时,一般有一个推导过程,如数学问题的来龙去脉、物理概念的抽象归纳、 语文课的分析等。感悟和理解推导过程是一个投入思维、感悟方法的过程,这有助于理解记忆结论,也有助于提高分析问题和运用知识的能力。
⑤ 搁置问题抓住老师的思路。碰到自己还没有完全理解老师所讲内容的时候,最好是做个记号,姑且先把这个问题放在一边,继续听老师讲后面 的内容,以免顾此失彼。来自:学习方法网
⑥ 利用笔记抓住老师的思路。记笔记不仅有利于理解和记忆,而且有利于抓住老师的思路。
2019/8/16
最新中小学教学课件
19
谢谢欣赏!
2019/8/16
最新中小学教学课件
20
4
24
讲授新课
例2 已经知函数y=
2 x1
(x∈[2,6]),
求函数的最大值和最小值.
讲授新课
例2 已经知函数y=
2 x1
(x∈[2,6]),
求函数的最大值和最小值.
x
2
1 0.4
O 1 2 3 4 5 6y
课堂小结
1. 最值的概念;
课堂小结
1. 最值的概念; 2. 应用图象和单调性求最值的一般步骤.
第一章 集合与函数概念
1.3 函数的基本性质 ——最大(小)值
复习引入
问题1 函数f (x)=x2. 在(-∞, 0]上是减函数, 在[0, +∞)上是增函数. 当x≤0时,f (x)≥f (0),
x≥0时, f (x)≥f (0). 从而x∈R,都有f (x) ≥f (0). 因此x=0时,f (0)是函数值中的最小值.
复习引入
问题2 函数f (x)=-x2. 同理可知x∈R, 都有f (x)≤f (0). 即x=0时,f (0)是函数值中的最大值.
⑤ 搁置问题抓住老师的思路。碰到自己还没有完全理解老师所讲内容的时候,最好是做个记号,姑且先把这个问题放在一边,继续听老师讲后面 的内容,以免顾此失彼。来自:学习方法网
⑥ 利用笔记抓住老师的思路。记笔记不仅有利于理解和记忆,而且有利于抓住老师的思路。
2019/8/16
最新中小学教学课件
19
谢谢欣赏!
2019/8/16
最新中小学教学课件
20
4
24
讲授新课
例2 已经知函数y=
2 x1
(x∈[2,6]),
求函数的最大值和最小值.
讲授新课
例2 已经知函数y=
2 x1
(x∈[2,6]),
求函数的最大值和最小值.
x
2
1 0.4
O 1 2 3 4 5 6y
课堂小结
1. 最值的概念;
课堂小结
1. 最值的概念; 2. 应用图象和单调性求最值的一般步骤.
第一章 集合与函数概念
1.3 函数的基本性质 ——最大(小)值
复习引入
问题1 函数f (x)=x2. 在(-∞, 0]上是减函数, 在[0, +∞)上是增函数. 当x≤0时,f (x)≥f (0),
x≥0时, f (x)≥f (0). 从而x∈R,都有f (x) ≥f (0). 因此x=0时,f (0)是函数值中的最小值.
复习引入
问题2 函数f (x)=-x2. 同理可知x∈R, 都有f (x)≤f (0). 即x=0时,f (0)是函数值中的最大值.
