七年级下册数学几何题大全
七年级数学下册专题08 期中-几何综合大题必刷(压轴题)(原卷版)
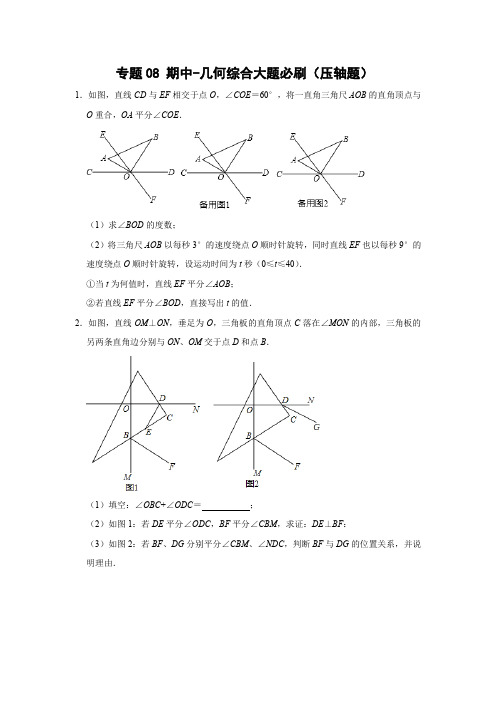
专题08 期中-几何综合大题必刷(压轴题)1.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.(1)求∠BOD的度数;(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).①当t为何值时,直线EF平分∠AOB;②若直线EF平分∠BOD,直接写出t的值.2.如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.(1)填空:∠OBC+∠ODC=;(2)如图1:若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF:(3)如图2:若BF、DG分别平分∠CBM、∠NDC,判断BF与DG的位置关系,并说明理由.3.如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM 时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过秒后边OC 与边ON互相垂直.(直接写出答案)4.【学科融合】物理学中把经过入射点O并垂直于反射面的直线ON叫做法线,入射光线与法线的夹角i叫做入射角,反射光线与法线的夹角r叫做反射角(如图①).由此可以归纳出如下的规律:在反射现象中,反射光线、入射光线和法线都在同一平面内;反射光线、入射光线分别位于法线两侧;反射角等于入射角.这就是光的反射定律(reflection law).【数学推理】如图1,有两块平面镜OM,ON,且OM⊥ON,入射光线AB经过两次反射,得到反射光线CD.由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即:∠1=∠2,∠3=∠4.在这样的条件下,求证:AB∥CD.【尝试探究】两块平面镜OM,ON,且∠MON=α,入射光线AB经过两次反射,得到反射光线CD.(1)如图2,光线AB与CD相交于点E,则∠BEC=;(2)如图3,光线AB与CD所在的直线相交于点E,∠BED=β,则α与β之间满足的等量关系是.5.已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG =30°,求∠MGN+∠MPN的度数;(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.6.“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B 射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.(1)填空:∠BAN=°;(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.7.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF(1)求∠EOB的度数;(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.8.如图1,MN∥EF,C为两直线之间一点.(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.(2)如图2,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.(3)如图3,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请直接写出∠ACB与∠ADB之间的数量关系:.9.(1)【问题】如图1,若AB∥CD,∠BEP=25°,∠PFC=150°.求∠EPF的度数;(2)【问题迁移】如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;(3)【联想拓展】如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.10.如图,已知直线AB∥射线CD,∠CEB=100°.P是射线EB上一动点,过点P作PQ ∥EC交射线CD于点Q,连接CP.作∠PCF=∠PCQ,交直线AB于点F,CG平分∠ECF.(1)若点P,F,G都在点E的右侧.①求∠PCG的度数;②若∠EGC﹣∠ECG=40°,求∠CPQ的度数.(2)在点P的运动过程中,是否存在这样的情形,使?若存在,求出∠CPQ 的度数;若不存在,请说明理由.11.如图,AB∥CD,∠ABE=120°.(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.12.已知:AB∥CD,点E在直线AB上,点F在直线CD上.(1)如图(1),∠1=∠2,∠3=∠4.①若∠4=36°,求∠2的度数;②试判断EM与FN的位置关系,并说明理由;(2)如图(2),EG平分∠MEF,EH平分∠AEM,试探究∠GEH与∠EFD的数量关系,并说明理由.13.已知M、N分别为直线AB,直线CD上的点,且AB∥CD,E在AB,CD之间.(1)如图1,求证:∠BME+∠DNE=∠MEN;(2)如图2,P是CD上一点,连PM,作MQ∥EN,若∠QMP=∠BME.试探究∠E与∠AMP的数量关系,并说明理由;(3)在(2)的条件下,作NG⊥CD交PM于G,若MP平分∠QME,NF平分∠ENG,若∠MGN=m°,∠MFN=n°,直接写出m与n的数量关系.14.如图,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.(1)试说明:∠BAG=∠BGA;(2)如图1,点F在AG的反向延长线上,连接CF交AD于点E,若∠BAG﹣∠F=45°,求证:CF平分∠BCD.(3)如图2,线段AG上有点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,求的值.15.已知:如图,直线PQ∥MN,点C是PQ,MN之间(不在直线PQ,MN上)的一个动点.(1)若∠1与∠2都是锐角,如图1,请直接写出∠C与∠1,∠2之间的数量关系.(2)若小明把一块三角板(∠A=30°,∠C=90°)如图2放置,点D,E,F是三角板的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数.(3)将图2中的三角板进行适当转动,如图3,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,给出下列两个结论:①的②∠GEN﹣∠BDF的值不变.其中只有一个是正确的,你认为哪个是正确的?并求出不变的值是多少.16.已知AB∥CD,解决下列问题:(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.(2)如图②,若∠ABP=∠ABE,∠CDP=∠CDE,试写出∠P与∠E的数量关系并说明理由.(3)如图③,若∠ABP=∠ABE,∠CDP=∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).17.如图1,AM∥CN,点B为平面内一点,AB⊥BC于B,过B作BD⊥AM.(1)求证:∠ABD=∠C;(2)如图2,在(1)问的条件下,分别作∠ABD、∠DBC的平分线交DM于E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,①求证:∠ABF=∠AFB;②求∠CBE的度数.18.已知AB∥CD,点M在直线AB上,点N、Q在直线CD上,点P在直线AB、CD之间,连接PM、PN、PQ,PQ平分∠MPN,如图①.(1)若∠PMA=α、∠PQC=β,求∠NPQ的度数(用含α,β的式子表示);(2)过点Q作QE∥PN交PM的延长线于点E,过E作EF平分∠PEQ交PQ于点F,如图②,请你判断EF与PQ的位置关系,并说明理由;(3)在(2)的条件下,连接EN,如图③,若∠NEF=∠PMA,求证:NE平分∠PNQ.19.如图1,AB∥CD,G为AB、CD之间一点.(1)若GE平分∠AEF,GF平分∠EFC.求证:EG⊥FG;(2)如图2,若∠AEP=∠AEF,∠CFP=∠EFC,且FP的延长线交∠AEP的角平分线于点M,EP的延长线交∠CFP的角平分线于点N,猜想∠M+∠N的结果并且证明你的结论;(3)如图3,若点H是射线EB之间一动点,FG平分∠EFH,MF平分∠EFC,过点G 作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.20.如图1,直线AB∥CD,直线EF交AB于点E,交CD于点F,点G和点H分别是直线AB和CD上的动点,作直线GH,EI平分∠AEF,HI平分∠CHG,EI与HI交于点I.(1)如图1,点G在点E的左侧,点H在点F的右侧,若∠AEF=70°,∠CHG=60°,求∠EIH的度数.(2)如图2,点G在点E的右侧,点H也在点F的右侧,若∠AEF=α,∠CHG=β,其他条件不变,求∠EIH的度数.(3)如图3,点G在点E的右侧,点H也在点F的右侧,∠GHC的平分线HJ交∠KEG 的平分线EJ于点J.其他条件不变,若∠AEF=α,∠CHG=β,求∠EJH的度数.21.如图1,已知直线EF分别与直线AB,CD相交于点E,F,AB∥CD,EM平分∠BEF,FM平分∠EFD(1)求证:∠EMF=90°.(2)如图2,若FN平分∠MFD交EM的延长线于点N,且∠BEN与∠EFN的比为4:3,求∠N的度数.(3)如图3,若点H是射线EA之间一动点,FG平分∠HFE,过点G作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.22.已知直线AB∥CD,直线EF分别交AB、CD于A、C,CM是∠ACD的平分线,CM交AB于H,过A作AG⊥AC交CM于G.(1)如图1,点G在CH的延长线上时,①若∠GAB=36°,则∠MCD=.②猜想:∠GAB与∠MCD之间的数量关系是.(2)如图2,点G在CH上时,(1)②猜想的∠GAB与∠MCD之间的数量关系还成立吗?如果成立,请给出证明;如果不成立,请写出∠GAB与∠MCD之间的数量关系,并说明理由.23.已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.(1)如图1,∠BME,∠E,∠END的数量关系为;(直接写出答案)(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数.(用含m的式子表示)(3)如图3点G为CD上一点,∠BMN=n•∠EMN,∠GEK=n•∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)24.如图1,AB∥CD,P为AB、CD之间一点(1)若AP平分∠CAB,CP平分∠ACD.求证:AP⊥CP;(2)如图(2),若∠BAP=∠BAC,∠DCP=∠ACD,且AE平分∠BAP,CF平分∠DCP,猜想∠E+∠F的结果并且证明你的结论;(3)在(1)的条件下,当∠BAQ=∠BAP,∠DCQ=∠DCP,H为AB上一动点,连HQ并延长至K,使∠QKA=∠QAK,再过点Q作∠CQH的平分线交直线AK于M,问当点H在射线AB上移动时,∠QMK的大小是否变化?若不变,求其值;若变化,求其取值范围.25.如图1,AB∥CD.G为AB、CD之间一点.(1)若GE平分∠AEF,GF平分∠EFC.求证:EG⊥FG;(2)如图2.若∠AEP=∠AEF,∠CFP=∠EFC,且FP的延长线交∠AEP的角平分线于点M,EP的延长线交∠CFP的角平分线于点N,猜想∠M+∠N的结果并且证明你的结论;(3)如图3,若点H是射线EB之间一动点,FG平分∠EFH,MF平分∠EFC,过点G 作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系;并证明你的结论.26.已知,BC∥OA,∠B=∠A=100°,试回答下列问题:(1)如图1所示,求证:OB∥AC;(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,此时∠EOC的度数等于(直接写出答案即可);(3)在(2)的条件下,若平行移动AC,如图3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,求此时∠OCA度数.27.如图1,AB∥CD,点E、F分别在AB、CD上,点O在直线AB、CD之间,且∠EOF =80°.(1)求∠BEO+∠OFD的值;(2)如图2,直线MN分别交∠BEO、∠OFC的角平分线于点M、N,直接写出∠EMN ﹣∠FNM的值(3)如图3,EG在∠AEO内,∠AEG=m∠OEG;FH在∠DFO内,∠DFH=m∠OFH,直线MN分别交EG、FH分别于点M、N,且∠FMN﹣∠ENM=80°,直接写出m的值.28.已知,两直线AB,CD,且AB∥CD,点M,N分别在直线AB,CD上,放置一个足够大的直角三角尺,使得三角尺的两边EP,EQ分别经过点M,N,过点N作射线NF,使得∠ENF=∠ENC.(1)转动三角尺,如图①所示,当射线NF与NM重合,∠FND=45°时,求∠AME的度数;(2)转动三角尺,如图②所示,当射线NF与NM不重合,∠FND=60°时,求∠AME 的度数.(3)转动直角三角尺的过程中,请直接写出∠FND与∠AME之间的数量关系.29.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.(1)如图1,求证:AB∥CD;(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.30.如图1,BC⊥AF于点C,∠A+∠1=90°.(1)求证:AB∥DE;(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.31.已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.(1)如图1,求证:EF∥GH;(2)如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;(3)如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.32.如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF 交CD于点M,且∠FEM=∠FME.(1)判断直线AB与直线CD是否平行,并说明理由;(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.①当点G在点F的右侧时,若β=56°,求α的度数;②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.33.如图1,G,E是直线AB上两点,点G在点E左侧,过点G的直线GP与过点E的直线EP交于点P.直线PE交直线CD于点H,满足点E在线段PH上,∠PGB+∠P=∠PHD.(1)求证:AB∥CD;(2)如图2,点Q在直线AB,CD之间,PH平分∠QHD,GF平分∠PGB,点F,G,Q在同一直线上,且2∠Q+∠P=120°,求∠QHD的度数;(3)在(2)的条件下,若点M是直线PG上一点,直线MH交直线AB于点N,点N 在点B左侧,请直接写出∠MNB和∠PHM的数量关系.(题中所有角都是大于0°且小于180°的角)34.已知,DE平分∠ADB交射线BC于点E,∠BDE=∠BED.(1)如图1,求证:AD∥BC;(2)如图2,点F是射线DA上一点,过点F作FG∥BD交射线BC于点G,点N是FG 上一点,连接NE,求证:∠DEN=∠ADE+∠ENG;(3)如图3,在(2)的条件下,连接DN,点P为BD延长线上一点,DM平分∠BDE 交BE于点M,若DN平分∠PDM,DE⊥EN,∠DBC﹣∠DNE=∠FDN,求∠EDN的度数.35.综合应用题:如图,有一副直角三角板如图①放置(其中∠D=45°,∠C=30°),P A、PB与直线MN重合,且三角板P AC,三角板PBD均可以绕点P逆时针旋转.(1)∠DPC=;(2)如图②,若三角板PBD保持不动,三角板∠P AC绕点P逆时针旋转,转速为10°/秒,转动一周三角板P AC就停止转动,在旋转的过程中,当旋转时间为多少时,有PC ∥DB成立;(3)如图③,在图①基础上,若三角板P AC的边P A从PN.处开始绕点P逆时针旋转,转速为3°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2°/秒,(当PC转到与PM重合时,两三角板都停止转动),在旋转过程中,当∠CPD=∠BPM,求旋转的时间是多少?36.已知E,F分别是AB、CD上的动点,P也为一动点.(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD;(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD;(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求的值.37.“一带一路”让中国和世界联系更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视若灯A转动的速度是每秒2°,灯B转动的速度是每秒1°.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.(1)填空:∠BAN=°;(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)若两灯同时开始转动,两灯射出的光束交于点C,且∠ACB=120°,则在灯B射线到达BQ之前,转动的时间为秒.38.已知AB∥CD,点E在AB上,点F在DC上,点G为射线EF上一点.(1)【基础问题】如图1,试说明:∠AGD=∠A+∠D.(完成图中的填空部分)证明:过点G作直线MN∥AB,又∵AB∥CD,∴∥CD∵MN∥AB,∴∠=∠MGA.∵MN∥CD,∴∠D=()∴∠AGD=∠AGM+∠DGM=∠A+∠D.(2)【类比探究】如图2,当点G在线段EF延长线上时,请写出∠AGD、∠A、∠D三者之间的数量关系,并说明理由.(3)【应用拓展】如图3,AH平分∠GAE,DH交AH于点H,且∠GDH=2∠HDF,∠HDF=22°,∠H=32°,直接写出∠DGA的度数为°.39.如图1,直线AB、CD被直线EF截,分别交AB于点G,交CD于点H,∠AGE与∠EHC互补.(1)求证:AB∥CD;(2)如图2,点P在直线AB、CD内部直线EF上,点M、N分别在直线AB、CD上,连接PM、PN,点K在∠PMB的角平分线上,连接KN,若∠MKN=180°∠MPN,求证:∠PNK=∠CNK;(3)如图3,在(2)的条件下,点O为AB上一点,连接ON、MN,MN平分∠PNO,若∠MNK:∠PMK=2:7,2∠MKN﹣∠PNO=180°,求∠NOM的度数.40.已知,AB∥CD,点F、G分别在AB、CD上,且点E为射线FG上一点.(1)如图1:当点E在线段FG上时,连接AE、DE,易得∠AED=∠EAF+∠EDG.小明给出的理由是:如图1,过E作EH∥AB,∵AB∥CD,∴AB∥CD∥EH,(平行于同一条直线的两条直线互相平行)∴∠EAF=∠AEH,∠EDG=∠DEH,(依据1)∴∠AED=∠AEH+∠DEH=∠EAF+∠EDG;(依据2)填空:依据1:.依据2:.(2)如图2,当点E在FG延长线上时,求证:∠EAF=∠AED+∠EDG;(3)如图3,AI平分∠BAE,DI交AI于点I,交AE于点K,且∠EDI:∠CDI=2:1,∠AED=20°,∠I=30°,求∠EKD的度数.41.如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠P AC=50°,∠ADC=30°,AE平分∠P AD,CE平分∠ACD,AE与CE相交于E.(1)求∠AEC的度数;(2)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠P AC=50°,∠A1D1C=30°,求∠A1EC 的度数.(3)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(2)相同,求此时∠A1EC的度数.42.阅读下面材料:小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是.参考小亮思考问题的方法,解决问题:(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,作∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M=(直接用含α的式子表示).。
七年级数学(下册)几何典型题
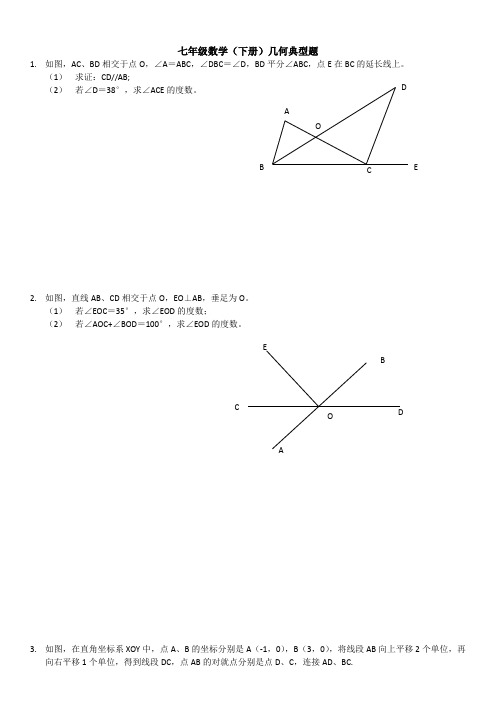
七年级数学(下册)几何典型题1. 如图,AC 、BD 相交于点O ,∠A =ABC ,∠DBC =∠D ,BD 平分∠ABC ,点E 在BC 的延长线上。
(1) 求证:CD//AB;(2) 若∠D =38°,求∠ACE 的度数。
2. 如图,直线AB 、CD 相交于点O ,EO ⊥AB ,垂足为O 。
(1) 若∠EOC =35°,求∠EOD 的度数;(2) 若∠AOC+∠BOD =100°,求∠EOD 的度数。
3. 如图,在直角坐标系XOY 中,点A 、B 的坐标分别是A (-1,0),B (3,0),将线段AB 向上平移2个单位,再向右平移1个单位,得到线段DC ,点AB 的对就点分别是点D 、C ,连接AD 、BC.(1) 直接写出点C 、D 的坐标; (2) 求四边形ABCD 的面积;(3) 点P 为线段BC 上任意一点(与点B 、C 不重合),连接PD 、PO.求证:∠CDP+∠BOP=∠OPD.4. 如图,直接EF 分别与直线AB ,CD 相交于点P 和点Q ,PG 平分∠APQ, QH 平分∠DQP ,并且∠1=∠2,说出图中哪些直线平行。
5. 平面内的两条直线有相交和平行两种位置关系。
(1) 如图1,若AB//CD ,点P 在AB 、CD 内部,∠B =50°,∠D =30°,求∠BPD 的度数。
(2) 如图2,将点P 移到AB 、CD 外部,则∠BPD 、∠B 、∠D 之间有何数量关系?请写出你的结论并加以证6. 如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A (1,2),解答以下问题。
(1) 请在图中建立适当的直角坐标系,并写出图书馆(B )的位置坐标。
(2) 若体育馆位置坐标为C (-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC ,求△ABC 的面积。
7. 如圖,CE ⊥AB 于E ,DF ⊥AB 于F ,AC ∥A CE FB8. 如图,在平面直角坐标系中,已知点A (-3,3),B (-5,1),C (-2,0),P (a,b )是△ABC 的边AC 上任意一点,△ABC 经过平移后得到△A ’B ’C ’,点P 的对应点为P ’(a+6,b-2). (1) 直接写出点C ’的坐标; (2) 在图中画出△A ’B ’C ’; (3) △AOA ’的面积。
七年级(下)北师大版数学几何易错题集

北师大版七年级(下)数学几何易错题集班级:姓名:得分:1,已知△ABC与△DEF全等,∠A=∠D=90°,∠B=37°,则∠E的度数是;2,已知△DEF≌△ABC,AB=AC,且△ABC的周长为23cm,BC=4 cm,则△DEF(第3题图)(第4题图)(第5题图)7,长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm 的两根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为()A.一个人取6cm的木条,一个人取8cm的木条;B.两人都取6cm的木条;C.两人都取8cm的木条;D.B, C 两种取法都可以8,下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是()A. ①②B. ②③C. ①③D. ①②③9,如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有()A. 2对B. 2对C. 4对D. 5对10,下列说法中,正确的有()①三角对应相等的2个三角形全等;②三边对应相等的2个三角形全等;③两角、一边相等的2个三角形全等;④两边、一角对应相等的2个三角形全等.A. 1个B. 2个C. 3个D. 4个11,如图,D在AB上,E在AC上,且∠B=∠C,则在下列条件:①AB=AC;②AD=AE;③BE=CD.其中能判定△ABE≌△ACD的有()A. 0个B. 1个C. 2个D. 3个12,△ABC中,AB=AC,三条高AD,BE,CF相交于O那么图中全等的三角形有()A. 5对B. 6对C. 7对D. 8对13,如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对()A.1B.2C.3D.414,不能判断△ABC≌△DEF的条件是()A.∠A=∠F,BA=EF,AC=FDB.∠B=∠E,BC=EF,高AH=DGC.∠C=∠F=90°,∠A=60°,∠E=30°,AC=DFD.∠A=∠D,AB=DE,AC=DF15,如图,在△ABC与△ADE中,∠BAD=∠CAE,BC=DE,且点C在DE上,若添加一个条件,能判定△ABC≌△ADE,这个条件是()A.∠BAC=∠DAE B.∠B=∠DC.AB=AD D.AC=AE16,如图,FD⊥AO于D,FE⊥BO于E,下列条件:①OF是∠AOB的平分线;②DF=EF;③DO=EO;④∠OFD=OFE.其中能够证明△DOF≌△EOF的条件的个数有()A.1个B.2个C.3个D.4个17,如图,AB=AC,AD=AE,∠B=50°,∠AEC=120°则∠DAC的度数等于()A.120° B.70° C.60° D.50°18,如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是()A.相等 B.互余 C.互补或相等 D.不相等19,七(7)班徐同学想利用下列长度的木棒制成一个三角形工具,下列各组你认为可行的是()A.5,2,2 B.2,3,6 C.5,3,4 D.7,13,6 20,在△ABC中,∠A=47°,高BE、CF所在直线交于点O,且点E、F不与点B、 C重合,则∠BOC= ;21, 下列说法中:①只有两个三角形才能完全重合;②如果两个图形全等,它们的形状和大小一定都相同;③两个正方形一定是全等图形;④边数相同的图形一定能互相重合; 错误的有()A.4个 B.3个 C.2个 D.1个22,对于条件:①两条直角边对应相等;②斜边和一锐角对应相等;③斜边和一直角边对应相等;④直角边和一锐角对应相等;以上能断定两直角三角形全等的有()A.1个 B.2个 C.3个 D.4个23,下列说法中,正确的个数是()○1斜边和一直角边对应相等的两个直角三角形全等;○2有两边和它们的对应夹角相等的两个直角三角形全等;○3一锐角和斜边对应相等的两个直角三角形全等;○4两个锐角对应相等的两个直角三角形全等;A.1个B.2个C.3个D.4个24,如图,∠1=70°,若m ∥n,则∠2= 度25,如图,AB∥CD,∠B=28°,∠D=47°,则∠BED= 度(第24题图)(第25题图)(第26题图)26,如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2= 度;27,如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.28,下列所示的四个图形中,∠1和∠2是同位角的是()A.②③ B.①②③ C.①②④ C.①②④29,在图中,∠1与∠2是同位角的有()A.①② B.①③ C.②③ D.②④30,已知:x+y=-1,xy=-6,求:x2+y2及x-y的值;31,解方程:(2x+3)(x-4)-(x+2)(x-3)= x2+6推理填空:32,已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.证明:∵DG⊥BC,AC⊥BC(已知)∴∠DGB=∠ACB=90°(垂直定义)∴DG∥AC()∴∠2= ()∵∠1=∠2(已知)∴∠1=∠(等量代换)∴EF∥CD()∴EF∥CD()∴∠AEF=∠()∵EF⊥AB(已知)∴∠AEF=90°()∴∠ADC=90°()∴CD⊥AB()33,如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE;解:∵∠A=∠F()∴AC∥DF()∴∠D=∠1()又∵∠C=∠D()∴∠1=∠C()∴BD∥CE()。
七年级数学下册平行线相交线经典例题

七年级数学下册平行线相交线经典例题在七年级数学下册的学习中,平行线和相交线是一个非常基础且重要的概念。
理解这一概念不仅有助于我们解决实际问题,还可以帮助我们更好地理解几何学的其他知识。
在本文中,我将共享一些关于平行线和相交线的经典例题,以便能够更全面地掌握这一知识点。
1.平行线的性质我们要了解什么是平行线。
平行线是指在同一个平面上,永远也不会相交的两条直线。
了解平行线的性质对于解决相关问题非常重要。
例题1:已知平行线l1和l2,以及一条与l1相交的线m,求证直线m与l2相交的角和与直线l1与l2相交的角相等。
解析:根据平行线的定义,我们知道在同一个平面上,如果两条直线不相交,那么它们必定是平行线。
在这个例题中,我们可以利用已知的平行线性质来证明所求。
以l1和l2为平行线,m为相交线。
根据平行线的性质,可以得出直线m与l1相交的角等于直线m与l2相交的角。
这是因为在平行线与一条相交线所形成的交点处,对应角是相等的。
直线m与l2相交的角和与直线l1与l2相交的角相等。
2.相交线的性质除了平行线的性质,相交线也有一些独特的特点。
了解相交线的性质可以帮助我们更好地理解几何学知识,并能够更好地解决相关问题。
例题2:已知两条相交线l1和l2,以及直线m分别与l1和l2相交,求证直线m与l1或l2的交点的垂直角相等。
解析:相交线的性质是我们要理解和熟练运用的知识点。
在这个例题中,我们可以利用相交线的性质来解决问题。
根据相交线的性质,我们可以得出结论:相交线上的垂直角相等。
以l1和l2为相交线,m为另一条相交线。
根据相交线的性质,可以得出直线m与l1或l2的交点的垂直角相等。
这是因为在两条相交线所形成的交点处,垂直角是相等的。
直线m与l1或l2的交点的垂直角相等。
总结回顾:通过上面的两个例题,我们可以深入地理解平行线和相交线的性质。
对于平行线的性质,我们要了解在同一个平面上,永远也不会相交的两条直线是平行线。
利用平行线的性质可以帮助我们证明相关的几何问题。
(完整版)七年级下册数学几何压轴题集锦(最新整理)

在矩形ABCD 中,点E 为BC 边上的一动点,沿AE 翻折,△ABE 与△AFE 重合,射线AF 与直线CD 交于点G 。
1、当BE :EC=3:1时,连结EG ,若AB=6,BC=12,求锐角AEG 的正弦值。
2、以B 为原点,直线BC 和直线AB 分别为X 轴、Y 轴建立平面直角坐标系,AB=5,BC=8,当点E 从原点出发沿X 正半轴运动时,是否存在某一时刻使△AEG 成等腰三角形,若存在,求出点E 的坐标。
1、2a b m b a-+b+3=0=14.ABC A S A 如图,已知(0,),B (0,),C (,)且(4),o y =DC FD ADO ⊥∠∠∠(1)求C 点坐标(2)作D E ,交轴于E 点,E F 为A E D 的平分线,且D FE 90。
求证:平分;(3)E 在y 轴负半轴上运动时,连EC ,点P 为AC 延长线上一点,EM 平分∠AEC ,且PM ⊥EM,PN ⊥x 轴于N 点,PQ 平分∠APN ,交x 轴于Q 点,则E 在运动过程中,的大小是否发生变化,若不变,求出其值。
MPQECA ∠∠2、如图1,AB//EF, ∠2=2∠1(1)证明∠FEC=∠FCE;(2)如图2,M 为AC 上一点,N 为FE 延长线上一点,且∠FNM=∠FMN ,则∠NMC 与∠CFM 有何数量关系,并证明。
图1 图23、(1)如图,△ABC, ∠ABC 、∠ACB 的三等分线交于点E 、D ,若∠1=130°,∠2=110°,求∠A 的度数。
BCA BCABC(2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D,E 若∠1=110°,∠2=130°,求∠A 的度数。
AC4、如图,∠ABC+∠ADC=180°,OE 、OF 分别是角平分线,则判断OE 、OF 的位置关系为?FEA5、已知∠A=∠C=90°.(1)如图,∠ABC 的平分线与∠ADC 的平分线交于点E ,试问BE 与DE 有何位置关系?说明你的理由。
华师版七年级下册几何应用题

华师版七年级下册几何应用题例题1:一个圆形花坛的直径是8米,要在花坛周围铺设一条2米宽的小路,求小路的面积是多少平方米?解答:首先计算出圆形花坛的半径为8÷2=4米,加上小路宽度后的新半径为4+2=6米。
利用圆的面积公式S=πr²,可得原来花坛面积为π4²=16π平方米,加上小路后的总面积为π6²=36π平方米,所以小路面积为36π-16π=20π平方米。
例题2:一个直角三角形的两条直角边分别是6厘米和8厘米,现以这个直角三角形的直角边为轴旋转一周,形成的立体图形是什么?其体积是多少立方厘米?解答:以直角边为轴旋转一周后会形成两个圆锥体,若以6厘米的直角边为轴,则形成的圆锥底面半径是8厘米,高是6厘米;若以8厘米的直角边为轴,则底面半径是6厘米,高是8厘米。
根据圆锥体积公式V=1/3πr²h,分别计算出两个圆锥体积,选取其中一个进行解答,如以6厘米直角边为轴的圆锥体积V=1/3π8²6=128π/3立方厘米。
例题3:一个梯形的上底是10厘米,下底是20厘米,高是8厘米。
如果在这个梯形内画出一个最大的正方形,求这个正方形的面积是多少平方厘米?解答:在梯形中画出的最大正方形,其一边必然与梯形的上底或下底平行且等长,因此这里最大正方形的边长应等于梯形的高,即8厘米。
所以正方形的面积为边长的平方,即8厘米×8厘米=64平方厘米。
例题4:一个长方体容器的长、宽、高分别是10厘米、6厘米和5厘米,里面装满了水。
现在将一个棱长为4厘米的正方体铁块完全浸入水中,水面会上升多少厘米?解答:首先计算长方体容器的体积V1=长×宽×高=10cm×6cm×5cm=300立方厘米,这是原来水的体积。
正方体铁块的体积V2=4cm×4cm×4cm=64立方厘米。
由于铁块完全浸入水中,所以它排开的水体积就是它的体积,即水面升高部分的体积也是64立方厘米。
2022-2023学年人教版数学七年级下册期末几何解答题专题练习
2022-2023学年人教版七年级下学期期末数学几何解答题专题练习1、如图,AB∥CD,∠A=∠C,BE平分∠ABC交AD的延长线于点E,(1)证明:AD∥BC;(2)若∠ADC=118°,求∠E的度数.2、如图,已知∠1=∠BDC,∠2+∠3=180°.(1)AD与EC平行吗?试说明理由.(2)若DA平分∠BDC,CE⊥AE于点E,∠1=80°,试求∠F AB的度数.3、小聪把一副三角尺ABC,DCE按如图1的方式摆放,其中边BC,DC在同一条直线上,过点A向右作射线AP∥DE.(1)如图2,求∠P AC的度数;(2)如图3,点Q是线段BC上一点,若∠AQB=53∠PAQ,求∠QAB的度数.4、已知:在四边形ABCD中,AD∥BC,AE平分∠DAB交BC于点E,点M为线段BC上一点,且AM∥DC.(1)如图(1),若点M与点E重合,求证:∠C=∠BAE;(2)如图(2),若AN平分∠BAM交BC于点N,且∠NAE=25°,求∠C的度数;(3)在(1)的条件下,F为线段BA的延长线上一点,∠DCB=75°,若∠DCB的三等分线与∠F AD的角平分线交于点P,请直接写出∠APC的度数.5、直线AB∥CD,BE﹣EC是一条折线段,BP平分∠ABE.(1)如图1,若BP∥CE,求证:∠BEC+∠DCE=180°;(2)CQ平分∠DCE,直线BP,CQ交于点F.①如图2,写出∠BEC和∠BFC的数量关系,并证明;②当点E在直线AB,CD之间时,若∠BEC=40°,直接写出∠BFC的大小.6、如图1,AB∥CD,点E在AB上,点H在CD上,点F在直线AB,CD之间,连接EF,FH,∠BEF=α,∠FHD=β.(1)直接写出∠EFH的度数为;(2)如图2,若HM平分∠CHF,MN平分∠BEF,证明:∠EFH+2∠M=180°;(3)如图3,若∠BEN=1n∠BEF,∠MHC=1n∠FHC,则∠M=.(用含有n,α,β的式子表示)7、如图,已知A(0,a),B(b,0),且满足|a−4|+√b+6=0.(1)求A、B两点的坐标;(2)点P(m,n)在线段AB上,当PB=2P A时,求P点的坐标;(3)若点M(c,6),△ABM的面积记作S△ABM,当S△ABM>10时,直接写出c的取值范围.8、在平面直角坐标系中,已知点A(a,0),B(0,b),若a,b满足(a﹣b+6)2+|2a﹣3b+14|=0.(1)求点A,B的坐标;(2)将线段AB向右平移2个单位至CD,线段CD与y轴交于点E,求点E的坐标;(3)点P为直线CD上一动点,连接BC,PB,若4≤S△BCP<6,则点P的横坐标x P的取值范围是.9、如图,已知AB∥CD,M,N分别是直线AB,CD上一点,点E在直线AB,CD之间.(1)如图1,求证:∠BME+∠DNE=∠MEN;(2)如图2,F是EM上一点,NE平分∠FND,FH平分∠NFE,试探究∠NHF与∠BME 之间的数量关系?并证明你的结论;(3)如图3,P为直线MN上一动点(不与点N重合),过点P作PG⊥MN交直线CD 于点G,∠PNG的角平分线和∠PGC的角平分线交于点O,则∠O的度数为(直接写出结果).10、平面直角坐标系中,A(a,0),B(0,b),a,b均为整数,且满足b=√2a−4−√4−a,点C在y轴负半轴上且S△ABC=10,将线段AB平移到DE,其中点A的对应点是点D.(1)请直接写出点A ,B ,C 的坐标;(2)如图(1),若点D 的坐标为(﹣1,0),点F (m ,n )为线段DE 上一点,且△ACF 的面积大于12,求m 的取值范围;(3)如图(2),若DE 与y 轴的交点G 在B 点上方,点P 为y 轴上一动点,请直接写出∠EBO ,∠BPD ,∠PDA 之间的数量关系.11、在平面直角坐标系中,A (a ,0),B (1,b ),a ,b 满足|a +b ﹣1|+√2a −b +10=0,连接AB 交y 轴于C .(1)直接写出a = ,b = ;(2)如图1,点P 是y 轴上一点,且三角形ABP 的面积为12,求点P 的坐标;(3)如图2,直线BD 交x 轴于D (4,0),将直线BD 平移经过点A ,交y 轴于E ,点Q (x ,y )在直线AE 上,且三角形ABQ 的面积不超过三角形ABD 面积的13,求点Q 横坐标x 的取值范围.12、已知,AB ∥DE ,点C 是直线AB ,DE 下方一点,连接BC ,DC .(1)如图1,求证:∠B +∠D ﹣∠C =180°;(2)如图2,若BF ,DG 分别平分∠ABC 和∠CDE ,BF 、DG 所在的直线相交于点H ,若∠H =α°,求∠C 的度数;(用含α的式子表示)(3)如图3,若BF ,DG 分∠ABC 和∠CDE 为两部分,且∠ABF =n ∠FBC ,∠EDG =n ∠CDG ,直线BF ,DG 相交于点H ,则∠H = .(用含n 和∠C 的式子表示)13、已知,在平面直角坐标系中,点A 在y 轴上,OA =a ,点B (b ,b ),且a 、b 满足√a +b −8+(a −b −4)2=0.(1)则a = ;b = ;(2)如图1,在x 轴上是否存在点C ,使三角形ABC 的面积等于三角形ABO 面积的一半?若存在,请求出点C 的坐标;若不存在,请说明理由;(3)如图2,将线段AB 向左平移m 个单位(m >0),得到线段A 'B ',其中点A ,点B 的对应点分别为点A ',点B '.若点N (﹣1,n )在射线A 'B '上,连接ON ,BN 得到三角形BON ,若三角形BON 的面积大于三角形ABO 面积的12并且小于三角形ABO 面积,则m 的取值范围是 .14、如图1,已知点A (﹣2,0),B (0,﹣4),C (﹣4,﹣6),过点C 作x 轴的平行线m ,一动点P 从C 点出发,在直线m 上以1个单位长度/秒的速度向右运动,与此同时,直线m 以2个单位长度/秒的速度竖直向上运动.(1)直接写出:运动1秒时,点P 的坐标为 ;运动t 秒时,点P 的坐标为 ;(用含t 的式子表示)(2)若点P 在第三象限,且S △ABP =8,求点P 的坐标;(3)如图2,如果将直线AB 沿y 轴负半轴向下平移n 个单位长度,恰好经过点C ,求n 的值.15、已知BE 平分∠ABD ,DE 平分∠BDC ,且∠BED =∠ABE +∠EDC .(1)如图1,求证:AB ∥CD ;(2)如图2,若∠ABE =3∠ABF ,且∠BFD =30°时,试求∠CDF ∠FDE 的值;(3)如图3,若H 是直线CD 上一动点(不与D 重合),BI 平分∠HBD ,画出图形,并探究出∠EBI 与∠BHD 的数量关系.问题探究:(1)如图1,∠CFP +∠EPF =∠AEP ,证明:AB ∥CD ;问题拓展:(2)如图2,AB ∥CD ,∠AEP 的角平分线EK 所在的直线和∠DFP 的角平分线FR 所在的直线交于Q 点,请写出∠EPF 和∠EQF 之间的数量关系,并证明.问题迁移:(3)如图3,AB ∥CD ,直线MN 分别交AB ,CD 于点M ,N ,若点H 在线段MN 上,且∠MEF =α,请直接写出∠HFE ,∠MEH 和∠EHF 之间满足的数量关系(用含α的式子表示).16、当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等例如:在图①、图②中,都有∠1=∠2,∠3=∠4.设镜子AB 与BC 的夹角∠ABC =α.(1)如图①,若α=90°,判断入射光线EF 与反射光线GH 的位置关系,并说明理由.(2)如图②,若90°<α<180°,入射光线EF 与反射光线GH 的夹角∠FMH =β.探索α与β的数量关系,并说明理由.(3)如图③,若α=120°,设镜子CD 与BC 的夹角∠BCD =γ(90°<γ<180°),入射光线EF 与镜面AB 的夹角∠1=m (0°<m <90°),已知入射光线EF 从镜面AB 开始反射,经过n (n 为正整数,且n ≤3)次反射,当第n 次反射光线与入射光线EF 平行时,请直接写出γ的度数.(可用含有m 的代数式表示)17、在平面直角坐标系中,点A ,C 均在x 轴上,点B 在第一象限,直线AB 上所有点的坐标(x ,y )都是二元一次方程x ﹣y =﹣2的解,直线BC 上所有点的坐标(x ,y )都是二元一次方程2x +y =8的解.(1)求B 点的坐标时,小明是这样想的:先设B 点坐标为(m ,n ),因为B 点在直线AB 上,所以(m ,n )是方程x ﹣y =﹣2的解;又因为B 点在直线BC 上,所以(m ,n )也是方程2x +y =8的解,从而m ,n 满足{m −n =−22m +n =8.据此可求出B 点坐标为 ,再求出A 点坐标为 ;C 点坐标为 .(均直接写出结果)(2)若线段BC 上存在一点D ,使S △OCD =12S △ABC (O 为原点),求D 点坐标;(3)点E (a ,﹣3)是坐标平面内的动点,若满足S △ABE ≤13S △ABC ,求a 的取值范围.18、已知:点E 在直线AB 上,点F 在直线CD 上,AB ∥CD .(1)如图1,连EF ,EP 平分∠AEF ,FP 平分∠CFE ,求∠P 的度数.(2)如图2,若∠EGF =160°,射线EH ,FH 分别在∠AEG ,∠CFG 的内部,且∠EHF =40°,当∠AEG =4∠AEH 时,求∠GFH ∠CFG 的值.(3)如图3,在(1)的条件下,在直线CD 上有一动点M (点M 不与点F 重合),EN 平分∠MEF ,若∠PEN =α(0°<α<90°),请直接写出∠EMF = (结果用含α的式子表示).19、在平面直角坐标系中,A (a ,0),B (b ,b ),C (0,c ).(其中a ,b ,c 均为正数),且a ,b ,c 满足{3a −b +2c =8a −2b −c =−9,若√b 的算术平方根为√2. (1)求a ,b ,c 的值.(2)如图1,在第二象限内有一点P (m ,12),若四边形ACPO 的面积与△ABC 的面积相等,求不等式:x−32≥2x−m 3的解集.(3)如图2,BO 平分∠AOC ,过点C 作CD ∥AB 交BO 的延长线于点D ,AE 平分∠BAX ,AE 的反向延长线交BO 的延长线于点F ,设∠CDB =α,∠F =β(其中α,β均为锐角),请直接写出:α+2β3= .23.(10分)如图1,已知直线l1∥l2,点A、B在直线l1上,点C、D在l2上,线段AD交线段BC于点E,且∠BED=60°.(1)求证:∠ABE+∠EDC=60°;(2)如图2,当F、G分别在线段AE、EC上,且∠ABF=2∠FBE,∠EDG=2∠GDC,标记∠BFE为∠1,∠BGD为∠2.①若∠1﹣∠2=16°,求∠ADC的度数;②当k=时,(k∠1+∠2)为定值,此时定值为.24.(12分)如图1,在平面直角坐标系中,已知A(a,1),B(0,b),且实数a,b满足√a+b−2+|a+2b|=0.(1)直接写出两点坐标:A(),B();(2)如图2,将线段AB沿着横坐标均为m的点组成的直线l对折,A与C对应,B与D 对应,若凸四边形ABDC的面积为18,求m的值;(3)如图3,点P在第二、四象限的角平分线上,设P点坐标为(h,﹣h),其中h≠0.①当P在线段AB上时,求h的值;②若S△ABP≥2+32S△OBP.直接写出h的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级下册数学几何题大全
七年级下册数学几何题是中学生在学习数学时需要经常练习的基
础性难题。
它们能够帮助学生们掌握计算、演绎以及图形思维的技能。
下面就来介绍一些七年级下册数学几何题:
(1)带标号的线段:这是一项常见的几何练习,要求学生们判
断线段长度,标记出从远到近的道路段号。
(2)三角形面积计算:要求学生根据给定的三个边长的面积,
利用三角公式计算三角形的面积。
(3)多边形和圆形:这是一项数学考试中的普遍几何题,要求
学生计算出一个多边形或圆形的周长,或者求出多边形或圆形的面积。
(4)正方体面积、体积计算:要求学生根据给定的边长,利用
立体几何公式计算出正方体的面积和体积。
(5)求三维图形体积:要求学生根据给定的三维坐标,求出三
维图形的体积。
(6)平面图形综合练习:这个练习十分有益,不仅能帮助学生
掌握平面几何知识,而且还能熟悉坐标系统,可以算出二维和三维图
形的面积等指标,便于学生在算术和几何的实践和应用中进行合理的
推理。
以上就是七年级下册数学几何题的一些典型例子,是中学生在学
习数学时必不可少的练习题目,可以帮助学生更好地掌握几何知识,
并且在抽象思维和应用能力上有所提高。
