应用光学复习题
应用光学第二版胡玉禧课件第二章

−l
β =
y' y
y' nl ' = β = y n ' l (2.15) -------垂轴放大率仅取决于共轭面的位置。
l'
第二章
高斯光学
四、近轴光学公式的实际意义 1、作为衡量光学系统成像质量的标准; 2、近似确定光学系统的成像尺寸。 例1.(习题1)一根长500mm, n =1.5的玻璃棒,两端面为凸 球面,半径分别为50mm和100mm,高1mm的物体位于左端 球面顶点之前200mm处,
图2.11 过节点的光线
第二章
高斯光学
B A′ A F H H′ F′ B′
§2-5 由基面、基点求理想像
一、作图法求像 1、典型光线及性质 2、用作图法求光学系统的理想像 1) 轴外 点B或 一垂 轴线 段AB 的像 (图2.14-5)
B′ B A′ F A N H M M ′ N′ H′ F′
M 2 ' A2 ' // N 2 ' F2 '
图(d):为(a)、(b)、(c)的总结果图。
B′ A2 F2 H2 H F1′ 2′ A2′ F2′ A1′ A1 F1 M1′
M1 H1 F2
M2
M2′ A2′ F ′ 2
H1′ H2 F1′ 2′ H
图 (c)
图 (d )
第二章
二、解析法求像
高斯光学
3、作图注意几点(P.37)
图2. 16
作图法求轴上点的像
第二章
高斯光学
图(b):同2)中法一;
轴上点经两个光组的像 图(a):作A1M1 ;
M1
A F1 F2 H1 H1′H2 F ′H2′ 1 F2′ A1
物理光学与应用光学第二版课件及课后习题答案

由式(1-12)
2 所以有: ( E ) ) E
由式(1-16)得:
2
即 E 0
E 2 E 2 t
(1-17)
同理对式(1-15)两边 取旋度,得
2 2 D B E H ( D) 2 2 t t t t
即:
E E 2 t
2
(1-16)
利用矢量微分恒等式
2 ( A) ( A) A
有:
2 ( E ) ( E ) E
D 0
可知 E 0
同理,利用矢量微分恒等式,可得:
2 有以上两式得: H H 2 t
2
2 ( H ) H
(1-18)
v 令
1
可将式(1-17)式(1-18)变为:
2 1 2E 2 E 2 2 0 (1-19) 2 H 1 H 0 v t v 2 t 2
4.波动方程
麦克斯韦方程组描述了电磁现象的变化规律, 指出随时间变化的电场将在周围空间产生变化的磁 场,随时间变化的磁场将在周围空间产生变化的电 场,变化的电场和磁场之间相互联系,相互激发, 并且以一定速度向周围空间传播。因此,时变电磁 场就是在空间以一定速度由近及远传播的电磁波。
一、 电磁场波动方程:
D H j t
符号的意义:
哈密顿算符:
i j k x y z
具有矢量和求导的双重功能 Dx Dy Dz 散度: D D
x y z
《物理光学与应用光学》习题及选解2

《物理光学与应⽤光学》习题及选解2《物理光学与应⽤光学》习题及选解第⼀章习题1-1. ⼀个线偏振光在玻璃中传播时,表⽰为:i E ))65.0(10cos(10152t cz-??=π,试求该光的频率、波长,玻璃的折射率。
1-2. 已知单⾊平⾯光波的频率为z H 1014=ν,在z = 0 平⾯上相位线性增加的情况如图所⽰。
求f x , f y , f z 。
1-3. 试确定下列各组光波表⽰式所代表的偏振态: (1))sin(0kz t E E x -=ω,)cos(0kz t E E y -=ω; (2) )cos(0kz t E E x -=ω,)4cos(0πω+-=kz t E E y ;(3) )sin(0kz t E E x -=ω,)sin(0kz t E E y --=ω。
1-4. 在椭圆偏振光中,设椭圆的长轴与x 轴的夹⾓为α,椭圆的长、短轴各为2a 1、2a 2,E x 、E y 的相位差为?。
求证:?αcos 22tan 220000y x y x E E E E -=。
1-5.已知冕牌玻璃对0.3988µm 波长光的折射率为n = 1.52546,11m 1026.1/--?-=µλd dn ,求光在该玻璃中的相速和群速。
1-6. 试计算下⾯两种⾊散规律的群速度(表⽰式中的v 表⽰是相速度):(1)电离层中的电磁波,222λb c v +=,其中c 是真空中的光速,λ是介质中的电磁波波长,b 是常数。
(2)充满⾊散介质()(ωεε=,)(ωµµ=)的直波导管中的电磁波,222/a c c v p -=εµωω,其中c 真空中的光速,a 是与波导管截⾯有关的常数。
1-7. 求从折射率n = 1.52的玻璃平板反射和折射的光的偏振度。
⼊射光是⾃然光,⼊射⾓分别为?0,?20,?45,0456'?,? 90。
1-8. 若⼊射光是线偏振的,在全反射的情况下,⼊射⾓应为多⼤⽅能使在⼊射⾯内振动和垂直⼊射⾯振动的两反射光间的相位差为极⼤?这个极⼤值等于多少?=501θ,n 1 = 1,n 2 = 1.5,则反射光的光⽮量与⼊射⾯成多⼤的⾓度?若?=601θ时,该⾓度⼜为多1-2题⽤图⼤?1-10. 若要使光经红宝⽯(n = 1.76)表⾯反射后成为完全偏振光,⼊射⾓应等于多少?求在此⼊射⾓的情况下,折射光的偏振度P t 。
物理光学与应用光学习题解

第七章●习题7-1. 有一玻璃球,折射率为3,今有一光线射到球面上,入射角为60°,求反射光线和折射光线的夹角。
7-2. 水槽有水20cm深,槽底有一个点光源,水的折射率为1.33,水面上浮一不透明的纸片,使人从水面上任意角度观察不到光,则这一纸片的最小面积是多少?7-3. 空气中的玻璃棒,n’=1.5163,左端为一半球形,r=-20mm。
轴上有一点光源,L =-60mm。
求U=-2°的像点的位置。
7-4. 简化眼把人眼的成像归结为只有一个曲率半径为5.7mm,介质折射率为1.333的单球面折射,求这种简化眼的焦点的位置和光焦度。
7-5. 有一玻璃球,折射率为n=1.5,半径为R,放在空气中。
(1)物在无穷远时,经过球成像在何处?(2) 物在球前2R处时像在何处?像的大小如何?7-6. 一个半径为100mm的玻璃球,折射率为1.53。
球内有两个气泡,看来一个恰好在球心,另一个在球的表面和球心之间,求两个气泡的实际位置。
7-7. 一个玻璃球直径为60mm,折射率为1.5,一束平行光入射在玻璃球上,其会聚点应该在什么位置?7-8. 一球面反射镜,r=-100mm,求β=0,-0.1,-1,5,10情况下的物距和像距。
7-9. 一球面镜对其前面200mm处的物体成一缩小一倍的虚像,求该球面镜的曲率半径。
7-10. 垂直下望池塘水底的物时,若其视见深度为1m,求实际水深,已知水的折射率为4/3。
7-11. 有一等边折射率三棱镜,其折射率为1.65,求光线经该棱镜的两个折射面折射后产生最小偏向角时的入射角和最小偏向角。
●部分习题解答7-2. 解:水中的光源发出的光波在水——空气界面将发生折射,由于光波从光密介质传播到光疏介质,在界面将发生全反射,这时只有光波在界面的入射角小于水——空气界面的全反射的临界角,光线才有可能进入空气,因此界面的透光区域为一个以光源在界面上的垂7-2题用图直投影点为心的圆面,如右图,该圆面的面积即为所求纸片的最小面积。
物理光学与应用光学习题解第二章
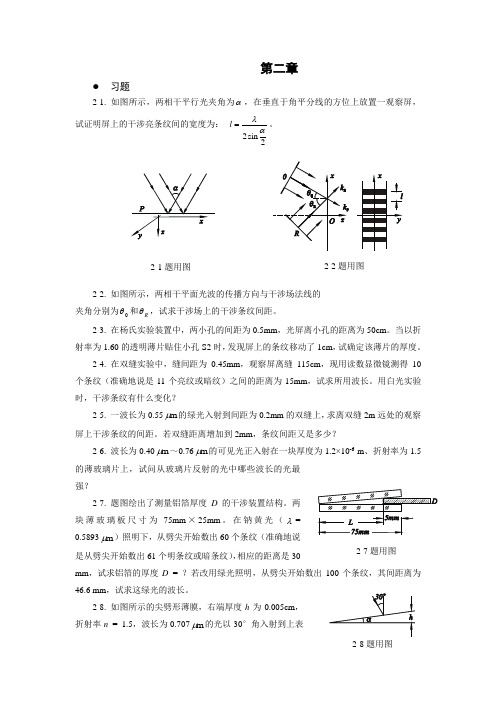
第二章习题2-1. 如图所示,两相干平行光夹角为α,在垂直于角平分线的方位上放置一观察屏,试证明屏上的干涉亮条纹间的宽度为: 2sin2αλ=l 。
2-2. 如图所示,两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ,试求干涉场上的干涉条纹间距。
2-3. 在杨氏实验装置中,两小孔的间距为0.5mm ,光屏离小孔的距离为50cm 。
当以折射率为1.60的透明薄片贴住小孔S2时,发现屏上的条纹移动了1cm ,试确定该薄片的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现用读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝距离增加到2mm ,条纹间距又是多少?2-6. 波长为0.40m μ~0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。
两块薄玻璃板尺寸为75mm ×25mm 。
在钠黄光(λ=0.5893m μ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改用绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所示的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径,结构如图所示。
物理光学与应用光学习题解第二章概要

物理光学与应⽤光学习题解第⼆章概要第⼆章习题2-1. 如图所⽰,两相⼲平⾏光夹⾓为α,在垂直于⾓平分线的⽅位上放置⼀观察屏,试证明屏上的⼲涉亮条纹间的宽度为: 2 sin2αλ=l 。
2-2. 如图所⽰,两相⼲平⾯光波的传播⽅向与⼲涉场法线的夹⾓分别为0θ和R θ,试求⼲涉场上的⼲涉条纹间距。
2-3. 在杨⽒实验装置中,两⼩孔的间距为0.5mm ,光屏离⼩孔的距离为50cm 。
当以折射率为1.60的透明薄⽚贴住⼩孔S2时,发现屏上的条纹移动了1cm ,试确定该薄⽚的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现⽤读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所⽤波长。
⽤⽩光实验时,⼲涉条纹有什么变化?2-5. ⼀波长为0.55m µ的绿光⼊射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上⼲涉条纹的间距。
若双缝距离增加到2mm ,条纹间距⼜是多少?2-6. 波长为0.40m µ~0.76m µ的可见光正⼊射在⼀块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃⽚上,试问从玻璃⽚反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的⼲涉装置结构。
两块薄玻璃板尺⼨为75mm ×25mm 。
在钠黄光(λ=0.5893m µ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改⽤绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所⽰的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m µ的光以30°⾓⼊射到上表2-1题⽤图2-2题⽤图2-7题⽤图2-8题⽤图⾯,求在这个⾯上产⽣的条纹数。
物理光学与应用光学习题解第三章
第三章习题3-1. 由氩离子激光器发出波长λ= 488 nm 的蓝色平面光,垂直照射在一不透明屏的水平矩形孔上,此矩形孔尺寸为0.75 mm ×0.25 mm 。
在位于矩形孔附近正透镜(f = 2.5 m )焦平面处的屏上观察衍射图样。
试描绘出所形成的中央最大值。
3-2. 由于衍射效应的限制,人眼能分辨某汽车两前灯时,人离汽车的最远距离l = ?(假定两车灯相距1.22 m 。
)3-3. 一准直的单色光束(λ= 600 nm )垂直入射在直径为1.2 cm 、焦距为50 cm 的汇聚透镜上,试计算在该透镜焦平面上的衍射图样中心亮斑的角宽度和线宽度。
3-4. (1)显微镜用紫外光(λ= 275 nm )照明比用可见光(λ= 550 nm )照明的分辨本领约大多少倍?(2)它的物镜在空气中的数值孔径为0.9,用用紫外光照明时能分辨的两条线之间的距离是多少?(3)用油浸系统(n = 1.6)时,这最小距离又是多少?3-5. 一照相物镜的相对孔径为1:3.5,用λ= 546 nm 的汞绿光照明。
问用分辨本领为500线 / mm 的底片来记录物镜的像是否合适?3-6. 用波长λ= 0.63m μ的激光粗测一单缝的缝宽。
若观察屏上衍射条纹左右两个第五级极小的间距是6.3cm ,屏和缝之间的距离是5 m ,求缝宽。
3-7. 今测得一细丝的夫琅和费零级衍射条纹的宽度为 1 cm ,已知入射光波长为0.63m μ,透镜焦距为50 cm ,求细丝的直径。
3-8. 考察缝宽b = 8.8×10-3 cm ,双缝间隔d = 7.0×10-2 cm 、波长为0.6328m μ时的双缝衍射,在中央极大值两侧的两个衍射极小值间,将出现多少个干涉极小值?若屏离开双缝457.2 cm ,计算条纹宽度。
3-9.在双缝夫琅和费衍射实验中,所用波长λ= 632.8 nm ,透镜焦距f = 50 cm ,观察到两相邻亮条纹之间的距离e = 1.5 mm ,并且第4级亮纹缺级。
《物理光用与应用光学》第二版习题解答
进行坐标变换:
ïìEx = Ex 'cosa - E y 'sina ïîíE y = Ex 'sina + E y 'cosa
代入上面的椭圆方程:
(Ex
'2
cos 2
a
+
E
y
'2
sin
2
a
-
2Ex
'
E
y
'sina
cos a
)E
2
y0
+
(Ex
'2
sin 2
a
+
Ey
'2
cos 2
a
+
2Ex
'
Ey
' sin a
解:(1)∵ k = w / v
d (kv)
dv
∴vg =
dk
=v+k dk
∵ k = 2p / l
∴ dk = -(2p / l2 )dl
∴ vg
=
v-l
dv dl
=v-l
b2l c2 + b2l2
= c2 + b2l2 - b2l2
=
c2
c2 =
c 2 + b2l2
c 2 + b2l2 v
(2)∵
2 cosq1 sinq 2
Ei0 p sin(q1 + q 2 ) cos(q1 - q2 )
①、②依据题意,介质平板处在同一种介质中,由 Fresnel's Fomula 的前两项,可以看
旺旺:yulingcici QQ:985673089 专业提供中科院中科大考研考博资料
应用光学所有题目
15
Applied Optics
l 解: 1
50
f 1 ' 14
l1 '
f 1 ' l 1 l1 f 1 '
19 . 44
l 2 ( 19 . 44 32 ) 51 . 44
l2 ' l2 f2 ' l2 f2 ' 51 . 44 42 51 . 44 42
1 l' 1 l 1 f' 1 60 1 150 1 f'
f ' 42 . 86
12
Applied Optics
例题11.
f '1
一个成像光学系统由相隔50毫米,焦距 =100毫米、
f '2
=200毫米的两个薄透镜组
成,直径为5毫米的物体位在第一透镜的物方焦平面上。 求物体通过这两个薄透镜后所成像的大小为多少?如果要 求保持两个透镜的间隔不变,所成的像平面与第二透镜的 距离即像距变为250毫米,采用移动物平面的方法,问物
n ' n r
解:鱼先经水面成像 n 水 1
r n' 1 n 1 . 33
l 1000
n' l'
n l
l ' 751 . 88
再经照相物镜成像 x 1000 751 . 88 1751 . 88
f x 75 1751 . 88 0 . 0428
平面距离第一透镜的距离为多少?
13
Applied Optics
解:
1
1 l
y' y
西电《物理光学与应用光学》真题与要点
专业课复习参考
课后题要好好做还有那些例题要弄明白,考试基本上都是课后题。
首选把这些弄明白有些太复杂的不要研究了,基本题就行。
第一章光在各向同性介质中的传播特性
1.2重点
课后例题必须看
第二章光的干涉
2.1 2.4 2.5 2.5是重点中的重点
第三章光的衍射
3.1-3.4
第四章光在各向异性介质中的传播特性
第四章的结论的东西要记住 4.1-4.4 4.5.1
第五章晶体的感应双折射
5.1
第六章光的吸收、色散和散射
第六章基本概念看看就行了
第七章几何光学基础
第七章都看
第八章理想光学系统
8.1-8.4
第九章光学系统像差基础和光路计算
第九章光阑的计算方法要会可以参考山东大学出版的《光学》其他了解一下概念就行
第十章光学仪器的基本定理
10.2-10.5
在强调一遍课后的例题一定要仔细看要弄明白
(说明:西电光工初试专业课09年开始使用《物理光学与几何光学》一书)
2009物理光学与应用光学考研真题
09-1
09-2
09-3
2010物理光学与应用光学考研真题
10-1
10-2
10-3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
真诚为您提供优质参考资料,若有不当之处,请指正。
1 / 3
1、 一束光由玻璃(n=1.5)进入水(n=1.33),若以45°角入射,试求折射角。(52.6°)
2、 一薄透镜焦距为200mm,一物体位于透镜前300nm,求像的位置和垂轴放大率。
(`600,2lmm)
3、 一组合系统由薄正透镜(前)和薄负透镜(后)组成,1`20fmm,2`20fmm,两透镜之
间的距离10dmm,当一物体位于正透镜前方100mm处,求组合系统的垂轴放大率和像的位
置。(可用两种方法解)。(2`60,1lmm)
4、 一双凸薄透镜的两表面半径分别为1250,50rmmrmm,求该透镜位于空气中和浸入水
(01.33n)中的焦距分别为多少?(透镜材料折射率n=1.5)
(`50fmm空,`195.6fmm水)
5、 符号规则标注
6、 作图求物像:掌握第二章作业里作图题
7、 棱镜成像方向的判断。
8、 一凹球面反射镜浸没在水中,物在镜前300mm,像在像前90mm,求球面反射镜的曲率半径和
焦距。(138.46,`69.23rmmffmm)
9、 有一正薄透镜对某一物体成实像时,像高为物高的一半;若将物体向透镜移近100mm时,则所
得的实像与物大小相同,求透镜的焦距。(`100fmm)
10、 已知显微镜的视放大率为-300,目镜的焦距为20mm,求显微镜物镜的倍率。假定人眼的
视角分辨率为60``,问使用该显微镜观察时,能分辨的两物点的最小距离等于多少?
(24,0.00024mm)
11、 用两个焦距都是50mm的正透镜组成一个10倍的显微镜,问目镜的倍率,物镜的倍率以
及物镜和目镜之间的间隔为多少?
12、 有一焦距为150mm的望远物镜,其口径为10mm,像的直径为20mm。在物镜后方80mm
处放置一直角棱镜(n1.5),假如系统没有渐晕,求棱镜入射表面的通光口径及像平面离开棱镜
出射表面的距离。(D=29.33,l`=50.44mm)
13、
6倍双目望远镜系统中,物镜焦距为108mm,物镜口径为30mm,目镜口径为20mm,如
果系统中没有视场光阑,问该望远镜最大极限视场角等于多少?渐晕系数KD=0.5时的视场角等
于多少?(max0.5211.33,29.08)
(理解)
14、
7倍望远系统,视场28,目镜焦距为25mm,出瞳直径为5mm,假定无渐晕,求孔径
光阑、入瞳、出瞳位置,物镜和目镜的口径,视场光阑口径/位置。
(理解)
真诚为您提供优质参考资料,若有不当之处,请指正。
2 / 3
(D视阑=24.5,`28.58zlmm,D物镜=35mm) 图见下图。
14、(理解)有一薄透镜焦距为50mm,通光孔径为40mm,在透镜左侧30mm处放置一个直径为
20mm的圆孔光阑,一轴上物点位于光阑左方200mm处,求:
(1)限制光束口径的是圆孔光阑还是透镜框?
(2)此时该薄透镜的相对孔径多大?
(3)出瞳离开透镜多远,出瞳直径多大?
15、掌握第三章作业;
16、第四章反射棱镜,掌握书上的像坐标判断;
17、已知220V,60W的充气钨丝灯泡均匀发光,辐射的总光通量为900lm,求该灯泡的光视效能和
发光强度?2m处的光照度?
18、有一均匀磨砂球形灯,它的直径为17cm,光通量为220lm,求该球形灯的光亮度?
19、有一直径为20mm的球形磨砂灯泡,各方向均匀发光,其光视效能为15lm/W,若在灯泡正下
方2m处的光照度为30lx,问该灯泡的功率多大?灯泡的光亮度多大?
20、像差:掌握各种像差的概念、产生的原因、各种像差与什么物理量有关?
21、已知一球面的半径为100mm,n=1,n`=1.52,若200,10lmmymm。
求:`?,`?ly
22、已知一个同心透镜r1=50mm,厚度d=10mm,n=1.5163,求它的主平面和焦点位置。
23、某透镜将位在它前面的高为20mm的物体成一倒立的高为120mm的实像,若把物向透镜方向
移动10mm,则像成在无限远,求透镜的焦距及移动前原位置时的物距和像距。
24、要求用两个焦距分别为1210,`50fmmfmm的薄透镜组成一个总焦距为`80fmm 的镜
头,问两透镜之间的间隔应等于多少?
25、有一折射率n=1.52的玻璃板,若有一光线以30°的入射角射到其表面发生反射
和折射,求:
(1)反射角?(2)折射角?(3)当玻璃板顺时针转过3°,问反射光线变化了多
少?
26、一平行细光束平行于光轴入射到曲率半径r=100mm的折射球面上,试求:(1)它的
-ω=4°
f`物
l`
z
-f
目
真诚为您提供优质参考资料,若有不当之处,请指正。
3 / 3
像点位置?(2)像方焦点的位置?(n=1;n`=1.52)
27、有一个物体高度为y=20mm,被一焦距f`=100mm透镜成像,已知物距l=-200mm,
求:(1)像距?(2)像高?
28、某显微镜目镜焦距25mm,物镜垂轴放大率-3×,物镜的共轭距离为180mm,试求:
1)物镜的焦距;3)显微镜的视放大率?(主平面之间距离忽略不计)
29、10cd的点光源发出的光通量是多少?离开光源2m处的光照度是多少?在该处通过
0.5m²的面积(与光照射方向垂直)的光通量为多少?
30、假定望远镜物镜的焦距为80mm,通光口径为20mm,半视场角ω=5°,在它后面50m
处放一个直角棱镜,求棱镜的尺寸和像面位置?(n=1.52)
31、每章的基本概念和基本定律
