解答题训练1(2015-3-6 15.22.57)
2015年中考数学专项训练--选择题(二)-1.doc

2015年中考数学专项训练--选择题(二)答案附:上表中共有20种可能的组合,相同组合(同种颜色表示相同组合)只算一种,余10种组合,其中1男1女的组合有6组,所以一男一女的概率()53106==一男一女P11.解:根据题意,画出树状图如下:一共有36种情况,当x=1时,y=﹣x 2+3x=﹣12+3×1=2,当x=2时,y=﹣x 2+3x=﹣22+3×2=2,当x=3时,y=﹣x 2+3x=﹣32+3×3=0,当x=4时,y=﹣x 2+3x=﹣42+3×4=﹣4,当x=5时,y=﹣x 2+3x=﹣52+3×5=﹣10,当x=6时,y=﹣x 2+3x=﹣62+3×6=﹣18, 所以,点在抛物线上的情况有2种, P (点在抛物线上)181362==故选A .21.解:作AE ⊥y 轴于E ,CF ⊥y 轴于F ,如图,∵四边形OABC 是平行四边形,∴S △AOB =S △COB ,∴AE =CF ,∴OM =ON , ∵S △AOM =21|k 1|=21OM •AM ,S △CON =21|k 2|=21ON •CN , ∴21k k CN AM,所以①正确; ∵S △AOM =21|k 1|,S △CON =21|k 2|, ∴S 阴影部分=S △AOM +S △CON =21(|k 1|+|k 2|),而k 1>0,k 2<0, ∴S 阴影部分=21(k 1﹣k 2),所以②错误; 当∠AOC =90°,∴四边形OABC 是矩形, ∴不能确定OA 与OC 相等, 而OM =ON ,∴不能判断△AOM ≌△CNO , ∴不能判断AM =CN ,∴不能确定|k 1|=|k 2|,所以③错误; 若OABC 是菱形,则OA =OC , 而OM =ON ,∴Rt △AOM ≌Rt △CNO ,∴AM =CN ,∴|k 1|=|k 2|,∴k 1=﹣k 2,∴两双曲线既关于x 轴对称,也关于y 轴对称,所以④正确. 故答选择C .22.解:过点C 作CE ⊥x 轴于点E ,过点D作DF ⊥x 轴于点F , 设OC =3x ,则BD =x , 在Rt △OCE 中,∠COE =60°,则OE =23x ,CE =233x , 则点C 坐标为(23x ,233x ), 在Rt △BDF 中,BD =x ,∠DBF =60°, 则BF =21x ,DF =23x , 则点D 的坐标为(x 215-,23x ), 将点C 的坐标代入反比例函数解析式可得:k =439x 2, 将点D 的坐标代入反比例函数解析式可得:243235x x k -=, 则2243235439x x x -=, 解得:x 1=1,x 2=0(舍去), 故43914392=⨯=k 故选择A24.解:如图,∵A 点坐标为(﹣1,1), ∴k=﹣1×1=﹣1,∴反比例函数解析式为xy 1-=, ∵OB=AB=1,∴△OAB 为等腰直角三角形,∴∠AOB=45°, ∵PQ ⊥OA ,∴∠OPQ=45°,∵点B 和点B ′关于直线l 对称,∴PB=PB ′,BB ′⊥PQ , ∴∠BPQ=∠B ′PQ=45°,即∠B ′PB=90°, ∴B ′P ⊥y 轴,∴B 点的坐标为(t1-,t ),∵PB=PB ′,∴t ﹣1=|﹣t 1|=t1,。
解答题专项训练

■ HE ;;『数 5数U船 矗 专 学 -U 档 题 一X0K£ 1 鳅 学 》司 乏
l 如 图3 Q 所示 .在 正方形AB D C 中. 是 上 一 点 是 D延 长线上 一
点 . D = E 且 FB . l.已知 , 同 一 直 角 坐 标 系 中 , 3 在
x -1 l
6 某 工 程 队 在 社 会 主 义 新 农 村 无 建 设 过 程 中 承 包 了 一 项 拆 迁 工 程 .原 计 划 每 天 拆 迁 1 5 平 方 米 , 因 为 准 0 2 但
的任 意 一点 , 点P / C上 过  ̄P 轴于 点C, -
P) 轴 于 点 n 求 四 边 形ABC ,上 D面 积 的 最 小 值 , 并 说 明 此 时 四边 形 AB D C
卖 出3 0 , 准 备 降价 处理 , 经 市 0件 现 且
场 调 查 , 降 价 1 . 星 期 可多 卖 每 元 每 2 件.在确 保赢 利 的前 提下 ,解答 下 0
列 问题.
(- ) 0i 有 一 个整 数 解 , a a2 = Z少  ̄ 且 是整 数 , 的值 . 求a
5 .如 图 1 示 .张 琪 家 居 住 在 甲 所
图2
\
,.
C 一
() 1求这 个不 等式 组 的整数 解. ( ) 上述 不 等式 组 的整 数 解 满 2若 足 方程a + = 一 a求 a x 6x 2 。 的值.
解 答 一 个 问 题 后 , 结 论 作 为 将
(计 代 式 一 ) 3 算数 ( ・ )
的值
楼AB, 现计划 在他 家居住 的楼 前修 建
一
座 乙楼 C 乙 楼高 约 为 1米 , 楼 D, 8 两
解答题专题练习一 1-6
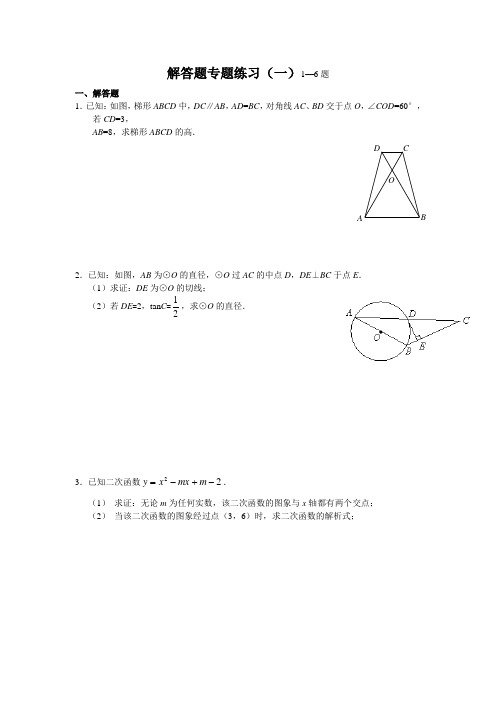
解答题专题练习(一)1—6题一、解答题1.已知:如图,梯形ABCD 中,DC ∥AB ,AD =BC ,对角线AC 、BD 交于点O ,∠COD =60°,若CD =3,AB =8,求梯形ABCD 的高.2.已知:如图,AB 为⊙O 的直径,⊙O 过AC 的中点D ,DE ⊥BC 于点E .(1)求证:DE 为⊙O 的切线;(2)若DE =2,tan C =21,求⊙O 的直径.3.已知二次函数22-+-=m mx x y .(1) 求证:无论m 为任何实数,该二次函数的图象与x 轴都有两个交点;(2) 当该二次函数的图象经过点(3,6)时,求二次函数的解析式;B C D OA4.如图,直线3+-=x y 与x 轴,y 轴分别交于B ,C 两点,抛物线c bx x y ++-=2经过点B 和点C ,点A 是抛物线与x 轴的另一个交点.(1)求抛物线的解析式和顶点坐标;(2)若点Q 在抛物线的对称轴上,能使△Q AC 的周长最小,请求出Q 点的坐标;5某工厂计划招聘A 、B 两个工种的工人共120人,A 、B 两个工种的工人月工资分别为800元和1000元.(1)若某工厂每月支付的工人工资为ll000O 元,那么A 、B 两个工种的工人各招聘多少人?设招聘A 工种的工人x 人。
根据题设完成下列表格,并列方程求解.(2)若要求B 工种的人数不少于A 工种人数的2倍,那么招聘A 工种的工人多少人时,可使工厂每月支付的工人工资最少?6.如图,已知一次函数b kx y +=的图象经过)1,2(--A ,)3,1(B 两点,并且交x 轴于点C ,交y 轴于点D ,(1)求该一次函数的解析式;(2)求OCD ∠tan 的值;(3)求证:︒=∠135AOB .。
解答题限时训练6(参考答案)

高三年级理科数学解答题限时训练6参考答案1.【解析】(1)因为211n n n S S a λ+++=,①所以当2n ≥时,21n n n S S a λ-+=, ②……………………………………………………1分 -①②得:2211n n n n a a a a λλ+++=-,即111()()n n n n n n a a a a a a λ++++=+-,因为{}n a 的各项均为正数,所以10n n a a ++>,且0λ>,所以11n n a a λ+-=.……3分由①知,2212S S a λ+=,即21222a a a λ+=,又因为11a λ=,所以22a λ=.所以211a a λ-=.……………………………………………………………………4分故11()n n a a n N λ*+-=∈,所以数列{}n a 是首项为1λ,公差为1λ的等差数列.……5分所以11(1)n na n λλλ=+-=.………………………………………………………………6分(2)由(1)得n na λ=,所以1n n b n λ-=⋅,……………………………………………7分所以221123(1)n n n T n n λλλλ--=++++-+, ③23123(1)n n n T n n λλλλλ-=++++-+, ④……………………………………8分-③④,得21(1)1n n n T n λλλλλ--=++++-,……………………………………9分当0λ>且1λ≠时,1(1)1nn n T n λλλλ--=--,……………………………………………10分 解得21(1)1n nn n T λλλλ-=---;……………………………………………………………………11分 当1λ=时,由③得2(1)123(1)22n n n n nT n n ++=++++-+==;综上,数列{}n b 的前n 项和22,121,0,1(1)1n n nn nT n λλλλλλλ⎧+=⎪⎪=⎨-⎪->≠⎪--⎩……………………12分 2.解:在图1中,连结DP 交AE 于点O .因为ABCD 是矩形,所以在Rt PDC △中,CD AB ==又22CP BC BP=-==,所以1tan2CPPDCCD∠==;在Rt ADE△中,AD BC DE===1tan2DEADEAD∠==.所以PDC DAE∠=∠,所以2DAE ADP PDC ADPπ∠+∠=∠+∠=,所以2DOAπ∠=.…………………………………………………………………………2分从而,AO OD AO OP⊥⊥,那么在图2中,AE OD AE OP'⊥⊥,…………………3分又因为D O PO O'=,所以AE⊥平面POD',……………………………………4分又因为D P'⊂平面POD',所以AE D P'⊥.……………………………………5分(2)由(1)知OD AE'⊥,OP AE⊥,所以D OP'∠是二面角B AE D'--的平面角,从而23D OPπ'∠=.……………………………………………………………………6分在图2中延长,AE BC交于点Q,连结D Q',则Q∈平面AD E',Q∈平面BCD',又D'∈平面AD E',D'∈平面BCD',所以平面AD E '平面BCD D Q''=,D Q'即为直线l.………………………………7分在平面POD'内过点O作OF OP⊥交D P'于F,由(1)知AE⊥平面POD',从而AE OF⊥,故,,OA OP OF两两垂直,以O为原点,分别以,,OA OP OF为x轴、y轴、z轴正方向建立如图所示空间直角坐标系.…………8分在图1中,CE DC DE=-=Rt ADE△中,AD DE==所以5,2,1AE OD OE===;在ABQ△中,//EC AB,所以EQ CEQA AB=,即23EQAE EQ=+,所以10EQ=,所以11OQ OE EQ=+=.从而(0,1(1,0,0),(3,4,0),(11,0,0)D E C Q'----,所以(1,1,3),(2,4,0),(11,1ED EC QD''=-=-=-,…………………………9分设(,,)n x y z=为平面D CE'的法向量,则20n ED x yn EC x y⎧'⋅=-=⎪⎨⋅=-=⎪⎩,取x =1y z ==-,所以(23,1)n =-是平面D CE '的一个法向量.………………………………11分设l 与平面D CE '所成角为θ,则sin cos ,55QD n QD nQD n θ'⋅'===='⋅,所以l 与平面D CE '所成角的正弦值为5.…………………………………………12分3.解:(Ⅰ)2×2列联表:………………………………………………………………………………………………………2分2250(311729) 6.27 6.635,10403218K ⨯⨯-⨯=≈<⨯⨯⨯………………………………………………… 4分∴没有99%的把握认为以45岁为分界点对了解《民法总则》政策有差异.…………………5分(Ⅱ)X 的所有可能取值为0,1,2,3,22842210584(0),225C C P x C C ===211128482422105104(1),225C C C C C P x C C +=== 11122824242210535(2),225C C C C C P x C C +===2124221052(3),225C C P x C C ===………………10分则X 的分布列为所以X 的数学期望是0.2252252255EX =+++=……………………………12分 4.【解析】:(1)依题意,直线l 的极坐标为()R θαρ=∈.………………………………1分由1cos 1sin x y ϕϕ=+⎧⎨=+⎩,消去ϕ,得22(1)(1)1x y -+-=,……………………………………3分将cos ,sin x y ρθρθ==代入上式,得22cos 2sin 10ρρθρθ--+=,故M 的极坐标方程为22cos 2sin 10ρρθρθ--+=.…………………………………………………………5分 (2)依题意可设12344(,),(,),,,,66A B C C ππραραραρα⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭, 且1234,,,ρρρρ均为正数.将θα=代入22cos 2sin 10ρρθρθ--+=,得22(cos sin )10ρααρ-++=, 所以122(cos sin )ρραα+=+,…………………………………………………………6分 同理可得,342cos sin 66ππρραα⎡⎤⎛⎫⎛⎫+=+++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,………………………………7分 所以点O 到,,,A B C D 四点的距离之和为OA OB OC OD +++1234ρρρρ=+++()2cos sin αα=+2cos sin 66ππαα⎡⎤⎛⎫⎛⎫++++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦(1(3αα=+2(13πα⎛⎫=+ ⎪⎝⎭…………………………………………………………9分因为0,6πα⎛⎤∈ ⎥⎝⎦,所以当6πα=时,1234ρρρρ+++取得最大值2+所以点O 到,,,A B C D 四点的距离之和的最大值为2+10分。
解答题专项训练

解答题专项训练 一、勾股定理 1.(5分)如图18-9所示,在四边形ABCD中,AB=BC=2,CD=1,AD=3,∠ABC=900,求∠BCD的度数?
2.(5分)在△ABC中,BC=m2-n2,AC=2mn,AB=m2+n2(m>n) 求证:△ABC是直角三角形。
3.(5分)如图18-10,已知△ABC中,∠B=450,∠C=300,AB= 求AC的长? 4. (5分)如图18-11,四边形ABCD是正方形,AE= AB,BF= BC,求证:DE⊥EF 5. (8分)如图18-12, 在△ABC中, AD⊥BC于D, AB=3, BD=2, DC=1, 求AC2的值.
6. (8分) “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过千米/小时,如图18-13,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方米处,过了秒后,测得小汽车与车速检测仪间距离为米,这辆小汽车超速了吗?
7.(8分)如图18-15,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域. 1. A城是否受到这次台风的影响?为什么? 2. 若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间? 二、分式方程应用题 1、某化肥厂计划在规定日期内生产化肥120吨,由于采用了新技术,每天多生产化肥3吨,实际生产180吨与原计划生产120吨的时间相等,求计划每天生产多少吨化肥?
2、陈明同学准备在课外活动时间组织部分同学参加电脑网络培训,按原定的人数估计共需费用300元,后因人数增加到原定人数的2倍,享受优惠,一共只需480元,参加活动的每个同学平均分摊的费用比原计划少4元,求原定的人数是多少?
3、甲、乙两组学生去距学校4.5千米的敬老院打扫卫生,甲组学生步行出发半小时后,乙组学生骑自行车开始出发,结果两组学生同时到达敬老院,如果步行的速度是骑自行车的速
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.已知 (1)求函数的最小正周期及在区间的最大值;
(2)在中,所对的边分别是,,求周长的最大值.
2.已知函数的图象过点();
(1)求A的值; (2)已知,求的值。
3.已知是等差数列,,.
(1)求数列的通项公式;(2)对一切正整数,设,求数列的前项和.
宝鸡市东风路高级中学导学单
年 级: 高三 班级:2.4班 小 组: 姓名:
创建人: 周粉粉 使用时间:
4.如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
5.从某小区抽取100个家庭进行月用电量调查,发现其月用电量都在50度至350度之间,频率分布直方图如图
所示.
(1)根据直方图求的值,并估计该小区100个家庭的月均
用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100个家庭中, 随机抽取月用电量超
过300度的2个家庭,参加电视台举办的环保互动活动,求
家庭甲(月用电量超过300度)被选中的概率.
