2001-2012年安徽省中考数学试题分类解析汇编(12专题) 专题8平面
安徽省2001-2012年中考数学试题分类解析专题5:数量和位置变化

新世纪教育网 精品资料 版权所有@新世纪教育网新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。
版权所有@新世纪教育网 九年级一模科学参考答案 2013.3.151~10:ABABB CDBBC 11~20:DDDBB CBDCD21. (1)亚欧 (2)热能22. (1)C 2H 8N 2 (2)D (3)反应可在常温下进行,可吸收CO 2(答对一条即得分)23. (3)不相同 24. 电压 525. (1)群落 (2)植物→鼠→蛇(或植物→鸟→蛇)26. (1)见光易分解 (2)O 2 27. (1)A 、D 、F (2)CO 228. (1)浓H2SO4 (2)无水硫酸铜不变色 29. 6000 3030. (1)BaCO 3+2Hcl=BaCl 2+H 2O+CO 2↑ (2)C31. (1)对照 在37℃下酶活性较强 (2)Cl- 32. (1)根据二力平衡,拉力等于摩擦力 (2)未控制鞋子的重力(或对地面的压力)相等(3)增大与地面的摩擦力 (4) B33. (2)C (3)O2(4)将带火星的木条伸入所收集的气体中,带火星的木条复燃,说明收集气体为氧气。
34. (1) (2)1.8 (3)100Ω,2A (4)先增大后减小35. (1)大于 光照 (2)消费者、分解者36. (1)(1)酸性 BaCl 2、HCl(2)设与BaCl 2反应的K 2CO 3质量为xK 2CO 3+BaCl 2=BaCO 3↓+kCl138 197x 9.85g138x =1979.85g得x =6.9g 质量分数=6.9g 30g×100%=23% 37. (1)0.8(2)CaCO 3%=4g-0.8g 4g×100%=80% (3)设可得CO 2质量为xCaCO 3____________高温 CaO+CO 2↑100 441000kg ×80% x1001000kg ×80% = 44x得x =352kg 38. (1)解:I=P U =1100w 220v=5A R 总=PU I =220v 5A=44Ω R 0=R 总-R T =44Ω-34Ω=10Ω(2)温度130℃时,R T =100ΩI=U R 总=U R T +R 0=220v 100Ω+10Ω=2A P=I 2×R T =(2A)2×100Ω=400W。
2001-2012年镇江市中考数学试题分类解析专题12:押轴题

2001-2012年江苏镇江中考数学试题分类解析汇编(12专题)专题12:押轴题一、选择题1. (2001江苏镇江3分)如图,直角三角形AOB 中,AB ⊥OB ,且AB =OB =3,设直线a :x=t 截此三角形所得的阴影部分的面积为S ,则S 与t 之间的函数关系的图像为【 】【答案】D 。
【考点】二次函数的图象。
【分析】由直角三角形AOB 中,AB ⊥OB ,且AB =OB =3,知直线a :x=t 截此三角形所得的阴影部分也为等腰直角三角形,所以()21S=a 0a 32≤≤。
则S 与t 之间的函数关系的图像为D 。
故选D 。
2. (2002江苏镇江3分)如图,正方形ABCD 内接于⊙O ,E 为 DC 的中点,直线BE 交⊙O 于点F ,若⊙O 的半径为2,则BF 的长为【 】A 、23B 、22C 、556D 、554 【答案】C 。
【考点】正方形的性质,圆周角定理,勾股定理,相交弦定理。
【分析】连接BD ,∵由正方形的性质∠DCB=90°,∴BD 是直径。
∵⊙O的半径为2,∴BD=22。
∴根据正方形的性质和勾股定理得BC=DC=2。
∵E为DC的中点,∴DE=CE=1。
∴根据勾股定理得BE=4+15=。
由相交弦定理得DE CE15 EF?BE55⋅===。
∴BF=BE+EF=655。
故选C。
3. (2003江苏镇江3分)如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H 分别在AD、AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则矩形ABCD的面积为【】A、2B、43C、32D、53【答案】D。
【考点】矩形和正方形的性质【分析】设小正方形的边长a,那么矩形的面积=(S△AEF+S△BFG)×2+S四边形EFGH,即:2a a a4a3a5a2122⋅⋅⋅=+⨯+(),解得1a3=(a>0)。
∴矩形的面积=3a×5a=53a5a3⋅=。
江苏省连云港市2001-2012年中考数学试题分类解析 专题08 平面几何基础

[中考12年]连云港市2001-2012年中考数学试题分类解析专题08平面几何基础一、选择题1. (2001年江苏连云港3分)在比例尺1∶n的某市地图上,规划出一块长5cm、宽2cm的矩形工业园区,则该园区的实际面积是【】(单位:平方米)(A)n1000(B)2n1000(C)10n (D)210n2. (2001年江苏连云港3分)下列四个命题中的真命题是【】(A)同位角相等,则它们的平分线互相垂直(B)内错角相等,则它们的平分线互相垂直(C)同旁内角互补,则它们的平分线互相垂直(D)同旁内角相等,则它们的平分线互相垂直3. (2002年江苏连云港3分)下面给出四个命题,其中假命题是【】A.两条直线被第三直线所截,同位角相等B .不相等的两角不是对顶点C .平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧D .以已知线段AB 为弦的圆的圆心的轨迹是线段AB 的垂直平分线4. (2004年江苏连云港3分)下列图案中,既是中心对称又是轴对称的图案是【 】A .B .C .D .5. (2005年江苏连云港3分)如图,直线1l ∥2l ,3l ⊥4l .有三个命题:①︒=∠+∠9031;②︒=∠+∠9032;③42∠=∠.下列说法中,正确的是【 】(A )只有①正确 (B )只有②正确 (C )①和③正确 (D )①②③都正确6. (2006年江苏连云港3分)下列图案中,不是..中心对称图形的是【】A、 B、 C、 D、7. (2006年江苏连云港3分)多边形的内角和不可能...为【】A、180°B、680°C、1080°D、1980°8. (2008年江苏连云港3分)已知AC为矩形ABCD的对角线,则图中1∠一定不相等∠与2的是【】A. B. C.D.9. (2010年江苏连云港3分)下列四个多边形:①等边三角形;②正方形;③正五边形;④正六边形.其中,既是轴对称图形又是中心对称图形的是【】A.①② B.②③ C.②④ D.①④10. (2011年江苏连云港3分)小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是【】A.B.C.D.11.(2012年江苏连云港3分)下列图案是轴对称图形的是【】A. B. C. D.12.(2012年江苏连云港3分)如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为【】A.50° B.60° C.70° D.80°二、填空题1. (2004年江苏连云港3分)如图,两平面镜OA与OB之间的夹角为110°,光线经平面镜OA反射到平面镜OB上,再反射出去,其中∠1=∠2,则∠1的度数为▲ 度.2. (2005年江苏连云港3分)已知一个五边形的4个内角都是100,则第5个内角的度数是▲ .3. (2006年江苏连云港3分)如图,∠BAC=30°,AB=10。
2001-2012年镇江市中考试题分类解析专题8:平面几何基础
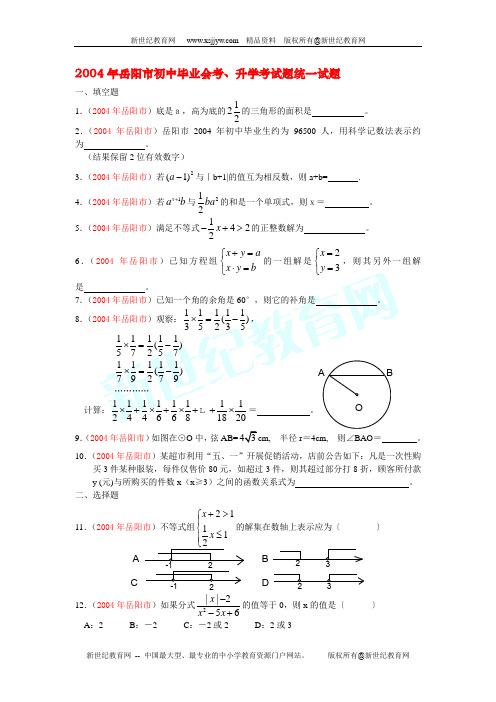
CA B DOAB2004年岳阳市初中毕业会考、升学考试题统一试题一、填空题1.(2004年岳阳市)底是a,高为底的122的三角形的面积是 。
2.(2004年岳阳市)岳阳市2004年初中毕业生约为96500人,用科学记数法表示约为 。
(结果保留2位有效数字)3.(2004年岳阳市)若2(1)a -与|b+1|的值互为相反数,则a+b= .4.(2004年岳阳市)若1x ab +与212ba 的和是一个单项式,则x= 。
5.(2004年岳阳市)满足不等式1422x -+>的正整数解为 。
6.(2004年岳阳市)已知方程组x y a x y b +=⎧⎨⋅=⎩的一组解是23x y =⎧⎨=⎩,则其另外一组解是 。
7.(2004年岳阳市)已知一个角的余角是60°,则它的补角是 。
8.(2004年岳阳市)观察:11111()35235⨯=-, 11111()57257⨯=- 11111()79279⨯=- …………计算:111111112446681820⨯+⨯+⨯++⨯L = 。
9.(2004年岳阳市)如图在⊙O 中,弦AB= 半径r =4cm, 则∠BAO = 。
10.(2004年岳阳市)某超市利用“五、一”开展促销活动,店前公告如下:凡是一次性购买3件某种服装,每件仅售价80元,如超过3件,则其超过部分打8折,顾客所付款y (元)与所购买的件数x (x ≥3)之间的函数关系式为 。
二、选择题11.(2004年岳阳市)不等式组2111x x +>⎧⎪⎨≤⎪的解集在数轴上表示应为〔 〕12.(2004年岳阳市)如果分式2||256x x x --+的值等于0,则x 的值是〔 〕A :2B :-2C :-2或2D :2或313.(2004年岳阳市)下列运算正确的是〔 〕 A :235()a a = B :326(3)6a a -=C :32()a a a -÷=D :991001222⎛⎫⨯= ⎪⎝⎭14.(2004年岳阳市)下列各项正确的是〔 〕A 3π=-B :若a>b, c<0. 则ac>bcC 是最简二次根式D :分解因式:3322()ab a b ab b a -=-15.(2004年岳阳市)由小到大的一组数:1,2,x,5,6,7中,这组数的中位数是4,则x为〔 〕A :2B :3C :4D :5 16.(2004年岳阳市)下列轴对称图形中,对称轴只有2条的图形是〔 〕 A :角 B :等边三角形 C :菱形 D :圆 17.(2004年岳阳市)给出下列4 个命题,正确的个数为〔 〕①平行四边形的对角线相互垂直平分 ②两条对角线互相垂直的矩形是正方形 ③菱形的对角线互相垂直 ④对角线互相垂直的四边形是菱形 A :4 B :3 C :2 D :1 18.(2004年岳阳市)20人一行外出旅游住旅社,因特殊原因,服务员在安排房间时每间比原来多住1人,结果比原来少用了一个房间,若原来每间住x人,则x应满足的关系式为〔 〕A :202011x x -=+ B :202011x x -=- C :202011x x -=- D :202011x x-=+ 三、解答题(3×6=18分)19.(2004年岳阳市)计算:23111(2)||21)83-+-⨯-+÷20.(2004年岳阳市)化简求值:22111())2x y x y xyx y -÷+-=(其中21.(2004年岳阳市)如图在△ABC 中,已知∠B=45°,∠A=105°,AB 求BC 的长。
【中考12年】江苏省镇江市2001-中考数学试题分类解析 专题11 圆

2001-2012年江苏镇江中考数学试题分类解析汇编(12专题)专题11:圆一、选择题1. (2001江苏镇江3分)如图,PA切⊙O于A,PBC是经过圆心O的一条割线,PA=4,PB=2,则⊙O的半径等于【】A.8 B. 6 C. 4 D. 3【答案】D。
【考点】切割线定理。
【分析】设⊙O的半径为r,∵PA切⊙O于A,PBC是经过圆心O的一条割线,∴根据切割线定理得PA2=PB·PC=PB·(PB+2r)。
又∵PA=4,PB=2,∴42=2(2+2r),解得r=3。
故选D。
2. (2001江苏镇江3分)圆锥的侧面积是8лcm2,其轴截面是一个等边三角形,则该轴截面的面积是【】A.43cm 2 B. 83cm 2 C. 83лcm 2 D.43лcm 2【答案】A。
【考点】圆锥的计算,等边三角形的性质,含30度角直角三角形的性质。
【分析】如图,∵圆锥的轴截面是一个等边三角形,∴圆锥的底面直径BD=2r等于母线AB=l。
∵圆锥的侧面积是8лcm2,∴12r2r=82ππ⋅⋅,即2r=4r=2,。
由等边三角形和含30度角直角三角形的性质,可得圆锥的高∴该轴截面的面积是212r 2⋅cm 2)。
故选A 。
3. (2001江苏镇江3分)已知a 1、a 2表示直线,给出下列四个论断:①a 1∥a 2;②a 1切⊙O 于点A ;③a 2切⊙O 于点B ;④AB 是⊙O 的直径。
若以其中三个论断作为条件,余下的一个作为结论,可以构造出一些命题,在这些命题中,正确的个数为【 】 A .1个 B. 2个 C.3个 D.4个4. (2002江苏镇江3分)如图,正方形ABCD 内接于⊙O,E 为 DC 的中点,直线BE 交⊙O 于点F ,若⊙O 的半径为2,则BF 的长为【 】A 、23 B 、22 C 、556 D 、5545. (2003江苏镇江3分)一个圆锥的底面半径为52,母线长为6,则此圆锥侧面展开图扇形的圆心角的度数是【 】A 、1800B 、1500C 、1200D 、900【答案】B 。
【中考12年】江苏省南通市2001-2012年中考数学试题分类解析 专题4 图形的变换

2001-2012年某某某某中考数学试题分类解析汇编(12专题)专题4:图形的变换一、选择题1.(某某省某某市2002年3分)如图,有一块直角三角形纸片,两直角边AC=6cm, BC=8cm ,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于【】A.2cm B.3cm C.4cm D.5cm【答案】B。
【考点】折叠的性质,勾股定理。
【分析】根据勾股定理求得AB的长,再根据折叠的性质求得AE,BE的长,从而利用勾股定理可求得CD 的长:∵AC=6cm,BC=8cm,∴AB=10cm。
∵AE=6cm,∴BE=4cm。
设CD=x,则在Rt△DEB中,42+x2=(8-x)2,解得x=3(cm)。
故选B。
2.(某某省某某市2004年3分)某中学新科技馆铺设地面,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则该学校不应该购买的地砖形状是【】A、正方形B、正六边形C、正八边形D、正十二边形【答案】C。
【考点】平面镶嵌(密铺),多边形内角和定理。
【分析】根据密铺的条件得,两多边形内角和必须凑出360°,进而判断即可:A、正方形的每个内角是90°,90°×2+60°×3=360°,∴能密铺;B、正六边形每个内角是120°,120°+60°×4=360°,∴能密铺;C、正八边形每个内角是180°-360°÷8=135°,135°与60°无论怎样也不能组成360°的角,∴不能密铺;D、正十二边形每个内角是150°,150°×2+60°=360°,∴能密铺。
故选C。
3.(某某省某某市课标卷2005年2分)“圆柱与球的组合体”如下图所示,则它的三视图是【】【答案】A。
浙江省温州市2001-2012年中考数学试题分类解析 专题12 押轴题
2001-2012年浙江温州中考数学试题分类解析汇编(12专题)专题12:押轴题一、选择题1. (2001年浙江温州3分)在Rt△ABC中,∠C=90°,BC=4,AC=3,则tanA的值是【】A.43B.34C.35D.45【答案】A。
【考点】锐角三角函数定义。
【分析】根据正切函数定义,得tanA=BC4AC3。
故选A。
2. (2002年浙江温州4分)如图,在梯形ABCD中,AD∥BC,AB=DC,∠C=60°,BD平分∠ABC,如果这个梯形的周长为30,则AB的长是【】A.4 B.5 C.6 D.7【答案】C。
【考点】等腰梯形的性质,角平分线的定义,三角形内角和定理,含30度角直角三角形的性质,平行的性质,等腰三角形的判定。
【分析】∵在梯形ABCD中,AB=DC,∠C=60°,∴∠ABC=60°。
∵BD平分∠ABC,∴∠CBD=∠ABD=30°。
∴∠BDC=90°。
设AB=DC=x,则BC=2x。
∵AD∥BC,∴∠CBD=∠ADB。
∴∠ABD=∠ADB。
∴AD=AB= x。
∵梯形的周长为30,∴AD+BC+AB+DC=30,即5x=30,x=6。
故选C。
3. (2003年浙江温州4分)如图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于【】A.140° B.110° C.120° D.130°【答案】 D。
【考点】圆周角定理,圆内接四边形的性质。
【分析】设点D是优弧 AC上一点,连接AD,CD。
∵∠AOC=100°,∴∠AEC=12∠AOC=50°。
∴∠ABC=180°-∠AEC=130°。
故选D。
4. (2004年浙江温州4分)甲、乙、丙三位同学进行立定跳远比赛,每人轮流跳一次称为一轮,每轮按名次从高到低分别得3分、2分、1分(没有并列名次),他们一共进行了五轮比赛,结果甲共得14分;乙第一轮得3分,第二轮得1分,且总分最低。
【中考12年】江苏省镇江市2001-2012年中考数学试题分类解析 专题5 数量和位置变化
2001-2012年江苏镇江中考数学试题分类解析汇编(12专题)专题5:数量和位置变化一、选择题1. (2001江苏镇江3分)函数y=x 2+5x --的自变量x 的取值范围在数轴上表示应为【 】2. (2001江苏镇江3分)如图,直角三角形AOB 中,AB⊥OB,且AB =OB =3,设直线a :x=t 截此三角形所得的阴影部分的面积为S ,则S 与t 之间的函数关系的图像为【 】【答案】D 。
【考点】二次函数的图象。
【分析】由直角三角形AOB 中,AB⊥OB,且AB =OB =3,知直线a :x=t 截此三角形所得的阴影部分也为等腰直角三角形,所以()21S=a 0a 32≤≤。
则S 与t 之间的函数关系的图像为D 。
故选D 。
3. (2002江苏镇江3分)函数y=2x 1x 1+-的自变量x 的取值范围【 】 A 、 x≥-21. B 、x≠1. C、x≥-21,且x≠1. D、x >-21,且x≠1. 【答案】C 。
【考点】函数自变量的取值范围,二次根式和分式有意义的条件。
【分析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使2x 1x 1+-在实数范围内有意义,必须12x 10x 1x 2x 102x 1⎧+≥≥-⎧⎪⇒⇒≥-⎨⎨-≠⎩⎪≠⎩且x≠1。
故选C 。
4. (2005江苏镇江3分)图1是水滴进玻璃容器的示意图(滴水速度不变),图2是容器中水高度随滴水时间变化的图象.给出下列对应:(1):(a )--(e )(2):(b )--(f )(3):(c )--h (4):(d )--(g )其中正确的是【 】A .(1)和(2)B .(2)和(3)C .(1)和(3)D .(3)和(4) 【答案】B 。
【考点】跨学科问题,函数的图象【分析】根据容器的形状,判断对应的函数图象,再对题中的每一种结论进行判断:在只有容器不同的情况下,容器中水高度随滴水时间变化的图象与容器的形状有关。
【中考12年】江苏省镇江市2001-2012年中考数学试题分类解析 专题2 代数式和因式分解
2001-2012年某某某某中考数学试题分类解析汇编(12专题)专题2:代数式和因式分解一、选择题1. (2001某某某某3分)用代数式表示“比a 的平方的2倍小1的数”为【 】 A .2a 2-1 B. (2a)2-1 C. 2(a -1)2D.(2a -1)2【答案】A 。
【考点】列代数式。
【分析】a 的平方的2倍表示为2a 2,比它1的数为2a 2-1。
故选A 。
2. (2002某某某某3分)下列运算中,正确的是【 】A 、 a 2·a 4=a 8. B 、1a b --=-1a b -C 、= 、(tan300-31)0=1.【答案】C 。
【考点】同底幂乘法,分式化简,二次根式化简,0次幂的意义,特殊角的三角函数值。
【分析】根据同底幂乘法,分式化简,二次根式化简,0次幂的意义逐一计算作出判断: A. a 2·a 4=a 6,选项错误; B.11=a b a+b---,选项错误;知a <0D. ∵tan300==,∴(tan300)0无意义,选项错误。
故选C 。
3. (2003某某某某3分)下列运算正确的是【 】A 、2a 3·3ab=5a 4b B 、10-3÷102=10-1C =D 、11b a a b=--- 【答案】D 。
【考点】单项式的乘法,同底数幂的除法,二次根式的化简,分式的基本性质。
【分析】根据二次根式的化简、单项式的乘法、同底数幂的除法法则和分式的基本性质,逐一检验:A 、错误,2a 3•3ab=6a 4b ;B 、错误,10-3÷102=10-5;C 、错误,261a a 6a 393==; D 、正确。
故选D 。
4. (2004某某某某3分)下列运算中,正确的是【 】(A )11x y x y=---- (B )127 与3是同类根式 (C )236(a )a -= (D )2x 2x 1x 1-+=-5. (2004某某某某3分)如果x 3-是多项式22x 5x m -+的一个因式,则m 等于【 】(A )6 (B )6- (C )3 (D )3- 【答案】D 。
【中考12年】江苏省南京市2001-2012年中考数学试题分类解析 专题2 代数式和因式分解【中考1
2001-2012年江苏南京中考数学试题分类解析汇编(12专题)专题2:代数式和因式分解一、选择题1. (江苏省南京市2002年2分)计算a6÷a2 的结果是【】A、a3B、a4C、a8D、a12【答案】B。
【考点】同底数幂的除法。
【分析】根据同底数幂的除法法则,同底数幂相除,底数不变,指数相减计算即可:a6÷a2=a6-2=a4。
故选B。
2. (江苏省南京市2002年2分)下列二次根式中,属于最简二次根式的是【】A【答案】C。
【考点】最简二次根式。
【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件(1)被开方数的因数是整数,因式是整式; (2)被开方数中不含能开得尽方的因数或因式是否同时满足,同时满足的就是最简二次根式,否则就不是:A、,被开方数含能开得尽方的因数,不是最简二次根式;BC、满足(1)被开方数的因数是整数,因式是整式; (2)被开方数中不含能开得尽方的因数或因式,所以是最简二次根式;D、2,被开方数含能开得尽方的因数,不是最简二次根式。
故选C。
3. (江苏省南京市2003年2分)计算()32a的结果是【】(A)5a(B)6a(C)8a(D)9a【考点】幂的乘方。
【分析】根据幂的乘方,底数不变,指数相乘,计算后直接选取答案:23236a a a ⨯==()。
故选B 。
4. (江苏省南京市2003年2分) x 2-,那么x 的取值范围是【 】.(A ) x≤2 (B ) x <2 (C )x ≥ 2 (D ) x >2【答案】C 。
【考点】二次根式的性质与化简。
【分析】已知等式左边为算术平方根,结果x -2为非负数,列不等式求范围:x 2-,∴必有x -2≥0,即x≥2。
故选C 。
5. (江苏省南京市2004年2分)计算x 6÷x 3的结果是【 】 A 、x 9B 、x 3C 、x 2D 、2【答案】B 。
【考点】同底数幂的除法【分析】根据同底数幂相除,底数不变,指数相减,计算即可:x 6÷x 3=x6﹣3=x 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2001-2012年安徽省中考数学试题分类解析汇编(12专题)专题8:平面几何基础一、选择题1. (2001安徽省4分)如图,长方体中,与棱AA′平行的面是▲。
【答案】面BC′和面CD′。
【考点】认识立体图形。
【分析】在长方体中,面与棱之间的关系有平行和垂直两种,且与棱平行的面有两个:面BC′和面CD′。
2. (2001安徽省4分)如图所示,要把角钢(1)弯成120°的钢架(2),则在角钢(1)上截去的缺口是▲度。
【答案】60。
【考点】角的计算,平角的定义。
【分析】因为在截取之前的角是平角180°,截完弯折后左右两边重合,所组成的新角是120°,所以缺口角等于180°﹣120°=60°。
3. (2002安徽省4分)如图,AB、CD相交于点O,OB平分∠DOE.若∠DOE=60°,则∠AOC的度数是▲.【答案】30°。
【考点】角平分线的定义,对顶角的性质【分析】∵AB、CD相交于点O,∠DOE=60°,OB平分∠DOE,∴∠BOD=12∠DOE=12×60°=30°。
又∵∠AOC与∠BOD是对顶角,∴∠AOC=∠BOD=30°。
4. (2003安徽省4分)如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有【】A:1个B:2个C:3个D:4个【答案】C。
【考点】平行线的性质,余角和补角,对顶角的性质,直角三角形两锐角的关系。
【分析】∵AB∥CD,∴∠ABC=∠BCD。
设∠ABC的对顶角为∠1(如图),则∠ABC=∠1。
又∵AC⊥BC,∴∠ACB=90°。
∴∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°。
∴与∠CAB互余的角为∠ABC,∠BCD,∠1。
故选C。
12的是【】5. (2005安徽省课标4分)下列图中能够说明∠>∠A.B.C.D.【答案】D。
【考点】对顶角的性质,圆周角定理,直角三角形的内角,三角形的外角性质。
【分析】根据对顶角、圆周角、直角三角形的内角、三角形的外角性质等分析作出判断:A、根据对顶角相等,得∠1=∠2;B、根据同弧所对的圆周角相等,得∠1=∠2;C、直角三角形中,直角最大,则∠1<∠2;D、由于三角形的任何一个外角>和它不相邻的内角,故∠1>∠2。
故选D。
6. (2006安徽省课标4分)如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为【】A.35°B.45°C.55°D.125°【答案】A。
【考点】平行线的的性质,平角的定义。
【分析】∵a∥b,∠1=55°,∴∠3=∠1=55°(两条直线平行,同位角相等)。
又AB⊥BC,∴∠ABC=180°。
∴根据平角的定义,得∠2=180°-90°-55°=35°。
故选A。
7. (2006安徽省课标4分)如图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为【】A.36°B.42°C.45°D.48°【答案】D。
【考点】多边形内角和定理,等腰三角形的性质。
【分析】如图,折扇的顶角的度数是:360°÷3=120°,两底角的和是:180°-120°=60°,正五边形的每一个内角=(5-2)•180°÷5=108°,∴梅花图案中的五角星的五个锐角均为:108°-60°=48°。
故选D。
8. (2007安徽省4分)下列图形中,既是中心对称又是轴对称的图形是【】A.B.C.D.【答案】C。
【考点】轴对称图形和中心对称图形。
【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。
因此,A、不是轴对称图形,也不是中心对称图形;B、是轴对称图形,不是中心对称图形;C、是轴对称图形,也是中心对称图形;D、是轴对称图形,不是中心对称图形。
故选C。
9. (2009安徽省4分)如图,直线l1∥l2,则α为【】A.150°B.140°C.130°D.120°【答案】D。
【考点】平行线的性质,对顶角的性质。
【分析】∵l1∥l2,∴130°所对应的同旁内角为∠1=180°-130°=50°。
又∵α与(70°+50°)的角是对顶角,∴∠α=70°+50°=120°。
故选D。
10. (2009安徽省4分)如图,直线l1∥l2,∠1=55°,∠2=65°,则∠3为【】A.50°B.55°C.60°D.65°【答案】C。
【考点】平行线的性质,对顶角的性质,三角形内角和定理。
【分析】如图所示:∵l1∥l2,∠2=65°,∴∠6=65°。
∵∠1=55°,∴∠1=∠4=55°。
在△ABC中,∠6=65°,∠4=55°,∴∠3=180°-65°-55°=60°。
故选C。
二、填空题1. (2002安徽省4分)下列图案既是中心对称,又是轴对称的是【】A.B.C.D.【答案】D。
【考点】轴对称图形和中心对称图形。
【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。
因此,A.是轴对称图形,不是中心对称图形;B.既不是轴对称图形,也不是中心对称图形;C.不是轴对称图形,是中心对称图形;D.既是轴对称图形,也是中心对称图形。
故选D。
2. (2004安徽省4分)(华东版教材实验区试题)如图,已知AB∥DE,∠ABC=80°,∠CDE=140°,则∠BCD= ▲.【答案】40°。
【考点】平行线的的性质,平角定义,三角形的外角性质。
【分析】如图,反向延长DE交BC于M,∵AB∥DE,∠ABC=80°,∴∠BMD=∠ABC=80°。
∴∠CMD=180°-∠BMD=100°。
又∵∠CDE=∠CMD+∠C,∠CDE=140°,∴∠BCD=∠CDE-∠CMD=140°-100°=40°。
3. (2007安徽省5分)如图,已知∠1=100°,∠2=140°,那么∠3= ▲度。
【答案】60。
【考点】多边形的外角性质,平角定义。
【分析】根据多边形的外角性质,三角形三个外角的和为360°,因此,如图,∵∠4=360°-∠1-∠2=360°-100°-140°=120°,∴∠3=180°-120°=60°。
4. (2008安徽省5分)如图,已知a∥b,∠1=70°,∠2=40°,则∠3= ▲。
【答案】70°。
【考点】平行线的性质,对顶性质,三角形内角和定理。
【分析】由对顶角相等可得∠ACB=∠2=40°。
在△ABC中,由三角形内角和知∠ABC=180°-∠1-∠ACB=70°。
又∵a∥b,∴∠3=∠ABC=70°。
三、解答题1. (2003安徽省10分)如图,在五边形A1A2A3A4A5中,B1是A1对边A3A4的中点,连结A1B1,我们称A1B1是这个五边形的一条中对线。
如果五边形的每条中对线都将五边形的面积分成相等的两部分。
求证:五边形的每条边都有一条对角线和它平行。
【答案】证明:取A 1A 5中点B 3,连接A 3B 3、A 1A 3、A 1A 4、A 3A 5,∵A 3B 1=B 1A 4,∴131114A A B A B A S S ∆∆=。
又∵四边形A 1A 2A 3B 1与四边形A 1B 1A 4A 5的面积相等, ∴123145A A A A A A S S ∆∆=。
同理123345A A A A A A S S ∆∆=。
∴145345A A A A A A S S ∆∆=。
∴△A 3A 4A 5与△A 1A 4A 5边A 4A 5上的高相等。
∴A 1A 3∥A 4A 5。
同理可证A 1A 2∥A 3A 5,A 2A 3∥A 1A 4,A 3A 4∥A 2A 5,A 5A1∥A 2A 4。
