2014届高三数学试题(理科)
2014届高三年级12月月考 数学试题
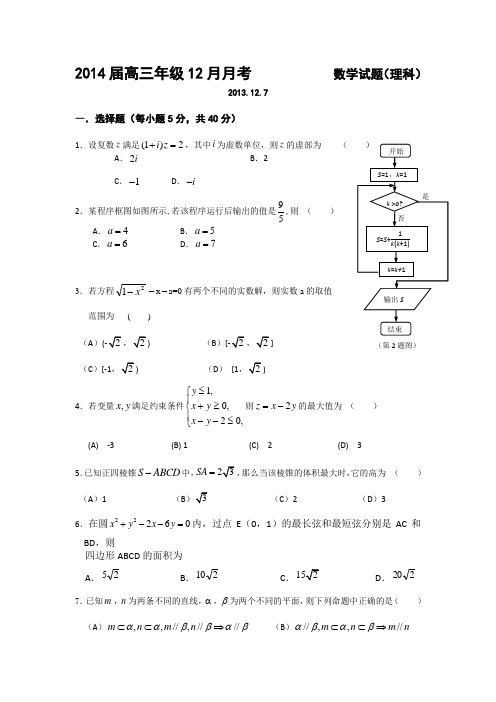
2014届高三年级12月月考 数学试题(理科)2013.12.7一.选择题(每小题5分,共40分)1.设复数z 满足(1)2i z +=,其中i 为虚数单位,则z 的虚部为 (A .2iB .2C .1-D .i -2.某程序框图如图所示,若该程序运行后输出的值是59,则 ( ) A .4=a B .5=aC .6=aD .7=a3.若方程21x--x -a=0有两个不同的实数解,则实数a 的取值范围为 ( )(A ) (B )] (C )[-1 (D ) [1)4.若变量,x y 满足约束条件1,0,20,y x y x y ≤⎧⎪+≥⎨⎪--≤⎩则2z x y =-的最大值为 ( )(A) -3 (B) 1 (C) 2 (D) 35.已知正四棱锥S ABCD -中,SA =,那么当该棱锥的体积最大时,它的高为 ( )(A )1 (B (C )2 (D )3 6.在圆22260x y x y +--=内,过点E (0,1)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为A .25B .210C .D .2207.已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( ) (A ),,//,////m n m n ααββαβ⊂⊂⇒ (B )//,,//m n m n αβαβ⊂⊂⇒(第2题图)(C ),//m m n n αα⊥⊥⇒ (D )//,m n n m αα⊥⇒⊥8.已知圆O 的半径为1,PA 、PB 为该圆的两条切线,A 、B 为两切点,那么PA PB ∙的最小值为( )(A) 3-+(B)3-(C) 4-+ (D)4-+二.填空题(每小题5分,共30分)9.若函数()f x ax b =-的零点是1, 则2()g x bx ax =-的零点是 .10.例6. 某几何体的三视图如图所示,则它的体积为______11.直线2cos 1ρθ=与圆2cos ρθ=相交的弦长为 .12.设f(x)是定义在R 上的奇函数,且当x ≤0时,f(x)=-x 2,若对任意的x ∈[t ,t +2],不等式f(x+t) ≥2f(x)恒成立,则实数t 的取值范围为__ 13.在直角坐标系xOy 中,M 是曲线1C :1,12x t y t =+⎧⎨=-⎩(t 为参数)上任意一点,N 是曲线2C :1cos ,sin x y θθ=-+⎧⎨=⎩(θ为参数)上任意一点,则MN 的最小值为 .14.已知关于x 的方程x 3+ax 2+bx+c=0有三个实数根可作为一个椭圆、一个双曲线、一个抛物线的离心率(抛物线的离心率为1),则1a 1+-b 的取值范围为 三.解答题(共80分)15.(本小题共13分)已知函数2()22sin f x x x =-. (Ⅰ)求函数()f x 的最大值; (II )求函数()f x 的零点的集合。
湖南省桑植一中皇仓中学2014届高三第一次联考(9月)数学试题(理科) word版含答案

湖南省桑植一中皇仓中学2014届高三第一次联考(9月)数学试卷 理 科第Ⅰ卷(选择题,共40分)一、本大题8小题,每小题5分,共40分。
在每小题给出的四个选项中,选出符合题目要求的一项。
1.若复数2()()x x x iz x R i+-=∈为纯虚数,则x 等于( )A .0B .1C .-1D .0或12.给出下列三个命题: ①2,0;x R x ∀∈>②2000,x R x x ∃∈≤使得成立;③对于集合,,M N x M N ∈若,则.x M x N ∈∈且其中真命题的个数是( )A .0B .1C .2D .33.沿一个正方体三个方面的对角线截得的几何体如图所示,则该几何体的左视图为( )4.“13x -<<”是“0)3(<-x x 成立”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.已知正整数列{}n a 中,22212111,2,2(2)n n n a a a a a n +-===+≥,则6a 等于( )A .16B .8C.D .46.已知双曲线22221(0,0)x y a b a b-=>>,过其右焦点且垂直于实轴的直线与双曲线交于M ,N 两点,O为坐标原点,若OM ON ⊥,则双曲线的离心率为 ( )ABCD7.ABC ∆外接圆的半径为1,圆心为O ,且20,||||OA AB AC OA AB ++==,则CA CB ⋅等于( )A .32BC .3D.8.已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数[()1]y f f x =+的零点个数是( )A .4B .3C .2D .1第Ⅱ卷(共110分)二、填空题:本大题共7小题,每小题5分,共35分。
9.251()x x+的展开式中,4x 的系数为 。
(用数字作答)10.某地为了调查职业满意度,决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中,抽取若干人组成调查小组,有关数据见下表,则调查小组的总人数为 ;若从调查小组中的公务员和教师中随机选2人撰写调查报告,则其中恰好有1人来自公务员的概率11.在ABC ∆中,若,,4B bC ∠==∠则= 。
鄂州市2014届高三摸底考试数学(理科)试题

鄂州市2014届高三摸底考试数学试题(理科)命题人:廖红武 审题人:林春宝注意事项:1、答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卷上,并将准考证号条形码粘贴在答题卡上的指定位置。
2、选择题的作答:每小题选出答案后,用统一提供的2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3、非选择题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4、考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:(每小题5分,共50分)1.已知集合}0,0{},1log {2><<=<=c c x x B x x A ,若B B A =⋃,则c 的取值范围是 A .(]1,0B .[)+∞,1C .(]2,0D .[)+∞,22.化简[]()02161)2(---的结果是A .-9B .7C .-10D .93.由曲线x y =,直线2-=x y 及y 轴所围成的图形面积为A .310B .4C .316 D .64.曲线13-+=bx ax y 在点(1,f(1))处的切线方程为=-=a b x y 则, A .-3 B .4 C .3 D .6 5.等比数列{a n }的前n 项和S n ,已知S 3=a 2+10a 1,a 5=9,则a 1= A .31B .31-C .91D .91-6.若3sin θ+cos θ=0,则θθ2sin cos 12+的值为A .310 B .31 C .32 D .-27.设a ,b ,c ,x ,y ,z 是正数,且a 2+b 2+c 2=10,x 2+y 2+z 2=40,ax +by +cz =20,则z y x cb a ++++=A .41B .31C .21 D .43 8.将函数y =sin(2x +φ)的图象沿x 轴向左平移8π个单位后得到一个偶函数的图象,则φ的一个可能取值为 A .π43B .π41C .0D .π41-9.放射性元素由于不断有原子放射出微粒子而变成其它元素,其含量不断减少,这种现象称为衰变。
2014年高考真题——理科数学(全国大纲卷)解析版 Word版含解析

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.设103i z i=+,则z 的共轭复数为 ( )A .13i -+B .13i --C .13i +D .13i -2.设集合2{|340}M x x x =--<,{|05}N x x =≤≤,则M N =I ( )A .(0,4]B .[0,4)C .[1,0)-D .(1,0]-3.设sin 33,cos55,tan 35,a b c =︒=︒=︒则 ( )A .a b c >>B .b c a >>C .c b a >>D .c a b >>4.若向量,a b r r 满足:()()1,,2,a a b a a b b =+⊥+⊥r r r r r r r 则b =r ( )A .2B .2C .1D .225.有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )A .60种B .70种C .75种D .150种6.已知椭圆C :22221x y a b +=(0)a b >>的左、右焦点为1F 、2F 3,过2F 的直线l 交C 于A 、B 两点,若1AF B ∆的周长为43C 的方程为 ( )A .22132x y +=B .2213x y +=C .221128x y +=D .221124x y +=7.曲线1x y xe-=在点(1, 1)处切线的斜率等于( ) A .2e B .e C .2 D .18.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( )A .814πB .16πC .9πD .274π 【答案】A .【解析】考点:1.球的内接正四棱锥问题;2. 球的表面积的计算.9.已知双曲线C 的离心率为2,焦点为1F 、2F ,点A 在C 上,若122F A F A =,则21cos AF F ∠=( )A .14B .13C .24D .23 10.等比数列{}n a 中,452,5a a ==,则数列{lg }n a 的前8项和等于 ( )图2A .6B .5C .4D .311.已知二面角l αβ--为60︒,AB α⊂,AB l ⊥,A 为垂足,CD β⊂,C l ∈,135ACD ∠=︒,则异面直线AB 与CD 所成角的余弦值为 ( )A .14B 2C 3D .12【答案】B.【解析】12.函数()y f x =的图象与函数()y g x =的图象关于直线0x y +=对称,则()y f x =的反函数是( )A .()y g x =B .()y g x =-C .()y g x =-D .()y g x =--第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 8y x 的展开式中22x y 的系数为 . 【答案】70.14.设,x y 满足约束条件02321x y x y x y -≥⎧⎪+≤⎨⎪-≤⎩,则4z x y =+的最大值为.15.直线1l 和2l 是圆222x y +=的两条切线,若1l 与2l 的交点为()1,3,则1l 与2l 的夹角的正切值等于 .2l的夹角的正切值:12124 tan13k kk kθ-==+.考点:1.直线与圆的位置关系(相切);2.两直线的夹角公式.16.若函数()cos2sinf x x a x=+在区间(,)62ππ是减函数,则a的取值范围是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分)ABC∆的内角A,B,C的对边分别为a,b,c,已知3cos2cosa C c A=,1tan3A=,求B.18. (本小题满分12分)等差数列{}na的前n项和为nS,已知110a=,2a为整数,且4nS S≤.(I )求{}n a 的通项公式; (II )设11n n n b a a +=,求数列{}n b 的前n 项和n T . 19. (本小题满分12分) 如图,三棱柱111ABC A B C -中,点1A 在平面ABC 内的射影D 在AC 上,090ACB ∠=,11,2BC AC CC ===. (I )证明:11AC A B ⊥; (II )设直线1AA 与平面11BCC B 31A AB C --的大小.20. (本小题满分12分)设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立.(I)求同一工作日至少3人需使用设备的概率;(II)X表示同一工作日需使用设备的人数,求X的数学期望.21.(本小题满分12分)已知抛物线C :22(0)y px p =>的焦点为F ,直线4y =与y 轴的交点为P ,与C 的交点为Q ,且5||||4QF PQ =. (I )求C 的方程;(II )过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l '与C 相较于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.【答案】(I )24y x =;(II )直线l 的方程为10x y --=或10x y +-=.22. (本小题满分12分)函数()()()ln 11ax f x x a x a=+->+. (I )讨论()f x 的单调性;(II )设111,ln(1)n n a a a +==+,证明:23+22n a n n <≤+. 【答案】(I )(i )当12a <<时,()f x 在()21,2a a --上是增函数,在()22,0a a -上是减函数,在()0,+∞上是增函数;(ii )当2a =时,()f x 在()1,-+?上是增函数;(iii )当2a >时,()f x 在是()1,0-上是增函数,在()20,2a a -上是减函数,在()22,a a -+∞上是增函数;(II)详见试题分析.1n k=+时有2333kak k<?++,结论成立.根据(i)、(ii)知对任何n N*Î结论都成立.考点:1.利用导数研究函数的单调性;2.利用数学归纳法证明数列不等式.。
2014年辽宁省高考数学试卷(理科)答案与解析

2014年辽宁省高考数学试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2014•辽宁)已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=()A.{x|x≥0} B.{x|x≤1} C.{x|0≤x≤1} D.{x|0<x<1}考点:交、并、补集的混合运算.专题:集合.分析:先求A∪B,再根据补集的定义求C U(A∪B).解答:解:A∪B={x|x≥1或x≤0},∴C U(A∪B)={x|0<x<1},故选:D.点评:本题考查了集合的并集、补集运算,利用数轴进行数集的交、并、补运算是常用方法.2.(5分)(2014•辽宁)设复数z满足(z﹣2i)(2﹣i)=5,则z=()A.2+3i B.2﹣3i C.3+2i D.3﹣2i考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:把给出的等式两边同时乘以,然后利用复数代数形式的除法运算化简,则z可求.解答:解:由(z﹣2i)(2﹣i)=5,得:,∴z=2+3i.故选:A.点评:本题考查了复数代数形式的除法运算,是基础的计算题.3.(5分)(2014•辽宁)已知a=,b=log2,c=log,则()A.a>b>c B.a>c>b C.c>a>b D.c>b>a考点:对数的运算性质.专题:计算题;综合题.分析:利用指数式的运算性质得到0<a<1,由对数的运算性质得到b<0,c>1,则答案可求.解答:解:∵0<a=<20=1,b=log2<log21=0,c=log=log23>log22=1,∴c>a>b.故选:C.点评:本题考查指数的运算性质和对数的运算性质,在涉及比较两个数的大小关系时,有时借助于0、1这样的特殊值能起到事半功倍的效果,是基础题.4.(5分)(2014•辽宁)已知m,n表示两条不同直线,α表示平面,下列说法正确的是()A.若m∥α,n∥α,则m∥n B.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α考点:空间中直线与直线之间的位置关系.专题:空间位置关系与距离.分析:A.运用线面平行的性质,结合线线的位置关系,即可判断;B.运用线面垂直的性质,即可判断;C.运用线面垂直的性质,结合线线垂直和线面平行的位置即可判断;D.运用线面平行的性质和线面垂直的判定,即可判断.解答:解:A.若m∥α,n∥α,则m,n相交或平行或异面,故A错;B.若m⊥α,n⊂α,则m⊥n,故B正确;C.若m⊥α,m⊥n,则n∥α或n⊂α,故C错;D.若m∥α,m⊥n,则n∥α或n⊂α或n⊥α,故D错.故选B.点评:本题考查空间直线与平面的位置关系,考查直线与平面的平行、垂直的判断与性质,记熟这些定理是迅速解题的关键,注意观察空间的直线与平面的模型.5.(5分)(2014•辽宁)设,,是非零向量,已知命题p:若•=0,•=0,则•=0;命题q:若∥,∥,则∥,则下列命题中真命题是()A.p∨q B.p∧q C.(¬p)∧(¬q)D.p∨(¬q)考点:复合命题的真假;平行向量与共线向量.专题:简易逻辑.分析:根据向量的有关概念和性质分别判断p,q的真假,利用复合命题之间的关系即可得到结论.解答:解:若•=0,•=0,则•=•,即(﹣)•=0,则•=0不一定成立,故命题p为假命题,若∥,∥,则∥平行,故命题q为真命题,则p∨q,为真命题,p∧q,(¬p)∧(¬q),p∨(¬q)都为假命题,故选:A.点评:本题主要考查复合命题之间的判断,利用向量的有关概念和性质分别判断p,q的真假是解决本题的关键.6.(5分)(2014•辽宁)6把椅子排成一排,3人随机就座,任何两人不相邻的坐法种数为()A.144 B.120 C.72 D.24考点:计数原理的应用.专题:应用题;排列组合.分析:使用“插空法“.第一步,三个人先坐成一排,有种,即全排,6种;第二步,由于三个人必须隔开,因此必须先在1号位置与2号位置之间摆放一张凳子,2号位置与3号位置之间摆放一张凳子,剩余一张凳子可以选择三个人的左右共4个空挡,随便摆放即可,即有种办法.根据分步计数原理可得结论.解答:解:使用“插空法“.第一步,三个人先坐成一排,有种,即全排,6种;第二步,由于三个人必须隔开,因此必须先在1号位置与2号位置之间摆放一张凳子,2号位置与3号位置之间摆放一张凳子,剩余一张凳子可以选择三个人的左右共4个空挡,随便摆放即可,即有种办法.根据分步计数原理,6×4=24.故选:D.点评:本题考查排列知识的运用,考查乘法原理,先排人,再插入椅子是关键.7.(5分)(2014•辽宁)某几何体三视图如图所示,则该几何体的体积为()A.8﹣2πB.8﹣πC.8﹣D.8﹣考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:几何体是正方体切去两个圆柱,根据三视图判断正方体的棱长及切去的圆柱的底面半径和高,把数据代入正方体与圆柱的体积公式计算.解答:解:由三视图知:几何体是正方体切去两个圆柱,正方体的棱长为2,切去的圆柱的底面半径为1,高为2,∴几何体的体积V=23﹣2××π×12×2=8﹣π.故选:B.点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.8.(5分)(2014•辽宁)设等差数列{a n}的公差为d,若数列{}为递减数列,则()A.d<0 B.d>0 C.a1d<0 D.a1d>0考点:数列的函数特性.专题:函数的性质及应用;等差数列与等比数列.分析:由于数列{2}为递减数列,可得=<1,解出即可.解答:解:∵等差数列{a n}的公差为d,∴a n+1﹣a n=d,又数列{2}为递减数列,∴=<1,∴a1d<0.故选:C.点评:本题考查了等差数列的通项公式、数列的单调性、指数函数的运算法则等基础知识与基本技能方法,属于中档题.9.(5分)(2014•辽宁)将函数y=3sin(2x+)的图象向右平移个单位长度,所得图象对应的函数()A.在区间[,]上单调递减B.在区间[,]上单调递增C.在区间[﹣,]上单调递减D.在区间[﹣,]上单调递增考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:直接由函数的图象平移得到平移后的图象所对应的函数解析式,然后利用复合函数的单调性的求法求出函数的增区间,取k=0即可得到函数在区间[,]上单调递增,则答案可求.解答:解:把函数y=3sin(2x+)的图象向右平移个单位长度,得到的图象所对应的函数解析式为:y=3sin[2(x﹣)+].即y=3sin(2x﹣).当函数递增时,由,得.取k=0,得.∴所得图象对应的函数在区间[,]上单调递增.故选:B.点评:本题考查了函数图象的平移,考查了复合函数单调性的求法,复合函数的单调性满足“同增异减”原则,是中档题.10.(5分)(2014•辽宁)已知点A(﹣2,3)在抛物线C:y2=2px的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为()A.B.C.D.考点:直线与圆锥曲线的关系.专题:圆锥曲线的定义、性质与方程.分析:由题意先求出准线方程x=﹣2,再求出p,从而得到抛物线方程,写出第一象限的抛物线方程,设出切点,并求导,得到切线AB的斜率,再由两点的斜率公式得到方程,解出方程求出切点,再由两点的斜率公式求出BF的斜率.解答:解:∵点A(﹣2,3)在抛物线C:y2=2px的准线上,即准线方程为:x=﹣2,∴p>0,=﹣2即p=4,∴抛物线C:y2=8x,在第一象限的方程为y=2,设切点B(m,n),则n=2,又导数y′=2,则在切点处的斜率为,∴即m=2m,解得=2(舍去),∴切点B(8,8),又F(2,0),∴直线BF的斜率为,故选D.点评:本题主要考查抛物线的方程和性质,同时考查直线与抛物线相切,运用导数求切线的斜率等,是一道基础题.11.(5分)(2014•辽宁)当x∈[﹣2,1]时,不等式ax3﹣x2+4x+3≥0恒成立,则实数a的取值范围是()C.[﹣6,﹣2]D.[﹣4,﹣3] A.[﹣5,﹣3]B.[﹣6,﹣]考点:函数恒成立问题;其他不等式的解法.专题:综合题;导数的综合应用;不等式的解法及应用.分析:分x=0,0<x≤1,﹣2≤x<0三种情况进行讨论,分离出参数a后转化为函数求最值即可,利用导数即可求得函数最值,注意最后要对a取交集.解答:解:当x=0时,不等式ax3﹣x2+4x+3≥0对任意a∈R恒成立;当0<x≤1时,ax3﹣x2+4x+3≥0可化为a≥,令f(x)=,则f′(x)==﹣(*),当0<x≤1时,f′(x)>0,f(x)在(0,1]上单调递增,f(x)max=f(1)=﹣6,∴a≥﹣6;当﹣2≤x<0时,ax3﹣x2+4x+3≥0可化为a≤,由(*)式可知,当﹣2≤x<﹣1时,f′(x)<0,f(x)单调递减,当﹣1<x<0时,f′(x)>0,f(x)单调递增,f(x)min=f(﹣1)=﹣2,∴a≤﹣2;综上所述,实数a的取值范围是﹣6≤a≤﹣2,即实数a的取值范围是[﹣6,﹣2].故选:C.点评:本题考查利用导数研究函数的最值,考查转化思想、分类与整合思想,按照自变量讨论,最后要对参数范围取交集;若按照参数讨论则取并集.12.(5分)(2014•辽宁)已知定义在[0,1]上的函数f(x)满足:①f(0)=f(1)=0;②对所有x,y∈[0,1],且x≠y,有|f(x)﹣f(y)|<|x﹣y|.若对所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,则m的最小值为()A.B.C.D.考点:函数恒成立问题;绝对值不等式的解法.专题:综合题;函数的性质及应用.分析:依题意,构造函数f(x)=(0<k<),分x∈[0,],且y∈[0,];x∈[0,],且y∈[,1];x∈[0,],且y∈[,1];及当x∈[,1],且y∈[,1]时,四类情况讨论,可证得对所有x,y∈[0,1],|f(x)﹣f(y)|<恒成立,从而可得m≥,继而可得答案.解答:解:依题意,定义在[0,1]上的函数y=f(x)的斜率|k|<,依题意,k>0,构造函数f(x)=(0<k<),满足f(0)=f(1)=0,|f(x)﹣f(y)|<|x﹣y|.当x∈[0,],且y∈[0,]时,|f(x)﹣f(y)|=|kx﹣ky|=k|x﹣y|≤k|﹣0|=k×<;当x∈[0,],且y∈[,1],|f(x)﹣f(y)|=|kx﹣(k﹣ky)|=|k(x+y)﹣k|≤|k(1+)﹣k|=<;当y∈[0,],且x∈[,1]时,同理可得,|f(x)﹣f(y)|<;当x∈[,1],且y∈[,1]时,|f(x)﹣f(y)|=|(k﹣kx)﹣(k﹣ky)|=k|x﹣y|≤k×(1﹣)=<;综上所述,对所有x,y∈[0,1],|f(x)﹣f(y)|<,∵对所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,∴m≥,即m的最小值为.故选:B.点评:本题考查函数恒成立问题,着重考查构造函数思想、分类讨论思想、函数方程思想与等价转化思想的综合运用,考查分析、推理及运算能力,属于难题.二、填空题:本大题共4小题,每小题5分。
2014届高三数学试题

江西省2014届高三数学试题(理科)(测试时间:120分钟 卷面总分:150分)一.选择题(每小题5分,共50分)1.设集合]}5,5[,sin 2|{-∈==x x y y M ,}lg |{)1(2-==x y x N ,则=N M ( )A . }51|{≤<x xB . }01|{≤<-x xC . }02|{≤≤-x xD . }21|{≤<x x2.设5.03=a ,35log =b ,3cos =c ,则( )A .c b a <<B . b a c <<C .a b c <<D .a c b <<3.函数),(4sin )(322R b a bx x a x f ∈++=,若2013)20141(lg =f ,则=)(lg 2014f ( ) A .2018 B .-2009 C .2013 D .-20134.要得到函数)32cos(π+=x y 的图像,只需将函数x x y 2cos 232sin 21+=的图像( ) A .向左平移4π B .向左平移8π C .向右平移2π D .向右平移3π 5.在等差数列}{n a 中,首项a 1=0,公差d ≠0,若7321a a a a a k ++++= ,则k=( )A .22B .23C .24D .256.设R y x ∈,,向量)1,(x a =,),1(y =,)4,2(-=,且⊥,c b //,则=+||( ) A .5 B .10 C .52 D .107.已知m 和n 是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m ⊥β的是( )A .α⊥β且α⊂mB .α⊥β且α//mC .n m //且n ⊥βD .m ⊥n 且βα//8.在ABC ∆中,若)sin()cos(21)sin(C A C B B A +++=-,则ABC ∆的形状一定是( )A .等边三角形B .不含60°的等腰三角形C .钝角三角形D .直角三角形第13题 第14题9.定义域为R 的连续函数)(x f ,对任意x 都有)2()2(x f x f -=+,且其导函数)(x f '满足0)()2(>'-x f x ,则当42<<a 时,有( )A .)(log )2()2(2a a f f f <<B .)(log )2()2(2a a f f f <<C .)2()2()(log 2f f f a a<< D .)2()(log )2(2a a f f f <<10.已知函数,1log )10(sin )(2014⎪⎩⎪⎨⎧>≤≤=x x x x f x π若a 、b 、c 互不相等,且)()()(c f b f a f ==,则a +b +c 的取值范围是( )A .(1,2014)B .(1,2015)C .(2,2015)D .[2,2015]二.填空题(每小题5分,共25分)11.若x x x x f ln 42)(2--=,则0)(>'x f 的解集为 。
河南省中原名校2014届高三高考仿真模拟统一考试 数学(理)扫描版试题Word版答案
中原名校2014年高考仿真模拟统一考试数学试题(理科)参考答案一、选择题1. D2. B3. C4. C5. A6. A7. D8. D9. A 10. C 11. C 12. B 二、填空题13. -784 14. 43- 15. 16π 16. 100711134⎛⎫- ⎪⎝⎭三.解答题.17、解(1)设三边分别为,,a b c由cos sinB sinC A =可得cos 02C C π=⇒=又cos 9162AB AC AB AC A S AB AC inA ⎧⋅⎪⎨=⎪⎩=||||==||||s 两式相除可得4tan 3aA b== 令4,3(0)a k b k k ==> 则1612S ab k ==⇒=∴三边长分别为3,4,5,………………(8分)(2)有两角差的正切公式可得tan BAD ∠=913…………(12分)18. 甲取胜的概率为32233323()()()5555P A C =+⋅⋅ =297625………………(4分)(2)224(3)()525P X ===132232351(4)()5555125P X C ==⋅⋅+=12223323232354(5)()()555555125P X C C ==⋅⋅+⋅⋅= X ∴的分布列为:534125EX ∴=………………………………….12分所以:平面ABCD ⊥平面AED ;………..5分1(0,1,0),0)2A B D -(3,0,1)AF =-则cos ,AF m <>=所以cos θ=………………(12分)20.解:(1)由题意22421,c e a a b==+= 又222,a b c =+解得228,4a b ==,故椭圆的标准方程为221.84x y += ................ (4分)(2)设直线AB 的方程为1122,(,),(,),y kx m A x y B x y =+联立2228y kx m x y =+⎧⎨+=⎩,得222(12)4280,k x kmx m +++-= 22222(4)4(12)(28)8(84)0,km k m k m ∆=-+-=-+>① 1222122412.2812km x x k m x x k -⎧+=⎪⎪+⎨-⎪=⎪+⎩2122122212122211,,2211284.221212AC BDy y b k k a x x m m y y x x k k⋅=-=-∴=---∴=-=-⋅=-++又1212()()y y kx m kx m =++22121222222222()28412128,12k x x km x x m m km k km mk k m k k=+++--=++++-=+ 222222222248,(4)8,121242.m m k m m k k kk m --∴-=∴--=-++∴+=……………….. (8分) (ⅰ)222212122222284442412121212m m m k OA OB x x y y k k k k ---+-⋅=+=-==++++ 242,12k =-+224 2.OA OB ∴-=-≤⋅<当0k =(此时22m =满足①式),即直线AB 平行于x 轴时,OA OB ⋅的最小值为-2.又直线AB 的斜率不存在时,2OA OB ⋅=,∴OA OB ⋅的最大值为2. (ⅱ)设原点到直线AB 的距离为d ,则211||2||AOB S AB d x x ∆=⋅=-=====∴S 四边形ABCD = 4S ΔAOB=即四边形ABCD 的面积为定值. ………………………….(12分)1,2EBC OCD EB OC AB ∴∆≅∆∴==E ∴是AB 的中点。
(完整版)2014年北京市高考数学试卷(理科)答案与解析
2014年北京市高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项)1.(5分)(2014•北京)已知集合A={x|x2﹣2x=0},B={0,1,2},则A∩B=()A.{0} B.{0,1} C.{0,2} D.{0,1,2}考点:交集及其运算.专题:集合.分析:解出集合A,再由交的定义求出两集合的交集.解答:解:∵A={x|x2﹣2x=0}={0,2},B={0,1,2},∴A∩B={0,2}故选C点评:本题考查交的运算,理解好交的定义是解答的关键.2.(5分)(2014•北京)下列函数中,在区间(0,+∞)上为增函数的是()A.y=B.y=(x﹣1)2C.y=2﹣x D.y=log0.5(x+1)考点:对数函数的单调性与特殊点.专题:函数的性质及应用.分析:根据基本初等函数的单调性,判断各个选项中函数的单调性,从而得出结论.解答:解:由于函数y=在(﹣1,+∞)上是增函数,故满足条件,由于函数y=(x﹣1)2在(0,1)上是减函数,故不满足条件,由于函数y=2﹣x在(0,+∞)上是减函数,故不满足条件,由于函数y=log0.5(x+1)在(﹣1,+∞)上是减函数,故不满足条件,故选:A.点评:本题主要考查函数的单调性的定义和判断,基本初等函数的单调性,属于基础题.3.(5分)(2014•北京)曲线(θ为参数)的对称中心()A.在直线y=2x上B.在直线y=﹣2x上C.在直线y=x﹣1上D.在直线y=x+1上考点:圆的参数方程.专题:选作题;坐标系和参数方程.分析:曲线(θ为参数)表示圆,对称中心为圆心,可得结论.解答:解:曲线(θ为参数)表示圆,圆心为(﹣1,2),在直线y=﹣2x上,点评:本题考查圆的参数方程,考查圆的对称性,属于基础题.4.(5分)(2014•北京)当m=7,n=3时,执行如图所示的程序框图,输出的S的值为()A.7B.42 C.210 D.840考点:循环结构.专题:计算题;算法和程序框图.分析:算法的功能是求S=7×6×…×k的值,根据条件确定跳出循环的k值,计算输出S的值.解答:解:由程序框图知:算法的功能是求S=7×6×…×k的值,当m=7,n=3时,m﹣n+1=7﹣3+1=5,∴跳出循环的k值为4,∴输出S=7×6×5=210.故选:C.点评:本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答本题的关键.5.(5分)(2014•北京)设{a n}是公比为q的等比数列,则“q>1”是“{a n}”为递增数列的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断;等比数列.专题:等差数列与等比数列;简易逻辑.分析:根据等比数列的性质,结合充分条件和必要条件的定义进行判断即可得到结论.解答:解:等比数列﹣1,﹣2,﹣4,…,满足公比q=2>1,但“{a n}”不是递增数列,充分性不成立.若a n=﹣1为递增数列,但q=>1不成立,即必要性不成立,故“q>1”是“{a n}”为递增数列的既不充分也不必要条件,点评:本题主要考查充分条件和必要条件的判断,利用等比数列的性质,利用特殊值法是解决本题的关键.6.(5分)(2014•北京)若x,y满足且z=y﹣x的最小值为﹣4,则k的值为()A.2B.﹣2 C.D.﹣考点:简单线性规划.专题:数形结合;不等式的解法及应用.分析:对不等式组中的kx﹣y+2≥0讨论,当k≥0时,可行域内没有使目标函数z=y﹣x取得最小值的最优解,k<0时,若直线kx﹣y+2=0与x轴的交点在x+y﹣2=0与x轴的交点的左边,z=y﹣x的最小值为﹣2,不合题意,由此结合约束条件作出可行域,化目标函数为直线方程的斜截式,由图得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.解答:解:对不等式组中的kx﹣y+2≥0讨论,可知直线kx﹣y+2=0与x轴的交点在x+y﹣2=0与x轴的交点的右边,故由约束条件作出可行域如图,由kx﹣y+2=0,得x=,∴B(﹣).由z=y﹣x得y=x+z.由图可知,当直线y=x+z过B(﹣)时直线在y轴上的截距最小,即z最小.此时,解得:k=﹣.故选:D.点评:本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.7.(5分)(2014•北京)在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C (0,2,0),D(1,1,),若S1,S2,S3分别表示三棱锥D﹣ABC在xOy,yOz,zOx 坐标平面上的正投影图形的面积,则()A.S1=S2=S3B.S2=S1且S2≠S3C.S3=S1且S3≠S2D.S3=S2且S3≠S1考点:空间直角坐标系.专题:空间向量及应用.分析:分别求出三棱锥在各个面上的投影坐标即可得到结论.解答:解:设A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,),则各个面上的射影分别为A',B',C',D',在xOy坐标平面上的正投影A'(2,0,0),B'(2,2,0),C'(0,2,0),D'(1,1,0),S1=.在yOz坐标平面上的正投影A'(0,0,0),B'(0,2,0),C'(0,2,0),D'(0,1,),S2=.在zOx坐标平面上的正投影A'(2,0,0),B'(2,0,0),C'(0,0,0),D'(1,0,),S3=,则S3=S2且S3≠S1,故选:D.点评:本题主要考查空间坐标系的应用,求出点对于的投影坐标是解决本题的关键.8.(5分)(2014•北京)学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,则这一组学生最多有()A.2人B.3人C.4人D.5人考点:进行简单的合情推理.专题:推理和证明.分析:分别用ABC分别表示优秀、及格和不及格,根据题干中的内容推出文成绩得A,B,C的学生各最多只有1个,继而推得学生的人数.解答:解:用ABC分别表示优秀、及格和不及格,显然语文成绩得A的学生最多只有1个,语文成绩得B得也最多只有一个,得C最多只有一个,因此学生最多只有3人,显然(AC)(BB)(CA)满足条件,故学生最多有3个.故选:B.点评:本题主要考查了合情推理,关键是找到语句中的关键词,培养了推理论证的能力.二、填空题(共6小题,每小题5分,共30分)9.(5分)(2014•北京)复数()2=﹣1.考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:由复数代数形式的除法运算化简括号内部,然后由虚数单位i的运算性质得答案.解答:解:()2=.故答案为:﹣1.点评:本题考查了复数代数形式的除法运算,考查了虚数单位i的运算性质,是基础题.10.(5分)(2014•北京)已知向量,满足||=1,=(2,1),且+=(λ∈R),则|λ|=.考点:平面向量数量积的坐标表示、模、夹角.专题:平面向量及应用.分析:设=(x,y).由于向量,满足||=1,=(2,1),且+=(λ∈R),可得,解出即可.解答:解:设=(x,y).∵向量,满足||=1,=(2,1),且+=(λ∈R),∴=λ(x,y)+(2,1)=(λx+2,λy+1),∴,化为λ2=5.解得.故答案为:.点评:本题考查了向量的坐标运算、向量的模的计算公式、零向量等基础知识与基本技能方法,属于基础题.11.(5分)(2014•北京)设双曲线C经过点(2,2),且与﹣x2=1具有相同渐近线,则C的方程为;渐近线方程为y=±2x.考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:利用双曲线渐近线之间的关系,利用待定系数法即可得到结论.解答:解:与﹣x2=1具有相同渐近线的双曲线方程可设为﹣x2=m,(m≠0),∵双曲线C经过点(2,2),∴m=,即双曲线方程为﹣x2=﹣3,即,对应的渐近线方程为y=±2x,故答案为:,y=±2x.点评:本题主要考查双曲线的性质,利用渐近线之间的关系,利用待定系数法是解决本题的关键,比较基础.12.(5分)(2014•北京)若等差数列{a n}满足a7+a8+a9>0,a7+a10<0,则当n=8时,{a n}的前n项和最大.考点:等差数列的性质.专题:等差数列与等比数列.分析:可得等差数列{a n}的前8项为正数,从第9项开始为负数,进而可得结论.解答:解:由等差数列的性质可得a7+a8+a9=3a8>0,∴a8>0,又a7+a10=a8+a9<0,∴a9<0,∴等差数列{a n}的前8项为正数,从第9项开始为负数,∴等差数列{a n}的前8项和最大,故答案为:8.点评:本题考查等差数列的性质和单调性,属中档题.13.(5分)(2014•北京)把5件不同产品摆成一排,若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有36种.考点:排列、组合的实际应用;排列、组合及简单计数问题.专题:排列组合.分析:分3步进行分析:①用捆绑法分析A、B,②除去A、B相邻又满足A、C相邻的情况.解答:解:先考虑产品A与B相邻,把A、B作为一个元素有种方法,而A、B可交换位置,所以有2=48种摆法,又当A、B相邻又满足A、C相邻,有2=12种摆法,故满足条件的摆法有48﹣12=36种.故答案为:36.点评:本题考查分步计数原理的应用,要优先分析受到限制的元素,如本题的A、B、C.14.(5分)(2014•北京)设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)若f(x)在区间[,]上具有单调性,且f()=f()=﹣f(),则f(x)的最小正周期为π.考点:由y=Asin(ωx+φ)的部分图象确定其解析式;三角函数的周期性及其求法.专题:三角函数的图像与性质.分析:由f()=f()求出函数的一条对称轴,结合f(x)在区间[,]上具有单调性,且f()=﹣f()可得函数的半周期,则周期可求.解答:解:由f()=f(),可知函数f(x)的一条对称轴为x=,则x=离最近对称轴距离为.又f()=﹣f(),则f(x)有对称中心(,0),由于f(x)在区间[,]上具有单调性,则≤T⇒T≥,从而=⇒T=π.故答案为:π.点评:本题考查f(x)=Asin(ωx+φ)型图象的形状,考查了学生灵活处理问题和解决问题的能力,是中档题.三、解答题(共6小题,共80分,解答应写出文字说明、演算步骤或证明过程)15.(13分)(2014•北京)如图,在△ABC中,∠B=,AB=8,点D在边BC上,且CD=2,cos∠ADC=.(1)求sin∠BAD;(2)求BD,AC的长.考点:余弦定理的应用.专题:解三角形.分析:根据三角形边角之间的关系,结合正弦定理和余弦定理即可得到结论.解答:解:(1)在△ABC中,∵cos∠ADC=,∴sin∠ADC====,则sin∠BAD=sin(∠ADC﹣∠B)=sin∠ADC•cosB﹣cos∠ADC•sinB=×﹣=.(2)在△ABD中,由正弦定理得BD==,在△ABC中,由余弦定理得AC2=AB2+CB2﹣2AB•BCcosB=82+52﹣2×8×=49,即AC=7.点评:本题主要考查解三角形的应用,根据正弦定理和余弦定理是解决本题本题的关键,难度不大.16.(13分)(2014•北京)李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立);场次投篮次数命中次数场次投篮次数命中次数主场1 22 12 客场1 18 8主场2 15 12 客场2 13 12主场3 12 8 客场3 21 7主场4 23 8 客场4 18 15主场5 24 20 客场5 25 12(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;(3)记是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X为李明在这场比赛中的命中次数,比较EX与的大小(只需写出结论).考点:离散型随机变量的期望与方差;相互独立事件的概率乘法公式.专题:概率与统计.分析:(1)根据概率公式,找到李明在该场比赛中超过0.6的场次,计算即可,(2)根据互斥事件的概率公式,计算即可.(3)求出平均数和EX,比较即可.解答:解:(1)设李明在该场比赛中投篮命中率超过0.6的概率为事件A,由题意知,李明在该场比赛中超过0.6的场次有:主场2,主场3,主场5,客场2,客场4,共计5场所以李明在该场比赛中投篮命中率超过0.6的概率P(A)=,(2)设李明的投篮命中率一场超过0.6,一场不超过0.6的概率为事件B,同理可知,李明主场命中率超过0.6的概率,客场命中率超过0.6的概率,故P(B)=P1×(1﹣P2)+P2×(1﹣P1)=;(3)=(12+8+12+12+8+7+8+15+20+12)=11.4EX=点评:本题主要考查了概率的计算、数学期望,平均数,互斥事件的概率,属于中档题.17.(14分)(2014•北京)如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P﹣ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.(1)求证:AB∥FG;(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.考点:直线与平面所成的角.专题:计算题;证明题;空间位置关系与距离;空间角.分析:(1)运用线面平行的判定定理和性质定理即可证得;(2)由于PA⊥底面ABCDE,底面AMDE为正方形,建立如图的空间直角坐标系Axyz,分别求出A,B,C,E,P,F,及向量BC的坐标,设平面ABF的法向量为n=(x,y,z),求出一个值,设直线BC与平面ABF所成的角为α,运用sinα=|cos|,求出角α;设H(u,v,w),再设,用λ表示H的坐标,再由n=0,求出λ和H的坐标,再运用空间两点的距离公式求出PH的长.解答:(1)证明:在正方形AMDE中,∵B是AM的中点,∴AB∥DE,又∵AB⊄平面PDE,∴AB∥平面PDE,∵AB⊂平面ABF,且平面ABF∩平面PDE=FG,∴AB∥FG;(2)解:∵PA⊥底面ABCDE,∴PA⊥AB,PA⊥AE,如图建立空间直角坐标系Axyz,则A(0,0,0),B(1,0,0),C(2,1,0),P(0,0,2),E(0,2,0),F(0,1,1),,设平面ABF的法向量为n=(x,y,z),则即,令z=1,则y=﹣1,∴n=(0,﹣1,1),设直线BC与平面ABF所成的角为α,则sinα=|cos|=||=,∴直线BC与平面ABF所成的角为,设H(u,v,w),∵H在棱PC上,∴可设,即(u,v,w﹣2)=λ(2,1,﹣2),∴u=2λ,v=λ,w=2﹣2λ,∵n是平面ABF的法向量,∴n=0,即(0,﹣1,1)•(2λ,λ,2﹣2λ)=0,解得λ=,∴H(),∴PH==2.点评:本题主要考查空间直线与平面的位置关系,考查直线与平面平行、垂直的判定和性质,同时考查直线与平面所成的角的求法,考查运用空间直角坐标系求角和距离,是一道综合题.18.(13分)(2014•北京)已知函数f(x)=xcosx﹣sinx,x∈[0,](1)求证:f(x)≤0;(2)若a<<b对x∈(0,)上恒成立,求a的最大值与b的最小值.考点:利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(1)求出f′(x)=cosx﹣xsinx﹣cosx=﹣xsinx,判定出在区间∈(0,)上f′(x)=﹣xsinx<0,得f(x)在区间∈[0,]上单调递减,从而f(x)≤f(0)=0.(2)当x>0时,“>a”等价于“sinx﹣ax>0”,“<b”等价于“sinx﹣bx<0”构造函数g(x)=sinx﹣cx,通过求函数的导数讨论参数c求出函数的最值,进一步求出a,b的最值.解答:解:(1)由f(x)=xcosx﹣sinx得f′(x)=cosx﹣xsinx﹣cosx=﹣xsinx,此在区间∈(0,)上f′(x)=﹣xsinx<0,所以f(x)在区间∈[0,]上单调递减,从而f(x)≤f(0)=0.(2)当x>0时,“>a”等价于“sinx﹣ax>0”,“<b”等价于“sinx﹣bx<0”令g(x)=sinx﹣cx,则g′(x)=cosx﹣c,当c≤0时,g(x)>0对x∈(0,)上恒成立,当c≥1时,因为对任意x∈(0,),g′(x)=cosx﹣c<0,所以g(x)在区间[0,]上单调递减,从而,g(x)<g(0)=0对任意x∈(0,)恒成立,当0<c<1时,存在唯一的x0∈(0,)使得g′(x0)=cosx0﹣c=0,g(x)与g′(x)在区间(0,)上的情况如下:x (0,x0)x0(x0,)g′(x)+ ﹣g(x)↑↓因为g(x)在区间(0,x0)上是增函数,所以g(x0)>g(0)=0进一步g(x)>0对任意x∈(0,)恒成立,当且仅当综上所述当且仅当时,g(x)>0对任意x∈(0,)恒成立,当且仅当c≥1时,g(x)<0对任意x∈(0,)恒成立,所以若a<<b对x∈(0,)上恒成立,则a的最大值为,b的最小值为1 点评:本题考查利用导数求函数的单调区间;利用导数求函数的最值;考查解决不等式问题常通过构造函数解决函数的最值问题,属于一道综合题.19.(14分)(2014•北京)已知椭圆C:x2+2y2=4,(1)求椭圆C的离心率(2)设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,求直线AB与圆x2+y2=2的位置关系,并证明你的结论.考点:圆与圆锥曲线的综合;椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(1)化椭圆方程为标准式,求出半长轴和短半轴,结合隐含条件求出半焦距,则椭圆的离心率可求;(2)设出点A,B的坐标分别为(x0,y0),(t,2),其中x0≠0,由OA⊥OB得到,用坐标表示后把t用含有A点的坐标表示,然后分A,B的横坐标相等和不相等写出直线AB的方程,然后由圆x2+y2=2的圆心到AB的距离和圆的半径相等说明直线AB 与圆x2+y2=2相切.解答:解:(1)由x2+2y2=4,得椭圆C的标准方程为.∴a2=4,b2=2,从而c2=a2﹣b2=2.因此a=2,c=.故椭圆C的离心率e=;(2)直线AB与圆x2+y2=2相切.证明如下:设点A,B的坐标分别为(x0,y0),(t,2),其中x0≠0.∵OA⊥OB,∴,即tx0+2y0=0,解得.当x0=t时,,代入椭圆C的方程,得.故直线AB的方程为x=,圆心O到直线AB的距离d=.此时直线AB与圆x2+y2=2相切.当x0≠t时,直线AB的方程为,即(y0﹣2)x﹣(x0﹣t)y+2x0﹣ty0=0.圆心O到直线AB的距离d=.又,t=.故=.此时直线AB与圆x2+y2=2相切.点评:本题考查椭圆的简单几何性质,考查了圆与圆锥曲线的综合,训练了由圆心到直线的距离判断直线和圆的位置关系,体现了分类讨论的数学思想方法,考查了计算能力和逻辑思维能力,是压轴题.20.(13分)(2014•北京)对于数对序列P:(a1,b1),(a2,b2),…,(a n,b n),记T1(P)=a1+b1,T k(P)=b k+max{T k﹣1(P),a1+a2+…+a k}(2≤k≤n),其中max{T k﹣1(P),a1+a2+…+a k}表示T k﹣1(P)和a1+a2+…+a k两个数中最大的数,(Ⅰ)对于数对序列P:(2,5),(4,1),求T1(P),T2(P)的值;(Ⅱ)记m为a,b,c,d四个数中最小的数,对于由两个数对(a,b),(c,d)组成的数对序列P:(a,b),(c,d)和P′:(c,d),(a,b),试分别对m=a和m=d两种情况比较T2(P)和T2(P′)的大小;(Ⅲ)在由五个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P使T5(P)最小,并写出T5(P)的值(只需写出结论).考点:分析法和综合法.专题:新定义;分析法.分析:(Ⅰ)利用T1(P)=a1+b1,T k(P)=b k+max{T k﹣1(P),a1+a2+…+a k}(2≤k≤n),可求T1(P),T2(P)的值;(Ⅱ)T2(P)=max{a+b+d,a+c+d},T2(P′)=max{c+d+b,c+a+b},分类讨论,利用新定义,可比较T2(P)和T2(P′)的大小;(Ⅲ)根据新定义,可得结论.解答:解:(Ⅰ)T1(P)=2+5=7,T2(P)=1+max{T1(P),2+4}=1+max{7,6}=8;(Ⅱ)T2(P)=max{a+b+d,a+c+d},T2(P′)=max{c+d+b,c+a+b}.当m=a时,T2(P′)=max{c+d+b,c+a+b}=c+d+b,∵a+b+d≤c+d+b,且a+c+d≤c+b+d,∴T2(P)≤T2(P′);当m=d时,T2(P′)=max{c+d+b,c+a+b}=c+a+b,∵a+b+d≤c+a+b,且a+c+d≤c+a+d,∴T2(P)≤T2(P′);∴无论m=a和m=d,T2(P)≤T2(P′);(Ⅲ)数对(4,6),(11,11),(16,11),(11,8),(5,2),T5(P)最小;T1(P)=10,T2(P)=26;T3(P)42,T4(P)=50,T5(P)=52.点评:本题考查新定义,考查学生分析解决问题的能力,正确理解与运用新定义是解题的关键.。
数学理卷·2014届山东省德州一中高三1月月考试题(2014.01)
(2)法一:∵当 ∠ AHB 的角平分线垂直 x 轴时,点 H (4,2) ,∴ kHE = −kHF ,
设 E(x1, y1) , F ( x2 , y2 ) ,
∴ yH − y1 = − yH − y2 ,
xH − x1
xH − x2
∴
yH
y
2 H
− y1 − y12
=
−
yH y H2
2
解得 k = ±1 ,故直线 AB 的方程为 y = x 或 y = −x
……12 分
解法二
uuuv
A, B uuv
两点的坐标分别记为
(
xA
,
yA
),
(xB , yB )
由 OB = 2OA 及(1)知, O, A, B 三点共线且点 A , B 不在 y 轴上,
因此可以设直线 AB 的方程为 y = kx
根据上述分解规律,若 n2=1+3+5+…+19, m3(m∈N*)的分解中最小的数是 21,则 m+n 的值为________.
x2 + y2 ≤ 4
16.已知 x, y 满足约束条件 x − y + 2 ≥ 0 ,则目标函数 z = 2x + y 的最大值是_______.
y≥0
三、解答题(共 6 个小题,17-21 题各 12 分,22 题 14 分,共 74 分)
= 1+ 4k2
解得 k = ±1 ,故直线 AB 的方程为 y = x 或 y = −x .
22、解(1)∵点 M 到抛物线准线的距离为 4 + p = 17 , 24
∴ p = 1 ,即抛物线 C 的方程为 y 2 = x .----------------------------------------------2 分 2
河北冀州中学2014届高三上学期期末考试 数学理试题B卷 Word版含答案
试卷类型:B 河北冀州中学2013-2014学年上学期期末考试 高三年级数学试题(理科)考试时间 120分钟 满分150分命题人:戴洪涛第I 卷(共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设不等式20x x -≤的解集为M ,函数()ln(1||)f x x =-的定义域为N ,则M N ⋂为( )A . [0,1)B .(0,1)C .[0,1]D .(-1,0]2.如果复数21z i=-+,则( ) .A |z|=2 .B z 的实部为1 .C z 的虚部为﹣1 .D z 的共轭复数为1+i3.已知等比数列{}n a 的公比2q =,且42a ,6a ,48成等差数列,则{}n a 的前8项和( )A .127B .255C .511D .10234.设,a b 是两条直线,,αβ是两个平面,则a b ⊥的一个充分条件是( ) A .,//,a b αβαβ⊂⊥ B .,,//a b αβαβ⊂⊥ C .,,//a b αβαβ⊥⊥D .,//,a b αβαβ⊥⊥5.已知菱形ABCD 的边长为4,150ABC ∠=,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( ) A.4π B. 14π- C. 8πD. 18π-6.在平面直角坐标平面上,(1,4),(3,1)OA OB ==-,且O A 与OB 在直线l 上的射影长度相等,直线l 的倾斜角为锐角,则l 的斜率为 ( ) A .43 B .52C .25D .347.已知点(,)a b 在圆221x y +=上,则函数2()cos sin cos 12af x a x b x x =+--的最小正周期和最小值分别为( )A.2π,3-2B. π,3-2C. π,5-2D. 2π,5-28.设函数()sin()f x A x ωϕ=+(0,0,)22A ππωϕ≠>-<<的图像关于直线23x π=对称,它的周期是π,则( ) A .()f x 的一个对称中心是5(,0)12πB .()f x 的最大值是AC .()f x 的图象过点1(0,)2D . ()f x 在2123ππ⎡⎤⎢⎥⎣⎦,上是减函数9.已知球的直径SC=4,A ,B 是该球球面上的两点,AB=2.45ASC BSC ∠=∠=︒则棱锥S —ABC 的体积为 ( ) ABCD. 10.函数()cos f x x π=与()2log 1g x x =-的图像所有交点的横坐标之和为 A.2 B.4 C.6 D.811.如图,A ,F 分别是双曲线2222C 1 (0)x y a b a b-=:,>的左顶点、右焦点,过F 的直线l 与C 的一条渐近线垂直且与另一条渐近线和y 轴分别交于P ,Q 两点.若AP ⊥AQ ,则C 的离心率是( ) ABD12.在三棱锥P ABC -中,PA 垂直于底面ABC ,090ACB ∠=AE PB ⊥于E ,AF PC ⊥于F ,若2PA AB ==,BPC θ∠=,则当AEF ∆的面积最大时,tan θ的值为( )A.2B .2C .12 D第Ⅱ卷(共90分)本卷包括必考题和选考题两部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014届高三数学试题(理科) 出卷人: 班别: 姓名: 学号: 分数: 一、选择题:本大题共8小题,每小题5分,满分40分.
1.集合{|lg0}Mxx,2{|9}Nxx,则MN( )
A.(1,3) B.[1,3) C.(1,3] D.[1,3] 2. 已知复数(1)zii (为虚数单位),则复数z在复平面上所对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3. 设抛物线的顶点在原点,准线方程为-2,x则抛物线的方程是( )
A.28yx B. 28yx C. 24yx D. 24yx 4.如图是某简单组合体的三视图,则该组合体的体积为( ) A. 363(2) B. 363(2)
C. 1083 D. 108(32) 5.已知向量(1,1)a,(3,)bm,//()aab, 则m( ) A. 2 B.2 C.3 D.3
6.设随机变量服从正态分布(3,4)N,若
(23)(2)PaPa,则a( )
A. 3 B. 53 C.5 D.73 7.在△ABC中,已知b=4 ,c=2 ,∠A=120°,则a ( )
A.2 B.6 C.2 或6 D.27
8.函数,),(Dxxfy若存在常数C ,对任意的,1Dx存在唯一的Dx2使得 ,)()(21Cxfxf则称函数)(xf在D上的几何平均数为C .已知],2,1[,)(3xxxf 则函数3)(xxf在[1,2]上的几何平均数为( ) A.2 B.2 C.4 D.22 二.填空题:本大题共7小题,每小题5分,满分30分. (一)必做题:第9、10、11、12、13题为必做题,每道试题考生都必须作答.
9.在等差数列{}na中,有67812aaa,则此数列的前13项之和为 .
10.62()xx展开式中,常数项是 . 11.执行如图的程序框图,那么输出S的值是 . 12.已知集合ABC、、,A={直线},B={平面},
CAB. 若,,aAbBcC,给出下列四个命题:
①//////abaccb ②//abaccb ③//abaccb
④//abaccb 其中所有正确命题的序号是 . 13.设变量x,y满足约束条件22024010xyxyx,则目标函
数32zxy的最小值为 . (二)选做题:第14、15题为选做题,考生只能选做一题. 14.(坐标系与参数方程选做题)若直线的极坐标方程为cos()324,曲线C:1上的点到直线的距离为d,则d的最大值为 .
15.(几何证明选讲选做题) 如图圆O的直径6AB,P是AB的延长线上一点,过点P 作圆O的切线,切点为C,连接AC,若30CPA,则PC . 三、解答题: 本大题共6小题,共80分.解答应写出文
开始 2,1Sk
2013k 否
1kk是 输出S
结束 1
1SS 字说明,证明过程或演算步骤. 16.(本小题满分12分) 已知()sin()1fxAx ,(xR,其中
0,0,02A)的周期为,且图像上一个最低点为2(,1)3M
(1)求()fx的解析式; (2)当[0,]12x时,求()fx的值域. 17.(本小题满分13分) 在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表: 科目甲 科目乙 总计 第一小组 1 5 6 第二小组 2 4 6 总计 3 9 12 现从第一小组、第二小组中各任选2人分析选课情况. (1)求选出的4 人均选科目乙的概率; (2)设为选出的4个人中选科目甲的人数,求的分布列和数学期望. 18.(本题满分13分) 数列na的前n项和为122nnS,数列nb是首项为1a,公差为(0)dd的等差数
列,且1311,,bbb成等比数列. (1)求数列na与nb的通项公式;
(2)设nnnbca,求数列nc的前n项和nT. 19.(本小题满分14分) 如图5所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点 E在线段PC上,PC⊥平面BDE (1)、证明:BD⊥平面PAC; (2)、若PA=1,AD=2,求二面角B-PC-A的正切值;
20. (本小题满分14分) 已知椭圆22122:1(0)xyCabab的离心率为
33e,直线:2lyx与以原点为圆心、以椭圆1C的短半轴长为半径的圆O相切.
(1)求椭圆C1的方程; (2)设椭圆1C的左焦点为1F,右焦点为2F,直线1l过点1F,且垂直于椭圆的长轴,动直线2l垂直于1l,垂足为点P,线段2PF的垂直平分线交2l于点M,求点M的轨迹2C的方程;
21.(本小题满分14分) 设函数2()ln(),fxxxaaR.
(Ⅰ)若0a,求函数()fx在[1,e]上的最小值; (Ⅱ)若函数()fx在1[,2]2上存在单调递增区间,试求实数a的取值范围;
一、选择题.本大题共8小题,每小题5分,满分40分. 题号 l 2 3 4 5 6 7 8 答案 C B A B C D D D
二、填空题;本大题共7小题,考生作答6小题,每小题5分,满分30分. 9. 52 10. 60 111.2 12. ④ 13.-4 14.321 15. 33 三、解答题: 本大题共6小题,共80分. 16. (本小题满分12分) 解:(1)由()sin()1fxAx的周期为,知2T,则有2; 所以()sin(2)1fxAx,因为函数图像有一个最低点2(,1)3M,0A, 所以2A 且 2sin(2)13, „„„„„„„„„„ 3分 则有2322()32kkZ „„„„„„„„„„„ 4分 解得2()6kkZ, 因为02,所以6 „„„.6分 所以()2sin(2)16fxx xR „„„„„„„„„„„ 7分 (2)当[0,]12x时,2[,]663x, „„„„„„„„„„„ 8分 则有13sin(2)[,]622x,所以()2sin(2)1[2,13]6fxx„„11分 即()fx的值域为[2,13]。 „„„„„„„„„ 12分 17. (本小题满分12分) 解:(1)设“从第一小组选出的2人选科目乙”为事件A, “从第二小组选出的2人选科目乙””为事件B.由于事 件A、B相互独立,
且25262()3CPAC, 24262()5CPBC.„„„„„„„„„„„„4分 所以选出的4人均选科目乙的概率为 224()()()3515PABPAPB„„„„„„„„„„„ 6分
(2)设可能的取值为0,1,2,3.得 4(0)15P, 21112524542222666622(1)45CCCCCPCCCC,15226611(3)45CPCC,
2(2)1(0)(1)(3)9PPPP„ 9分
的分布列为
0 2
3
P 415 2245 29 145
∴的数学期望42221012311545945E „„„„13分 18.(本题满分13分) 解析:(1)当2n,时11222nnnnnnaSS,
又111112222aS,也满足上式,所以数列{na}的通项公式为2nna.
112ba,设公差为d,则由1311,,bbb成等比数列,2(22)2(210)dd,
得0d(舍去)或3d ,所以数列}{nb的通项公式31nbn.
(2)由(1)可得312123nnnbbbbTaaaa123258312222nn,
121583122222nnnT,
两式式相减得
1213333122222nnnnT,
131(1)3135222512212nnnnnnT
,
20(本小题满分14分) 解:(1)由直线:2lyx与圆222xyb相切,得|002|2b,即2b. (2分) 由33e,得222213bea,所以3a, (3分)
所以椭圆的方程是221:132xyC. (4分) (2)由条件,知2||||MFMP,即动点M到定点2F的距离等于它到直线1:1lx的距离,由抛物线的定义得点M的轨迹2C的方程是xy42. (7分) 21. (本小题满分14分) (1) 证:由题意()2(1)22nfnna,即log2mnna, „„1分 2nnma
. „„2分
2()2nnnnbafanm
,
当22m时,11()()2nnnnbafan. „„„„3分 ∴012111111()2()3()()2222nnSn, ① 123111111()2()3()()22222nnSn
② „„4分
①-②,得012311111111()()()()()()2222222nnnSn 11(1())12()121()2nnn
„„6分
∴11(2)()42nnSn „„7分 (2) 解:由(1)知,2lg2lgnnnncaanmm,要使1nncc对一切nN成立, 即2lg(1)lgnmnmm对一切nN成立. „„8分 201,lg0(1)mmnnm
,对一切nN恒成立,
只需2min()1nmn,„„10分 1111nnn单调递增,∴当1n时,min1()12nn. „„12分
