时间序列分析基于R——习题答案
时间序列分析作业及答案-精共16页PPT

36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
谢谢!
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
应用时间序列分析习题答案
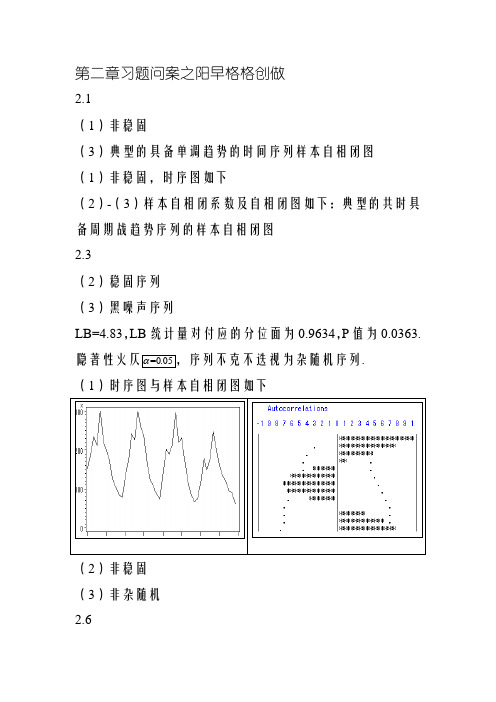
第二章习题问案之阳早格格创做2.1(1)非稳固(3)典型的具备单调趋势的时间序列样本自相闭图(1)非稳固,时序图如下(2)-(3)样本自相闭系数及自相闭图如下:典型的共时具备周期战趋势序列的样本自相闭图2.3(2)稳固序列(3)黑噪声序列LB=4.83,LB统计量对付应的分位面为0.9634,P值为0.0363.隐著性火仄=0.05,序列不克不迭视为杂随机序列.(1)时序图与样本自相闭图如下(2)非稳固(3)非杂随机2.6(1)稳固,非杂随机序列(拟合模型参照:ARMA(1,2)) (2)好分序列稳固,非杂随机 第三章习题问案3.13.2解:对付于AR (2)模型:3.3 解:根据该AR(2)3.4 解:本模型可变形为:型稳固.由此可知c即当-1<c<0时,该AR(2)模型稳固. 3.5说明:已知本模型可变形为:不管c 与何值,皆市有一特性根等于1,果此模型非稳固.3.6 解:(1 (2(3 (4(5)3.7MA(1)3.8解法1解法2展启等号左边的多项式,整治为 合并共类项,本模型等价表黑为3.9解:3.10解法1:(1隐然模型的AR 部分的特性根是1,模型非稳固. (2MA(1)模型,稳固.解法2:(1固序列.(2自相闭系数只与时间隔断少度有闭,与起初时间无闭所以该好分序列为稳固序列.3.11解:(1(2.(3.+0.2693i(4.(5(6.3.12 解法1解法23.13Green函数3.14的递推公式得:3.15 (1)创造(2)创造(3)创造(4)不可坐3.16 解:(1已知AR(1)模型的Green9.9892+即[3.8275,16.1509](210.045+即[3.9061,16.1839].3.17 (1)稳固非黑噪声序列(2)AR(1)(3) 5年预测截止如下:3.18 (1)稳固非黑噪声序列(2)AR(1)(3) 5年预测截止如下:3.19 (1)稳固非黑噪声序列(2)MA(1)(3) 下一年95%的置疑区间为(80.41,90.96)3.20 (1)稳固非黑噪声序列(2)ARMA(1,3)序列(3)拟合及5年期预测图如下:第四章习题问案4.1 解:4.2 解由代进数据得解得4.3解:(1)(2.其(3)正在移动仄衡法下:正在指数仄滑法中:4.4 解:根据指数仄滑的定义有(1)式创造,(1)式等号二2)式创造(1)-(2)得limtttxt→∞⎛=⎝4.5 该序列为隐著的线性递加序列,利用本章的知识面,不妨使用线性圆程大概者holt二参数指数仄滑法举止趋势拟合战预测,问案不唯一,简直截止略.4.6 该序列为隐著的非线性递加序列,不妨拟合二次型直线、指数型直线大概其余直线,也能使用holt二参数指数仄滑法举止趋势拟合战预测,问案不唯一,简直截止略.4.7 本例正在混同模型结构,季节指数供法,趋势拟合要领等处均有多种可选规划,如下干法仅是可选要领之一,截止仅供参照(1)该序列有隐著趋势战周期效力,时序图如下(2)该序列周期振幅险些不随着趋势递加而变更,所以测(注:如果用乘法模型也不妨)最先供季节指数(不与消趋势,本去不是最透彻的季节指数)序列趋势做用(要领不唯一)(注:该趋势模型截距偶尔思,主假如斜率蓄意思,反映了少久递加速率)残好序列基础无隐著趋势战周期残留.预测1971年奶牛的月度产量序列为得到(3)该序列使用x11要领得到的趋势拟合为趋势拟合图为4.8 那是一个有着直线趋势,然而是有不牢固周期效力的序列,所以不妨正在赶快预测步调中用直线拟合(stepar)大概直线指数仄滑(expo)举止预测(trend=3).简直预测值略.第五章习题预计下一天5.1 拟合好分稳固序列,的支盘价为2895.2 拟合模型不唯一,问案仅供参照.拟合ARIMA(1,1,0)模型,五年预测值为:5.4 (1)AR(1),(2)有同圆好性.最后拟合的模型为5.5(1)非稳固(2)与对付数与消圆好非齐,对付数序列一节好分后,拟合疏系数模型AR(1,3)所以拟合模型为(3)预测截止如下:5.6 本序列圆好非齐,好分序列圆好非齐,对付数变更后,好分序列圆好齐性.第六章习题6.1 单位根考验本理略.例2.1 本序列不仄稳,一阶好分后稳固例2.2 本序列不仄稳,一阶与12步好分后稳固例2.3 本序列戴漂移项稳固例2.4 本序列不戴漂移项稳固例2.5固.6.2 (1)二序列均为戴漂移项稳固(2)谷物产量为戴常数均值的杂随机序列,落雨量不妨拟合AR(2)疏系数模型.(3)二者之间具备协整闭系(46.3 (1)掠食者战被掠食者数量皆浮现出隐著的周期特性,二个序列均为非稳固序列.然而是掠食者战被掠食者延缓2阶序列具备协整闭系..模型心径为:已去一周的被掠食者预测序列为:Forecasts for variable xObs Forecast Std Error 95% Confidence Limits 掠食者预测值为:Forecasts for variable yObs Forecast Std Error 95% Confidence Limits 6.4(1)出进心总数序列均不仄稳,然而对付数变更后的一阶好分后序列稳固.所以对付那二个序列与对付数后举止单个序列拟合战协整考验.(2简直心径为:简直心径为:(3(4(5。
《时间序列分析》第二章 时间序列预处理习题解答[1]
![《时间序列分析》第二章 时间序列预处理习题解答[1]](https://img.taocdn.com/s3/m/afd770ef524de518964b7d1f.png)
∧
, 24)
225.0 131.6 63.2 86.4
95.3 112.8 181.6 136.9
1 100.6 8 81.8 7 73.9 3 31.5
48.3 31.0 64.8 35.3
112.3 160.8 52.3 ; 26.2 112.8
143.0 80.5 144.3 62.5 49.5 158.2 116.1 7.6 165.9 54.1 106.7 92.2 63.2 67.3 77.0 148.6 159.3 85.3 59.4
时间序描述程序 data example1; input number@@; time=intnx('year','01jan1980'd, _n_-1); format time date.; cards; 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ; proc gplot data=example1; plot number*time=1; symbol1 c=black v=star i=join; run;
析: 分析 自相关图显示序列自 自相关系数 数长期位于零 零轴的一边 边, 这是具有 有单调趋势序 序列 的典 典型特征。
由下图可知 知,自相关系 系数长期位于 于零轴的一边 边,且自相关 关系数递减到 到零的速度较慢, 在 5 个延期中,自相关系数 数一直为正,说明这是一个 个有典型单调 调趋势的非平 平稳序列。
分析 析:自相关图显示该序 序列自相关系数较小,大致在零轴 轴附近波动 动,大多数控 控制 在 2 倍标准差 差范围内,所 所以认为该 该序列是平稳 稳的。
3.1945 年-19 950 年费城 城月度降雨量 量数据如下 下(单位:m mm) ,见教材 材 P35 表 2-8.
《时间序列分析》第二章 时间序列预处理习题解答[1]
![《时间序列分析》第二章 时间序列预处理习题解答[1]](https://img.taocdn.com/s3/m/afd770ef524de518964b7d1f.png)
ppm 342 341 340 339 338 337 336 335 334 333 332 331 330 329 328 01JAN75 01MAY75 01SEP75 01JAN76 01MAY76 01SEP76 01JAN77 01MAY77 01SEP77 01JAN78 01MAY78 01SEP78 01JAN79 01MAY79 01SEP79 01JAN80 01MAY80 01SE分析 自相关图显示序列自 自相关系数 数长期位于零 零轴的一边 边, 这是具有 有单调趋势序 序列 的典 典型特征。
由下图可知 知,自相关系 系数长期位于 于零轴的一边 边,且自相关 关系数递减到 到零的速度较慢, 在 5 个延期中,自相关系数 数一直为正,说明这是一个 个有典型单调 调趋势的非平 平稳序列。
∧
, 24)
225.0 131.6 63.2 86.4
95.3 112.8 181.6 136.9
1 100.6 8 81.8 7 73.9 3 31.5
48.3 31.0 64.8 35.3
112.3 160.8 52.3 ; 26.2 112.8
143.0 80.5 144.3 62.5 49.5 158.2 116.1 7.6 165.9 54.1 106.7 92.2 63.2 67.3 77.0 148.6 159.3 85.3 59.4
时间序列分析与预测课后习题答案

22 7336 18 0766 20 2040
第八章 时间序列分析与预测
练习题第五题答案
2000
季度 销售量
长期趋势
一季度 13 1
9 3324
二季度 13 9
9 9722
三季度 79
10 6121
四季度 86
11 2519
2001
Y/T 销售量 长期趋势
1 4037 10 8
11 8918
1 3939 11 5
9
2 10
10
2 50
Y 1 1 = 0 . 3 6 5 3 3 3 + 0 . 1 9 2 6 4 8 1 1 = 2 . 4 8 6 6 6 7
2024/1/18
第八章 时间序列分析与预测
练习题第五题
某县2000—2003年各季度鲜蛋销售量如表所示单位:万公斤 1用移动平均法消除季节变动 2拟合线性模型测定长期趋势 3预测2004年各季度鲜蛋销售量
13 95 0 987174
2024/1/18
第八章 时间序列分析与预测
练习题第五题答案
2用线形趋势模型法测定时间序列的长期趋势
年份 2000 2001 2002 2003
季度 一 二 三 四 一 二 三 四 一 二 三 四 一 二 三 四
2024/1/18
销售量
13 1 13 9
t 1 3 6 , t= 8 .5 , t2 = 1 4 9 6
0 9177 17 5
15 0910 1 1596
20 0 17 6504 1 1331 1 1511 1 1472 20 2099
0 7364 16 0
15 7309 1 0171
16 9 18 2903 0 9240 0 8555 0 8526 20 8497
《时间序列分析——基于R》王燕,读书笔记

《时间序列分析——基于R》王燕,读书笔记笔记:⼀、检验:1、平稳性检验:图检验⽅法:时序图检验:该序列有明显的趋势性或周期性,则不是平稳序列⾃相关图检验:(acf函数)平稳序列具有短期相关性,即随着延迟期数k的增加,平稳序列的⾃相关系数ρ会很快地衰减向0(指数级指数级衰减),反之⾮平稳序列衰减速度会⽐较慢衰减构造检验统计量进⾏假设检验:单位根检验adfTest()——fUnitRoots包2、纯随机性检验、⽩噪声检验(Box.test(data,type,lag=n)——lag表⽰输出滞后n阶的⽩噪声检验统计量,默认为滞后1阶的检验统计量结果)1、Q统计量:type=“Box-Pierce”2、LB统计量:type=“Ljung-Box”⼆、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf(),pacf(),auto.arima()⾃动定阶1.3建模arima()1.4模型显著性检验:残差的⽩噪声检验Box.test();参数显著性检验t分布2、⾮平稳确定性分析2.1趋势拟合:直线、曲线(⼀般是多项式,还有其它函数)2.2平滑法移动平均法:SMA()——TTR包指数平滑法:HoltWinters()3、⾮平稳随机性分析3.1ARIMA1平稳性检验,差分运算2拟合ARMA3⽩噪声检验3.2疏系数模型arima(p,d,f)3.3季节模型可以叠加的模型4、残差⾃回归模型:4.1建⽴线性模型4.2对滞后的因变量间拟合线性模型,对模型做残差⾃相关DW检验。
dwtest()——lmtest包,增加选项order.by指定延迟因变量4.3对残差建⽴ARIMA模型5、条件异⽅差模型:异⽅差检验:LM检验ArchTest()——FinTS包,⽤ARCH、GARCH模型建模第⼀章简介统计时序分析⽅法:1、频域分析⽅法2、时域分析⽅法步骤:1、观察序列特征2、根据序列特征选择模型3、确定模型的⼝径4、检验模型,优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展⽅向:1、AR,MA,ARMA,ARIMA(Box-Jenkins模型)2、异⽅差场合:ARCH,GARCH等(计量经济学)3、多变量场合:“变量是平稳”不再是必需条件,协整理论3、⾮线性场合:门限⾃回归模型,马尔科夫转移模型第⼆章时间序列的预处理预处理内容:对它的平稳性和纯随机性进⾏检验,最好是平稳⾮⽩噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述⼀个随机变量的统计特征,同样⼀个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。
时间序列习题(含答案)
一、单项选择题1.时间数列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的,后者是根据变量值大小排列的D 前者是根据变量值大小排列的,后者是根据时间顺序排列的 2.时间数列中,数值大小与时间长短有直接关系的是( )A 平均数时间数列B 时期数列C 时点数列D 相对数时间数列 3.发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数 4.计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平5.某车间月初工人人数资料如下:则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6.某地区某年9月末的人口数为150万人,10月末的人口数为150.2万人,该地区10月的人口平均数为( )A150万人 B150.2万人 C150.1万人 D 无法确定 7.由一个9项的时间数列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 8.采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度 9.某企业的产值2005年比2000年增长了58.6%,则该企业2001—2005年间产值的平均发展速度为( )A 5%6.58 B 5%6.158 C 6%6.58 D 6%6.158 10.根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数,采用的公式是( )A 简单平均法B 几何平均法C 加权序时平均法D 首末折半法 11、时间序列在一年内重复出现的周期性波动称为( )A 、长期趋势B 、季节变动C 、循环变动D 、随机变动1.C 2.B 3.C 4.B 5.C 6.C 7.A 8.A 9.B 10.D 11、B 二、多项选择题1.对于时间数列,下列说法正确的有( )A 数列是按数值大小顺序排列的B 数列是按时间顺序排列的C 数列中的数值都有可加性D 数列是进行动态分析的基础E 编制时应注意数值间的可比性 2.时点数列的特点有( )A 数值大小与间隔长短有关B 数值大小与间隔长短无关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的3.下列说法正确的有( )A 平均增长速度大于平均发展速度B 平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14.下列计算增长速度的公式正确的有( )A %100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100%D %100⨯-=基期水平基期水平报告期水平增长速度E %100⨯=基期水平报告期水平增长速度 5.采用几何平均法计算平均发展速度的公式有( )A1231201-⨯⨯⨯⨯=n n a a a a a a a a nx Ba a nx n =C 1a a nx n= D nR x = E n x x ∑=6.某公司连续五年的销售额资料如下:根据上述资料计算的下列数据正确的有( )A 第二年的环比增长速度=定基增长速度=10%B 第三年的累计增长量=逐期增长量=200万元C 第四年的定基发展速度为135%D 第五年增长1%绝对值为14万元E 第五年增长1%绝对值为13.5万元 7.下列关系正确的有( )A 环比发展速度的连乘积等于相应的定基发展速度B 定基发展速度的连乘积等于相应的环比发展速度C 环比增长速度的连乘积等于相应的定基增长速度D 环比发展速度的连乘积等于相应的定基增长速度E 平均增长速度=平均发展速度-1 8.测定长期趋势的方法主要有( )A 时距扩大法B 方程法C 最小平方法D 移动平均法E 几何平均法9.关于季节变动的测定,下列说法正确的是( ) A 目的在于掌握事物变动的季节周期性 B 常用的方法是按月(季)平均法 C 需要计算季节比率D 按月计算的季节比率之和应等于400%E 季节比率越大,说明事物的变动越处于淡季 10.时间数列的可比性原则主要指( )A时间长度要一致 B经济内容要一致 C计算方法要一致 D总体范围要一致E计算价格和单位要一致1.BDE 2.BD 3.BC 4.ACD 5.ABD 6.ACE 7.AE8.ACD 9.ABC 10.ABCDE三、判断题1.时间数列中的发展水平都是统计绝对数。
时间序列习题答案
时间序列习题答案时间序列习题答案时间序列分析是一种用来研究随时间变化的数据模式和趋势的方法。
它在经济学、金融学、统计学等领域中被广泛应用。
下面我将给出一些时间序列分析的习题,并附上详细的答案解析。
习题一:某公司过去一年的销售额如下:100, 120, 130, 140, 150, 160, 170, 180, 190, 200。
请计算该公司的平均销售额和年度增长率。
答案解析:首先,计算平均销售额的方法是将所有销售额相加,然后除以销售额的个数。
在这个例子中,销售额的个数为10,总销售额为100+120+130+140+150+160+170+180+190+200=1540。
因此,平均销售额为1540/10=154。
接下来,计算年度增长率的方法是将最后一年的销售额减去第一年的销售额,然后除以第一年的销售额,并乘以100%。
在这个例子中,最后一年的销售额为200,第一年的销售额为100。
因此,年度增长率为(200-100)/100*100%=100%。
习题二:某股票的每日收盘价如下:10.2, 10.5, 10.7, 10.9, 11.1, 11.3, 11.5, 11.7, 11.9, 12.1。
请计算该股票的平均收盘价和收益率。
答案解析:计算平均收盘价的方法与计算平均销售额的方法相同。
将所有收盘价相加,然后除以收盘价的个数。
在这个例子中,收盘价的个数为10,总收盘价为10.2+10.5+10.7+10.9+11.1+11.3+11.5+11.7+11.9+12.1=113.9。
因此,平均收盘价为113.9/10=11.39。
计算收益率的方法是将每日的收盘价减去前一日的收盘价,然后除以前一日的收盘价,并乘以100%。
在这个例子中,第二天的收盘价为10.5,第一天的收盘价为10.2。
因此,第二天的收益率为(10.5-10.2)/10.2*100%=2.94%。
习题三:某城市过去十年的月度平均气温如下:15, 18, 20, 22, 25, 28, 30, 29, 26, 23。
《时间序列分析》第二章 时间序列预处理习题解答[1]
97.0 105.4
proc print data=example2_3; proc arima data=example2_3; identify var=rain; run;
分析: (1) 如上图所示: (2) 根据样本时序图和样本自相关图可知,该序列平稳 (3) 根据白噪声检验,P 值都较大,可以判断该序列为白噪声序列,即该序列具有纯随 机性。
析: 分析 自相关图显示序列自 自相关系数 数长期位于零 零轴的一边 边, 这是具有 有单调趋势序 序列 的典 典型特征。
由下图可知 知,自相关系 系数长期位于 于零轴的一边 边,且自相关 关系数递减到 到零的速度较慢, 在 5 个延期中,自相关系数 数一直为正,说明这是一个 个有典型单调 调趋势的非平 平稳序列。
data example2; input ppm@@; time=intnx('month','01jan1975'd, _n_-1); format year year4.; cards; 330.45 331.90 331.63 333.05 332.81 334.65 334.66 336.25 335.89 337.41 337.81 339.25 330.97 330.05 332.46 330.87 333.23 332.41 335.07 334.39 336.44 335.71 338.16 337.19 331.64 328.58 333.36 329.24 334.55 331.32 336.33 332.44 337.63 333.68 339.88 335.49 332.87 328.31 334.45 328.87 335.82 330.73 337.39 332.25 338.54 333.69
时间序列分析基于r
时间序列分析基于r时间序列分析是一种用于分析时间序列数据的统计方法。
R 是一种流行的编程语言和环境,广泛用于数据分析和统计建模。
下面是一些基于R的时间序列分析的常见步骤和函数。
1. 导入数据:首先,你需要将时间序列数据导入到R中。
你可以使用`read.csv()`函数或其他适用的函数来导入数据。
2. 创建时间序列对象:在R中,你可以使用`ts()`函数来创建时间序列对象。
这个函数需要指定数据和时间间隔参数。
例如,如果你的数据是每个月的销售量,你可以使用`ts(data, frequency = 12)`来创建一个每年12个观测值的时间序列对象。
3. 可视化时间序列:使用`plot()`函数可以将时间序列数据可视化。
你可以添加标题、轴标签和其他自定义选项来改进图形的可读性。
4. 时间序列分解:时间序列可以被分解成趋势、季节和随机成分。
你可以使用`decompose()`函数来进行时间序列分解。
这个函数将返回一个包含趋势、季节和随机成分的对象。
5. 平稳性检验:在进行时间序列分析之前,你需要确保时间序列是平稳的。
你可以使用`adf.test()`函数来进行单位根检验。
如果序列是非平稳的,你可以使用差分操作来使其平稳。
6. 自相关和偏自相关函数:自相关函数(ACF)和偏自相关函数(PACF)是用于识别时间序列模型的重要工具。
你可以使用`acf()`和`pacf()`函数来绘制ACF和PACF图。
7. 拟合时间序列模型:根据ACF和PACF图的结果,你可以选择适当的时间序列模型。
常见的时间序列模型包括AR (自回归)、MA(滑动平均)、ARMA(自回归滑动平均)和ARIMA(差分自回归滑动平均)模型。
你可以使用`arima()`函数来拟合ARIMA模型。
8. 模型诊断:拟合时间序列模型后,你需要对模型进行诊断,以确保模型的拟合质量。
你可以使用`checkresiduals()`函数来检查模型的残差是否符合正态分布和白噪声的假设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*** ** 第一章习题答案 略
第二章习题答案 2.1 (1)非平稳
(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376 (3)典型的具有单调趋势的时间序列样本自相关图
2.2 (1)非平稳,时序图如下
(2)- (3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相 关图***
** 2.3 (1)自相关系数为: 0.2023 0.013 0.042 -0.043 -0.179 -0.251
-0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.70 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118 (2)平稳序列 (3)白噪声序列
2.4 LB=4.83 ,LB 统计量对应的分位点为 0.9634 ,P 值为 0.0363 。显著性水平 =0.05 ,序列 不能视为纯随机序列。
2.5 (1)时序图与样本自相关图如下***
** (2) 非平稳 (3)非纯随机
2.6 (1)平稳,非纯随机序列(拟合模型参考: ARMA(1,2)) (2)差分序列平稳,非纯随机
第三章习题答案 0.71 E( x ) 0 ,
t
1 Var (x ) 1.96 ,
t 2 1 0.7
2 2 0.7 0.49, 22 0
0.72 1
7 15 , 2 1
15
0.73 E( x ) 0 ,
t
1 0.15 Var (x ) 1.98 t (1 0.15)(1 0.8 0.15)(1 0.8 0.15)
1 0.8
1 0.15 0.70 , 2 0.8 1 0.15 0.41,
3
0.8 2 0.15 1 0.22
11 1 0.70, 22 2 0.15, 33 0
1 ,
0.74 1 c 0, 1 1
c
c ,k 2 k k 1
k 2
0.75 证明: 该序列的特征方程为: 3 - 2-c c 0,解该特征方程得三个特征根:
1 1, 2 c , 3
c*** ** 无论 c取什么值,该方程都有一个特征根在单位圆上, 所以该序列一定是非平稳序列。 证毕。 2.7 (1) 错 (2)错 (3)对 (4)错 (5) 1 2.8 该模型有两种可能的表达式: x 1 和 t t t 2
x 2 。
t t t 1
2.9 将 x 10 0.5x 0.8 C 等价表达为
t t 1 t t 2 t 3
2 3 1 0.8B CB
x 20 t t 1 0.5B
2 3 2 2 3 3 1 0.8 B CB (1 0.5 B 0.5 B 0.5 B ) t
展开等号右边的多项式,整理为 2 2 3 3 4 4 1 0.5 B 0.5 B 0.5 B 0.5 B
2 3 2 4 0.76B 0.8 0.5B 0.8 0.5 B
3 4 CB 0.5CB
合并同类项,原模型等价表达为
2 k 3 3 k x 20 [1 0.5 B 0.55B 0.5 (0.5 0.4 C)B ]
t t k 0
当 3 0.9 0.4 C 0时,该模型为 MA (2) 模型,解出 C
0.275 。
2.10 E( x ) 0 ,
t
2 2 Var ( xt ) 1 0.7 0.4 1.65
1 0.71 0.7 0.4 0.59 1.65 , 2 0.4 0.24 1.65 ,
k 0,k 3
2.11 (1)证明:因为 2 2 Var (xt ) lim(1 kC )
k
,所以该序列为非平稳序列。
(2) y x x 1 (C 1)
1,该序列均值、方差为常数,
t t t t t
E( y ) 0,
t
2 2
Var ( yt ) 1 (C 1)
自相关系数只与时间间隔长度有关,与起始时间无关 C 1 1 2 1 (C 1)
, 0,k 2
k
所以该差分序列为平稳序列。 *** ** 2.12 (1)非平稳,(2)平稳,(3)可逆,(4)不可逆,(5)平稳可逆, (6)不平稳不可逆***
** 2.13 k 1 k 1 G0 1,G1 1G0 1 0.6 0.3 0.3, 1 1 1 1
0.3 0.6 , 2
G G G k k k 所以该模型可以等价表示为: k x 0.3 0.6
t t t k k 0
1
3 2.14 0
1 1 1 0.25
1 2
12
2.15 证明:已知 1
1 2 , 1 1
4 ,根据 ARMA(1,1)模型 Green 函数的递推公式得:
G0 1,
2 G G , 1 1 0 1 0.5 0.25 1 k 1 k 1
G G G k
1 1 1 1 1 , 2 k k
0 1 5 2 2 j 3 2 1 G G
j j 1 1 1 1 2 2 4 5 j j 0 1 1 1 1 1 1 7
1 4 2 4 1 26
2 2( 1) 1 1 1 j G 1 1
j 1 2 1
j 0 j 1 1
0.77
G G G G G G j j k j 1 j k 1 j j k 1 j 0 j 0 j 0 ,k 2 k 1 1 k
1 2 2 2 G G G
j j j j 0 j 0 j 0
2.16 (1)成立 (2)成立 (3)成立 (4)不成立 2.17 (1)95%置信区间为( 3.83,16.15 ) (2)更新数据后 95%置信区间为( 3.91,16.18 )
2.18 (1)平稳非白噪声序列 (2)AR(1) (3) 5 年预测结果如下: *** ** 2.19 (1)平稳非白噪声序列 (2)AR(1) (3) 5 年预测结果如下:***
** 2.20 (1)平稳非白噪声序列 (2)MA(1) (3) 下一年 95%的置信区间为( 80.41,90.96 )
2.21 (1)平稳非白噪声序列 (2)ARMA(1,3)序列 (3)拟合及 5 年期预测图如下:
第四章习题答案 0.78 x 的系数为 T 3 1 16 , x 的系数为
T 1
5
16
0.79 解下面的方程组,得到 0.4 0.10 5(1 ) t
0.11 5.5 (1 ) t
0.80 (1)11.04 (2)11.79277 (3) b a 0.4 0.24 0.16
0.81 根据指数平滑的定义有( 1)式成立,(1)式等号两边同乘 (1 ) 有(2)式成立 2 3 x t (t 1) (1 ) (t 2) (1 ) (t 2) (1 ) (1)
t 2 3 (1 )x t (1 ) (t 1) (1 ) (t 2) (1 ) (2)
t (1)- (2)得*** ** x t t
2
(1 ) (1 )
x t t (1 ) (1 ) 2
1 t
则 1 t
x t lim lim 1
。 t t t t
2.22 该序列为显著的线性递增序列,利用本章的知识点,可以使用线性方程或者 holt 两参 数指数平滑法进行趋势拟合和预测,答案不唯一,具体结果略。
2.23 该序列为显著的非线性递增序列, 可以拟合二次型曲线、 指数型曲线或其他曲线, 也能 使用 holt 两参数指数平滑法进行趋势拟合和预测,答案不唯一,具体结果略。
2.24 本例在混合模型结构, 季节指数求法, 趋势拟合方法等处均有多种可选方案, 如下做法 仅是可选方法之一,结果仅供参考 (1)该序列有显著趋势和周期效应,时序图如下
(2)该序列周期振幅几乎不随着趋势递增而变化, 所以尝试使用加法模型拟合该序 列: xt Tt St It 。(注:如果用乘法模型也可以)
首先求季节指数(没有消除趋势,并不是最精确的季节指数) 0.82 0.912575 1.038169 1.064302 1.153627 1.116566 0.12 0.984162 0.930947 0.938549 0.902281 0.955179
消除季节影响, 得序列 yt xt St x,使用线性模型拟合该序列趋势影响 (方法不唯一) :
T 97.70 1.79268t ,t 1,2,3,
t
(注:该趋势模型截距无意义,主要是斜率有意义,反映了长期递增速率)
