19.2特殊的平行四边形课时练
19.2 特殊的平行四边形—菱形(1)

1 2
BD平分∠ABC、 BD平分∠ABC、∠ADC 平分
A
O
5 6 3 4 7 8
D
C
已知:菱形ABCD的对角线AC和BD相交于点O, 已知:菱形ABCD的对角线AC和BD相交于点O ABCD的对角线AC 相交于点 如图。 如图。
第十九章
平行四边形
19.2 特殊的平行四边形
义务教育课程标准实验教科书——人教版——八年级下册
19.2.2 菱形的性质
义务教育课程标准实验教科书——人教版——八年级下册
两次, 将一张矩形的纸对折两次,然后 沿图中的虚线剪下, 沿图中的虚线剪下,得到一个直角三 角形,打开即得到一个四边形。 角形,打开即得到一个四边形。
1.菱形ABCD的周长是20cm,则菱形ABCD的边 1.菱形ABCD的周长是20cm,则菱形ABCD的边 菱形ABCD的周长是20cm,则菱形ABCD 长是 5cm ; 2.下面性质中菱形有而矩形没有的是( ) 2.下面性质中菱形有而矩形没有的是( 下面性质中菱形有而矩形没有的是 (A)邻角互补 (B)四个角都为直角 (C)对角线相等 (D)对角线互相垂直
A O B C D
∴AC⊥BD,AC平分∠ ∴AC⊥BD,AC平分∠BAD 平分
同理: AC平分 BCD; 平分∠ 同理: AC平分∠BCD; BD平分 ABC和 平分∠ BD平分∠ABC和∠ADC
菱形是特殊的平行四边形,既具有平行四边 的平行四边形, 形的所有性质,又具有自己的特殊性质:
八年级数学下册特殊的平行四边形课时练

八年级数学下册特殊的平行四边形课时练课时一矩形1·矩形具有而平行四边形不具有的性质是( )A ·对边相等B ·对角相等C ·对角互补D ·对角线平分2·直角三角形中,两直角边长分别为12和5,则斜边中线长是( ) A ·26 B ·13 C ·8·5 D ·6·53·矩形ABCD 对角线AC 、BD 交于点O ,AB=5,12,cm BC cm =则△ABO 的周长为等于 ·4· 如图所示,四边形ABCD 为矩形纸片.把纸片ABCD 折叠, 使点B 恰好落在CD 边的中点E 处,折痕为AF .若CD =6, 则AF 等于 ( )A ·34B ·33C ·24D ·85· 如图所示,矩形ABCD 的对角线AC 和BD 相交于点O ,过点O 的直线分别交AD 和BC 于点E 、F ,23AB BC ==,,则图中阴影部分的面积为 .6·已知矩形的周长为40cm ,被两条对角线分成的相邻两个三角形的周长 的差为8cm ,则较大的边长为 ·7· 如图,矩形ABCD 中,AC 与BD 交于O 点,BE AC ⊥于E ,CF BD ⊥于F 。
求证BE=CF 。
8· 如图所示,E 为□ABCD 外,AE ⊥CE,BE ⊥DE , 求证:□ABCD 为矩形9·已知矩形ABCD 和点P ,当点P 在图1中的位置时,则有结论:S △PBC =S △PAC +S △PCD 理由:过点P 作EF 垂直BC ,分别交AD 、BC 于E 、F 两点.ABC DEF 第4题图 AB CD EFO第5题图第7题图 第8题图图l ∵ S△PBC+S△PAD=12BC·PF+12AD·PE=12BC(PF+PE)=12BC·EF=12S矩形ABCD又∵ S△PAC+S△PCD+S△PAD=12S矩形ABCD∴ S△PBC+S△PAD= S△PAC+S△PCD+S△PAD.∴ S△PB C=S△PA C+S△P CD.请你参考上述信息,当点P分别在图2、图3中的位置时,S△PB C、S△PAC、S PCD又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.图2 图310·如图所示,△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于点F·(1)求证:EO=FO(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论·课时一答案:1·C;2·D,提示:由勾股定理求得斜边为:1351222=+,斜边的中线长为5.6213=;3·18,提示:AB=5,BC=12,AC=13,cmACABOBOAABLABO18513=+=+=++=∆;4·A,提示:DE=3,AB=AE=6,在直角三角形ADE中,∠DAE=30 ,由折叠的性质得∠BAF=∠EAF=30,设BF=x,则AF=2x,342,32,36422====-xAFxxx;5·3;6·14;7证明:∵四边形ABCD为矩形,∴AC=BD,BO=CO,∵BE AC⊥,CF BD⊥,∴∠BEO=∠CFO=90 ,又∵∠BOE=∠COF第10题图则∆∆BOE COF ≅ ∴BE=CF8·连接AC 、BD ,AC 与BD 相交于点O ,连接OE 在□ABCD 中,AO=OC,BO=DO · 在DEB Rt ∆中,OE=BD 21, 在AEC Rt ∆中,OE=AC 21,∴BD=AC, ∴□ABCD 为矩形· 9· 猜想结果:图2结论S △PBC =S △PAC +S △PCD ; 图3结论S △PBC =S △PAC -S △PCD 证明:如图2,过点P 作EF 垂直AD ,分别交AD 、BC 于E 、F 两点. ∵ S △PBC =12BC·PF=12BC·PE+12BC·EF=12AD·PE+12BC·EF=S △PAD +12S 矩形ABCD S △PAC +S △PCD =S △PAD +S △ADC =S △PAD +12S 矩形ABCD∴ S △PBC =S △PAC +S △P CD10· (1)证明:∵MN ∥BC ,∴∠BCE =∠CEO 又∵∠BCE =∠ECO∴∠OEC =∠OCE ,∴OE =OC ,同理OC =OF ,∴OE =OF(2)当O 为AC 中点时,AECF 为矩形,∵EO =OF (已证),OA =OC ∴AECF 为平行四边形,又∵CE 、CF 为△ABC 内外角的平分线 ∴∠EOF =90°,∴四边形AECF 为矩形 课时二菱形1· 如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,E 为BC 的 中点,则下列式子中一定成立的是( ) A .AC=2OE B .BC=2OE C .AD=OE D .OB=OE2· 如图,在菱形ABCD 中,不一定成立的( ) A ·四边形ABCD 是平行四边形B ·AC ⊥BDC ·△ABD 是等边三角形D ·∠CAB =∠CAD3· 如图,如果要使ABCD 成为一个菱形,需要添加一个条件,那么你添加的条件是 .4· 菱形的两条对角线长分别是6和8,则菱形的边长为 。
2019-2020年八年级数学课时练:特殊四边形
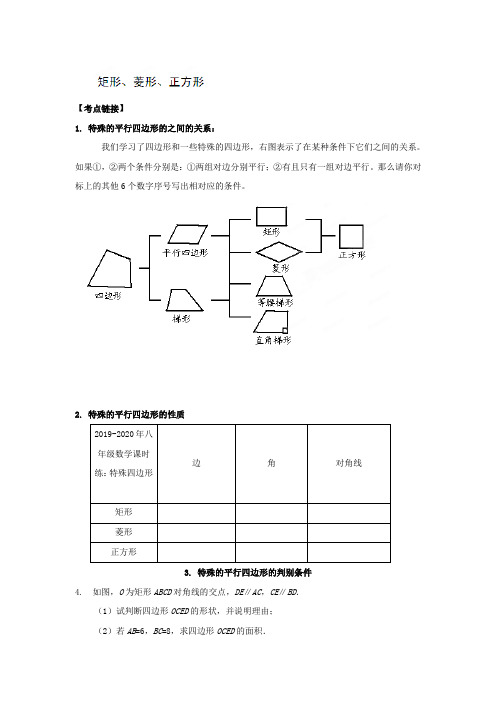
【考点链接】1. 特殊的平行四边形的之间的关系:我们学习了四边形和一些特殊的四边形,右图表示了在某种条件下它们之间的关系。
如果①,②两个条件分别是:①两组对边分别平行;②有且只有一组对边平行。
那么请你对标上的其他6个数字序号写出相对应的条件。
2. 特殊的平行四边形的性质3. 特殊的平行四边形的判别条件4. 如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)试判断四边形OCED的形状,并说明理由;(2)若AB=6,BC=8,求四边形OCED的面积.DC B AOE5.如图,在等腰梯形ABCD 中,点E 、F 、G 、H 分别是边AB 、BC 、CD 、AD 的中点. 试判断四边形EFGH 的形状,并说明理由;6.如图,在△ABC 中,点O 是AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN 交∠BCA 的角平分线于点E ,交∠BCA 的外角平分线于点F .(1)求证:EO =FO ;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.(3)在(2)的条件下,若要使矩形AECF 成为正方形,则△ABC 需满足的条件是________。
ABCEF M NOB C【自我挑战】7.如图所示,正方形ABCD 的面积为12,ABE △是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD PE +的和最小,则这个最小值为___________8.如图,抛物线232y ax x =--与x 轴正半轴交于点(30)A ,,以OA 为边在x 轴上方作正方形OABC ,延长CB 交抛物线于点D ,再以BD 为边向上作正方形BDEF . (1)求a 的值. (2)求点F 的坐标.A EPB C9.如图甲,分别以两个彼此相邻的正方形OABC 与CDEF 的边OC 、OA 所在直线为x 轴、y 轴建立平面直角坐标系(O 、C 、F 三点在x 轴正半轴上).若⊙P 过A 、B 、E 三点(圆心在x 轴上),抛物线c bx x y ++=241经过A 、C 两点,与x 轴的另一交点为G ,M 是FG 的中点,正方形CDEF 的面积为1. (1)求B 点坐标;(2)求证:ME 是⊙P 的切线;(3)设直线AC 与抛物线对称轴交于N ,Q 点是此对称轴上不与N 点重合的一动点,①求△ACQ周长的最小值;②若FQ=t,S△ACQ=s,直接写出....s与t之间的函数关系式.图甲图乙(备用图)24.解:(1)如图甲,连接PE 、PB ,设PC =n∵正方形CDEF 面积为1∴CD =CF =1根据圆和正方形的对称性知OP =PC =n ∴BC =2PC =2n ………1分而PB =PE ,22222254n n n PC BC PB =+=+=1)1(2222++=+=n EF PF PE∴2251)1(n n =++解得n=1 (21-=n 舍去) ……………2分 ∴BC =OC =2 ∴B 点坐标为(2,2)………3分 (2)如图甲,由(1)知A (0,2),C (2,0) ∵A ,C 在抛物线上∴2412++=bx x y ∴23-=b ∴抛物线的解析式为223412+-=x x y 即41)3(412--=x y ∴抛物线的对称轴为3x =,即EF 所在直线 ∵C 与G 关于直线3x =对称, ∴CF =FG =1 ∴FM =21FG =21在Rt △PEF 与Rt △EMF 中EF PF =2,221:1==FM EF ∴EF PF =FMEF∴△PEF ∽△EMF …………5分 ∴∠EPF =∠FEMPEM =∠PEF +∠FEM =∠PEF +∠EPF =90°∴ME 与⊙P 相切……………………………………………………………………6分 (注:其他方法,参照给分)(3)①如图乙,延长AB 交抛物线于A ',连A C '交对称轴x=3于Q ,连AQ则有AQ =A 'Q ,△ACQ 周长的最小值为(AC +A 'C )的长……………………………7分∵A 与A '关于直线x=3对称∴A (0,2),A '(6,2)图甲P∴A 'C =522)26(22=+-,而AC =222222=+…………………8分∴△ACQ 周长的最小值为5222+ ……………………………9分②当Q 点在F 点上方时,S =t+1 ……10分当Q 点在线段FN 上时,S =1-t ……11分当Q 点在N 点下方时,S =t-1 ……12分【关键词】正方形的性质、待定系数法、二次函数2y ax bx c =++(a ≠0)与a ,b ,c 的关系 【答案】解:(1)∵抛物线232y ax x =--与x 轴正半轴交于点(30)A ,∴把(30)A ,的坐标代入232y ax x =--得:9a -3-23=0∴a =21(2)设正方形BDEF 的边长为x ,则D (3+x ,3)∵点D 在抛物线上∴32333212=-+-+)()(x x 解这个方程得:x 1=210-,2102--=x (不合题意,舍去)F (3,110+)。
19.2平行四边形(第一课时)
平行四边形的有关概念
平行四边形定义:两组对边分别平行的四边形叫做平行四边形
平行四边形的表示:平行四边形用符号“□ “表示。
如图1所示,平行四边形ABCD记作“□ABCD”,读作”平 行四边形ABCD”。
A
B
注意:顶点字母按顺时针或逆时针方向来排列。
对边: AB与CD,AD与BC
B
图3
C
(2)由(1)知 ∠AEB=∠ABE=40°, ∴∠A=180°- (40°+40°)=100° ∵∠C=∠A(平行四边形的对角相等) ∴∠C=100°
练一练:
1.如图,AB∥EF∥DC,AD∥GH∥BC, A E
D
那么图中共有__9__个平行四边形。 G
K
H
BF
C
2.填一填:在□ABCD中,AB=a,BC=b,∠B=60°,那么
平行四边形。 (2)性质定理1 平行四边形的对边相等。 (3)性质定理2 平行四边形的对角相等。 (4)推论1 夹在两条平行线间的平行线段相等。 (5)推论2 平行线间的距离处处相等。
布置作业 & 课后反馈
课堂作业:习题20.2 2、3题 家庭作业:习题20.2 第1题
对角: ∠A与∠C, ∠B与∠D
D
邻角: ∠A与∠B,∠B与∠C,∠C与∠D,∠D与∠A 等。(平行四边形的邻角互补)
C 图1
实验操作 & 猜想性质
画一画:你能根据定义快速地画一个平行四边形吗?
量一量:用刻度尺和量角器测量一下你所画的平行四边
形的对边和对角,你发现了什么?
推理论证 & 归纳性质
例2.已知:如图4,过△ABC的三个顶点,分别作对边的平行
19.2平行四边形的判定定理(2)

如图 A( 3, 2 ), B( 1, 1), C( 3, 2 ), D(1, 1)
四边形ABCD是不是平行四边形?请给出证明.
3, 2 ) 与 C( 3, 2 )关于原点O对称
A(
y
D
B( 1, 1) 与 D(1, 1) 关于原点O 对称
∴O平分AC,O平分BD 连接对角线AC,BD则有 OA=OC,OB=OD
A
E O F
D
B
C
讨论:根据现有条件,说说你准备选用哪种方法证明? 大概的步骤是怎样的?
例1:已知:E、F是平行四边形ABCD对角线AC 上的两点,并且AE=CF。
大 显 身 手
B
求证:四边形BFDE是平行四边形 证明: 连接对角线BD,交AC于点O
A
E
O F
D
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO ∵AE=CF ∴AO-AE=CO-CF ∴EO=FO
19.2平行四边形的判定(2)
A
D
平行四边形有哪些性质?
B
C
Ⅰ.边: 平行四边形对边平行且相等 Ⅱ.角:
平行四边形对角相等、邻角互补
Ⅲ. 对角线: 平行四边形对角线互相平分.
我们学过平行四边形有哪些判定方法?
两组对边分别平行 从边看: 两组对边分别相等 一组对边平行且相四边形是否还有其它的方法?
方法四该如何证明?
A
O B C D
A
D
B
C
已知:在四边形ABCD中,对角线AC,BD交于点O, 且OA=OC,OB=OD, 求证:四边形ABCD是平行四边形 证明∵在三角形AOD与三角形COB中
∵ AO=CO,OD=OB,∠AOD=∠COB
新课标人教版初中数学八年级下册第十九章19.2特殊的平行四边形--正方形的判定-精品课件
练习1:判断 (1)四个角都相等的四边形是正方形 (2)四条边都相等的四边形是正方形 (3)对角线相等的菱形正方形 (4)对角线互相垂直的矩形是正方形 (5)对角线垂直且相等的四边形是正方形 (6)四边相等,有一角是直角的四边形是 正方形
例2 已知:在正方形ABCD中,A′、B ′、C ′、 D ′分别从顶点A、B、C、D沿AB、BC、CD、 DA方向同时以同样速度向B、C、D、A移动。
D
M
A
E
F
C
N
B
练习2(2019年山东省济南市中考试题)如图,是 一块在电脑屏幕上出现的矩形色块图,由5种颜色 不同的正方形组成。设中间最小的一个正方形边 长为1,则这个矩形的面积是
练习4 (2019年陕西省中考题)如图,在矩形 ABCD中,点E、F分别在AB、CD上,BF平行 于DE。若AD=12cm,AB=7cm,且AE:EB=5: 2,求阴影部分的面积。
例题3:已知正方形ABCD中,Q在CD上,且 DQ=QC,P在BC上,AP=CD+CP; 求证:AQ 平分∠DAP.
证明:延长AQ交BC延长线与E,
∵四边形ABCD是正方形, ∴AD=CD,AD∥CD;
A
D
∴∠D=∠QCE,∠DAQ=∠E, 又∵DQ=CQ,
Q
∴⊿ADQ≌⊿ECQ (AAS).
∴∴ACDD==CCEE,,又∴AADP==CCDD,+CP=CE+CP=EPB.
①AE与BF相等吗?为什么?
②AE与BF是否垂直?说明你的理由。
A
D
F G
BE
C
练习7:如图,已知正方形ABCD中,
E、F分别为BC和DC上的点,且
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学:19.2特殊的平行四边形
课时一矩形
1.矩形具有而平行四边形不具有的性质是( )
A.对边相等 B.对角相等 C.对角互补 D.对角线平分
2.直角三角形中,两直角边长分别为12和5,则斜边中线长是( )
A.26 B.13 C.8.5 D.6.5
3.矩形ABCD对角线AC、BD交于点O,AB=5,12,cmBCcm则△ABO的周长为等于
.
4. 如图所示,四边形ABCD为矩形纸片.把纸片ABCD折叠,
使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,
则AF等于 ( )
A.34 B.33 C.24 D.8
5. 如图所示,矩形ABCD的对角线AC和BD相交于点O,
过点O的直线分别交AD和BC于点E、F,23ABBC,,
则图中阴影部分的面积为 .
6.已知矩形的周长为40cm,被两条对角线分成的相邻两个三角形的周长
的差为8cm,则较大的边长为 .
7. 如图,矩形ABCD中,AC与BD交于O点,BEAC于E,CFBD于F。
求证BE=CF。
8. 如图所示,E为□ABCD外,AE⊥CE,BE⊥DE,
求证:□ABCD为矩形
9.已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+S△PCD理由:过点P
作EF垂直BC,分别交AD、BC于E、F两点.
A
B
C
D
E
F
第4题图
A
B
C
D
E
F
O
第5题图
第7题图
第8题图
课时二菱形
1. 如图,在菱形ABCD中,对角线AC、BD相交于点O,E为BC的
中点,则下列式子中一定成立的是( )
A.AC=2OE B.BC=2OE
C.AD=OE D.OB=OE
2. 如图,在菱形ABCD中,不一定成立的( )
A.四边形ABCD是平行四边形
B.AC⊥BD
C.△ABD是等边三角形
D.∠CAB=∠CAD
3. 如图,如果要使ABCD成为一个菱形,需要添加一个条件,那么你添加的条件是 .
4. 菱形的两条对角线长分别是6和8,则菱形的边长为 。
5.□ABCD的对角线相交于点O,分别添加下列条件:①AC⊥BD;②AB=BC;③AC平分∠BAD;
④AO=DO,使得□ABCD是菱形的条件有( )
A.1个 B.2个 C.3个 D.4个
6.菱形的周长为20cm,一条对角线长为8cm,则菱形的面积为 .
7. 在四边形ABCD中,对角线AC、BD交于点O,从(1)AB=CD;(2)AB∥CD;(3)OA=OC;(4)OB=OD;
(5)AC⊥BD;(6)AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形。如
(1)(2)(5)ABCD是菱形,再写出符合要求的两个:________ABCD是菱形;________ABCD
是菱形。
8. 如图所示,AD是△ABC的角平分线.DE∥AC交AB于E,DF∥AB交
AC于F.四边形AEDF是菱形吗?说明你的理由.
9..□ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F,
四边形AFCE是否是菱形?为什么?
10.. 已知:如图,在□ABCD 中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB
的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
第1题图
A
B
C
D
第2题图
A
D
C B
第3题图
第10题图
第8题图
第9题图
课时三正方形
1. 四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
2. 在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,则△ABO的周长是( )
A.12+122 B.12+62 C.12+2 D.24+62
3. 已知四边形ABCD是菱形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件
即可).
4. 下列命题中的假命题是( ).
A.一组邻边相等的平行四边形是菱形
B.一组邻边相等的矩形是正方形
c 一组对边平行且相等的四边形是平行四边形
D.一组对边相等且有一个角是直角的四边形是矩形
5. 正方形的一条边长是3,那么它的对角线长是_______.
6.
如图,依次连结一个边长为1的正方形各边的中点,得到第二个正方形,再依次连结第二个正方形各
边的中点,得到第三个正方形,按此方法继续下去, 则第六个正方形的面积是 .
7. 如图,四边形ABCD为正方形,△ADE为等边三角形,AC为正方形ABCD的对角线,
则∠EAC=___度.
8. 已知如下图,正方形ABCD中,E是CD边上的一点,
F为BC延长线上一点,CE=CF.
(1)求证:△BEC≌△DFC;
(2)若∠BEC=60°,求∠EFD的度数.
9如图所示,.四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
第6题图
A 第7题图 B C D
E
第8题图
第9题图
10. 把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如
图).试问线段HG与线段HB相等吗?
请先观察猜想,然后再证明你的猜想.
11.如图,点E在正方形ABCD的边CD上运动,AC与BE交于点F.
(1)如图1,当点E运动到DC的中点时,求△ABF与四边形ADEF的面积之比;
(2)如图2,当点E运动到CE:ED=2:1时,求△ABF与四边形ADEF的面积之比.
(3)当点E运动到CE:ED=3:1时,写出△ABF与四边形ADEF的面积之比;当点E•运动到CE:
ED=n:1(n是正整数)时,猜想△ABF与四边形ADEF的面积之比(只写结果,不要求写出计算过
程);
(4)请你利用上述图形,提出一个类似的问题(根据提出的问题给附加分,•最多4分,计入
总分,但总分不超过120分).
D C
A
B
G
H
F
E
第10题图
