相交线与平行线提高篇
(完整)人教版相交线与平行线提高题(含答案),推荐文档

①2121②12③12④人教版相交线与平行线提高题(含答案)一、选择题:1.下列所示的四个图形中,1∠和2∠是同位角...的是( C )A. ②③B. ①②③C. ①②④D. ①④2.如右图所示,点E 在AC 的延长线上,下列条件中能判断...CD AB //( B ) A. 43∠=∠ B. 21∠=∠ C. DCE D ∠=∠ D. ο180=∠+∠ACD D3.一学员练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( A )A. 第一次向左拐ο30,第二次向右拐ο30B. 第一次向右拐ο50,第二次向左拐ο130 C. 第一次向右拐ο50,第二次向右拐ο130 D. 第一次向左拐ο50,第二次向左拐ο130 4.两条平行直线被第三条直线所截,下列命题中正确..的是( D ) A. 同位角相等,但内错角不相等 B. 同位角不相等,但同旁内角互补 C. 内错角相等,且同旁内角不互补 D. 同位角相等,且同旁内角互补 5.下列说法中错误..的个数是( C ) (1)过一点有且只有一条直线与已知直线平行。
(2)过一点有且只有一条直线与已知直线垂直。
(3)在同一平面内,两条直线的位置关系只有相交、平行两种。
(4)不相交的两条直线叫做平行线。
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A. 1个 B. 2个 C. 3个 D. 4个 6.下列说法中,正确..的是( B ) A. 图形的平移是指把图形沿水平方向移动。
B. 平移前后图形的形状和大小都没有发生改变。
C. “相等的角是对顶角”是一个真命题。
D. “直角都相等”是一个假命题。
7.如右图,CD AB //,且ο25=∠A ,ο45=∠C ,则E ∠的度数是( B ) A. ο60 B. ο70 C. ο110 D. ο80E DC BA4321EDC BA8.如右图所示,已知BC AC ⊥ ,AB CD ⊥,垂足分别是C 、D ,那 么以下线段大小的比较必定成立....的是( C ) A. AD CD > B. BC AC < C. BD BC > D. BD CD <9.在一个平面内,任意四条直线相交,交点的个数最多有( B )A. 7个B. 6个C. 5个D. 4个10. 如右图所示,BE 平分ABC ∠,BC DE //,图中相等的角共有( C )A. 3对B. 4对C. 5对D. 6对二、填空题1.把命题“等角的余角相等”写成“如果……,那么……。
相交线与平行线精选综合提高试题

相交线与平行线综合提高一、教学内容:相交线与平行线综合提高1. 了解对顶角的概念,掌握其性质,并会用它们进行推理和计算.2. 了解垂线、垂线段等概念,了解垂线段最短的性质,体会点到直线距离的意义.3. 知道过一点有且仅有一条直线垂直于已知直线,会用三角尺或量角器过一点画一条直线的垂线.4. 知道两直线平行同位角相等,并进一步探索平行线的特征.5. 知道过直线外一点有且仅有一条直线平行于已知直线.会用三角尺和直尺过已知直线外一点画这条直线的平行线.6. 掌握平行线的三个判定方法,并会用它们进行直线平行的推理.二、知识要点:1. 两条直线的位置关系(1)在同一平面内,两条直线的位置关系有两种:相交与平行.(2)平行线:在同一平面内,不相交的两条直线叫平行线.2. 几种特殊关系的角(1)余角和补角:如果两个角的和是直角,称这两个角互为余角.如果两个角的和是平角,称这两个角互为补角.(2)对顶角:①定义:一个角的两边分别是另一个角两边的反向延长线,这两个角叫对顶角.②性质:对顶角相等.(3)同位角、内错角、同旁内角两条直线分别与第三条直线相交,构成八个角.①在两条直线之间并且在第三条直线的两旁的两个角叫做内错角.②在两条直线的同一侧并且在第三条直线同旁的两个角叫做同位角.③在两条直线之间并且在第三条直线同旁的两个角叫做同旁内角.3. 主要的结论(1)垂线①过一点有且只有一条直线与已知直线垂直.②直线外一点与直线上各点连结的所有线段中,垂线段最短.简称:垂线段最短.(2)平行线的特征及判定平行线的判定平行线的特征同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补经过直线外一点,有且只有一条直线与已知直线平行4. 几个概念(1)垂线段:过直线外一点,作已知直线的垂线,这点和垂足之间的线段.(2)点到直线的距离:从直线外一点到这条直线的垂线段的长度.5. 几个基本图形(1)相交线型.①一般型(如图①);②特殊型(垂直,如图②).AB C DOABCD O ①②(2)三线八角.①一般型(如图①);②特殊型(平行,如图②).A BCDEFAB CDEF ①②三、重点难点:重点有两个:一方面要掌握关于相交线和平行线的一些基本事实,另一方面学会借助三角尺上的直角或量角器画已知直线的垂线,用移动三角尺的方法画平行线.难点是是利用对顶角的性质、平行线的特征、两直线平行的条件等进行推理和计算.四、考点分析:考查(1)对顶角的性质;(2)平行线的识别方法;(3)平行线的特征,其中依据平行线的识别与特征解决一类与平行线有关的几何问题是历届中考命题的重要考点.常见题型有填空题、选择题和解答题,单纯考查一个知识点的题目并不难,属于中低档题,将平行线的特征与其他知识综合起来考查的题目难度较大,属高档题.【典型例题】例1. 如图所示,已知FC ∥AB ∥DE ,∠α∶∠D ∶∠B =2∶3∶4,求∠α、∠D 、∠B 的度数.ABCDEF 12α分析:由条件∠α∶∠D ∶∠B =2∶3∶4.可以分别设出∠α、∠D 、∠B ,再根据题目给出的条件建立方程求解.解:设∠α=2x ,∠D =3x ,∠B =4x . ∵FC ∥AB ∥DE ,∴∠2+∠B =180°,∠1+∠D =180°, ∴∠2=180°-4x ,∠1=180°-3x , 又∵∠1+∠α+∠2=180°,∴180°-3x +2x +180°-4x =180°, ∴5x =180°,x =36°,∴∠α=2x =72°,∠D =3x =108°,∠B =4x =144°.评析:解答这类计算题不仅要熟悉图形的性质,还要善于进行等量转化,把待求的角逐步和已知条件建立起联系来,当待求结论要经过复杂过程才能求得时,一定要思路清晰、叙述表达严密.例2. 如图所示,直线a ∥b ,则∠A =__________.AB C Ea b28°50°ABCDEa b28°50°分析:已知条件a ∥b 能转化为三线八角,过A 作AD ∥a ,那么已知的两个角可转换到顶点A (都用内错关系转化),可求∠A. 由AD ∥a ,a ∥b ,可知AD ∥b ,由两直线平行内错角相等得:∠DAB =∠ABE =28°,∠DAE =50°,∴∠EAB =50°-28°=22°.解:22°评析:用平行线三线八角把已知角转化成以A 为顶点的角即可.例3. 已知:如图所示,DF ∥AC ,∠1=∠2.试说明DE ∥AB.ABC DEF 12分析:要说明DE ∥AB ,可以证明∠1=∠A ,而由DF ∥AC ,有∠2=∠A ,又因为∠1=∠2,故有∠1=∠A ,从而结论成立.解:∵DF ∥AC (已知),∴∠2=∠A (两直线平行,同位角相等). ∵∠1=∠2(已知), ∴∠1=∠A (等式性质),∴DE ∥AB (同位角相等,两直线平行).评析:说明两直线平行的方法有:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行;④平行于同一条直线的两条直线互相平行;⑤垂直于同一条直线的两条直线互相平行.例4. 试说明:两条平行线被第三条直线所截,一对内错角的平分线互相平行. 分析:先根据题意画出图形,标注字母,找出已知条件和问题,再进行说明.ABCDG HMN EF12解:已知:如图所示,AB ∥CD ,EF 分别交AB 、CD 于G 、H ,GM 、HN 分别平分∠BGF 、∠EHC. 说明GM ∥HN .∵GM 、HN 分别平分∠BGF 、∠EHC (已知), ∴∠1=∠BGF ,∠2=∠EHC (角平分线定义). ∵AB ∥CD ,∴∠BGF =∠EHC (两直线平行,内错角相等). ∴∠1=∠2.∴GM ∥HN (内错角相等,两直线平行).评析:(1)上题把内错角平分线改为同位角平分线,原结论也成立,请同学们自己试着解一解.(2)此题为文字题,首先应根据题意画出图形,再根据已知条件和结论结合图形写出解题过程.例5. 如图所示,已知CE ∥DF ,说明∠ACE =∠A +∠ABF .ABCDEFG分析:结论中∠ACE ,∠A 与∠ABF 在三个顶点处,条件CE ∥DF 不能直接运用,结论形式启示我们用割补法,即构造一个角等于∠A +∠ABF ,因此想到在点A 处补上一个∠GAB =∠ABF ,只要GA ∥DF 即可,同时可得GA ∥CE ,∠GAC =∠ACE ,结论便成立.解:过A 作AG ∥DF ,∴∠GAB =∠ABF (两直线平行,内错角相等) 又∵AG ∥DF ,CE ∥DF (已知)∴AG ∥CE (平行于同一直线的两条直线互相平行) ∴∠GAC =∠ACE (两直线平行,内错角相等) 又∵∠GAC =∠BAC +∠GAB (已知) ∴∠ACE =∠BAC +∠ABF (等量代换). 评析:(1)割补法是一种常用方法.(2)此题还可以过点C 作一条直线与AB 平行,把∠ACE 分成两个角后,分别说明这两个角与∠A 、∠ABF 相等.例6. 解放战争时期,有一天江南某游击队在村庄A 点出发向正东行进,此时有一支残匪在游击队的东北方向B 点处(如图所示,残匪沿北偏东60°角方向,向C 村进发.游击队步行到A’处,A’正在B 的正南方向上,突然接到上级命令,决定改变行进方向,沿北偏东30°方向赶往C 村.问游击队进发方向A ’C 与残匪行进方向BC 至少是多少角度时,才能保证C 村村民不受伤害?A BCA'北东A BCA'北东D E分析:如图可知A ’C 与BC 的夹角最小值是∠BCA ’.本题关键是引辅助线,延长A’B 到D ,过C 作CE ∥A’D ,通过平行线特征来求解.解:根据题意∠DBC =60°,∠BA’C =30°. 过点C 作CE ∥A’B ,则∠BCE =∠DBC =60°,∠A’CE =∠BA’C =30°. ∴∠BCA’=∠BCE -∠A’CE =60°-30°=30°. 夹角至少为30°时才能保证C 村村民不受伤害.评析:本题较综合地运用了角、方位角、平行线的有关知识.【方法总结】 1. 方程的思想几何图形中常见一些已知线段、角,而要求未知线段和角,我们可以把它们分别视为已知量、未知量,用方程的思想方法求解.2. 比较的思想方法利用比较这一思想方法,分清易混概念和性质,加深对概念性质的理解和认识.例如平行线的性质是理解判定定理时最易混淆的,学习时,可通过比较其异同弄清它们的区别和联系.3. 推理的方法推理是一个思维形式,它是从一个或几个判断得出新判断的思维形式.推理时要时刻明确最终目标,最后推出结论,推理过程要步步有根据,不能“想当然”,推理的根据,可以是已知条件、定义、性质、基本事实等.【模拟试题】(答题时间:60分钟)一. 选择题1. 如图所示,下列说法中正确的是()A. 图中没有同位角、内错角、同旁内角B. 图中没有同位角和内错角,但有一对同旁内角C. 图中没有内错角和同旁内角,但有三对同位角D. 图中没有同位角和内错角,但有三对同旁内角AB C2. 一条公路两次转弯后又回到原来的方向(即AB∥CD,如图),如果第一次转弯时的∠B=140°,那么,∠C应是()A. 140°B. 40°C. 100°D. 180°140°AB CD3. 如图所示,下列说法正确的是()A. 若AB∥CD,则∠B+∠A=180°B. 若AD∥BC,则∠B+∠C=180°C. 若AB∥CD,则∠B+∠D=180°D. 若AD∥BC,则∠B+∠A=180°AB CD4. 如图所示,要得到DE∥BC,需要条件()A. CD⊥AB,GF⊥ABB. ∠DCE+∠DEC=180°C. ∠EDC=∠DCBD. ∠BGF=∠DCBABC D EF G5. 如图所示,AB ⊥AC ,AD ⊥BC ,DE ∥AB ,则∠CDE 与∠BAD 的关系是( ) A. 互余 B. 互补 C. 相等 D. 不能确定ABCDE6. 如图所示,已知AB ∥CD ,CE 平分∠ACD ,∠A =110°,则∠ECD 的度数等于( ) A. 110° B. 70° C. 55° D. 35°C ABED*7. 两条平行线被第三条直线所截,角平分线互相垂直的是( ) A. 内错角 B. 同旁内角 C. 同位角 D. 内错角或同位角**8. 学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)):P(1)P(2)P(3)P(4)从图中可知,小敏画平行线的依据有:( )①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.( )A. ①②B. ②③C. ③④D. ①④二. 填空题1. 如图所示,A 、B 之间是一座山,一条铁路要通过A 、B 两地,在A 地测得B 地在北偏东70°,如果A 、B 两地同时开工修建铁路,那么在B 地应按__________方向开凿,才能使铁路在山腹中准确接通.AB北70°北2. 如图所示,A 、C 、B 在同一直线上,DC ⊥CE 于C ,∠ACD =53°,则∠BCE =_______.ABCDE3. 如图所示,四边形ABCD 中,∠1=∠2,∠D =72°,则∠BCD =__________.ABCD12*4. 如图所示,AB ∥CD 、BEFD 是AB 、CD 之间的一条折线,则∠1+∠2+∠3+∠4=__________.ABCDE F12345. 如图所示,a ∥b ,∠1=3∠2,则∠1=__________,∠2=__________.ab 12*6. 已知,如图,AD 与BC 相交于点O ,AB ∥CD ,如果∠B =20°,∠D =40°,那么∠BOD 为__________度.ABCD O7. 如图所示,若AE ∥BD ,那么相等的角有__________;若AB ∥EC ,那么互补的角有__________.A CDB1234567E**8. 设a 、b 、c 为平面内三条不同的直线.(1)若a ∥b ,c ⊥a ,则c 与b 的位置关系是__________;(2)若c ⊥a ,c ⊥b ,则a 与b 的位置关系是__________;(3)若a ∥b ,则c 与b 的位置关系是__________.三. 解答题1. 如图所示,已知AB ⊥BC ,BC ⊥CD ,∠1=∠2,试判断BE 与CF 的关系,并说明理由.ABCD12EF2. 如图所示,已知AB ∥CD ,直线EF ⊥CD 于F ,∠1=2∠2,求∠2的度数.CDEF A B12G*3. 如图所示,已知AB ∥DE ,∠ABC =60°,∠CDE =140°,求∠BCD 的度数.AB CDE4. 如图所示,小刚准备在C 处牵牛到河边AB 饮水.(1)请用三角板作出小刚的最短路线(不考虑其他因素);(2)如图乙,若小刚在C 处牵牛到河边AB 饮水,并且必须到河边D 处观察河水的水质情况,请作出小刚行走的最短路线(不写作法,保留作图痕迹).甲ABC乙ABCD典型例题例1 如图2-45是梯形的有上底的一部分,已知量得∠A =115°,∠D=100°,梯形另外两个角各是多少度?图2-45分析:已知是梯形,可知它的上、下两底平行,要求另外两个角的度数,直接应用平行线的特征即可求出.解:因为梯形上、下两底平行,所以,∠A 与∠B 互补,∠D 与∠C 互补,于是∠B =180°-115°=65°,∠C =180°-100°=80°梯形的另外两个角分别是65°、80°.例2 已知,如图2-46,直线a ∥b ,c ∥d ,∠1=70°,求∠2、∠3的度数.图2-46分析:这是平行线的特征的应用的计算题,要注意格式.解:∵a∥b(已知),∴∠2=∠1=70°(两直线平行,内错角相等)∵c∥d(已知),∴∠3=∠2=70°(两直线平行,同位角相等)参考例题[2.2.1探索直线平行的条件(一) ][例1]若∠1=52°,如图2-18,问应使∠C为多少度时,能使直线AB∥CD?图2-18分析:要使直线AB∥CD,则需使同位角相等,即∠1=∠C.这样即可求出.解:若∠1=52°,当∠C=52°时,直线AB∥CD.[例2]如图2-19,若∠1=∠4,∠1+∠2=180°,则AB、CD、EF的位置关系如何?图2-19分析:由已知∠1=∠4,可知:AB∥EF,∴可猜想:AB∥CD∥EF.由图中可知:∠2+∠3=180°,而已知:∠1+∠2=180°.∴由同角的补角相等可得∠1=∠3,这样得到AB∥CD.由“两条直线都与第三条直线平行,则这两条直线平行”可得:AB∥CD∥EF.解:⎪⎭⎪⎬⎫→∠=∠→∠=∠→⎭⎬⎫︒=∠+∠︒=∠+∠EF||CD||AB AB 41311802318021 →AB ∥CD ∥EF . 二、参考练习1.如图2-20,∠1=45°,∠2=135°,则l 1∥l 2吗?为什么? 解:平行.∵∠1+∠3=180°,∠1=45°. ∴∠3=135°,又∵∠2=135°. ∴∠2=∠3,因此l 1∥l 2.图2-20 图2-212.如图2-21,∠1=120°,∠2=60°,问直线a 与b 的关系? 解:直线a 与b 平行.∵:∠2+∠3=180°,∠2=60°, ∴∠3=120°, 又∵∠1=120°.∴∠1=∠3,因此a ∥b .3.在三角形ABC 中,∠B =90°,D 在AC 边上,DF ⊥BC 于F ,DE ⊥AB 于E ,则线段AB 与DF 平行吗?BC 与DE 平行吗?为什么?图2-22解:线段AB 与DF 平行.线段BC 与DE 也平行. ∵:DF ⊥BC 于F ,则∠DFC =90°, 又∵∠B =90°,∴∠B =∠DFC , 因此AB ∥DF .BC 与ED 平行的理由同上.专业资料参考【试题答案】一. 选择题1. D2. A3. D4. C5. A6. D7. B8. C二. 填空题1. 南偏西70°2. 37°3. 108°4. 540°分别过点E、F作AB的平行线.5. 135°,45°6. 607. ∠1=∠3,∠5=∠6;∠B与∠BCE,∠BAE与∠68. 垂直,平行,平行或相交三. 解答题1. ∵AB⊥BC,BC⊥CD,∴∠ABC=∠BCD=90°,又∵∠1=∠2,∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF,∴BE∥CF.2. ∵AB∥CD,∴∠1=∠CFG=2∠2,∵EF⊥CD,∴∠CFE=∠CFG+∠2=2∠2+∠2=3∠2=90°,∴∠2=30°.3. 延长ED交BC于点G,过点C作CF∥AB,则∠BCD=∠BCF-∠DCF=∠ABC-∠GDC=60°-(180°-∠CDE)=20°.4. (1)甲:过C作AB的垂线,垂足与C点之间的线段为最短路线,根据是:垂线段最短.(2)乙:连结CD得线段CD就是最短线段,根据是:两点之间线段最短.word格式整理。
相交线与平行线提高训练题
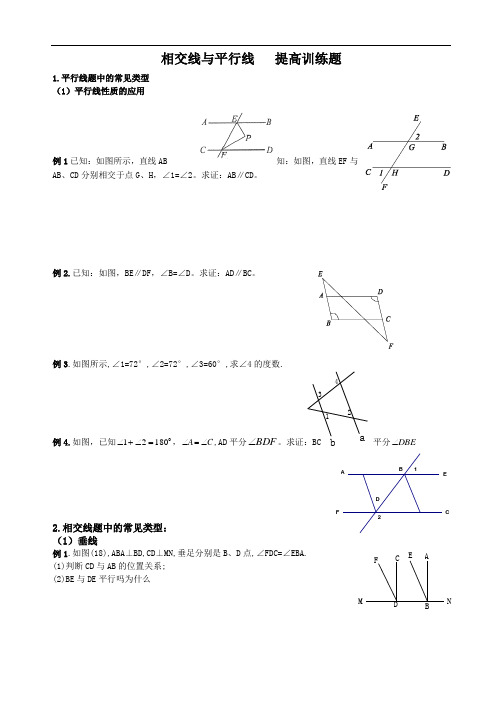
1DE2CFABba3412NMFE DCBA相交线与平行线 提高训练题1.平行线题中的常见类型 (1)平行线性质的应用例1已知:如图所示,直线AB知:如图,直线EF 与AB 、CD 分别相交于点G 、H ,∠1=∠2。
求证:AB∥CD。
例2.已知:如图,BE∥DF,∠B=∠D。
求证:AD∥BC。
例3.如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.例4.如图,已知018021=∠+∠,C A ∠=∠,AD 平分BDF ∠。
求证:BC 平分DBE ∠2.相交线题中的常见类型: (1)垂线例1.如图(18),ABA⊥BD,CD⊥MN,垂足分别是B 、D 点,∠FDC=∠EBA. (1)判断CD 与AB 的位置关系; (2)BE 与DE 平行吗为什么例2. 已知:如图,AO BO ⊥∠=∠,12。
求证:CO DO ⊥。
例3.如图,已知,DA AB DE ⊥平分,ADC CE ∠平分,1290,BCD ∠∠+∠=求证:BC AB ⊥.(2)相交例1.已知:如图,∠1=35°,AB⊥CD,垂足为O ,EF 经过点O.求∠2、∠3、∠4的度数。
例2. 如图,直线AB 、CD 、EF 交于点O ,是它的余角的2倍,∠=∠AOE DOF 2,且有OG OA ⊥,求∠EOG 的度数。
3、练习1.已知:如图1所示,AB 图所示,已知AB图所示,已知AB ∥CD,直线EF 分别交AB,CD 于E,F,EG•平分∠BEF,若∠1=72°,则∠2=_______.ED CBA21OEFB C D2 3 1O AAD E O F CG BFEDC B A 12GF EDCBA 124.如图所示,已知直线AB,CD 被直线EF 所截,若∠1=∠2,•则∠AEF+∠CFE=________.5.如图,已知11,,,44AB CD EAF EAB ECF ECD ∠=∠∠=∠求证:34AFC AEC ∠=∠FEDC BA。
《相交线与平行线》提高练习题

《相交线与平行线》提高练习题、选择题:4 .两条平行直线被第三条直线所截,下列命题中正确的是()5. 下列说法中错误 的个数是( )(1) 过一点有且只有一条直线与已知直线平行。
(2) 过一点有且只有一条直线与已知直线垂直。
(3) 在同一平面内,两条直线的位置关系只有相交、平行两种。
(4) 不相交的两条直线叫做平行线。
(5) 有公共顶点且有一条公共边的两个角互为邻补角。
A. 1 个B. 2 个C. 3 个D. 4 6.下列说法中,正确的是()A.图形的平移是指把图形沿水平方向移动。
C. “相等的角是对顶角”是一个真命题。
7 .如右图,AB//CD ,且 A 25 , C 45个B. 平移前后图形的形状和大小都没有发生改变。
D.“直角都相等”是一个假命题。
,贝U E 的度数是( ) AB>E2 •如右图所示,点 AB//CD (A. 34 B.1C. D DCED. D3. 一学员练习驾驶汽车, 两次拐弯后,2ACD 180行驶的方向与原来的方向相同, A. 第一次向左拐30,第二次向右拐30 B. 第一次向右拐50,第二次向左拐130 C.第一次向右拐50,第二次向右拐130 D.第一次向左拐50,第二次向左拐130 A.同位角相等,但内错角不相等 B. 同位角不相等,但同旁内角互补 C.内错角相等,且同旁内角不互补D.同位角相等,且同旁内角互补1.E 在AC 的延长线上,下列条件中能判断)BD这两次拐弯的角度可能是30°角的斜坡,如图②,现要在斜坡上竖一电线杆,当电线杆与斜坡成的1=°时,电线杆与地面垂直。
4 .如图③,按角的位置关系填空:A 与1是6.如图⑤,已知a//b ,若 1 50,则____ ;若 3=100,则 2___A. 60B.70 C. 110D.808 •如右图所示,已知 AC BC , CD么以下线段大小的比较必定成立.的是( A. CD AD B. AC BC C.BC BDD.CDBDAB ,垂足分别是C 、 )D ,那BA. 7个B. 6 个C. 5 个D. 4 个 10.如右图所示,BE 平分 ABC , DE // BC , 图中相等的角共有( )A. 3对B. 4对 C. 5 对 D. 6 对 9 .在一个平面内,任意四条直线相交,交点的个数最多有() 、填空题 1.把命题“等角的余角相等”写成“如果……,那么 的形式为 2 .用吸管吸易拉罐内的饮料时,如图①,1=110,则 2=(拉罐的上下底面互相平行) 图①5.如图④,若 12=220 ,贝V 3=a b3 .有一个与地面成7•如图⑥,为了把ABC平移得到A B C,可以先将ABC向右平移____ 格,再向上平移____ 格。
人教版相交线与平行线提高题(含答案)

①2121②12③12④人教版相交线与平行线提高题(含答案)一、选择题:1.下列所示的四个图形中,1∠和2∠是同位角...的是( C )A 。
②③ B. ①②③ C. ①②④ D 。
①④2.如右图所示,点E 在AC 的延长线上,下列条件中能判断...CD AB //( B ) A. 43∠=∠ B 。
21∠=∠ C 。
DCE D ∠=∠ D.180=∠+∠ACD D3.一学员练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( A )A 。
第一次向左拐 30,第二次向右拐 30B 。
第一次向右拐 50,第二次向左拐130 C 。
第一次向右拐50,第二次向右拐130 D. 第一次向左拐50,第二次向左拐130 4.两条平行直线被第三条直线所截,下列命题中正确..的是( D ) A. 同位角相等,但内错角不相等 B. 同位角不相等,但同旁内角互补 C. 内错角相等,且同旁内角不互补 D 。
同位角相等,且同旁内角互补 5.下列说法中错误..的个数是( C ) (1)过一点有且只有一条直线与已知直线平行. (2)过一点有且只有一条直线与已知直线垂直。
(3)在同一平面内,两条直线的位置关系只有相交、平行两种。
(4)不相交的两条直线叫做平行线。
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A. 1个 B. 2个 C 。
3个 D. 4个 6.下列说法中,正确..的是( B ) A. 图形的平移是指把图形沿水平方向移动。
B. 平移前后图形的形状和大小都没有发生改变. C 。
“相等的角是对顶角"是一个真命题. D 。
“直角都相等”是一个假命题. 7.如右图,CD AB //,且25=∠A ,45=∠C ,则E ∠的度数是( B ) A.60 B 。
70 C 。
110 D.80E DC BA4321EDCBA8.如右图所示,已知BC AC ⊥ ,AB CD ⊥,垂足分别是C 、D ,那 么以下线段大小的比较必定成立....的是( C ) A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
b
a
3
4
1
2
相交线与平行线提高篇
1.平行线题中的常见类型
(1)平行线性质的应用
例1已知:如图所示,直线AB//CD,直线EF分别交AB、CD于点E、F,BEF的平分线与DFE的平分
线相交于点P。试说明P为什么等于90°。
例2:如果两个角的两边分别平行,而其中一个角比另一个角的3倍少40°,求这两个角的度数。
(2)平行线判定的应用
例1.已知:如图,直线EF与AB、CD分别相交于点G、H,∠1=∠2。求证:AB∥CD。
例2.已知:如图,BE∥DF,∠B=∠D。求证:AD∥BC。
例3.如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
2
1
D
E
2
C
F
A
B
NM
F
E
D
C
B
A
例4.如图,已知018021,CA,AD平分BDF。求证:BC平分DBE
2.相交线题中的常见类型:
(1)垂线
例1.如图(18),ABA⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
(1)判断CD与AB的位置关系;
(2)BE与DE平行吗?为什么?
例2. 已知:如图,AOBO,12。求证:CODO。
例3.如图,已知,DAABDE平分,ADCCE平分,1290,BCD求证:BCAB.
(2)相交
例1.已知:如图,∠1=35°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3、∠4
的度数。
E
D
CB
A
2
1
O
E
F
B
C
D
2 3
1
O A
3
例2. 如图,直线AB、CD、EF交于点O,DOB是它的余角的2倍,AOEDOF2,且有OGOA,
求EOG的度数。
3、练习
1.已知:如图1所示,AB//CD,11102120°,°,则_______。
2.如图所示,已知AB//CD,请你观察EBD、、之间有什么关系?证明你所得到的结论。
3.如图所示,已知AB∥CD,直线EF分别交AB,CD于E,F,EG•平分∠BEF,若∠1=72°,则∠2=_______.
GFEDCBA12
A
D
E O F
C
G B
4
F
E
D
C
B
A
1
2
4.如图所示,已知直线AB,CD被直线EF所截,若∠1=∠2,•则∠AEF+∠CFE=________.
5.如图,已知11,,,44ABCDEAFEABECFECD求证:34AFCAEC
F
E
D
C
BA
