河南省南阳市第一中学高二数学下学期期末考前模拟试题理(扫描版)
河南省南阳市第一中学_学年高二数学下学期开学考试试题理(PDF)【含答案】
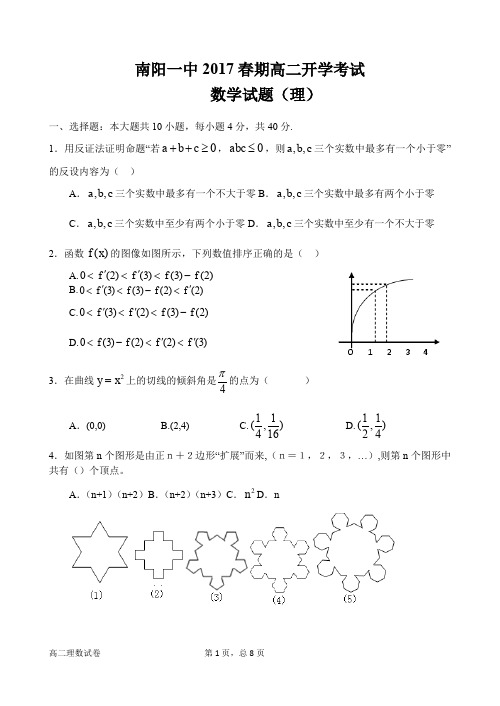
南阳一中2017春期高二开学考试数学试题(理)一、选择题:本大题共10小题,每小题4分,共40分.1.用反证法证明命题“若0a b c ++≥,0abc ≤,则,,a b c 三个实数中最多有一个小于零”的反设内容为( )A .,,a b c 三个实数中最多有一个不大于零B .,,a b c 三个实数中最多有两个小于零C .,,a b c 三个实数中至少有两个小于零D .,,a b c 三个实数中至少有一个不大于零 2.函数)(x f 的图像如图所示,下列数值排序正确的是( )A.)2()3()3()2(0f f f f -<'<'<B.)2()2()3()3(0f f f f '<-<'<C.)2()3()2()3(0f f f f -<'<'<D.)3()2()2()3(0f f f f '<'<-<3.在曲线2y x =上的切线的倾斜角是4π的点为( ) A .(0,0) B.(2,4) C.11(,)416 D.11(,)244.如图第n 个图形是由正n+2边形“扩展”而来,(n=1,2,3,…),则第n 个图形中共有()个顶点。
A .(n+1)(n+2)B .(n+2)(n+3)C .2n D .n5.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,如果x 1+x 2=6,那么|AB|等于( )A .8B .10C .6D .46.如图所示,椭圆中心在坐标原点,F 为左焦点,当F B →⊥A B →时,其离心率为5-12,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e 等于( )A.5+12 B.5-12C.5-1D.5+1 7.已知双曲线22221x y a b-=(a>0,b>0)的两条渐近线均和圆C :x 2+y 2-6x+5=0相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为( )A .22154x y -= B .22145x y -= C .221x y 36-=D .221x y 63-= 8.在∆ABC 中,c b a ,,为C B A ∠∠∠,,的对边,且1)cos(cos 2cos =-++C A B B ,则( )A .c b a ,,成等差数列B .b c a ,,成等差数列C .b c a ,,成等比数列D .c b a ,,成等比数列9.已知椭圆)20(1cos sin 22πααα<≤=-y x 的焦点在y 轴上,则α的取值范围是( )A .34ππ(,) B.1344ππ(,) C.12ππ(,) D.1324ππ(,)10.抛物线C 1:y=12px 2(p >0)的焦点与双曲线C 2:2213x y -=的右焦点的连线交C 1于第一象限的点M.若C 1在点M 处的切线平行于C 2的一条渐近线,则p=( )A.16 B.8 C.3 D.3二、填空题:本大题共4小题,每小题4分,共16分.11.已知函数的导函数为,若,则 .()f x ()'f x ()()2'1ln f x f x x =+()1f =12.现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为24a .类比到空间,有两个棱长均为a 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为.13.已知数列{2n -1·a n }的前n 项和S n =9-6n ,则数列{a n }的通项公式是______14.曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >的点的轨迹.给出下列三个结论:①曲线C 过坐标原点;②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则12F PF ∆的面积不大于212a . 其中所有正确的结论的序号是 .三、解答题:本大题共4小题,共44分.解答应写出必要的文字说明或推理、验算过程.15.(本小题满分10分)已知函数26()ax f x x b-=+的图像在点M (-1,(1)f -)处的切线方程为250x y ++=,求函数()y f x =解析式。
河南省南阳市第一中学2018_2019学年高二数学下学期开学考试试题文(扫描版)

河南省南阳市第一中学2018-2019学年高二数学下学期开学考试试题文(扫描版)高二文科数学开学考试参考答案1-5 DABAB6-10CCBDC 11-12DB13. 14.[-1,]15.16.217.(Ⅰ);(Ⅱ)或.解:(Ⅰ)若为假命题,则为真命题.若命题p真,即对∀x∈[0,1],恒成立⇔所以.(Ⅱ)命题q:方程表示焦点在x轴上的椭圆∴⇒或.∵p∨q为真命题,且p∧q为假命题∴p、q一真一假①如果p真q假,则有;②如果p假q真,则有.综上实数m的取值范围为或.18.(1)(2)解:(1)由及正弦定理,得. 因为为锐角,所以.(2)由余弦定理,得,又,所以,所以.考点:正余弦定理的综合应用及面积公式.19.解:(1)由题得a n2+a n=2S n,a n+12+a n+1=2S n+1,两式子相减得:结合a n>0得a n+1﹣a n=1,令n=1得a12+a1=2S1,即a1=1,所以{a n}是首项为1,公差为1的等差数列,即a n=n(2)因为b n ==(n ≥2),所以T n =+…+①T n =+…++②①﹣②得T n =1++…+﹣=﹣,所以数列{b n }的前n 项和T n =3﹣.20.(1)y 2=4x .(2)﹣12<k <0.解:(1)设P (x ,y ),由题意可得,P 在直线x +2=0右边,所以P 点到直线x =﹣1和到F (1,0)距离相等,所以P 点的轨迹是顶点在原点,F 为焦点,开口向右的抛物线,∵F 和顶点的距离1,2p =4,所以轨迹C 的方程是y 2=4x .(2)由题意知直线l 的斜率存在设为k ,所以直线l 的方程y =kx+2(k≠0),M (),N ()联立得消去x 得ky2﹣4y+8=0∴,,且△=16﹣32k >0即k . ∴()•()=()•()+y1y2∵,∴﹣12<k <0,满足k ,∴﹣12<k <0.21解:(1)f ′(x )=ax +(1-a )x -b .由题设知f ′(1)=0,解得b =1, (2)f (x )的定义域为(0,+∞), 由(1)知,f (x )=a ln x +1-a2x 2-x ,f ′(x )=a x +(1-a )x -1=()xa x a x )1)(1(---.(i)若a ≤12,则a1-a ≤1,故当x ∈(1,+∞)时,f ′(x )>0,f (x )在(1,+∞)上单调递增.所以,存在x 0≥1,使得f (x 0)<a 1-a 的充要条件为f (1)<aa -1,即1-a 2-1<aa -1,解得-2-1<a <2-1.(ii)若12<a <1,则a1-a >1,故当x ∈⎝ ⎛⎭⎪⎫1,a 1-a 时,f ′(x )<0;当x ∈⎝ ⎛⎭⎪⎫a 1-a ,+∞时,f ′(x )>0. f (x )在⎝ ⎛⎭⎪⎫1,a 1-a 上单调递减,在⎝ ⎛⎭⎪⎫a 1-a ,+∞上单调递增. 所以,存在x 0≥1,使得f (x 0)<aa -1的充要条件为f ⎝ ⎛⎭⎪⎫a 1-a <aa -1.而f ⎝ ⎛⎭⎪⎫a 1-a =a ln a 1-a +a 22(1-a )+a a -1>a a -1,所以不合题意.(iii)若a >1, 则f (1)=1-a 2-1=-a -12<aa -1,符合题意. 综上,a 的取值范围是(-2-1,2-1)∪(1,+∞).22.解:(1)椭圆:的离心率为,可得,,点在椭圆上,可得,解得,,椭圆的标准方程为:; (2)假设在轴上存在定点,使得为定值.设,, 椭圆的右焦点为,设直线的方程为,联立椭圆方程,化为,则,,.令,解得,可得,因此在轴上存在定点,使得为定值.。
南阳市2022-2023学年高二下学期期末数学试题参考答案

南阳市2022-2023学年高二下学期期末数学参考答案一.选择题.1-8.BCAD CCCA 二.选择题.9.AD 10.ABD11.BD12.AC三.填空题.13.17114.13-=x y 15.73+16.22(本空2分)324+=n n a (本空3分)提示16.由题知,若n 为奇数,则n n f =)(;若n 为偶数,则).2()(n f n f =故,21=a )()()()()()()()(n n n f f f f f f f f a 264212531+++++-++++= )()()()()1232112(531-+++++-++++=n n f f f f 11114,222----=-∴+⋅=n n n n nn a a a 112211)()()(2a a a a a a a a n n n n n n +-++-+-=≥∴--- 时,324241)41(42444121+=+--=++++=---n n n n ,又21=a 符合上式324+=∴n n a 四.解答题:17.解:(1)由题知,5)76543(51=++++=x ................1分,54.1)2.29.15.11.11(51=++++=y ................2分32.05513554.1557.41ˆ2=⨯-⨯⨯-=∴b,................5分06.0532.054.1ˆ-=⨯-=a................6分故y 关于x 的线性回归方程为06.032.0-=x y ................7分(2)由(1)知,当10=x 时,14.306.01032.0=-⨯=y 所以预测该月用户为3.14万人.................10分18.解:(1)由题得................2分成绩低于110分不低于110分合计感兴趣91625不感兴趣21425合计302050828.101220302525)211694(5022>=⨯⨯⨯⨯-⨯=χ................4分所以有99.9%的把握认为“该校高二年级学生对数学的感兴趣程度与成绩不低于110分有关”.................5分(2)由题意知,X 的可能取值为0,1,2,3.,141)0(484503===C C C X P ,73146)1(483513====C C C X P ,73146)2(482523====C C C X P 141)3(481533===C C C X P .................9分X 的分布列为X 0123P1417373141故期望2314137327311410)(=⨯+⨯+⨯+⨯=X E ................12分19.解:(1)1=n 时,1,121111=∴=-=a a a S .....2分2≥n 时,1122---=-=n n n n n a a S S a ,21=∴-n na a .....4分∴数列}{n a 是以1为首项,2为公比的等比数列故*12N n a n n ∈=-,.....6分(2)由(1)得12)1(-∙-=n n n b .....7分12102)1(222120-∙-++∙+∙+∙=∴n n n T =n T 2n n n n 2)1(2)2(2120121∙-+∙-++∙+∙- .....9分nn n n T 2)1(2222132--++++=-∴- 22)2(2)1(21)21(21---=----=-n n n n n .....11分*,22)2(N n n T n n ∈+-=∴.....12分20.解:(1)证明: AC C A C A AC AA AC A ⊥=∴==︒=∠1111,2,2,22,45.....2分又因为平面⊥11A ACC 平面ABC ,交线为AC,111A ACC C A 平面⊂,ABC C A 平面⊥∴1,.....4分BC A C A 11平面⊂,∴平面⊥BC A 1平面ABC.....5分(2)以C 为坐标原点,建立空间直角坐标系如图所示则)2,3,1(),2,0,2(),0,3,1(),2,0,0(111--B C B A .....7分)2,0,2(),2,3,1(),2,3,3(111-=--=--=∴BB BA BC 设平面11BC A 的法向量),,(111z y x m =,则⎪⎩⎪⎨⎧=∙=∙,0,011BA m BC m 即⎩⎨⎧=+--=+--,023,023*******z y x z y x 令21=y ,则)3,2,0(=m .....9分设平面11C BB 的法向量),,(222z y x n =,则⎪⎩⎪⎨⎧=∙=∙,0,011BB n BC n 即⎩⎨⎧=+-=+--,022,023322222z x z y x 令12-=y ,则)3,1,3(-=n .....11分71||||,cos =∙>=<∴n m n m n m 二面角111B BC A --的余弦值为71......12分21.解:(1)设直线l 的方程为:,n my x +=代入x y =2得02=--n my y ,设),(),,(2211y x B y x A ,则ny y m y y -==+2121,.....3分由6)(2212212121=-=+=+=∙n n y y y y y y x x OB OA 2-=∴n (舍去)或3=n 故点M 的坐标为(3,0)......5分(2)由(1)知321-=y y ,不妨设01>y ,123y y -=.....6分)323)(23||||21112121y y y y y y OM S OAB +=-=-=∆(.....8分1283||||21y y OF S S OBF OBC ===∆∆.....10分∴2133134283)1348383923111111=∙⨯≥+=+=+=∆∆y y y y y y S S S OBC OAB OABC (四边形当且仅当11134y y =,即2131=y 时等号成立故四边形OABC 面积的最小值为2133......12分22.解:(1)函数)(ln )(2R k kx x x f ∈-=有两个零点化为2ln xxk =有两个正根,设2ln )(x xx g =,),0(+∞∈x ,3ln 21)(x x x g -=',.....2分由0)(>'x g 得),0(e x ∈,由0)(<'x g 得)(∞+∈,e x )(x g ∴在,0(e 单增,在)(∞+,e 单减.....4分又,0)1(=g ee g 21)(=当1>x 时0)(>x g 故实数k 的取值范围为21,0(e.....6分(2)由(1)知211x e x <<<由题得⎩⎨⎧==222211ln ln kx x kx x ∴⎩⎨⎧-=-+=+)()(212212212212ln ln ln ln x x k x x x x k x x .....8分12212212122122212221ln 1)(1)(ln ln ln x x x x x x x x x x x x x x -+=-+=+∴,设),1(12+∞∈=t x x 由题知,需证明,1ln 1122>-+t t t 对),1(+∞∈t 恒成立即,011ln 22>+--t t t 对),1(+∞∈t 恒成立,.....10分记11ln )(22+--=t t t t ϕ,0)1()1()1(41)(222222>+-=+-='t t t t t t t ϕ)(t ϕ∴在),1(+∞上单调递增且0)1(=ϕ,故0)(>t ϕ对),1(+∞∈t 恒成立综上所述,1ln ln 21>+x x 成立......12分。
河南省南阳市第一中学高二数学下学期第二次月考试题理(扫描(2021年整理)

河南省南阳市第一中学2017-2018学年高二数学下学期第二次月考试题理(扫描版)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(河南省南阳市第一中学2017-2018学年高二数学下学期第二次月考试题理(扫描版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为河南省南阳市第一中学2017-2018学年高二数学下学期第二次月考试题理(扫描版)的全部内容。
河南省南阳市第一中学高二下学期期末考前模拟数学(文)试题

2016年春期高二文科数学期末考前模拟试卷参考答案一选择题 ACABB BBAAB AA二填空题 5;16; S BCD2=S ABC2+S ACD2+S ADB2 ; 4三解答题17解:设复数a=x+yi,(x,y 为实数),则错误!未找到引用源。
,得方程错误!未找到引用源。
,解方程得:错误!未找到引用源。
,所以复数a=错误!未找到引用源。
(10分) 18解:(1)由框图可知∵a i+1=a i +d ,∴{a n }是等差数列,设公差为d ,则有∴=,由题意可知,k=5时,∴得或(舍去)故a n =a 1+(n ﹣1)d=2n ﹣1 (6分) (2)由(1)可得:b n =2an=22n ﹣1∴b 1+b 2+......+b m =21+23+......+22m ﹣1==所以当m=5时,答案为682 (也可逐项求出再求和) (12分) 19 解:(Ⅰ)曲线C 1的参数方程式(t 为参数),得(x ﹣4)2+(y ﹣5)2=25即为圆C 1的普通方程, 即x 2+y 2﹣8x ﹣10y+16=0.将x=ρcos θ,y=ρsin θ代入上式,得.ρ2﹣8ρcos θ﹣10ρsin θ+16=0,此即为C 1的极坐标方程; (6分) (Ⅱ)曲线C 2的极坐标方程为ρ=2sin θ化为直角坐标方程为:x 2+y 2﹣2y=0, 由,解得或.∴C1与C2交点的极坐标分别为(,),(2,).(12分)20解:(1)X=2即为甲连赢两场或者乙连赢两场,两者之间互斥,概率为错误!未找到引;(4分)用源。
(2)X=4的可能情况为甲一赢二输三赢四赢,概率错误!未找到引用源。
一输二赢三赢四赢,概率错误!未找到引用源。
乙一赢二输三赢四赢,概率错误!未找到引用源。
一输二赢三赢四赢,概率,错误!未找到引用源。
(12分)四种情况之间彼此互斥,所以P(X=4)=错误!未找到引用源。
21 解:(Ⅰ)把C1,C2的参数方程消去参数,化为普通方程分别为,C1为圆心是(﹣4,3),半径是1的圆;C2为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.(4分)(Ⅱ)当时,P(﹣4,4),设Q(8cosθ,3sinθ),故,C3为直线x﹣2y﹣7=0,求得M到C3的距离=|cosθ﹣sinθ﹣|=|sin(θ+α)﹣|,其中,sinα=,cosα=﹣.从而当sin(θ+α)=1,即当时,d取得最小值为.) (此处最值4分,Q点坐标4分)(12此时Q(错误!未找到引用源。
河南省南阳市第一中学高二数学下学期开学考试试题 理(

高二春期开学考试理科数学参考答案一、选择题1-5 CDACB 6-10 BCCDD 11-12 CD二、填空题13.()()11216n n n ++ 14.2 15.-4 16.43三、解答题17.(1)由22430x ax a -+<得(3)()0x a x a -⋅-< 又0a >,所以3a x a <<当1a =时,13x <<,即p 为真命题时,实数x 的取值范围是13x <<由2560x x -+≤得23x ≤≤ 所以q 为真时,实数x 的取值范围是23x ≤≤.若p q ∧为真,则23x ≤<,所以实数x 的取值范围是[)2,3(2)设{}|3A x a x a =<<,{}|23B x x =≤≤ q 是p 的充分不必要条件,则B A⊂所以021233a a a <<⎧⇒<<⎨>⎩,所以实数a 的取值范围是()1,2 .18.(1)由cos 2A -3cos(B +C)=1,得2cos 2A +3cos A -2=0,即(2cos A -1)(cos A +2)=0.解得cos A =12或cos A =-2(舍去).因为0<A<π,所以A =3π.(2)由S =12bcsin A =12bc·2=4bc =,得bc =20. 又b =5,所以c =4.由余弦定理,得a 2=b 2+c 2-2bccos A =25+16-20=21,故a又由正弦定理,得sin Bsin C =b a sin A·c a sin A =2bc a·sin 2A =2021×34=57. 19.(I )因为1121121,22222S a S a a ⨯==+⨯=+,41143424122S a a ⨯=+⨯=+, 由题意,得2111(22)(412)a a a +=+,解得11a =,所以21n a n =-.(II )11144(1)(1)(21)(21)n n n n n n n b a a n n --+=-=--+111(1)()2121n n n -=-+-+ 当n 为偶数时,1111111(1)()()()33523212121n T n n n n =+-+++--+---+L 1121n =-+221n n =+ 当n 为奇数时,1111111(1)()()()33523212121n T n n n n =+-++++-+---+L 1121n =++2221n n +=+ 所以22,212,21n n n n T n n n +⎧⎪⎪+=⎨⎪⎪+⎩为奇数为偶数,(或1n 21(1)2+1n n T n -++-=) 20.解:(1)依题得,根据长方体的表面积公式可知,xy y x p 200400900++=S S S S xy y x p xy S 12002002004009002200400900+=+⨯≥++=∴=,Θ 又因为0160632000120020032000≤-+≤+≤S S S S p ,化简得,所以,解得01016>≤≤-S S ,又,1000≤<∴S ,当且仅当320100400900=⎩⎨⎧==x xy y x ,即时S 取得最大值。
河南省南阳市近年-近年学年高二数学下学期期末考试试题文(扫描版)(最新整理)
2019年春期高中二年级期终质量评估数学试题(文)参考答案一、选择题1.A 2.A 3.D 4.B 5.D 6.C 7.A 8. B 9。
D 10.C 11.B 12.C 二、填空题13.丁 14.4+3i 15. 16.②④三、解答题 17.解析:(1)∵为纯虚数,∴∴,所以……………………………………………………………5分(2),∴。
∴复数. ……………………………………………………………10分18。
解析:(1)曲线的普通方程为, ………………………………………2分,曲线表示焦点在轴上的椭圆. …………………………………………4分(2)将直线的参数方程(为参数)代入椭圆方程,整理得,即, …………………………………………6分,设对应的参数分别为、,则……………………………………………………8分 由的几何意义知,,,ωxl21212286.1at t t t a++⋅=+于是,,, …………………………10分若,,成等比数列,则有,即,解得,所以实数的值为。
……………………………………………………………12分19.解析:(1)由已知得错误!解得d =2, …………………2分故a n =2n -1+错误!,S n =n (n +错误!). …………………………………………6分 (2)证明:由(1)得b n =错误!=n +错误!.假设数列{b n }中存在三项b p ,b q ,b r (p ,q ,r∈N *,且互不相等)成等比数列,则b 2q =b p b r 。
即(q +错误!)2=(p +错误!)(r +错误!).∴(q 2-pr)+错误!(2q -p -r )=0. ……………………………………………8分 ∵p,q ,r∈N *,∴q 2-pr 为有理数.而若2q -p -r≠0,则错误!(2q -p -r )为无理数.显然(q 2-pr )+错误!(2q -p -r )=0不成立.…………………………………10分 ∴错误!∴,(p -r)2=0。
河南省南阳市第一中学2015-2016学年高二下学期期末考前模拟数学(文)试题扫描版含答案
2016年春期高二文科数学期末考前模拟试卷参考答案一选择题 ACABB BBAAB AA二填空题 5;16; S BCD2=S ABC2+S ACD2+S ADB2 ; 4三解答题17解:设复数a=x+yi,(x,y 为实数),则121213,2(24),(2612)(246)1z i z x y i z z x y y x i =-=++∙=++++-=,得方程261212460x y y x ++=⎧⎨+-=⎩,解方程得:1203720x y ⎧=⎪⎪⎨⎪=-⎪⎩,所以复数a=1372020i - (10分) 18解:(1)由框图可知∵a i+1=a i +d ,∴{a n }是等差数列,设公差为d ,则有∴=,由题意可知,k=5时,∴得或(舍去)故a n =a 1+(n ﹣1)d=2n ﹣1 (6分) (2)由(1)可得:b n =2an=22n ﹣1∴b 1+b 2+......+b m =21+23+......+22m ﹣1==所以当m=5时,答案为682 (也可逐项求出再求和) (12分) 19 解:(Ⅰ)曲线C 1的参数方程式(t 为参数),得(x ﹣4)2+(y ﹣5)2=25即为圆C 1的普通方程, 即x 2+y 2﹣8x ﹣10y+16=0.将x=ρcos θ,y=ρsin θ代入上式,得.ρ2﹣8ρcos θ﹣10ρsin θ+16=0,此即为C 1的极坐标方程; (6分) (Ⅱ)曲线C 2的极坐标方程为ρ=2sin θ化为直角坐标方程为:x 2+y 2﹣2y=0,由,解得或.∴C1与C2交点的极坐标分别为(,),(2,).(12分)20解:(1)X=2即为甲连赢两场或者乙连赢两场,两者之间互斥,概率为22115 33339⨯+⨯=;(4分)(2)X=4的可能情况为甲一赢二输三赢四赢,概率21228 333381⨯⨯⨯=一输二赢三赢四赢,概率12228 333381⨯⨯⨯=乙一赢二输三赢四赢,概率12112 333381⨯⨯⨯=一输二赢三赢四赢,概率21112 333381⨯⨯⨯=,四种情况之间彼此互斥,所以P(X=4)= 2081(12分)21 解:(Ⅰ)把C1,C2的参数方程消去参数,化为普通方程分别为,C1为圆心是(﹣4,3),半径是1的圆;C2为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.(4分)(Ⅱ)当时,P(﹣4,4),设Q(8cosθ,3sinθ),故,C3为直线x﹣2y﹣7=0,求得M到C3的距离=|cosθ﹣sinθ﹣|=|sin(θ+α)﹣|,其中,sinα=,cosα=﹣.从而当sin(θ+α)=1,即当时,d取得最小值为.此时Q(329,55-) (此处最值4分,Q点坐标4分)(12分)22解:(1)因为f(x)=x3+bx2+cx+2,所以f′(x)=3x2+2bx+c.由已知得f ′(1)=0,f (1)=-1,所以⎩⎪⎨⎪⎧3+2b +c =0,1+b +c +2=-1,解得b =1,c =-5.经验证:b =1,c =-5符合题意. (5分) (2)由(1)知f (x )=x 3+x 2-5x +2,f ′(x )=3x 2+2x -5. 由f ′(x )=0得x 1=-53,x 2=1.当x 变化时,f ′(x ),f (x )的变化情况如下表:根据上表,当x =-3时函数取得极大值且极大值为f ⎝ ⎛⎭⎪⎫-3=27,当x =1时函数取得极小值且极小值为f (1)=-1.根据题意结合上图可知k 的取值范围为⎝ ⎛⎭⎪⎫-1,22927.(12分)。
2020-2021学年河南省南阳市高二下学期阶段检测考试数学(理)试题(解析版)
2020-2021学年河南省南阳市高二下学期阶段检测考试数学(理)试题一、单选题1.已知复数z 满足()51213i i z +=,则z =( )A .15B .12C .1D .5【答案】C 【分析】化简1251313z i =+,即得解. 【详解】因为13(512)125512131313i i i z i i -===++, 所以1z =. 故选:C2.已知函数2()6f x x =-,且()02f x '=,则0x =( )A B .C .D .【答案】B【分析】依题意求出函数的导函数,再解方程即可;【详解】解:由题意可得()6f x '=-+,因为()0062f x '=-+=,所以0x = 故选:B3.已知x 为正数,随机变量ξ的分布列为则x =( ) A .19B .112 C .16D .18【答案】C【分析】利用分布列的概率和为1,即可求解. 【详解】由分布列可知,321x x x ++=,得16x =. 故选:C4.下面给出的类比推理中(其中R 为实数集,C 为复数集),结论正确的是( )A .由“已知,a b ∈R ,若a b =,则a b =±”类比推出“已知,a b C ∈,若a b =,则a b =±”B .由“若直线a ,b ,c 满足//a b ,//b c ,则//a c ”类比推出“若向量a →,b →,c →满足//a b →→,//b c →→,则//a c →→”C .由“已知,a b ∈R ,若0a b ->,则a b >”类比推出“已知,a b C ∈,若0a b ->,则a b >”D .由“平面向量a →满足22a a →→=”类比推出“空间向量a →满足22a a →→=” 【答案】D【分析】根据复数知识判断选项A ;根据平面向量知识判断选项B ;根据复数不一定可以比较大小判断C ;根据空间向量知识判断选项D ;【详解】在复数集C 中,若两个复数满足||||a b =,则只表示它们的模相等,a ,b 不一定相等或相反,所以A 不正确;当b →为零向量,a →,c →为不共线的非零向量时,不满足向量平行的传递性,所以B 不正确;在复数集C 中,例如2a i =+,1b i =+,此时10a b -=>,但a ,b 都是虚数,无法比较大小,所以C 不正确;平面向量或空间向量a →,均满足22a a →→=,所以D 正确. 故选:D.5.某篮球运动员投篮的命中率为0.8,现投了7次球,则恰有5次投中的概率为( ) A .520.80.2⨯ B .5527C 0.80.2⨯⨯C .0.85D .557C 0.8⨯【答案】B【分析】根据独立重复试验的概率计算公式直接计算出结果.【详解】根据独立重复试验的概率计算公式()()1n kkk nP X k C p p -==⋅-⋅可知:恰有5次投中的概率为55270.80.2P C =⨯⨯.故选:B.6.已知函数2()ln 21f x x x x =-+,则曲线()y f x =在点()()1,1f 处的切线方程为( )A .0x y +=B .20x y --=C .210x y +-=D .240x y --=【答案】A【分析】根据导数的几何意义求解切线的斜率,最后写出切线方程即可.【详解】因为()2ln 2f x x x x '=+-, 所以(1)121f '=-=-. 因为()11f =-,所以曲线()y f x =在点()()1,1f 处的切线方程为()11y x +=--, 即0x y +=. 故选:A.【点睛】本题主要考查导数的几何意义,导数在切点处的取值为切线的斜率,这类问题需要注意题目中的关键信息,是在这个点处还是过这个点,注意区别对待.7.一颗骰子连续掷两次,设事件A 为“两次的点数不相等”,B 为“第一次为奇数点”,则()|P B A =( ) A .1011 B .56C .12D .512【答案】C【分析】根据已知条件先分析事件A 对应的情况数,然后分析事件,A B 同时发生的情况数,由此求解出()(),P A P AB 的值,再根据公式()()()P AB P B A P A =求解出结果.【详解】由题知,事件A 出现的情况有66630⨯-=种,事件A ,B 同时出现的情况有3515⨯=种,所以()1536P AB =,30()36P A =,()()()151302P AB P B A P A ===. 故选:C.8.A ,B ,C ,D ,E ,F 六名同学进行劳动技术比赛,决出第1名到第6名的名次.A ,B ,C 去询问成绩,回答者对A 说:“很遗憾,你们三个都没有得到冠军.”对B 说:“你的名次在C 之前.”对C 说:“你不是最后一名.”从以上的回答分析,6人的名次排列情况种数共有( ) A .108 B .120 C .144 D .156【答案】A【分析】先选冠军有13C 种可能,最后一名有13C 种可能,再排剩下4个位置,即得解. 【详解】因为A ,B ,C 都没有得到冠军,所以从D ,E ,F 中选一个为冠军,有13C 种可能.因为C 不是最后一名,B 的名次又在C 之前,所以最后一名有13C 种可能,剩下4个位置.因为B ,C 定序,所以有442212 A A =种可能,所以6人的名次排列有3312108⨯⨯=种不同情况. 故选:A9.已知()272901291(21)(1)(1)(1)x x a a x a x a x +-=+-+-++-,则2468a a a a +++=( ) A .10935 B .5546 C .5468 D .5465【答案】D【分析】令1x t -=,则()2729012922(12)t t t a a t a t a t +++=++++,令0t =,得02a =;令1t =,可得0129a a a a ++++;令1t =-,可得0129a a a a -++-,进而可得结果.【详解】令1x t -=,则()2729012922(12)t t t a a t a t a t +++=++++,令0t =,则02a =. 令1t =,则012910935a a a a ++++=,令1t =-,则01291a a a a -++-=-,所以024********54672a a a a a -++++==, 所以246805467546725465a a a a a +++=-=-=. 故选:D.10.已知函数32()ln 2e f x x x x ax =-+-,若对任意的(0,)x ∈+∞,()0f x ≤恒成立,则实数a 的取值范围为( ) A .21e ,e ⎡⎫++∞⎪⎢⎣⎭B .210,e e ⎛⎤+ ⎥⎝⎦C .21e ,e ⎡⎫-+∞⎪⎢⎣⎭D .)2e ,⎡+∞⎣【答案】A【分析】问题转化为22lnx a x ex x-++,令2()2lnx h x x ex x =-++,求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的最大值,从而求出a 的取值范围即可.【详解】2()()2lnxf xg x a x ex x⇔-++, 令2()2lnxh x x ex x=-++,则2211()222()lnx lnxh x x e x e x x --'=-++=--+, 当0x e <<时,()0h x '>,当x e >时,()0h x '<, ()h x ∴在(0,)e 上单调递增,在(,)e +∞上单调递减, ()h x ∴的最大值为21()h e e e=+,则21a e e+,故选:A11.十九大报告提出实施乡村振兴战略,要“推动城乡义务教育一体化发展,高度重视农村义务教育”.为了响应报告精神,某师范大学5名毕业生主动申请到某贫困山区的乡村小学工作.将这5名毕业生分配到该山区的A ,B ,C 三所小学,每所学校至少分配1人( ).A .若甲不去A 小学,则共有120种分配方法B .若甲、乙去同一所小学,则共有36种分配方法C .若有一所小学分配了3人,则共有90种分配方法D .共有120种分配方法 【答案】B【分析】A .分析A 小学分别分配1,2,3人的分配方法数且甲不在A 小学,由此可计算出总的分配方法数;B .分别考虑甲、乙所去的小学仅有2人,甲、乙所去的小学有3人,计算出对应的分配方法数再相加即可;C .考虑将5人分成3,1,1三组,然后再将三组人分配给三所小学,计算出对应的分配方法数;D .考虑5名毕业生分配到三所小学可以分成3,1,1或2,2,1两种情况,计算出总的分配方法数即可.【详解】5名毕业生分配到三所小学可以分成3,1,1或2,2,1两种情况,若A 小学安排1人且甲不在A 小学,则有()1322442456C C A C ⨯+=种分配方法,若A 小学安排2人且甲不在A 小学,则有21243236C C A =种分配方法, 若A 小学安排3人且甲不在A 小学,则有32428C A =种分配方法, 所以甲不去A 小学共有56368100++=种分配方法,所以A 错误;若甲、乙同去A ,当A 中仅有2人时,则将剩下3人分到B ,C 小学共有1223226C C A =种分配方法,当A 中有3人时,则将剩下3人平均分到A ,B ,C 三所小学共有336A =种分配方法,所以甲、乙去同一所小学共有()136636C +⋅=种分配方法,所以B 正确;若有一所小学分配了3人,先将5人分成3,1,1三组,再将三组人分配到三所小学,所以共有335360C A =种分配方法,所以C 错误; 由上根据部分平均分组可知一样共有311221352153132222150C C C C C C A A A ⎛⎫+⋅= ⎪⎝⎭种分配方法,所以D 错误; 故选:B.12.现有11棵树径(绕树底部围一圈得到的周长)均不相等的国槐需要种植在新办公楼的前面,种成一排,若要求从中间往两边看时,树径都依次变小,则树径排第五的那棵树和树径排第一(树径最大)的那棵树相邻的概率为( ) A .27B .29C .584D .542【答案】D【分析】首先基本事件有510252C =,然后树径排第五的那棵树和树径排第一(树径最大)的那棵树相邻有46230C =,进而根据概率公式即可求得结果.【详解】将树径从高到低的11棵树依次编号为1,2,3,4,5,6,7,8,9,10,11,则1号必须排在正中间,从其余10棵中任选5棵排在1号的左边,剩下的5棵树排在1号的右边,有510252C =种排法.当排名第五的5号排在最高的1号的左边时,从6,7,8,9,10,11中任选4棵排在5号的左边,其余五棵排在1号的右边,有4615C =种排法,同理当排名第五的5号排在最高的1号的右边时,也有15种排法.所以树径排第五的那棵树和树径排第一的那棵树相邻的概率为30525242=. 故选:D.二、填空题13.已知z 为纯虚数,若()()12z i ++在复平面内对应的点在直线0x y -=上,则z =________.【答案】13i【分析】根据z 为纯虚数设()z ai a R =∈,由此计算出()()12z i ++并将其对应的点的坐标代入0x y -=,由此求解出a 的值,则z 可知.【详解】设()z ai a R =∈,则()()()()()1212221z i ai i a a i ++=++=-++. 因为()221a a i -++对应的点为()2,21a a -+,所以221a a -=+,解得13a =,故13z i =.故答案为:13i .14.在()622y x y x ⎛⎫ ⎪⎝⎭-+的展开式中,34x y 的系数为________.【答案】58-【分析】求出62y x ⎛⎫+ ⎪⎝⎭展开式的通项,即可求出系数.【详解】因为62y x ⎛⎫+ ⎪⎝⎭展开式的通项为61612rr r rr T C x y -+⎛⎫= ⎪⎝⎭,所以34x y 的系数为4343661152228C C ⎛⎫⎛⎫⨯-=- ⎪ ⎪⎝⎭⎝⎭. 故答案为:58-.15.已知函数ln ,1,()1(7),14x x f x x x ≥⎧⎪=⎨+<⎪⎩,若21x x >且()()12f x f x =,则21x x -的最小值是________. 【答案】118ln 2-【分析】首先画出函数的图象,由()()12f x f x t ==,解出12,x x ,并将21x x -转化为关于t 的函数,利用导数求函数的最小值. 【详解】作出函数()f x 的大致图象如图所示,设()()12f x f x t ==,则02t ≤<.由()()11174f x x t =+=,可得147x t =-;由()22ln f x x t ==,可得2t x e =. 令21()47tg t x x e t =-=-+,其中02t ≤<,则()4t g t e '=-.由()0g t '=,得2ln 2t =.当02ln 2t ≤<时,()0g t '<,则()g t 在[0,2ln 2)上单调递减; 当2ln 22t <<时,()0g t '>,则()g t 在[2ln 2,2]上单调递增. 所以min ()(2ln 2)118ln 2g t g ==-.即21x x -的最小值为118ln 2-. 故答案为:118ln 2-【点睛】关键点点睛:本题考查函数零点,利用导数求函数的最值的综合问题,属于中档题型,本题的关键是结合函数的图象,得到t 的取值范围,并得到147x t =-,2tx e =.三、双空题16.毕达哥拉斯学派是古希腊哲学家毕达哥拉斯及其信徒组成的学派,他们把美学视为自然科学的一个组成部分.美表现在数量比例上的对称与和谐,和谐起于差异的对立,美的本质在于和谐.他们常把数描绘成沙滩上的沙粒或小石子,并由它们排列而成的形状对自然数进行研究.如图所示,图形的点数分别为1,5,12,22,,总结规律并以此类推下去,第8个图形对应的点数为________,若这些数构成一个数列,记为数列{}n a ,则322112321a a a a ++++=________.【答案】92 336【分析】记第n 个图形的点数为n a ,由图形,归纳推理可得113(1)n n a a n --=+-,再根据累加得可得(31)2n n a n =-,进而求出8a .由于(31)2n na n =-可得312n a n n -=,根据等差数列的前n 项和即可求出322112321a a a a ++++的结果. 【详解】记第n 个图形的点数为n a ,由题意知11a =,214131a a -==+⨯, 32132a a -=+⨯,43133a a -=+⨯,…,113(1)n n a a n --=+-,累加得147[13(1)](31)2n na a n n -=++++-=-,即(31)2n na n =-,所以892a =.又312n a n n -=, 所以3221111262(25862)213362321222a a a a +++++=++++=⨯⨯=.四、解答题17.2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱贫攻坚取得重大胜利.为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础,在产业扶贫政策的大力支持下,西部某县新建了甲、乙两家农产品加工厂加工同一种农产品.已知食品安全监管部门随机抽检了两个加工厂生产的产品各100件,在抽取的200件产品中,根据检测结果将它们分为A ,B ,C 三个等级,A ,B 等级都是合格品,C 等级是次品,统计结果如下表(表一)所示.(表一)(表二)在相关政策的扶持下,确保每件合格品都有对口销售渠道,从安全起见,所有的次品必须由原厂家自行销毁.(1)请根据所提供的数据,完成上面的22⨯列联表(表二),若从抽取的100件乙产品中选取2件,求刚好1件合格品,1件次品的概率;(2)用频率代替概率,从甲、乙两加工厂各抽取2件产品,求甲抽到的合格产品件数比乙多的概率.【答案】(1)填表见解析;1633;(2)2150.【分析】(1)结合表(一)完成列联表即可,由排列组合可得古典型概率;(2)依题意可得,从甲、乙两加工厂各抽取1件产品,抽到合格品的概率分别为34,35.从甲、乙两加工厂各抽取2件产品,设抽到合格品的件数分别为X ,Y ,记事件A 为“从甲,乙两加工厂各抽取2件产品,甲抽到的合格产品件数比乙多”,则()()()()()()()102021P A P X P Y P X P Y P X P Y ===+==+==.进而可得结果. 【详解】(1)22⨯列联表如下因为100件乙产品中合格品60件,次品40件,所以所求概率为11604021001633C C C =.(2)因为用频率近似概率,所以从甲、乙两加工厂各抽取1件产品,抽到合格品的概率分别为34,35.从甲、乙两加工厂各抽取2件产品,设抽到合格品的件数分别为X ,Y ,记事件A 为“从甲,乙两加工厂各抽取2件产品,甲抽到的合格产品件数比乙多”,则()()()()()()()102021P A P X P Y P X P Y P X P Y ===+==+==.因为12333(1)1448P X C ⎛⎫==⨯⨯-= ⎪⎝⎭,239(2)416P X ⎛⎫=== ⎪⎝⎭,234(0)1525P Y ⎛⎫==-= ⎪⎝⎭,123312(1)15525P Y C ⎛⎫==⨯⨯-= ⎪⎝⎭, 所以349491221()8251625162550P A =⨯+⨯+⨯=.18.已知函数23215()6132f x a x ax x =-++在2x =处取得极大值.(1)求a ;(2)求经过点()()0,0f 且与曲线()y f x =相切的直线斜率. 【答案】(1)1a =;(2)6或2116. 【分析】(1)由题意可知0a ≠,求出函数的导函数,令()0f x '=,即可求出参数的值,还需判断函数的单调性进行检验;(2)由(1)知3215()6132f x x x x =-++,求出函数的导函数,设切点为()()00,x f x ,表示出切线方程,最后将点()0,1代入切线方程,求出0x ,即可得解;【详解】解:(1)由题意可知0a ≠,22()56(2)(3)f x a x ax ax ax '=-+=--. 令()0f x '=,得2x a =或3x a=. 当0a >时,23a a<,则22a =,得1a =,所以()(2)(3)f x x x '=--,所以当()(),23,x ∈-∞+∞时()0f x '>,()2,3x ∈时()0f x '<,即()f x 的单调递增区间是(,2)-∞和(3,)+∞,单调递减区间是()2,3, 当2x =时()f x 取得极大值,满足题意; 当0a <时,320a a<<,显然不合题意.故1a =. (2)由(1)知3215()6132f x x x x =-++,则(0)1f =,2()56f x x x '=-+.设切点为()()00,x f x ,则()200056f x x x '=-+,所以切线方程为()()32200000015615632y x x x x x x x ⎛⎫--++=-+- ⎪⎝⎭,将点()0,1代入,得320025032x x -=,所以00x =,或0154x =.因为(0)6f '=,1521416f ⎛⎫'= ⎪⎝⎭,所以经过点()()0,0f 且与曲线()y f x =相切的直线斜率为6或2116. 19.某校针对高一学生安排社团活动,周一至周五每天安排一项活动,活动安排表如下:要求每位学生选择其中的三项,学生甲决定选择篮球,不选择书法;乙和丙无特殊情况,任选三项.(1)求甲选排球且乙未选排球的概率;(2)用X 表示甲、乙、丙三人选择排球的人数之和,求X 的分布列. 【答案】(1)415;(2)答案见解析. 【分析】(1)利用古典概型计算公式可得:甲选排球的概率,乙未选排球的概率,再利用相互独立概率计算公式即可求出结果;(2)首先求出X 的可能取值,然后求出丙选排球的概率,进而求出对应概率,即可列出分布列.【详解】解:(1)设A 表示事件“甲选排球”,B 表示事件“乙选排球”,则12232()3C P A C ==,24353()5C P B C ==.因为事件A ,B 相互独立,所以甲选排球且乙未选排球的概率234()()()13515P AB P A P B ⎛⎫==⨯-= ⎪⎝⎭.(2)设C 表示事件“丙选排球”,则24353()5C P C C ==.X 的可能取值为0,1,2,3.1224(0)35575P X ==⨯⨯=;2221321234(1)35535535515P X ==⨯⨯+⨯⨯+⨯⨯=;23222313311(2)35535535525P X ==⨯⨯+⨯⨯+⨯⨯=;2336(3)35525P X ==⨯⨯=.所以X 的分布列为20.某单位为丰富员工的业余生活,利用周末开展趣味野外拉练,此次拉练共分A ,B ,C 三大类,其中A 类有3个项目,每项需花费2小时,B 类有3个项目,每项需花费3小时,C 类有2个项目,每项需花费1小时.要求每位员工从中选择3个项目,每个项目的选择机会均等.(1)求小张在三类中各选1个项目的概率;(2)设小张所选3个项目花费的总时间为X 小时,求X 的分布列. 【答案】(1)928;(2)答案见解析. 【分析】(1)在三类项目中各选一个有111332C C C 种选法,总的选法数有38C 种,两者相除即可求得所求概率;(2)先分析X 的可取值,对于每一个X 的取值,利用该值对应的选法数除以总的选法数即可求得对应概率,由此可得X 的分布列. 【详解】解:(1)记事件M 为在三类中各选1个项目则111332389()28C C C P M C ==,所以小张在三类中各选1个项目的概率为928. (2)X 的可能取值为4,5,6,7,8,9,则2123383(4)56C C P X C ===;21212332389(5)56C C C C P X C +===; 111323333819(6)56C C C C P X C +===; 212132333815(7)56C C C C P X C +===; 2133389(8)56C C P X C ===;33381(9)56C P X C ===.所以分布列如下表所示:21.已知数列{}n a ,{}n b 满足16a =,2154a =,12n n n a b a ++=,1n n n n n b a b +=+.(1)证明:{}n n a b 为常数数列,且13n n a a +>>.(2)设数列21n b ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,证明:499n nS <+.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)首先利用递推关系,两式相乘证明{}n n a b 为常数数列,进而得到9n nb a =, 通过基本不等式证明3n a >,接着证明10n n a a +-<即可; (2)利用13n n a a +<<,放缩得到()2211994n n a a +-<-,进而得到121111349n n b -⎛⎫≤⨯+⎪⎝⎭, 最后求和证明不等式即可. 【详解】证明:(1)因为1122n n n nn n n n n na b a b a b a b a b +++=⨯=+, 所以数列{}n n a b 为常数数列,因为16a =,2154a =,且1122a b a +=,所以132b =,故119n n a b a b ==,9n nb a =. 易知0n a >,则11932n n n a a a +⎛⎫=+≥ ⎪⎝⎭(当且仅当3n a =时取等号).因为163a =≠,所以3n a >.因为21902nn n na a a a +--=<,所以13n n a a +<<. (2)由()281n n a b =,得221181n n a b =, 因为13n n a a +<<,所以()222121811182744n n n n a a a a +⎛⎫=++<+ ⎪⎝⎭, 则()2211994n n a a +-<-, 所以()1122111992744n n na a --⎛⎫⎛⎫-≤-=⨯ ⎪⎪⎝⎭⎝⎭,即1212794n na -⎛⎫≤⨯+ ⎪⎝⎭,所以122111181349n n n a b -⎛⎫=≤⨯+ ⎪⎝⎭. 当1n =时,211441999b =<+; 当2n ≥时,11111111144113449399914nn n n S n n -⎛⎫- ⎪⎡⎤⎛⎫⎝⎭<++++=⨯+<+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦-,故499n n S <+. 【点睛】本题主要考查数列不等式的证明,在处理中要用到不等式的放缩,这类问题有一定的难度,适当的进行放缩是解决问题的关键,在备考中要多总结提高. 22.已知函数2()2e 1x f x ax =-+.(1)若()f x 在(0,)+∞上不单调,求a 的取值范围.(2)若()f x 在区间(0,)+∞上存在极大值M ,证明:1M a <+. 【答案】(1)(,)e +∞;(2)证明见解析.【分析】(1)求出函数的导函数()2x e f x x a x ⎛⎫'=- ⎪⎝⎭,再令()xe g x x =,利用导数说明其单调性与最小值,即可求出参数a 的取值范围.(2)由(1)可知a e >,令()()h x f x =',利用导数说明()f x '的单调性,即可得到存在0(0,1)x ∈,使得()00f x '=,从而得到当0x x =时,()f x 取得极大值,即02021x M e ax =-+,再利用基本不等式计算可得;【详解】(1)解:()()22x xe f x e ax x a x ⎛⎫'=-=- ⎪⎝⎭.令()xe g x x =,则2(1)()x x e g x x -'=.当01x <<时,()0g x '<,()g x 在()0,1上单调递减; 当1x >时,()0g x '>,()g x 在(1,)+∞上单调递增. 故min ()(1)g x g e ==.因为()f x 在(0,)+∞上不单调,即()0f x '=在(0,)+∞有变号零点,所以a e >,即a 的取值范围为(,)e +∞.(2)证明:由(1)可知当a e ≤时,()f x 在(0,)+∞上单调递增,则不存在极大值.当a e >时,1ln a <.()()2x f x e ax '=-,令()()h x f x =',则()()2xh x e a '=-.令()0h x '=,则ln x a =.易知()f x '在()0,ln a 上单调递减,在(ln ,)a +∞上单调递增. 因为(0)20f '=>,(1)2()0f e a '=-<,所以存在0(0,1)x ∈,使得()()00020xf x e ax '=-=.则当()00,x x ∈时,()0f x '>;当()0,1x x ∈时()0f x '<. 故()f x 在()00,x 上单调递增,在()0,1x 上单调递减,所以当0x x =时,()f x 取得极大值,即02021x M e ax =-+.因为001x <<,所以0102x ->,且00122x x ≠-. 因为000x e ax -=,所以00xe ax =,则0220002121x M e ax ax ax =-+=-+2000122411411222x x x x a a a ⎛⎫+- ⎪⎛⎫=⋅⋅-+<+=+ ⎪ ⎪⎝⎭⎪⎝⎭,即1M a <+.【点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.。
2023-2024学年河南省南阳市六校高二下学期期末考试数学试题
2023-2024学年河南省南阳市六校高二下学期期末考试数学试题1.已知随机变量服从正态分布,且,则()A.0.05B.0.1C.0.3D.0.42.如图,均为直角三角形,为直角顶点,,且,设这些直角三角形的周长从小到大组成的数列为,则()A.B.C.D.3.已知函数,且,则实数()A.1B.2C.D.4.已知是正项等比数列,若成等差数列,则()A.3B.4C.5D.65.已知为虚数单位,则的展开式中的系数为()A.-10B.10C.-15D.156.已知数列满足,且,设,则数列的前2024项和为()A.674B.673C.-673D.-6747.已知函数若恒成立,则实数的取值范围是()A.B.C.D.8.已知双曲线,如图,过的右焦点作直线与的两条渐近线分别交于点,与轴交于点,若,且,则的离心率为()A.B.C.2D.9.假定生男孩和生女孩是等可能的,已知一个家庭中共有3个孩子,用表示事件“该家庭中既有男孩又有女孩”,用表示事件“该家庭中最多有1个女孩”,则()A.B.C.D.与相互独立10.已知数列的前项和,则下列说法中正确的是()A.一定为等差数列B.可能为等比数列C.若,则一定为递增数列D.若,则存在,使得11.已知函数,若不等式恰有一个整数解,则实数的取值不可能是()A.B.C.D.12.将4个不同编号的球放到3个不同的盒子中,每个盒子至少放一个球,则不同的分配方法共有________种.13.已知点在圆上运动,则的最小值是__________.14.已知函数及其导函数的定义域均为,且为偶函数,若时,,且,则不等式的解集为__________.15.如图,在四棱锥中,四边形为正方形,平面.(1)若,求;(2)若,求直线与平面所成角的正弦值.16.扬子鳄是中国特有的一种小型鳄类,是国家一级重点保护野生动物,活动区域主要在长江下游流域.研究人员为了解扬子鳄的生长发育情况,随机抽取了6只扬子鳄,测量它们的头长(单位与体长(单位:),得到如下数据:样本编号123456头长1515.315.316.616.817体长125128130138142153并计算得(1)求这6只扬子鳄的平均头长与平均体长;(2)求扬子鳄的头长与体长的样本相关系数;(精确到0.01)(3)已知与可以用模型进行拟合,若某只扬子鳄的头长为,利用所给数据估计这只扬子鳄的体长.附:相关系数.17.已知数列满足,当时,.(1)求的通项公式;(2)设为数列的前项和,证明:.参考结论:当时,.18.已知函数,其中.(1)讨论在区间上的单调性;(2)若,函数在区间内存在唯一的极值点,求实数的取值范围.19.已知抛物线的焦点到直线的距离为为直线上的动点,过点作直线分别与相切于点.(1)求的方程;(2)证明:直线过定点;(3)若直线分别交轴于点,求的最小值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省南阳市第一中学2015-2016学年高二数学下学期期末考前模拟
试题理(扫描版)
理数参考答案
一.选择题(每题5分,共计60分) 1-5BBAAD 6-10DBADB 11-12CB 二.填空题(每题5分,共计20分)
13.185 14. 1683 15. 1:8 16. ②、④ 三.解答题
17.证明:①当n=1时,左边=1,右边=2,∴n=1不等式成立. ②假设当n=k (k≥2)时成立,即*)(2
1312
11N k k k ∈<+
++
+
那么当n=k+1时,左边=1
121
1
13
12
11++
<+++++
+
k k k k
∵4k 2
+4k <4k 2
+4k+1,可得k k +2
212+<k , 即:12
1
221
1
2
11
1
2
1
122
+=++<
+++=
+++=++
k k k k k k
k k k k k
.这就是说n=k+1时不等式也成立.综上①②可知不等式对所有的n ∈N *
18.(1)136.(2)10
3
19解 k =65×[a 30+a - 20-a 15-a ]2
20×45×15×50=60× 65a -300 2
20×45×15×50=13× 13a -60
2
60×90.
由k ≥2.706得a ≥7.19或a ≤2.04. 又a >5且15-a >5,a ∈Z ,即a =8,9.
故a 为8或9时,在犯错误的概率不超过0.1的前提下认为x 与y 之间有关系.
21.设Y :
(1)A 表示事件“第三个顾客恰好等待4分钟开始办理业务”,则事件A 对应三种情形:
①第一个顾客办理业务所需的时间为1分钟,且第二个顾客办理业务所需的时间为3分钟; ②第一个顾客办理业务所需的时间为3分钟,且第二个顾客办理业务所需的时间为1分钟; ③第一个、第二个顾客办理业务所需的时间均为2分钟.所以P (A )=P (Y=1)P (Y=3)+P (Y=3)P (Y=1)+P (Y=2)P (Y=2)=0.1×0.3+0.3×0.1+0.4×0.4=0.22.
(2)X 所有可能的取值为0,1,2.X=0对应第一个顾客办理业务所需的时间超过2分钟,所以P (X=0)=P (Y>2)=0.5;
X=1对应第一个顾客办理业务所需的时间为1分钟且第二个顾客办理业务所需的时间超过1分钟,或第一个顾客办理业务所需的时间为2分钟,
所以P (X=1)=P (Y=1)P (Y>1)+P (Y=2)=0.1×0.9+0.4=0.49; X=2对应两个顾客办理业务所需的时间均为1分钟, 所以P (X=2)=P (Y=1)P (Y=1)=0.1×0.1=0.01. 所以X 的分布列为:
EX=0×0.5+1×0.49+2×0.01=0.51.
22解:(1)若2-=a ,则,2)(2x e x f x --=,22)(x e x f x
--='当),0(+∞∈x 时0)(<'
x f
故函数)(x f 在区间),0(+∞上是单调递减的 。
3分
(2)函数
)
(x f 有两个极值点
2
1,x x ,则
2
1,x x 是
2)(=-='x ae
x f x
的两个根
即方程x
e
x a 2=
有两个根,设x
e
x x h 2)(=
则x
e
x x h 22)(-=
'
要使x
e
x a 2=
有两个根,只需
e h a 2
)1(0=
<<故实数a 的取值范围是
)
2,
0(e 。
8分
(3)证明有(2)可知,函数)(x f 的两个极值点21,x x 满足2110x x <<<
由
2)(111
=-='x ae
x f x 得1
12x e
x a =
所以
1
2
12112)(1
x x x ae
x f x +-=-=
由于
1
2
112)(x x x f +-=在区间
)
1,0(上是增函数,由
101
x <<知
10(0)()(1)1
f f x f =<<= 。
12分。
