河海大学概率论与数理统计试卷2009
12 132期中测试题谜底1
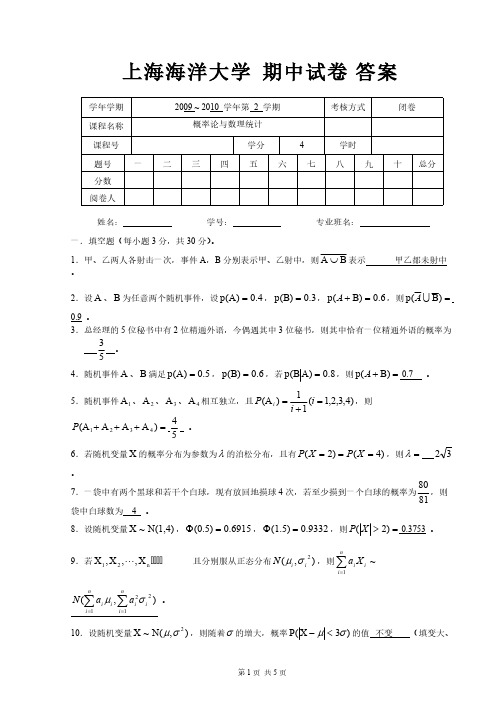
上海海洋大学期中试卷答案学年学期2009 ~ 2010 学年第 2 学期考核方式闭卷课程名称概率论与数理统计课程号学分4学时题号一二三四五六七八九十总分分数阅卷人姓名:学号:专业班名:一.填空题(每小题3分,共30分)。
1.甲、乙两人各射击一次,事件A ,B 分别表示甲、乙射中,则表示甲乙都未射中B A ⋃。
2.设、为任意两个随机事件,设,,,则A B 4.0)A (p =3.0)B (p =6.0)B (p =+A =)B (p A 0.9 。
3.总经理的5位秘书中有2位精通外语,今偶遇其中3位秘书,则其中恰有一位精通外语的概率为。
534.随机事件、满足,,若,则 0.7 。
A B 5.0)A (p =6.0)B (p =8.0)A B (p ==+)B (p A 5.随机事件、、、相互独立,且,则1A 2A 3A 4A )4,3,2,1(11)(A =+=i i P i 。
=+++)A A A (A 4321P 546.若随机变量的概率分布为参数为的泊松分布,且有,则X λ)4()2(===X P X P =λ32。
7.一袋中有两个黑球和若干个白球,现有放回地摸球4次,若至少摸到一个白球的概率为,则8180袋中白球数为 4 。
8.设随机变量,,,则 0.3753 。
N(1,4)~X 0.6915(0.5)=Φ0.9332(1.5)=Φ=>)2(X P 9.若且分别服从正态分布,则且且且且n 21X ,,X ,X ),(2i i N σμ~1∑=ni ii Xa 。
),(2121i ni i ni i i a a N σμ∑∑==10.设随机变量,则随着的增大,概率的值 不变(填变大、),N(~X 2σμσ)3X P(σμ<-气系试高中资料试卷方案。
变小、或者不变)。
二、选择题(每小题3分,共30分)1.若,则(C )B ⊂A A ) B )C )未发生则A 必不发生D )B 发生则A 可能不发生)((A)B P P <0)(>-A B P B 2.下列概率的性质中不属于概率的公理化定义的是( C )。
2009年全国统一高考数学试卷(文科)(全国卷ⅰ)(含解析版)

2009年全国统一高考数学试卷(文科)(全国卷Ⅰ)一、选择题(共12小题,每小题5分,满分60分)1.(5分)sin585°的值为( )A.B.C.D.2.(5分)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合∁U(A∩B)中的元素共有( )A.3个B.4个C.5个D.6个3.(5分)不等式<1的解集为( )A.{x|0<x<1}∪{x|x>1}B.{x|0<x<1}C.{x|﹣1<x<0}D.{x|x<0}4.(5分)已知tana=4,cotβ=,则tan(a+β)=( )A.B.﹣C.D.﹣5.(5分)已知双曲线﹣=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率为( )A.B.2C.D.6.(5分)已知函数f(x)的反函数为g(x)=1+2lgx(x>0),则f(1)+g(1)=( )A.0B.1C.2D.47.(5分)甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( )A.150种B.180种C.300种D.345种8.(5分)设非零向量、、满足,则=( )A.150°B.120°C.60°D.30°9.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为( )A.B.C.D.10.(5分)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为( )A.B.C.D.11.(5分)已知二面角α﹣l﹣β为60°,动点P、Q分别在面α、β内,P到β的距离为,Q到α的距离为,则P、Q两点之间距离的最小值为( )A.1B.2C.D.412.(5分)已知椭圆C:+y2=1的右焦点为F,右准线为l,点A∈l,线段AF 交C于点B,若=3,则||=( )A.B.2C.D.3二、填空题(共4小题,每小题5分,满分20分)13.(5分)(x﹣y)10的展开式中,x7y3的系数与x3y7的系数之和等于 .14.(5分)设等差数列{a n}的前n的和为S n,若S9=72,则a2+a4+a9= .15.(5分)已知OA为球O的半径,过OA的中点M且垂直于OA的平面截球面得到圆M.若圆M的面积为3π,则球O的表面积等于 .16.(5分)若直线m被两平行线l1:x﹣y+1=0与l2:x﹣y+3=0所截得的线段的长为,则m的倾斜角可以是①15°②30°③45°④60°⑤75°其中正确答案的序号是 (写出所有正确答案的序号)三、解答题(共6小题,满分70分)17.(10分)设等差数列{a n}的前n项和为S n,公比是正数的等比数列{b n}的前n项和为T n,已知a1=1,b1=3,a3+b3=17,T3﹣S3=12,求{a n},{b n}的通项公式.18.(12分)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2﹣c2=2b ,且sinAcosC=3cosAsinC,求b.19.(12分)如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=,DC=SD=2,点M在侧棱SC上,∠ABM=60°(I)证明:M是侧棱SC的中点;(Ⅱ)求二面角S﹣AM﹣B的大小.20.(12分)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束.假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立.已知前2局中,甲、乙各胜1局.(Ⅰ)求再赛2局结束这次比赛的概率;(Ⅱ)求甲获得这次比赛胜利的概率.21.(12分)已知函数f(x)=x4﹣3x2+6.(Ⅰ)讨论f(x)的单调性;(Ⅱ)设点P在曲线y=f(x)上,若该曲线在点P处的切线l通过坐标原点,求l的方程.22.(12分)如图,已知抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点.(Ⅰ)求r的取值范围;(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.2009年全国统一高考数学试卷(文科)(全国卷Ⅰ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)sin585°的值为( )A.B.C.D.【考点】GE:诱导公式.【分析】由sin(α+2kπ)=sinα、sin(α+π)=﹣sinα及特殊角三角函数值解之.【解答】解:sin585°=sin(585°﹣360°)=sin225°=sin(45°+180°)=﹣sin45°=﹣,故选:A.【点评】本题考查诱导公式及特殊角三角函数值.2.(5分)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合∁U(A∩B)中的元素共有( )A.3个B.4个C.5个D.6个【考点】1H:交、并、补集的混合运算.【分析】根据交集含义取A、B的公共元素写出A∩B,再根据补集的含义求解.【解答】解:A∪B={3,4,5,7,8,9},A∩B={4,7,9}∴∁U(A∩B)={3,5,8}故选A.也可用摩根律:∁U(A∩B)=(∁U A)∪(∁U B)故选:A.【点评】本题考查集合的基本运算,较简单.3.(5分)不等式<1的解集为( )A.{x|0<x<1}∪{x|x>1}B.{x|0<x<1}C.{x|﹣1<x<0}D.{x|x<0}【考点】7E:其他不等式的解法.【分析】本题为绝对值不等式,去绝对值是关键,可利用绝对值意义去绝对值,也可两边平方去绝对值.【解答】解:∵<1,∴|x+1|<|x﹣1|,∴x2+2x+1<x2﹣2x+1.∴x<0.∴不等式的解集为{x|x<0}.故选:D.【点评】本题主要考查解绝对值不等式,属基本题.解绝对值不等式的关键是去绝对值,去绝对值的方法主要有:利用绝对值的意义、讨论和平方.4.(5分)已知tana=4,cotβ=,则tan(a+β)=( )A.B.﹣C.D.﹣【考点】GP:两角和与差的三角函数.【专题】11:计算题.【分析】由已知中cotβ=,由同角三角函数的基本关系公式,我们求出β角的正切值,然后代入两角和的正切公式,即可得到答案.【解答】解:∵tana=4,cotβ=,∴tanβ=3∴tan(a+β)===﹣故选:B.【点评】本题考查的知识点是两角和与差的正切函数,其中根据已知中β角的余切值,根据同角三角函数的基本关系公式,求出β角的正切值是解答本题的关键.5.(5分)已知双曲线﹣=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率为( )A.B.2C.D.【考点】KC:双曲线的性质;KH:直线与圆锥曲线的综合.【专题】11:计算题.【分析】先求出渐近线方程,代入抛物线方程,根据判别式等于0,找到a和b 的关系,从而推断出a和c的关系,答案可得.【解答】解:由题双曲线的一条渐近线方程为,代入抛物线方程整理得ax2﹣bx+a=0,因渐近线与抛物线相切,所以b2﹣4a2=0,即,故选:C.【点评】本小题考查双曲线的渐近线方程直线与圆锥曲线的位置关系、双曲线的离心率,基础题.6.(5分)已知函数f(x)的反函数为g(x)=1+2lgx(x>0),则f(1)+g(1)=( )A.0B.1C.2D.4【考点】4R:反函数.【专题】11:计算题.【分析】将x=1代入即可求得g(1),欲求f(1),只须求当g(x)=1时x的值即可.从而解决问题.【解答】解:由题令1+2lgx=1得x=1,即f(1)=1,又g(1)=1,所以f(1)+g(1)=2,故选:C.【点评】本小题考查反函数,题目虽然简单,却考查了对基础知识的灵活掌握情况,也考查了运用知识的能力.7.(5分)甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( )A.150种B.180种C.300种D.345种【考点】D1:分类加法计数原理;D2:分步乘法计数原理.【专题】5O:排列组合.【分析】选出的4人中恰有1名女同学的不同选法,1名女同学来自甲组和乙组两类型.【解答】解:分两类(1)甲组中选出一名女生有C51•C31•C62=225种选法;(2)乙组中选出一名女生有C52•C61•C21=120种选法.故共有345种选法.故选:D.【点评】分类加法计数原理和分类乘法计数原理,最关键做到不重不漏,先分类,后分步!8.(5分)设非零向量、、满足,则=( )A.150°B.120°C.60°D.30°【考点】9S:数量积表示两个向量的夹角.【分析】根据向量加法的平行四边形法则,两个向量的模长相等可构成菱形的两条相邻边,三个向量起点处的对角线长等于菱形的边长,这样得到一个含有特殊角的菱形.【解答】解:由向量加法的平行四边形法则,∵两个向量的模长相等∴、可构成菱形的两条相邻边,∵∴、为起点处的对角线长等于菱形的边长,∴两个向量的夹角是120°,故选:B.【点评】本小题考查向量的几何运算、考查数形结合的思想,基础题.向量知识,向量观点在数学.物理等学科的很多分支有着广泛的应用,而它具有代数形式和几何形式的“双重身份”能融数形于一体.9.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC 上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为( )A.B.C.D.【考点】LO:空间中直线与直线之间的位置关系.【分析】首先找到异面直线AB与CC1所成的角(如∠A1AB);而欲求其余弦值可考虑余弦定理,则只要表示出A1B的长度即可;不妨设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1,利用勾股定理即可求之.【解答】解:设BC的中点为D,连接A1D、AD、A1B,易知θ=∠A1AB即为异面直线AB与CC1所成的角;并设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1,则|AD|=,|A1D|=,|A1B|=,由余弦定理,得cosθ==.故选:D.【点评】本题主要考查异面直线的夹角与余弦定理.10.(5分)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为( )A.B.C.D.【考点】HB:余弦函数的对称性.【专题】11:计算题.【分析】先根据函数y=3cos(2x+φ)的图象关于点中心对称,令x=代入函数使其等于0,求出φ的值,进而可得|φ|的最小值.【解答】解:∵函数y=3cos(2x+φ)的图象关于点中心对称.∴∴由此易得.故选:A.【点评】本题主要考查余弦函数的对称性.属基础题.11.(5分)已知二面角α﹣l﹣β为60°,动点P、Q分别在面α、β内,P到β的距离为,Q到α的距离为,则P、Q两点之间距离的最小值为( )A.1B.2C.D.4【考点】LQ:平面与平面之间的位置关系.【专题】11:计算题;16:压轴题.【分析】分别作QA⊥α于A,AC⊥l于C,PB⊥β于B,PD⊥l于D,连CQ,BD 则∠ACQ=∠PBD=60°,在三角形APQ中将PQ表示出来,再研究其最值即可.【解答】解:如图分别作QA⊥α于A,AC⊥l于C,PB⊥β于B,PD⊥l于D,连CQ,BD则∠ACQ=∠PDB=60°,,又∵当且仅当AP=0,即点A与点P重合时取最小值.故选:C.【点评】本题主要考查了平面与平面之间的位置关系,以及空间中直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题. 12.(5分)已知椭圆C:+y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若=3,则||=( )A.B.2C.D.3【考点】K4:椭圆的性质.【专题】11:计算题;16:压轴题.【分析】过点B作BM⊥x轴于M,设右准线l与x轴的交点为N,根据椭圆的性质可知FN=1,进而根据,求出BM,AN,进而可得|AF|.【解答】解:过点B作BM⊥x轴于M,并设右准线l与x轴的交点为N,易知FN=1.由题意,故FM=,故B点的横坐标为,纵坐标为±即BM=,故AN=1,∴.故选:A.【点评】本小题考查椭圆的准线、向量的运用、椭圆的定义,属基础题.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(x﹣y)10的展开式中,x7y3的系数与x3y7的系数之和等于 ﹣240 .【考点】DA:二项式定理.【专题】11:计算题.【分析】首先要了解二项式定理:(a+b)n=C n0a n b0+C n1a n﹣1b1+C n2a n﹣2b2++C n r a n﹣r b r++C n n a0b n,各项的通项公式为:T r+1=C n r a n﹣r b r.然后根据题目已知求解即可.【解答】解:因为(x﹣y)10的展开式中含x7y3的项为C103x10﹣3y3(﹣1)3=﹣C103x7y3,含x3y7的项为C107x10﹣7y7(﹣1)7=﹣C107x3y7.由C103=C107=120知,x7y3与x3y7的系数之和为﹣240.故答案为﹣240.【点评】此题主要考查二项式定理的应用问题,对于公式:(a+b)n=C n0a n b0+C n1a n﹣1b1+C n2a n﹣2b2++C n r a n﹣r b r++C n n a0b n,属于重点考点,同学们需要理解记忆.14.(5分)设等差数列{a n}的前n的和为S n,若S9=72,则a2+a4+a9= 24 .【考点】83:等差数列的性质.【分析】先由S9=72用性质求得a5,而3(a1+4d)=3a5,从而求得答案.【解答】解:∵∴a5=8又∵a2+a4+a9=3(a1+4d)=3a5=24故答案是24【点评】本题主要考查等差数列的性质及项与项间的内在联系.15.(5分)已知OA为球O的半径,过OA的中点M且垂直于OA的平面截球面得到圆M.若圆M的面积为3π,则球O的表面积等于 16π .【考点】LG:球的体积和表面积.【专题】11:计算题;16:压轴题.【分析】由题意求出圆M的半径,设出球的半径,二者与OM构成直角三角形,求出球的半径,然后可求球的表面积.【解答】解:∵圆M的面积为3π,∴圆M的半径r=,设球的半径为R,由图可知,R2=R2+3,∴R2=3,∴R2=4.∴S球=4πR2=16π.故答案为:16π【点评】本题是基础题,考查球的体积、表面积的计算,理解并能够应用小圆的半径、球的半径、以及球心与圆心的连线的关系,是本题的突破口,解题重点所在,仔细体会.16.(5分)若直线m被两平行线l1:x﹣y+1=0与l2:x﹣y+3=0所截得的线段的长为,则m的倾斜角可以是①15°②30°③45°④60°⑤75°其中正确答案的序号是 ①或⑤ (写出所有正确答案的序号)【考点】I2:直线的倾斜角;N1:平行截割定理.【专题】11:计算题;15:综合题;16:压轴题.【分析】先求两平行线间的距离,结合题意直线m被两平行线l1与l2所截得的线段的长为,求出直线m与l1的夹角为30°,推出结果.【解答】解:两平行线间的距离为,由图知直线m与l1的夹角为30°,l1的倾斜角为45°,所以直线m的倾斜角等于30°+45°=75°或45°﹣30°=15°.故填写①或⑤故答案为:①或⑤【点评】本题考查直线的斜率、直线的倾斜角,两条平行线间的距离,考查数形结合的思想.三、解答题(共6小题,满分70分)17.(10分)设等差数列{a n}的前n项和为S n,公比是正数的等比数列{b n}的前n项和为T n,已知a1=1,b1=3,a3+b3=17,T3﹣S3=12,求{a n},{b n}的通项公式.【考点】8M:等差数列与等比数列的综合.【专题】11:计算题.【分析】设{a n}的公差为d,数列{b n}的公比为q>0,由题得,由此能得到{a n},{b n}的通项公式.【解答】解:设{a n}的公差为d,数列{b n}的公比为q>0,由题得,解得q=2,d=2∴a n=1+2(n﹣1)=2n﹣1,bn=3•2n﹣1.【点评】本小题考查等差数列与等比数列的通项公式、前n项和,基础题.18.(12分)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2﹣c2=2b ,且sinAcosC=3cosAsinC,求b.【考点】HR:余弦定理.【分析】根据正弦定理和余弦定理将sinAcosC=3cosAsinC化成边的关系,再根据a2﹣c2=2b即可得到答案.【解答】解:法一:在△ABC中∵sinAcosC=3cosAsinC,则由正弦定理及余弦定理有:,化简并整理得:2(a2﹣c2)=b2.又由已知a2﹣c2=2b∴4b=b2.解得b=4或b=0(舍);法二:由余弦定理得:a2﹣c2=b2﹣2bccosA.又a2﹣c2=2b,b≠0.所以b=2ccosA+2①又sinAcosC=3cosAsinC,∴sinAcosC+cosAsinC=4cosAsinCsin(A+C)=4cosAsinC,即sinB=4cosAsinC由正弦定理得,故b=4ccosA②由①,②解得b=4.【点评】本题主要考查正弦定理和余弦定理的应用.属基础题.19.(12分)如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=,DC=SD=2,点M在侧棱SC上,∠ABM=60°(I)证明:M是侧棱SC的中点;(Ⅱ)求二面角S﹣AM﹣B的大小.【考点】LO:空间中直线与直线之间的位置关系;MJ:二面角的平面角及求法.【专题】11:计算题;14:证明题.【分析】(Ⅰ)法一:要证明M是侧棱SC的中点,作MN∥SD交CD于N,作NE⊥AB交AB于E,连ME、NB,则MN⊥面ABCD,ME⊥AB,设MN=x,则NC=EB=x,解RT△MNE即可得x的值,进而得到M为侧棱SC的中点;法二:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,并求出S点的坐标、C点的坐标和M点的坐标,然后根据中点公式进行判断;法三:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,构造空间向量,然后数乘向量的方法来证明.(Ⅱ)我们可以以D为坐标原点,分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,我们可以利用向量法求二面角S﹣AM﹣B的大小.【解答】证明:(Ⅰ)作MN∥SD交CD于N,作NE⊥AB交AB于E,连ME、NB,则MN⊥面ABCD,ME⊥AB,设MN=x,则NC=EB=x,在RT△MEB中,∵∠MBE=60°∴.在RT△MNE中由ME2=NE2+MN2∴3x2=x2+2解得x=1,从而∴M为侧棱SC的中点M.(Ⅰ)证法二:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz ,则.设M(0,a,b)(a>0,b>0),则,,由题得,即解之个方程组得a=1,b=1即M(0,1,1)所以M是侧棱SC的中点.(I)证法三:设,则又故,即,解得λ=1,所以M是侧棱SC的中点.(Ⅱ)由(Ⅰ)得,又,,设分别是平面SAM、MAB的法向量,则且,即且分别令得z 1=1,y1=1,y2=0,z2=2,即,∴二面角S﹣AM﹣B的大小.【点评】空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;20.(12分)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束.假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立.已知前2局中,甲、乙各胜1局.(Ⅰ)求再赛2局结束这次比赛的概率;(Ⅱ)求甲获得这次比赛胜利的概率.【考点】C8:相互独立事件和相互独立事件的概率乘法公式.【专题】12:应用题.【分析】根据题意,记“第i局甲获胜”为事件A i(i=3,4,5),“第j局甲获胜”为事件B i(j=3,4,5),(1)“再赛2局结束这次比赛”包含“甲连胜3、4局”与“乙连胜3、4局”两个互斥的事件,而每局比赛之间是相互独立的,进而计算可得答案,(2)若“甲获得这次比赛胜利”,即甲在后3局中,甲胜2局,包括3种情况,根据概率的计算方法,计算可得答案.【解答】解:记“第i局甲获胜”为事件A i(i=3,4,5),“第j局甲获胜”为事件B i(j=3,4,5).(Ⅰ)设“再赛2局结束这次比赛”为事件A,则A=A3•A4+B3•B4,由于各局比赛结果相互独立,故P(A)=P(A3•A4+B3•B4)=P(A3•A4)+P(B3•B4)=P(A3)P(A4)+P(B3)P (B4)=0.6×0.6+0.4×0.4=0.52.(Ⅱ)记“甲获得这次比赛胜利”为事件H,因前两局中,甲、乙各胜1局,故甲获得这次比赛胜利当且仅当在后面的比赛中,甲先胜2局,从而B=A3•A4+B3•A4•A5+A3•B4•A5,由于各局比赛结果相互独立,故P(H)=P(A3•A4+B3•A4•A5+A3•B4•A5)=P(A3•A4)+P(B3•A4•A5)+P(A3•B4•A5)=P(A3)P(A4)+P(B3)P(A4)P(A5)+P(A3)P(B4)P(A5)=0.6×0.6+0.4×0.6×0.6+0.6×0.4×0.6=0.648【点评】本小题考查互斥事件有一个发生的概率、相互独立事件同时发生的概率,解题之前,要分析明确事件间的关系,一般先按互斥事件分情况,再由相互独立事件的概率公式,进行计算.21.(12分)已知函数f(x)=x4﹣3x2+6.(Ⅰ)讨论f(x)的单调性;(Ⅱ)设点P在曲线y=f(x)上,若该曲线在点P处的切线l通过坐标原点,求l的方程.【考点】6B:利用导数研究函数的单调性;6H:利用导数研究曲线上某点切线方程.【专题】16:压轴题.【分析】(1)利用导数求解函数的单调性的方法步骤进行求解.(2)根据已知,只需求出f(x)在点P处的导数,即斜率,就可以求出切线方程.【解答】解:(Ⅰ)令f′(x)>0得或;令f′(x)<0得或因此,f(x)在区间和为增函数;在区间和为减函数.(Ⅱ)设点P(x0,f(x0)),由l过原点知,l的方程为y=f′(x0)x,因此f(x0)=f′(x0)x0,即x04﹣3x02+6﹣x0(4x03﹣6x0)=0,整理得(x 02+1)(x02﹣2)=0,解得或.所以的方程为y=2x或y=﹣2x【点评】本题比较简单,是一道综合题,主要考查函数的单调性、利用导数的几何意义求切线方程等函数基础知识,应熟练掌握.22.(12分)如图,已知抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点.(Ⅰ)求r的取值范围;(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.【考点】IR:两点间的距离公式;JF:圆方程的综合应用;K8:抛物线的性质.【专题】15:综合题;16:压轴题.【分析】(1)先联立抛物线与圆的方程消去y,得到x的二次方程,根据抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是此方程有两个不相等的正根,可求出r的范围.(2)先设出四点A,B,C,D的坐标再由(1)中的x二次方程得到两根之和、两根之积,表示出面积并求出其的平方值,最后根据三次均值不等式确定得到最大值时的点P的坐标.【解答】解:(Ⅰ)将抛物线E:y2=x代入圆M:(x﹣4)2+y2=r2(r>0)的方程,消去y2,整理得x2﹣7x+16﹣r2=0(1)抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是:方程(1)有两个不相等的正根∴即.解这个方程组得,.(II)设四个交点的坐标分别为、、、.则直线AC、BD的方程分别为y﹣=•(x﹣x 1),y+=(x﹣x1),解得点P的坐标为(,0),则由(I)根据韦达定理有x1+x2=7,x1x2=16﹣r2,则∴令,则S2=(7+2t)2(7﹣2t)下面求S2的最大值.由三次均值有:当且仅当7+2t=14﹣4t,即时取最大值.经检验此时满足题意.故所求的点P的坐标为.【点评】本题主要考查抛物线和圆的综合问题.圆锥曲线是高考必考题,要强化复习.。
考研数学三(概率论与数理统计)历年真题试卷汇编1(题后含答案及解析)

考研数学三(概率论与数理统计)历年真题试卷汇编1(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(87年)若二事件A和B同时出现的概率P(AB)=0,则【】A.A和B不相容(互斥).B.AB是不可能事件.C.AB未必是不可能事件.D.P(A)=0或P(B)=0.正确答案:C解析:由P(AB)=0不能推出AB=的结论,故A、B均排除.而D明显不对,应选C.知识模块:概率论与数理统计2.(89年)以A表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件为:【】A.“甲种产品滞销,乙种产品畅销”.B.“甲、乙两种产品均畅销”.C.“甲种产品滞销”.D.“甲种产品滞销或乙种产品畅销”.正确答案:D 涉及知识点:概率论与数理统计3.(90年)议A、B为随机事件,且BA,则下列式子正确的是【】A.P(A+B)=P(A).B.P(AB)=P(A).C.P(B|A)=P(B).D.P(B-A)=P(B)-P(A).正确答案:A解析:∵AB,∴A+B=A,故选A.知识模块:概率论与数理统计4.(91年)设A和B是任意两个概率不为零的互不相容事件,则下列结论中肯定正确的是:【】A.不相容.B.相容.C.P(AB)=P(A)P(B).D.P(A-B)=P(A).正确答案:D 涉及知识点:概率论与数理统计5.(92年)设当事件A与B同时发生时,事件C必发生,则【】A.P(C)≤P(A)+P(B)-1.B.P(C)≥P(A)+P(B)-1.C.P(C)=P(AB).D.P(C)=P(A∪B).正确答案:B 涉及知识点:概率论与数理统计6.(93年)设两事件A与B满足P(B|A)=1,则【】A.A是必然事件.B.P(B|)=0C.AB.D.AB.正确答案:C 涉及知识点:概率论与数理统计7.(94年)设0<P(A)<1,0<P(B)<1,P(A|B)+P()=1,则事件A和B 【】A.互不相容.B.互相对立.C.不独立.D.独立.正确答案:D 涉及知识点:概率论与数理统计8.(96年)已知0<P(B)<1,且P[(A1+A2)|B]=P(A1|B)+P(A2|B),则下列选项成立的是【】A.P[(A1+A2)|]=P(A1|)+P(A2|)B.P(A1B+A2B)=P(A1B)+P(A2B)C.P(A1+A2)=P(A1|B)+P(A2|B)D.P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)正确答案:B解析:由已知得,化简得B项正确.知识模块:概率论与数理统计9.(00年)在电炉上安装了4个温控器,其显示温度的误差是随机的.在使用过程中,只要有两个温控器显示的温度不低于临界温度t0,电炉就断电.以E 表示事件“电炉断电”,而T(1)≤T(2)≤T(3)≤T(4)为4个温控器显示的按递增顺序排列的温度值,则事件E等于【】A.{T(1)≥t0}B.{T(2)≥t0}C.{T(3)≥t0}D.{T(4)≥t0}正确答案:C 涉及知识点:概率论与数理统计填空题10.(88年)设P(A)=0.4,P(A∪B)=0.7,那么(1)若A与B互不相容,则P(B)=_______;(2)若A与B相互独立,则P(B)=_______.正确答案:0.3;0.5.解析:由P(A∪B)=P(A)+P(B)-P(AB) (1)若A、B互不相容,则AB =,∴P(AB)=0,代入上式得0.7=0.4+P(B)-0,故P(B)=0.3 (2)若A、B相互独立,则P(AB)=P(A)P(B),代入得0.7=0.4+P(B)-0.4×P(B),故P(B)=0.5.知识模块:概率论与数理统计11.(88年)若事件A,B,C满足等式A∪C=B∪C,则A=B.该命题是否正确_______.(填正确或不正确)正确答案:不正确涉及知识点:概率论与数理统计12.(90年)一射手对同一目标独立地进行4次射击,若至少命中一次的概率为,则该射手的命中率为_______.正确答案:解析:设该射手的命中率为p,则4次射击(独立重复)中命中k次的概率为C4kpk(1-p)4-k.由题意=P(他至少命中一次)=1-P(他命中0次)=1-C40p0(1-p)4-0=1-(1-p)4 解得p=知识模块:概率论与数理统计13.(92年)将C,C,E,E,I,N,S这七个字母随机地排成一行,则恰好排成SCIENCE的概率为_______.正确答案:解析:这7个字母排一行共有71种排法(第1位置有7种放法,第2位置有6种放法,余类推,用乘法原则),这是总样本点个数.而在有利场合下,第1位置有1种放法(1个S),第2位置有2种放法(2个C中选1个),同理,第3位置有1种放法(1个D,第4位置有2种放法(2个E中选1个),后边都是1种选法(即使是C或E,只剩1个了),故有1×2×1×2×1×1×1=4种放法,这是有利样本点个数.故所求概率为知识模块:概率论与数理统计14.(07年)在区间(0,1)中随机地取两个数,则这两个数之差的绝对值小于的概率为_______.正确答案:解析:设这两个数分别为χ,y,则二维点(χ,y)可能取的点为图4.3中的正方形内部(面积为1),而符合要求(即题中“两数之差的绝对值<”)的点集合{(χ,y):0<χ<1,0<y<1,|χ-y|<}为图中阴影部分G,而G的面积为1-2×.故所求概率为知识模块:概率论与数理统计15.(12年)设A,B,C是随机事件,A与C互不相容,P(AB)=,P(C)=,则P(AB|)=_______.正确答案:解析:∵AC=,∴A,得P(AB)=P(AB)=,又P()=1-P(C)=,故知识模块:概率论与数理统计16.(16年)设袋中有红、白、黑球各1个,从中有放回地取球,每次取1个,直到三种颜色的球都取到时停止,则取球次数恰好为4的概率为_______.正确答案:解析:用古典概型,4次取球共有34种取法;而“第1次取红球,第2、3次至少取得1白球且未取得黑球,第4次取黑球”共有3种取法:(按顺序)“红红白黑,红白红黑,红白白黑”,故上述事件(引号内的事件)的概率为.而红、白、黑3种颜色排列有31种,故本题所求概率为.知识模块:概率论与数理统计解答题解答应写出文字说明、证明过程或演算步骤。
考研数学三(概率论与数理统计)历年真题试卷汇编5(题后含答案及解析)

考研数学三(概率论与数理统计)历年真题试卷汇编5(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(03年)将一枚硬币独立地掷两次,引进事件:A1={掷第一次出现正面},A2={掷第二次出现正面},A3={正、反面各出现一次},A4={正面出现两次},则事件【】A.A1,A2,A3相互独立.B.A2,A3,A4相互独立.C.A1,A2,A3两两独立.D.A2,A3,A4两两独立.正确答案:C 涉及知识点:概率论与数理统计2.(07年)某人向同一目标独立重复射击,每次射击命中目标的概率为p(0<P<1),则此人第4次射击恰好第2次命中目标的概率为【】A.3p(1-p)2.B.6p(1-p)2.C.3p2(1-p)2.D.6p2(1-p)2.正确答案:C解析:P{第4次射击恰好第2次命中目标}=P{前3次射击恰中1枪,第4次射击命中目标} =P{前3次射击恰中1枪}.P{第4次射击命中目标}=C31p(1-p)2.P=3p2(1-p)2 知识模块:概率论与数理统计3.(09年)设事件A与事件B互不相容,则【】A.P()=0.B.P(AB)=P(A)P(B).C.P(A)=1-P(B).D.P()-1.正确答案:D 涉及知识点:概率论与数理统计4.(14年)设随机事件A与B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=【】A.0.1B.0.2C.0.3D.0.4正确答案:B解析:∵A与B独立,∴P(AB)=P(A)P(B).故0.3=P(A-B)=P(A)-P(AB)=P(A)-P(A)P(B) =P(A)[1-P(B)]=P(A)(1-0.5)=0.5(P(A) 得P(A)==06,P(B-A)=P(B)-P(AB)=P(B)-P(A)P(B)=0.5-0.6×0.5=0.2.知识模块:概率论与数理统计5.(15年)若A,B为任意两个随机事件,则【】A.P(AB)≤P(A)P(B).B.P(AB)≥P(A)P(B).C.P(AB)≤.D.P(AB)≥.正确答案:C解析:由ABA,ABB得P(AB)≤P(A),P(AB)≤P(B),两式相加即得:P(AB)≤.知识模块:概率论与数理统计6.(16年)设A,B为两个随机事件,且0<P(A)<1,0<P(B)<1,如果P(A|B)=1,则【】A.P()=1.B.P(A|)=0.C.P(A∪B)=1.D.P(B|A)=1.正确答案:A解析:由1=P(A|B)=,有P(B)=P(AB) 于是知识模块:概率论与数理统计7.(90年)设随机变量X和Y相互独立,其概率分布为则下列式子正确的是:【】A.X-YB.P{X-Y}=0C.P{X-Y}=D.P{X=Y}=1正确答案:C解析:P(X=Y)=P(X=-1,Y=-1)+P(X=1,Y=1) =P(X=-1)P(Y =-1)+P(X=1)P(Y=1) =知识模块:概率论与数理统计8.(93年)设随机变量X的密度函数为φ(χ),且φ(-χ)-φ(χ),F(χ)为X的分布函数,则对任意实数a,有【】A.F(-a)=1-∫0aφ(χ)dχB.F(-a)=-∫0aφ(χ)dχC.F(-a)=F(a)D.F(-a)=2F(a)-1正确答案:B解析:由概率密度的性质和已知,可得故选B.知识模块:概率论与数理统计9.(95年)设随机变量X~N(μ,σ2),则随着σ的增大,概率P(|X-μ|<σ) 【】A.单调增大.B.单调减小.C.保持不变.D.增减不定.正确答案:C解析:由已知X~N(μ,σ),得~N(0,1) 故P{|X-μ|<σ}==(1)Ф-Ф(-1) 故选C.知识模块:概率论与数理统计填空题10.(89年)设随机变量X的分布函数为则A=_______,P{|X|<}=_______.正确答案:1;解析:∵分布函数是右连续的,故得1=Asin ∴A=1 这时,F(χ)在(-∞,+∞)上都连续,于是知识模块:概率论与数理统计11.(91年)设随机变最X的分布函数为则X的概率分布为_______.正确答案:解析:F(χ)为一阶梯状函数,则X可能取的值为F(χ)的跳跃点:-1,1,3.P(X=-1)=F(-1)-F(-1-0)=0.4 P(X=1)=F(1)-F(1-0)=0.8-0.4=0.4 P(X=3)=F(3)-F(3-0)=1-0.8=0.2 知识模块:概率论与数理统计12.(94年)设随机变量X的概率密度为以Y表示对X的三次独立重复观察中事件{X≤}出现的次数P{Y=2}=_______.正确答案:解析:由题意,Y~B(3,p).其中p=故知识模块:概率论与数理统计13.(00年)设随机变量X的概率密度为若k使得P{X≥k}=,则k的取值范围是_______.正确答案:[1,3]解析:∵P(X≥k)=∫k+∞f(χ)dχ.可见:若k≤0,则P(X≥k)=1 若0<k<1,则P(X≥k)=若k>6,则P(X≥k)=0 若3<k≤6,则P(X ≥k)=若1≤k≤3,则P(X≥k)=综上,可知K∈[1,3].知识模块:概率论与数理统计14.(05年)从数1,2,3,4中任取一个数,记为X,再从1,…,X中任取一个数,记为Y,则P(Y=2}=_______.正确答案:解析:由题意,X的概率分布为而P(Y=2|X=1)=0,P(Y=2|X=2)=,P(Y=2|X=3)=,P(Y=2|X=4)=,故由全概率公式得知识模块:概率论与数理统计15.(05年)设二维随机变量(X,Y)的概率分布为若随机事件{X=0}与{X+Y=1}相互独立,则a=_______,b=_______.正确答案:0.4;0.1.解析:由题意知0.4+a+b+0.1=1,∴a+b=0.5 而P{X=0}=0.4+a,P{X+Y=1}=P{X=0,Y=1}+P{X=1,Y=0}=a+b=0.5,P{X =0,X+Y=1}=P{X=0,Y=1}=a 由P{X=0,X+Y=1)=P{X=0)P{X +Y=1} ∴a=(0.4+a)0.5,得a=0.4,从而b=0.1.知识模块:概率论与数理统计16.(06年)设随机变量X与Y相互独立,且均服从区间[0,3]上的均匀分布,则P{max(X,Y)≤1}=_______.正确答案:解析:由题意知X与Y的概率密度均为:则P(X≤1}=P{Y≤1}=∫-∞1f(χ)dχ=故P{max(X,Y)≤1}=P{X≤1,y≤1}=P{X≤1}P{y≤1}=知识模块:概率论与数理统计17.(99年)设随机变量Xij(i=1,2,…,n;n≥2)独立同分布,Eij=2,则行列式Y=的数学期望EY=_______.正确答案:0解析:由n阶行列式的定义知Y=,P1,…,Pn为(1,…,n)的排列,τ(p1p2…pn)为排列p1p2…pn的逆序数.而Xij(i,j=1,2,…,n)独立同分布且EXij=2,故知识模块:概率论与数理统计解答题解答应写出文字说明、证明过程或演算步骤。
2009届高考数学名校试题精选概率与统计部分

2009届高考数学名校试题精选——概率与统计部分专项训练一、选择题:1、4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( ) A .13B .12C .23D .342、调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据表: 你认为婴儿的性别与出生时间有关系的把握为( ) A.80% B.90% C.95% D.99%3、在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为( ) (A )511(B )681 (C )3061(D )40814、某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是( ) A. 256625B. 192625C.96625D.166255、已知样本7,8,9,,x y 的平均数是8xy 的值为( )A、8 B、32 C、60 D、806、把一根匀均匀木棒随机地按任意点拆成两段,则“其中一段的长度大于另一段长度的2倍”的概率为( )(A)23 (B)25 (C)35 (D)137、如图,四边形ABCD 为矩形,3=AB ,1=BC ,以A 为圆心,1为半径作四分之一个圆弧DE ,在圆弧DE 上任取一点P ,则直线AP 与线段BC 有公共点的概率是( ). (A)31 (B)23 (C)25 (D)358.某学生通过计算初级水平测试的概率为21,他连续测试两次, 则恰有1次获得通过的概率为 ( )43.41.21.31.D C B A 9.下面事件①若a 、b ∈R ,则a ·b=b·a ;②某人买彩票中奖;③6+3>10;④抛一枚硬币出现正面向上,其中必然事件有 ( ) A .① B .② C .③④ D .①②10.在4次独立重复实验中,随机事件A 恰好发生1次的概率不大于其恰好发生两次的概率,则事件A 在一次试验中发生的概率的范围是 ( )A .[O .4,1]B .(O ,0.4]C .(O ,0.6]D .[0.6,1)11.设袋中有8个球,其中3个白球,3个红球,2个黑球,除了颜色不同外,其余均相同.若取得1个白球得1分,取得1个红球扣1分,取得一个黑球既不得分,也不扣分,则任摸3个球后的所得总分为正分的概率为( )5623.289.74.5619.D C B A 12.从1、2、3、4、5中随机抽取3个数字(允许重复)组成一个三位数,则和等于9的概率为 ( )12513.12416.12518.12519.D C B A 13.甲、乙两人独立地对同一目标各射击一次,其命中率一分别为0.6和0.5,现已知目标被击中,则它恰是甲射中的概率为 ( )A .0.45B .0.6C .0.65D .0.7514. 教某气象站天气预报的准确率为80%.则5次预报中至少有4次准确的概率为 ( ) A ,0.2 B .0.41 C .0.74 D .0.6715.有一道试题,A 解决的概率为21,B 解决的概率为31,C 解决的概率为41,则A 、B 、C 三人独立解答此题,只有1人解出的117111则两人射击成绩的稳定程度是__________________。
考研数学三(概率论与数理统计)历年真题试卷汇编6(题后含答案及解析)

考研数学三(概率论与数理统计)历年真题试卷汇编6(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(2000年)在电炉上安装了4个温控器,其显示温度的误差是随机的。
在使用过程中,只要有两个温控器显示的温度不低于临界温度t0,电炉就断电,以E表示事件“电炉断电”,而T(1)≤T(2)≤T(3)≤T(4)为4个温控器显示的按递增顺序排列的温度值,则事件E等于事件( )A.{T(1)≥t0}。
B.{T(2)≥t0}。
C.{T(3)≥t0}。
D.{T(4)≥t0}。
正确答案:C解析:随机变量T(1),T(2),T(3),T(4)为4个温控器显示的按递增顺序排列的温度值,事件E表示事件“电炉断电”,即有两个温控器显示的温度不低于t0,此时必定两个显示较高的温度大于等于t0,即T(4)≥T(3)≥t0。
所以说断电事件就是{T(3)≥t0}。
2.(2009年)设事件A与事件B互不相容,则( )A.B.P(AB)=P(A)P(B)。
C.P(A)=1-P(B)。
D.正确答案:D解析:因为A,B互不相容,所以P(AB)=0。
选项A:=1-P(A∪B),因为P(A ∪B)不一定等于1,所以A不正确;选项B:当P(A),P(B)不为0时,选项B 不成立,故排除B;选项C:只有当A、B互为对立事件的时候才成立,故排除C;选项D:=1-P(AB)-1,故D正确。
3.(2014年)设随机事件A与B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=( )A.0.1。
B.0.2。
C.0.3。
D.0.4。
正确答案:B解析:P(A-B)=0.3,则P(A)-P(AB)=0.3,又随机事件A与B相互独立,则有P(AB)=P(A)P(B)。
因此有P(A)-P(A)P(B)=0.3,又P(B)=0.5,故P(A)=0.6,且P(AB)=P(A)P(B)=0.3。
淮海工学院09-11概率论与数理统计试卷和答案
第1页 共30页淮 海 工 学 院09 - 10 学年 第2学期 概率论与数理统计 试卷(A闭卷)答案及评分标准1.一袋中有6个白球,4个红球,任取两球都是白球的概率是-----------------( B ) ()A 1/2 ()B 1/3 ()C 1/4 ()D 1/6 2.设随机变量~(3,)X b p ,且{1}{2}P X P X ===,则p 为---------------(A )()A 0.5 ()B 0.6 ()C 0.7 ()D 0.83.设),(Y X 的联合概率密度为(,)f x y ,则边缘概率密度()X f x =----------( C )()A (,)f x y dx +∞-∞⎰()B (,)xf x y dx +∞-∞⎰()C (,)f x y dy +∞-∞⎰()D (,)yf x y dy +∞-∞⎰4.设X 是一随机变量,则下列各式中错误的是----------------------------------( C )()A [()]()E D X D X = ()B [()]()E E X E X = ()C [()]()D EX E X = ()D [()]0D E X =5.已知()0E X =,()3D X =,则由切比雪夫不等式得{||6}P X ≥≤------( B )()A 1/4()B 1/12 ()C 1/16 ()D 1/366.设总体()21,2XN ,12,,,n X X X 为X 的一个样本,则---------------( C )()A()10,12X N - ()B ()10,14X N - ()C ()0,1N ()D ()0,1N7.设总体2~(,)X N μσ,2,μσ未知,n X X X ,,,21 为来自X 的样本,样本均值为X ,样本标准差为S ,则μ的置信水平为α-1的置信区间为-------( D )()A 2()X z α±()B 2((1))X z n α±-()C 2(())X n α±()D 2((1))X n α- 8.设总体2~(,)X N μσ,2,μσ未知,检验假设22220010:,:H H σσσσ=≠的拒绝域为--------------------------------------------------------------------------------------( A )()A 2222122(1)(1)n n ααχχχχ-≥-≤-或 ()B 22(1)n αχχ≥-()C 22221(1)(1)n n ααχχχχ-≥-≤-或 ()D 221(1)n αχχ-≤-二、填空题(本大题共4小题,每题4分,共16分)1.设,,A B C 表示三个随机事件,则事件“,,A B C 不都发生”可用,,A B C 的运算关系表示为ABC .2.随机变量X 的数学期望()2E X =,方差()4D X =,则2()E X = 8第2页 共30页3.设X Y 和相互独立,且()~0,1X U ,Y 的概率密度为121,0()20,y Y e y f y -⎧>⎪=⎨⎪⎩其他,则(,)X Y 的概率密度为121,(0,1),0(,)20,y ex y f x y -⎧∈>⎪=⎨⎪⎩其他.4.设n X X X ,,,21 是来自正态总体),(~2σμN X 的一个简单随机样本,2,X S 分别为样本均值和样本方差,则()E X =μ,2()E S =2σ.三、计算题(本大题共4小题,每题7分,共28分)1.已知()()0.4,0.7P A P AB ==,分别在下列两种条件下,求()P B 的值.(1)若A 与B 互不相容;(2)若A 与B 相互独立. 解 由加法公式()()()()P AB P A P B P AB =+- ------------2'(1)A 与B 互不相容,即()0AB P AB =∅⇒=,代入加法公式得,()0.70.40.3P B =-= ------------2' (2)A 与B 相互独立,即()()()P AB P A P B =代入加法公式得,0.70.4()0.4()P B P B =+-,得()0.5P B = ------------3'2.已知随机变量X 的概率密度函数为2,01,()0,,ax x f x ⎧<<=⎨⎩其他 求(1)常数a ;(2){0.3}.P X > 解 (1)120()1,13f x dx ax dx a +∞-∞=∴=∴=⎰⎰ -----------------4'(2) 11230.30.3{0.3}30.973.P X x dx x >===⎰-----------------3'3.已知随机变量~(0,1)X U ,求随机变量ln Y X =的概率密度函数)(y f Y . 解 1,01,()0,X x f x <<⎧=⎨⎩其他,---------------------2'1()ln ,()0y g x x g x x'===>,()g x 在(0,1)严格单调增, 反函数(),()yyx h y e h y e '==={}{}min (0),(1),max (0),(1)0.g g g g αβ==-∞==----------------------2'[()]|'()|,,()0,X Y f h y h y y f y αβ⋅<<⎧=⎨⎩其他,,0,0,0y e y y ⎧<=⎨≥⎩ ---------------------3'4.设随机变量X求(1)(),X Y 的分布律;(2){3}.P X Y += 解 (1)-------------------5'(2){3}{1,2}{2,1}P X Y P X Y P X Y +====+==0.210.210.42.=+= ---------------------2'第3页 共30页四、应用题(本题8分)某商店将同牌号同瓦数的一、二、三级灯泡混在一起出售,三个级别的灯泡比例为1:2:1,出售灯泡时需试用. 一、二、三级品在试用时被烧毁的概率分别为0.1, 0.2, 0.3. 现有一顾客买一灯泡试用正常,求该灯泡为三级品的概率. 解: 设1A =“一级品”,2A =“二级品”,3A =“三级品”,B =“灯泡正常”,------------------2'123123121(),(),(),444(|)0.9,(|)0.8,(|)0.7,P A P A P A P B A P B A P B A ====== ------------------2' 313112233()(|)(|)()(|)()(|)()(|)P A P B A P A B P A P B A P A P B A P A P B A ∴=++10.940.281.1210.90.80.7444⨯==⨯+⨯+⨯ ----------------4'五、计算题(本题8分)设随机变量X 在[2,5]上服从均匀分布,现对X 进行三次独立观测,试求其中至少有一次“观测值大于3”的概率.解 1,25,()30,X x f x ⎧≤≤⎪=⎨⎪⎩其他,---------------2'5312{3}33p P X dx =>==⎰ ---------------2'设Y 表示三次独立观测中“观测值大于3”的次数,则2~(3,)3Y b ---------------2'3126{1}1{0}1()327P Y P Y ∴≥=-==-= -----------------2'六、计算题(本题8分)设总体X 的概率密度为1,0,(;)0,0.xe xf x x θθθ-⎧>⎪=⎨⎪≤⎩其中0>θ为未知参数,12,,,n X X X 为来自X 的样本,12,,,n x x x 为相应的样本值,(1)求θ的最大似然估计量1ˆθ; (2)试问1ˆθ与21ˆ2X X θ=-是不是θ的无偏估计量?当1n >时,上述两个估计量哪一个较为有效?解 (1) 似然函数112111()(;),,,,0nii x nnin ni i L f x ex x x θθθθ=-==∑==>∏∏ -------2'11ln ()ln nii L n x θθθ==--∑,令21ln ()10()ni i d L n x d θθθθ==-+=∑,解得11ˆni i x x n θ===∑, 所以θ的最大似然估计量为1ˆ.X θ= ----------------2' (2) 1ˆ()(),E E X θθ== 21ˆ()(2)2,E E X X θθθθ=-=-= ∴估计量12ˆˆθθ与都是θ的无偏估计量。
率论与数理统计09年6月重修答案
重庆大学概率论与数理统计(重修)试卷课程试卷A卷B卷2008 ~2009学年 第 二 学期 开课学院: 数理学院考试日期: 2009年6考试方式:开卷闭卷 其他 考试时间:120 分钟 题 号一 二 三 四 五 六 七 八 九 十 总 分 得 分一、 填空题(每空3分,共39分)1、已知A ,B 两个事件满足条件()()P AB P A B =,且()P A P =,则()P B =1-P2、.一袋中装有4个红球3个白球,现不放回从中摸两个球,令A 表示“第一次摸到白球”,B 表示“第二次摸到红球”。
则P(B|A)= ;P(B)= 。
解: P(B|A) = 3264=;7463746473)|()()|()()()()(=⋅+⋅=+=+=A B P A P A B P A P B A P AB P B P 3 设P(A) = , P(B) = .1) 如果A 与B 互斥,则)(B A P = ;)(B A P ⋃= 。
2) 如果A B ⊂,则)(B A P = ;)(B A P ⋃= 。
解:1)75.0)()()()()()()()(25.0)()(,==-+=-+=⋃==∴⊂⊂Φ=B P A P B P A P B A P B P A P B A P B P B A P BA AB AB2)如果A B ⊂,35.025.06.0)()()()()(=-=-=-=B P A P AB P A P B A P ;1)()()()()()()()()()(=+=+-+=-+=⋃B P B P AB P A P B P A P B A P B P A P B A P4 设25,36,0.4XY DX DY ρ=== 则(,)COV X Y = 12 ,(2)D X Y += 885设1,2,3,4X X X X 是来自正态总体(0,1)N 样本,则统计量212234()()X X Y X X +=+ F (1,1)6设()XP λ,其中λ未知,则未知参数λ的矩估计量λ=λ7设相互独立的两个随机变量,X Y 具有同一分布律,且X 的分布律为X 0 1P2121则随机变量min(,)Z X Y =的分布律为解:z 01P43418设随机变量X 与Y 相互独立,且P{X ≤1}=12,P{Y>1}=13,则 P{X ≤1, Y ≤1}=13二、 计算题(每小题7分,共35分)1、设设随机变量X 具有分布密度⎩⎨⎧≤≤-=其它,010 ),1(6)(x x x x ϕ 求:① EX ;② DX ; ③ })(5|{|X D EX X P <- 解:命题人:组题人:审题人:命题时间:学院 专业 年级 学号 姓名封线密1)1(6}10{}201521{}5{201)1()21(6)()(21)1(6)(1012212=-=<<=<-=<-=--=-==-==⎰⎰⎰⎰⎰∞∞-∞∞-dx x x X P X P DX EX X P dx x x x dx x EX x DX dx x x dx x x EX ϕϕ2、设二维随机变量(X,Y)的密度函数为⎩⎨⎧<<<<-=其它 , 020,20 , )2(),(2y x y y Ax y x ϕ(1)求常数A; (2)问X与Y是否独立? 解:(1)由密度函数的完备性可得Ady y y dx x A dxdy y y Ax dxdy y x 932)2()2(),(1220220202=-=-==⎰⎰⎰⎰⎰⎰∞-+∞∞-+∞∞-ϕ所以 A=329。
09年概率论与数理统计A试卷(天津科技大学)
7. 若随机变量X 与Y ,满足1DX DY ==,相关系数 ()1,2R X Y -=,则(4)D X Y -= .8.某品牌清漆的干燥时间(小时)2~(, 0.6)X N μ,现随机抽取9个样品,算得样本均值6x =,求μ的置信水平为0.95的置信区间为 . 9. 若随机变量12, X X 相互独立,且都服从标准正态()0, 1N 分布,记12534Y X X =+-, 则Y 服从的为 分布.10. 设总体()~,4X N μ,从中抽取容量为16的样本1216,,,X X X ,则()26.6656P S <= ____.二、某工厂有甲、乙、丙三个车间生产同一种产品,由于设备差别,各车间的生产量分别占总产量的60% 、 25%、 15% ;各车间生产的产品优质品率分别为70%、 80%、 90% 。
现从总产品中随机挑选一件,(1)求此产品为优质品的概率;(2)若此产品不是优质品,求它是甲车间生产的概率. (10分)概率密度() 66,0,0,0.y Y e y f y y -⎧>=⎨≤⎩ ,写出二维随机变量(), X Y 的联合分布函数(), f x y ,并求概率()P X Y ≤ . (8分)六、设连续总体X 的概率密度函数为 1,01( )0,x x f x θθθ-⎧<<=⎨⎩;其它, 其中0θ>。
n X X X ,,,21 为来自总体X 的样本,求未知参数θ的最大似然估计量。
(7分)x的关系,将同样条件下繁殖的7只老鼠注射不同剂量的胰岛素A ,依据观测数据经计算得0.35x =,44.14y =,0.07xx S =,9.2xy S =,1372.8572yy S =. 求回归方程ˆˆˆyx αβ=+. (7分) 十. 设连续型随机变量X 的概率密度为:()sin ,0,20,a x b x f x π⎧⋅+≤≤⎪=⎨⎪⎩其它, 且48E X π+=,求a 和b . (7分)。
2009考研数学真题及答案详解
2009年全国硕士研究生入学统一考试数学一试题答案解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)当0x ®时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则()A 11,6a b ==-.()B 11,6a b ==.()C 11,6a b =-=-.()D 11,6a b =-=.【答案】 A【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小,则222200000()sin sin 1cos sinlim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx ®®®®®---==-×---洛洛230sin lim 166x aax a b b ax a®==-=-× 36a b \=- 故排除,B C 。
另外201cos lim 3x a axbx ®--存在,蕴含了1cos 0a ax -®()0x ®故 1.a =排D 。
所以本题选A 。
(2)如图,正方形(){},1,1x y x y ££被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =òò,则{}14max k k I ££=()A 1I .()B 2I . ()C 3I .()D 4I .【答案】A【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。
24,D D 两区域关于x 轴对称,而(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,而(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是-1 -1 1 1 xy 1D 2D3D4D关于x 的偶函数,所以{}1(,),012cos 0x y y x x I y xdxdy ³££=>òò;{}3(,),012cos 0x y y x x I y xdxdy £-££=<òò.所以正确答案为A. (3)设函数()y f x =在区间[]1,3-上的图形为:则函数()()0x F x f t dt =ò的图形为()A ()B()C ()D【答案】D【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征:①[]0,1x Î时,()0F x £,且单调递减。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河海大学2009~2010学年第一学期《概率论与数理统计》试卷(A)(供全校2008级工科学生用)(2009年12月)专业、班级姓名学号成绩一、(每空2分,本题满分18分)填空题1.一批电子元件共有100个,次品率为0.05,连续两次不放回地从中任取一个,则第二次才取到正品的概率为。
2.设随机变量X ~)1.0,20(B ,则==)}({X E X P 。
3.假设随机事件A 与B 相互独立,5.0)(=A P ,α-=2)(B P ,96)(=⋃B A P ,则=α。
4.设随机变量),10(~2σN X ,且3.0}2010{=<<X P ,则=<<}200{X P 。
5.设二维随机变量),(Y X 的联合分布律为则==}0{XY P 。
6.已知随机变量)1,3(~-N X ,)3,1(~U Y ,且X 与Y 相互独立,设随机变量232+-=Y X Z ,则=)(Z E ,=)(Z D 。
7.设随机变量)1)((~>n n t X ,21XY =,则~Y 。
8.设总体),(~2σμN X ,μ和2σ均未知,n X X X ,,,21 为来自该总体的一个简单随机样本,则2σ的置信度为α-1的置信区间为。
二、(本题满分12分)某厂卡车运送防“非典”用品下乡,顶层装10个纸箱,其中5箱民用口罩、2箱医用口罩、3箱消毒棉花。
到目的地时发现丢失了1箱,但不知丢失了哪一箱,现从剩下的9箱中任意打开2箱检查。
(1)求任意打开的2箱都是民用口罩的概率;(2)在任意打开的2箱都是民用口罩的情况下,求丢失的一箱也是民用口罩的概率。
三、(本题满分12分)已知随机变量X 的概率密度函数为⎪⎩⎪⎨⎧<≤-<≤=其他,021,210,)(x x x x A x f求(1)常数A ;(2)X 的分布函数)(x F ;(3))23(2+-X X E ;(4)}5.15.0{≤<X P 。
四、(本题满分8分)设随机变量X服从参数为3的泊松(Poisson)分布,Y 服从参数为4的泊松分布,且X 与Y 相互独立,证明XY+服从参数为7的泊松分布。
五、(本题满分8分)设X 、Y 是相互独立的随机变量,概率密度函数分别为⎩⎨⎧≤≤=其它,010,1)(x x f X,⎩⎨⎧≤>=-0,00,)(y y e y f y Y求Y X Z +=的概率密度函数)(z f Z 。
六、(本题满分12分)设二维连续型随机变量),(Y X 的联合概率密度函数为:⎩⎨⎧≤≤≤≤=其它,01,10,2),(y x x y x f求:(1)关于X 和Y 的边缘密度函数)(x f X 和)(y f Y ;(2)X 和Y 的相关系数XY ρ;(3)X 与Y 是否独立?为什么?七、(本题满分16分)设总体X 的密度函数为⎪⎩⎪⎨⎧>=-其它,00,1);(x e x f xθθθ其中θ为未知参数。
(1)求θ的矩估计量M θˆ和极大似然估计量MLE θˆ; (2)问MLE θˆ是否为θ的无偏估计量?为什么?(3)若给出来自该总体的一个容量为8的样本的观测值:1、3、3、2、6、5、7、9,求}1{>X P 的极大似然估计值。
八、(本题满分14分)某电子制造厂生产的产品额定质量为500克,某日开工后随机抽查了9件进行测量,测量结果经计算得其平均值为499=x ,样本方差为292=S ,设该天生产的产品质量服从正态分布),(2σμN 。
(1)试问该天生产机器工作是否正常?)05.0(=α(2)若已知该天生产的产品质量的方差为302=σ,求产品平均质量μ的置信度为95%的置信区间。
(283.11.0=z ,645.105.0=z ,960.1025.0=z ,3968.1)8(1.0=t ,3830.1)9(1.0=t ,3722.1)10(1.0=t ,8695.1)8(05.0=t ,8331.1)9(05.0=t ,8125.1)10(05.0=t ,3060.2)8(025.0=t ,2622.2)9(025.0=t ,2280.2)10(05.0=t )2009-2010学年第一学期《概率论与数理统计》(工科)参考解答A 卷一(每空2分,共18分).1.19/396或0.048;2.1822209.01.0C ≈0.285;3.4/3;4.0.6;5.0.5;6.-10,7;7.F (n,1);8.))1()1(,)1()1((22/1222/2-χ--χ-α-αn S n n S n 。
二(12分).A -----任取2箱都是民用口罩,kB ----丢失的一箱为k ,3,2,1=k 分别表示民用口罩,医用口罩,消毒棉花.则(1)3685110321)()()(29252925292431=⋅+⋅+⋅==∑=C C C C C C B A P B P A P kk k(2).83368363)(/21)(/)()()(2924111=÷=⋅==A P C C A P B A P B P A BP三(12分).(1)由1)(=⎰+∞∞-dx x f ,又=⎰+∞∞-dx x f )(1)2(2110=-+⎰⎰dx x Axdx ,所以1=A(2)当0≤x 时, )(x F =0;当10≤<x 时, )(x F 221)(x xdx dx x f xx===⎰⎰∞-,当21≤<x 时, 122)2()(211--=-+=⎰⎰xx dx x xdx x F x,当2>x 时,)(x F =1,所以X的分布函数为)(x F ⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<--≤<≤=xx x x x x x 2121,12210,210,022;(3))23(2+-X XE =61)2)(23()23(212102=-+-++-⎰⎰dx x x xxdx x x;(4)}5.15.0{≤<X P ⎰⎰-+=5.1115.0)2(dx x xdx =0.75四(8分).)3(~P X ,所以X 的分布律为!3)(3k ek X P k-==,,...3,2,1,0=k ;又因为)4(~P Y ,所以Y 的分布律为!4)(4k ek Y P k -==,,...3,2,1,0=k ;令YX Z +=,所以Z的取值为,...3,2,1,0,且有∑∑=∞==========km m m X P m X k Z P m X P m X k Z P k Z P 0)()|()()|()(!7!3)!(4)()(734k em em k em X P m k Y P kkm mmk km -=---==⋅-==-==∑∑,,...3,2,1,0=k。
从而X Y+服从参数为7的泊松分布。
五(8分).法1: ⎪⎩⎪⎨⎧>≤≤=-⋅,,0,0,10,),(其它y x e y x f y⎰⎰⎰⎰⎰⎰≤+--------⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≥+-=<<+-=≤==z y x xz zz y z x z zy Z z e e dy e dx z e z dy e dx z dxdy y x f z F 10)1(00,1,1,10,1,0,0),()(⎪⎪⎩⎪⎪⎨⎧≤<<-≥-=∴--.0,0,10,1,1,)1()(z z e z e e z f zz Z法2:⎰+∞∞--=dyy f y z fz f Y XZ)()()(,0,10><-<∴y y z ,;0)(,0=≤∴z fz Z时;1)(,100zzyZ edy ez f z ---==<<⎰时;)1()(,11z zz y Z e e dy e z f z ----==≤⎰时⎪⎪⎩⎪⎪⎨⎧≤<<-≥-=∴--.0,0,10,1,1,)1()(z z e z e e z f zz Z六(12分).(1)⎰+∞∞-=dy y x f x f X),()(⎪⎩⎪⎨⎧<<-==⎰其它,010),1(221x x dy x ;⎰+∞∞-=dx y x f y fY),()(⎪⎩⎪⎨⎧<<==⎰其它,010,220y y dx y(2)⎰+∞∞-=dx x xfX E X)()(⎰-⋅=1)1(2dxx x =31,⎰+∞∞-=dx x f xXE X )()(22⎰-⋅=12)1(2dxx x=61,所以)()()(22X EXE X D -=1819161=-=;⎰+∞∞-=dyy yf Y E Y )()(3221=⋅=⎰ydy y ,⎰+∞∞-=dyy f yYE Y )()(2221212=⋅=⎰ydy y,181)()()(22=-=Y EYE Y D 又412),()(11===⎰⎰⎰⎰xDdy xy dx dxdy y x xyf XY E ,所以361323141)()()(),(=⨯-=-=Y E X E XY E Y X Cov ,XYρ=2118/136/1)()(),(==Y D X D Y X Cov(3)因为)()(),(y f x f y x f YX≠,所以X 与Y 不独立。
七(16分).(1)令X X E =)(,又θ=)(X E ,所以MθˆX =;∏==θni i x f L 1)()(,当ni xi ,...,2,1,0=>时,∏∏=θ-=θ==θni x n i i i e x f L 111)()(,所以∑=θ-θ-=θni i x L 1)ln ()(ln ,令)1()(ln 12=+-=∑=ni ix d L d θθθθ有MLEθˆX=;(2)因为θ===θ)()()ˆ(X E X E E MLE,所以MLEθˆX=为θ的无偏估计。
(3)因为}1{>X P θ-θ-∞+=θ=⎰111e dx e x,所以XMLE e eXP MLE1ˆ1}1{-θ-∧==>,另5.4=x ,所以}1{>X P 的极大似然估计值为5.41-e。
八(14分).(1)构造假设500:00=μ=μH,500:1≠μH,取检验统计量)1(~/00-μ-=n t nS X T H 为真,由α=->α)}1(|{|2/n tT P 得拒绝域为: )1(||2/->αn t T .又9=n ,499=x ,292=s ,05.0=α,3060.2)8(025.0=t,3060.256.09/29|500499|<=-=T ,故应接受0H ,即认为包装机工作正常.(2)因为302=σ已知,所以总体均值μ的置信度为α-1的置信区间为),(2/2/n z x nzx σ+σ-αα,又96.1025.02/==αz z,故),(2/2/nz x nz x σ+σ-αα=)93096.1499,93096.1499(⨯+⨯-)578.502,422.495(=.。
