中考数学补充复习训练题4无答案
专题04 中考数学专题复习最值问题(隐圆)练习(解析版)-备战2022年中考数学复习专题最值问题训练

中考数学专题复习最值问题(隐圆)练习1.如图,在Rt ABC D 中,ACB Rt Ð=Ð,8AC =cm ,3BC =cm .D 是BC 边上的一个动点,连接AD ,过点C 作CE AD ^于E ,连接BE ,在点D 变化的过程中,线段BE 的最小值是( )A .1BC .2D 【答案】A 【分析】由∠AEC =90°知,点E 在以AC 为直径的⊙M 的 CN 上(不含点C 、可含点N ),从而得BE 最短时,即为连接BM 与⊙M 的交点(图中点E ′点),BE 长度的最小值BE ′=BM −ME ′.【解析】如图,由题意知,90AEC Ð=°,E \在以AC 为直径的Me 的 CN上(不含点C 、可含点)N ,BE \最短时,即为连接BM 与M e 的交点(图中点E ¢点),在Rt BCM D 中,3BC cm =,142CM AC cm ==,则5BM cm ==.4ME MC cm ¢==Q ,BE \长度的最小值1BE BM ME cm ¢=-¢=,故选:A .【点睛】本题主要考查了勾股定理,圆周角定理,三角形的三边关系等知识点,难度偏大,解题时,注意辅助线的作法.2.如图,△ACB中,CA=CB=4,∠ACB=90°,点P为CA上的动点,连BP,过点A作AM⊥BP 于M.当点P从点C运动到点A时,线段BM的中点N运动的路径长为()ABπCD.2π【答案】A【解析】解:设AB的中点为Q,连接NQ,如图所示:∵N为BM的中点,Q为AB的中点,∴NQ为△BAM的中位线,∵AM⊥BP,∴QN⊥BN,∴∠QNB=90°,∴点N的路径是以QB的中点O为圆心,14AB长为半径的圆交CB于D的 QD,∵CA=CB=4,∠ACB=90°,∴AB==QBD=45°,∴∠DOQ=90°,∴ QD为⊙O的14周长,∴线段BM的中点N=故选:A.3.如图,在△ABC 中,∠ACB =90°,AC =BC ,AB =4cm ,CD 是中线,点E 、F 同时从点D 出发,以相同的速度分别沿DC 、DB 方向移动,当点E 到达点C 时,运动停止,直线AE 分别与CF 、BC 相交于G 、H ,则在点E 、F 移动过程中,点G 移动路线的长度为( )A .2B .πC .2πDπ【答案】D 【解析】解:如图,∵CA =CB ,∠ACB =90°,AD =DB ,∴CD ⊥AB ,∴∠ADE =∠CDF =90°,CD =AD =DB ,在△ADE 和△CDF 中,AD CD ADE CDF DE DF =ìïÐ=Ðíï=î,∴△ADE ≌△CDF (SAS ),∴∠DAE =∠DCF ,∵∠AED =∠CEG ,∴∠ADE =∠CGE =90°,∴A 、C 、G 、D四点共圆,∴点G的运动轨迹为弧CD,∵AB=4,AB=,∴AC=∴OA=OC=∵DA=DC,OA=OC,∴DO⊥AC,∴∠DOC=90°,∴点G=π.故选:D.4.如图,在等腰Rt∆ABC中,AC BC==,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是()A.4+B.2p C.2+D.4p【答案】B【解析】分析:取AB的中点O、AC的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图,利用等腰直角三角形的性质得到AB BC=8,则OC=12AB=4,OP=12AB=4,再根据等腰三角形的性质得OM⊥PC,则∠CMO=90°,于是根据圆周角定理得到点M在以OC为直径的圆上,由于点P 点在A点时,M点在E点;点P点在B点时,M点在F点,则利用四边形CEOF为正方得到EF=OC=4,所以M点的路径为以EF为直径的半圆,然后根据圆的周长公式计算点M运动的路径长.解析:取AB的中点O、AC的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图,∵在等腰Rt△ABC中,AC=BC AB BC=8,∴OC=12AB=4,OP=12AB=4.∵M为PC的中点,∴OM⊥PC,∴∠CMO=90°,∴点M在以OC为直径的圆上,点P点在A点时,M点在E点;点P点在B点时,M点在F点,易得四边形CEOF为正方形,EF=OC=4,∴M点运动的路径为以EF为直径的半圆,∴点M运动的路径长=12•4π=2π.故选B.点睛:本题考查了轨迹:点按一定规律运动所形成的图形为点运动的轨迹.解决此题的关键是利用等腰三角形的性质和圆周角定理确定M点的轨迹为以EF为直径的半圆.5.如图,在Rt V ABC中,∠ACB=90°,D为AC的中点,M为BD的中点,将线段AD绕A点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=8,BC=6,那么在旋转过程中,线段CM长度的取值范围是____.【答案】3≤CM≤7【分析】由勾股定理可求AB=10,由三角形中位线定理可求OM=2,点M在以O为圆心,OM长为半径的圆上运动,即可求解.【解析】解:如图,取AB中点O,连接OC,OM,∵AC=8,BC=6,∴AB10=,∵D为AC的中点,点O是AB中点,∴AD=4,CO=5,∵M为BD的中点,点O是AB中点,AD=2,∴OM=12∴点M在以O为圆心,OM长为半径的圆上运动,∴当点M在线段OC上时,CM有最小值=5﹣2=3,当点M在线段CO的延长线时,CM有最大值=5+2=7,∴线段CM长度的取值范围3≤CM≤7,故答案为:3≤CM≤7.【点睛】本题主要考查三角形中位线及隐圆问题,熟练掌握三角形的中位线及动点的运动轨迹是解题的关键.6.如图,在锐角△ABC中,AB=2,AC,∠ABC=60°.D是平面内一动点,且∠ADB=30°,则CD的最小值是________【答案】33【分析】作AH⊥BC于H,证明△ACH为等腰直角三角形,求得BC,在BC上截取BO=AB=2,则△OAB 为等边三角形,以O为圆心,2为半径作⊙O,根据∠ADB=30°,可得点D在⊙O上运动,当DB经过圆心O时,CD最小,其最小值为⊙O的直径减去BC的长.【解析】解:如图,作AH⊥BC于H,∵AB=2,AC,∠ABC=60°,∴BH=12AB=1,∴AH==,CH==∴△ACH为等腰直角三角形,∴∠ACB=45°,BC=CH+BH,在BC上截取BO=AB=2,则△OAB为等边三角形,以O为圆心,2为半径作⊙O,∵∠ADB=30°,∴点D在⊙O上运动,当DB经过圆心O时,CD最小,最小值为4-)故答案为:3【点睛】本题考查了勾股定理,含30度角的直角三角形的性质,等腰直角三角形的判定和性质,圆周角定理.解题的关键是得出点D在⊙O上运动.7.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD=2,E是AC的中点,连接DE,则线段DE长度的最小值为______.【答案】1)## (1-【分析】先判断出四边形ABCD是圆内接四边形,得到∠ACD=∠ABD=30°,根据题意知点E在以FG为直径的⊙P上,连接PD交⊙P于点E,此时DE长度取得最小值,证明∠APD=90°,利用含30度角的直角三角形的性质求解即可.【解析】解:∵∠BAD=∠BCD=90°,∴四边形ABCD是圆内接四边形,∴∠ACD=∠ABD=30°,∴∠ADB=60°,∵AD=2,∴BD=2AD=4,分别取AB、AD的中点F、G,并连接FG,EF,EG,∵E是AC的中点,∴EF∥BC,EG∥CD,∴∠AEF=∠ACB,∠AEG=∠ACD,∴∠AEF+∠AEG=∠ACB+∠ACD=90°,即∠FEG =90°,∴点E在以FG为直径的⊙P上,如图:当点E恰好在线段PD上,此时DE的长度取得最小值,连接PA,∵F、G分别是AB、AD的中点,BD=2,∴FG∥BD,FG=12∴∠ADB=∠AGF=60°,∵PA=PG,∴△APG是等边三角形,∴∠APG=60°,∵PG=GD=GA,且∠AGF=60°,∴∠GPD=∠GDP=30°,∴∠APD=90°,∴PD==∴DE长度的最小值为1) .故答案为:1).【点睛】本题考查了圆周角定理,圆内接四边形的性质,等边三角形的判定和性质,含30度角的直角三角形的性质,得到点E在以FG为直径的⊙P上是解题的关键.8.如图,△ABC为⊙O的内接等边三角形,BC=12,点D为 BC上一动点,BE⊥OD于E,当点D 由点B沿 BC运动到点C时,线段AE的最大值是____.【答案】【分析】连接BO,取BO中点M,连接ME,求得12ME OB=,点E在以M为圆心,以12OB为半径的圆上,求得当A M E、、共线且点E在AM的延长线上时,AE最大,求解即可.【解析】解:连接BO,取BO中点M,连接ME,如下图:∵BE OD ^,M 为BO 中点∴12ME OB=∴点E 在以M 为圆心,以12OB 为半径的圆上∴当A M E 、、共线且点E 在AM 的延长线上时,AE 最大延长BO 交AC 于点H ,如上图:∵△ABC 为⊙O 的内接等边三角形∴HB 垂直平分AC ,12AC BC ==∴162AH CH AC ===∴BH =23OB BH ==∴12OM OB ==MH =∴AM ==∴AE 的最大值为故答案为:【点睛】此题考查了圆与内接正三角形的性质,涉及了直角三角形的性质,勾股定理,三角形外心的性质,解题的关键是理解题意,利用性质确定出点E 的运动轨迹.9.如图,点A ,B 的坐标分别为()4,0A ,()0,4B ,C 为坐标平面内一动点,且2BC =,点M 为线段AC 的中点,连接OM ,当AC 取最大值时,点M 的纵坐标为____.【答案】2【分析】根据同圆的半径相等可知:点C 在半径为2的⊙B 上,通过画图可知,C在AB 的延长线上时,AC 最大,根据中点坐标公式可得结论.【解析】解:如图,∵点C 为坐标平面内一点,BC =2,∴C 在⊙B 上,且半径为2,∴当C 在AB 的延长线上时,AC 最大,过点C 作CD ⊥x 轴,∵点A ,B 的坐标分别为()4,0A ,()0,4B ,∴4OA OB ==,∵=90BOA а,∴BOA △是等腰直角三角形,∴45A Ð=°,AB ==∴2AC BC AB =+=+.∵CD ⊥x 轴,∴CDA V 是等腰直角三角形,∴CD AD =,∵222=CD AD AC +,即(222=2CD +,解得:4CD =,∴C 4,∵点M 为线段AC 的中点,∴点M 2+.2.【点睛】本题考查了坐标和图形的性质,动点线段最值问题,勾股定理等知识,确定AC 为最大值时点C 的位置是解题的关键.10.如图,⊙O 的半径为2,弦AB =2,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的最大面积是_________.【分析】连接OA 、OB ,如图1,由OA =OB =AB =2可判断△OAB 为等边三角形,则∠AOB =60°,根据圆周角定理得∠APB =12∠AOB =30°,由于AC ⊥AP ,所以∠C =60°,因为AB =2,则要使△ABC 的最大面积,点C 到AB 的距离要最大;由∠ACB =60°,可根据圆周角定理判断点C 在⊙D 上,且∠ADB =120°,如图2,于是当点C 优弧AB 的中点时,点C 到AB 的距离最大,此时△ABC 为等边三角形,从而得到△ABC 的最大面积.【解析】解:连接OA 、OB ,如图1,∵OA=OB=2,AB=2,∴△OAB为等边三角形,∴∠AOB=60°,∠AOB=30°,∴∠APB=12∵AC⊥AP,∴∠C=60°,∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,作△ABC的外接圆D,∵∠ACB=60°,点C在⊙D上,∴∠ADB=120°,如图2,当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC2=∴△ABC【点睛】本题考查了圆的综合题:熟练掌握圆周角定理和等边三角形的判断与性质;记住等边三角形的面积公式.11.如图,AB是半圆O的直径,点D在半圆O上,AB=13,AD=5,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H.连接BH,在点C移动的过程中,BH的最小值是 ___.【分析】连接BD,取AD的中点E,连接BE,由题意先判断出点H在以点E为圆心,AE为半径的圆上,当B、H、E三点共线时,BH取得最小值,然后在直角三角形中,利用勾股定理求出BE的长,利用直角三角形中,斜边上的中线等于斜边的一半,求出EH的长,由BH BE EH=-即可算出BH的长度.【解析】解:连接BD,取AD的中点E,连接BE,如下图:∵DH⊥AC∴点H在以点E为圆心,AE为半径的圆上,当B、H、E三点共线时,BH取得最小值∵AB是直径∴90BDAÐ=o在Rt BDAV中,AB=13,AD=5由勾股定理得:222BD AB AD=-即:216925144BD=-=∵0BD>∴=12BD∵E为AD的中点∴1522 DE AD==在Rt BDEV中,=12BD,52 DE=由勾股定理得:222BE DE BD =+即:225601+144=44BE =∵0BE >∴BE 又∵DH ⊥AC ,且点E 为AD 的中点∴52EH =∴52BH BE =-=【点睛】本题考查勾股定理解三角形,直径所对的圆周角为直角,直角三角形斜边上的中线等于斜边的一半,隐圆问题的处理等相关知识点,能够判断出从动点的运动轨迹是解题的关键.12.如图,Rt △ABC 中,∠ACB =90°,∠CAB =60°,AB =4,点P 是BC 边上的动点,过点c 作直线记的垂线,垂足为Q ,当点P 从点C 运动到点B 时,点Q 的运动路径长为_______.【答案】23p 【解析】解:∵AQ ⊥CQ ,∴∠AQC =90°,∴当点P 从点C 运动到点B 时,点Q 的运动的轨迹是以AC 为直径的半圆上,路径是120度的弧长,在Rt△ABC 中,∵AB =4,∠B =30°,∴AC 12=AB =2,∴点Q 的运动路径长为120121803p ××=π13.如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D 的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为_____.【答案】3p【解析】解:画出点O运动的轨迹,如图虚线部分,则点P从B到A的运动过程中,PQ的中点O所经过的路线长等于3224p´´=3π,故答案为:3π.14.如图,△ABC为等边三角形,AB=2,若P为△ABC内一动点,且满足∠PAB=∠ACP,则点P运动的路径长为_________.【解析】解:∵△ABC 是等边三角形,∴∠ABC =∠BAC =60°,AC =AB =2,∵∠PAB =∠ACP ,∴∠PAC +∠ACP =60°,∴∠APC =120°,∴点P 的运动轨迹是 AC ,如图所示:连接OA 、OC ,作OD ⊥AC 于D ,则AD =CD 12=AC =1,∵ AEC 所对的圆心角=2∠APC =240°,∴劣弧AC 所对的圆心角∠AOC =360°﹣240°=120°,∵OA =OC ,∴∠OAD =30°,∵OD ⊥AC ,∴OD =2OD =,∴ AC=π;15.△ABC 中,AB =4,AC =2,以BC 为边在△ABC 外作正方形BCDE ,BD 、CE 交于点O ,则线段AO 的最大值为______.【答案】【解析】解:如图:以AO为边作等腰直角△AOF,且∠AOF=90°∵四边形BCDE是正方形∴BO=CO,∠BOC=90°∵△AOF是等腰直角三角形∴AO=FO,AF=∵∠BOC=∠AOF=90°∴∠AOB=∠COF,且BO=CO,AO=FO∴△AOB≌△FOC(SAS)∴AB=CF=4若点A,点C,点F三点不共线时,AF<AC+CF;若点A,点C,点F三点共线时,AF=AC+CF∴AF≤AC+CF=2+4=6∴AF的最大值为6∵AF=∴AO的最大值为故答案为:16.如图一,等边△ABC中,AB=6,P为AB上一动点,PD⊥BC,PE⊥AC,求DE的最小值.【答案】92DE =【分析】由题意易得∠PEC =∠PDC =90°,所以P 、D 、C 、E 四点共圆,又因为∠EOD =120°,所以当直径最小时,弦DE 的值最小.【解析】解:∵PD ⊥BC ,PE ⊥AC ,∴∠PEC =∠PDC =90°,∴四边形PDCE 对角互补,∴P 、D 、C 、E 四点共圆,如图2.∴∠EOD =2∠ECD =120°,要使得DE 最小,则要使圆的半径最小,故直径PC 最小,则当CP ⊥AB 时,PC 最短,∵△ABC 是等边三角形,∴60,3B BP Ð=°=,∴CP ==,∵60DOP Ð=°,∴92sin 2DE OD DOP =×Ð=.【点睛】本题主要考查圆的基本性质、三角函数及等边三角形的性质,熟练掌握圆的基本性质、三角函数及等边三角形的性质是解题的关键.17.问题发现:(1)如图①,点A和点B均在⊙O上,且∠AOB=90°,点P和点Q均在射线AM上,若∠APB =45°,则点P与⊙O的位置关系是;若∠AQB<45°,则点Q与⊙O的位置关系是.问题解决:如图②、图③所示,四边形ABCD中,AB⊥BC,AD⊥DC,∠DAB=135°,且AB=1,AD=,点P是BC边上任意一点.(2)当∠APD=45°时,求BP的长度.(3)是否存在点P,使得∠APD最大?若存在,请说明理由,并求出BP的长度;若不存在,也请说明理由.【答案】(1)点P在⊙O上,点Q在⊙O外;(2)PB2;(3−1【分析】(1)如图①中,根据圆周角与圆心角的关系即可判断;(2)如图2中,造等腰直角三角形△AOD,与O为圆心作⊙O交BC于P、P′,易知∠APD=∠AP′D=45°.求出BP′和BP的长即可解决问题;(3)作线段AD的垂直平分线,交AD于E,交BC于F,点O在EF上,以OA为半径作⊙O,当⊙O与BC相切于点P时,∠APD最大,求出此时BP的值即可;【解析】解:(1)如图①中,∠AOB=45°,∵∠APB=12∴点P在⊙O上,∵∠AQB<45°,∴点Q在⊙O外.故答案为点P在⊙O上,点Q在⊙O外.(2)如图2中,如图构造等腰直角三角形△AOD,与O为圆心,OA为半径作⊙O交BC于P、P′,易知∠APD=∠AP′D=45°.延长DO交BC于H,∵∠DAB=135°,∠DAO=45°,∴∠OAB=∠B=90°,∴OA∥BC,∴∠DOA=∠OHB=90°,∴四边形ABHO是矩形,∴AB=OH=1,OA=BH,∵AD=∴OA=OD=OP=OP′=2,在Rt△OPH和Rt△OP′H中,易知HP =HP =,∴BH =OA =2,∴BP ′=2,PB =2.(3)如图③中,存在.作线段AD 的垂直平分线,交AD 于E ,交BC 于F ,点O 在EF 上,以OA 为半径作⊙O ,当⊙O 与BC 相切于点P 时,∠APD 最大,理由:在BC 上任意取一点M ,连接MA 、MD ,MD 交⊙O 于N ,连接AN .∵∠AND >∠AMD ,∠APD =∠AND ,∴∠APD >∠AND ,连接OP ,延长DA 交CB 的延长线于点G .∵AB ⊥BC ,∠DAB =135°,∴∠G =∠EFG =45°,∴△ABG ,△EFG 都是等腰直角三角形,∵AB =BG =1,∴AG∵AD =OE ⊥AD ,∴AE =ED∴EG =EF =GF EG =4,设OP =PF =r ,则OF ,OE =EF −OF =r ,在Rt △AOE 中,AE 2+OE 2=OA 2,∴()222+r =,解得r =4 或4(舍弃),∴BP =GF −GB −PF =4−1−r −1.【点睛】本题考查圆综合题、圆周角与圆心角的关系、点与圆的位置关系、矩形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,利用辅助圆解决问题.18.如图,在平面直角坐标系xOy 中,点A 与点B 的坐标分别是(1,0),(7,0).(1)对于坐标平面内的一点P ,给出如下定义:如果∠APB =45°,则称点P 为线段AB 的“等角点”.显然,线段AB 的“等角点”有无数个,且A 、B 、P 三点共圆.①设A 、B 、P 三点所在圆的圆心为C ,直接写出点C 的坐标和⊙C 的半径;②y 轴正半轴上是否有线段AB 的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;(2)当点P 在y 轴正半轴上运动时,∠APB 是否有最大值?如果有,说明此时∠APB 最大的理由,并求出点P 的坐标;如果没有请说明理由.【答案】(1)①(4,3)或(4,−3),半径为②存在,(0,) 或(0,3),见解析;(2)有,见解析,(0【分析】(1)①在x 轴的上方,作以AB 为斜边的等腰直角三角形△ACB ,易知A ,B ,P 三点在⊙C 上,圆心C 的坐标为(4,3),半径为,根据对称性可知点C (4,−3)也满足条件;②当圆心为C (4,3)时,过点C 作CD ⊥y 轴于D ,则D (0,3),CD =4,根据⊙C 的半径得⊙C 与y 轴相交,设交点为1P ,2P ,此时1P ,2P 在y 轴的正半轴上,连接1CP 、2CP 、CA ,则1CP =2CP =CA =r得2DP (2)如果点P 在y 轴的正半轴上,设此时圆心为E ,则E 在第一象限,在y 轴的正半轴上任取一点M (不与点P 重合),连接MA ,MB ,PA ,PB ,设MB 交于⊙E 于点N ,连接NA ,则∠APB=∠ANB,∠ANB是△MAN的外角,∠ANB>∠AMB,即∠APB>∠AMB,过点E作EF⊥x轴于AB=3,OF=4,四边形OPEF是矩形,OP=EF,PE=OF=4,得EF=F,连接EA,EP,则AF=12则OP=【解析】(1)①如图1中,在x轴的上方,作以AB为斜边的等腰直角三角形△ACB,易知A,B,P三点在⊙C上,圆心C的坐标为(4,3),半径为,根据对称性可知点C(4,−3)也满足条件;②y轴的正半轴上存在线段AB的“等角点“。
中考数学补充复习训练题5无答案1

一元二次方程一。
填空题(每小题2分,共24分)1. 方程x x 3122=-的二次项系数是 ,一次项系数是 ,常数项是 ;2. 方程)0(02≠=++a c bx ax 的判别式是 ,求根公式是 ;3. 把一元二次方程x x x 2)1)(1(=-+化成二次项系数大于零的一般式是 ,其中二次项系数是 ,一次项的系数是 ,常数项是 ;4. 一元二次方程12)1(2=-+mx x m 的一个根是3,则=m ;5. 方程022=-x x 的根是 ,方程05022=-x 的根是 ;6. 已知方程032=+-mx x 的两个实根相等,那么=m ; 7. +-x x 222 =2)(-x , 22)(41)(-=+-x x x ; 8. a 是实数,且0|82|42=--+-a a a ,则a 的值是 ; 9. 方程)34(342-=x x 中,⊿= ,根的情况是 ; 10.已知322--x x 与7+x 的值相等,则x 的值是 ;11.关于x 的方程03)3(12=+---x x m m 是一元二次方程,则=m ; 12.设b a ,是一个直角三角形两条直角边的长,且12)1)((2222=+++b a b a ,则这个直角三角形的斜边长为 ; 3A. 3,121-==x x B. 2,421-==x x C. 3,121=-=x x D. 2,421=-=x x2. 关于x 的一元二次方程02322=-+-m x x 的根的情况是A. 有两个不相等的实根B. 有两个相等的实根C. 无实数根D. 不能确定 3. 方程:①13122=-x x ②05222=+-y xy x ③0172=+x ④022=y 中一元二次方程是A. ①和②B. ②和③C. ③和④D. ①和③4. 一元二次方程0624)2(2=-+--m mx x m 只有一个实数根,则m 等于A. 6-B. 1C. 6-或1D. 25. 关于x 的方程0)(242=---ab x b a x 的判别式是A. 2)(4b a +B. 2)(b a +C. 2)(b a -D. ab b a 4)(2--6. 已知0和1-都是某个方程的解,此方程是A. 012=-xB. 0)1(=+x xC. 02=-x xD. 1+=x x7. 等腰三角形的两边的长是方程091202=+-x x 的两个根,则此三角形的周长为A. 27B. 33C. 27和33D. 以上都不对8. 如果01)3(2=+-+mx x m 是一元二次方程,则A. 3-≠mB. 3≠mC. 0≠mD. 03≠-≠m m 且9. 关于x 的方程0)()(=---x b b x ax 的解为 A. b a , B.b a ,1 C. b a,1- D. b a -, 10.已知06522=+-y xy x ,则x y :等于 A. 161或 B. 16或 C. 2131或 D. 32或 三、按指定的方法解方程(每小题3分,共12分)1.02522=-+)(x (直接开平方法) 2. 0542=-+x x (配方法)3.025)2(10)2(2=++-+x x (因式分解法) 4. 03722=+-x x (公式法)四、用适当的方法解方程(每小题4分,共12分)1.036252=-x 2.0223)12(22=-+-+x x3.0)4()52(22=+--x x五、(本题5分)已知)0(04322≠=-+y y xy x ,求yx y x +-的值。
中考数学复习专题训练精选试题及答案

中考数学复习专题训练精选试题及答案一、选择题1. 以下哪一个数是最小的无理数?A. √2B. πC. 3.14D. √9答案:A2. 若一个等差数列的首项是2,公差是3,则第8项是多少?A. 17B. 18C. 19D. 20答案:A3. 一个二次函数的图像开口向上,顶点坐标为(3,-4),则该二次函数的一般式为:A. y = x² + 6x - 13B. y = x² - 6x + 13C. y = -x² + 6x - 13D. y = -x² - 6x + 13答案:B4. 在三角形ABC中,a = 5,b = 7,C = 60°,则边c 的长度等于:A. 6B. 8C. 10D. 12答案:C二、填空题1. 已知a = 3,b = 4,则a² + b² = _______。
答案:252. 已知一个等差数列的前5项和为35,首项为7,求公差d = _______。
答案:23. 在梯形ABCD中,AB // CD,AB = 6,CD = 8,AD = BC = 5,求梯形的高h = _______。
答案:34. 若函数f(x) = x² - 2x + 1的最小值为m,求m =_______。
答案:0三、解答题1. 已知一元二次方程x² - 4x - 12 = 0,求解该方程。
解:首先,将方程因式分解为(x - 6)(x + 2) = 0。
然后,解得x = 6或x = -2。
答案:x = 6或x = -22. 已知一个长方体的长为a,宽为b,高为c,且a、b、c成等差数列。
若长方体的体积为V,求V的表达式。
解:由题意可知,a + c = 2b,所以c = 2b - a。
长方体的体积V = abc = ab(2b - a)。
答案:V = ab(2b - a)3. 已知三角形ABC,AB = AC,∠BAC = 40°,BC = 6,求三角形ABC的周长。
2021届中考数学专题复习训练——二次函数 专题4二次函数综合之线段最值,成比

类型一:线段最值问题【经典例题1改编】抛物线y=-x 2+bx +c 与直线y=-x +5一个交点A (2,m ),另一个交点B 在x 轴上,点P 是线段AB 上异于A 、B 的一个动点,过点P 做x 轴的垂线,交抛物线于点E ;(1)求抛物线的解析式;(2)是否存在这样的点P ,使线段PE 长度最大?若存在求出最大值及此时点P 的坐标,若不存在说明理由;(3)在y 轴右侧,当EP 平行于y 轴时,设点E 的横坐标为m ,当点E 到y 轴的距离等于线段EP 的长时,求m 的值;【解析】(1)A(2,-3),抛物线解析式y=-x 2+6x -5(2)设点P 的横坐标为m ,E(m ,-m 2+6m -5),P(m ,-m+5)∴EP=y E -y P=(-m 2+6m -5)-(-m +5)=-m 2+7m -10=-(m -27)2+49 当m=27时,EP 长度有最大值49,此时,P(27,23) (3)根据题意分两种情况∴当0<x <2或x >5时,EP=m 2-7m +10,所以m=m 2-7m +10,即m 2-8m +10=0,解得m1=4+6,m2=4-6;∴当2<x<5时,EP=-m2+7m-10,所以m=-m2+7m-10,即m2-6m+10=0,此方程无解。
综上,m1=4+6,m2=4-6【经典例题2】如图所示,抛物线y=ax2+bx-3(a≠0)与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,直线y= -x与抛物线交于E,F两点.(1)求抛物线的解析式;(2)P是直线EF下方抛物线上的一个动点,作PH∴EF于点H,求PH的最大值;【解析】(1)抛物线的表达式为:y=a(x+3)(x−1)=a(x2+2x−3),即−3a=−3,解得:a=1,故抛物线的表达式为:y=x2+2x−3;(2)过点P作PM∴y轴交直线EF于点M,设点P(x ,x 2+2x −3)、点M(x ,−x ),则PH=22PM=22(−x −x 2−2x +3), 当x =−23时,PH 的最大值为:8221;【经典例题3】已知抛物线l 1:y 1=ax 2−2的顶点为P ,交x 轴于A. B 两点(A 点在B 点左侧),且sin∴ABP=55. (1)求抛物线l 1的函数解析式;(2)过点A 的直线交抛物线于点C ,交y 轴于点D ,若∴ABC 的面积被y 轴分为1:4两个部分,求直线AC 的解析式;【解析】(1)当x =0时,y 1=ax 2-2=-2∴顶点P (0,-2),OP=2∴∴BOP=90° ∴sin∴ABP=BP OP =55 ∴BP=5OP=25 ∴OB=442022=-=-OP BP∴B (4,0),代入抛物线l 1得:16a -2=0,解得:a =81 ∴抛物线l 1的函数解析式为y 1=81x 2-2 (2)∴知抛物线l 1交x 轴于A 、B 两点∴A 、B 关于y 轴对称,即A (-4,0)∴AB=8设直线AC 解析式:y=kx +b点A 代入得:-4k +b =0∴b =4k∴直线AC :y=kx +4k ,D (0,4k )∴S ∴AOD =S ∴BOD =21×4×|4k |=8|k | ∴81x 2-2=kx +4k 整理得:x 2-8kx -32k -16=0∴x 1+x 2=8k∴x 1=-4∴x C =x 2=8k +4,y C =k (8k +4)+4k =8k 2+8k∴C (8k +4,8k 2+8k )∴S ∴ABC =21AB•|y C |=32|k 2+k | ∴若k >0,则S ∴AOD :S 四边形OBCD =1:4∴S ∴AOD =51S ∴ABC ∴8k =51×32(k 2+k ) 解得:k 1=0(舍去),k 2=41 ∴直线AC 解析式为y=41x +1 ∴若k <0,则S ∴AOD =S ∴BOD =-8k ,S ∴ABC =-32(k 2+k )∴-8k =51×[-32(k 2+k )] 解得:k 1=0(舍去),k 2=41(舍去) 综上所述,直线AC 的解析式为y=41x +1.【经典例题4】如图1,在平面直角坐标系中,直线y=x +4与抛物线y=21-x 2+bx +c (b ,c 是常数)交于A. B 两点,点A 在x 轴上,点B 在y 轴上。
2020重庆中考复习数学最值专题训练四(含答案解析)
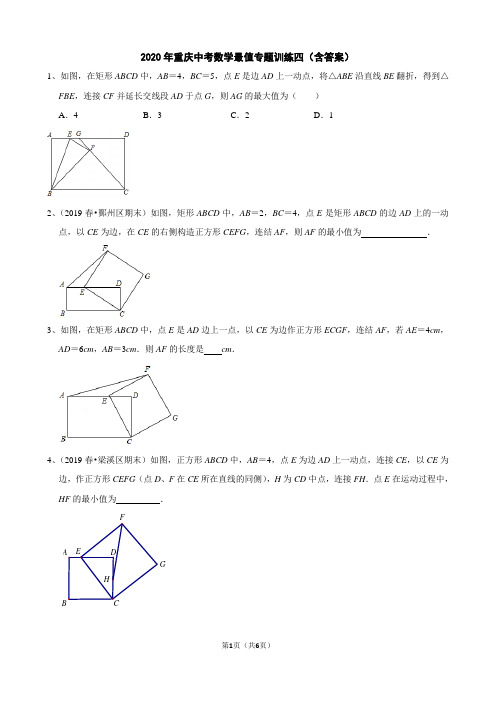
2020年重庆中考数学最值专题训练四(含答案)1、如图,在矩形ABCD 中,AB =4,BC =5,点E 是边AD 上一动点,将△ABE 沿直线BE 翻折,得到△FBE ,连接CF 并延长交线段AD 于点G ,则AG 的最大值为( )A .4B .3C .2D .12、(2019春•鄞州区期末)如图,矩形ABCD 中,AB =2,BC =4,点E 是矩形ABCD 的边AD 上的一动点,以CE 为边,在CE 的右侧构造正方形CEFG ,连结AF ,则AF的最小值为.3、如图,在矩形ABCD 中,点E 是AD 边上一点,以CE 为边作正方形ECGF ,连结AF ,若AE =4cm ,AD =6cm ,AB =3cm .则AF 的长度是 cm .4、(2019春•梁溪区期末)如图,正方形ABCD 中,AB =4,点E 为边AD 上一动点,连接CE ,以CE 为边,作正方形CEFG (点D 、F 在CE 所在直线的同侧),H 为CD 中点,连接FH .点E 在运动过程中,HF 的最小值为 .C DGE H5、如图,矩形ABCD中,已知AB=6,BC=8,点E是边AD上一点,以CE为直角边在与点D的同侧作等腰直角△CEG,连结BG,当点E在边AD上运动时,线段BG长度的最小值是()A.2B.10C.10D.146、(2017•龙华区二模)如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是.7、如图,矩形ABCD中,AB=3,AD=4,点E、F分别是边BC和对角线BD上的动点,且BE=DF,则AE+AF的最小值是.2020年重庆中考数学最值专题训练四(含答案)1、如图,在矩形ABCD中,AB=4,BC=5,点E是边AD上一动点,将△ABE沿直线BE翻折,得到△FBE,连接CF并延长交线段AD于点G,则AG的最大值为()A.4B.3C.2D.1解:如图:∵CF是⊙B切线,∴BF⊥CG,∵折叠,∴∠BAD=∠EFB=90°即BF⊥EF;根据过一点有且只有一条直线与已知直线垂直,∴CG与CE重合即E,G重合;∵四边形ABCD是矩形,∴AB=CD=4,BC=AD=5,AD∥BC;∵折叠,∴∠AEB=∠BEF;∵AD∥BC,∴∠AEB=∠CBE,∴∠CBE=∠BEF,∴BC=GC=5;在Rt△GCD中,DG==3,∴AG的最大值为AD﹣DG=2.故选:C.2、(2019春•鄞州区期末)如图,矩形ABCD中,AB=2,BC=4,点E是矩形ABCD的边AD上的一动点,以CE为边,在CE的右侧构造正方形CEFG,连结AF,则AF的最小值为3.解:过F作FH⊥ED,∵正方形CEFG,∴EF=EC,∠FEC=∠FED+∠DEC=90°,∵FH⊥ED,∴∠FED+∠EFH=90°,∴∠DEC=∠EFH,且EF=EC,∠FHE=∠EDC=90°,∴△EFH≌△EDC(AAS),∴EH=DC=2,FH=ED,∴AF===∴当AE=1时,AF的最小值为33、如图,在矩形ABCD 中,点E 是AD 边上一点,以CE 为边作正方形ECGF ,连结AF ,若AE =4cm ,AD =6cm ,AB =3cm .则AF的长度是 cm .解:如图,作FM ⊥AD 于M ,∵四边形EFGC 是正方形,∴EF =EC ,∠FEC =∠M =90°,∴∠FEM +∠EFM =90°,∠FEM +∠CED =90°,∴∠EFM =∠CED ,在△ECD 和△FEM 中,,∴△ECD ≌△FEM ,∴FM =ED ,CD =EM ,∵AB =CD =EM =3,AE =4.AD =6,∴ED =FM =2,在Rt △AFM 中,AF ===.4、(2019春•梁溪区期末)如图,正方形ABCD 中,AB =4,点E 为边AD 上一动点,连接CE ,以CE 为边,作正方形CEFG (点D 、F 在CE 所在直线的同侧),H 为CD 中点,连接FH .点E 在运动过程中,HF 的最小值为 .A B CDGE H图1 解:如图,连接DF ,过点F 作FM ⊥AD ,交AD 延长线于点M ,过点F 作FN ⊥CD 的延长线于点N , ∵△EFM ≌△CED ,∴CD =EM ,DE =FM ,∴CD =AD =EM ,∴AE =DM ,设AE =x =DM ,则DE =4﹣x =FM ,∵FN ⊥CD ,FM ⊥AD ,ND ⊥AD ,∴四边形FNDM 是矩形,∴FN =DM =x ,FM =DN =4﹣x∴NH =4﹣x +2=6﹣x ,在Rt △NFH 中,HF === ∴当x =3时,HF 有最小值==35、(2017秋•上虞区期末)如图,矩形ABCD中,已知AB=6,BC=8,点E是边AD上一点,以CE为直角边在与点D的同侧作等腰直角△CEG,连结BG,当点E在边AD上运动时,线段BG长度的最小值是()A.2B.10C.10D.14解:如图作GH⊥BA交BA的延长线于H,EM⊥HG于M,交BC于N.则MN⊥BC.设AE=m.∵∠EMG=∠ENC=∠CEG=90°,∴∠MEG+∠CEN=90°,∠CEN+∠ECN=90°,∴∠MEG=∠ECN,∵EG=EC,∴△MEG≌△NCE(AAS),∴EM=CN=AH=8﹣m,MG=EN=6,在Rt△BHG中,BG===,∴m=4时,BG有最大值,最大值为10,故选:B.6、(2017•龙华区二模)如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是5.解:如图所示:过点D作DG⊥OA,过点E作HE⊥DG.∵DG⊥OA,HE⊥DG,∴∠EHD=∠DGA=90°.∴∠GDA+∠DAG=90°.∵四边形ADEF为正方形,∴DE=AD,∠HDE+∠GDA=90°.∴∠HDE=∠GAD.在△HED和△GDA中,∴△HED≌△GDA.∴HE=DG=3,HD=AG.设D(a,3),则DC=a,DH=AG=4﹣a.∴E(a+3,7﹣a).∴OE==.当a=2时,OE有最小值,最小值为5.7、如图,矩形ABCD中,AB=3,AD=4,点E、F分别是边BC和对角线BD上的动点,且BE=DF,则AE+AF的最小值是.解:如图,作点D关于BC的对称点G,连接BG,在BG上截取BH,使得BH=AD,连接AH.作HM ⊥AB交AB的延长线于M.∵四边形ABCD是矩形,∴AB=CD=3,BC=AD=4,AD∥BC,∴∠ADF=∠DBC,∵DC=CG,BC⊥DG,∴BD=BG,∴∠DBC=∠CBG,∴∠ADF=∠HBE,∵DA=BH,DF=BE,∴△ADF≌△HBE(SAS),∴AF=EH,∴AE+AF=AE+EH≥AH,在Rt△BCD中,BD==5,由△BHM∽△DBC,可得==,∴==,∴BM=,MH=,∴AM=3+=,在Rt△AMH中,AH==,∴AE+AF≥,∴AE+AF的最小值为.。
人教版中考数学复习-- 数与式(训练)(附答案)

第一章数与式时间:45分钟满分:80分一、选择题(每题4分,共32分)1.-2的相反数是()A.2 B.-2 C.12D.-122.据报道,超过515 000 000名观众通过中国中央广播电视总台收看了2022年北京冬奥会开幕式,将515 000 000用科学记数法表示为()A.0.515×109B.5.15×108C.51.5×107D.515×1063.实数-3,12,0,2中,最大的数是()A.-3 B.12C.0 D. 24.下列运算正确的是()A.a2·a3=a6B.a8÷a2=a4C.(a+b)2=a2+b2D.(ab3)2=a2b65.如图,数轴上点P表示的数为x,则在该数轴上表示数1-2x的点可能是()(第5题)A.点A B.点B C.点C D.点D6.估计3×(23+5)的值应在()A.10和11之间B.9和10之间C.8和9之间D.7和8之间7.已知m为方程x2+3x-2 022=0的根,那么m3+2m2-2 025m+2 022的值为()A.-2 022 B.0C.2 022 D.4 0448.从边长为a 的大正方形纸板中挖去一个边长为b 的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )(第8题)A .a 2-b 2=(a -b )2B .(a +b )2=a 2+2ab +b 2C .(a -b )2=a 2-2ab +b 2D .a 2-b 2=(a +b )(a -b )二、填空题(每题4分,共16分)9.若要使代数式x x -4有意义,则x 的取值范围为________. 10. 因式分解:a 3-9a =__________________.11.对某种盒装牛奶进行质量检测,一盒装牛奶超出标准质量2 g ,记作+2 g ,那么低于标准质量3 g ,应记作________g.12.下面的解题过程中,第①步出现错误,但最后所求的值是正确的,则被污染的x 的值是________. 先化简,再求值:3-x x -4+1,其中x =★. 解:原式=3-x x -4·(x -4)+(x -4) ① =3-x +x -4=-1.三、解答题(共32分)13.(10分)计算:(1)⎝ ⎛⎭⎪⎫120+|1-2|-8;3(2)-14+⎝ ⎛⎭⎪⎫13-1×12-4cos 30°.14.(10分)(1)先化简,再求值:(m m -3+1m -3)÷m 2-1m 2-6m +9,其中m =2+1;(2) 先化简⎝ ⎛⎭⎪⎫x -x x +1·x +1x 2+4x +4÷ x 2-2x x 2-4,再从-2≤x ≤2中选一个合适的整数代入并求值.15.(12分)欣欣文具店出售的文具盒定价为每个20元,钢笔定价为每支5元.为了促销,该文具店制定了两种优惠方案.方案一:每买一个文具盒赠送一支钢笔;方案二:按总价的8折付款.某班欲购买x个文具盒和8支钢笔奖励给数学竞赛获奖的学生,且x≤8.(1)用含x的代数式分别表示两种方案所需的钱数;(2)当x=5时,哪种优惠方案更省钱?5 参考答案一、1.A 2.B 3.D 4.D 5.C 6.B 7.B 8.D二、9. x >4 10. a (a +3)(a -3) 11. -312.5 点拨:3-x x -4+1=3-x +x -4x -4=14-x. 由题意可知14-x =-1,可得x =5,检验:当x =5时,4-x ≠0, ∴图中被污染的x 的值是5.三、13.解:(1)原式=1-1+2-2 2 =- 2.(2) 原式=-1+3×23-4×32=43-1.14.解:(1)原式=m +1m -3÷(m +1)(m -1)(m -3)2=m +1m -3×(m -3)2(m +1)(m -1)=m -3m -1. 当 m =2+1时,原式=2+1-32+1-1=2-2 2=1- 2. (2)原式=⎣⎢⎡⎦⎥⎤x (x +1)x +1-x x +1·x +1(x +2)2·(x +2)(x -2)x (x -2) =x 2x +1·x +1(x +2)2·(x +2)(x -2)x (x -2)=x x +2. ∵-2≤x ≤2,且x 为整数,∴x =-2,-1,0,1,2.∵要使分式有意义,即分母x +1≠0,x +2≠0,x (x -2)≠0,∴x ≠-1,-2,2,0.∴应选x =1.当x=1时,原式=11+2=13.15.解:(1)方案一所需的钱数为20x+5(8-x)=15x+40(元).方案二所需的钱数为(20x+5×8)×80%=(20x+40)×80%=16x+32(元).(2)由(1)可知当x=5时,方案一所需的钱数为15x+40=15×5+40=115(元).方案二所需的钱数为16x+32=16×5+32=112(元).∵112<115,∴方案二更省钱.。
中考数学复习《整式的加减》专项提升训练题-附答案
中考数学复习《整式的加减》专项提升训练题-附答案学校:班级:姓名:考号:一、单选题1.整式中单项式的个数为()A.2 B.3 C.4 D.52.已知多项式,下面说法正确的是()A.它是四次五项式B.三次项式C.常数项是5 D.一次项系数是13.下列选项中,两个整式的结果相同的是()A.和B.和C.和D.和4.下列去括号正确的是()A.B.C.D.5.如果与是同类项,那么m,n的值是()A.m=2,n=1 B.m=0,n=1C.m=2,n=2 D.m=1,n=26.已知.若的值与无关,则的值为()A.B.4 C.D.27.已知一个多项式与的和等于,则这个多项式是()A.B.C.D.8.为落实“双减”政策,某校利用课后服务开展形式多样的活动,七、八、九年级共有50人参加书法学习,其中七年级的人数比八年级人数的2倍少1人,设八年级的人数为人,则九年级的人数为().A.B.C.D.二、填空题9.若,则括号内的式子为.10.若多项式是关于,的三次三项式,则常数.11.已知三角形第一边的长为,第二边比第一边长a-b,第三边比第二边短a,则这个三角形的周长是(用含字母的代数式表示)12.若多项式与多项式的和不含二次项,则等于.13.已知有理数a,b,c,其大小关系为:,化简代数式等于.三、计算题14.(1)(2)15.先化简,再求值:,其中.16.已知和.(1)求,结果用含m,n的式子表示;(2)若的值与字母m的取值无关,求n的值.17.某位同学做一道题:已知两个多项式,且,求的值,他误将“”看成“”,求得结果为.(1)求多项式;(2)求的正确结果.18.某公司生产一种电子产品和配件,已知该电子产品的售价为200元/台,配件的售价为20元/个,在促销活动期间,有如下两种优惠方案(顾客只能选择其中一种优惠方案):①买一台电子产品送一个配件;②电子产品每台降价10元出售,配件每个打9折.在促销活动期间,某学校计划到该公司购买台电子产品,个配件.(1)分别求该校选择优惠方案①,②购买该电子产品和配件所需的总费用;(用含x、y的代数式来表示)(2)若该校计划购买该电子产品10台,配件20个,请通过计算判断,选择哪种优惠方案更省钱?参考答案:1.【答案】B2.【答案】D3.【答案】D4.【答案】B5.【答案】A6.【答案】A7.【答案】A8.【答案】C9.【答案】10.【答案】-111.【答案】7a+b12.【答案】413.【答案】14.【答案】(1)解:原式=-(2m-3m+3n-3-2)-1=-(-m+3n-5)-1=m-3n+5-1=m-3n+4.(2)解:原式=5x2-6y2+10x2-4y2+7xy=15x2-10y2+7xy15.【答案】解:(1)==当时原式===.16.【答案】(1)解:因为所以====.(2)解:因为,的值与字母m的取值无关所以解得.17.【答案】略18.【答案】(1)解:选择①所需总费用为(元)选择②所需总费用为(元).(2)解:当,时选择优惠方案①需要的费用:(元);选择优惠方案②需要的费用:(元).因为故答案为:优惠方案①更省钱。
2021年中考九年级数学第一轮专题复习:三角形 综合压轴题强化训练(无答案)
2021年中考九年级数学第一轮专题复习:三角形综合压轴题强化训练1、已知,在Rt△ABC中,∠A=90°,点D在BC边上,点E在AB边上,,过点B作BF⊥DE交DE的延长线于点F.(1)如图1,当AB=AC时:①∠EBF的度数为;②求证:DE=2BF.(2)如图2,当AB=kAC时,求的值(用含k的式子表示).2、在等腰Rt△ABC中,∠BAC=90°,AB=AC,点P为AC上一点,M为BC上一点.(1)若AM⊥BP于点E.①如图1,BP为△ABC的角平分线,求证:PA=PM;②如图2,BP为△ABC的中线,求证:BP=AM+MP.(2)如图3,若点N在AB上,AN=CP,AM⊥PN,求的值.3、如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.解答下列问题:(1)当t为何值时,以点E、P、Q为顶点的三角形与△ADE相似?(2)当t为何值时,△EPQ为等腰三角形?(直接写出答案即可).4、如图,在△ABC中,∠ACB=90°,AC=BC=6cm,等腰RT△DEF中,∠D=90°,EF=4cm.EF在BC 所在直线L上,开始时点F与点C重合,让等腰RT△DEF沿直线L向右以每秒1cm的速度做匀速运动,最后点E和点B重合。
(1)请直接写出等腰RT△DEF运动6S时与△ABC重叠部分面积(2)设运动时间为xS,运动过程中,等腰RT△DEF与△ABC重叠部分面积为ycm²①在等腰RT△DEF运动6S后至运动停止前这段时间内,求y与x之间的函数关系式②在RT△DEF整个运动过程中,求当x为何值时,y=1/2.5、【操作发现】如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=45°,连接AC,BD交于点M.①AC与BD之间的数量关系为;②∠AMB的度数为;【类比探究】如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算的值及∠AMB的度数;【实际应用】如图(3),是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE组成的图形,其中∠ACB=∠DCE=90°,∠A=∠D=30°且D、E、B在同一直线上,CE=1,BC=,求点A、D之间的距离.6、如图1,在△ABC 中,AB =AC =10,,点D 为BC 边上的动点(点D 不与点B ,C 重合).以D 为顶点作∠ADE =∠B ,射线DE 交AC 边于点E ,过点A 作AF ⊥AD 交射线DE 于点F ,连接CF .(1)求证:△ABD ∽△DCE ;(2)当DE ∥AB 时(如图2),求AE 的长;(3)点D 在BC 边上运动的过程中,是否存在某个位置,使得DF =CF ?若存在,求出此时BD 的长;若不存在,请说明理由.7、如图,在△ABC 中,AB =AC ,△BAC =120°,D 为BC 边上的点,将DA 绕D 点逆时针旋转120°得到DE .(1)如图1,若△DAC =30°.△求证: AB =BE ;△直接写出BE 2+CD 2与AD 2的数量关系为 ;(2)如图2,点D 为BC 边上任意一点,线段BE 、CD 、AD 是否依然满足(1)中△的关系,请给出结论并证明.MBAABEDC DC B A8、已知△ABC≌△ADE,∠BAC=∠DAE=90°.(1)如图(1)当C、A、D在同一直线上时,连CE、BD,判断CE和BD位置关系,填空:CE_____BD.(2)如图(2)把△ADE绕点A旋转到如图所示的位置,试问(1)中的结论是否仍然成立,写出你的结论,并说明理由.(3)如图(3)在图2的基础上,将△ACE绕点A旋转一个角度到如图所示的△AC′E′的位置,连接BE′、DC′,过点A 作AN⊥BE′于点N,反向延长AN交DC′于点M.求的值.9、△ABC中,AC=BC,∠ACB=α,点D是平面内不与点A和点B重合的一点,连接DB,将线段DB绕点D顺时针旋转α得到线段DE,连接AE、BE、CD.(1)如图①,点D与点A在直线BC的两侧,α=60°时,的值是;直线AE与直线CD相交所成的锐角的度数是度;(2)如图②,点D与点A在直线BC两侧,α=90°时,求的值及直线AE与直线CD相交所成的锐角∠AMC的度数;DMDC(3)当α=90°,点D 在直线AB 的上方,S △ABD =S △ABC ,请直接写出当点C 、D 、E 在同一直线上时,的值.10、(1)问题发现如图1,在△OAB 和△OCD 中,OA =OB ,OC =OD ,△AOB =△COD =40°,连接AC ,BD 交于点M .填空: △BDAC的值为 ; △△AMB 的度数为 . (2)类比探究如图2,在△OAB 和△OCD 中,△AOB =△COD =90°,△OAB =△OCD =30°,连接AC 交BD 的延长线于点M .请判断BDAC的值及△AMB 的度数,并说明理由; (3)拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=7,请直接写出当点C与点M重合时AC的长.11、几何探究:【问题发现】(1)如图1所示,ABC∆是有公共顶点的等边三角形,BD、CE的关系是(选填“相等”∆和ADE或“不相等”);(请直接写出答案)【类比探究】(2)如图2所示,ABC∆是有公共顶点的含有30︒角的直角三角形,(1)中的结论还成立吗?∆和ADE请说明理由;【拓展延伸】(3)如图3所示,ADE∆和ABC∆绕点∆是有公共顶点且相似比为1:2的两个等腰直角三角形,将ADEA自由旋转,若BC=B、D、E三点共线时,直接写出BD的长.。
2021年中考九年级数学第一轮强化训练:一次函数 压轴题专题复习(无答案)
2021年中考九年级数学第一轮强化训练:一次函数压轴题专题复习1、如图,一次函数y=x+3的函数图象与x轴,y轴分别交于点A,B.(1)若点P(﹣2,m)为第三象限内一个动点,请问△OPB的面积会变化吗?若不变,请求出面积;若变化,请说明理由.(2)在(1)的条件下,试用含m的代数式表示四边形APOB的面积;若△APB的面积是6,求m的值.2、如图,在平面直角坐标系中,直线l的解析式为y=﹣x,直线l2与l1交于点A(a,﹣a)与y轴交于点B(0,b),其中a,b满足(a+2)2+=0(1)求直线l2的解析式;(2)若在第二象限中有一点P(m,5)使得S△AOP=S△AOB,请求出点P的坐标;(3)已知直线y=2x﹣2分别交x轴、y轴于E、F两点,M、N分别是直线l1、l2上的动点,请直接写出能使E、F、M、N四点构成平行四边形的点M的坐标.3、如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.(1)求一次函数的解析式.(2)求(1)中一次函数与矩形的交点坐标.(3)设点D(﹣1,0),在一次函数图象上求一点P,使△ADP为直角三角形,求点P坐标.4、如图,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.(1)填空:点C的坐标是(,),点D的坐标是(,);(2)设直线CD与AB交于点M,求线段BM的长;(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.5、如图,直线和x轴、y轴的交点分别为B、C,点A的坐标是(﹣2,0).(1)试说明△ABC是等腰三角形;(2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S.①求S与t的函数关系式;②设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t值;若不存在请说明理由;③在运动过程中,当△MON为直角三角形时,求t的值.6、如图,在平面直角坐标系中,一次函数y=kx+b的图象与y轴的正半轴交于点A,与x 轴交于点B(﹣2,0),△ABO的面积为2.动点P从点B出发,以每秒1个单位长度的速度在射线BO上运动,动点Q从O出发,沿x轴的正半轴与点P同时以相同的速度运动,过P 作PM⊥X轴交直线AB于M.(1)求直线AB的解析式.(2)当点P在线段OB上运动时,设△MPQ的面积为S,点P运动的时间为t秒,求S与t 的函数关系式(直接写出自变量的取值范围).(3)过点Q作QN⊥x轴交直线AB于N,在运动过程中(P不与B重合),是否存在某一时刻t(秒),使△MNQ是等腰三角形?若存在,求出时间t值.7、如图,在平面直角坐标系中,函数y=2x+12的图象分别交x轴,y轴于A,B两点过点A 的直线交y轴正半轴于点M,且点M为线段OB的中点.(1)求直线AM的函数解析式.(2)试在直线AM上找一点P,使得S△ABP=S△AOB,请直接写出点P的坐标.(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A,B,M,H为顶点的四边形是等腰梯形?若存在,请直接写出点H的坐标;若不存在,请说明理由.8、、如图,直线l1的解析表达式为:y=3x﹣3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求△ADC的面积;(2)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,则点P的坐标为;(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H 为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.9、如图,直线l1:y=﹣x+b分别与x轴、y轴交于A、B两点,与直线l2:y=kx﹣6交于点C(4,2).(1)求A点坐标及k,b的值;(2)在直线BC上有一点E,过点E作y轴的平行线交直线l2于点F,设点E的横坐标为m,当m为何值时,以O、B、E、F为顶点的四边形是平行四边形;(3)若点P为x轴上一点,在坐标系中是否存在一点Q,使得P、Q、A、B四个点能构成一个菱形?若存在,求出所有符合条件的Q的坐标;若不存在,请说明理由.10、如图,在平面直角坐标系xOy中,已知直线l1:y=x与直线l2:y=﹣x+6相交于点M,直线l2与x轴相交于点N.(1)求M,N的坐标.(2)矩形ABCD中,已知AB=1,BC=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动,设矩形ABCD与△OMN的重叠部分的面积为S,移动的时间为t (从点B与点O重合时开始计时,到点A与点N重合时计时开始结束).直接写出S与自变量t之间的函数关系式(不需要给出解答过程).(3)在(2)的条件下,当t为何值时,S的值最大?并求出最大值.11、已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=x﹣与x轴交于点B,直线l1、l2交于点C,且C点的横坐标为1.(1)如图1,过点A作x轴的垂线,若点P(x,2)为垂线上的一个点,Q是y轴上一动点,若S△CPQ=5,求此时点Q的坐标;(2)若P在过A作x轴的垂线上,点Q为y轴上的一个动点,当CP+PQ+QA的值最小时,求此时P的坐标;(3)如图2,点E的坐标为(﹣2,0),将直线l1绕点C旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M点为直角顶点的等腰直角三角形?若存在,求出N点的坐标;若不存在,请说明理由.12、如图,直线y=kx+b与x轴和y轴交于A、B两点,AB=4,∠BAO=45°.(1)如图1,求直线AB的解析式.(2)如图1,直线y=2x﹣2交x轴于点E.且P为该直线在直线AB上方一动点,当△PAB 的面积等于10时,将线段PE沿着x轴平移得到线段P1E1,连接OP1.求OP1+P1E1+的最小值.(3)如图2,在(2)问的条件下,若直线y=2x﹣2与y轴的交点是C,连接CE1,得到△OCE1,将△OCE1绕着原点O逆时针旋转α°(0<α<180),旋转过程中直线OC与直线AB 交于点M,直线CE1与直线AB交于点N,当△CMN为等腰三角形时,直接写出α的值.13、已知直线y=﹣x+6与x轴,y轴分别相交于点A,B,将∠OBA对折,使点O的对应点E落在直线AB上,折痕交x轴于点C.(1)求点C的坐标和直线BC的函数表达式;(2)若已知x轴上有一点D(4,0),点M为直线AB上一点,点N为直线BC上一点,是否存在这样的点M、N,使得以点A、D、M、N为顶点的四边形是平行四边形?若存在,求出点M的坐标:若不存在,说明理由;(3)已知y轴上有点P(0,2),点Q为直线BC上一点,点K为直线y=﹣x上一点,是否存在合适的点Q,K,使得PQ+KQ最小?若存在,求出PQ+KQ的最小值以及此时K点的坐标;若不存在,请说明理由.14、如图1.在平面直角坐标系中,四边形OBCD是正方形,D(0,3),点E是OB延长线上一点,M是线段OB上一动点(不包括O、B),作MN⊥DM,交∠CBE的平分线于点N.(1)①直接写出点C的坐标:②求证:MD=MN;(2)如图2,若M(2,0),在OD上找一点P,使四边形MNCP是平行四边形,求直线PN的解析式;(3)如图,连接DN交BC于F,连接FM,下列两个结论:①FM的长为定值:②MN平分∠FMB,其中只有一个正确,选择并证明.15、在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).(1)已知点A(﹣,0),B为y轴上的一个动点,①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;②直接写出点A与点B的“非常距离”的最小值;(2)已知C是直线y=x+3上的一个动点,①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;11/ 11。
初中学业数学补考试卷
1. 下列数中,是负数的是()A. -3B. 3C. -3.5D. 3.52. 下列代数式中,正确的是()A. 3a + 2b = 5a - 2bB. 2a + 3b = 3a + 2bC. 3a - 2b = 5a - 3bD. 2a - 3b = 5a + 2b3. 若x + 2 = 5,则x的值为()A. 3B. 4C. 5D. 64. 下列方程中,无解的是()A. 2x + 3 = 7B. 3x - 5 = 2C. 4x + 1 = 0D. 5x - 2 = 05. 下列图形中,是轴对称图形的是()A. 等腰三角形B. 等边三角形C. 长方形D. 正方形6. 下列计算正确的是()A. (a + b)² = a² + b²B. (a - b)² = a² - b²C. (a + b)² = a² + 2ab + b²D. (a - b)² = a² - 2ab + b²7. 下列函数中,是反比例函数的是()A. y = x²B. y = 2xC. y = kxD. y = k/x8. 下列数中,是质数的是()A. 4B. 5C. 6D. 79. 若等腰三角形的底边长为6cm,腰长为8cm,则其高为()A. 4cmB. 5cmC. 6cmD. 7cm10. 下列不等式中,正确的是()A. 2x > 3B. 3x < 4C. 4x ≤ 5D. 5x ≥ 611. 若x - 3 = 5,则x = _______。
12. 若a² = 4,则a = _______。
13. (-2)×(-3)×(-4)= _______。
14. 3a + 2b - 4c = 5a + 2b - 4c,则a = _______。
15. 下列函数中,是正比例函数的是 y = _______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金戈出品必属精品
学 习 资 料 汇编
1
一元二次方程训练题 4
一、选择题:(每小题6分,共24分)
1. 一元二次方程022xax方程有两个相等实数根,则a------------------
( )
A 81 B 81 C 81 D 0
2. 若方程0522mxx有两个相等实数根,则m= -------------------------
( )
A 2 B 0 C 2 D 813
3. 若方程0624)2(2mmxxm有相等实数根,则m-----------------
( )
A 6m B 1m C 2m D 6m或
1m
4. 方程07)1(82kxkx的一个根为零,则
k
--------------------------( )
A 1 B 163 C 4 D 7
二、填空题:(每小题6分,共30分)
4. 当_________k时,方程0)12(22kkxkx有实数根;
5. 当_________m时,方程032)1(2mmxxm有两个实数根;
6. 当_________k时,方程01222kkxx有重根;
7. 0 是方程01032mxx的一个根,则________m时才能满足这一条件;
8. 方程02)6(92mxmx的两根相等,则_______m;
三、求证:方程074)1(3222mmxmx对于任何实数m,永远有两个不
相等的实数根;(15分)
金戈出品必属精品
学 习 资 料 汇编
2
四、墙的一边,再用13米长的铁丝挡三边围成一个面积是20平方米的长方形,问长
方形
长和宽各是多少才能刚好合适?(15分)
五、相邻两数是自然数,它们的平方和比这两数中较小者的2倍大51,求这两数:(16
分)
选作题:
1. 已知acb2,求证:关于x的一元二次方程
0)(2)(22222cbxcabxba
有两个相等实数根;(10分)
2. 已知a、b、c为⊿ABC的三边,试判断关于x的方程
金戈出品必属精品
学 习 资 料 汇编
3
)(02)(2cbcbaxxcb
的根的情况(10分)
亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……
