基于神经网络的非线性系统辨识
一种非线性系统参数辨识的耦合算法研究

一种非线性系统参数辨识的耦合算法研究付华;乔德浩;池继辉【摘要】针对工程复杂性、时变性、非线性的特点,提出了基于混沌免疫粒子群算法(CIPSO)与El-man神经网络的耦合算法(CIPSD-ENN),用于非线性动态模型参数辨识.CIPSO优化算法将人工免疫系统中的克隆选择和混沌优化机制引入粒子群算法,在粒子群种群进化过程中.该算法对粒子进行克隆选择,提高其收敛速度,对克隆后的粒子混沌变异以增强种群局部搜索能力,最后,CIPSO与动态反馈型Elman神经网络融合,对其权值、阈值寻优,建立了基于CIPSO和ENN的耦合算法系统辨识模型.实验结果表明,算法具有收敛速度快、收敛精度高、鲁棒性强的特点,与单纯Elman网络辨识相比,模型收敛速度提高了10倍,拟合精度提高了2个数量级.%Aiming at the complexity, time varying and nonlinearity of the projects, a CIPSO-ENN coupling algorithm for identifying the parameters of nonlinear dynamic models is proposed, where the clonal selection of artificial immune system and chaotic mutation mechanism are embedded into standard particle swarm optimization.In the evolution of the particle swarm optimization population, this algorithm accelerates convergence of particle clonal selection and enhances the particle swarm local search capability after cloned particle chaotic mutation.Then CIPSO algorithm is merged with dynamic feedback Elman neural network to construct system identification model based on the CIPSO-ENN.The experiment results show that the identification model convergence rate is increased by 10 times and fitting accuracy is increased by 2 orders of magnitude compared with the pure Elman network identification method.【期刊名称】《西安交通大学学报》【年(卷),期】2011(045)002【总页数】5页(P49-53)【关键词】混沌算法;克隆选择;Elman神经网络;耦合算法;非线性动态系统【作者】付华;乔德浩;池继辉【作者单位】辽宁工程技术大学电气与控制工程学院,125105,辽宁,葫芦岛;辽宁工程技术大学电气与控制工程学院,125105,辽宁,葫芦岛;辽宁工程技术大学电气与控制工程学院,125105,辽宁,葫芦岛【正文语种】中文【中图分类】TP183动态反馈型Elman神经网络(ENN)具有很强的非线性动态映射能力,是一种极具潜力的非线性系统辨识工具,能为非线性参数的辨识提供一种行之有效的方法[1].为了提高Elman网络模型的辨识性能,避免出现参数辨识过程中收敛速度慢和易收敛于局部极小点导致辨识误差过大的问题,本文将擅长全局搜索的混沌免疫粒子群算法(CIPSO)与Elman神经网络进行有机结合,提出基于CIPSO的Elman神经网络的耦合算法(简称CIPSO-ENN),采用数学方式建立CIPSO-ENN非线性参数辨识模型.通过CIPSO搜寻ENN最合适的一组权值和阈值,使辨识的目标函数值最小,实现辨识模型的输出接近输出的目标期望值,达到非线性参数辨识的目的.SPSO算法是将群体中的每个个体视为多维搜索空间中一个没有质量和体积的粒子,这些粒子在搜索空间以一定的速度飞行,并根据粒子本身的飞行经验以及同伴的飞行经验,对自己的飞行速度进行动态调整,即每个粒子通过统计迭代过程中自身的最优值和群体的最优值不断地修正自己的前进方向和速度,从而形成群体巡游的正反馈机制[2-5].设在一个D维搜索空间中,存在一个由N个粒子组成的群体,群体中第t次迭代时粒子i的位置表示为Xi=(xi1,xi2,…,xiD),相应的飞行速度表示为Vi=(vi1,vi2,…,viD),i=1,2,…,N.将 Xi带入目标函数可得到其适应值.记第i个粒子搜索到的最优位置为Pi=(pi1,pi2,…,piD),整个粒子群搜索到的最优位置为Pg=(pg1,pg2,…,pgD),粒子状态更新操作为式中:i=1,2,…,N;d=1,2,…,D;r1、r2为[0,1]之间的随机数;c1、c2为加速度因子;w为惯性因子.为加快收敛速度,同时保持粒子群的多样性,本文引入混沌算法和人工免疫系统中的克隆选择机制.将目标函数和约束条件视为抗原,粒子群视为抗体,将亲和度高的抗体按与其亲和度成正比进行克隆[6],与亲和度成反比进行混沌变异;将亲和度低的抗体按一定比例重新初始化,以保证多样性.基于混沌克隆选择的PSO算法的基本思路是:抗体在初始化后,首先利用式(1)、式(2)指导其“飞行”的方向,为加快收敛速度,选择亲和度高的抗体进行克隆操作,使抗体更多的聚集在“好”位置的附近;再对克隆后的抗体进行混沌变异,使抗体往“好”位置附近的各个方向进行搜索;最后抛弃亲和度最差的抗体,将它们重新初始化,以保证种群的多样性.本文针对克隆扩增和超突变现象设计混沌克隆算子,设当前群体按式(1)、式(2)对所有粒子(抗体)的速度和位置进行更新后得到新的种群PK={X1,X2,…,Xn}.根据抗体抗原亲和度排序,亲和度最高的M个抗体组成精英克隆种群SK,剩下的(N-M)个抗体组成种群LK,精英种群规模M是一个变量,设抗体亲和度函数为f(X),则SK表示为精英种群SK中的M 个抗体X1,X2,…,XM的亲和度为f1,f2,…,fM,根据种群规模N 和抗体亲和度,Xj克隆为qj个相同的点Xj1,Xj2,…,Xjqj由式(4)可知,抗体 Xi的亲和度越高,抗体克隆的数目越多.则由dj组成种群D′K,由子代种群D′K和初始种群SK合并,选择竞赛规模Q,通过锦标联赛的方式[8],形成新一代精英种群SK+1.混沌克隆算子通过空间的扩展与压缩,有效地提高局部寻优能力.对于种群LK,模拟生物克隆选择中B细胞自然消亡的过程,在LK中选择d个亲和度最低的抗体,运用消亡算子Γ(*)予以抛弃,将其重新初始化,得到LK+1,可保持种群的多样性式中:L、U分别表示抗体X的取值范围的下、上界.对种群进行更新、克隆、变异等操作后,得到新一代种群如此循环进行下一次种群更新操作,直到达到期望结果.为了验证CIPSO算法的寻优性能,采用多峰、非凸的peaks函数作为优化问题的测试对象,分别用CIPSO算法与SPSO算法对其求解优化peaks的minf(x,y).函数表达式为粒子群规模为20,加速因子c1=c2=2,最大迭代次数为50,惯性权值w随迭代次数从0.9到0.4线性减小,竞赛规模Q=10.经过50次迭代实验结果如图1所示由图1可以看出,本文提出的CIPSO算法比标准PSO算法的全局寻优能力以及收敛精度、收敛速度都有明显改进.静态前馈神经网络对时变、动态系统进行辨识,其实质是将动态时间建模问题变为一个静态空间建模问题,这必然存在许多问题[9].在系统辨识过程中,为提高辨识的准确性,常以网络的结构膨胀为代价,导致系统学习速度下降.具有动态特性和递归作用的Elman神经网络则具有内部反馈、存储和利用过去时刻输入、输出信息的特点,除了能解决静态系统的建模问题外,还能实现动态系统的映射并更加直接地反映系统的动态特性,比前向神经网络系统具有更强的计算能力和网络稳定性[10].如图2所示,Elman神经网络一般分为4层:输入层、隐含层、结构层和输入层.对于非线性系统,Elman神经网络的隐含层单元个数就是状态变量的个数,即系统的阶次.Elman神经网络只需一个输入单元和一个输出单元.如果有n个结构单元,则隐含层的输入有n+l个,与静态网络所要求的神经元个数相比大为减少.Elman神经网络自身具有动态环节,无需使用过多的系统状态输入,从而减少了输入层的单元个数.此外,Elman神经网络的动态特性仅由内部的连接提供,无需使用状态作为输入或训练信号,这也是Elman神经网络相对于静态前馈网络的优越之处,非常适合于动态系统辨识[11].但是,在执行过程中,Elman神经网络算法网络参数每次调整的幅度为一个与网络误差函数或其对权值的导数成正比的项乘以固定的学习率η,在误差曲面平坦处误差下降很慢,在曲面曲率大处,误差函数最小点附近会发生过调整现象,从而引起震荡.大量的数值仿真研究表明,由于Elman神经网络结构的复杂性,不同权值和阈值对同一样本的收敛速度不同[12],从而使Elman神经网络算法存在学习速度慢、精度低和鲁棒性差等缺陷,无法满足工程应用的需要.CIPSO的搜索能够遍及整个解空间,容易得到全局最优解,且不要求目标函数连续、可微,甚至不要求目标函数有显函数的形式,只要求问题可计算.因此,将擅长全局搜索的CIPSO与 Elman神经网络进行有机结合,形成CIPSO-ENN算法,能有效提高Elman神经网络辨识性能.在CIPSO训练Elman神经网络时,首先定义粒子群位置向量X是以Elman网络全体节点之间的连接权值和节点的阈值组成粒子的位置参数式中:W1为神经网络输入层与隐含层间的连接权值;W2为结构层与隐含层间的连接权值;W3为隐含层与输出层间的连接权值;θ1为隐含层阈值;θ2为输出层阈值.若Elman网络输入节点数是V1,结构层节点数是V2,隐含层节点是V3,输出节点数是V4,则CIPSO搜索空间维数为采用CIPSO搜寻Elman网络最合适的一组权值和阈值,是通过参数的调整和优化,从而使得Elman网络的输出最接近输出的目标期望值,使网络输出和理想输出的误差平方和指标(适应值)达到最小,实现非线性动态系统的辨识.定义适应度函数为式中:N为训练样本数;O为输出神经元数;ydji为输出样本值;yji为实际值.(1)确定种群规模Na,适应阈值ε,最大迭代次数 Gmax,学习因子 c1、c2.(2)随机初始化种群,确定每个粒子(抗体)的初始位置和速度.(3)根据粒子(抗体)Xi和训练样本,按式(14)计算每个粒子(抗体)的亲和度,并更新Pi 和Pg.(4)若达到结束条件,算法终止.(5)按式(1)、式(2)对所有粒子(抗体)的速度和位置进行更新,并限制其不超过边界.(6)对于当前种群Pk,根据抗体抗原亲和度排序,选出亲和度最高的M个粒子(抗体)组成精英克隆种群SK,剩下的(N-M)个粒子(抗体)组成种群LK.(7)对种群SK中的粒子(抗体)进行克隆、混沌变异和选择操作,得到新一代精英种群SK+1.(8)在种群LK中取得d个亲和度最低的粒子(抗体),运用消亡算子予以抛弃,将其重新初始化得到新种群LK+1.分别采用CIPSO-ENN耦合算法、Elman网络算法对非线性函数 f1(x)进行计算,并比较其拟合程度与收敛性能.f1(x)表达式为在数值实验中,两种算法均随机选取100个样本作为网络的训练输入,其输出作为相对应的测试输出,以此构成网络的训练样本集.网络的输入节点数V1=1,隐含层节点数V2=20,结构层节点数V3=20,输出层节点数V4=1,网络的隐含层神经元的激发函数选用sigrnofd函数,输出层神经元的激发函数采用Pureline函数.粒子群规模为20,加速因子c1=c2=2,最大迭代次数Iter max=600,惯性权值w随迭代次数从0.9到0.4线性减小,竞赛规模Q=10.由图3、图4可以看出,CIPSO-ENN耦合算法得到的拟合曲线几乎与原函数完全重合,比Elman网络算法具有更好的逼近效果.CIPSO-ENN辨识模型最大拟合误差为2.385×e-6,Elman辨识模型最大拟合误差为1.267×e-2.为了使结果更加直观,对最大拟合误差取自然对数,结果见图5.由图5可以看出,CIPSO-ENN算法收敛速度明显快于Elman算法,而且在迭代次数相同的情况下,具有相对更高的精度和收敛效果.显然,本文提出的算法具有很高的搜索效率和很强的鲁棒性,能够实现任意非线性函数的逼近以及对非线性多参数的实时辨识.本文将克隆选择和混沌算法与粒子群优化算法结合,提出了一种混沌免疫粒子群优化算法.该算法具有收敛速度快、收敛精度高、鲁棒性强的特点,将其与具有动态反馈型Elman神经网络算法相结合,对Elman网络的权值与阈值进行训练.实验表明,本文提出的CIPSO-ENN耦合算法对动态非线性模型的辨识比传统Elman算法具有明显的优越性.【相关文献】[1] GERNASKY M,BENUSKOVA L.Simple recurrent network trained by RTRL and extended Kalmann filter algorithm[J].Neural Network World,2003,13(3):223-234.[2] 陈贵敏,贾建援,韩琪.粒子群优化算法的惯性权值递减策略研究[J].西安交通大学学报,2006,40(1):53-56.CHEN Guimin,JIA Jianyuan,HAN Qi.Study on the strategy of decreasing inertial weight in particle swarm optimization algorithm[J].Journal of Xi′an JiaotongUniversity,2006,40(1):53-56.[3] 潘峰,陈杰,甘明刚,等.粒子群优化算法模型分析[J].自动化学报,2006,32(3):368-377.PAN Feng,CHEN Jie,GAN Minggang,et al.Model analysis of particle swarmoptimizer[J].Acta Automatica Sinica,2006,32(3):368-377.[4] HOLAND J.Emergence:from chaos to order[M].Redwood City,California:Addison Wesley,1998.[5] 杨维,李歧强.粒子群优化算法综述[J].中国工程科学,2004,6(5):87-94.YANG Wei,LI Qiqiang.Survey on particle swarm optimization algorithm [J].EngineeringScience,2004,6(5):87-94.[6] 陈曦,蒋加伏.免疫粒子群优化算法求解旅行商问题[J].计算机与数字工程,2006,34(6):10-29. CHEN Xi,JIANG Jiafu.Particle swarm optimization algorithms with immunity for traveling salesman problems[J].Computer and Digital Engineering,2006,34(6):10-29.[7] 尤勇,王孙安,盛万兴.新型混沌优化方法的研究及应用[J].西安交通大学学报,2003,37(1):69-72. YOU Yong,WAN G Sun′an,SHENG Wanxing.New chaos optimization algorithm with application[J].Journal of Xi′an Jiaotong University,2003,37(1):69-72.[8] SCHWEFEL H P.Evolution and optimum seeking[M].New York,USA:Wiley,1995.[9] 王峰,邢科义,徐小平.系统辨识的粒子群优化方法[J].西安交通大学学报,2009,43(2):116-119. WANG Feng,XING Keyi,XU Xiaoping.A system identification method using particle swarm optimization[J].Journal of Xi′an Jiaotong University,2009,43(2):116-119.[10]葛宏伟,梁艳春.进化Elman神经网络模型与非线性系统辨识[J].吉林大学学报:工学版,2005,35(5):511-519.GE Hongwei,LIANG Yanchun.Evolutionary Elman neural network model and identification for non-linear systems[J].Journal of Jilin University:Engineering and Technology Edition,2005,35(5):511-519.[11]李秀英,韩志刚.非线性系统辨识方法的新进展[J].自动化技术与应用,2004,23(10):5-7.LI Xiuying,HAN Zhigang.Advances in nonlinear system identification[J].Techniques of Automation&Application,2004,23(10):5-7.[12]时小虎,梁艳春,徐旭.改进的Elman模型与递归反传控制神经网络[J].软件学报,2003,14(6):1110-1119.SHI Xiaohu,LIANG Yanchun,XU Xu.An improved Elman model and recurrent back-propagation control neural networks[J].Journal of Software,2003,14(6):1110-1119.。
智能控制

1、智能控制: 即设计一个控制器(或系统),使之具有学习、抽象、推理、决策等功能,并能根据环境(包括被控对象或被控过程)信息的变化做出适应性反应,可以有各种人工智能的水平,从而实现由人来完成的任务。
2、智能控制由哪几部分组成?各自的特点是什么?①模糊控制(通过模拟人脑的思维方法设计控制器,可实现复杂系统的控制)②神经网络控制(从机理上对人脑生理系统进行简单结构的模拟,具有并行机制、模式识别、记忆和自学习能力的特点,能充分逼近任意复杂的非线性系统,能够学习与适应不确定系统的动态特性,有很强的鲁棒性和容错性)③遗传算法(可用于模糊控制规则的优化及神经网络参数及权值的学习)3、比较智能控制和传统控制的特点传统控制和智能控制的主要区别:①传统控制方法在处理复杂化和不确定性问题方面能力很低;智能控制在处理复杂性、不确定性方面能力较高。
智能控制系统的核心任务是控制具有复杂性和不确定性的系统,而控制的最有效途径就是采用仿人智能控制决策。
②传统控制是基于被控对象精确模型的控制方式;智能控制的核心是基于知识进行智能决策,采用灵活机动的决策方式迫使控制朝着期望的目标逼近。
传统控制和智能控制的统一:智能控制擅长解决非线性、时变等复杂控制问题,而传统控制适于解决线性、时不变等相对简单的控制问题。
智能控制的许多解决方案是在传统控制方案基础上的改进,因此,智能控制是对传统控制的扩充和发展,传统控制是智能控制的一个组成部分。
在这个意义上,传统控制和智能控制可以统一在智能控制的框架下,而不是被智能控制所取代。
智能控制研究对象的特点:(1)不确定性的模型 (2)高度的非线性 (3)复杂的任务要求智能控制的特点:(1)分层递阶的组织结构 (2)自学习能力 (3)自适应能力 (4)自组织能力(5)优化能力4、专家系统:是一类包含着知识和推理的智能计算机程序,其内部含有大量的某个领域的专家水平的知识和经验,具有解决专门问题的能力。
专家控制:是将专家系统的理论和技术同控制理论、方法与技术相结合,在未知环境下,仿效专家的经验,实现对系统的控制。
非线性系统辨识与鲁棒控制设计

非线性系统辨识与鲁棒控制设计近年来,随着科技的迅猛发展,越来越多的实际控制系统呈现出非线性特性。
非线性系统在实际生活和工业生产中无处不在,如机械系统、电力系统和化学过程等。
为了更好地实现对非线性系统的控制,非线性系统辨识和鲁棒控制设计成为研究热点。
非线性系统辨识是指通过对系统输入输出数据进行分析和处理,建立系统的数学模型。
在非线性系统中,系统的动力学特性可能会因为非线性关系而变得复杂,因此,非线性系统辨识是非常具有挑战性的任务。
非线性系统辨识可以通过两种常用方法来实现:基于物理模型的辨识和基于数据的辨识。
基于物理模型的辨识方法是指通过对系统的运动方程和控制原理进行建模和推导,得到系统的数学模型。
这种方法适用于已知系统结构和动力学特性的情况下,可以较好地描述系统的行为。
然而,实际系统经常难以精确建模,因此,基于物理模型的辨识方法在非线性系统中的应用受到一定限制。
基于数据的辨识方法是指通过对系统输入输出数据进行数学处理和分析,从而推断出系统的数学模型。
这种方法不依赖于对系统的结构和动力学特性的先验知识,可以适用于各种非线性系统。
基于数据的辨识方法在非线性系统的辨识中具有广泛的应用,例如神经网络模型、支持向量机模型和遗传算法等。
在完成非线性系统辨识之后,鲁棒控制设计成为实现系统稳定性和性能要求的关键任务。
鲁棒控制设计是指通过设计适应非线性系统变化和不确定性的控制器,实现对系统的稳定性和鲁棒性能的改进。
在鲁棒控制设计中,一种常见的方法是通过将非线性系统转化为线性化系统,然后设计线性控制器进行控制。
鲁棒控制设计的核心思想是对系统不确定性和外部扰动进行补偿。
对于非线性系统的鲁棒控制,常用的方法包括滑模控制、自适应控制和模糊控制等。
滑模控制通过引入滑模面,实现对非线性系统的鲁棒控制;自适应控制通过在线调整参数,以适应非线性系统的变化;模糊控制通过建立模糊模型和设计模糊规则,实现对非线性系统的鲁棒控制。
除了上述方法,近年来,深度学习技术也开始应用于非线性系统的辨识和控制中。
非线性动态系统模型与辨识

、 、g :非线性算子; u( k ) 、 y( k ) 、 x( k ) :系统在采样点 k 的输入、输出和状态向量。
两种模型,设: (1)系统具有能观、能控性,是 BIBO 系统; (2)输入向量 m 维
u ( k ) [u1 ( k ), u 2 ( k ), , u m ( k )] T
网络模型:
x o ( k 1) H Wy c ( k 1) 1 Wu( k ) 1 y c ( k ) o( k 1) f (x o ( k 1)) ( k ) 2 Wo( k ) y
实时调整权值动态 BP 算法: 2
u (k )
y c (k )
o(k 1) ˆ (k 1) y
f ( x ) (1 e x ) / (1 e x )
j 0 2
输出层节点输出 :
ˆ ( k 1) 2 wi ( k )oi ( k ) , n=3 x
1
n
i 1
wij :节点 j 至 i 的权值(第一至第二层节点); 1 wi 0 2 wi :第二层节点 i 的阈值;
(SPM3) (SPM4) (SPM5)
( k ) Ng[ y ( k 1), , y ( k n); V]u( k m) y
( k ) wi y ( k i ) N[u( k 1), , u( k m); W ] y
i 1
n
( k ) Ng[ y ( k 1), y ( k n); V] wi u( k i ) y
W 、 2 W 、 H W :输入至隐层、隐层至输出层、隐层节点间权矩阵; f(x) :对称型 S 函数。
1
机械系统动力学系统辨识方法综述

机械系统动力学系统辨识方法综述在机械工程领域,对机械系统动力学特性的准确了解是优化设计、故障诊断、性能预测和控制策略制定的关键。
机械系统动力学系统辨识作为获取系统动态特性的重要手段,一直以来都是研究的热点。
本文将对常见的机械系统动力学系统辨识方法进行综述。
机械系统动力学系统辨识的基本任务是根据系统的输入和输出数据,建立能够准确描述系统动态特性的数学模型。
常见的辨识方法可以大致分为基于时域的方法和基于频域的方法。
时域辨识方法中,脉冲响应函数法是一种常用的技术。
它通过对系统施加一个短脉冲输入,并测量系统的输出响应,从而得到系统的脉冲响应函数。
脉冲响应函数直接反映了系统的动态特性,通过对其进行分析和处理,可以得到系统的数学模型参数。
最小二乘法在时域辨识中也应用广泛。
它基于输入输出数据,通过最小化误差的平方和来估计模型参数。
这种方法计算相对简单,并且在一定条件下具有较好的估计精度。
然而,它对噪声比较敏感,当测量数据中存在噪声时,可能会导致辨识结果的偏差。
卡尔曼滤波法是一种基于状态空间模型的时域辨识方法。
它能够在存在测量噪声和系统不确定性的情况下,对系统状态进行最优估计,并同时估计模型参数。
这种方法在处理多变量系统和时变系统时具有优势。
在频域辨识方法中,频率响应函数法是基础且重要的手段。
通过对系统施加不同频率的正弦输入,并测量系统的稳态输出响应,可以得到系统的频率响应函数。
频率响应函数包含了系统在不同频率下的幅频和相频特性,通过对其进行拟合和分析,可以获得系统的模型参数。
谐波平衡法常用于非线性系统的频域辨识。
它假设系统的响应可以表示为多个谐波的叠加,通过求解非线性方程来确定谐波的系数,从而得到系统的模型。
相干函数分析则用于评估输入和输出之间的线性相关性,帮助判断辨识结果的可靠性。
除了上述传统的辨识方法,近年来还发展出了一些新的技术和方法。
例如,基于神经网络的辨识方法利用神经网络强大的非线性拟合能力,能够处理复杂的非线性机械系统。
大庆石油学院继续教育学院部分主讲教师及其学术研究方向简介z
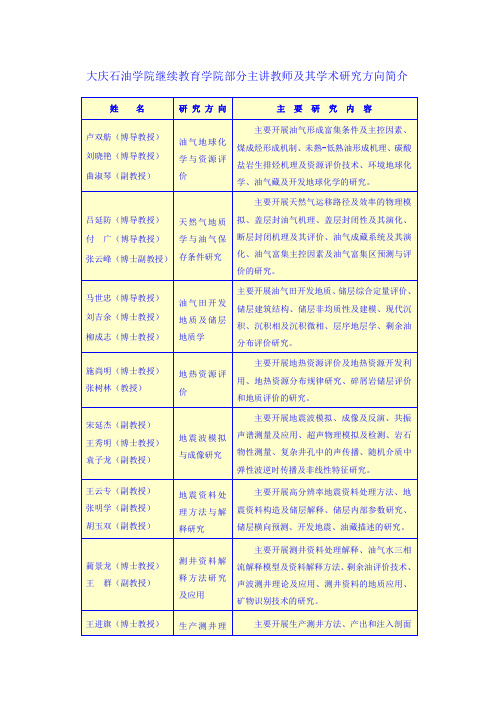
吴文祥(博导教授)
康万利(博士教授)
化学驱油技术研究
聚合物驱、三元复合驱、泡沫复合驱、微生物采油原理与应用技术等;各种化学驱油方法的注入剂的研制。
刘永健(博导教授)
陈涛平(博士教授)
范洪富(博士教授)
稠油热采及物理法采油技术
稠油水热裂解降粘提高采收率技术,稠油裂解催化剂研究;利用震动、电磁场、加热等方法,对低渗透油田提高采收率的技术。
栾庆德(教授)
刘树林(博导教授)
崔旭明(副教授)
钻采机械设计及理论
地面机械设计及理论(抽油机、钻机等)、井下机械设计及理论(抽油泵、抽油杆与螺纹、定向井工具等)、机械装备失效与可靠性设计分析技术。
张永弘(教授)
任福山(教授)
李其(副教授)
实验力学及应用技术
断裂力学与疲劳分析技术、光弹力学及应用技术
郝文森(教授)
吕延防(博导教授)
付广(博导教授)
张云峰(博士副教授)
天然气地质学与油气保存条件研究
主要开展天然气运移路径及效率的物理模拟、盖层封油气机理、盖层封闭性及其演化、断层封闭机理及其评价、油气成藏系统及其演化、油气富集主控因素及油气富集区预测与评价的研究。
马世忠(博导教授)
刘吉余(博士教授)
柳成志(博士教授)
蒋明虎(博导教授)
王尊策(教授)
赵立新(博士)
旋流分离理论与应用技术
地面油水分离技术与应用、工业污水分离技术、井下油水分离技术。
刘巨保(教授)
李国义(副教授)
李崇志(副教授)
计算力学及应用技术
井下管柱力学与数值仿真、石油设备有限元分析
朱军(博士教授)
姜民政(副教授)
系统工程理论及节能技术
使用Matlab进行非线性系统辨识与控制的技巧
使用Matlab进行非线性系统辨识与控制的技巧在控制系统领域,非线性系统一直是研究的重点和难点之一。
与线性系统不同,非线性系统具有复杂的动力学特性和响应行为,给系统的建模、辨识和控制带来了挑战。
然而,随着计算机技术的快速发展,现在可以利用强大的软件工具如Matlab来进行非线性系统辨识与控制的研究。
本文将分享一些使用Matlab进行非线性系统辨识与控制的技巧,希望对相关研究人员有所帮助。
一、非线性系统辨识非线性系统辨识是指通过实验数据来确定系统的数学模型,以描述系统的动态行为。
在非线性系统辨识中,最常用的方法是基于系统响应的模型辨识技术。
这种方法通常包括以下几个步骤:1. 数据采集和预处理:首先,需要采集实验数据以用于系统辨识。
在数据采集过程中,应尽量减小噪声的影响,并确保数据的可靠性。
然后,对采集到的数据进行预处理,如滤波、采样等,以消除噪声和干扰。
2. 模型结构选择:在进行非线性系统辨识时,应选择合适的模型结构来描述系统的动态特性。
常见的模型结构包括非线性自回归移动平均模型(NARMA),广义回归神经网络(GRNN)等。
选择合适的模型结构对于准确地描述系统非线性特性至关重要。
3. 参数估计:根据选定的模型结构,使用最小二乘法或其他参数估计算法来估计模型的参数。
MATLAB提供了多种估计算法和工具箱,如系统辨识工具箱(System Identification Toolbox)等,可方便地进行参数估计。
4. 模型验证与评估:在参数估计完成后,应对辨识的模型进行验证和评估。
常用的方法是计算模型的均方根误差(RMSE)和决定系数(R-squared),进一步提高模型的准确性和可靠性。
二、非线性系统控制非线性系统控制是指通过设计控制策略来实现对非线性系统的稳定和性能要求。
与非线性系统辨识类似,非线性系统控制也可以利用Matlab进行研究和设计。
以下是一些常用的非线性系统控制技巧:1.反馈线性化控制:线性化是将非线性系统近似为线性系统的一种方法。
人工神经网络系统辨识综述
人工神经网络系统辨识综述摘要:当今社会,系统辨识技术的发展逐渐成熟,人工神经网络的系统辨识方法的应用也越来越多,遍及各个领域。
首先对神经网络系统辨识方法与经典辨识法进行对比,显示出其优越性,然后再通过对改进后的算法具体加以说明,最后展望了神经网络系统辨识法的发展方向。
关键词:神经网络;系统辨识;系统建模0引言随着社会的进步,越来越多的实际系统变成了具有不确定性的复杂系统,经典的系统辨识方法在这些系统中应用,体现出以下的不足:(1)在某些动态系统中,系统的输入常常无法保证,但是最小二乘法的系统辨识法一般要求输入信号已知,且变化较丰富。
(2)在线性系统中,传统的系统辨识方法比在非线性系统辨识效果要好。
(3)不能同时确定系统的结构与参数和往往得不到全局最优解,是传统辨识方法普遍存在的两个缺点。
随着科技的继续发展,基于神经网络的辨识与传统的辨识方法相比较具有以下几个特点:第一,可以省去系统机构建模这一步,不需要建立实际系统的辨识格式;其次,辨识的收敛速度仅依赖于与神经网络本身及其所采用的学习算法,所以可以对本质非线性系统进行辨识;最后可以通过调节神经网络连接权值达到让网络输出逼近系统输出的目的;作为实际系统的辨识模型,神经网络还可用于在线控制。
1神经网络系统辨识法1.1神经网络人工神经网络迅速发展于20世纪末,并广泛地应用于各个领域,尤其是在模式识别、信号处理、工程、专家系统、优化组合、机器人控制等方面。
随着神经网络理论本身以及相关理论和相关技术的不断发展,神经网络的应用定将更加深入。
神经网络,包括前向网络和递归动态网络,将确定某一非线性映射的问题转化为求解优化问题,有一种改进的系统辨识方法就是通过调整网络的权值矩阵来实现这一优化过程。
1.2辨识原理选择一种适合的神经网络模型来逼近实际系统是神经网络用于系统辨识的实质。
其辨识有模型、数据和误差准则三大要素。
系统辨识实际上是一个最优化问题,由辨识的目的与辨识算法的复杂性等因素决定其优化准则。
基于Hopfield神经网络的非线性系统故障估计方法
W a g an h n Zh s an,Zha g n Enln,Zh g u gua g ,Fe g an i an H a n n Ji
( c o l fI f r to ce c n g n e i g,No t e s e n Un v r i S h o n o ma i n S i n e a d En i e rn o r h a t r ie st y,S e y n h n a g,1 0 0 1 0 4,Ch n ) ia
f u t e tma i n p o l m o v r e o t es a i t r b e o h e u r n e r l e wo k .Th r — a l s i t r b e i c n e t d t h t b l y p o l m ft e r c r e t u a t r s o s i n n ep o
()= ()一 A ()一 ,( ()“ £)一 f f x £ , ()
B x() ( ) () g( t , £ ) f () 2
Y()= C £ £ x()+ Dg( , ) ( ) x() () £
令 参 数 的估 计值 为 () 则 含估 计 值 的方 () ,
ce l i h e r i g c p biiy a d s a lt he r f r c r e e a n t inty usng t e l a n n a a l n t biiy t o y o e u r nt n ur l e wor s, t p r me e t k he a a t r
J1 01 u .2 1
基于神经网络的伺服系统辨识与内模控制
下 M D 03 1 编码 器每转脉冲数为 250 4倍频 S A 8 D A; 0 , 反馈 , 到 编 码 器 每 转 脉 冲 数 为 1 0 。② 电 得 0 00 机控制 卡 : 采用 凌华P I 6 ③ 工控机 :et m1 C .1 。 83 Pn u i 1 1
K e r s: o ln a ;s se i e tf a in;h g p e n ih p e iin;n u a e r s y wo d n n i e r y tm d nii t c o ih s e d a d h g rcso e r ln two k
为获得高性能的运动控制伺服系统 , 首先需要确
13G z . H 。④ 附加惯性:.0 ga 1638k.m 。 为了使过程是可辨识的, 选择 M序列信号作为系 统辨识的输入信号 ]为避免信号失真 , , 且保证数据
一
定 的信噪比, 经试验确定输出幅值 a 300 输入信 = 0 ,
号为 : 1 0 和 一1 0 两种数值。通过输入正弦信 + 0 5 0 5
S se i n i c to n n e n lmo lc n r lo e v o t o y t m s y t m de tf a i n a d i t r a de o t o f s r o c n r ls s e i b s d o u a e r s a e n ne r ln two k
Wu a 30 4 C ia hn4 0 7 , o a s to e td t fS r o Co to y tms,t ep p rh sma es se i e t iainso sr c : c r i gt e fts aao e v nrlS se h a e a d y tm d n ic t f o f poiiea d i v remo e a e n n ua e r s n n ls si e t iain rs l a d p t owa d p si stv n n es d lb s d o e rln twok ,a d a ay e d ni c to e u t n usfr r o s— f b e s h me t e lz g p e n g r cso to l c e o r aie Hih S e d a d Hih P e iin Moin.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于神经网络的非线性系统辨识随着人工智能技术的不断发展,神经网络技术成为人工智能领域中
一个重要的研究方向。
神经网络具有自主学习、自适应和非线性等特点,因此在实际应用中有很大潜力。
本文将介绍神经网络在非线性系
统辨识中的应用。
一、什么是非线性系统辨识?
非线性系统辨识是指对一些非线性系统进行建模与识别,通过参数
估计找到最佳的系统模型以进行预测分析和控制。
在许多实际应用中,非线性系统是比较常见的,因此非线性系统辨识技术的研究和应用具
有重要的意义。
二、神经网络在非线性系统辨识中的应用
神经网络在非线性系统辨识中具有很好的应用效果。
其主要原因是
神经网络具有强大的非线性建模和逼近能力。
常用的神经网络模型包
括前馈神经网络、递归神经网络和卷积神经网络等。
下面主要介绍前
馈神经网络在非线性系统辨识中的应用。
1. 神经网络模型建立
前馈神经网络由输入层、隐含层和输出层组成。
在非线性系统辨识中,输入层由外部输入量组成,隐含层用于提取输入量之间的非线性
关系,输出层则用于输出系统的状态变量或输出变量。
模型建立的关
键是隐含层神经元的个数和激活函数的选取。
2. 系统建模
在非线性系统的建模过程中,需要将输出变量与输入变量之间的非线性关系进行建立。
可以使用最小二乘法、最小均方误差法等方法,对神经网络进行训练和学习,在一定的误差范围内拟合系统模型。
此外,也可以使用遗传算法、粒子群算法等优化算法来寻找最优的神经网络参数。
3. 系统预测和控制
在系统建模和参数估计后,神经网络可以用于非线性系统的预测和控制。
在预测过程中,将系统的状态量输入前馈神经网络中,通过输出层的计算得到系统的输出量。
在控制过程中,将前馈神经网络与控制器相结合,在控制对象输出量和期望值不同时,自动调节控制器参数的值来实现系统的控制。
三、神经网络在非线性系统辨识中的优势和挑战
与传统的线性系统模型相比,神经网络模型可以更好地描述非线性系统,并且可以用于对于非线性系统的建模和控制。
但是,在实际应用中,神经网络模型的设计和参数调节都需要大量的实验操作,而且面临着过拟合和欠拟合等问题。
四、结论
基于神经网络的非线性系统辨识是一项非常重要的研究技术。
在实际应用中,神经网络能够很好地进行非线性系统的建模和控制,具有
广泛的应用前景和研究价值。
未来,如何进一步提高神经网络的建模和预测能力,将会是非线性系统辨识研究的重点。
