五年级下册数学奥数题(含答案)-小学五年级奥数题大全及答案(更新版)-通用版
五年级下册数学奥数题及答案

五年级下册数学奥数题及答案一、选择题1.下列数中,哪一个不能整除30? A. 5 B. 6 C. 10 D. 15答案:A2.小明买了3双袜子,每双袜子花费5元,他还剩下多少元? A. 10 B.12 C. 15 D. 18答案:C3.一个长方形的长是8cm,宽是4cm,它的面积是多少平方厘米? A.16 B. 20 C. 30 D. 32答案:D4.下列数字中,哪一个是奇数? A. 10 B. 15 C. 20 D. 24答案:B5.如果一个三角形的三条边长度分别是3cm、4cm和5cm,那么它是什么三角形? A. 等边三角形 B. 直角三角形 C. 锐角三角形 D. 钝角三角形答案:B二、填空题1. 5 × 6 = ____ 答案:302.下列数字中,最小的是____ 答案:03.7 ÷ 2 = ____ 答案:3.54. 2 + 4 × 3 = ____ 答案:145.12 ÷ 3 = ____ 答案:4三、解答题1. 计算题小明在商场购买了两本数学书,每本书的价格分别是35元和20元。
他付给售货员一张50元的钞票,请问他应该找给小明多少零钱?解答:两本书的总价格:35元+ 20元= 55元小明给了售货员50元的钞票,所以需要找给小明的零钱是:50元- 55元= -5元小明应该还需要给售货员5元。
2. 推理题一辆汽车前进了200公里,然后返回原点,再往前走100公里,最后又返回原点。
请问汽车最终所在的位置与原点的位置相比,是在原点的左边还是右边?解答:汽车前进了200公里,然后返回原点,所以汽车回到了原点。
再往前走100公里,又返回原点,所以汽车依然在原点。
因此,汽车最终所在的位置与原点的位置重合,即汽车最终位置与原点相同。
四、总结本文列出了五年级下册数学奥数题及答案。
选择题包括了求除数、数字判断、图形面积、奇偶数、三角形分类等题型。
填空题涵盖了乘法、最小数、除法以及复杂的运算顺序。
人教版【精选】小学五年级下册数学奥数题带答案

人教版【精选】小学五年级下册数学奥数题带答案一、拓展提优试题1.如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.2.松鼠A、B、C共有松果若干,松鼠A原有松果26颗,从中拿出10颗平分给B、C,然后松鼠B拿出自己的18颗松果平均分给A、C,最后松鼠C把自己现有松果的一半平分给A、B,此时3只松鼠的松果数量相同,则松鼠C原有松果颗.3.如图,若长方形S长方形ABCD=60平方米,S长方形XYZR=4平方米,则四边形S四边=平方米.形EFGH4.李双骑车以320米分钟的速度从A地驶向B地,途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车,15分钟后以原来骑车速度的1.5倍继续向前驶向B地,到达B地时,比预计时间多用17分钟,则李双推车步行的速度是米/分钟.5.解放军战士在洪水不断冲毁大坝的过程中要修好大坝,若10人需45分钟,20人需要20分钟,则14人修好大坝需分钟.6.四位数的所有因数中,有3个是质数,其它39个不是质数.那么,四位数有个因数.7.对于自然数N,如果1﹣9这九个自然数中至少有六个数可以整除N,则称N是一个“六合数”,则在大于2000的自然数中,最小的“六合数”是.8.一次数学竞赛中,某小组10个人的平均分是84分,其中小明得93分,则其他9个人的平均分是分.9.两个数的最大公约数和最小公倍数分别是3和135,求这两个数的差最小是.10.(15分)甲、乙两船顺流每小时行8千米,逆流每小时行4千米,若甲船顺流而下,然后返回;乙船逆流而上,然后返回,两船同时出发,经过3小时同时回到各自的出发点,在这3小时中有多长时间甲、乙两船同向航行?11.如图,在梯形ABCD中,若AB=8,DC=10,S△AMD=10,S△BCM=15,则梯形ABCD的面积是.12.(8分)有一个特殊的计算器,当输入一个数后,计算器先将这个数乘以3,然后将其结果是数字逆序排列,接着再加2后显示最后的结果,小明输入了一个四位数后,显示结果是2015,那么小明输入的四位数是.13.定义新运算:θa=,则(θ3)+(θ5)+(θ7)(+θ9)+(θ11)的计算结果化成最简真分数后,分子与分母的和是.14.如图六角星的6个顶点恰好是一个正六边形的6个顶点,那么阴影部分面积是空白部分面积的倍.15.小明准备和面包饺子,他在1.5千克面粉中加入了5千克的水,发现面和得太稀了,奶奶告诉他,包饺子的面需要按照3份面,2份水和面,于是小明分三次加入相同分量的面粉,终于将面按按要求和好了,那么他每次加入了千克面粉.16.(8分)小胖把这个月的工资都用来买了一支股票.第一天该股票价格上涨,第二天下跌,第三天上涨,第四天下跌,此时他的股票价值刚好5000元,那么小胖这个月的工资是元.17.A、B两桶水同样重,若从A桶中倒2.5千克水到B桶中,则B桶中水的重量是A桶中水的重量的6倍,那么B桶中原来有水千克.18.同学们去春游,带水壶的有80人,带水果的有70人,两样都没带的有6人.若既带水壶又带水果的人数是所有参加春游人数的一半,则参加春游的同学共有人.19.如图,在△ABC中,D、E分别是AB、AC的中点,且图中两个阴影部分(甲和乙)的面积差是5.04,则S△ABC=.20.从1、2、3、4、5中任取3个组成一个三位数,其中不能被3整除的三位数有个.21.有白球和红球共300个,纸盒100个.每个纸盒里都放3个球,其中放1个白球的纸盒有27个,放2个或3个红球的纸盒共有42个,放3个白球和3个红球的纸盒数量相同.那么,白球共有个.22.如图所示,P为平行四边形ABDC外一点。
【强烈推荐】小学五年级奥数题100题(附答案)

【强烈推荐】小学五年级奥数题100题(附答案)五年级奥数题100题(附答案)1.765×213÷27+765×327÷27解:原式=765÷27×(213+327)= 765÷27×540=765×20=153002.(9999+9997+...+9001)-(1+3+ (999)解:原式=(9999-999)+(9997-997)+(9995-995)+……+(9001-1)=9000+9000+…….+9000(500个9000)=45000003.19xx19xx×19x x19xx-19xx19xx×19xx19xx解:(19xx19xx+1)×19xx19xx-19xx19xx×19xx19xx=19xx19xx×19xx19xx-19xx19xx×19xx19xx+19xx19xx=19xx19xx-19xx19xx=100004.(873×477-198)÷(476×874+199)解:873×477-198=476×874+199因此原式=15.20xx×19xx-19xx×19xx+19xx×19xx-19xx×1996+…+2×1解:原式=19xx×(20xx-19xx)+19xx×(19xx-1996)+…+3×(4-2)+2×1=(19xx+19xx+…+3+1)×2=20xx000。
6.297+293+289+…+209解:(209+297)*23/2=58197.计算:解:原式=(3/2)*(4/3)*(5/4)*…*(100/99)*(1/2)*(2/3)*(3/4)*…*(98/99)=50*(1/99)=50/998.解:原式=(1*2*3)/(2*3*4)=1/49.有7个数;它们的平均数是18。
人教版【精选】小学五年级下册数学奥数题带答案图文百度文库

人教版【精选】小学五年级下册数学奥数题带答案图文百度文库一、拓展提优试题1.如图,7×7的表格中,每格填入一个数字,使得相同的数字所在的方格都连在一起(相连的两个方格必须有公共边),现在已经给出了1,2,3,4,5各两个,那么,表格中所有数的和是.12533421542.(15分)如图,正六边形ABCDEF的面积为1222,K、M、N分别AB,CD,EF的中点,那么三角形PQR的边长是.3.(15分)一个自然数恰有9个互不相同的约数,其中3个约数A,B,C满足:①A+B+C=79②A×A=B×C那么,这个自然数是.4.幼儿园给小朋友派礼物,如果有2人各派4个,其余各派3个,则还剩余11个,如果4人各派3个,其余各派6个,则剩余10个,问一共有多少件礼物?5.请从1、2、3、…、9、10中选出若干个数,使得1、2、3、…、19、20这20个数中的每个数都等于某个选出的数或某两个选出的数(可以相等)的和.那么,至少需要选出个数.6.(8分)有四个人甲、乙、丙、丁,乙欠甲1元,丙欠乙2元,丁欠丙3元,甲欠丁4元.要想把他们之间的欠款结清,只因要甲拿出元.7.三位偶数A、B、C、D、E满足A<B<C<D<E,若A+B+C+D+E=4306,则A最小.8.某商店的同种点心有大小两种包装礼盒,大盒85.6元一盒,内有点心32块,小盒46.8元一盒,内有点心15块,若王雷用654元买了9盒点心,则他可得点心块.9.两个数的最大公约数和最小公倍数分别是3和135,求这两个数的差最小是.10.对于自然数N,如果1﹣9这九个自然数中至少有六个数可以整除N,则称N是一个“六合数”,则在大于2000的自然数中,最小的“六合数”是.11.(8分)一个大于1的正整数加1能被2整除,加2能被3整除,加3能被4整除,加4能被5整除,这个正整数最小是.12.如图是一个正方体的平面展开图,若该正方体相对的两个面上的数值相等,则a﹣b×c的值是.13.如图,在△ABC中,D、E分别是AB、AC的中点,且图中两个阴影部分(甲和乙)的面积差是5.04,则S=.△ABC14.(7分)如图,按此规律,图4中的小方块应为个.15.(7分)对于a、b,定义运算“@”为:a@b=(a+5)×b,若x@1.3=11.05,则x=.【参考答案】一、拓展提优试题1.解:首先理解题目,找出唯一填法的空格,例如第一行第一个1,与其唯一相邻的空白空格必须为1,以此类推,第二行第一个5也具有唯一相邻空格.逆推得出唯一图形.相加求和为150.故答案为150.2.解:如图延长BA和EF交于点O,并连接AE,由正六边形的性质,我们可知S ABCM=S CDEN=S EF AK=六边形面积,根据容斥原理,重叠部分三个三角形面积和等于阴影部分面积,且因为对称,△AKP,△CMQ,△ENR三个三角形是一样的,有KP=RN,AP=ER,RP=PQ,=,则=,=,由鸟头定理可知道3×KP×AP=RP×PQ,综上可得:PR=2KP=RE,那么由三角形AEK是六边形面积的,且S△APK ,=S△AKES△APK=S ABCDEF=47,所以阴影面积为47×3=141故答案为141.3.解:一个自然数N恰有9个互不相同的约数,则可得N=x2y2,或者N=x8,(1)当N=x8,则九个约数分别是:1,x,x2,x3,x4,x5,x6,x7,x8,其中有3个约数A、B、C且满足A×A=B×C,不可能.(2)当N=x2y2,则九个约数分别是:1,x,y,x2,xy,y2,x2y,xy2,x2y2,其中有3个约数A、B、C且满足A×A=B×C,①A=x,B=1,C=x2,则x+1+x2=79,无解.②A=xy,B=1,C=x2y2,则xy+1+x2y2=79,无解.③A=xy,B=x,C=xy2,则xy+x+xy2=79,无解.④A=xy,B=x2,C=y2,则xy+x2+y2=79,解得:,则N=32×72=441.⑤A=x2y,B=x2y2,C=x2,则x2y+x2y2+x2=79,无解.故答案为441.4.【分析】假设第一次每人都派3个,则还剩余2×(4﹣3)+11=13个,第二次如每人都派6个,同时少了4×(6﹣3)﹣10=2个,就是每人多派6﹣3=3个,则需要13+2=15个礼物,据此可求出人数,进而可求出礼物数.解:[2×(4﹣3)+11+4×(6﹣3)﹣10]÷(6﹣3)=[2×1+11+4×3﹣10]÷3=[2+11+12﹣10]÷3=15÷3=5(人)2×4+(5﹣2)×3+11=8+3×3+11=8+9+11=28(件)答:一共有28件礼物.5.解:列举如下:1=1;2=2;3=1+2;4=2+2;5=5;6=1+5;7=2+5;8=8;9=9;10=10;11=1+10;12=2+10;13=5+8;14=7+7;15=5+10;16=8+8;17=8+9;18=8+10;19=9+10;通过观察,可看出从1、2、3、…、9、10中选出若干个数分别为{1,2,5,8,9,10};就能使得1、2、3、…、19、20这20个数中的每个数都等于某个选出的数或某两个选出的数(可以相等)的和.故至少需要选出6个数.故答案为6.6.解:根据分析,从甲开始,乙欠甲1元,故甲应得1元,甲欠丁4元,故甲应还4元;清算时,甲还应拿出4﹣1=3元,此时甲的账就结清了;再看看丁的账,丁得到甲的4元后,还给丙3元,即可结清;再看看丙的账,丙得到丁的3元后,还给乙2元,丙的账也清了;再看看乙的账,乙得到丙的2元后,还给甲1元,乙的账也结清;综上,甲只须先拿出4元还给丁,后得到乙的1元,故而甲总共只须拿出3元.故答案是:3.7.解:最大的三位偶数是998,要满足A最小且A<B<C<D<E,则E最大是998,D最大是996,C最大是994,B最大是992,4306﹣(998+996+994+992)=4306﹣3980=326,所以此时A最小是326.故答案为:326.8.设大合x盒,小盒y盒,依题意有方程:85.6x+46.8(9﹣x)=654解方程得x=6,9﹣6=3.所以大合6盒,小盒3盒,共有32×6+15×3=237块.答:可得点心237块.9.解:因为135÷3=45,45分解成两个互质的数有两种情况即1和45、9与5,所以差最小的是:9和5,所以这两个数分别是:9×3=275×3=1527﹣15=12答:这两个数的差最小是12.故答案为:12.10.解:依题意可知:要满足是六合数.分为是3的倍数和不是3的倍数.如果不是3的倍数那么一定是1,2,4,8,5,7的倍数,那么他们的最小公倍数为:8×5×7=280.那么280的倍数大于2000的最小的数字是2240.如果是3的倍数.同时满足是1,2,3,6的倍数.再满足2个数字即可.大于2000的最小是2004(1,2,3,4,6倍数)不符合题意;2010是(1,2,3,5,6倍数)不符合题意;2016是(1,2,3,4,6,7,8,9倍数)满足题意.2016<2240;故答案为:201611.解:根据分析:这个数除以2,3,4,5均余1,那么这个数减去1后就能同时被2,3,4,5整除;2,3,4,5的最小公倍数是60,则这个数为60的倍数加1.又因为这个数大于1,所以这个数最小是61.故答案为:61.12.解:依题意可知:3a+2与17是对立面,3a+2=17,所以a=5;7b﹣4与10是对立面,7b﹣4=10,所以b=2;a+3b﹣2c与11的对立面,5+3×2﹣2c=11,所以c=0;所以a﹣b×c=5故答案为:513.解:根据分析,S△BDC=S△EBC⇒S△DOB=S△EOC,∴S甲﹣S乙=(S甲+S△DOB)﹣(S乙+S△EOC)=5.04,又∵S△BDC :S△DEC=BC:DE=2:1即:S△BDC=2S△DEC∴S四边形DECB =3S△DEC;S△ADE=S△DEC∴S△ABC =S四边形DECB+S△ADE=4S△DEC,设S△DEC =X,则S△BDC=2X,故有2X﹣X=5.04,∴X=5.04,S△ABC =4S△DEC=4X=4×5.04=20.16故答案是:20.1614.解:因为图1中小方块的个数为1+2×3=7个,图2中小方块的个数为1+(1+2)+3×4=16个,图3中小方块的个数为1+(1+2)+(1+2+3)+4×5=30个,所以图4中小方块的个数为1+(1+2)+(1+2+3)+(1+2+3+4)+5×6=50个,故答案为:50.15.解:由定义可知:x@1.3=11.05,(x+5)1.3=11.05,x+5=8.5,x=8.5﹣5=3.5故答案为:3.5。
苏教版小学五年级下册数学奥数题带答案图文百度文库
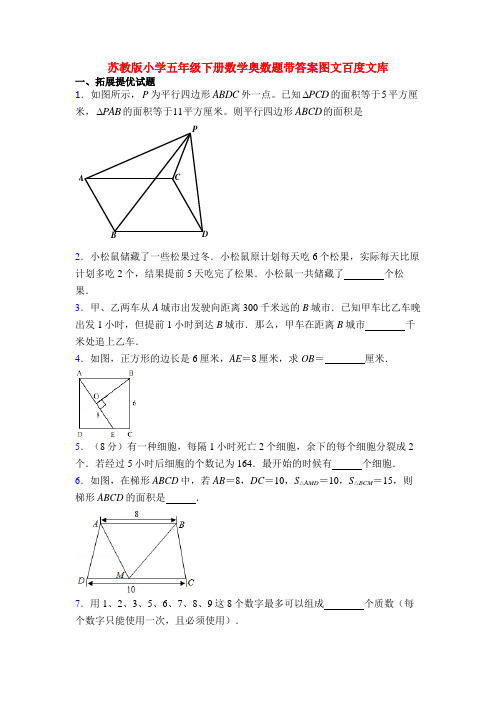
苏教版小学五年级下册数学奥数题带答案图文百度文库一、拓展提优试题1.如图所示,P为平行四边形ABDC外一点。
已知PCD∆的面积等于5平方厘米,PAB∆的面积等于11平方厘米。
则平行四边形ABCD的面积是CADBP2.小松鼠储藏了一些松果过冬.小松鼠原计划每天吃6个松果,实际每天比原计划多吃2个,结果提前5天吃完了松果.小松鼠一共储藏了个松果.3.甲、乙两车从A城市出发驶向距离300千米远的B城市.已知甲车比乙车晚出发1小时,但提前1小时到达B城市.那么,甲车在距离B城市千米处追上乙车.4.如图,正方形的边长是6厘米,AE=8厘米,求OB=厘米.5.(8分)有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.若经过5小时后细胞的个数记为164.最开始的时候有个细胞.6.如图,在梯形ABCD中,若AB=8,DC=10,S△AMD=10,S△BCM=15,则梯形ABCD的面积是.7.用1、2、3、5、6、7、8、9这8个数字最多可以组成个质数(每个数字只能使用一次,且必须使用).8.大于0的自然数n是3的倍数,3n是5的倍数,则n的最小值是.9.如果2头牛可以换42只羊,3只羊可以换26只兔,2只兔可以换3只鸡,则3头牛可以换多少只鸡?10.(15分)甲、乙两船顺流每小时行8千米,逆流每小时行4千米,若甲船顺流而下,然后返回;乙船逆流而上,然后返回,两船同时出发,经过3小时同时回到各自的出发点,在这3小时中有多长时间甲、乙两船同向航行?11.如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.12.定义新运算:θa=,则(θ3)+(θ5)+(θ7)(+θ9)+(θ11)的计算结果化成最简真分数后,分子与分母的和是.13.小明准备和面包饺子,他在1.5千克面粉中加入了5千克的水,发现面和得太稀了,奶奶告诉他,包饺子的面需要按照3份面,2份水和面,于是小明分三次加入相同分量的面粉,终于将面按按要求和好了,那么他每次加入了千克面粉.14.如图,在△ABC中,D、E分别是AB、AC的中点,且图中两个阴影部分=.(甲和乙)的面积差是5.04,则S△ABC15.某场考试共有7道题,每道题问的问题都只与这7道题的答案有关,且答案只能是1、2、3、4中的一个.已知题目如下:①有几道题的答案是4?②有几道题的答案不是2也不是3?③第⑤题和第⑥题的答案的平均数是多少?④第①题和第②题的答案的差是多少?⑤第①题和第⑦题的答案的和是多少?⑥第几题是第一个答案为2的?⑦有几种答案只是一道题的答案?那么,7道题的答案的总和是 .【参考答案】一、拓展提优试题1.12[解答]作PF AB ⊥,由于//AB DC ,所以PF CD ⊥。
小学五年级奥数题30道(附答案)

小学五年级奥数题30道(附答案)在小学五年级学习奥数的过程中,练习题是非常重要的。
通过解答奥数题,可以增强逻辑思维能力、提升解决问题的能力。
下面给大家分享30道小学五年级奥数题,并附上详细的解答,帮助大家更好地理解和掌握解题技巧。
题目1:小明有5块巧克力,小红有3块巧克力,他们一共有多少块巧克力?解答1:小明有5块,小红有3块,所以总共有5+3=8块巧克力。
题目2:5艘船将100个水桶分给海盗们,每艘船上都要有相同数量的水桶,问每艘船上装了多少个水桶?解答2:要将100个水桶平均分给5艘船,所以每艘船上装了100÷5=20个水桶。
题目3:有一辆公交车上有18个座位,现在已经有10个人上车了,还有多少个座位空着?解答3:公交车上一共有18个座位,已经有10个人上车了,空着的座位数为18-10=8个。
题目4:一年有365天,这些天分成几个星期和几天?解答4:一周有7天,所以365天可以分成52个星期和1天。
题目5:小明和小红共有50颗糖果,小明比小红多15颗,小红有多少颗糖果?解答5:小明比小红多15颗,小明和小红共有50颗,所以小红有50-15=35颗糖果。
题目6:一个矩形的长是5米,宽是3米,这个矩形的面积是多少平方米?解答6:矩形的面积可以通过长乘以宽计算,所以这个矩形的面积为5×3=15平方米。
题目7:一个正方形的边长是8厘米,这个正方形的周长是多少厘米?解答7:正方形的周长可以通过边长乘以4计算,所以这个正方形的周长为8×4=32厘米。
题目8:有40个苹果,每个篮子装8个苹果,问最多可以装多少个篮子?解答8:如果每个篮子装8个苹果,那么40个苹果可以装40÷8=5个篮子。
题目9:某商店的西瓜每公斤4元,小明买了3.5公斤的西瓜,他应该付多少钱?解答9:小明买了3.5公斤的西瓜,每公斤4元,所以他应该付3.5×4=14元。
题目10:一个三角形的底是6厘米,高是4厘米,这个三角形的面积是多少平方厘米?解答10:三角形的面积可以通过底乘以高再除以2计算,所以这个三角形的面积为6×4÷2=12平方厘米。
(完整版)五年级奥数题100题(附答案)
五年级奥数题100题(附答案)1. 765×213÷27+765×327÷27解:原式=765÷27×(213+327)= 765÷27×540=765×20=153002. (9999+9997+...+9001)-(1+3+ (999)解:原式=(9999-999)+(9997-997)+(9995-995)+……+(9001-1) =9000+9000+…….+9000 (500个9000)=45000003.19981999×19991998-19981998×19991999解:(19981998+1)×19991998-19981998×19991999=19981998×19991998-19981998×19991999+19991998=19991998-19981998=100004.(873×477-198)÷(476×874+199)解:873×477-198=476×874+199因此原式=15.2000×1999-1999×1998+1998×1997-1997×1996+…+2×1解:原式=1999×(2000-1998)+1997×(1998-1996)+…+3×(4-2)+2×1=(1999+1997+…+3+1)×2=2000000。
6.297+293+289+…+209解:(209+297)*23/2=58197.计算:解:原式=(3/2)*(4/3)*(5/4)*…*(100/99)*(1/2)*(2/3)*(3/4)*…*(98/99)=50*(1/99)=50/998.解:原式=(1*2*3)/(2*3*4)=1/49.有7个数,它们的平均数是18。
小学数学五年级下册《奥数题》练习(共五大类,含答案解析)
五年级数学下册奥数题练习班级考号姓名总分一、排列组合问题1、有五对夫妇围成一圈,使每一对夫妇的夫妻二人都相邻的排法有( )A、768种B、32种C、24种D、2的10次方种2、若把英语单词hello的字母写错了,则可能出现的错误共有( )A、119种B、36种C、59种D、48种二、容斥原理问题1、有100种赤贫.其中含钙的有68种,含铁的有43种,那么,同时含钙和铁的食品种类的最大值和最小值分别是( )A、43,25B、32,25C、32,15D、43,112、在多元智能大赛的决赛中只有三道题。
已知:(1)某校25名学生参加竞赛,每个学生至少解出一道题;(2)在所有没有解出第一题的学生中,解出第二题的人数是解出第三题的人数的2倍;(3)只解出第一题的学生比余下的学生中解出第一题的人数多1人;(4)只解出一道题的学生中,有一半没有解出第一题,那么只解出第二题的学生人数是( )A、5B、6C、7D、83、一次考试共有5道试题。
做对第1、2、3、4、5题的分别占参加考试人数的95%、80%、79%、74%、85%。
如果做对三道或三道以上为合格,那么这次考试的合格率至少是多少?三、抽屉原理、奇偶性问题1、一只布袋中装有大小相同但颜色不同的手套,颜色有黑、红、蓝、黄四种,问最少要摸出几只手套才能保证有3副同色的?2、有四种颜色的积木若干,每人可任取1-2件,至少有几个人去取,才能保证有3人能取得完全一样?3、某盒子内装50只球,其中10只是红色,10只是绿色,10只是黄色,10只是蓝色,其余是白球和黑球,为了确保取出的球中至少包含有7只同色的球,问:最少必须从袋中取出多少只球?4、地上有四堆石子,石子数分别是1、9、15、31如果每次从其中的三堆同时各取出1个,然后都放入第四堆中,那么,能否经过若干次操作,使得这四堆石子的个数都相同?(如果能请说明具体操作,不能则要说明理由)四、路程问题1、狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。
五年级下册奥数应用题100道及答案解析
五年级下册奥数应用题100道及答案解析1. 有一块长方形草地,长18 米,宽12 米,在它的四周每隔3 米种一棵桃树,一共要种多少棵桃树?答案:20 棵解析:长方形草地的周长为:(18 + 12)×2 = 60(米),每隔3 米种一棵桃树,所以共种60 ÷3 = 20(棵)2. 一辆汽车从甲地开往乙地,每小时行60 千米,5 小时到达。
若要4 小时到达,则每小时需要多行多少千米?答案:15 千米解析:甲乙两地的距离为60×5 = 300(千米),若 4 小时到达,速度应为300÷4 = 75(千米/小时),每小时多行75 - 60 = 15(千米)3. 小明买5 本日记本比买1 本故事书多用5.8 元,已知一本故事书的价钱正好是一本日记本价钱的3 倍。
一本日记本的价钱是多少元?答案:2.9 元解析:设一本日记本的价钱为x 元,则一本故事书的价钱为3x 元。
5x - 3x = 5.8,2x = 5.8,x = 2.94. 某工厂有一堆煤,如果每天烧2.5 吨,可以烧30 天,如果每天节约0.5 吨,可以多烧多少天?答案:6 天解析:煤的总量为2.5×30 = 75(吨),每天节约0.5 吨,每天烧2.5 - 0.5 = 2(吨),可以烧75÷2 = 37.5(天),多烧37.5 - 30 = 7.5 天,约为6 天5. 学校买来8 张办公桌和6 把椅子,共花去1650 元。
每张办公桌的价钱是每把椅子的2 倍,每张办公桌和每把椅子各多少元?答案:办公桌150 元,椅子75 元解析:设每把椅子的价钱为x 元,则每张办公桌的价钱为2x 元。
8×2x + 6x = 1650,22x = 1650,x = 75,2x = 1506. 甲乙两车同时从相距480 千米的两地相对而行,甲车每小时行45 千米,途中因汽车故障甲车停了1 小时,5 小时后两车相遇。
小学五年级奥数题及答案大全
小学五年级奥数题及答案大全奥数对很多人说都是数学的噩梦,但它确实最能体现你的数学能力。
下面由店铺给你带来关于小学五年级奥数题及答案大全,希望对你有帮助!小学五年级奥数题及答案大全一51. 一副扑克牌共54张,最上面的一张是红桃K。
如果每次把最上面的12张牌移到最下面而不改变它们的顺序及朝向,那么,至少经过多少次移动,红桃K才会又出现在最上面?解:因为[54,12]=108,所以每移动108张牌,又回到原来的状况。
又因为每次移动12张牌,所以至少移动108÷12=9(次)。
52. 爷爷对小明说:“我现在的年龄是你的7倍,过几年是你的6倍,再过若干年就分别是你的5倍、4倍、3倍、2倍。
”你知道爷爷和小明现在的年龄吗?解:爷爷70岁,小明10岁。
提示:爷爷和小明的年龄差是6,5,4,3,2的公倍数,又考虑到年龄的实际情况,取公倍数中最小的。
(60岁)53. 某质数加6或减6得到的数仍是质数,在50以内你能找出几个这样的质数?并将它们写出来。
解:11,13,17,23,37,47。
54. 在放暑假的8月份,小明有五天是在姥姥家过的。
这五天的日期除一天是合数外,其它四天的日期都是质数。
这四个质数分别是这个合数减去1,这个合数加上1,这个合数乘上2减去1,这个合数乘上2加上1。
问:小明是哪几天在姥姥家住的?解:设这个合数为a,则四个质数分别为(a-1),(a+1),(2a-1),(2a+1)。
因为(a-1)与(a+1)是相差2的质数,在1~31中有五组:3,5;5,7;11,13;17,19;21,31。
经试算,只有当a=6时,满足题意,所以这五天是8月5,6,7,11,13日。
55. 有两个整数,它们的和恰好是两个数字相同的两位数,它们的乘积恰好是三个数字相同的三位数。
求这两个整数。
解:3,74;18,37。
提示:三个数字相同的三位数必有因数111。
因为111=3×37,所以这两个整数中有一个是37的倍数(只能是37或74),另一个是3的倍数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级下册数学奥数题(含答案) 小学五
年级奥数题大全及答案(更新版)-通用版
1、一块草地,可以供24匹马吃6天,20匹马吃10天。
问12天时多少匹马可以吃尽这块草地?
假设草地单位为“1”,所以24*6=144,20*10=200.因此每
天草地长草14个单位“1”。
200-14*10=60,因此草地原有草60个单位"1"。
所以,60/12+14=19,即19匹马12天可以吃尽这块草地。
2、一块草地,可以供5只羊吃40天,6只羊吃30天。
如果4只羊吃30天后又增加2只羊一起吃,那么这块草地还
可以再吃多少天?
同理,40*5=200,30*6=180.因此每天草地长草2个单位“1”。
200-2*40=120是原有草。
120-(4-2)*30=60是剩余草。
因此,60/(6+2)=7.5,即再吃7.5天。
3、每小时有3000人到书店买书。
如果设一个售书口,每分钟可以让50人买完离开;如果设2个售书口,1小时后就
没有人排队了。
那么如果设4个口,多长时间后就没有人排队了?
每分钟有3000/60=50人来买书。
如果设一个售书口,每分钟可以卖出50本书。
因此,每分钟的人数和卖出的书数相等,不会有排队。
如果设2个售书口,每分钟可以卖出100本书。
因此,每分钟有50人来买书,需要排队等待。
但是,2个售书口可以同时处理,所以不会有排队。
同理,如果设4个售书口,每分钟可以卖出200本书。
因此,每分钟有100人来买书,需要排队等待。
但是,4个售书口可以同时处理,所以不会有排队。
4、一口井,用3部抽水机40分钟可以抽干;6部抽水机16分钟可以抽干。
那么5部同样的抽水机,多少分钟可以抽干?
设5部抽水机可以在x分钟内抽干这口井。
则有
3*40=6*16,即120=96.
因此,每分钟5部抽水机可以抽干的水量为120/5=24.所以,用5部抽水机抽干这口井需要24x的时间。
又因为6部抽水机可以在16分钟内抽干,每分钟抽干的水量为120/16=7.5.因此,5部抽水机每分钟可以抽干的水量为7.5*5/6=6.25.
所以,24x=120,即x=5,用5部抽水机可以在5分钟内抽干这口井。
5、一个水池,池内除原有的水外,每天都流入同样多的水。
如果用池中的水每天浇50亩地,10天用完;如果每天浇45亩地,20天用完。
那么,用这些水浇多少亩地,正好可用25天?
设每天流入的水量为x,池中原有的水量为y。
则
10x+y=50*10,20x+y=45*20.解得x=5,y=50.
因此,用这些水浇25天的水量为25*5=125.即用这些水可以浇125亩地。
6、一个大水坑,每分钟从四周流掉一定数量的水。
如果用5台水泵,6小时抽干;用10台,4小时抽干。
现在要2小时抽干,要多少水泵?
设用n台水泵可以在2小时内抽干这个大水坑。
则有
5*6=10*4,即30=40.
因此,每分钟5台水泵可以抽干的水量为30/(5*60)
=0.1,每分钟10台水泵可以抽干的水量为40/(10*60)
=0.067.
所以,n*2=0.1*2*60+n*0.067*2*60,解得n=15,需要15
台水泵。
7、仓库装满水泥时,可用30天。
现在仓库是空的,用大车运水泥,除每天供工地使用外,要装5天才可装满;用小车,除每天供工地使用外,要装10天才可装满。
如果大车小车一
起用,除每天供工地使用外,要装几天才可装满?
设用大车和小车一起装满仓库需要x天。
则有5(1/5+1/x)=1,10(1/10+1/x)=1.解得x=7.5.
因此,大车小车一起用需要7.5天才能将仓库装满。
8、甲、乙、丙、丁四人加工同样的零件,甲先加工了一
段时间,然后乙、丙、丁三人一起参加加工,6小时后乙和甲
加工的一样多;9小时后丙和甲加工的一样多,12小时后丁和甲加工的一样多。
又知乙每小时加工27个零件,丙每小时加
工23个零件。
那么,丁每小时加工零件多少个?
设甲先加工了t小时,因此乙、丙、丁三人一起参加加工的时间为6-t小时。
设乙、丙、丁三人一起加工的效率为x。
则有:
t+6-x(6-t)=27(6-t)。
t+9-x(9-t)=23(9-t)。
t+12-x(12-t)=x(12-t)。
解得x=3,t=3.
因此,丁每小时加工零件数为x+23=26.
设父亲和儿子的现在年龄分别为x和y,则:
15年前,父亲的年龄为x-15,儿子的年龄为y-15,且x-15=7(y-15);
十年后,父亲的年龄为x+10,儿子的年龄为y+10,且
x+10=2(y+10)。
解以上方程组,得到x=70,y=15,因此父亲现在70岁,儿子现在15岁。
二。
设父亲和儿子的年龄差为d,则:
15年前,父亲的年龄是儿子的7倍,即d-15=6(7d-15),解得d=9;
十年后,父亲的年龄是儿子的2倍,即d+10=2(2d+10),解得d=20.
因此,父亲现在年龄为29岁,儿子现在年龄为9岁。
本文介绍了一道数学问题——差倍问题,并通过画图和列方程的方式进行了分析和解答。
在图中,黑色线段表示父亲和儿子15年前的年龄,当时父亲是儿子的7倍。
经过25年后,父亲是儿子的2倍。
通过观察图形可以发现,绿色分界线前后的线段相等,都等于原来儿子的年龄加上25,而25年等于原来儿子的5倍。
因此,可以得出儿子原来的年龄为5岁,今年为20岁;父亲原来的年龄为35岁,今年为50岁。
为了更直观地解答问题,我们还可以列方程。
假设儿子今年X岁,则儿子15年前为(X-15),10年后为X+10.父亲15年前为(X-15)×7,今年为(X-15)×7+15.根据10年后的条件,可以列出方程(X+10)×2=(X-15)×7+15+10,进一步解得X=20岁。
因此,父亲今年50岁。
通过以上两种方法,我们都得出了相同的答案,解决了这道差倍问题。
