高精度差分格式及可压缩湍流数值模拟(一)
cfd高精度格式
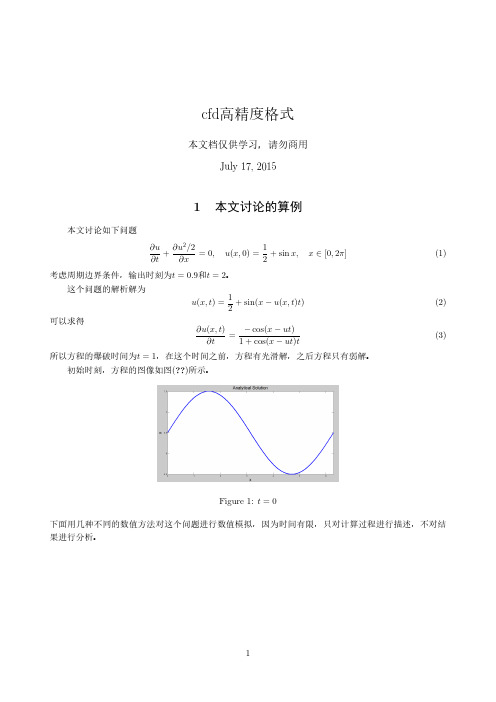
Figure 10: t = 0.9
cfd高精度格式
本文档仅供学习，请勿商用 July 17, 2015
1 本文讨论的算例
本文讨论如下问题
∂u ∂u2/2
1
+
= 0, u(x, 0) = + sin x, x ∈ [0, 2π]
(1)
∂t ∂x
2
考虑周期边界条件，输出时刻为t = 0.9和t = 2。
这个问题的解析解为
1
u(x, t) = + sin(x − u(x, t)t)
unj +1
=
unj
−
λ(fj+
1 2
−
fj−
1 2
),
∆t λ=
∆x
(12)
其中
fj+
1 2
=
1 2
[f
(unj )
+
f
(unj+1
)
−
1 λ
Q(λaj+
1 2
)(unj+1
−
unj )]
aj
+
1 2
=
f
(unj+1) unj+1
− −
f (unj unj
)
,
a(unj ),
当unj+1 = unj 当unj+1 = unj
Figure 2: t = 0.9
Figure 3: t = 2 况。
3 Roe格式
对于单个守恒律方程
∂u ∂f (u)
df
+
= 0, a(u) =
(6)
∂t ∂x
du
一维不可压缩navier_stokes方程_理论说明
一维不可压缩navier stokes方程理论说明1. 引言1.1 概述本文将讨论一维不可压缩Navier-Stokes方程的理论说明。
Navier-Stokes方程是描述流体运动的基本方程之一，其在各个领域都具有重要应用价值。
本文将从介绍Navier-Stokes方程的基本概念开始，逐步展开对一维流动特征和不可压缩流体模型假设的理论说明。
1.2 文章结构文章分为五个主要部分：引言、一维不可压缩Navier-Stokes方程理论说明、理论推导和分析、数值方法和模拟研究以及结论与展望。
其中，引言部分将概述文章的目标和结构，提供读者对整篇文章内容的预览。
1.3 目的本文旨在深入探讨一维不可压缩Navier-Stokes方程，并通过理论推导和数值模拟研究解析该方程对流体运动行为的描述能力。
通过阐明不同数值方法在求解此类方程时的差异和优劣，我们可以更好地了解该方程在实践中的应用，并为进一步研究提供展望。
以上是关于引言部分的详细内容，请根据需要进行修改或补充。
2. 一维不可压缩Navier Stokes方程理论说明2.1 Navier Stokes方程简介Navier Stokes方程是描述流体运动的基本方程之一，它由质量守恒和动量守恒两个方程组成。
同时考虑流体的黏性和压力力作用，Navier Stokes方程能够准确描述流体在各种复杂情况下的运动。
2.2 一维流动特征描述在一维流动中，流体只在一个空间方向上（通常为x轴）有速度分量变化，而在其余两个空间方向上（通常为y轴和z轴）没有速度分量变化。
这样简化后的一维问题可以更容易地推导出Navier Stokes方程的解析解，并且提供了更直观的物理图像。
2.3 不可压缩流体模型假设不可压缩流体是指在任何情况下密度保持不变，即密度是常数。
这个假设适用于许多情况下，例如液体的非常小压缩性以及稳态条件下气体的高马赫数等。
通过这个假设，我们可以将Navier Stokes方程进一步简化为不含密度项的形式，并且使问题更具可行性。
对流方程的四阶中心差分格式
对流方程的四阶中心差分格式流体动力学中，流体动力学方程是用来描述流体在非平衡状态下的运动特性的常微分方程。
它描述的是物质的密度和流动速度的变化，作为时间变化的外力的影响。
流体动力学方程的四阶中心差分格式是一种在数值模拟中应用广泛的解析方法。
一、四阶中心差分格式的简介四阶中心差分格式是一种应用于数值模拟的新方法，它利用中心差分法将流体动力学方程式划分为一系列离散的微分方程，从而能够更准确地描述流体动力学过程。
有一组离散的普通微分方程以及一组离散的非线性方程构成了四阶中心差分格式的核心。
四阶中心差分格式与传统的中心差分格式相比，能够更快更准确地收敛，因此是一种实际应用中的优良方法。
二、优势1、四阶中心差分格式具有较好的精度、可靠性和通用性。
与传统的中心差分格式相比，该方法更加准确地收敛，以及更快地收敛。
2、操作简单，实施方便。
和传统的中心差分格式相比，四阶中心差分格式不仅具有准确性，而且操作简单，实施方便。
3、运算量较小，性能稳定。
对于四阶中心差分格式，其运算量比传统的中心差分格式要小，且性能稳定，更容易用于模拟流体动力学过程。
三、应用1、应用于流体动力学模拟。
四阶中心差分格式可以应用于地形线、边界条件、热流和微外质，从而模拟流体动力学过程。
2、用于求解复杂的流体动力学问题。
该格式由微分方程和非线性方程构成，可以用于求解复杂的流体动力学问题，如湍流流动、不规则流动等。
3、用于水力参数的表达。
此外，四阶中心差分格式也可以用来表达不同的水力参数，如流速、湍流度、温度分布等。
四、缺陷1、四阶中心差分格式伴随着较大的计算量，可能会导致计算速度下降。
2、四阶中心差分格式实施起来可能会比较复杂，可能会消耗更多的精力和时间。
3、四阶中心差分格式可能会受到流体边界条件等外部影响，从而产生模拟误差。
大型客机复杂可压缩流的大涡模拟主要研究方法
大型客机复杂可压缩流的大涡模拟主要研究方法一、大涡模拟基础1. 大涡模拟简介大涡模拟是一种将流场分解成小尺度湍流和大尺度湍流的方法。
在LES中，大尺度结构通过直接数值模拟来求解，而小尺度结构则通过子网格模型（sub-grid model）进行建模。
由于小尺度结构不再需要直接求解，因此可以使用更粗的网格来进行计算，从而减少计算量。
同时，LES还能够提供更加真实的湍流统计数据，如湍流强度、湍流长度等。
2. LES的优点和局限性与其他流体力学方法相比，LES有以下几个优点：（1）能够考虑湍流中的时间和空间尺度差异，提供更加真实的湍流信息；（2）计算结果对于网格的依赖性相对较小，使得计算可以在较粗的网格上进行；（3）LES能够模拟复杂流场，如湍流燃烧、多相流等。
虽然LES具有很多优点，但它也有一些局限性：（1）计算量较大，需要使用高性能计算机进行计算；（2）由于需要建立子网格模型，LES的结果可能受到模型误差的影响；（3）由于直接数值模拟只考虑了大尺度结构，因此对于小尺度结构的预测可能存在误差。
二、大涡模拟在大型客机流场研究中的应用1. 大涡模拟在飞行器气动力学研究中的应用大型客机的外形复杂，流场也非常复杂。
对于这样的流场，传统的计算流体力学方法可能无法准确地预测气动力学行为。
因此，大涡模拟成为研究大型客机流场的一种重要方法。
在大涡模拟中，通过将流场分解成大尺度结构和小尺度结构，可以更加准确地模拟大型客机流场中的湍流现象。
大涡模拟还能够提供更加真实的气动力学数据，如升阻比、气动力矩等。
这些数据对于飞机设计和优化非常重要。
2. 大涡模拟在飞行器噪声研究中的应用随着人们对噪声污染的关注度不断提高，飞机噪声研究也越来越受到关注。
大型客机飞行时产生的噪声主要来自于引擎和机翼表面的湍流。
由于湍流现象非常复杂，传统的计算流体力学方法无法准确地预测噪声的产生和传播。
因此，大涡模拟成为研究飞机噪声的一种重要方法。
通过大涡模拟，可以更加准确地模拟湍流现象，从而预测噪声的产生和传播方式。
有限体积WENO格式及其应用
有限体积WENO格式及其应用在数值模拟领域，有限体积WENO（Weighted EssentiallyNon-Oscillatory）格式是一种广泛使用的非线性数值逼近方法，适用于解决流体力学中的各种问题。
由于其具有高精度、低振荡和低数值弥散等优点，有限体积WENO格式在气象预报、气候模拟、流体动力学等领域中得到了广泛应用。
本文将详细介绍有限体积WENO格式的定义、特点、应用、优势、不足以及结论。
有限体积WENO格式是一种基于有限体积方法的气象预报和流体动力学数值模拟算法。
该方法通过非线性加权差分函数，在每个控制体网格中心进行积分，进而得到流体的宏观量如速度、压力等在该网格中心的数值近似。
高精度：有限体积WENO格式具有高精度的特点，能够准确捕捉到流体的详细变化特征。
低振荡：由于有限体积WENO格式采用非线性加权差分函数，因此能够有效避免数值振荡现象，提高模拟结果的稳定性。
低数值弥散：有限体积WENO格式在模拟过程中产生的数值弥散较小，能够更好地保持流场的结构特征。
有限体积WENO格式在气象预报、气候模拟、流体动力学等领域中得到了广泛应用。
例如，在气象预报领域，有限体积WENO格式被广泛应用于天气预报和气候预测。
在流体动力学领域，有限体积WENO格式被用于模拟湍流、燃烧等复杂流动现象。
在这些应用中，有限体积WENO格式都展现出了其高精度、低振荡和低数值弥散等优点。
有限体积WENO格式在实际应用中具有以下优势：高精度：有限体积WENO格式能够准确捕捉到流体的变化特征，提高模拟结果的精度。
适用范围广：有限体积WENO格式适用于各种复杂流动现象的模拟，能够适应不同领域的需求。
稳定性好：由于有限体积WENO格式采用非线性加权差分函数，能够有效避免数值振荡现象，提高模拟结果的稳定性。
计算效率高：有限体积WENO格式的计算效率较高，适用于大规模并行计算，能够处理大规模问题。
虽然有限体积WENO格式具有许多优点，但也存在一些不足之处：计算成本较高：由于有限体积WENO格式需要进行非线性加权差分函数的计算，因此需要消耗更多的计算资源，导致计算成本较高。
6-通量差分.
§6. 通量差分 6.1 Godunov 格式简介Godunov 格式是可压缩流动数值算法发展过程中的一个重要成果，对通量差分等方法的产生和发展起到了直接的促进作用。
这一方法还是非线性问题（一维气体力学方程组）数值方法中第一个被证明能够收敛到方程弱解的格式，在这之前都是用线化模型方程研究格式的收敛性。
但由于这种方法的计算量现在看起来都很大，以当时计算机的发展水平更是难以承受，所以其实用性较差。
考虑守恒律方程组()t x¶¶+=抖f w w 0 Godunov 方法的求解过程中有两个关键步骤：• 精确求解Riemann 问题：在Godunov 格式中，每一个网格上的计算是通过求Riemann 问题的解析解来完成的，得到的是在整个网格内处处有定义的函数解（间断除外）。
而通常的差分格式得到的是仅在网格点上有定义的离散解。
• 平均：由于Godunov 格式给出的是函数解，为了让计算能够进行下去，需要计算解函数在网格上的平均值。
这一做法后来发展成各种高阶重构方法，到现在还在使用。
上图给出了Godunov 方法的示意图，计算的步骤简述如下。
设在 n t t = 时刻，已经得到数值解函数 (),n x t w% 。
在以 j x 为中心的网格 1122,j j x x -+轾犏臌上，将 (),n x t w % 看成常数 n jw 。
当然，最简单的做法就是取 (),n x t w % 在网格点上的值 (),n nj jx t =w w % 。
但是，取 (),n x t w% 在网格上的平均值()12121,j j xn n jxt d x+-=D òw w%ξξ 精度更高一些。
事实上，由泰勒展开()()()()2221,,2nn jj j j jt x t x x x x 抖=+?+?+¶¶wwww%%%%L ξξξ代入上述积分，有()()()()()1212112211222222211,21,1 2j j j j j j xn n jjj j xj jx x nj j x xj j x t x x d x x x x t d x d xx x +-++--轾抖犏=+?+?+犏D ?¶犏臌ì骣ï¶÷ïç÷ç=??í÷ç÷ïçD ?÷桫ïïî骣÷¶ç÷ç+?÷ç÷ç¶÷ç桫ò蝌w ww w w w w %%%L %%%ξξξξξξ()12122j j x j x x d +-üïïï-+ýïïïþòL ξξ令 j y x =-ξ ，继续计算，()()11122211122222223211,2111,2120x xxnn j j x xx j j n j j j x t dy ydyy dy xx x x t x x x x x D D D -D -D -D 禳骣骣镲÷抖秣?çç镲÷÷çç=???÷睚÷çç÷÷ç镲çD ?÷¶÷ç桫镲桫镲铪ì骣骣ï÷抖秣ççï÷÷çç=譊+?譊+÷í÷çç÷÷ççD ?÷¶÷ç桫桫蝌?w w w w w w w %%%L%%%L ()()2,n j x t x üïïïý镲镲镲铪=+D w%O由此可见，作为函数 (),n x t w % 在网格上的常数近似，网格平均比网格点处的值 (),n j x t w% 精度更高。
可压缩平板边界层转捩的大涡模拟
为了解释小涡无序化的过程，文献［1］最先提出了高剪切层的概念。文献［2］采用直接数值模拟精确计算了槽道内层流向湍流发展的全过程。文献［3］采用大涡模拟（Large eddy simulation，LES）方法观察了自然转捩过程中Tollmien-Schlichting（T-S）波的增长。文献［4～7］通过直接数值模拟方法研究了边界层自然转捩过程，并对转捩晚期的涡系结构的演化进行了深入研究，发现了发卡涡、U型涡、桶型涡等多种涡结构形式，探讨了次生流向涡的生成机理。文献［8］则分析了直接数值模拟结果与实验结果之后，确定了T-S波感受性问题以及其非线性发展阶段对转捩的影响。
关于平板层流转捩过程也有众多的学者进行了大量的实验研究。这些研究不仅实现了边界层流动的可视化，并且对涡系结构的空间发展进行了描述。文献［9］通过实验研究观测了三维非线性波包、发卡涡、二次涡环以及涡链的形成过程。文献［10］实验研究发现边界层转捩晚期可以分为H型和K型两种扰动，尽管它们的涡结构有着不同的空间排列方式，但它们的涡系演化规律在转捩的后期是相似的。
2.2 进口边界条件
入口边界条件为二维布拉修斯相似解，叠加设定的T-S扰动波，具体形式为
式中：q1am为二维层流平板边界层的布拉修斯相似解，扰动为一个二维T-S波（方程（5）右边第2项）和一对三维T-S波（方程（5）右边第3项），这里通过求解可压缩平板边界层的线性稳定性方程，分别得到了二维扰动和三维扰动的特征值和特征扰动形状函数；A2d和A3d为扰动振幅；q′2d和q′3d为相应的扰动形状函数（特征向量）；α，β，ω分别为扰动波的流向波数、展向波数和频率。
【国家自然科学基金】_高精度格式_基金支持热词逐年推荐_【万方软件创新助手】_20140731
科研热词 数值模拟 高精度 非结构网格 紧致格式 摄动法 拉弯成形 辛时域有限差分 稳定性 有限差分格式 新型数值计算方法 数值色散性 大涡模拟 基函数法 加权本质无振荡(weno) weno格式 kelvin-helmhohz不稳定性 黏性可压缩流动 高超声速钝锥边界层 高精度计算格式 高精度紧致差分格式 高精度格式 高精度有限差分法 高精度数值模拟 高精度分析 高精度ppm格式 颗粒轨道模型 频谱 频域相邻系数 预处理方法 非静力模式 非结构 非线性波 非线性抛物型方程 非定常流 非均匀网格 障碍物 闸门瞬间全开 间断有限元 间断galerkin(dg) 重映技术 迎风格式 边界层 辛数值流形时间子域法 辛传播子技术 超音速流体 资料同化 谱微分矩阵 计算网格 计算流体力学 计算气动声学 计算效率 虚拟仿真
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
科研热词 推荐指数 高精度 6 数值模拟 5 高精度格式 3 直接数值模拟 3 高精度计算格式 2 边界层 2 绝热效率 2 气膜冷却 2 冷气射流 2 高阶紧致格式 1 高阶差分格式 1 高阶godullov格式 1 高速飞行器气动热计算 1 高速流动 1 高精度紧致差分方法 1 高分辨率格式 1 频率 1 预处理 1 非结构网格 1 非线性抛物积分微分方程 1 非等距网格离散 1 非振荡 1 非平行性 1 非均匀网格 1 非交错网格 1 间断流函数 1 钝锥 1 部分半粗化 1 迎风紧致格式 1 边界层湍流 1 超收敛 1 谱积分 1 误差分析 1 航空、航天推进系统 1 自适应网格 1 自适应 1 羽流 1 组合紧致迎风格式 1 组合格式 1 组合型超紧致差分格式(cscd) 1 紧致差分格式 1 紧致差分方案 1 精细积分 1 简化计算 1 稳定性 1 直接积分 1 病态方程组 1 界面捕捉 1 界面不稳定性 1 特征正交分解 1 物质输运 1 激波装配法 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
23
Suresh A & Huynh HT (1997) 的高阶MP格式
fj 1/2=fj 1/2 min mod(f min fj 1/2, f max fj 1/2)
High-order (linear) part
MP part (limiter)
f
j 1/ 2
f j1/2 f min
if if
5% 误差
1 0.5
00
1
2
3
17
4） 分辨率优化
原则： 牺牲精度、提高分辨率
方法： 1） 构造含自由参数的差分格式 u j F ( ,uk ) 2） 计算出格式的色散、耗散误差特性； 3） 调整自由参数，使得色散、耗散特性最优
ki
3 2.5
2 1.5
1 0.5
00
1st order upwind 2nd order center 3rd order upwind 5th order upwind 5th order upwind compact 6th order central 6th order central compact exact
精度： 充分小网格 情况下的误差特性 分辨率： 有限尺度网格 情况下的误差特性
x 0
例：
格式1 格式2
u x
j
a1u j3
a2u j2
.......10
5u x5
x4
u x
j
b1u j3
b2u j2
....... 0.1
4u x4
x3
误差
4阶精度 3阶精度
显然： x 足够小的情况下， 格式1误差更小 x 并非足够小的情况下，格式2 有可能误差更小
后面的数据必须等待前一步计算完成，难以直接并行
20
B) 并行方法1： 流水线法
流水线示意图
步骤： 1) 计算 d(:,:) 2) for k=1,M { 如果 myid=0, 计算 F(k,0), 否则 从myid-1接收 F(k,0); for i=1,N1 (N1=N/P) 计算 F(k,i); 如果myid ≠P-1 向 myid+1 发送 F(k,N1) }
YF-23，风洞实验5,500小时，CFD计算15,000机时
YF17
YF17
YF23
6
● 90年代， CFD 在飞机设计中发挥了主力作用 波音777， CFD占主角
● 2000 之后， CFD 取代了大部分风洞实验 波音787：全机风洞实验仅3次
● 航天领域，CFD发挥着实验无法取代的作用 实验难点：复现高空高速流动条件
f MD
f AV
1 2
d
M j
1/2
A. Suresh, H.T. Huynh, Accurate Monotonicity-Preserving Schemes with Runge-Kutta Time Stepping. J. Comput.
单
度计算
精度不易提高
复杂外形的工程 计算
9
➢ 差分法 vs 有限体积法
… j-2 j-1 j j+1 …
差分法： 离散微分方程（一维离散）
U F1 F2 0 t x y
坐标变换 计算空间
每一维独立处理 一维重构（一维Taylor展开）
例如：
f x
j
a1 f j2
a2
f j1
a3
fj
a4 f j1
PPW 2 2 x kx
= PPW 2
每个波长里面2个网格点， 谱方法的分辨率， 差分法的极限
16
3） 格式的分辨率： Fourier分析
u(x j ) eikxj
du ikeikxj dx
uj
k x
eikx j
k kr iki 修正波数 k ikx i
精确解 差分解
耗散误差
商飞北研培训讲座 2018-10-10
高精度差分格式及 可压缩湍流数值模拟
（一）
李新亮 中国科学院力学研究所
1
提纲
Part 1. 高精度差分格式 Part 2. 湍流模拟方法 Part 3. OpenCFD及可压缩湍流直接数值模拟 Part 4. 激波-边界层干扰的数值研究
2
提纲
Part 1. 高精度差分格式 1. 前言 2. 高精度高分辨率差分格式 格式的精度、分辨率及优化 常用的高分辨率格式： 紧致格式、TVD/保单调格式； WENO格式 3. 群速度控制格式
➢ 新方法： 迎风紧致格式；群速度控制格式； 加权群速度控制格式(WGVC-M); 优化的保单调格式OMP; 优化的MUSCL方法
13
二、 高精度、高分辨率差分格式
1. 格式的精度、 分辨率及优化 1) 差分格式精度： 截断误差的阶数
u x
j
1 2x
(u j2
4u j1
3u j )
7
6
f j ( f j+1 f j1) / 2x
5 阶迎风差分格式
f j (2 f j3 15 f j2 60 f j1 20 f j 30 f j1 3 f j2 ) / 60x
优点： 易于推广到高阶格式 不足： 要求网格足够光滑， 不易处理复杂外形
10
有限体积： 离散积分方程 （多维离散）
1
2
3
18
2. 常用的高分辨率格式 1） 紧致格式
✓引入导数信息、 联立求解
j-1
j
j+1
Fj
f x
j
普通格式： Fj =af j1 bf j cf j1
显式给出差分表达式；
紧致格式： Fj1+Fj + Fj1=af j1 bf j cf j1 隐式给出差分表达式；
6阶对称紧致 1/ 3Fj1 Fj 1/ 3Fj1 (28( f j1 f j1) ( f j2 f j2 )) / 36x 5阶迎风紧致 2 / 5Fj1 3/ 5Fj (3 f j1 44 f j1 36 f j 12 f j1 f j2 ) /120x
0
1
x0 , y0
11
➢高精度差分法： 复杂流动的精细模拟 典型应用： 湍流精细模拟 （直接数值模拟、 大涡模拟）
湍射流的涡量分布：DNS
RANS
12
➢ 湍流精细模拟 与 高精度格式
➢ 激波给可压湍流DNS的数值方法带来巨大挑战 矛盾： 低耗散 vs. 抑制振荡（需要耗散）
➢ 2003年以前， 多采用人工粘性（或滤波); 近期, 多采用WENO 格式 不足： 耗散较大， 计算量大
3u x3
j
x2
O(x3)
截断误差
方法1： Taylor展开，计算截断误差项 （非线性格式推导困难）
方法2： 数值实验
ln err
给定一测试函数（可精确求导），计算 误差对网格尺度的依赖关系
n = 斜率
err Axn
ln err ln A nln x
ln(x)
14
2) 差分格式的分辨率
ki
色散误差
1st order upwind
2nd order center
3
3rd order upwind
5th order upwind
5th order upwind compact
2.5
6th order central 6th order central compact
exact
2
1.5
精度高、守恒性好、易于 处理复杂网格
精度高
算法简单，可处理复杂外 形
缺点
适用范围
处理复杂网格不够 相对简单外形的
灵活
高精度计算
不易提高精度（二 复杂外形的工程 阶以上方法复杂） 计算
对于复杂方程处理 多用于固体力学
困难
等
计算量大；
复杂外形的高精
捕捉激波（限制器）度计算
难度大
外形、边界条件简 简单外形的高精
MP bound, using lower
f max min[max(fj, fj 1, f MD ), max(fj, f UL, f LC )]
order interpolation
f UL
fj 4(fj fj 1) f LC
fj
1 2
(fj
fj 1)
4 3
d
M j
1/2
f AV
1 2
(fj
fj 1)
U 1 F nds 0
t
k
控制体边界上进行重构
u(x,
y)
u
x0
,
y0
(x
x0
)
x
+(
y
y0
)
y
u
1 2!
(x
x0
)
x
(
y
y0
)
y
2
u
...
•多维重构（多维Taylor展开）， 推广到高阶精度复杂
优点： 对网格光滑性要求不高，可处理复杂外形 不足： 推广到高阶精度难度大
实验 优点： 直接、可靠、最终验证方式 不足： 周期长、费用高
计算
优点： 周期短、费用低 不足： 受模型及算法限制，需验证
5
计算流体力学(CFD): 在航空航天领域得到广泛应用 ● 1970 年代， 飞机设计主要依赖风洞实验
YF-17研制，风洞实验13,500小时 ● 1980年代，CFD逐渐发展， 部分取代实验
3
一、 前言
• 计算流体力学: Computational Fluid Dynamics 简称CFD
计算流体力学是通过数值方法求解流体力学控 制方程，得到流场的离散的定量描述，并以此 预测流体运动规律的学科