吉林省松原高中高三数学第一次模拟考试题(一)文
2022年吉林省松原市高中高三下第一次测试数学试题含解析

2021-2022高考数学模拟试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某几何体的三视图如图所示,若图中小正方形的边长均为1,则该几何体的体积是( )A .16163π+B .8163π+C .32833π+ D .321633π+ 2.在区间[]1,1-上随机取一个实数k ,使直线()3y k x =+与圆221x y +=相交的概率为( )A .12B .14C .22D .243.已知变量的几组取值如下表:x1 2 3 4 y2.4 4.3 5.37若y 与x 线性相关,且ˆ0.8yx a =+,则实数a =( ) A .74 B .114 C .94D .1344.某学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n 的样本,其频率分布直方图如图所示,其中支出在[20,40)(单位:元)的同学有34人,则n 的值为( )A .100B .1000C .90D .905.已知椭圆()222210x y a b a b+=>>的左、右焦点分别为1F 、2F ,过1F 的直线交椭圆于A ,B 两点,交y 轴于点M ,若1F 、M 是线段AB 的三等分点,则椭圆的离心率为( ) A .12B .32C .255D .556.双曲线22:21C x y -=的渐近线方程为( ) A .20x y ±= B .20x y ±= C .20x y ±=D .20x y ±=7.金庸先生的武侠小说《射雕英雄传》第12回中有这样一段情节,“……洪七公道:肉只五种,但猪羊混咬是一般滋味,獐牛同嚼又是一般滋味,一共有几般变化,我可算不出了”.现有五种不同的肉,任何两种(含两种)以上的肉混合后的滋味都不一样,则混合后可以组成的所有不同的滋味种数为( ) A .20B .24C .25D .268.已知函数()2cos sin 6f x x x m π⎛⎫=⋅++ ⎪⎝⎭(m ∈R )的部分图象如图所示.则0x =( )A .32π B .56π C .76π D .43π-9.设,a b 为非零向量,则“a b a b +=+”是“a 与b 共线”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件10.设1F ,2F 分别为双曲线22221x y a b-=(a >0,b >0)的左、右焦点,过点1F 作圆222x y b += 的切线与双曲线的左支交于点P ,若212PF PF =,则双曲线的离心率为( ) A .2B .3C .5D .611.过抛物线22x py =(0p >)的焦点且倾斜角为α的直线交抛物线于两点A B ,.2AF BF =,且A 在第一象限,则cos2α=( ) A .55B .35C .79D .23512.现有甲、乙、丙、丁4名学生平均分成两个志愿者小组到校外参加两项活动,则乙、丙两人恰好参加同一项活动的概率为 A .12B .13C .16D .112二、填空题:本题共4小题,每小题5分,共20分。
吉林省松原市数学高三上学期理数第一次质量检测试卷

吉林省松原市数学高三上学期理数第一次质量检测试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2019高一上·淄博期中) 若集合,,则图中阴影部分表示的集合为()A .B .C .D . 或2. (2分)(2020·化州模拟) 复数满足,则复数的虚部为()A . -1B . 1C .D .3. (2分) (2016高一上·绵阳期中) 已知a=0.42 , b=30.4 , c=log40.3,则()A . a<b<cB . a<c<bC . c<a<bD . c<b<a4. (2分)定义在R上的函数f(x)对任意x1 , x2(x1≠x2)都有<0,且函数y=f(x+1)的图象关于原点对称,若s,t满足不等式f(s2﹣2s)≤﹣f(2t﹣t2+2),则当1≤s≤4时,的取值范围是()A . [﹣3,﹣)B . [﹣3,﹣ ]C . [﹣5,﹣)D . [﹣5,﹣ ]5. (2分)(2017·东北三省模拟) 已知实数a,b满足﹣2≤a≤2,﹣2≤b≤2,则函数y= x3﹣ ax2+bx ﹣1有三个单调区间的概率为()A .B .C .D .6. (2分) (2020高二上·黄陵期末) 阅读右面的程序框图,则输出的S等于()A . 40B . 20C . 32D . 387. (2分) =()A . 1B . ﹣1C .D .8. (2分)已知为等比数列,是它的前项和. 若,且与2 的等差中项为,则 = ()A . 31B . 32C . 33D . 349. (2分)(2017·新乡模拟) 已知双曲线C:﹣ =1(a>0,b>0)的右焦点为F,点B是虚轴上的一个顶点,线段BF与双曲线C的右支交于点A,若 =2 ,且| |=4,则双曲线C的方程为()A . ﹣ =1B . ﹣ =1C . ﹣ =1D . ﹣ =110. (2分)(2018·临川模拟) 若函数在上单调递减,则的取值范围是()A .B .C .D .11. (2分)若,对任意实数x都有且,则实数a的值等于()A . -1B . -7或-1C . 7或1D . ±712. (2分)(2020·上饶模拟) 已知,不等式对成立,则的取值范围为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)(2019·深圳模拟) 设满足约束条件,则目标函数的最大值为________.14. (1分)(2017·安徽模拟) 已知向量,与的夹角为30°,则最大值为________.15. (1分)直线y=kx﹣1与曲线y=﹣有交点,则k的取值范围是________.16. (1分)如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC= ,则球O的体积等于________.三、解答题 (共7题;共70分)17. (10分)(2020·嘉祥模拟) 已知的内角、、的对边分别为、、,满足.有三个条件:① ;② ;③ .其中三个条件中仅有两个正确,请选出正确的条件完成下面两个问题:(1)求;(2)设为边上一点,且,求的面积.18. (10分)(2017·广西模拟) 据相关规定,24小时内的降水量为日降水量(单位:mm),不同的日降水量对应的降水强度如表:日降水量(0,10)[10,25)[25,50)[50,100)[100,250)[250,+∞)降水强度小雨中雨大雨暴雨大暴雨特大暴雨为分析某市“主汛期”的降水情况,从该市2015年6月~8月有降水记录的监测数据中,随机抽取10天的数据作为样本,具体数据如下:16 12 23 65 24 37 39 21 36 68(1)请完成以如表示这组数据的茎叶图;(2)从样本中降水强度为大雨以上(含大雨)天气的5天中随机选取2天,求恰有1天是暴雨天气的概率.19. (10分)如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,且点M和N分别为B1C和DD1的中点.(1)求证:MN∥平面ABCD;(2)求直线AD1和平面ACB1所成角的正弦值;(3)求点M到平面ACD1的距离.20. (10分) (2019高二上·大庆月考) 已知双曲线两个焦点分别是,点在双曲线上.(1)求双曲线的标准方程;(2)过双曲线的右焦点且倾斜角为的直线与双曲线交于两点,求的周长.21. (10分)函数(1)讨论函数的单凋性;(2)若存在使得对任意的不等式(其中e为自然对数的底数)都成立,求实数的取值范围.22. (10分)(2018·南宁模拟) 在直角坐标系xOy中,曲线的参数方程为(为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求曲线的普通方程和的直角坐标方程;(2)已知曲线的极坐标方程为,点A是曲线与的交点,点B是曲线与的交点,且A,B均异于原点O,且,求的值.23. (10分)选修4-5:不等式选讲, 已知关于x的不等式|x+a|<b的解集为{x|2<x<4}.(1)求实数a,b的值;(2)求+的最大值.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共70分) 17-1、17-2、18-1、18-2、19-1、19-2、19-3、20-1、20-2、21-1、22-1、22-2、23-1、23-2、。
2025届吉林省高中学高三六校第一次联考数学试卷含解析
2025届吉林省高中学高三六校第一次联考数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
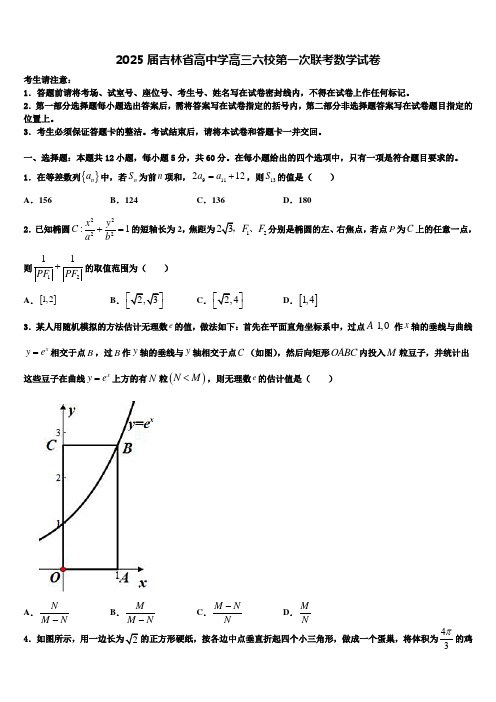
1.在等差数列{}n a 中,若n S 为前n 项和,911212a a =+,则13S 的值是( ) A .156B .124C .136D .1802.已知椭圆2222:1x y C a b+=的短轴长为2,焦距为1223F F ,、分别是椭圆的左、右焦点,若点P 为C 上的任意一点,则1211PF PF +的取值范围为( ) A .[]1,2B .2,3⎡⎤⎣⎦C .2,4⎡⎤⎣⎦D .[]1,43.某人用随机模拟的方法估计无理数e 的值,做法如下:首先在平面直角坐标系中,过点1,0A 作x 轴的垂线与曲线x y e =相交于点B ,过B 作y 轴的垂线与y 轴相交于点C (如图),然后向矩形OABC 内投入M 粒豆子,并统计出这些豆子在曲线xy e =上方的有N 粒()N M <,则无理数e 的估计值是( )A .NM N-B .MM N-C .M NN- D .M N42的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为43π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )A .212 B .212C 61- D 31-5.设()f x 是定义在实数集R 上的函数,满足条件()1y f x =+是偶函数,且当1x ≥时,()112xf x ⎛⎫=- ⎪⎝⎭,则()3log 2a f =,312b f ⎛⎫=- ⎪⎝⎭,()3c f =的大小关系是( ) A .a b c >>B .b c a >>C .b a c >>D .c b a >>6.已知向量(2,4)a =-,(,3)b k =,且a 与b 的夹角为135︒,则k =( ) A .9-B .1C .9-或1D .1-或97.过抛物线()2:20E x py p =>的焦点F 作两条互相垂直的弦AB ,CD ,设P 为抛物线上的一动点,(1,2)Q ,若111||||4AB CD +=,则||||PF PQ +的最小值是( ) A .1B .2C .3D .48.已知,a b 为非零向量,“22a b b a =”为“a a b b =”的( ) A .充分不必要条件 B .充分必要条件C .必要不充分条件D .既不充分也不必要条件9.函数()cos2xf x π=与()g x kx k =-在[]6,8-上最多有n 个交点,交点分别为(),x y (1i =,……,n ),则()1nii i xy =+=∑( )A .7B .8C .9D .1010.已知等差数列{}n a 的公差不为零,且11a ,31a ,41a 构成新的等差数列,n S 为{}n a 的前n 项和,若存在n 使得0n S =,则n =( ) A .10B .11C .12D .1311.函数ln ||()xx x f x e=的大致图象为( ) A . B .C .D .12.本次模拟考试结束后,班级要排一张语文、数学、英语、物理、化学、生物六科试卷讲评顺序表,若化学排在生物前面,数学与物理不相邻且都不排在最后,则不同的排表方法共有( ) A .72种B .144种C .288种D .360种二、填空题:本题共4小题,每小题5分,共20分。
吉林省松原市乾安县第七中学高三数学第一次模拟考试试题 理

乾安七中2016-2017学年度高三第一次模拟考试数学试题(理)一、选择题(每小题5分,满分60分.在每题给出的四个选项中,只有一项是符合题目要求的) 1.已知命题:,sin p x x x ∀∈>R ,则p 的否定形式为( ) A .000,sin x x x ∃∈≤R B .000,sin x x x ∃∈<RC .,sin x x x ∀∈≤RD .,sin x x x ∀∈<R2.函数)1(log 232)(22---=x x x x f 的定义域是( )A. (-21,2) B. ),2[]21,(+∞⋃--∞ C. (2,+∞) D. [1,+∞)3.曲线y = 2+x x在点(-1,-1)处的切线方程为( )A y=2x+1B y = 2x-1C y= -2x-3D y=-2x-24. 已知三次函数f(x)=13x 3-(4m -1)x 2+(15m 2-2m -7)x +2在x ∈(-∞,+∞)上是单调函数,则m 的取值范围是( )A .m < 2或m > 4B .-4< m <-2C .2< m <4D .以上皆不正确 5. 函数xx x f 2)1ln()(-+= 的零点所在的大致区间是( ) A .(3,4) B .(2,e ) C .(1,2) D .(0,1)6.已知二次函数4)(2+-=ax x x f ,若)1(+x f 是偶函数,则实数a 的值为( )A. -1B. 1C. -2D. 27.已知函数y=f(x)是定义在R 上的偶函数,对任意x ∈R ,都有)(1)3(x f x f -=+成立,当[]2,3--∈x 时,x x f 4)(=则f (107.5)= ( )A .10B . 101C . -10D .101-8. 函数)1(),1|(|log >+=a x y a 的图像大致是( )9. 若点P 在曲线y =x 3-3x 2+(3-3)x +34上移动,经过点P 的切线的倾斜角为α,则角α的取值范围是( ) A .[0,π2)B . [0,π2)∪(π2,2π3]C . [2π3,π)D . [0,π2)∪[2π3,π)10.已知函数⎩⎨⎧≤<+-<≤---=)10(1)01(1)(x x x x x f ,则1)()(->--x f x f 的解集为( )A .(-∞,-1)∪(1,+∞) B. [-1,-21)∪(0,1] C .(-∞,0)∪(1,+∞) D. [-1,-21]∪(0,1) 11.设函数⎪⎩⎪⎨⎧<-≥-=)2(1)21()2()2()(x x x a x f x 是R 上的单调递减函数,则实数a 的取值范围( )A .(-∞,2)B .(-∞,813] C .(0,2) D .[813,2) 12.已知()y f x =是定义在R 上的奇函数,且当0x >时不等式()()'0f x xf x +<成立,若()0.30.333a f =⋅, (),log 3log 3b f ππ=⋅3311,log log 99c f ⎛⎫=⋅ ⎪⎝⎭,则 , , a b c 大小关系是( )A .c a b >>B .c b a >>C .b c a >>D .a c b >> 二.填空题:(本题共4小题,每小题5分。
吉林省松原市2021届新高考数学仿真第一次备考试题含解析
吉林省松原市2021届新高考数学仿真第一次备考试题一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
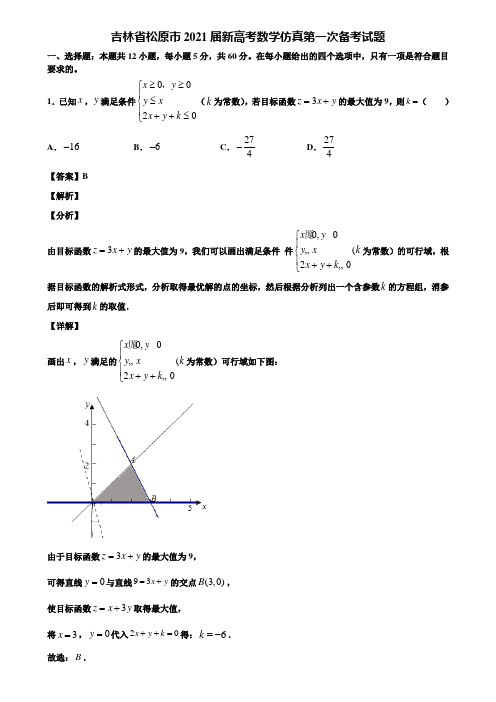
1.已知x ,y 满足条件0020x y y x x y k ≥≥⎧⎪≤⎨⎪++≤⎩,(k 为常数),若目标函数3z x y =+的最大值为9,则k =( )A .16-B .6-C .274-D .274【答案】B 【解析】 【分析】由目标函数3z x y =+的最大值为9,我们可以画出满足条件 件0,0(20x y y xk x y k ⎧⎪⎨⎪++⎩厖……为常数)的可行域,根据目标函数的解析式形式,分析取得最优解的点的坐标,然后根据分析列出一个含参数k 的方程组,消参后即可得到k 的取值. 【详解】画出x ,y 满足的0,0(20x y y xk x y k ⎧⎪⎨⎪++⎩厖……为常数)可行域如下图:由于目标函数3z x y =+的最大值为9, 可得直线0y =与直线93x y =+的交点(3,0)B , 使目标函数3z x y =+取得最大值, 将3x =,0y =代入20x y k ++=得:6k =-.【点睛】如果约束条件中含有参数,我们可以先画出不含参数的几个不等式对应的平面区域,分析取得最优解是哪两条直线的交点,然后得到一个含有参数的方程(组),代入另一条直线方程,消去x ,y 后,即可求出参数的值.2.命题“(0,1),ln x x e x -∀∈>”的否定是( ) A .(0,1),ln x x e x -∀∈≤ B .000(0,1),ln x x e x -∃∈> C .000(0,1),ln x x e x -∃∈<D .000(0,1),ln x x ex -∃∈≤【答案】D 【解析】 【分析】根据全称命题的否定是特称命题,对命题进行改写即可. 【详解】全称命题的否定是特称命题,所以命题“(0,1)x ∀∈,ln x e x ->”的否定是:0(0,1)x ∃∈,00ln x e x -≤.故选D . 【点睛】本题考查全称命题的否定,难度容易.3.若0a b <<,则下列不等式不能成立的是( ) A .11a b> B .11a b a>- C .|a|>|b|D .22a b >【答案】B 【解析】 【分析】根据不等式的性质对选项逐一判断即可. 【详解】选项A :由于0a b <<,即0ab >,0b a ->,所以110b aa b ab --=>,所以11a b>,所以成立; 选项B :由于0a b <<,即0a b -<,所以110()b a b a a a b -=<--,所以11a b a<-,所以不成立; 选项C :由于0a b <<,所以0a b ->->,所以||||a b >,所以成立;选项D :由于0a b <<,所以0a b ->->,所以||||a b >,所以22a b >,所以成立.本题考查不等关系和不等式,属于基础题.4.直线l 过抛物线24y x =的焦点且与抛物线交于A ,B 两点,则4||||AF BF +的最小值是 A .10 B .9C .8D .7【答案】B 【解析】 【分析】根据抛物线中过焦点的两段线段关系,可得1121AF BF p+==;再由基本不等式可求得4AF BF +的最小值. 【详解】由抛物线标准方程可知p=2因为直线l 过抛物线24y x =的焦点,由过抛物线焦点的弦的性质可知1121AF BF p+== 所以4AF BF +()114AF BF AF BF ⎛⎫=+⋅+ ⎪ ⎪⎝⎭ 441BF AF AF BF ⎛⎫=+++ ⎪ ⎪⎝⎭因为AF BF 、为线段长度,都大于0,由基本不等式可知4415BF AF AF BF ⎛⎫+++≥+ ⎪ ⎪⎝⎭522≥+⨯9≥,此时2BF AF =所以选B 【点睛】本题考查了抛物线的基本性质及其简单应用,基本不等式的用法,属于中档题. 5.若ABC ∆的内角A 满足2sin 23A =-,则sin cos A A -的值为( )A .3B .-3 C .3D .5-3【解析】 【分析】由2sin 22sin cos 3A A A ==-,得到1sin cos 03A A =-<,得出(,)2A ππ∈,再结合三角函数的基本关系式,即可求解. 【详解】由题意,角A 满足2sin 22sin cos 3A A A ==-,则1sin cos 03A A =-<, 又由角A 是三角形的内角,所以(,)2A ππ∈,所以sin cos A A >,因为()225sin cos 12sin cos 1()33A A A A -=-=--=,所以sin cos A A -=. 故选:A. 【点睛】本题主要考查了正弦函数的性质,以及三角函数的基本关系式和正弦的倍角公式的化简、求值问题,着重考查了推理与计算能力.6.已知集合{}2|2150A x x x =-->,{}|07B x x =<<,则()R A B ðU 等于( )A .[)5,7-B .[)3,7-C .()3,7-D .()5,7-【答案】B 【解析】 【分析】解不等式确定集合A ,然后由补集、并集定义求解. 【详解】由题意{}2|2150A x x x =-->{|3x x =<-或5}x >,∴{|35}R A x x =-≤≤ð,(){|37}R A B x x =-≤<U ð.故选:B. 【点睛】本题考查集合的综合运算,以及一元二次不等式的解法,属于基础题型.7.在直角坐标系中,已知A (1,0),B (4,0),若直线x+my ﹣1=0上存在点P ,使得|PA|=2|PB|,则正A .13B .3C D【答案】D 【解析】 【分析】设点()1,P my y -,由2PA PB =,得关于y 的方程.由题意,该方程有解,则0∆≥,求出正实数m 的取值范围,即求正实数m 的最小值. 【详解】由题意,设点()1,P my y -.222,4PA PB PA PB =∴=Q ,即()()222211414my y my y ⎡⎤--+=--+⎣⎦,整理得()2218120m y my +++=,则()()22841120m m ∆=-+⨯≥,解得m ≥或m ≤.min 0,m m m >∴∴=Q .故选:D . 【点睛】本题考查直线与方程,考查平面内两点间距离公式,属于中档题.8.已知双曲线2222:1(0,0)x y E a b a b-=>>满足以下条件:①双曲线E 的右焦点与抛物线24y x =的焦点F 重合;②双曲线E 与过点(4,2)P 的幂函数()f x x α=的图象交于点Q ,且该幂函数在点Q 处的切线过点F 关于原点的对称点.则双曲线的离心率是( )A .12B .12C .32D 1【答案】B 【解析】 【分析】由已知可求出焦点坐标为(1,0)(-1,0),,可求得幂函数为()f x =设出切点通过导数求出切线方程的斜率,利用斜率相等列出方程,即可求出切点坐标,然后求解双曲线的离心率.依题意可得,抛物线24y x =的焦点为(1,0)F ,F 关于原点的对称点(1,0)-;24α=,12α=,所以12()f x x ==,()f x '=,设0(Q x0=01x =,∴ ()1,1Q ,可得22111a b -=,又1c =,222c a b =+,可解得a =故双曲线的离心率是12ce a ===. 故选B . 【点睛】本题考查双曲线的性质,已知抛物线方程求焦点坐标,求幂函数解析式,直线的斜率公式及导数的几何意义,考查了学生分析问题和解决问题的能力,难度一般. 9.已知()22log 217y xx =-+的值域为[),m +∞,当正数a ,b 满足2132m a b a b+=++时,则74a b +的最小值为( ) A .94B .5 C.54+ D .9【答案】A 【解析】 【分析】 利用()22log 217y xx =-+的值域为[),m +∞,求出m,再变形,利用1的代换,即可求出74a b +的最小值.【详解】解:∵()()2222log 217log 116y x x x ⎡⎤=-+=-+⎣⎦的值域为[),m +∞, ∴4m =, ∴414622a b a b+=++,∴()()141746224622a b a b a b a b a b ⎛⎫+=++++⎡⎤ ⎪⎣⎦++⎝⎭()()4216219554426244a b a b a b a b +⎡⎤+=++≥⨯+=⎢⎥++⎣⎦, 当且仅当()4262262a b a b a b a b++=++时取等号, ∴74a b +的最小值为94.本题主要考查了对数复合函数的值域运用,同时也考查了基本不等式中“1的运用”,属于中档题. 10.设命题p:n ∃>1,n 2>2n ,则⌝p 为( ) A .21,2n n n ∀>> B .21,2n n n ∃≤≤ C .21,2n n n ∀>≤ D .21,2n n n ∃>≤【答案】C 【解析】根据命题的否定,可以写出p ⌝:21,2nn n ∀>≤,所以选C.11.已知函数()cos f x x m x =+,其图象关于直线3x π=对称,为了得到函数()g x x =的图象,只需将函数()f x 的图象上的所有点( )A .先向左平移6π个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变 B .先向右平移6π个单位长度,再把所得各点横坐标缩短为原来的12,纵坐标保持不变 C .先向右平移3π个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变 D .先向左平移3π个单位长度,再把所得各点横坐标缩短为原来的12,纵坐标保持不变 【答案】D 【解析】 【分析】由函数()f x 的图象关于直线3x π=对称,得1m =,进而得()cos 2sin 2cos 63f x x x x x ππ⎛⎫⎛⎫=+=+=- ⎪ ⎪⎝⎭⎝⎭,再利用图像变换求解即可【详解】由函数()f x 的图象关于直线3x π=对称,得3f π⎛⎫=⎪⎝⎭322m +=1m =,所以()cos 2sin 2cos 63f x x x x x ππ⎛⎫⎛⎫=+=+=- ⎪ ⎪⎝⎭⎝⎭,()2cos2g x x =,故只需将函数()f x 的图象上的所有点“先向左平移3π个单位长度,得2cos ,y x =再将横坐标缩短为原来的12,纵坐标保持不变,得()2cos2g x x =”即可.本题考查三角函数的图象与性质,考查图像变换,考查运算求解能力,是中档题12.函数的图象可能是下面的图象( )A .B .C .D .【答案】C【解析】因为,所以函数的图象关于点(2,0)对称,排除A,B .当时,,所以,排除D.选C.二、填空题:本题共4小题,每小题5分,共20分。
吉林省松原市2021届新高考第一次模拟数学试题含解析

吉林省松原市2021届新高考第一次模拟数学试题一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.甲乙丙丁四人中,甲说:我年纪最大,乙说:我年纪最大,丙说:乙年纪最大,丁说:我不是年纪最大的,若这四人中只有一个人说的是真话,则年纪最大的是( ) A .甲 B .乙 C .丙 D .丁【答案】C 【解析】 【分析】分别假设甲乙丙丁说的是真话,结合其他人的说法,看是否只有一个说的是真话,即可求得年纪最大者,即可求得答案. 【详解】①假设甲说的是真话,则年纪最大的是甲,那么乙说谎,丙也说谎,而丁说的是真话,而已知只有一个人说的是真话,故甲说的不是真话,年纪最大的不是甲;②假设乙说的是真话,则年纪最大的是乙,那么甲说谎,丙说真话,丁也说真话,而已知只有一个人说的是真话,故乙说谎,年纪最大的也不是乙;③假设丙说的是真话,则年纪最大的是乙,所以乙说真话,甲说谎,丁说的是真话,而已知只有一个人说的是真话,故丙在说谎,年纪最大的也不是乙;④假设丁说的是真话,则年纪最大的不是丁,而已知只有一个人说的是真话,那么甲也说谎,说明甲也不是年纪最大的,同时乙也说谎,说明乙也不是年纪最大的,年纪最大的只有一人,所以只有丙才是年纪最大的,故假设成立,年纪最大的是丙. 综上所述,年纪最大的是丙 故选:C. 【点睛】本题考查合情推理,解题时可从一种情形出发,推理出矛盾的结论,说明这种情形不会发生,考查了分析能力和推理能力,属于中档题.2.对于函数()f x ,若12,x x 满足()()()1212f x f x f x x +=+,则称12,x x 为函数()f x 的一对“线性对称点”.若实数a 与b 和+a b 与c 为函数()3xf x =的两对“线性对称点”,则c 的最大值为( )A .3log 4B .3log 41+C .43D .3log 41-【答案】D 【解析】 【分析】根据已知有333b c a b c a ++++=,可得13131ca b+=+-,只需求出3a b +的最小值,根据333a b a b +=+,利用基本不等式,得到3a b +的最小值,即可得出结论.【详解】依题意知,a 与b 为函数()3xf x =的“线性对称点”,所以33323323a b a b a b a b ++=+=≥⋅, 故34a b +≥(当且仅当a b =时取等号). 又+a b 与c 为函数()3xf x =的“线性对称点,所以333b c a b c a ++++=,所以3143131313a b ca b a b +++==+≤--,从而c 的最大值为3log 41-. 故选:D. 【点睛】本题以新定义为背景,考查指数函数的运算和图像性质、基本不等式,理解新定义含义,正确求出c 的表达式是解题的关键,属于中档题.3.如图,在矩形OABC 中的曲线分别是sin y x =,cos y x =的一部分,,02A π⎛⎫⎪⎝⎭,()0,1C ,在矩形OABC 内随机取一点,若此点取自阴影部分的概率为1P ,取自非阴影部分的概率为2P ,则( )A .12P P <B .12P P >C .12P P =D .大小关系不能确定【答案】B 【解析】 【分析】先用定积分求得阴影部分一半的面积,再根据几何概型概率公式可求得. 【详解】根据题意,阴影部分的面积的一半为:()4cos sin 21x x dx π-=⎰,于是此点取自阴影部分的概率为)()114141.41122 3.22P ππ-=⨯=>=. 又21112P P =-<,故12P P >. 故选B . 【点睛】本题考查了几何概型,定积分的计算以及几何意义,属于中档题.4.设等差数列{}n a 的前n 项和为n S ,若5632a a a +=+,则7S =( ) A .28 B .14C .7D .2【答案】B 【解析】 【分析】根据等差数列的性质6345a a a a +=+并结合已知可求出4a ,再利用等差数列性质可得1774()772a a S a +==,即可求出结果. 【详解】因为6345a a a a +=+,所以5452a a a +=+,所以42a =, 所以17747()7142a a S a +===, 故选:B 【点睛】本题主要考查等差数列的性质及前n 项和公式,属于基础题. 5.设集合A 、B 是全集U 的两个子集,则“A B ⊆”是“UA B =∅”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】C 【解析】 【分析】作出韦恩图,数形结合,即可得出结论. 【详解】如图所示,⊆⇒⋂=∅UA B A B ,同时⋂=∅⇒⊆UA B A B .故选:C.【点睛】本题考查集合关系及充要条件,注意数形结合方法的应用,属于基础题.6.已知命题p :“关于x 的方程240x x a -+=有实根”,若p ⌝为真命题的充分不必要条件为31a m >+,则实数m 的取值范围是( )A .[)1,+∞ B .1,C .(),1-∞D .(],1-∞【答案】B 【解析】命题p :4a ≤,p ⌝为4a >,又p ⌝为真命题的充分不必要条件为31a m >+,故3141m m +>⇒> 7.已知复数z 满足1z =,则2z i +-的最大值为( ) A .23+ B .15+C .25+D .6【答案】B 【解析】 【分析】设i,,z a b a b R =+∈,2z i +-22(2)(1)a b =++-,利用复数几何意义计算. 【详解】设i,,z a b a b R =+∈,由已知,221a b +=,所以点(,)a b 在单位圆上, 而2i |(2)(1)i |=z a b +-=++-22(2)(1)a b ++-22(2)(1)a b ++-(,)a b到(2,1)-的距离,故222(2)11z i +-≤-++=15. 故选:B. 【点睛】本题考查求复数模的最大值,其实本题可以利用不等式|2||||2|z i z i +-≤+-来解决.8.在直角坐标平面上,点(),P x y 的坐标满足方程2220x x y -+=,点(),Q a b 的坐标满足方程2268240a b a b ++-+=则y bx a--的取值范围是( ) A .[]22-,B .474733⎡--+⎢⎣⎦C .13,3⎡⎤--⎢⎥⎣⎦ D .676733⎡-⎢⎣⎦【答案】B【解析】 【分析】由点(),P x y 的坐标满足方程2220x x y -+=,可得P 在圆()2211x y -+=上,由(),Q a b 坐标满足方程2268240a b a b ++-+=,可得Q 在圆()()22341x y ++-=上,则PQ y bk x a-=-求出两圆内公切线的斜率,利用数形结合可得结果. 【详解】点(),P x y 的坐标满足方程2220x x y -+=,P ∴在圆()2211x y -+=上,(),Q a b 在坐标满足方程2268240a b a b ++-+=,Q ∴在圆()()22341x y ++-=上,则PQ y bk x a-=-作出两圆的图象如图, 设两圆内公切线为AB 与CD , 由图可知AB PQ CD k k k ≤≤, 设两圆内公切线方程为y kx m =+,则2211343411k mkk m k m k m k ⎧+=⎪+⎪⇒+=-+-⎨-+-⎪=⎪+⎩, 圆心在内公切线两侧,()34k m k m ∴+=--+-, 可得2m k =+,2222111k m k kk++==++,化为23830k k ++=,47k -±=即4747,33AB CD k k ---+==, 4747PQ y b k x a ----+∴≤=≤-, y bx a --的取值范围4747,⎡⎤---+⎢⎥⎣⎦,故选B.【点睛】本题主要考查直线的斜率、直线与圆的位置关系以及数形结合思想的应用,属于综合题. 数形结合是根据数量与图形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法,尤其在解决选择题、填空题时发挥着奇特功效,大大提高了解题能力与速度.运用这种方法的关键是运用这种方法的关键是正确作出曲线图象,充分利用数形结合的思想方法能够使问题化难为简,并迎刃而解. 9.函数sin y x x =+在[]2,2x ππ∈-上的大致图象是( )A .B .C .D .【答案】D 【解析】 【分析】讨论x 的取值范围,然后对函数进行求导,利用导数的几何意义即可判断. 【详解】当0x ≥时,sin y x x =+,则cos 10y x '=+≥, 所以函数在[]0,2π上单调递增, 令()cos 1g x x =+,则()sin g x x '=-, 根据三角函数的性质,当[]0,x π∈时,()sin 0g x x '=-<,故切线的斜率变小, 当[],2x ππ∈时,()sin 0g x x '=->,故切线的斜率变大,可排除A 、B ;当0x <时,sin y x x =-+,则cos 10y x '=-+≥, 所以函数在[]2,0π-上单调递增, 令 ()cos 1h x x =-+,()sin h x x '=,当[]2,x ππ∈--时,()sin 0h x x '=>,故切线的斜率变大, 当[],0x π∈-时,()sin 0h x x '=<,故切线的斜率变小,可排除C , 故选:D 【点睛】本题考查了识别函数的图像,考查了导数与函数单调性的关系以及导数的几何意义,属于中档题. 10.在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,若1a =,c =,sin sin 3b A a B π⎛⎫=- ⎪⎝⎭,则sin C =( ) A.7B.C.12D【答案】B 【解析】 【分析】利用两角差的正弦公式和边角互化思想可求得tan 3B =,可得出6B π=,然后利用余弦定理求出b 的值,最后利用正弦定理可求出sin C 的值. 【详解】1sin sin cos sin 32b A a B B a B π⎛⎫=-=- ⎪⎝⎭,即1sin sin cos sin sin 2A B A B A B =-,即3sin sin cos A B A A =, sin 0A >,3sin B B ∴=,得tan 3B =,0B π<<,6B π∴=.由余弦定理得b === 由正弦定理sin sin c b C B=,因此,1sin sin 7c B C b ===. 故选:B.【点睛】本题考查三角形中角的正弦值的计算,考查两角差的正弦公式、边角互化思想、余弦定理与正弦定理的应用,考查运算求解能力,属于中等题.11.在边长为23的菱形ABCD 中,60BAD ∠=︒,沿对角线BD 折成二面角A BD C --为120︒的四面体ABCD (如图),则此四面体的外接球表面积为( )A .28πB .7πC .14πD .21π【答案】A 【解析】 【分析】画图取BD 的中点M ,法一:四边形12OO MO 的外接圆直径为OM ,即可求半径从而求外接球表面积;法二:根据13OO =,即可求半径从而求外接球表面积;法三:作出CBD ∆的外接圆直径CE ,求出AC 和sin AEC ∠,即可求半径从而求外接球表面积; 【详解】如图,取BD 的中点M ,CBD ∆和ABD ∆的外接圆半径为122r r ==,CBD ∆和ABD ∆的外心1O ,2O 到弦BD 的距离(弦心距)为121d d ==.法一:四边形12OO MO 的外接圆直径2OM =,7R =28S π=;法二:13OO =7R =,28S π=;法三:作出CBD ∆的外接圆直径CE ,则3AM CM ==,4CE =,1ME =,7AE =,AC 33=,cos 27427AEC∠==-⋅⋅,33sin 27AEC ∠=,33227sin 3327AC R AEC ===∠,7R =,28S π=. 故选:A 【点睛】此题考查三棱锥的外接球表面积,关键点是通过几何关系求得球心位置和球半径,方法较多,属于较易题目.12.函数tan 42y x ππ⎛⎫=-⎪⎝⎭ 的部分图象如图所示,则 ()OA OB AB +⋅=( )A .6B .5C .4D .3【答案】A 【解析】 【分析】根据正切函数的图象求出A 、B 两点的坐标,再求出向量的坐标,根据向量数量积的坐标运算求出结果. 【详解】由图象得,令tan 42y x ππ⎛⎫=- ⎪⎝⎭=0,即42x ππ-=kπ,k Z ∈k=0时解得x=2, 令tan 42y x ππ⎛⎫=-⎪⎝⎭=1,即424x πππ-=,解得x=3,∴A(2,0),B(3,1),∴()()()2,0,3,1,1,1OA OB AB ===, ∴()()()5,11,1516OA OB AB +⋅=⋅=+=. 故选:A. 【点睛】本题考查正切函数的图象,平面向量数量积的运算,属于综合题,但是难度不大,解题关键是利用图象与正切函数图象求出坐标,再根据向量数量积的坐标运算可得结果,属于简单题.二、填空题:本题共4小题,每小题5分,共20分。
吉林省松原市扶余县第一中学高三上学期第一次月考数学(文)试题.pdf
数学(文科) 本试卷分第I卷(选择题)、第II卷(非选择题)两部分。
共150分,考试时间120分钟。
第I卷(选择题共60分) 注意事项: 1、答第I卷前,考生务必将自己的姓名、考号用铅笔涂写在答题卡上。
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上。
3、不可以使用计算器。
一、选择题(每小题5分,共60分) 1. 已知集合A=,=,则A∩B=( )(0,1) .(0,2] (1,2).(1,2]p:x1,x2R,(f(x2)f(x1))(x2x1)≥0,则p是( ) A.x1, x2R,(f(x2)f(x1))(x2x1)≤0 B.x1,x2R,(f(x2)f(x1))(x2x1)≤0 C.x1,x2R,(f(x2)f(x1))(x2x1)<0 D.x1,x2R,(f(x2)f(x1))(x2x1)<0 3. 设为定义在上的奇函数,当时,,则( )A.-1B.-4C.1D.4 4.若 ( )A.关于直线y=x对称B.关于x轴对称C.关于y轴对称D.关于原点对称 5. 已知定义在R上的奇函数,满足,且在区间[0,2]上是增函数,则( ). A. B. C. D. 6. 若函数的图象上任意点处切线的倾斜角为,则的最小值是( ) A. B. C. D. 7.函数为奇函数,=( ) A.3 B.1C.D.5 8. 在①1{0,1,2};②{1}∈{0,1,2};③{0,2,1}={0,1,2};④φ{0} 上述四个关系中,错误的个数是: A.1个 B.2个 C.3个 D.4 9. “m3”的否定是“ ,使 3” 三.解答题: (解答应写出文字说明、证明过程或演算步骤) 17. (本题满分10分) 已知函数(为常数,且)的图象过点. (1)求实数的值; (2)若函数,试判断函数的奇偶性,并说明理由. 18. (本题满分12分) 据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度 v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴 的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).(1)当t=4时,求s的值; (2)将s随t变化的规律用数学关系式表示出来; (3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由. 19. (本题满分12分) (1)化简 (2)计算 20.(本题满分12分) 已知数处取得极值,其中为常数. ()的值; (2)讨论函数的单调区间;(),不等式恒成立,求(x,满足 (1)求;; (2)判断y=的奇偶性 22 (本题满分12分) 已知函数.a∈R (Ⅰ)当a=1时,求的单调区间; (Ⅱ)若函数在上无零点,求a的最小值. 此函数的定义域为,又, 所以函数为奇函数. 18. 解:(1)由图象可知:当t=4时,v=3×4=12∴s=×4×12=24. (2)当0≤t≤10时,s=·t·3t=t2, 当10<t≤20时,s=×10×30+30(t-10)=30t-150; 当20<t≤35时,s=×10×30+10×30+(t-20)×30-×(t-20)×2(t-20)=-t2+70t-550. 综上可知s=(3)∵t∈[0,10]时,smax=×102=150<650. t∈(10,20]时,smax=30×20-150=450<650. ∴当t∈(20,35]时,令-t2+70t-550=650. 解得t1=30,t2=40,∵20<t≤35,∴t=30,所以沙尘暴发生30 h后将侵袭到N城. 19. (1) -9a(2)100 22.解:(I)当由由 故 (II)因为上恒成立不可能, 故要使函数上无零点,只要对任意的恒成立, 即对恒成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2019届高三第一次模拟考试卷 文 科 数 学(一) 注意事项: 1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。 2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。 4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.[2018·陕西四校联考]已知复数312iz(i是虚数单位),则z的实部为( ) A.35 B.35 C.15 D.15 2.[2018·广西摸底]已知集合24Axxx,340Bxx,则AB( ) A.,0 B.40,3 C.4,43 D.,0 3.[2018·资阳一诊]空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表: AQI指数值 050~ 51100~ 101150~ 151200~ 201300~ 300
空气质量 优 良 轻度污染 中度污染 重度污染 严重污染 下图是某市10月1日—20日AQI指数变化趋势
下列叙述错误的是( ) A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占14
C.该市10月的前半个月的空气质量越来越好 D.总体来说,该市10月上旬的空气质量比中旬的空气质量好 4.[2018·长春质监]已知等差数列na中,nS为其前n项的和,45S,920S,则7a( ) A.3 B.5 C.3 D.5 5.[2018·曲靖一中]曲线ln20yaxa在1x处的切线与两坐标轴成的三角形的面积为4,则a的值为( ) A.2 B.2 C.4 D.8 6.[2018·衡水中学]如图,在平行四边形ABCD中,对角线AC与BD交于点O,且2AEEO,则ED( )
A.1233ADAB B.2133ADAB C.2133ADAB D.1233ADAB 7.[2018·遵义航天中学]如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )
A.13 B.23 C.1 D.43 8.[2018·黑龙江模拟]已知抛物线2:8Cyx的焦点为F,准线为l,P是l上一点,Q是直线PF
与C的一个交点,若3FPFQ,则QF( ) A.83 B.52 C.3 D.2 9.[2018·曲靖统测]若关于x的不等式210xkx在1,2区间上有解,则k的取值范围是( ) A.,0 B.3,02 C.3,2 D.3,2 10.[2018·广安诊断]在区间1,1上随机取一个数k,则直线2ykx与圆221xy有两个不 2
同公共点的概率为( ) A.29 B.36 C.13 D.33 11.[2018·赣州模拟]在平面直角坐标系xOy中,设1F,2F分别为双曲线222210,0xyabab的左、右焦点,P是双曲线左支上一点,M是1PF的中点,且1OMPF,122PFPF,则双曲线的离心率为( ) A.6 B.2 C.5 D.3 12.[2018·陈经纶中学]已知矩形ABCD,2AB,BCx,将ABD△沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,则( ) A.当1x时,存在某个位置,使得ABCD B.当2x时,存在某个位置,使得ABCD C.当4x时,存在某个位置,使得ABCD D.0x时,都不存在某个位置,使得ABCD 二、填空题:本大题共4小题,每小题5分. 13.[2018·三湘名校]已知:x,y满足约束条件1030210xyxyy,则2zxy的最小值为________. 14.[2018·拉萨中学]若数列na的前n项和2133nnSa,则na的通项公式____________. 15.[2018·山东师大附中]已知sinπ164x,则sin26πx___________. 16.[2018·湖北七校联盟]已知12sin,64πfxxxR,若fx的任何一条对称轴与x轴交点的横坐标都不属于区间π,2π,则的取值范围是___________. 三、解答题:本大题共6大题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(12分)[2018·衡水中学]如图,在ABC△中,P是BC边上的一点,60APC,23AB,4APPB. (1)求BP的长; (2)若534AC,求cosACP的值.
18.(12分)[2018·南昌模拟]中国海军,正在以不可阻挡的气魄向深蓝进军.在中国海军加快建设的大背景下,国产水面舰艇吨位不断增大、技术日益现代化,特别是国产航空母舰下水,航母需要大量高素质航母舰载机飞行员.为此中国海军在全国9省9所优质普通高中进行海航班建设试点培育航母舰载机飞行员.2017年4月我省首届海军航空实验班开始面向全省遴选学员,有10000名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收50名学员.培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”)并记录成绩.10月某次活动中海航班学员成绩统计如图所示:
(1)根据图表,试估算学员在活动中取得成绩的中位数(精确到0.1); (2)根据成绩从50,60、90,100两组学员中任意选出两人为一组,若选出成绩分差大于10, 则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率. 3
19.(12分)[2018·陕西四校联]如图,直三棱柱111ABCABC的所有棱长都是2,D,E分别是AC,1CC的中点. (1)求证:AE平面1ABD; (2)求三棱锥11BABD的体积.
20.(12分)[2018·南昌期末]已知椭圆C中心在坐标原点,焦点在x轴上,且过31,2,直线l与椭圆交于A,B两点(A,B两点不是左右顶点),若直线l的斜率为12时,弦AB的中点D在直线12yx上.
(1)求椭圆C的方程; (2)若以A,B两点为直径的圆过椭圆的右顶点,则直线l是否经过定点,若是,求出定点坐标,若不是,请说明理由. 4
21.(12分)[2018·南城一中]已知函数32fxxaxbxc(a,b,cR). (1)若函数fx在1x和2x处取得极值,求a,b的值; (2)在(1)的条件下,当2,3x时,2fxc恒成立,求c的取值范围.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】 [2018·齐鲁名校]在直角坐标系xoy中,已知曲线1C、2C的参数方程分别为
1
2cos3sn:ixCy
为参数,21cos: sinxtCtyt为参数.
(1)求曲线1C、2C的普通方程; (2)已知点1,0P,若曲线1C与曲线2C交于A、B两点,求PAPB的取值范围.
23.(10分)【选修4-5:不等式选讲】 [2018·陕西四校联考]已知函数2fxxax. (1)当1a时,求不等式3fx的解集; (2)0xR,03fx,求a的取值范围. 2019届高三第一次模拟考试卷 文科数学(一)答 案 一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】B 【解析】∵312i336i12i12i12i55z,∴z的实部为35,故应选B. 2.【答案】C 【解析】∵集合2404Axxxxx,43403Bxxxx, ∴444,433ABxx,故选C. 3.【答案】C 【解析】对A,因为第10天与第11天AQI指数值都略高100,所以中位数略高于100,正确; 对B,中度污染及以上的有第11,13,14,15,17天,共5天占14,正确; 对C,由图知,前半个月中,前4天的空气质量越来越好,后11天该市的空气质量越来越差,错误; 对D,由图知,10月上旬大部分AQI指数在100以下,10月中旬大部分AQI指数在100以上, 所以正确,故选C. 4.【答案】C 【解析】等差数列na中,nS为其前n项的和,42352Saa,95209Sa,5209a,2355252aaad,联立两式得到718d,75+23aad,故答案为C. 5.【答案】B 【解析】由ln2yfxax,得afxx,∴1fa, 又12f,∴曲线ln20yaxa在1x处的切线方程为21yax, 令0x,得2ya;令0y,得21xa. ∴切线与坐标轴围成的三角形面积为12122121422Saaaa,解得2a,故选B. 6.【答案】C 【解析】11213333EDEAADACADADABADADAB.故选C. 7.【答案】B 【解析】由已知中的三视图可得该几何体是一个三棱锥,其直观图如下图所示:
故其体积112122323V,故选B. 8.【答案】A 【解析】设l与x轴的交点为M,过Q向准线l作垂线,垂足为N,
3FPFQ,23NQMF,又4MFp,83NQ,NQQF,83QF.故选A. 9.【答案】D 【解析】210xkx,得1kxx,令1fxxx,则fx在1,2递减, 当2x时,fx取得最小值为32,所以32k.故选D. 10.【答案】D 【解析】圆221xy的圆心为0,0,圆心到直线2ykx的距离为221kk,要使直线
2ykx与圆221xy相交,则2211kk,解得3333k,在区间1,1上随机取一个
