实用堰水力计算公式
梯形堰实用流量计算公式

标题:梯形堰实用流量计算公式说明:图12-10所给出的堰口形状为梯形的堰叫做梯形堰。
在流量计算时,可以认为经过梯形堰的液流流量是相应的矩形堰和三角形堰的流量之和,于是由式(12-3)和式(1 2-11)得上式中,若C1=C2=Ce,则:这是梯形堰的一般表达式,当tanθ=1/4时,可得下列公式:这种tanθ=1/4的梯形堰也叫做希普列蒂堰,希普列蒂(Ci ppoletti)给出了流量的近似计算公式:上式的适用条件为:D≥2.5h;p≥2h;b≥3h标题:矩形堰和全宽堰实用流量计算公式说明:堰口形状为矩形的堰叫做矩形堰,而宽度等于明渠宽度的矩形堰就是全宽堰,如图12-4所示。
1)矩形堰、全宽堰测流量的原理及流量计算一般式在短形堰、全宽堰的堰口曲线方程为代入式(12-8),沿高度方向积分得2)矩形堰a)金德斯瓦特卡特(Kindsvater-Carter)公式金德斯瓦特卡特于1959年发表的这个公式,是在式(12-10)的基础上对流体的表面张力和粘性的影响进行了修正,把流量系数和修正值用图给出。
式中,Ce是流量系数,是b/B和h/p的函数,式中,p是短形堰或全宽堰的下缘到堰底的距离;B是堰的宽度;b e是有效堰口宽度,be=b+k b,b是实际堰口宽度;k b是宽度修正值对应于堰宽的修正值,取表12-1中的值。
h e是堰的有效水头,h e=h+k h,h是实际测量的水头;k h是对水头的修正值,一般取O. OO1m。
公式的适用条件是C e的值可以查图12-5,或按下列公式计算上式的适用条件为3)全宽堰a)金德斯瓦特一卡特(Kindsvater-Carter)公式上式的适用条件为:SIA公式上式的适用条件为b)雷包克(Rehbock)公式上式的适用条件为:上式中的U a是明渠上游侧的平均液流速度,U a=qv/Aa,Aa是水头测量处明渠的通流面积。
因为U a是qv的函数,所以必须用逐步近似法计算。
上式的适用条件为:村石花地水电站压力管前段为铁管,后段为水泥涵管(外径为1.26米),内径均为1.10米。
三角堰量水堰计算
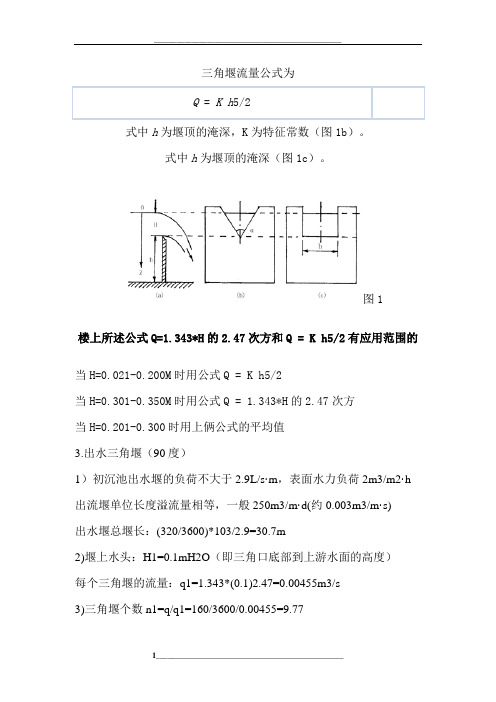
三角堰流量公式为Q = K h5/2式中h为堰顶的淹深,K为特征常数(图1b)。
式中h为堰顶的淹深(图1c)。
图1楼上所述公式Q=1.343*H的2.47次方和Q = K h5/2有应用范围的当H=0.021-0.200M时用公式Q = K h5/2当H=0.301-0.350M时用公式Q = 1.343*H的2.47次方当H=0.201-0.300时用上俩公式的平均值3.出水三角堰(90度)1)初沉池出水堰的负荷不大于2.9L/s·m,表面水力负荷2m3/m2·h 出流堰单位长度溢流量相等,一般250m3/m·d(约0.003m3/m·s)出水堰总堰长:(320/3600)*103/2.9=30.7m2)堰上水头:H1=0.1mH2O(即三角口底部到上游水面的高度)每个三角堰的流量:q1=1.343*(0.1)2.47=0.00455m3/s3)三角堰个数n1=q/q1=160/3600/0.00455=9.77q=出水流量。
取10个。
(每个池)4)三角堰中距L1=b/n1=3/10=0.3m通常三角堰之頂角為90°,tan(θ/2) =1,則(29)及(30)式變成Q=1.47H3/2(31)4.水堰流量的计算公式和计算表(1) 90°三角堰图6,7,890°三角堰流量计算公式式中 Q——流量(l/s)h——堰口水头(m)c——流量系数c=1354++(140+)(-0.09)2B——堰槽宽度(m)D——堰槽底面至堰口底点距离(m)流量系数公式在下述范围内适用:B=0.5~1.2(m) D=0.1~0.75(m)堰的水头测定方法(1)水头是指水流的上水面至堰口底点(90’三角堰)或堰口下边缘(矩形堰、全宽堰)的垂直距离。
(4)水堰的堰口至堰口外水池液面的高度不得小于100毫米。
b.三角堰设计计算每座UASB反应器处理水量7L/s,溢流负荷为1~2L/(m•s)设计溢流负荷取f=2L/(m•s),则堰上水面总长L=q/f=7/2=3.5m(3-7)设计90°三角堰,堰高H=50mm,堰口宽B=100mm,堰上水头h=25mm,则堰口水面宽b=50mm,三角堰数量n=L/b=3.5/0.05=70个.设计堰板长为8-0.3=7.7m,共6块,每块堰10个100mm堰口,10个670mm间隙.堰上水头校核:则每个堰出流率q=0.007/70=1×10-4m³/s按90°三角堰计算公式q=1.43h5/2(3-8)则堰上水头为h=(q/1.43)0.4=(1×10-4/1.43)0.4=0.022m。
08 堰顶高程的确定

Q A0
5500 5600
0.98(m / s)
堰前水头
Hd
H0
0v02
2g
11.53 0.05 11.48
堰顶高程 55.0 11.48 43.52
经校核,满足自由出流条件,以上按自由出游计算的 结果正确 。
/
水力分析与计算子项目
水力计算Excel展示厅
之八 堰顶高程的确定
/ 水利水电建筑工程
水力分析与计算子项目
一 计算公式
堰流的基本计算公式:
3
Q s mb 2g H02
式中: Q 为过堰流量,m3/s; σs为淹没系数,当自由出流时, σs=1; ε为侧收缩系数,无侧收缩时,ε =1 ; H0为堰上总水头,m。
=($A$3/($HBb$03*D18,*按$C1$计13*算$0D.$23*$ki1(in1 1)00.0Hn1b0
A$5*SQRT(2*9.8)))^(2/3)
3
Q s mb 2g H02 用上一次迭代出的
=($A$3/($B$3*$D$5*$C$3*$D$3*$
A$5*SQRT(=2I*F9(.B88)/)$)A^$(=521>/-130,).12,*B(8C/5$+A($D53)-1)*B5)*C8/D3
3
Q s mb H20gH10,2按1计 1算 用基本参数中b 的
0.2 k
(n
1) 0
H0 nb
/
/
水力分析与计算子项目
二 工程任务
某河道宽160m,设有WES型实用堰,堰上游面垂直。闸墩 头部为圆弧形,边墩头部为半圆形。共7孔,每孔净宽10m。当 设计流量为5500 m3/s时,相应的上游水位为55.0m,下游水位 为39.2 m,上、下游河床高程为20水力分析与计算子项目
堰水力计算

判别:条件:⑵m=0.32注意:条件:⑵m=0.36计算:7.4上游堰高P= 1.5堰前水头H=2墩间净宽b=5下游水头Hs 9系数α=0.19P/H=0.751、1)⑴0.342005⑵0.321、3)⑴1、2)⑴0.369677⑵0.362、b/B=0.555556P/H=0.751、0.9258392、多孔闸时:1、b/B 中=0.675676σcm=0.943168σc 平=0.9373922、hs/H O =0.4σs=自由出流:Q= 3.032874淹没出流Q=注意:其中系数的选取三、侧向收缩系数σc :上游边闸引渠宽B=(引渠为梯形,B=b o +mh/2,bo 为底宽,m 为边坡系为二、计算流量系数m (见《水力计算手册》P121)1.有底坎时:σc=1-α*(b/B )0.25*(1-b/B )/(0.2+P/H )0.3333一、基本数据:(b/B <0.2,用b/B=0.2;P/H >3.0,用P/H=3.0)多孔闸时取平均σc 平=(σcm(n-1)+σcs)/n 2.无底坎时:(见《水力计算手册》P126)宽 顶 堰 流堰顶厚度δ>2.5H 时hs/H <0.8,自由溢流⑴m=0.32+0.01*(3-P/H )/(0.46+0.75*P/H )⑵P/H ≥3.02)进口边缘修圆:(实用于r/H ≥0.2,r 为修圆半径)⑴0<P/H <3.0⑴m=0.36+0.01*(3-P/H )/(1.2+1.5*P/H )2.无底坎时:(分为直角、八字、圆弧、斜角型翼墙,见《水力计算手册》P122)二)侧向收缩系数σc :hs/H ≥0.8,淹没溢流⑵P/H ≥3.03)斜坡式进水口:五、流量计算Q :(只有一孔泄流时)四、淹没系数σs :(见《水力计算手册》P128)(包括行进流速水头H O )一)流量系数m 取值:1.有底坎时:1)进口为直角时:上游中闸引渠宽B=⑴0<P/H <3.00.8闸孔数n=3h/2,bo为底宽,m为边坡系数;闸墩(或边墩)墩头为矩形,堰进口边缘直角时,α=0.19,为曲线时而进口边缘为直角或圆弧,α=0.1。
淹没和非淹没矩形堰水力计算
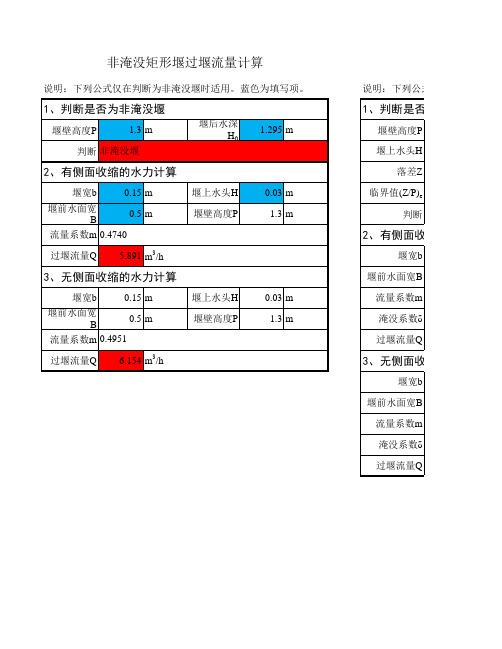
有侧面收缩的水力计算
0.15 m 0.5 m 0.4515 0.9135 7.893 m3/h 堰上水头H 堰壁高度P 0.04 m 1.3 m
无侧面收缩的水力计算
0.15 m 0.5 m 0.4727 0.9135 8.264 m3/h 堰上水头H 堰壁高度堰宽b 堰前水面宽B 流量系数m 淹没系数δ 过堰流量Q
淹没矩形堰过堰流量计算
:下列公式仅在判断为淹没堰时适用。蓝色为填写项。
判断是否为淹没堰
1.3 m 0.04 m 0.03 m 0.68 淹没 相对水头H/P 相对落差Z/P 1.750 m 0.023 堰后水深H0 1.31 m
非淹没矩形堰过堰流量计算
说明:下列公式仅在判断为非淹没堰时适用。蓝色为填写项。
淹没矩形
说明:下列公式仅在判断为淹
1、判断是否为非淹没堰
堰壁高度P 1.3 m 堰后水深H0 1.295 m
1、判断是否为淹没堰
堰壁高度P 堰上水头H 落差Z 堰上水头H 堰壁高度P 0.03 m 1.3 m 临界值(Z/P)e 判断
判断 非淹没堰
2、有侧面收缩的水力计算
堰宽b 堰前水面宽B 流量系数m 0.4740 过堰流量Q 5.891 m3/h 0.15 m 0.5 m
2、有侧面收缩的水力计算
堰宽b 堰前水面宽B 堰上水头H 堰壁高度P 0.03 m 1.3 m 流量系数m 淹没系数δ 过堰流量Q
3、无侧面收缩的水力计算
堰宽b 堰前水面宽B 流量系数m 0.4951 过堰流量Q 6.154 m3/h 0.15 m 0.5 m
进水口堰上水深计算

进水口堰上水深计算
进水口堰上水深的计算可以借助堰槽流量公式和进水口堰的几何特征来进行估算。
以下是一个简单的计算过程:
假设进水口堰的宽度为B(单位:米),水流速度为V(单位:米/秒),堰槽的底宽为b(单位:米),进水口堰的高度为H(单位:米)。
首先,可以通过堰槽流量公式计算出水流量Q(单位:立方米/秒):
Q=C*b*H*sqrt(2*g*H)
其中,C是流量系数(取决于堰的形状),g是重力加速度(约为9.8米/秒^2)。
一般来说,进水口堰的流量系数取值在0.4到1.0之间,可以根据具体的堰型和流量条件选择适当的数值。
接下来,可以根据流量Q和进水口堰的宽度B计算出标准速度v(单位:米/秒):
v=Q/(B*H)
最后,可以根据标准速度v和进水口堰的几何特征来计算进水口堰上水深h(单位:米)。
根据流体力学的原理,可以使用能量方程来计算h的值:
h=Hv^2/(2*g)
这样,就可以得到进水口堰上水深h的估算值。
需要注意的是,以上计算方法仅适用于一定的假设条件和理想化的情况。
在实际工程中,还需要考虑其他因素,如水流湍流、沉淀物的影响等。
同时,为了准确计算进水口堰上水深,可以借助数值模拟方法或进行实验测定来获取更精确的结果。
第八章-堰流-闸孔出流.讲义
三角形薄壁堰流量公式:
QC0H5/2
•当堰口夹角 900 时,
C 01.35 0 4 .H 00 4 0.1 40.P 2 1 H B0.0 9 2
或 C0 1.4
•当堰口夹角 900 时,
C 0 2 .3t6 g 2 1 0 .5 5 0 .0 31 tg 2 9 c 5 t2 g 0 .0 00 .0 5 H 0 1 0
0.5 1.0 2.0 0 0
ctg1
34 5
10
000
堰下游坡度
ctg2 0.5 0 0 1 2
0 0 0 0 3 5 10
/ H 0.4
流 量
~ =0.4 ~1 0.38
0.42 0.41 0.4
0.38 0.4
0.39 0.38 0.36 0.37 0.35 0.34
系 / H 0.36
数
淹没出流 Qmb2gH0 3/2
淹没系数
若堰顶的过流宽小于上游河宽,此时的堰流出现 有侧收缩,反之,为无侧收缩。
有侧收缩 Q1mb2gH0 3/2
1 侧收缩系数
17
(1)自由出流
hs
H
ht P2
堰下游水位较低( hs(0.7 50.8)5 H 0),堰的过 流能力不受影响。
18
H
C
hs
ht
自由出流特点:两次降落,一次微升;收缩断面 后的堰顶水流为急流。
6
堰流、闸孔出流共同点 1、水流或多或少受到水闸或溢流坝等建筑物的 约束,从而壅高上游水位。 2、过堰、过闸水流属于明渠急变流。 3、水头损失主要是局部水头损失。
7
堰、堰流的参数 0
H
V0
P1
P2
7.3 薄壁堰和实用堰——学习材料
学习单元三、薄壁堰和实用堰一、薄堰计算薄壁堰流的水头与流量的关系稳定,因此,常用作实验室或野外流量测量的一种工具。
根据堰口形状的不同,薄壁堰可分为三角形、矩形和梯形薄壁堰。
三角形薄壁堰常用于测量较小的流量,矩形和梯形薄壁堰常用于测量较大的流量。
1. 矩形薄壁堰实验表明矩形薄壁堰流在无侧向收缩、自由出流时,水流最稳定,测量精度也较高。
所以采用矩形薄壁堰测流量时,应注意以下几点。
(1) 矩形薄壁堰应与上游渠道等宽。
(2) 下游水位应低于堰顶。
(3) 堰顶水头不宜过小(一般应使H ≥2.5cm ),否则溢流水舌在表面张力作用下,出流会很不稳定。
(4) 水舌下面的空间应与大气相通。
否则溢流水舌会把其下面空气带走而形成局部真空,使出流不稳定。
图7-6是实验室中测得的无侧向收缩、非淹没矩形薄壁堰自由出流的水舌形状。
图7-6 无侧向收缩、非淹没矩形薄壁堰自由出流的水舌形状无侧向收缩、非淹没矩形薄壁堰的流量可按堰流基本计算公式公式计算。
2302H g b m Q = 两个计算0m 的经验公式。
雷伯克(Re hbock)公式:10053.00007.0403.0P H H m ++= 式中堰高1P 和堰顶水头H 必须以米代入。
此式适用范围为:H ≥0.025m ,2/1≤P H 及 P ≥0.3m 。
巴赞(Bazin)公式:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+++=21055.01)0027.0405.0(P H H H m 式中堰高 1 P 和堰顶水头H 必须以米代入。
此式适用范围为: H =0.1~0.6m ,B=0.2~2.0m 及12P H≤ 。
2. 三角形薄壁堰 当流量较小(例如Q <0.1m 3 /s )时,若用矩形薄壁堰来测量,则堰上水头H 太小,测量误差较大,为此改用三角形薄壁堰。
对于堰口两侧边对称的直角三角形薄壁堰自由出流的流量可按下列经验公式来计算。
图7-7 三角形薄壁堰250H C Q =式中0C 为三角形薄壁堰的流量系数。
实用堰流流量计算举例.
主持单位: 广东水利电力职业技术学院 黄河水利职业技术学院 参建单位: 杨凌职业技术学院 安徽水利水电职业技术学院 山西水利职业技术学院 四川水利职业技术学院 长江工程职业技术学院
薄壁堰流
水力分析与计算
0.67 / H 2.5
实用堰流
2.5 / H 10
宽顶堰流
实用堰流水力分析与计算
任务:
1.水流现象分析 2.过流能力计算
案例:
某溢流堰为WES剖面的曲线型实用堰,边墩头部为半圆形,闸墩 墩头型式采用圆弧型,共3孔,每孔净宽b=14m,堰与非溢流的混凝土 坝相接,堰高P1=P2=12m,下游水深ht=13m,设计水头Hd=3.11m。 试求闸门全开堰前水头H=3.36m时通过溢流堰的流量Q 。
水力分析与计算
实用堰流水力分析与计算
案例分析: 1.水流现象分析: 堰流 2.流量公式确定
H
相对开启高度 e/H e
Q s mB 2gH03/2
式中 B —堰顶过水净宽; H0—包括流速水头在内的堰前总水头,H0 H v02 / 2g ; m—堰的流量系数; σs—考虑下游水位对泄流影响的系数,称淹没系数,σs ≤ 1; ε —侧收缩系数,ε ≤1。
Q s mB 2gH0
3/2
3.流量系数m确定 4.侧收缩系数ε确定
水力分析与计算
(2)淹没系数确定 淹没系数与hs/H0、 P2/H0有关, 查图求得。
实用堰流水力分析与计算
淹没系数σs确定
淹没系数与hs/H0、 P2/H0有关,查 图求得。
水力分析与计算
实用堰流水力分析与计算
案例讲解: 1.水流现象分析
水力分析与计算
闸孔出流
2堰流公式讲解
第八章 堰流及闸孔出流水利工程中,为防洪、灌溉、航运、发电等要求,需修建溢流坝、水闸等控制水流的水工建筑物。
例如,溢流坝、 水闸底槛、桥孔和无压涵洞进口等。
堰是顶部过流的水工建筑物。
图1、2中过堰水流均未受闸门控制影响闸孔出流:过堰水流受闸门控制时,就是孔流堰流和闸孔出流是两种不同的水流现象。
它们的不同点在于堰流的水面线为一条光滑曲线且过水能力强,而孔流的闸孔上、下游水面曲线不连续且过水能力弱。
它们的共同点是壅高上游水位;在重力作用下形成水流运动;明渠急变流在较短范围内流线急剧弯曲,有离心力;出流过程的能量损失主要是局部损失。
相对性: 堰流和孔流是相对的,堰流和孔流取决于闸孔相对开度,闸底坎及闸门(或胸墙) 型式以及上游来流条件(涨水或落水)。
平顶堰: e /H ≤0.65 孔 流 曲线型堰:e/H ≤ 0.75 孔 流 e/H > 0.75 堰 流 e/H >0.65 堰 流 式中:e 为 闸孔开度; H 为 堰上水头堰流及孔流是水利工程中常见的水流现象,其水力计算的主要任务是研究过水能力。
它包括堰闸出流水力特性和堰闸水力计算。
图4 闸孔出流eHHv 0图1 堰流bH图2 堰流be图3 堰流及闸孔出流H第一节 堰流的分类及水力计算基本公式一、堰流的分类水利工程中,常根据不同建筑材料,将堰作成不同类型。
例如,溢流坝常用混凝土或石料作成较厚的曲线或者折线型;实验室量水堰一般用钢板、木板作成薄堰壁。
堰外形、厚度不同,能量损失及过水能力不同。
堰前断面:堰上游水面无明显下降的0-0 断面 堰上水头:堰前断面堰顶以上的水深,用H 表示行进流速:堰前断面的流速称为行进流速,用v 0 表示 堰前断面距离上游壁面的距离:L =(3~5) H研究表明,流过堰顶的水流型态随堰坎厚度与堰顶水头之比δ /H 而变,工程上,按δ与H 的大小将堰流分薄壁堰、实用堰、宽顶堰。
1. 薄壁堰:δ/H <0.67越过堰顶的水舌形状不受堰厚影响,水舌下缘与堰顶为线接触,水面呈降落线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、 游水位较低,水流在流出堰顶时将产生第二次跌落。 2、 4、 100H时,用明渠流理论解决不能用堰流理论。fh不可忽略。 同一堰,当堰上水头H较大时,视为实用堰;当堰上水头较小时,视为宽顶堰。
§8-2 堰流的基本方程
以宽顶堰为例来推求堰流的基本方程 取渐变流断面1-1 C-C(近似假设渐变流) 以堰顶为基准面, 列两断面能量方程:
gvgvhgvHccc22222000
000
2Hg
vH
作用水头
ch与H有关,引入一修正系数k。则00Hhkc机0kHhco。修正系数k取决于堰口的
形状和过流断面的变化。
代入上式,整理得:0021211gHkgHkvc 230021HgbkkbRHvbhvQccc
2302Hgmb
式中:b——堰宽
——流速系数 1
m——流量系数,kkm1
适用:堰流无侧向收缩 注:堰流存在侧向收缩或堰下游水位对堰流的出水能力产生影响时,可对此公式进行修正。
§8-3 薄壁堰
一、一、分类: 矩形薄壁堰→较大流量(Q>100L/S) 按堰口形状: 三角形薄壁堰→较小流量(Q<100L/S) 梯形薄壁堰→较大流量
1、 矩形薄壁堰 矩形薄壁堰上下游等宽,堰流无侧收缩。当自由出流时,水流最为稳定,测量精度较高。 为保证下游为自由出流,矩形薄壁堰应满足: ① H > 2.5 cm ,否则堰下形成贴壁流,出流不稳定 ② 水舌下与大气通,否则水舌下有真空,出流不稳定
① ① 矩形薄壁堰的自由出流;在无侧向收缩的影响时,其流量公式为: 2302HgmbQ 上式为关于流速的隐式方程,了;两边均含有流速,一般计算法进行计算,较复杂,于是,为计算简便,将上式改写成:
2302HgbmQ
0m——已考虑流速影响的薄壁堰的流量系数
0m的确定:
矩形薄壁8的流量系数由1898年法国工程师Basin提出经验公式为:
])(55.01)[0027.0405.0(20pHHHm
式中:H——堰上水头(m) p——上游堰高 (m)
适用条件:mH24.1~25.0 mp75.0~24.0 mb0.2~2.0 2、 2、 三角形薄壁堰: 当流量较小时,堰上水头较小时,采用三角形薄壁堰 ⑴公式:
取微元,则流量表达式为:dbhgmdQ2302 (*) 设h为db处水头,则由几何关系:2)(tghHb dhtgdb2 代入*式,得dhhgtgmdQ23022 积分得:dhhgtgmQH0230222 2502254Hgtgm
当90,mH25.0~05.0时,实验得395.00m。于是:254.1HQ 当90,mH55.0~25.0时,经验公式为:47.2343.1HQ
式中H——以顶点为起点的堰上水头(m)Q——流量(sm3) ⑵公式适用条件:①薄壁堰水面四周均为大气,必要时设通气管与大气相通。 ②无侧向收缩的影响。 ③堰流为自由出流。 ⑶薄壁堰是测量渠道流量的装置: 注意:①水面与大气相通, ②避免形成淹没式水流。
§8-4 实用堰
一、一、实用堰: 1、 1、 用途 挡水、泄流 (水利工程中) 2、 2、 分类: 曲线形实用堰 折线形实用堰
3、 3、 计算公式:2302HgmbQ m与实用堰的具体曲线类型有关,也与堰上水头有关
一般曲线型的实用堰可取45.00m 折线型实用堰可取42.0~35.00m 一、三、实用堰所受影响 1、 1、 淹没影响
淹没式出流:当堰下游水位超过堰顶标高时,即0phHs 淹没式出流公式:设s为淹没系数,与淹没程度有关,淹没式实用堰的流量公式为:302HgmbQs s具体见P169 表8-1 2、 2、 侧面收缩的影响: 堰宽﹤堰上游渠道 {过堰水流发生侧向收缩,泄流能力减小}
用侧面收缩系数表示,堰流流量为:2302HgbmQ 侧面收缩系数一般取值:95.0~85.0
§8-5 宽顶堰
一、一、自由出流: 1、 1、 分类: 直角形 按进口纵剖面的形式 圆弧形 ,阻力,泄流能力不同,流量系数不同。 斜角形
2、 2、 流量公式:2302HgmbQm流量系数,取决于堰口的类型和相对堰高。 m 的经验公式和经验数据如下:
⑴矩形直角进口宽顶堰:
当0.30Hp时,HpHpm75.046.0301.032.0 当0.3Hp时,32.0m ⑵矩形圆弧进口宽顶堰:
当0.30Hp时,HpHpm5.12.1301.036.0 当0.3Hp时,36.0m 二、二、淹没式出流: 下游水位高于堰顶且使堰顶水流由急流变缓流 1、特点:①过堰水流水位﹤下游水位 ②水流由急流→缓流(kkhhhh)充分条件 ③堰过水能力下降
2、淹没式堰流的充分条件是:0'8.0Hphhs
3、计算公式 2302HgmbQs s——淹没系数,取值范围见P171 表8-2
三、三、侧向收缩的影响: 1、 1、 侧向收缩:当堰宽小于上游渠道宽时,水流流入堰口后,A流道断面面积变化,水流在惯性的作用下,流线发生弯曲,产生附加的局部阻力,造成过流能力降低。其影响用收缩系数表示。 2、 2、 计算公式:
自由出流:2302HgmbQ ——收缩系数,与堰宽和渠道的比值Bb边墩的进口形状及进口断面变化有关。
的经验公式为:)1(2.0143BbBbHp
——墩形系数,矩形边缘19.0,圆形边缘10.0
例8-1 见P171
§8-6 小桥孔径的水力计算
一、 1、 1、 流经小桥孔径的水流特点:(水力现象) 与宽顶堰相同 ① ① 具有侧向影响,造成局部阻力 ② ② 桥孔前水位整齐,桥孔内流速增加,造成第一次水面跌落 ③ ③ 桥孔后流速减小,产生局部阻力,造成第二次水面跌落。 2、 2、 形成原因: 水流在缓流河道中,由于桥墩或桥的边墩侧向收缩,使水流过水断面减小造成的。 3、分类:自由出流 淹没出流 二、自由出流: 1、 1、 自由出流——当桥的下游水位不影响小桥的过水能力时,水面有明显的两次跌落,这时的小桥出流为自由出流。 2、 2、 特点(判断准则):
一般桥的下游水深,khh3.1(kh—桥下渠道的临界水深) 桥下水深 kahh
对于矩形桥进口断面:323322)(bgQgbQhk 把kahbvhbvQ)()(''代入上式,得gvhk2'2 3、 3、 公式推求: 列1-1、2-2能量方程: gvgvhgvHa2222200
式中令gvHH22000kzhh 垂直收缩系数1 具体数据由小桥进口形状而定
平滑进口:85.0~80.0 非平滑进口:80.0~75.0 v——流速
)(20ahHgv
——1
)(20aahHgmbhQ m
(小桥)
考虑侧向收缩 )(20aahHgmbhQ ——侧向收缩系数 小桥孔径流速系数与侧面收缩系数数据见P174 表8-3 三、淹没出流
1、淹没出流——当小桥下游水深khh3.1时,下游水位将影响桥的过水能力,此流动成为淹没出流。
2、特点: ①下游khh3.1 ②小桥水面上只发生一次跌水。hhb 3、计算公式:)(20hHgv)(20hHgmbhQ 例8-2 见0174 堰流 明渠缓流溢过建筑在渠道中的障碍物的流动。障碍物称为堰,在工程中,障碍物为坝、桥涵、溢流设备等,它们使上游水位壅高,对堰流起侧向收缩和底坎约束的作用。明渠急流流过障碍物,产生不同于堰流的水力现象。当流经侧收缩段时,发生冲击波。 堰流主要研究水流流经堰的流量 与其他特征量的关系。表示堰流特征量,除流量外,尚有:堰宽,即水流漫过堰顶宽度;堰顶水深,即堰上游水位在堰顶上的最大超高;堰壁厚度和它的剖面形状;下游水深及下游水位高出底坎的高度;为堰高;为堰下游坎高;0为趋近流速。如图[堰
流]所示。 堰的分类 根据堰壁的相对厚度/的大小分为:薄壁堰(/<0.67)、实用断面堰(0.67
