常见电池等效电路模型
电催化等效电路

电催化等效电路
电催化等效电路(Electrochemical Equivalent Circu it, EC Circuit)是一种用于描述和模拟电化学反应系统中电阻、电容和电荷转移现象的电路模型。
在电化学研究,尤其是电化学阻抗谱(EIS)分析中,等效电路模型能够帮助研究人员理解电池或电极表面的电荷传递过程以及界面动力学。
一个简单的电催化等效电路可能包括以下基本元件:
1. 串联电阻(Rs):代表电解液中的欧姆电阻或者外部连线电阻。
2. 电化学双层电容(Cdl):模拟电极-电解质界面的电荷储存效应,即双层电容。
3. 法拉第阻抗(Rct):也称为电荷转移电阻,反映了电子从电极转移到溶液中离子的难易程度。
4. Warburg 元件(ZW):模拟扩散过程中的阻抗,通常表现为非理想电容或称为 Warburg 电阻,尤其在涉及离子在电解液中的扩散时。
复杂的电催化等效电路可能包含多个并联或串联的这些基本元件,以适应更复杂的现象,如多步骤反应、多个界面层等。
通过拟合实验获得的阻抗谱数据与不同结构的等效电路模型,可以定量地提取出各个物理参数,并对电催化反应机理进行深入探讨。
常见几种电路的等效变换
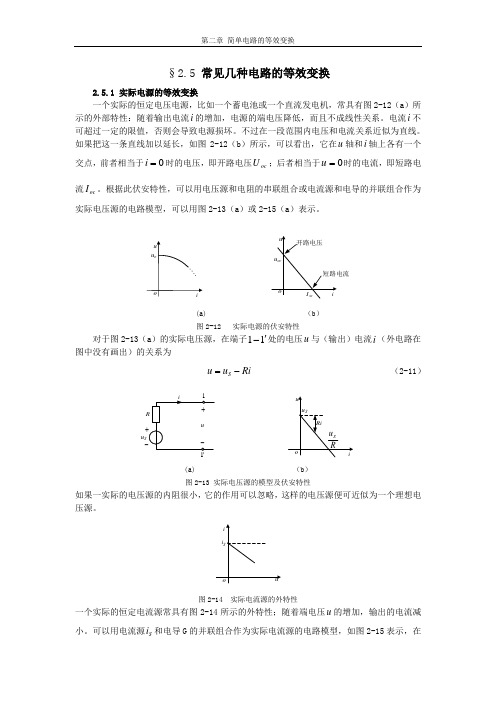
§2.5 常见几种电路的等效变换2.5.1 实际电源的等效变换一个实际的恒定电压电源,比如一个蓄电池或一个直流发电机,常具有图2-12(a )所示的外部特性:随着输出电流i 的增加,电源的端电压降低,而且不成线性关系。
电流i 不可超过一定的限值,否则会导致电源损坏。
不过在一段范围内电压和电流关系近似为直线。
如果把这一条直线加以延长,如图2-12(b )所示,可以看出,它在u 轴和i 轴上各有一个交点,前者相当于0=i 时的电压,即开路电压oc U ;后者相当于0=u 时的电流,即短路电流oc I 。
根据此伏安特性,可以用电压源和电阻的串联组合或电流源和电导的并联组合作为实际电压源的电路模型,可以用图2-13(a )或2-15(a )表示。
(a) (b ) 图2-12 实际电源的伏安特性对于图2-13(a )的实际电压源,在端子11'-处的电压u 与(输出)电流i (外电路在图中没有画出)的关系为Ri u u S -= (2-11)Su(a) (b ) 图2-13 实际电压源的模型及伏安特性如果一实际的电压源的内阻很小,它的作用可以忽略,这样的电压源便可近似为一个理想电压源。
图2-14 实际电流源的外特性一个实际的恒定电流源常具有图2-14所示的外特性;随着端电压u 的增加,输出的电流减小。
可以用电流源S i 和电导G 的并联组合作为实际电流源的电路模型,如图2-15表示,在端子11'-处的电压u 与(输出)电流i 的关系为(a) (b ) 图2-15 实际电流源的电路模型及伏安特性Gu i i S -= (2-12) 如果一实际的电流源的并联电导很小,它的作用可以忽略,这电源便可近似为一个理想电流源。
如果令RG 1=S S Gu i = (2-13)式(2-11)和(2-12)所示的两个方程将完全相同,也就是在端子11'-处的电压u 与电流i 的关系将完全相同。
电池等效电路

电池等效电路
电池等效电路是指将电池抽象为一个电路,以方便在电路中进行计算和分析。
电池等效电路包括理想电池模型和实际电池模型。
理想电池模型是指电池的内阻为零,电动势为固定值的电路模型。
实际电池模型则考虑了电池内阻的影响,将电池抽象为一个由电动势、内阻和电容组成的电路。
在实际电路中,电池等效电路的使用非常广泛。
例如,在设计电子产品时,需要对电池的寿命和性能进行评估,而电池等效电路可以帮助我们更准确地计算电路中电池的电压和电流。
此外,在设计太阳能电池板的充电系统时,也需要使用电池等效电路来优化系统性能。
在实际应用中,电池等效电路还需要考虑电池充电和放电的过程。
例如,在充电过程中,需要使用恰当的电路来控制电池的充电速度和电压,以避免电池过度充电并损坏电池。
同样,放电过程中也需要使用恰当的电路来控制电池的放电速度和电压,以避免电池被过度放电并损坏电池。
总之,电池等效电路是电路设计和优化中非常重要的一部分,它可以帮助我们更好地理解电池在电路中的运行机制,并优化电路性能。
- 1 -。
电池SOC/SOH

1.2 电池模型的研究现状对锂离子电池的建模有两种途径,一种是对电池进行大量的实验,积累实验数据,对采集到的数据进行模拟,总结得出锂离子电池的变化规律;另一种是对锂离子电池的微观行为进行研究,通过对微观行为的描述,借助计算机手段,建立具有理论基础的模型。
常用的电池模型主要有内阻模型,等效电路模型,遗传算法模型,神经网络模型以及电化学模型。
1.2.1 内阻模型内阻模型是最简单的电池模型,通常用来预测电池的容量[5]。
一般说来,电池容量随着电压和内阻变化。
由于电压在不同放电电流下会有不同的变化,研究者们就试图建立内阻与容量之间的关系。
然而内阻并非一个本征的数值,内阻模型需要大量的实验数据。
例如电池的最大容量在不同温度下的变化规律,电池输出端电压在不同电流倍率下的变化规律,电池内阻在不同温度下的变化规律。
根据实验得到的数据,根据电池使用环境的不同,依靠电池内阻来判定电池的容量,因此该模型更接近于一个数据库。
1.2.2 等效电路模型由于电池在电流的作用下会体现电阻以及电容的部分特征,v.Johsonl [6-7]等人提出可以用等效电路来建立电池模型,模拟电池的动态与静态性能。
基本的锂离子电池等效电路如图1所示,其中和分别代表电池的开路电压和输出o V V 电压,为电池内阻,并联电路模拟电池的外特性。
R 1R 1C oV 1C 1R RV 图1.1 电池等效电路模型1.2.3 遗传算法模型文献[8]研究了基于遗传算法的锂离子电池模型,一般情况下可以分析实验数据,求解方程等方法建立模型,模拟电池的特性。
但是由于电池内部的化学反应非常复杂,很难找到合适的函数来描述电池模型。
遗传算法计算方便,输出函数形式十分灵活,可以用来建立锂离子电池的模型。
1.2.4 神经网络模型Shen WX[9-10]等人研究了使用神经网络算法建立电池模型的可行性,建立了锂离子电池的模型,并且成功地预测电动汽车中电池的剩余电量。
K.T.Chau[11]将神经网络算法与模糊算法联合使用,取长补短,弥补两个算法各自的不足,用来估计锂离子电池的剩余容量,提高了单一算法的估计精度。
钙钛矿太阳电池等效电路

钙钛矿太阳电池等效电路
钙钛矿太阳电池是当前太阳电池领域的研究热点之一。
为了了解钙钛矿太阳电池的性能,需要建立其等效电路模型。
钙钛矿太阳电池的等效电路可以分为电荷输运层、势垒层和界面层三部分。
电荷输运层包括电子传输层和空穴传输层,它们分别负责电子和空穴的输运,具有一定的导电性。
势垒层是由于p-n结的形成而形成的,它的主要作用是阻止电荷的反向流动。
界面层则是光电转换的主要区域,其中包括阳极、阴极和钙钛矿层等。
通过对钙钛矿太阳电池等效电路的建立和分析,可以了解其电子和空穴的传输过程、光电转换效率以及输出特性等。
这对于钙钛矿太阳电池的性能优化和应用具有重要意义。
- 1 -。
太阳能电池等效电路分析

•太阳能电池等效电路分析•引言太阳能电池是利用光伏效应直接将光能转换为电能的器件。
其理想等效电路模型是一个电流源和一个理想二极管的并联电路,其输出特性可以用J—V曲线图表示。
如图1(略)。
在实际器件中,由于表面效应、势垒区载流子的产生及复合、电阻效应等因素的影响,其电流电压特性与理想特性有很大差异,这是因为理想模型不能正确反映实际器件的特点。
实际模型采用串联电阻及并联电阻来等效模拟实际器件中的各种非理想效应的影响。
本文针对太阳电池的等效电路模型,利用Matlab软件建立了仿真模块,模拟了太阳电池各输出参数受其内部电阻影响的程度。
太阳能电池等效电路分析实际太阳电池等效电路如图2所示,由一个电流密度为JL的理想电流源、一个理想二极管D和并联电阻Rsh,串联电阻Rs组合而成。
Rsh为考虑载流子产生与复合以及沿电池边缘的表面漏电流而设计的一个等效并联电阻,Rs为扩散顶区的表面电阻、电池体电阻及上下电极之间的欧姆电阻等复合得到的等效串联电阻。
太阳电池两端的电压为V,流过太阳电池单位面积的电流为J。
由图2可以得出其电流电压关系(公式略):式中,Js-—二极管反向饱和电流密度。
当太阳电池两端开路时,即负载阻抗为无穷大时,通过太阳电池的净电流J为零,此时的电压为太阳电池的开路电压VOC。
在(1)式中令J=0,则有(公式略)(2)式表明,开路电压不受串联电阻Rs,的影响,但与并联电阻Rsh有关。
可以看出,Rsh减小时,开路电压VOC会随之减小。
太阳电池两端短路即负载阻抗为零时,电压V为零,此时的电流为短路电流密度Jsc.在(1)式中令V=0,并且考虑到一般情况下R 〈<Rsh,(1)式可化为(公式略)由上式可以看出,短路电流基本与Rsh无关,但受Rs,的影响,随着Rs的增大,Js会减小。
太阳电池输出特性仿真以上定性分析了太阳电池等效电路中串联电阻和并联电阻对其伏安特性的影响,并讨论了短路电流和开路电压与电池内部的并联电阻及串联电阻之间的关系。
锂电池Thevenin(戴维南)一阶等效电路参数辨识

精品| 锂电池Thevenin一阶等效电路参数辨识一、参数辨识实验步骤(1)第一步:合理选择等效电路模型,如一阶、二阶电路模型,电化学模型等(2)第二步:选择电路元器件,定义元器件工作理原(3)第三步:对电池进行实验,本文参考HPPC测试原理(4)第四步:通过实验,计算各元器件参数(5)第五步:仿真与实测对比,算出误差二、等效电路模型Thevenin等效电路非线性特性好,能够快速便捷模拟仿真出锂电池的动静态电压特性,动锂电池系统的研究和仿真具有一定的帮助。
箭头为电流的流向,Thevenin一阶等效电路图如下所示三、等效电路元器件一阶等效电路主要由元器件R0、C1、R1、Em恒压源组成,其中:(1)R0为欧姆内阻(2)C1为极化电容(3)R1为极化内阻(4)Em为开路电压(5)Uoc为端电压(6)Uc为极化内阻两端电压四、电池HPPC实验HPPC测试计算各元器件参数,具体HPPC测试可以参照《Freedom CAR测试手册》。
采样数据可以参考如下原则进行五、计算元器件参数R0=U1−U2I在Thevenin电路中,时间常数J=R1*C1U3=U1∗(1−e t3/τ) (1)U4=U1∗(1−e t4/τ) (2)因此,由公式(1)、(2)递推出时间常数τ=t4−t3ln(U1−U4U1−U3)U3=U OC+i∗R0+U RC (3)U RC=i∗R1∗(1−e t/τ) (4)因此,由公式(3)、(4)推出R1=U3−U OC−i∗R0 i(1−e t2−t1/τ)进一步推出C1综上全部推出R0、R1、C1。
电源的两种模型及其等效变换

电源的两种模型及其等效变换
一个实际的直流电源(如直流发电机、蓄电池等)可以抽象成两种模型:
一种由独立电压源与线性时不变电阻元件串联而成;另一种由独立电流源与线性时不变电导并联而成。
在前一种电源模型中,电阻元件的电阻R称为原电源的内电阻,电压源的电压Us等于原电源的开路电压;在后一种电源模型中,线性时不变电阻元件的电导G称为原电源的内电导,电流源的电流Is等于原电源的短路电流。
由于它们代表同一个实际电源而有相同的外特性,所以它们能够等效互换。
两种模型等效互换的条件为Us和Is在电路计算中,为了计算方便,有时需要把一种电源模型变换成另一种电源模型。
把电压源模型换成电流源模型时,后者的电流源电流Is必须等于Us,内电导必须等于电阻的倒数;反之亦然。
1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常见电池等效电路模型
Rint模型将电池等效为理想电压源U oc与电阻R的串联:
Thevenin模型考虑了电池特性与电容相似的特点,模型中理想电压源U oc描述电池的开路电压,电阻R。
为电池内阻,电容CP与电阻RP并联描述电池的超电势
PNGV模型是2001年《PNGV电池试验手册》f3]中的标准电池模型,也沿用为2003年《FreedomCAR电池试验手册》中的标准电池模型。
模型中U oc为理想电压源,表示电池的开路电压;R0为电池欧姆电阻:RP为电池极化电阻;Cp为Rp旁的并联电容;Ip为极化电阻上的电流;电容Cb描述随着负载电流的时间累计而产生的开路电压的变化。
GNL模型,模型对电池的欧姆极化、电化学极化和浓差极化分别建模,并考虑自放电和过充电的影响。
模型中U oc为理想电压源,表示电池的开路电压;Cb为储能大电容,描述由于放电或充电引起的电池开路电压的变化,Ub为储能大电容两端的电压;R0为欧姆内阻;Re为电化学极化内阻,Ce为电化学极化电容,Re与Ce构成的电路网络模拟电池的电化学极化,Ue为电化学极化电容两端电压;Rp为浓差极化内阻,Cp为浓差极化电容,Rp与Cp构成的电路网络模拟电池的电化学极化,Up为浓差极化电容两端电压:Rs为自放电电阻或过充电电阻。
