圆柱与圆锥单元测试卷及答案
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷加精品答案
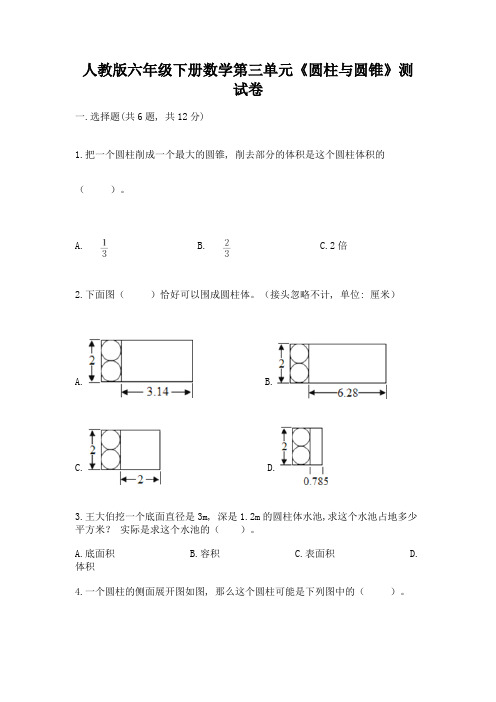
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷一.选择题(共6题, 共12分)1.把一个圆柱削成一个最大的圆锥, 削去部分的体积是这个圆柱体积的()。
A. B. C.2倍2.下面图()恰好可以围成圆柱体。
(接头忽略不计, 单位: 厘米)A. B.C. D.3.王大伯挖一个底面直径是3m, 深是1.2m的圆柱体水池,求这个水池占地多少平方米?实际是求这个水池的()。
A.底面积B.容积C.表面积D.体积4.一个圆柱的侧面展开图如图, 那么这个圆柱可能是下列图中的()。
A. B. C.5.用一个高36厘米的圆锥形容器盛满水, 倒入和它等底等高的圆柱形容器中, 水的高度是()厘米。
A.36B.18C.16D.126.下面第()个图形是圆柱的展开图。
A. B.C. D.二.判断题(共6题, 共12分)1.一个正方体木料, 加工成一个最大的圆锥, 圆锥的体积是正方体体积的/。
()2.圆柱的表面积等于底面积乘高。
()3.把一个土豆放在一个盛水的圆柱形容器里, 完全浸没, 土豆的体积等于上升的水的体积, 可以通过求圆柱的体积来计算。
()4.粉笔是最常见的圆柱。
()5.一个圆柱的直径和高相等, 则圆柱体的侧面展开图是正方形。
()6.一个圆锥和一个圆柱的高相等, 它们底面积的比是3:2, 圆锥的体积与圆柱的体积的比是1:2。
()三.填空题(共6题, 共11分)1.一根2米长的圆柱形木材, 锯成3段小圆柱后, 它们的表面积总和比原来增加了12.56dm2, 原来这根木材的体积是()dm3。
2.一个圆柱的体积是15立方厘米, 与它等底等高的圆锥的体积是()立方厘米。
3.圆锥的体积=()用字母表示()。
4.把圆柱的侧面沿高剪开, 得到一个(), 这个()的长等于圆柱底面的(), 宽等于圆柱的(), 所以圆柱的侧面积等于()。
5.一个圆柱的侧面积9.42平方厘米, 高4厘米, 这个圆柱的表面积是()平方厘米。
6.一个圆柱的底面直径是15 cm, 高是8 cm, 这个圆柱的侧面积是()cm2。
六年级第1单元《圆柱与圆锥》测试卷含答案
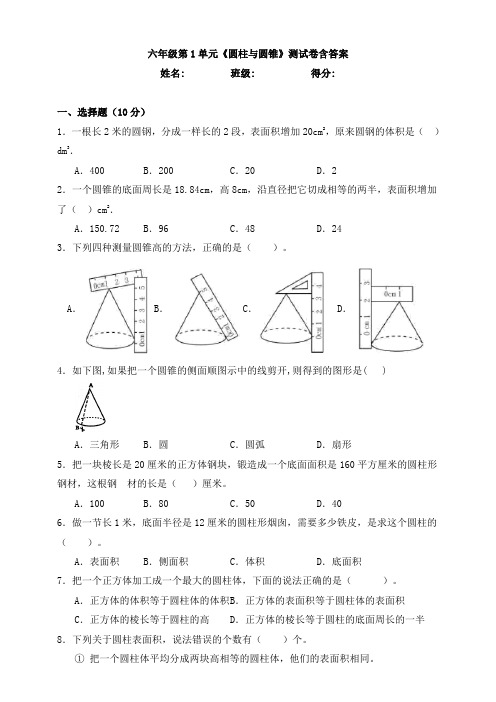
六年级第1单元《圆柱与圆锥》测试卷含答案姓名: 班级: 得分:一、选择题(10分)1.一根长2米的圆钢,分成一样长的2段,表面积增加20cm2,原来圆钢的体积是()dm3.A.400 B.200 C.20 D.22.一个圆锥的底面周长是18.84cm,高8cm,沿直径把它切成相等的两半,表面积增加了()cm2.A.150.72 B.96 C.48 D.243.下列四种测量圆锥高的方法,正确的是()。
A.B.C. D.4.如下图,如果把一个圆锥的侧面顺图示中的线剪开,则得到的图形是( )A.三角形B.圆C.圆弧D.扇形5.把一块棱长是20厘米的正方体钢块,锻造成一个底面面积是160平方厘米的圆柱形钢材,这根钢材的长是()厘米。
A.100 B.80 C.50 D.406.做一节长1米,底面半径是12厘米的圆柱形烟囱,需要多少铁皮,是求这个圆柱的()。
A.表面积B.侧面积C.体积D.底面积7.把一个正方体加工成一个最大的圆柱体,下面的说法正确的是()。
A.正方体的体积等于圆柱体的体积B.正方体的表面积等于圆柱体的表面积C.正方体的棱长等于圆柱的高D.正方体的棱长等于圆柱的底面周长的一半8.下列关于圆柱表面积,说法错误的个数有()个。
①把一个圆柱体平均分成两块高相等的圆柱体,他们的表面积相同。
②把一个圆柱体平均分成两块高相等的圆柱体,圆柱的表面积大小不变。
③把一个圆柱体平均分成三块高相等的圆柱体,每一块小圆柱的表面积是原来圆柱表面积的1/3。
A.0 B.1 C.2 D.39.把一个长、宽、高分别为7厘米、6厘米、4.5厘米的长方体铁块和一个棱长为5厘米的正方体铁块熔铸成一个底面直径为10厘米的圆柱,则圆柱的高是()。
A.4厘米B.6厘米C.8厘米10.如下图,将一个表面涂色的圆柱沿图中的线剖开后,没有涂色的面的面积一共是()cm²。
A.50.56 B.60.12 C.105.12二、填空题(37分)11.一个直角三角形,两条直角边分别是3cm和4cm,以它的短边为轴,形成的立体图形的体积是(_________)cm3。
小学人教版六年级下册数学(第三单元《圆柱与圆锥》达标测试卷(含参考答案)
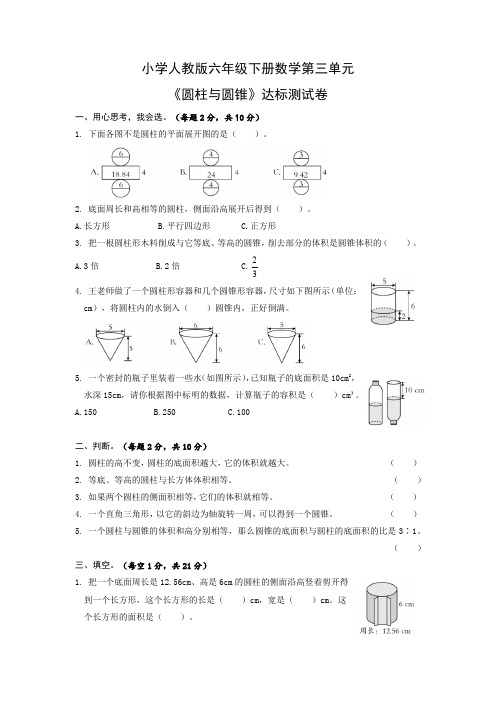
小学人教版六年级下册数学第三单元《圆柱与圆锥》达标测试卷一、用心思考,我会选。
(每题2分,共10分)1. 下面各图不是圆柱的平面展开图的是()。
2. 底面周长和高相等的圆柱,侧面沿高展开后得到()。
A.长方形B.平行四边形C.正方形3. 把一根圆柱形木料削成与它等底、等高的圆锥,削去部分的体积是圆锥体积的()。
2A.3倍B.2倍C.34. 王老师做了一个圆柱形容器和几个圆锥形容器,尺寸如下图所示(单位:cm),将圆柱内的水倒入()圆锥内,正好倒满。
5. 一个密封的瓶子里装着一些水(如图所示),已知瓶子的底面积是10cm2,水深15cm,请你根据图中标明的数据,计算瓶子的容积是()cm³。
A.150B.250C.100二、判断。
(每题2分,共10分)1. 圆柱的高不变,圆柱的底面积越大,它的体积就越大。
()2. 等底、等高的圆柱与长方体体积相等。
()3. 如果两个圆柱的侧面积相等,它们的体积就相等。
()4. 一个直角三角形,以它的斜边为轴旋转一周,可以得到一个圆锥。
()5. 一个圆柱与圆锥的体积和高分别相等,那么圆锥的底面积与圆柱的底面积的比是3∶1。
()三、填空。
(每空1分,共21分)1. 把一个底面周长是12.56cm、高是6cm的圆柱的侧面沿高竖着剪开得到一个长方形,这个长方形的长是()cm,宽是()cm。
这个长方形的面积是()。
2. 一个圆柱高是 8cm,侧面积是100.48cm2,它的底面积是()cm²,表面积是()cm²。
3. 把一个圆柱的底面分成许多相等的扇形,然后竖直切开拼成一个长方体,长方体的底面积等于圆柱的(),高等于圆柱的(),因为长方体的体积=()×(),所以圆柱的体积=()×()。
4. 把一个底面直径为12cm、高是20cm的圆柱,沿底面直径切割成同样大小的两半,表面积增加()cm²,体积是()cm³。
人教版六年级下册《圆柱圆锥》小学数学-有答案-单元测试卷

人教版六年级下册《圆柱圆锥》小学数学-有答案-单元测试卷一、圆柱和圆锥1. 一个圆柱形蓄水池,直径10米,深2米。
这个蓄水池的占地面积是多少?在池的一周及池底抹上水泥,抹水泥的面积是多少?2. 做十节长2米,直径8厘米的圆柱形铁皮烟囱,需要铁皮多少平方米?3. 压路机的滚筒是圆柱体,它的长是2米,滚筒横截面的半径是0.6米。
如果每分转动5周,每分可以压多大的路面?4. 大厅里有10根圆柱,圆柱底面直径1米,高8米。
在这些圆柱的侧面涂油漆,平均每平方米用油漆0.8千克,共需油漆多少千克?5. 一个圆柱的侧面积是25.12平方厘米,底面半径是2厘米,它的表面积是多少?6. 把两个底面直径都是4厘米、长都是3分米圆柱形钢材焊接成一个大的圆柱形钢材,焊接成的圆柱形钢材的表面积比原来两个小圆柱形钢材的表面积之和减少了多少?7. 将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体,这个物体的表面积是多少平方米?8. 一个蓄水池是圆柱形的,底面面积为31.4平方分米,高2.8分米,这个水池最多能容多少升水?9. 一个圆柱体的高是37.68厘米,它的侧面展开后恰好是正方形,这个圆柱体的体积是多少?(保留整数)10. 一个圆柱形水桶的体积是24立方分米,底面积是6平方分米,桶的装满了水,求水面高是多少分米?11. 一个圆柱形量筒,底面半径是5cm,把一块圆锥形铁块从量筒里取出后水面下降3cm.这块铁块的体积是多少立方厘米?12. 把一根长1.5米的圆柱形钢材截成三段后,表面积比原来增加9.6平方分米,这根钢材原来的体积是多少?13. 把一段长20分米的圆柱形木头沿着底面直径劈开,表面积增加80平方分米,原来这段圆柱形木头的表面积是多少?14. 砌一个圆柱形水池,底面周长是25.12米,深2米,要在它的底面和四周抹上水泥,如果每平方米用水泥10千克,共需水泥多少千克?15. 一堆圆锥形黄沙,底面周长是25.12m,高是1.5m,每立方米黄沙重1.5吨,这椎黄沙重多少吨?16. 一个无盖的圆柱形水桶,底面直径10厘米,高20厘米,制造这样一对水桶,至少要多少铁皮?如果用这对水桶盛水,能盛多少千克?(每升水重1千克,得数保留整千克)17. 大厅内有8根同样的圆柱形木柱,每根高5米,底面周长是3.2米,如果每千克油漆可漆4.5平方米,漆这些木柱需油漆多少千克?18. 一个圆锥形沙堆,底面周长是12.56米,高6米,将这些沙铺在宽10米的道路上铺0.04米厚,可以铺多少米长?19. 一个圆柱体和一个圆锥体等底等高,它们的体积相差50.24立方厘米。
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷及一套答案

人教版六年级下册数学第三单元《圆柱与圆锥》测试卷一.选择题(共6题,共12分)1.一个圆柱和一个圆锥,底面周长的比是2:3,体积比是5:6,那么这个圆柱和圆锥高的最简单的整数比是()。
A.8:5B.5:8C.12:5D.5:122.下面的说法错误的有()句。
①圆柱的底面积与高都扩大3倍,它的体积就扩大6倍②既是2的倍数又是5的倍数的数的特征是个位必须是0③一条线段绕着它的一个端点旋转120°,形成的图形是圆④在长方体上,我们找不到两条既不平行也不相交的线段⑤公式S梯形 =(a+b)h÷2,当a=b时,就是平行四边形的面积计算公式A.1B.2C.3D.43.下列图形绕虚线旋转一周,形成的几何体是圆锥的是()。
A. B. C. D.4.等底等高的圆柱、正方体、长方体的体积相比较()。
A.一样大B.长方体体积大C.圆柱体体积大D.正方体体积大5.一个圆柱体水桶的容积()圆锥体积。
A.相等B.大于C.小于D.无法确定6.如图,圆柱体的侧面积是()。
A.235.5cm2B.263.76cm2C.307.24cm2D.207.24cm2二.判断题(共6题,共12分)1.侧面积相等的两个圆柱,表面积也相等。
()2.如果圆锥的底面积是圆柱底面积的3倍,则圆锥和圆柱的体积相等。
()3.如果把一个圆柱的底面半径扩大到原来的3倍,高不变,那么他的体积就扩大到原来的9倍。
()4.圆柱的上下两个面都是圆形,大小不一样。
()5.把一个圆柱体削成一个最大的圆锥体,圆锥体的体积是削去部分的。
()6.圆柱体的底面周长和高相等时,沿着它的一条高剪开,侧面展开是一个正方形。
()三.填空题(共6题,共9分)1.一根2米长的圆柱形木材,锯成3段小圆柱后,它们的表面积总和比原来增加了12.56dm2,原来这根木材的体积是()dm3。
2.一个圆柱的直径和高都是2dm,这个圆柱的表面积是()平方分米。
3.从正面看到的图形是()形,从左面看是()形,从上面看是()形。
圆柱和圆锥单元综合测试(含答案)

圆柱和圆锥单元综合测试 一、填空题 1 .一个底面积是平方分米,高是 8 分米的圆柱,它的体积是 立方分米 . 2 .一个圆柱和一个圆锥等底等高,圆锥的体积是 8 立方分米,那么圆柱的体积是 立方分米. 3.把圆柱侧面睁开,获得的一个长方形,长方形的长是圆柱的 ,长方形的 宽是圆柱的 . 4 .一个圆锥和一个圆柱等底面积等体积,已知圆锥的高是 42 毫米,则圆柱的高是 毫米. 5 .一个圆柱和一个圆锥等底等高,它们的体积一共是 60 平方厘米,那么圆柱的体积是 立方厘米, 圆锥的体积是 立方厘米. 6 .一个圆柱形水桶,桶内直径是 4 分米,桶深 5 分米,现将 47.1 升水倒进桶内,水占水桶容积的 ℅. 7 .一个棱长是 4 分米的正方体容器装满水后,将水倒入一个底面积为 12 平方分米的圆锥形容器正好 装满,这个圆锥形容器的高是 分米. 8 .一个无盖的圆柱形水桶,底面半径是 2 分米,容积是立方分米,水桶的高是 分米做这个水桶 起码需要铁皮 平方分米. 9 .一支圆柱形新铅笔,需要涂漆的是 部分,假如铅笔长是 15 厘米,底面直径是厘米,涂 漆部分的面积是 平方厘米. 10.把圆锥的底面半径扩大到本来的 2 倍,高减小到本来的 1 倍,则圆锥的体积就 . 2 二、选择题 11.把圆柱的高扩大 2 倍,底面周长不变,圆柱的侧面积就扩大( ) A.2 倍 B.24 倍 C.12 倍 12.把一棱长为 2 分米的正方体,切割成最大的圆柱,圆柱的体积是( )立方分米. A. B.6.28 C. 13.把圆柱的底面半径扩大到本来的 2 倍,高不变,那么它的体积( ) A.扩大到本来的 2 倍 B.扩大到本来的 4 倍 C.扩大到本来的 8 倍 14.已知一个圆锥和一个圆柱高的比是 4:1,圆锥的底面半径是圆柱的底面半径的 1 ,圆锥和圆柱的 2 体积之比是( ) A. 1:3 B. 1:9 C. 1: 10 D. 1: 12 15.将一个正方体加工成最大的圆柱,这个正方体的棱长相当于圆柱的( )
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷及参考答案(综合卷)
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷一.选择题(共6题,共12分)1.下列说法,正确的有多少个?()①圆锥的体积等于圆柱体积的三分之一②长方体有12条棱和8个顶点③圆的半径扩大5倍,周长也扩大5倍④直线外一点与直线上各点连接的所有线段中,垂线段最短A.1个B.2个C.3个D.4个2.一个圆锥的体积是36立方米,底面积是12平方米,它的高是()米。
A.9B.6C.33.在半径为50cm的圆形铁皮上剪去一块扇形铁皮,用剩余部分制作成一个底面直径为80cm,母线长为50cm的圆锥形烟囱帽,则剪去的扇形的圆心角度数为()。
A.228°B.144°C.72°D.36°4.一个有盖圆柱形油桶的表面有()个面。
A.2B.3C.4D.65.把一块圆柱形状的木料削成一个最大的圆锥,削去部分的体积是4立方厘米.原来这块木料的体积是()。
A.12立方厘米B.8立方厘米C.6立方厘米6.圆柱的侧面沿直线剪开,在下列的图形中,不可能出现()。
A.长方形或正方形B.三角形C.平行四边形二.判断题(共6题,共12分)1.甲、乙两个圆柱的体积相等,如果甲圆柱的高是乙圆柱的,那么甲圆柱的半径则是乙圆柱的1.5倍。
()2.圆柱的表面积等于底面周长乘以高。
()3.压路机滚筒滚动一周能压多少路面是求滚筒的侧面积。
()4.一个矩形绕着其中一条边旋转360°,能得到一个圆柱;一个三角形绕着其中一条边旋转360°,也能得到一个圆锥。
()5.下图绕小棒转动,转出来的形状可能是圆柱。
()6.圆柱的体积一般比它的表面积大。
()三.填空题(共6题,共6分)1.一个圆锥形的沙堆,底面半径为1米,高为4.5分米,用这堆沙在5米宽的公路上铺2厘米厚的路面,可以铺()米。
2.已知一个圆锥的底面直径是4厘米,高是6厘米,这个圆锥的体积是()立方厘米。
3.一个圆锥形物体的底面积是50.24平方厘米,体积是301.44立方厘米,这个圆锥的高是()厘米。
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷带答案(完整版)
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷一.选择题(共6题, 共12分)1.边长是1厘米的正方形卷成一个圆柱体, 它的体积是()。
A.立方厘米B.立方厘米C.立方厘米D.立方厘米2.一个圆柱体的侧面展开图是正方形, 这个圆柱体的底面直径与高的比是()。
A.1∶πB.π∶1C.1∶2π3.它是由()。
A.两个大小不同的圆和曲面围成的圆柱B.由直角梯形旋转而得到的C.由半圆旋转而得到的4.圆柱的底面半径扩大3倍, 高不变, 体积扩大()。
A.3倍B.9倍C.6倍5.一个圆柱形容器内注有水, 它的底面半径是r厘米, 把一个圆锥形铜锤浸在水中, 水面上升h厘米, 这个圆锥形铜锤的体积是()。
6.圆锥的体积一定, 圆锥的底面积与高成()比例。
A.正B.反C.不成二.判断题(共6题, 共12分)1.如下图, 圆柱的底面是椭圆形。
()2.圆柱的侧面沿着高展开后会得到一个长方形或者正方形。
()3.圆锥的底面积扩大2倍, 体积也扩大2倍。
()4.圆锥的体积等于圆柱体积的。
()5.圆锥的侧面展开图是圆形。
()6.如果一个正方体和一个圆柱的底面积和高都相等, 那么它们的体积也相等。
()三.填空题(共6题, 共12分)1.一个直角三角形的两条直角边分别长6cm、8cm, 以8cm的直角边为轴旋转一周, 得到的立体图形是(), 它的体积是()cm3。
2.圆柱的两个底面是两个大小()的圆, 如果一个圆柱的底面周长和高相等, 那么它的侧面展开是一个()。
3.如右图所示, 把高是10厘米的圆柱切成若干等份, 拼成一个近似的长方体。
这个长方体的表面积比原来增加80cm2, 那么原来圆柱底面积半径是()厘米, 体积是()cm3。
4.一个圆锥体的体积是31.4立方分米, 高是5分米, 它的底面积是()平方分米。
5.有等底等高的圆柱和圆锥容器各一个, 将圆柱容器内装满水后, 倒入圆锥容器内。
当圆柱容器里的水全部倒光时, 溢出了36.2毫升, 这时圆锥容器里有水()升。
新人教版小学六年级数学下册第三单元《圆柱与圆锥》测试卷(含答案)
1 / 8 第3单元达标作业 1.认真想,仔细填。 (1)做一个圆柱形的竹笔筒,底面直径是8cm,高是12cm,至少需要( )cm²的竹片,笔筒的容积大约是( )cm³。 (2)等底、等高的圆柱和圆锥,如果圆锥的体积是18dm³,那么圆柱的体积是( )dm³;如果圆柱的体积是18dm³,那么圆锥的体积是( )dm³。 (3)一个圆柱和一个圆锥的体积相等,高也相等,若圆柱的底面积是12.56m²,则圆锥的底面积是( )m²。 (4)一支圆柱形铅笔,把这支铅笔用卷笔刀削尖(如图),笔尖(圆锥部分)的体积是削掉部分的( )。
2.我是小法官。(对的画“√”,错的画“×”) (1)圆柱有无数条高,圆锥也有无数条高。 ( ) (2)若把圆柱的侧面沿高展开得到一个正方形,则它的底面周长和高一定相等。 ( ) (3)把一个圆柱截成两段,它的表面积和体积都会增加。 ( ) (4)以一个三角形的任意一条边为轴,快速旋转一周,都可以得到一个圆锥。 ( ) (5)一个圆锥的高越长,体积就越大。 ( ) (6)正方体、长方体、圆柱和圆锥的底面积和高都相等时,体积也都相等。( ) 3.(1)计算下面圆柱的表面积和体积。
(2)计算下面圆锥的体积。 2 / 8
4.如图,一根长2米的圆柱形木头截开后表面积与原来相比增加了12dm²,它原来的体积是多少?
5.小玲在观看民俗表演时,看见一个叔叔在用力地敲击一个圆柱形鼓,声音低沉却异常浑厚。这面圆柱形鼓的侧面是铝皮,上、下底面是羊皮。已知底面直径是6分米,高是3分米,做这样一面鼓,两种材料各需要多少平方分米?
6.“1亿有多大?”张伟在家用黄豆做了一个实验,来感受1亿粒黄豆大约有多少。 (1)第一步,他数岀了1000粒黄豆,装在一个圆柱形玻璃杯中,正好装满。经测量,玻璃杯的底面周长是18.84cm,高4.5cm。1000粒黄豆约有多少立方厘米?这样算来,1亿粒黄豆约有多少立方米?(忽略玻璃杯的厚度) 3 / 8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱与圆锥单元测试卷及答案一、圆柱与圆锥1.具有近600年历史的北京天坛祈年殿为砖木结构,殿高38米,底层直径32米,三层重檐向上逐层收缩作伞状。
殿内有28根金丝楠木大柱,里圈的4根寓意春、夏、秋、冬四季,每根高约19米,直径1.2米。
因为它们是殿内最高的柱子,所以也叫通天柱,取的是和上天互通声息的意思。
(x取整数3)(1)请你根据上面信息,计算祈年殿的占地面积是多少平方米(2)如果要给4根通天柱刷油漆,则刷漆面积一共是多少平方米?【答案】(1)解:3x(32+2)2=768(平方米)答:计算祈年殿的占地面积是768平方米。
(2)解:3x1.2x19x4=273.6 (平方米)答:刷漆面积一共是273.6平方米。
【解析】【分析】(1)根据圆面积公式计算占地面积,底面直径是32米;(2)通天柱是圆柱形,刷漆的部分是侧面积,侧面积=底面周长x高,根据公式计算一个侧面积,再乘4就是刷漆的总面积。
2.工厂要生产一节烟囱,烟囱长2.5m,横截面是直径为40cm的圆。
(1)做一节烟囱一共需要铁皮多少平方米?(接头处忽略不计)(2)如果烟囱中充满废气,一节烟囱中最多可以容纳废气多少立方米?【答案】(1)解:40cm=0.4m3.14x0.4x2.5=3.14(m2)答:做一节烟囱一共需要铁皮3.14平方米。
(2)解:3.14x (0.4+2) 2x2.5=0.314 (m3)答:一节烟囱中最多可以容纳废气0.314立方米。
【解析】【分析】1cm=0.01m,(1)做一节烟囱一共需要铁皮的平方米数=这节烟囱横截面的周长x长,其中这节烟囱横截面的周长=横截面的半径x2xn;(2) 一节烟囱中最多可以容纳废气的立方米数=这节烟囱的容积=^2卜。
据此代入数据作答即可。
3.看图计算.(1)求圆柱的表面积(单位:dm)(2)求零件的体积(单位:cm)【答案】(1)解:3.14x10x20+3.14x (10“)2x2 = 628+3.14x25x2= 628+157= 785 (平方分米)答:圆柱的表面积是785平方分米。
(2)解:x3.14x (2“)2x3+3,14x (2“)2x4=x3.14x1x3+3.14x1x4=3.14+12.56=15.7(立方厘米)答:零件的体积是15.7立方厘米。
【解析】【分析】(1)圆柱的表面积是两个底面积加上一个侧面积,根据圆面积公式计算出底面积,用底面周长乘高求出侧面积;1(2)圆柱的体积=底面积x高,圆锥的体积=底面积x高x ,根据公式计算,用圆柱的体积加上圆锥的体积就是总体积。
4.如图,一个内直径是20cm的纯净水水桶里装有纯净水,水的高度是22cm.将水桶倒放时,空余部分的高度是3cm,无水部分是圆柱形.这个纯净水水桶的容积是多少升?【答案】解:3.14x (20+2) 2x22+3.14x (20+2) 2x3=3.14x100x(22+3) =3.14x100x25=7850(立方厘米)7850立方厘米=7.85升答:这个纯净水水桶的容积是7.85升。
【解析】【分析】水桶的容积包括水的体积和空余部分的体积,根据圆柱的体积公式分别计算后再相加即可求出水桶的容积。
5.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.【答案】解:3.14X (20“)2x2.24+314= 3.14x100x2.24+314= 703.36+314= 1017.36 (立方厘米),1017.36 + (3.14x92)= 1017.36x3+254.34= 3052.08+254.34=12(厘米),答:铅锤的高是12厘米。
【解析】【分析】根据题意可知,先求出圆锥形铅锥的体积,用圆柱形玻璃杯上面的空白1部分的体积+溢出的水的体积=圆锥形铅锥的体积,然后用圆锥形铅锥的体积+ +铅锥的底面积=铅锥的高,据此列式解答.6. 一个圆柱形钢管,内直径是20cm,水在钢管内的流速是每秒40cm,每秒流过的水是多少cm3?【答案】解:3.14x (20+2) 2x40=314x40=12560(cm3)答:每秒流过的水是12560cm3。
【解析】【分析】钢管是圆柱形,流出的水也是圆柱形。
用钢管的横截面面积乘每秒流出水的长度即可求出流过水的体积。
7.计算圆柱的表面积。
10cm【答案】解:3.14x (6+2) 2x2+3.14x6x10 =3.14x18+3.14x60 =56.52+188.4=244.92 (cm?)【解析】【分析】圆柱的表面积是两个底面积加上侧面积,根据圆面积公式计算底面积,用底面周长乘高求出侧面积。
8.我们熟悉的圆柱、长方体、正方体等立体的图形都称作直柱体,如图所示的三棱柱也是直柱体。
(1)通过比较,请你说说这类立体图形有什么样的共同特征呢?(至少写出3点)(2)我们已经学过圆柱、长方体、正方体的体积计算方法,请你大胆猜测一下,三棱柱的体积如何计算?若这个三棱柱的底面是一个直角三角形,两条直角边分别为2cm、3cm,高为5cm,请你计算出它的体积。
【答案】(1)答:①上下两个底面的大小和形状完全相同,并且它们相互平行。
②侧面与底面垂直,两个底面之间的距离就是直柱体的高。
③直柱体的侧面展开图是长方形。
④当底面周长与高相等时,侧面展开图是正方形。
(2)答:我们学过的长方体,正方体和圆柱体的体积都可以用“底面积x高〃来计算.因为三棱柱也是直柱体,所以我精测,三棱柱的体积计算方法也可以用“底面积x高〃来计算。
三棱柱的体积:2x3*x5=15cm3【解析】【分析】(1)根据每种直柱体的特征总结出它们共同的特征即可,例如:①它们的上下两个底面的大小和形状完全相同,并且它们相互平行;②它们的侧面与底面垂直,两个底面之间的距离就是直柱体的高;③它们的侧面展开图是长方形;④当底面周长与高相等时,侧面展开图是正方形;(2)长方体、正方体的体积都可以用“底面积x高〃来计算,而三棱柱也是直柱体,所以三棱柱的体积也可以用“底面积x高〃来计算,直角三角形的面积等于两条直角边乘积的一半,据此作答即可。
9.图“蒙古包〃是由一个近似的圆柱形和一个近似的圆锥形组成,这个蒙古包的空间大约是多少立方米?【答案】解:3.14x(8“)2x2+3.14x(8“)2x1x= 3.14x16x2+3.14x16x1x,100.48+16.75= 117.23 (立方米)答:这个蒙古包所占的空间大约是117.23立方米。
【解析】【分析】这个蒙古包是由圆锥和圆柱组成,所以这个蒙古包的空间是圆锥的体积和圆柱的体积,圆柱的底面半径=底面直径+2,圆柱的底面积=圆锥的底面积,所以圆柱的体积=nr2h,那么圆锥的体积=nr2h。
10. 一个圆锥体钢制零件,底面半径是3cm,高是2m,这个零件的体积是多少立方厘米?【答案】解:X3.14X32X2= 3.14x6=18.84(立方厘米)答:这个零件的体积是18.84立方厘米。
1【解析】【分析】圆锥的体积=底面积x高x ,根据公式计算体积即可。
11.把一个底面半径是4厘米,高是6分米的铁制圆锥体放入盛满水的桶里,将有多少立方厘米的水溢出?【答案】解:x3.14x42x6=x3.14x16x6=3.14x16x2=50.24x2=100.48(立方厘米)答:有100.48立方厘米的水溢出.【解析】【分析】根据题意可知,将圆锥放入盛满水的桶里,溢出的水的体积等于圆锥的1体积,依据圆锥的体积=x底面积x高,据此列式解答.12.有一个圆锥形沙堆,底面半径是10 米,高是4.8 米,把这些沙子均匀地铺在一条宽20米,厚40厘米的通道上,可以铺多长?【答案】40厘米=0.4米1314x102x4.8+3+(20x0.4)=502.4+8=62.8(米)答:可以铺62.8米。
【解析】【分析】可铺的米数=圆锥的底面积X高+3+ (宽X厚)13.一圆锥形小麦堆的底面周长为12.56米,高1.2米。
如果每立方米小麦约重30千克,这堆小麦约重多少千克?1【答案】解:12.56X1.2X X30=150.72 (千克)答:这腿小麦重150.72千克。
【解析】【分析】这堆小麦的重量=这堆小麦的体积X每立方米小麦大约重的千克数,其中这堆小麦的体积=xnr2h。
14.一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径2米的半圆.(1)搭建这个大棚大约要用多少平方米的塑料薄膜?(2)大棚内的空间大约有多大?【答案】(1)解:3.14X22+2X3.14X2X15+2=3.14X4+188.4+2= 12.56+94.2= 106.76 (平方米)答:搭建这个大棚大约要用106.76平方米的塑料薄膜。
(2)解:3.14X22X15+2=3.14x4x15+2=188.4+2=94.2(立方米)答:大棚内的空间大约有94.2立方米。
【解析】【分析】(1)搭建这个大棚大约要用塑料薄膜的平方米数=大棚的侧面积+半圆的面积x2,其中半圆的侧面积=横截面的半径x2xn+2,半圆的面积、2=圆的面积=横截面的半径2xn;(2)大棚内的空间=横截面的半径2xnx大棚的长度+2。
15.(1)请在下图中画出三角形八3。
已知其三个顶点的位置分别是:A(4, 3), B(-2, 0), C(4,0)。
(2)如果每个小方格的边长为1 cm,那么三角形ABC绕BC边旋转一周所得的立体图形的体积是多少?【答案】(1)解:如图:-3 -2 -] 0 | 2 ; jy二一国.或行=18五-56,能加(2)解:立体图形为圆锥,BC=2+4=6 cm AC=3 cm答:所得的立体图形的体积是56.52立方厘米.【解析】【分析】(1)数对中第一个数表示列,第二个数表示行,根据所在的列与行确定各点的位置后画出图形;(2)这个三角形是直角三角形,沿着一条直角边旋转一周后得到一个圆锥,圆锥的高是BC的长,底面半径是AC的长,根据圆锥的体积公式计算体积即可.。
