圆柱与圆锥试卷分析
《圆柱与圆锥》单元检测 试卷分析 试卷讲评课教案

《圆柱与圆锥》检测题试卷分析试卷讲评教案第三单元检测题姓名:等级:一、认真读题,谨慎填写。
1.沿着圆柱的高剪,侧面展开得到一个(),它的一条边就等于圆柱的(),另一条边就等于圆柱的()。
2.8050毫升=()升()毫升; 9时15分=()2.8立方米=()立方分米; 6000毫升=()升5平方米40平方分米=()平方米 5.4平方分米=()平方厘米3.把一段圆柱形木料削成一个最大的圆锥,削去部分是圆锥体积的()倍。
4.一个圆柱的底面周长是12.56厘米,高是5厘米,它的侧面积是()平方厘米,表面积是()平方厘米,体积是()立方厘米。
5.一个长方形长5厘米,宽4厘米,如果以宽为轴旋转一周得到一个立体图形,得到的是(),这个图形的体积是()立方厘米。
6.一个盛满水的圆锥体容器高9厘米,如果将水全部倒入与它等底等高的圆柱体容器中,则水高()厘米。
7.做一节底面直径为10分米,长40分米的烟筒,至少需要()平方分米铁片。
8.等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是()立方米,圆锥的体积是()立方米.9.一圆柱形罐头盒,高是1分米,底面周长6.28分米,罐头盒的侧面商标纸的面积最大是()平方分米,这个罐头盒至少要用()平方分米的铁皮。
10.一根长4米,横截面半径为2分米的圆柱形木料截成同样长的5段,表面积比原来增加()平方分米。
11.一个圆柱高减少4cm,则侧面积减少12.56cm²,这个圆柱底面积是()cm²12.一个圆柱高减少4厘米,则侧面积减少12.56平方厘米,这个圆柱底面积是()平方厘米。
13.如图,把一个圆柱沿半径切割成若干等份后拼成一个近似的长方体。
长方体的长是12.56cm,高是3cm.圆柱的底面积是()cm²,圆柱的体积是( )cm³二、反复比较,精心选择。
1.下面()图形是圆柱的展开图。
(单位:cm)2.求圆柱形木桶内盛多少升水,就是求水桶的()。
人教版数学六年级下册第三单元《圆柱与圆锥》单元卷附解析教师版
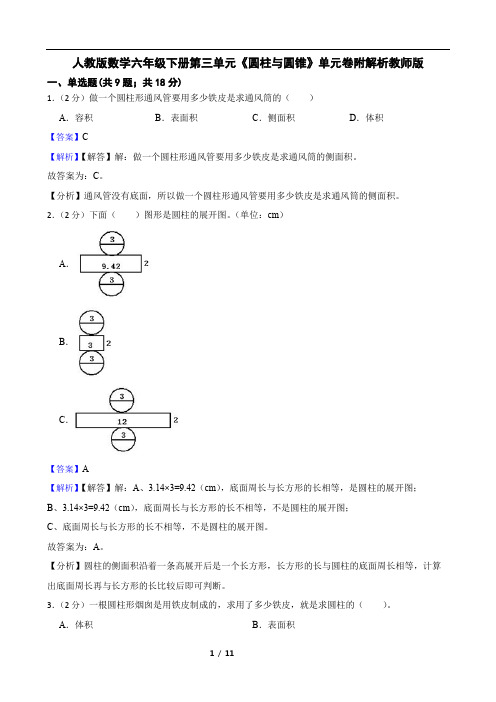
人教版数学六年级下册第三单元《圆柱与圆锥》单元卷附解析教师版一、单选题(共9题;共18分)1.(2分)做一个圆柱形通风管要用多少铁皮是求通风筒的()A.容积B.表面积C.侧面积D.体积【答案】C【解析】【解答】解:做一个圆柱形通风管要用多少铁皮是求通风筒的侧面积。
故答案为:C。
【分析】通风管没有底面,所以做一个圆柱形通风管要用多少铁皮是求通风筒的侧面积。
2.(2分)下面()图形是圆柱的展开图。
(单位:cm)A.B.C.【答案】A【解析】【解答】解:A、3.14×3=9.42(cm),底面周长与长方形的长相等,是圆柱的展开图;B、3.14×3=9.42(cm),底面周长与长方形的长不相等,不是圆柱的展开图;C、底面周长与长方形的长不相等,不是圆柱的展开图。
故答案为:A。
【分析】圆柱的侧面积沿着一条高展开后是一个长方形,长方形的长与圆柱的底面周长相等,计算出底面周长再与长方形的长比较后即可判断。
3.(2分)一根圆柱形烟囱是用铁皮制成的,求用了多少铁皮,就是求圆柱的()。
A.体积B.表面积C .侧面积D .1个底面积+侧面积【答案】C【解析】【解答】解:一根圆柱形烟囱是用铁皮制成的,求用了多少铁皮,就是求圆柱的侧面积。
故答案为:C 。
【分析】烟囱是圆柱形,但是烟囱没有底面,所以求制造烟囱需要铁皮的面积实际就是圆柱的侧面积。
4.(2分)制作一个长是20分米、底面直径是6分米的圆柱形通风管,至少需要铁皮( )平方分米。
A .376.8B .565.2C .753.6D .2260.8【答案】A【解析】【解答】解:3.14×6×20=3.14×120=376.8(平方分米) 故答案为:A 。
【分析】圆柱的底面周长=π×底面直径,圆柱的侧面积=底面周长×高。
5.(2分)一个圆柱,底面周长是25.12厘米,高是8厘米,如果沿底面直径垂直切开,它的截面是( )。
青岛版数学五年级下第四单元试卷分析

参考人数
58人
年 级
5(2)班
内 容
第四单元试卷分析
分
析
情
况
一、试卷总体分析:
本单元的主要内容是圆柱和圆锥。包括圆柱特征、侧面积、表面积、体积和圆锥特征、体积等知识。
基础知识掌握情况:本次单元检测难易程度适中,以基础题目为主,同时带着一些生活实际问题和概念性问题,从检测结果看,学生对本单元的基础性知识,如圆柱的侧面积、表面积、体积,还有圆锥体积计算等等掌握的不牢固,尤其后进生,学习困难导致低分。
3、练习的形式要多样,对于易混题加强辨析系生活实际,把数学知识应用于生活中去。
二、不足之处;
部分学生对于圆柱侧面积公式的推导不能理解,导致在做题过程中公式运用错误;等底等高圆柱和圆锥的体积关系不能熟练运用解决问题;不能灵活运用公式,出错率较高。
三、在今后的线上教学中,要注意从这几方面加以改进:
1、加强审题能力的培养,让学生从细节着手,分析每一道题。
2、注重灵活运用知识能力的培养,学会分析的方法,能够举一反三,不想当然做题。
第二单元《圆柱和圆锥》(原卷+解析)2022-2023学年六年级数学下册同步重难点讲义(苏教版)

第二单元《圆柱和圆锥》(原卷+解析)2022-2023学年六年级数学下册同步重难点讲义精讲精练(苏教版)一、教学目标1.学生能够了解圆柱和圆锥的基本定义和特征,能够有效地辨认和分类圆柱和圆锥;2.学生能够根据体积和表面积的公式,计算出给定圆柱和圆锥的体积和表面积;3.在探索型学习和讨论交流中,提高学生的数学思维能力和创新意识。
二、教学重点1.理解圆柱和圆锥的形状和特征;2.掌握圆柱和圆锥的公式及其应用;3. 教学的灵活性和实用性。
三、教学难点1.如何让学生理解圆锥的体积公式;2.如何让学生掌握圆柱和圆锥的应用。
四、教学准备1.教师:准备圆柱和圆锥的实物,计算圆柱和圆锥的体积和表面积的公式,预先准备演示板或PPT;2.学生:在老师的指导下,准备好笔、纸、尺和计算器等工具。
五、教学内容和步骤1. 教师进行导入(1)教师可以显示一些图像,让学生看看是否能够辨认出圆柱和圆锥。
显示后,可以让学生与同桌交流,让学生掌握圆柱和圆锥的基本概念。
(2)教师介绍圆柱和圆锥的基本形状,展示圆柱和圆锥的实物,让学生进行观察、感受和掌握。
2.教学内容(1)圆柱圆柱是由底面为圆的平行截面所限定的几何体,通俗来说,就是一根笔直的圆形棍子。
常见的圆柱有水杯、纸筒、柱形灯笼等。
圆柱的表面积公式为S=2πr²+2πrh,体积公式为V=πr²h。
(2)圆锥圆锥是由直角三角形沿直角边所在的直线旋转一周所得的几何体,通俗来说,就像是一个甜筒。
常见的圆锥有甜筒、角形锥灯笼等。
圆锥的表面积公式为S=πr²+πl(r+s),体积公式为V=1/3πr²h。
3.教学过程(1)让学生根据提供的图形辨认出圆柱和圆锥,并和同桌讨论说出一些常见的圆柱和圆锥。
(2)以圆柱为例,教师讲解圆柱的基本概念、公式及应用,通过实物演示,让学生理解并掌握圆柱的计算方法。
(3)以圆锥为例,教师讲解圆锥的基本概念、公式及应用,通过实物演示,让学生掌握圆锥的计算方法。
小升初必备:圆柱与圆锥典型及易错题型分析

小升初必备:圆柱与圆锥典型及易错题型分析圆柱与圆锥典型及易错题型(一)关于圆锥与圆柱相互之间的关系:1.若圆锥与圆柱等底等高,则它们的体积不等(圆锥的体积是圆柱的三分之一);2.若圆锥与圆柱等底等体积,则它们的高不等(圆锥的高是圆柱的3倍);3.若圆锥与圆柱等高等体积,则它们的底不等(圆锥的底面积是圆柱的3倍)。
练:1、一个圆柱和一个圆锥等底等高,它们的体积和是24立方分米,那么圆柱的体积是_________立方分米.2、一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,圆柱的体积是()立方分米。
A12B36C4D8(二)、关于圆柱、圆锥的典型实际问题:1.实质求圆柱的侧面积:通风管(如圆柱形烟囱)压路机1、做一根长1米,底面周长是2分米的圆柱形通风管,需要铁皮多少平方分米?(管壁厚度忽略不计)2.求的滚轮转动一周所压过的路面面积就是求圆柱(滚轮)的侧面积;(所压过的路面面积=圆柱(滚轮)的侧面积×转动速度×时间)1、压路机的滚筒是个圆柱,它的宽是3米,滚筒横截面半径是1米,那么滚筒转一周可压路面多少平方米?如果压路机的滚筒每分钟转10周,那么5分钟可以行驶多少米?3.求无盖的圆柱形表面积。
1、求圆柱形水桶能装水多少升,是求它的();做一节圆柱形通风管要多少铁皮,是求它的()A.侧面积B.表面积C.体积D.容积2、一个圆柱形儿童游泳池底面半径是4米,深0.5米.在它的四周和池底抹上水泥,每平方米需要水泥10千克,一共用水泥多少千克?3、一个无盖的圆柱形铁皮水桶,高50厘米,底面直径30厘米,做这个水桶约莫需用几何铁皮? (得数保留整数)4、做一个无盖的圆柱形鱼缸,底面半径3dm,高5dm。
(1)做这个鱼缸至少要几何平方分米?(得数保留整十平方分米)(2)这个鱼缸能装几何千克水?(1升水重1千克)5、圆柱的体积求底面积或高时,要用体积除以底面积或高,圆锥的体积求底面积或高时,要先乘以3再除以底面积或高。
圆柱与圆锥试卷分析5篇范文

圆柱与圆锥试卷分析5篇范文第一篇:圆柱与圆锥试卷分析圆柱与圆锥试卷分析一、计算错误1、带小数的计算容易错,计算表面积和体积的时候都会用到3.14,致使计算繁琐,导致计算错误较多。
2、没有注意到题目中单位的不统一,导致计算错误。
措施:加强小数乘除法计算练习,特别是对于和3.14相乘的计算练习;强制养成读题习惯。
二、概念不清1、圆柱中何时需要计算“两个底面”“一个底面”“没有底面”搞不清。
这个有些和生活经验有关,比如“通风管”。
2、极少数学生在应用的时候搞不清算的是表面积还是体积。
3、个别学生圆锥体积计算时没有乘三分之一。
三、等底等高的圆柱和圆锥的体积之间的关系。
1、前提:等底等高。
类似判断题:圆锥的体积等于圆柱体积的三分之一。
2、概念延伸。
(1)圆柱的体积是和它等底等高的圆锥体积的3倍。
(2)把一个圆柱削成一个最大的圆锥,削去部分的体积是圆锥体积的2倍。
(3)把一个圆柱削成一个最大的圆锥,削去部分的体积是圆柱体积的三分之二。
(4)把一个圆柱削成一个最大的圆锥,圆锥的体积是削去部分体积的二分之一。
(5)把一个圆柱削成一个最大的圆锥,圆柱的体积是削去部分体积的二分之三。
(6)等底等高的圆锥和长方体之间的体积关系。
类似题目:(1)一个圆柱的体积和它等底等高的圆锥的体积相差18立方分米,这个圆锥的体积是多少?(2)把一个圆柱形的木块削成一个最大的圆锥,削去部分的质量是24g。
这个圆锥重多少克?3、等体积等底的圆柱和圆锥的高之间的关系。
“圆锥的高是和它等体积等底的圆柱高的3倍。
” 这个要通过结合图让学生在大脑中建立两者之间的表象。
类似题目:(1)一个圆柱与一个圆锥体积相等,底面积也相等。
已知圆柱的高是12厘米,圆锥的高是()。
(2)一个圆柱与一个圆锥体积相等,圆柱的底面积是圆锥底面积的2倍,那么圆柱的高是圆锥高的()。
4、将一个形状的铁块铸成另一个形状时,它们的质量和体积不变。
类似题目:(1)将一块质量为156克的钢材铸成一个底面积是12平方厘米的圆锥形零件,这个零件的高是多少?(这种钢材每立方厘米质量是7.8克。
圆柱圆锥试卷分析0

2 ∶4 = 3 ∶6
4 ∶2 = 6 ∶3 4 ∶6 = 2 ∶3
判断:
(1)圆柱体、长方体和正方体的体积都可以用底面积乘以 高的方法来计算。 ( )
(2)圆柱的底面积扩大3倍,体积也扩大3倍 。
√ ( ) ×
(3)一个长方体与一个圆柱体,底面积相等,高也相等, 那么它们的体积也相等。 ( )
√ (4)圆柱体体积一定,圆柱体底面积和高成反比例。 ( √) (5) 两个圆柱体的侧面积相等,体积也一定相等。 ( ) × (6)一个圆柱形的水桶能装水15升,我们就说水桶的体积 是15立方分米。 ( ×)
试卷分析
1,计算错误 2,公式不熟
3,单位没统一
错题集:
4, 一个圆柱的底面半径是 5厘米,侧面展开正好是一个正 方形,圆柱的高是( )
5 , 将 一 个体积是 27 立方厘米的圆柱削成一 个最大的圆锥,这个圆 锥的体积是( )立方分 米
7,把一个长4米,横截面半 径为2厘米的圆柱形木料截 成同样长的4段,表面积比 原来增加了()平方厘米
判断:若圆锥的体积等于圆柱体 积的1/3,圆柱与圆锥就等底等高。
选择:圆柱的高不变,底面半径扩 大2倍,它的体积就扩大( ) 一个圆锥的体积是12.54立方厘米,
高是3厘米,它的底面积是( )
一个圆锥形的稻谷堆,量 得它的底面周长是12。56米,高 为1。5米,已知每立方米稻谷重 750千克,这堆稻谷共重多少千 克?
一个长5分米,宽3分米 ,高4分米的长方形铁块,将它 溶铸成底面积为6平方分米的圆 柱体,圆柱体的高为多少分米?
将一个圆柱体沿底面半径分 成许多相等的小块,拼成一 个底面积是628平方厘米, 高是4厘米的近似长方体。 原来圆柱体的体积是多少立 方厘米?
北师大版小学数学六年级下册圆柱和圆锥单元测试卷附答案与试题解析

北师大版小学数学六年级下册圆柱和圆锥单元测试卷附答案与试题分析一、填空:(24 分)1.(2 分)圆柱的上、下两个面叫做,他们是的两个圆,两个底面之间的距离叫做高.2.(2 分)圆锥的底面是一个,从圆锥的极点究竟面_________的距离是圆锥的高.3.(2 分)等底等高的圆柱和圆锥,它们的体积一共是48 立方分米,那么圆锥体积是_立方分米.4.(2 分) 3.2 立方米 =5.(2 分)一个圆锥体的底面半径是立方分米;3 分米,高是500 毫升 =10 分米,它的体积是升.立方分米.6.(2分)一个圆柱体,底面半径是 2 厘米,高是 6 厘米,它的侧面积是平方厘米.7.(2 分)(2012?平坝县)圆锥体底面直径是 6 厘米,高3 厘米,体积是立方厘米.8.(2 分)一个无盖的圆柱形铁水桶,高是0.3 米,底面直径是 0.2 米,做 10 个这样的水桶起码要用铁皮平方米.9.(2 分)假如一个圆柱体的侧面睁开是个正方形,则这个圆柱的底面周长和高_________.10.(2 分)一个圆柱和一个圆锥等底等高,它们的体积和是24 立方分米,那么圆柱的体积是立方分米.11.(2 分)把一段圆钢切削成一个最大的圆锥,切削掉的部分是 6 千克,这个圆锥的重量是千克.12.(2 分)一个圆柱形木材长 16 分米,半径是 3 分米,把它锯成两段后,表面积增添了分米.二、判断题:(10 分)13.(2 分)底面积相等,体积也相等的圆柱和圆锥,圆锥的高是圆柱的 3 倍.()14.(2 分)(2010?芜湖县)长方体、正方体、圆柱和圆锥的体积都能够用“底面积×高”计算.()15.(2 分)(2011?荣昌县)圆锥的体积是圆柱体积的.()16.(2 分)长方形一边为轴,旋转一周形成的图形是一个圆柱.17.(2 分)(2012?广州一模)圆锥的底面半径扩大为本来的3为本来体积的 9 倍.()()倍,它的体积就扩大三、选择( 10 分)18.( 2 分)求圆柱形水桶能装水多少升,是求它的(少铁皮,是求它的()A .侧面积B.表面积C.体积19.(2 分)一个圆柱的高是7.5 分米,底面半径是);做一节圆柱形通风管要多D.容积10 厘米,它的体积是()立方厘米.A .2355B.23550C.D.20.(2 分)一个圆柱体铁块能够浇铸成()个与它等底等高的圆锥形铁块.A .1B.2C.3D.421.(2 分)圆锥的体积是120 立方厘米,高是10 厘米,底面积是()平方厘米.A .12B.36C.4D.822.(2 分)把一圆柱形木材锯成两段,增添的底面有()A .1B.2C.3D.4四、解答题(共 1 小题,满分 16 分)23.(16 分)脱式计算:×+6250÷25+16×12(﹣)(+ )×.五、解答题(共 1 小题,满分 8 分)24.(8 分)填空:已知圆柱表面圆柱体积圆锥体积积底面半径 5 厘米高 1.2 厘米底面直径 3.6 分米高 2 分米底面周长 1.884 米高 3 米六、25.(8 分)计算下边各图形的体积(单位:cm)七、解决问题:(24 分)26.(4 分)一个圆柱形汽油桶,底面直径是12 厘米,高 2 厘米,这个油桶能装多少毫升汽油?27.(4 分)(2011?安平县)用铁皮制作一个圆柱形油桶,底面直径 6 分米,高 10 分米.制作这个油桶起码要用铁皮多少平方分米?28.(4 分)一个圆柱形小孩游泳池底面半径是 4 米,深 0.5 米.在它的周围和池底抹上水泥,每平方米需要水泥 10 千克,一共用水泥多少千克?29.(4 分)一个圆锥形沙堆,底面周长是 25.12 米,高 1.8 米.假如每立方米沙重 1.7 吨,这堆沙子重多少吨?(得数保存整吨数)假如用载重 3.4 吨的汽车来运,一共要运多少次?30.(4 分)一根圆柱形钢材,底面直径是 4 厘米,长是 80 厘米,将它铸成直径是 20 厘米的圆柱形部件,这个部件的高是多少厘米?31.(4 分)(2007?北塘区)一家饮料生产商生产一种饮料,采纳圆柱形易拉罐包装,从易拉罐外面量,底面直径 6 厘米,高 12 厘米.易拉罐侧面有“净含量 340 毫升”的字样,请问这家饮料商能否欺诈了花费者?(请你经过计算、比较后说明问题)北师大版六年级下数学素质测试卷一圆柱和圆锥参照答案与试题分析一、填空:(24 分)1.(2 分)圆柱的上、下两个面叫做底面,他们是完整相同的两个圆,两个底面之间的距离叫做高.考点:圆柱的特色.专题:立体图形的认识与计算.剖析:依据圆柱的特色,圆柱的上、下两个叫做底面,它们是完整相同的两个圆,侧面是一个曲面,两个底面之间的距离叫做圆柱的高.解答:解:圆柱的上、下两个叫做底面,它们是完整相同的两个圆,两个底面之间的距离叫做圆柱的高.故答案为:底面,完整相同.评论:本题考察的目的是使学生坚固掌握圆柱的特色.2.(2 分)圆锥的底面是一个圆,从圆锥的极点究竟面圆心的距离是圆锥的高.考点:圆锥的特色.专题:立体图形的认识与计算.剖析:依据圆锥的特色,圆锥的底面是一个圆,侧面是个曲面,侧面睁开是一个扇形,从圆锥的极点究竟面圆心的距离叫做圆锥的高.解答:解:圆锥的底面是一个圆,从圆锥的极点究竟面圆心的距离叫做圆锥的高.故答案为:圆,圆心.评论:本题主要考察圆锥的特色,考察目的是使学生坚固掌握圆锥的特色及圆锥各部分的名称.3.(2 分)等底等高的圆柱和圆锥,它们的体积一共是 48 立方分米,那么圆锥体积是 12 立方分米.考点:圆锥的体积;圆柱的侧面积、表面积和体积.剖析:等底等高的圆柱的体积是圆锥的体积的 3 倍,把它们的体积之和均匀分红四份,那么圆锥的体积就是此中的 1 份,由此即可解答.解答:解:48÷(3+1)=12(立方分米);答:圆锥的体积是12 立方分米.故答案为: 12.评论:本题考察了等底等高的圆柱与圆锥的体积倍数关系的灵巧应用.4.(2 分) 3.2 立方米 = 3200立方分米;500 毫升升.考点:体积、容积进率及单位换算.专题:长度、面积、体积单位.剖析:把 3.2 立方米转变立方分米数,用 3.2 乘进率 1000;把500 毫升转变为升数,用 500 除以 1000;据此解答即可.解答:解:3.2 立方米 =3200 立方分米;500 毫升 =0.5 升;故答案为: 3200,.评论:解决本题重点是要熟记单位间的进率,知道假如是高级单位的名数转变成初级单位的名数,就乘单位间的进率;反之,就除以进率来解决.5.(2 分)一个圆锥体的底面半径是 3 分米,高是 10 分米,它的体积是 94.2 立方分米.考点:圆锥的体积.剖析:2,由此代入公式即可计算.圆锥的体积 =×πr h解答:2解:××3×10,= ××9×10,(立方分米);答:它的体积是94.2 立方分米.故答案为:.评论:本题考察了圆锥的体积公式的计算应用.6.(2 分)一个圆柱体,底面半径是2 厘米,高是6 厘米,它的侧面积是75.36 平方厘米.考点:圆柱的侧面积、表面积和体积.剖析:依据圆柱体的侧面积公式:s 侧 =ch,圆的周长公式是: c=πd,或 c=2πr,已知底面半径是 2 厘米,高是 6 厘米,直接依据侧面积公式解答.解答:解:2××2×6×6(平方厘米);答:它的侧面积是75.36 平方厘米.故答案为:.评论:本题主要考察圆柱体的侧面积计算,直接依据侧面积公式解答即可.7.(2 分)(2012?平坝县)圆锥体底面直径是 6 厘米,高 3 厘米,体积是 28.26 立方厘米.考点:圆锥的体积.专题:立体图形的认识与计算.剖析:依据圆锥的体积公式: v= sh,第一依据圆的面积公式求出圆锥的底面积,再把数据代入圆锥的体积公式解答.解答:解:×(6÷2)2×3,=×9×3,(立方厘米);答:圆锥的体积是28.26 立方厘米.故答案为: 28.26 立方厘米.评论:本题考察的目的要修业生坚固掌握圆锥的体积公式,能够依据圆锥的体积公式正确快速地计算圆锥的体积.8.(2 分)一个无盖的圆柱形铁水桶,高是 0.3 米,底面直径是 0.2 米,做 10 个这样的水桶起码要用铁皮 2.198 平方米.考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.剖析:依据题意知道,先求出做一个圆柱形水桶需要的铁皮,其实是求水桶的侧面积加底面积,依照圆柱的侧面积 =底面周长×高,圆柱的底面积 =πr2,再乘 10 即可.解答:解:×(÷2)2××,×,,(平方米),×(平方米),答:做 10 个这样的水桶起码要用铁皮 2.198 平方米;故答案为:.评论:解答本题的重点是理解:做这类水桶要用铁皮的面积,其实是求水桶的侧面积加1个底面积.9.(2 分)假如一个圆柱体的侧面睁开是个正方形,则这个圆柱的底面周长和高相等.考点:圆柱的睁开图.专题:立体图形的认识与计算.剖析:由圆柱的侧面睁开图的特色可知:圆柱的侧面睁开后是一个长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高,又因睁开后是一个正方形,则圆柱的底面周长等于圆柱的高,据此即可进行解答.解答:解:由圆柱的侧面睁开图的特色可知:假如一个圆柱体的侧面睁开是个正方形,则这个圆柱的底面周长和高相等.故答案为:相等.评论:本题主要考察圆柱的侧面睁开图的特色.10.(2积是分)一个圆柱和一个圆锥等底等高,它们的体积和是18 立方分米.24 立方分米,那么圆柱的体考点:圆柱的侧面积、表面积和体积;圆锥的体积.剖析:依据等底等高的圆柱的体积与圆锥的体积之比是3:1,把它们的体积之和均匀分红4 份,那么圆柱占了此中 3 份,圆锥占了 1 份,由此即可解决问题.解答:解:因为等底等高的圆柱的体积与圆锥的体积之比是 3:1,3+1=4,因此圆柱的体积是: 24×=18(立方分米),答:圆锥的体积是 6 立方分米,圆柱的体积是18 立方分米.故答案为: 18.评论:本题考察了等底等高圆柱与圆锥的体积的倍数关系的灵巧应用.11.(2量是分)把一段圆钢切削成一个最大的圆锥,切削掉的部分是3 千克.6 千克,这个圆锥的重考点:简单的立方体切拼问题;圆锥的体积.专题:立体图形的认识与计算.剖析:圆柱内削出的最大的圆锥,与原圆柱等底等高,因此圆锥的体积是圆柱的体积的,则圆锥的体积就是削去部分的体积,削去的部分是 6 千克,依据分数乘法的意义即可求出圆锥的体积.解答:解:6× =3(千克),答:这个圆锥的体积是 3 千克.故答案为: 3.评论:本题考察了圆柱内最大的圆锥的特色以及等底等高的圆柱与圆锥的体积倍数关系的灵巧应用.12.(2 分)一个圆柱形木材长 16 分米,半径是 3 分米,把它锯成两段后,表面积增添了56.52 平方分米.考点:简单的立方体切拼问题;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.剖析:把圆柱切成相同长的 2 段后,表面积比本来增添了 2 个圆柱的底面积,由此依据圆柱的底面半径求出圆柱的底面积,再乘以2,即可解决问题.解答:解:×32×2,×2,(平方分米),答:表面积比本来增添了56.52 平方分米.故答案为: 56.52 平方.评论:抓住圆柱的切割特色,得出表面积是增添了圆柱的2 个底面积是解决此类问题的重点.二、判断题:(10 分)13.(2 分)底面积相等,体积也相等的圆柱和圆锥,圆锥的高是圆柱的3倍.正确.考点:圆柱的侧面积、表面积和体积;圆锥的体积.专题:立体图形的认识与计算.剖析:设圆锥和圆柱的底面积是S,体积是 V,依据圆柱与圆锥的体积公式可得出它们的高,由此即可解答.解答:解:设圆锥和圆柱的底面积是S,体积是 V,则:圆锥的高是:,圆柱的底面积是:,圆锥的高是圆柱的高的:÷=3,因此原题说法正确,故答案为:正确.评论:本题考察了圆柱与圆锥的体积公式的灵巧应用,这里可得结论:体积相等,底面积相等的圆锥的高是圆柱的高的 3 倍.14.(2 分)(2010?芜湖县)长方体、正方体、圆柱和圆锥的体积都能够用“底面积×高”计算.错误.考点:长方体和正方体的体积;圆柱的侧面积、表面积和体积;圆锥的体积.专题:压轴题.剖析:长方体、正方体、圆柱的体积都能够用底面积×高来计算,可是,圆锥的体积= ×底面积×高,由此即可判断.解答:解:因为圆锥的体积计算是×底面积×高,因此,原题说法错误.故答案为:错误.评论:本题考察了长方体、正方体、圆柱、圆锥的体积公式的灵巧应用.15.(2 分)(2011?荣昌县)圆锥的体积是圆柱体积的.错误.考点:圆柱的侧面积、表面积和体积;圆锥的体积.专题:压轴题.剖析:依据圆柱和圆锥的体积公式可知:等底等高的圆锥的体积是圆柱体积的,由此即可判断.解答:解:只有在等底等高的状况下,圆锥的体积是圆柱体积的,因此原题说法错误.故答案为:错误.评论:本题考察了等底等高的圆柱与圆锥的倍数关系的性质,要注意数学语言的严实性.16.(2 分)长方形一边为轴,旋转一周形成的图形是一个圆柱.正确.考点:将简单图形平移或旋转必定的度数;圆柱的特色.专题:立体图形的认识与计算.剖析:本题是一个长方形绕着它的一边旋转一周,依据面动成体的原理即可得解.解答:解:以长方形的一边所在直线为旋转轴,形成的旋转体叫做圆柱体.故答案为:正确.评论:依据圆柱体的形成可作出判断.本题主要考察圆柱的定义.17.(2 分)(2012?广州一模)圆锥的底面半径扩大为本来的来体积的 9 倍.正确.3 倍,它的体积就扩大为原考点:圆锥的体积;积的变化规律.专题:立体图形的认识与计算.剖析:因为圆锥的体积 = ×底面积×高,用公式表示为v= sh= πr2h,因此半径 r 扩大 3 倍,即:(3r)2=9r2,因此体积扩大9 倍.解答:解:圆锥的体积公式表示为v= sh= πr2h,因此半径 r 扩大 3 倍,即:(3r)2=9r2,因此体积扩大9 倍.因此原题说法正确.故答案为:正确.评论:本题考察了学生对圆锥体积公式的掌握状况,以及对问题的剖析判断能力.三、选择( 10 分)18.(2 分)求圆柱形水桶能装水多少升,是求它的(铁皮,是求它的()A .侧面积B.表面积C.体积);做一节圆柱形通风管要多少D.容积考点:圆柱的侧面积、表面积和体积;体积、容积及其单位.专题:立体图形的认识与计算.剖析:(1)依据容积的定义,即可解答;(2)因为圆柱形通风管没有底面只有侧面,要求做一节圆柱形通风管需要多少铁皮,就是求它的侧面积是多少,由此选择答案即可.解答:解:(1)依据容积的定义可知:求圆柱形水桶能装水多少升,就是求这个圆柱水桶的容积;(2)因为圆柱形通风管没有底面只有侧面,要求做一节圆柱形通风管需要多少铁皮,就是求它的侧面积是多少;应选: D;A.评论:本题是利用圆柱的知识解决实质问题,要仔细剖析题意,明确是利用圆柱的哪些知识来解答.19.(2分)一个圆柱的高是7.5 分米,底面半径是10 厘米,它的体积是()立方厘米.A .2355B.23550C.D.考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.剖析:圆柱的体积 V= πr2h,由此代入数据即可解答.解答:解:7.5 分米 =75 厘米,2×10 ×75,×100×75,答:它的体积是23550 立方厘米.应选: B.评论:本题考察了圆柱的体积公式的灵巧应用,要注意单位一致.20.(2 分)一个圆柱体铁块能够浇铸成()个与它等底等高的圆锥形铁块.A .1B.2C.3D.4考点:圆锥的体积;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.剖析:依据等底等高的圆柱的体积是圆锥体积的 3倍,可知 1 个圆柱形的铁块能够铸成 3个与它等底等高的圆锥形铁块;据此解答即可.解答:解:因为等底等高的圆柱的体积是圆锥体积的 3 倍,因此 1 个圆柱形的铁块能够铸成 3 个与它等底等高的圆锥形铁块;应选: C.评论:本题主要考察了等底等高的圆柱的体积与圆锥的体积的关系.21.(2 分)圆锥的体积是 120 立方厘米,高是 10 厘米,底面积是()平方厘米.A .12B.36C.4D.8考点:圆锥的体积.专题:立体图形的认识与计算.剖析:圆锥的底面积 =体积×3÷高,由此代入数据即可解答.解答:解:120×3÷10,=360÷10,=36(平方厘米),答:底面积是 36 平方厘米.应选: B.评论:本题考察了圆锥的体积 = πr2h 的灵巧应用.22.(2 分)把一圆柱形木材锯成两段,增添的底面有()A .1B.2C.3D.4考点:简单的立方体切拼问题.专题:立体图形的认识与计算.剖析:依据圆柱的切割特色可知,把一圆柱形木材锯成两段,表面积增添的是 2 个圆柱的底面,由此即可选择.解答:解:依据题干剖析可得:把一圆柱形木材锯成两段,表面积增添的是2 个圆柱的底面,应选: B.评论:抓住圆柱的切割特色即可解答问题.四、解答题(共 1 小题,满分 16 分)23.(16 分)脱式计算:×+6250÷25+16×12(﹣)(+ )×.考点:分数的四则混淆运算;整数四则混淆运算;运算定律与简易运算.专题:运算次序及法例;运算定律及简算.剖析:(1)把除法改为乘法,先算乘法,再算加法;(2)先算除法和乘法,再算加法;(3)(4)先算括号内的,再算括号外的.解答:解:(1)×÷ +,=×× + ,=+ ,=;(2)6250÷25+16×12,=250+192,=442;(3)(﹣),=(﹣)×,=×,=;(4)(+)× ,=× ,=.评论:在脱式计算中,特别注意运算次序和运算法例,在计算过程中,能约分的要约分.五、解答题(共 1 小题,满分8 分)24.(8 分)填空:已知圆柱表面圆柱体积圆锥体积积底面半径 5 厘米高 1.2 厘米底面直径 3.6 分米高 2分米底面周长 1.884 米高 3米考点:圆柱的侧面积、表面积和体积;圆锥的体积.专题:立体图形的认识与计算.剖析:2π ;圆柱的体积22因为圆柱的表面积 =2πrrh= r h= r h+2π ;圆锥的体积π ;因此题干中先利用直径除以 2 求出半径;利用底面周长÷π÷2求出半径,再利用上述公式代入数据,即可计算填空.解答:解:(1)圆柱的表面积是:×(5×2)××52×2=37.68+157,(平方厘米),圆柱的体积是:×52×(立方厘米),圆锥的体积是:×52××(立方厘米);(2)底面半径是:÷(分米),圆柱的表面积是:×××2×2,,(平方分米),圆柱的体积是:×2×(立方分米),圆锥的体积是:×2×2×(立方分米);(3)底面半径是:÷÷(米),圆柱的表面积是:××2×2,,圆柱的体积是:×2×(立方米),由以上计算能够填空:评论:本题考察了圆柱表面积、体积和圆锥的体积公式的灵巧应用,要修业生熟记公式即可解答.六、25.(8 分)计算下边各图形的体积(单位:cm)考点:圆柱的侧面积、表面积和体积;圆锥的体积.剖析:依据圆柱的体积公式: v=sh,圆锥的体积公式: v= sh,把数据代入公式计算即可.解答:解:×(10÷2)2×10,×25×10,=785(立方厘米);×(20÷2)2×15,=×100×15,=1570(立方厘米);答:圆柱体的体积是785 立方厘米,圆锥的体积是1570 立方厘米.评论:本题主要考察圆柱的体积和圆锥的体积计算,直接依据它们的体积公式解答即可.七、解决问题:(24 分)26.(4 分)一个圆柱形汽油桶,底面直径是12 厘米,高 2 厘米,这个油桶能装多少毫升汽油?考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.剖析:依据圆柱的体积公式 V=sh=πr2h,代入数据即可求出油桶的体积,即油桶的容积.解答:解:×(12÷2)2×2,×36×2,×72,(立方厘米),226.08 立方厘米 =226.08 毫升,答:这个油桶能装226.08 毫升汽油.评论:本题主要考察了圆柱的体积公式V=sh=πr2h 的灵巧应用.27.(4 分)(2011?安平县)用铁皮制作一个圆柱形油桶,底面直径 6 分米,高 10 分米.制作这个油桶起码要用铁皮多少平方分米?考点:圆柱的侧面积、表面积和体积.专题:压轴题;立体图形的认识与计算.剖析:要求制作这个油桶起码要用铁皮,实质是求圆柱形油桶的表面积,由此依据圆柱的侧面积公式 S=ch=πdh 与 S=πr2,列式解答即可.××18,×78,(平方分米);答:制作这个油桶起码要用铁皮244.92 平方分米.评论:本题主要考察了圆柱的表面积的计算方法:圆柱的表面积=侧面积 +2个底面积.28.(4 分)一个圆柱形小孩游泳池底面半径是 4 米,深 0.5 米.在它的周围和池底抹上水泥,每平方米需要水泥10 千克,一共用水泥多少千克?考点:对于圆柱的应用题.专题:立体图形的认识与计算.剖析:要求共需多少千克水泥,需求出涂水泥的面积,即求圆柱的侧面积和一个底面积(缺乏上边),由此列式解答即可.解答:解:×4×2××42,,(平方米);×10=628(千克);答:共需 628 千克水泥.评论:本题主要考察圆柱表面积的实质应用,重点要弄清是求圆柱哪些面的面积,再依条件列式解答即可.29.(4 分)一个圆锥形沙堆,底面周长是 25.12 米,高 1.8 米.假如每立方米沙重 1.7 吨,这堆沙子重多少吨?(得数保存整吨数)假如用载重 3.4 吨的汽车来运,一共要运多少次?考点:对于圆锥的应用题.专题:立体图形的认识与计算.剖析:依据圆锥的体积公式V= sh,求出圆锥形沙堆的体积,从而求出沙堆的重量,最后用沙堆的重量除以 3.4 吨就是要求的答案.解答:解:底面半径:÷÷2=4(米),××42××,= ××16××,×,,≈51(吨);51÷3.4=15(次),答:一共要运 15 次.评论:本题主要考察了圆锥的体积公式的实质应用,注意计算时不要忘了乘.30.(4 分)一根圆柱形钢材,底面直径是 4 厘米,长是 80 厘米,将它铸成直径是 20 厘米的圆柱形部件,这个部件的高是多少厘米?考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.剖析:先利用圆柱的体积公式求出这根钢材的体积,利用圆的面积公式求出圆柱形部件的底面积,则这个部件的高 =体积÷底面积.解答:解:××80÷×] ,÷314,(厘米),答:部件的高是 3.2 厘米.评论:本题考察了圆柱的体积公式的灵巧应用.31.(4 分)(2007?北塘区)一家饮料生产商生产一种饮料,采纳圆柱形易拉罐包装,从易拉罐外面量,底面直径 6 厘米,高 12 厘米.易拉罐侧面有“净含量 340 毫升”的字样,请问这家饮料商能否欺诈了花费者?(请你经过计算、比较后说明问题)考点:圆柱的侧面积、表面积和体积.专题:压轴题.剖析:先利用 V=sh 求出它的体积,再与“净含量 340 毫升”比较,从而判断真伪.解答:解:×(6÷2)2×12,×9×12,×108,(立方厘米);339.12 立方厘米 =339.12 毫升;339.12 毫升< 340 毫升.答:经过计算发现,这个圆柱形易拉罐的体积是 339.12 立方厘米,它里面的净含量应当比339.12 毫升还要小一些,跟产品注明的“净含量340 毫升”更是少些,因此该产品是欺诈了花费者.评论:本题考察的是运用圆柱知识解决实质问题,对于一个容器来说,它的容积要比它的体积小.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三单元《圆柱与圆锥》单元检测分析
一、试题的指导思想和原则
《圆柱与圆锥》是小学阶段几何知识的最后一部分内容,单元测试意在考查学生对圆柱和圆锥的有关知识的掌握情况,更加系统、牢固地掌握圆柱、圆锥的有关知识,能熟练地运用公式进行圆柱的体积和表面积以及圆锥的体积的计算,并进一步提高运用知识解决实际问题的能力。
二、试题分析
本次考试的命题范围只考本单元的知识。
试卷分填空、判断、选择、计算、解决问题五大类共29小题,每一道题的出现,考查的都是学生对新知的掌握情况以及对旧知的内化程度。
1、填空题:主要考查圆柱的底面积、侧面积和体积,有直接套公式计算,也有逆推计算,难度加深,层层深入,共18分。
2、判断题:考查了圆柱与圆锥的特征,让学生灵活解答问题,共6分。
3、选做题:考查了等底等高的圆柱与圆锥的关系,让学生灵活解答问题,共8分。
4、计算题:有2小题,给出了圆柱和圆锥的图形,并标明底面直径和高,要求学生求出圆柱的表面积和体积,圆锥的体积,考查学生的运用公式计算的基础能力,共14分。
5、应用题:占了试卷的大部分,这也是本单元的学习重点,内容涵盖了圆柱和圆锥的所有知识,也联系了生活的实际问题,内容变化、多样,基础占70%,稍有难度的占30%,共有7道题,共48分。
三、存在的问题以及原因分析
(一)、计算错误
1、带小数的计算容易错,计算表面积和体积的时候都会用到3.14,计算所得的积的位数也较多,计算的难度相当大!很多学生见到这些计算就感到头痛,所以计算错误相当多。
2、没有注意到题目中单位的不统一,导致计算错误;或者是结果计算正确,但单位写错。
(二)、概念不清
1、圆柱中何时需要计算“两个底面”“一个底面”“没有底面”搞不清。
这个有些和生活经验有关,比如“通风管”,比如“汽油桶”。
有些学生只记得表面积的公式,但遇到具体问题,就手忙脚乱,计算错误很多。
有些题目圆柱的表面积是要求三个面的面积,有些只要求圆柱的侧面积。
2、少数学生在应用的时候搞不清算的是表面积还是体积,。
3、部分学生圆锥体积计算时没有乘三分之一。
求圆柱和圆锥的体积,特别是等底等高的圆柱和圆锥两者之间的关系。
学生只记得公式,圆锥的体积是圆柱
体积的三分之一,遇到具体的应用,就不知如何下手。
四、重点讲解:
1、等底等高的圆柱和圆锥的体积之间的关系。
前提:等底等高。
类似判断题:圆锥的体积等于圆柱体积的三分之一()。
概念延伸。
(1)圆柱的体积是和它等底等高的圆锥体积的3倍。
(2)把一个圆柱削成一个最大的圆锥,削去部分的体积是圆锥体积的2倍。
(3)把一个圆柱削成一个最大的圆锥,削去部分的体积是圆柱体积的三分之二。
(4)把一个圆柱削成一个最大的圆锥,圆锥的体积是削去部分体积的二分之一。
(5)把一个圆柱削成一个最大的圆锥,圆柱的体积是削去部分体积的二分之三。
(6)等底等高的圆锥和长方体之间的体积关系。
举一反三:
(1)一个圆柱的体积和它等底等高的圆锥的体积相差18立方分米,这个圆锥的体积是多少?
(2)把一个圆柱形的木块削成一个最大的圆锥,削去部分的质量是24g。
这个圆锥重多少克?
2、等体积等底的圆柱和圆锥的高之间的关系。
“圆锥的高是和它等体积等底的圆柱高的3倍。
”
这个要通过结合图让学生在大脑中建立两者之间的表象。
举一反三:
(1)一个圆柱与一个圆锥体积相等,底面积也相等。
已知圆柱的高是12厘米,圆锥的高是()。
(2)一个圆柱与一个圆锥体积相等,圆柱的底面积是圆锥底面积的2倍,那么圆柱的高是圆锥高的()。
3、将一个形状的铁块铸成另一个形状时,它们的质量和体积不变。
举一反三:
(1)将一块质量为156克的钢材铸成一个底面积是12平方厘米的圆锥形零件,这个零件的高是多少?(这种钢材每立方厘米质量是7.8克。
)
(2)将一块底面积36平方厘米、高5厘米的圆锥形钢块和一块棱长6厘米的正方体铁块合铸成一根圆钢,圆钢的横截面是 2.3平方厘米。
这块圆钢的长度是多少?
四、对以后教学的几点改进措施
纵观这次考试情况,反思这个单元的教学内容和教学方法,我觉得本单元教学内容分两大板块——表面积和体积,但本单元的知识是简单的立体几何知识,很多知识都较为抽象,学生理解起来的确是不容易。
因此,在教学时我有意识地结合、围绕下面几点进行教学设计:
一是结合生活实际进行教学设计。
比如在教圆柱体的认识时,我先要求学生收集身边的圆柱体物体、观察生活中哪些物体是圆柱体,让学生在身边、在生活中学到数学知识。
二是加强动手操作,在做中学。
比如在教学圆柱体的表面积时,我要求学生动手用硬纸做一个圆柱体,然后进行分解撑握一般的圆柱体有三个表面,使学生理解圆柱体的表面积的含义,从而撑握圆柱体表面积的计算方法。
三是注意培养学生良好的学习习惯。
在本单元教学中,我有意识地对计算、易做错的题目进行反复的训练。
但是,由于本届学生基础的确较差,加上我教学上可能存在着急功好进的思想,勿视了学生的实际情况,因而导致学生测试成绩不好。
今后,应多加注意。
