哈尔滨工程大学信号与系统试卷与答案

合集下载

信号与系统a答案

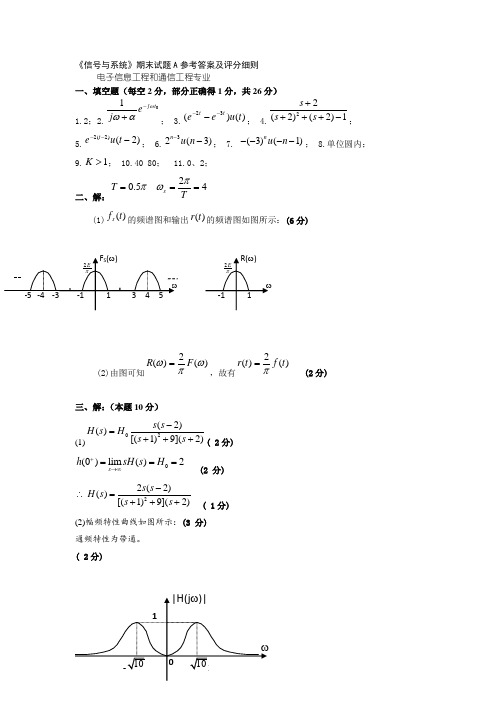
《信号与系统》期末试题A 参考答案及评分细则电子信息工程和通信工程专业一、填空题（每空2分，部分正确得1分，共26分）1.2；2.01t j ej ωαω-+； 3.)()(32t u eett---； 4.22(2)(2)1s s s ++++-；5.)2()2(2---t u et ； 6.32(3)n u n --； 7. (3)(1)n u n ----； 8.单位圆内；9.1K >； 10.40 80； 11.0、2；二、解：425.0===TT s πωπ(1))(t f s 的频谱图和输出)(t r 的频谱图如图所示：(6分)(2)由图可知)(2)(ωπωF R =，故有)(2)(t f t r π=(2分)三、解：（本题10分）(1)2(2)()[(1)9](2)s s H s H s s -=+++( 2分)0(0)lim ()2s h sH s H +→∞=== (2 分)22(2)()[(1)9](2)s s H s s s -∴=+++ ( 1分)(2)幅频特性曲线如图所示：(3 分) 通频特性为带通。

( 2分)四、解：3212()()(2)zH z z z -=-- (1)收敛域的三种情况：2z >12z <122z << (2分)(2) 12()2z zH z z z =--- (2分)2z >时 12()[()2]()nnh n u n =- 系统因果不稳定 (2分) 12z <时 12()[()2](1)nn h n u n =-+-- 系统非因果不稳定 (2分)122z <<时12()()()2(1)nnh n u n u n =+-- 系统非因果稳定 (2分)五、求解各题1.(1)电路的S 域模型为：525)(2++=s s s H (3分)极、零点图如图所示： (2分)极点位于左半平面系统是稳定系统。

哈尔滨工程大学2009年数字信号处理试卷

哈尔滨工程大学本科生考试试卷（ 2009 年秋季学期）一、（8分，每小题2分）判断系统的因果、稳定性。

(1) ()0.3()n h n u n =- (2) ()2[()(5)]n h n u n u n =--(3) 已知系统函数H()z 的收敛域为3z ≤≤∞(4) 已知系统的输入输出关系为：()()()y n x n u n =，其中()x n 为输入，()y n 为响应，()0, 0n y n ≤=时。

二、（6分，每小题2分）判断下列序列是否是周期序列，并判断周期序列的周期。

(1) ()cos()8n x n π=- (2) 6()sin(1)7x n n π=+ (3) 4π2π75()e e nnj j x n =-三、（18分，每小题6分）计算下列各小题。

(1)(){1,0,1,1,0,1}x n =的z 变换()X z 在单位圆上进行5等分取样，5()()k z W X k X z -==，0,1,2,3,4k =，求1()IDFT[()]x n X k =。

(2) 一个因果系统的系统函数为21()12z H z z z =-++，求系统的差分方程和单位脉冲响应。

(3) 设 ()a xt 是一个周期连续时间信号， ()cos(200π)cos(500π)a x t A t B t =+，以采样频率1kHz s f =对其进行采样，计算采样信号 ()()S a t nT x n x t ==的DFS 系数。

四、（12分）已知两个序列4()(1)()x n n R n =+，4()(4)()h n n R n =-(1) (5分)计算其线性卷积()*()x n h n ；(2) (5分)计算其圆周卷积()x n ④()h n ；(3) (2分)在什么条件下圆周卷积等于线性卷积结果？五、（20分，每小题4分）一线性时不变因果系统由下面差分方程描述：51()(1)(2)()(1)66y n y n y n x n x n --+-=-- 1. 确定该系统的系统函数()h z ，给出其收敛域，画出其零极点图。

哈尔滨工业大学信号与系统2006真题

T
2
T
t
其中的零输入响应、零状态响应响应、自由响应和受迫响应分量。（10 分）四、已知一连续线性时不变系统是因果系统，其系统函数的零极点分布如图二 (a ) 所示。当输入信号 e(t ) 如图二 (b) 时，系统输出的直流分量为 1。（10 分）（1）求该系统的系统函数 H ( s ) ；
，则原函数 f (t ) 2．已知 f (t ) 的 Fourier 变换 3．离散因果系统是稳定系统的充分必要条件是； 4．已知 x1 (n) u (n) u (n 3) ， x 2 (n) (3 n)[u (n) u (n 3)] ，
x3 (n) (n 2) (n 2) ，试画出 x1 (n) x 2 (n) x3 (n) 的波形；
进行抽样，得到抽样信号 f s (t ) 。求 f s (t ) 的频谱 Fs ( ) ，并画出频谱图；（3）若用同一抽样序列 T (t ) 对信号 f (4t ) 进行抽样，画出抽样信号的频谱图。六、求下列离散信号经过如图四所示滤波器后信号的频谱： 3 x 2 (n) 1 sin( n ) 8 4 （10 分）（1） x1 (n) (n 4) (n 4) （2）
m 0 图三
m

（1）求 f (4t ) 和 f (0.25t ) 的信号最高频率和 Nyquist 间隔（最大允许的抽样间隔）；（2）如果用序列 f (t )
T (t )
n
(t n 2s )

T
（ Ts 为信号 f (t ) 的 Nyquist ）对信号
5．求 k 0
F ( )
sin 3
； Leabharlann (n k ) ； cos t (t ) =

《信号与系统》试题及答案

2012年度教学质量综合评估测验卷《信号与系统》试题注：1、开课学院：信息工程学院学院。

命题组：电子信息教研组2、考试时间：120分钟，所有答案均写在答题纸上。

3、适用班级：信息工程学院通信工程专业及电子类专业。

4、在答题前，请在所发两张答题纸上认真填写所要求填写的个人信息。

1、下列说法不正确的是（）。

A 、一般周期信号为功率信号。

B 、时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。

C 、ε(t )是功率信号；D 、e t 为能量信号2、下列关于冲激函数性质的表达式不正确的是（）。

A 、)()0()()(t f t t f δδ=B 、()t a at δδ1)(=C 、)(d )(t tεττδ=⎰∞- D 、)()-(t t δδ=3、)2)(1()2(2)(-++=s s s s s H ，属于其极点的是（）。

A 、1B 、2C 、0D 、-2 4、If f 1(t ) ←→F 1(j ω)， f 2(t ) ←→F 2(j ω) Then[ ] A 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(j ω) *b F 2(j ω) ] B 、[a f 1(t ) + b f 2(t ) ] ←→ [a F1(j ω) - b F 2(j ω) ] C 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(j ω) + b F 2(j ω) ] D 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(j ω) /b F 2(j ω) ] 5、下列说法不正确的是（）。

A 、H(z)在单位圆内的极点所对应的响应序列为衰减的。

即当k →∞时，响应均趋于0。

B 、H(z)在单位圆上的一阶极点所对应的响应函数为稳态响应。

C 、H(z)在单位圆上的高阶极点或单位圆外的极点，其所对应的响应序列都是递增的。

即当k →∞时，响应均趋于∞。

完整版信号与系统试题附答案.doc

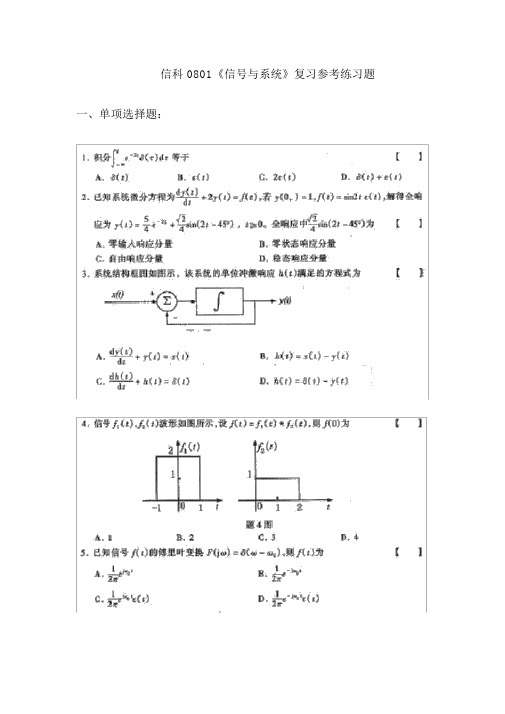
信科 0801《信号与系统》复习参考练习题一、单项选择题：14 、已知连续时间信号 f (t )sin 50(t2) ,则信号 f (t)·cos104t所占有的频带宽度（C）100(t 2)A ．400rad ／ sB 。

200 rad ／ s C。

100 rad ／ s D。

50 rad ／ s15 、已知信号 f (t) 如下图（a）所示，其反转右移的信号f1(t) 是（D）16 、已知信号f1 (t ) 如下图所示，其表达式是（ B ）A 、ε（ t）＋ 2ε (t－ 2) －ε (t－ 3)B 、ε (t－ 1) ＋ε (t－2) － 2ε (t－3)C 、ε (t)＋ε (t－ 2) －ε (t－ 3)D、ε (t－ 1) ＋ε －(t 2) －ε －(t 3)17 、如图所示： f（ t）为原始信号， f 1(t)为变换信号，则f1(t) 的表达式是（D）A、 f(－ t+1)B、 f(t+1)C、 f(－ 2t+1)D、 f( －t/2+1)18 、若系统的冲激响应为h(t), 输入信号为f(t), 系统的零状态响应是（C）19 。

信号f (t) 2 cos (t 2) 3sin (t 2) 与冲激函数(t 2) 之积为（ B ）4 4A、2B、 2 (t 2)C、 3 (t 2) D 、 5 (t 2)20．已知 LTI 系统的系统函数H( s )s 12 , Re[s ]＞－ 2，则该系统是（）s 5s 6因果不稳定系统非因果稳定系统C、因果稳定系统非因果不稳定系统21 、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ B ）A、常数B、实数 C 、复数D、实数 +复数22 、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ A ）A、阶跃信号B、正弦信号 C 、冲激信号 D 、斜升信号23. 积分 f (t ) (t )dt 的结果为( A )A f (0)B f (t ) C. f (t )(t) D. f ( 0)(t )24. 卷积(t) f (t ) (t ) 的结果为( C )A.(t)B.(2t )C.f (t)D. f ( 2t )25.零输入响应是 ( B )A. 全部自由响应B. 部分自由响应C.部分零状态响应D. 全响应与强迫响应之差2A 、e1e3、e3、127.信号〔ε (t)－ε －(t 2)〕的拉氏的收域( C )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知系二微分方程的零入响y zi (t ) 的形式Ae t Be 2t ，其 2 个特征根 ( A )A 。

《信号与系统》试题及答案,DOC

2012年度教学质量综合评估测验卷《信号与系统》试题注：1、开课学院：信息工程学院学院。

命题组：电子信息教研组2、考试时间：120分钟，所有答案均写在答题纸上。

3、适用班级：信息工程学院通信工程专业及电子类专业。

4、在答题前，请在所发两张答题纸上认真填写所要求填写的个人3、)2)(1()(-+=s s s H ，属于其极点的是（）。

A 、1B 、2C 、0D 、-2 4、If f 1(t )←→F 1(j ω)，f 2(t )←→F 2(j ω)Then[] A 、[a f 1(t )+b f 2(t )]←→[a F 1(j ω)*b F 2(j ω)] B 、[a f 1(t )+b f 2(t )]←→[a F 1(j ω)-b F 2(j ω)]C、[a f1(t)+b f2(t)]←→[a F1(jω)+b F2(jω)]D、[a f1(t)+b f2(t)]←→[a F1(jω)/b F2(jω)]5、下列说法不正确的是（）。

A、H(z)在单位圆内的极点所对应的响应序列为衰减的。

即当k→∞时，响应均趋于0。

67A、f(t)=cos(2t)+cos(4t)B、f(t)=sin(2t)+sin(4t)C、f(t)=sin2(4t)D、f(t)=cos2(4t)+sin(2t)8、已知某LTI连续系统当激励为)(t f时，系统的冲击响应为)(t h，零状态响应为)(t y zs ，零输入响应为)(t y zi ，全响应为)(1t y 。

若初始状态不变时，而激励为)(2t f 时，系统的全响应)(3t y 为（）。

A 、)(2)(t y t y zs zi +B 、()2()zi y t f t +C 、)(4t y zsD 、)(4t y zi 9、设有一个离散反馈系统，其系统函数为：)1(2)(k z zz H --=，问若要使该系统稳定，常数应k 该满足的条件是（）。

A 17、已知)21(2323)(22<<+-+=z z z z z X ，则=)(n x 。

哈尔滨工业大学信号与系统2005真题

哈尔滨工业大学2005年硕士研究生考试试题信号与信统适用专业：信息与通信工程一、回答下列各题（每小题3分，共21分）1．周期性连续时间信号的频谱特点是；2．试确定周期序列465sin(3)(ππ+=n n x 的周期；3．某系统的单位函数响应为)1(2)(+⋅=n u n n h n，试判断系统的因果性和稳定性；4．对一个连续时间信号)(t f 采样2秒，得到4096个采样点的序列。

如果采样后不发生频谱混叠，信号)(t f 的最高频率应小于；5．信号)(2n u n 的Z 变换的收敛域为；6．判断系统)2()2()(--+=n x n x n y 的线性、时不变性；7．若系统函数的极零点分布入图一所示，请说明它们分别具有那种滤波特性。

图一二、已知一线性时不变连续时间系统的激励信号)(]211[)(2t u e t e t --=，零状态响应为)(]1[)(22t u te e t r tt ----=。

（8分）)(a 求阶跃响应)(t g ；)(b 求系统的微分方程。

三、已知周期信号)(t f 如图二所示，试求其傅里叶级数，并画出响应的频谱图。

（10分）图二四、已知离散系统差分方程为：)1()(3)1(4)2(+=++++n x n y n y n y 输入信号为)1()2()(--=n u n x n，初始条件为0)0(=zi y ，1)1(=zi y 。

试求系统的全响应，并指出其中的零输入响应、零状态响应、自由响应、受迫响应、暂态响应、稳态响应分量。

（10分）五、某因果系统如图三所示，其中)()()(1t t t h δδ'+=、)()(3)(4)(222t t h t h t h δ=+'+"，写出系统的输出输入方程，并求)(t h 。

（8分）六、已知信号的频谱密度函数)(ωF 如图四所示，求原始信号)(t f 。

（8分）图五1．若系统的零输入响应为)(])31(5621(56[)(n u n y n n -=求常数a ，b ；2．若⎥⎦⎤⎢⎣⎡=)()()(n u n n x δ，系统初始状态为0，求⎥⎦⎤⎢⎣⎡=)()()(21n n n λλλ。

哈尔滨工业大学信号与系统2001真题

哈尔滨工业大学硕士研究生入学考试试题
2001年信号与系统试题
一、求解下列各题（每小题5分）
1.已知信号)(1t f 和)(2t f 如图一所示，试求)()()('21t t f t f δ**，并画出波形
图。

2.已知某系统的激励)(n x 与响应)(n y 之间的关系为)()(n nx n y =，试说明该系统是否为线性时不变系统，并说明原因。

3.试确定周期信号n j n j e e
n x )4/3()5/2()(ππ+=的周期N 。

4.已知)()5.0()(n u n x n =，求其付里叶变换)(ωj e X ，并大致画出幅度频谱
图。

5.已知某系统的极、零点分布如图二所示，且幅频特性的最大值为1，求系统函数)(s H 的表达式。

6.设系统输入)(n x 为因果序列，响应)()()()(n x n u n u n y **=，求系统单位样值响应。

二、（10分）已知周期信号)(t f 如图三所示，试求其傅里叶级数和傅里叶变
换，并画出相应的（傅里叶级数和傅里叶变换）频谱图。

T -2-
42T 图三三、（10分）系统如图四所示，Ω==121R R 、H L 5.0=、F C 5.0=，系统的初
始状态为零。

系统的激励为)(2)(t u
t e =，响应为电容电压)(t u c 。

试求：（1）列出系统的微分方程；（2）求)(t u c ，并指出其中的自由响应、强迫响应、暂态响应和稳态响应各分量。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第2页共 4页
y 1(t)；
4. 写出描述该系统的系统方程。

四、（12分）
设一因果连续时间LTI 系统输入x (t)和输出y (t)关系为：
y ''(t)＋3y '(t)+2y (t)=x (t)
1. 求该系统的系统函数H (s)，画出其零极点图，并判别系统的稳定性；
2. 确定此系统的冲激响应h (t)；
3. 求系统的幅频特性与相频特性表达式。

五、（8分）
一个离散LTI 系统的单位样值响应为：h (n )=αn
u (n )
1. 试用时域卷积方法求该系统的单位阶跃响应g(n );
2. 确定该系统的系统方程。

六、（24分）
已知函数x (t)和y (t)分别为：
∑∞
-∞
=-=
n n t t x )4()(δ ，t t t y 6sin 4cos )(+=
1. 求y (t)的指数傅立叶级数表示，说明其频带宽度；
2. 求x (t)的傅立叶级数展开表达式，简略画出其幅度谱线图；
3. 求x (t)的傅立叶变换表达式X (j ω)，简略画出X (j ω)；
4. 求y (t)的傅立叶变换表达式Y (j ω)，简略画出Y (j ω)；
5. 确定信号y (t)的奈奎斯特频率与奈奎斯特间隔。

6.
确定信号s (t)=x (t)y (t)的频谱。

七、（16分）
一个因果的离散时间LTI 系统描述如下：
)()2(2
1
)1(43)(n x n y n y n y =-+--
其中x (n)为输入，y (n)为输出。

1. 试求该系统的系统函数H (z)，画出H (z)的零、极点图；
2. 求系统的单位样值响应h (n)，并说明系统的稳定性；
3. 用求和器、数乘器和延时器画出其结构框图；
4. 如)(31)(,1)2(,2)1(n u n x y y n
⎪⎭
⎫
⎝⎛==-=-，求y (n)。

第3页共4页第4页共 4页
八、（8分）
假设x (t)的傅立叶变换X (j ω)＝0，|ω| >ωm ，而信号g(t )可表示成
)}sin (
]cos )({[cos )()(t
t
t t x t t x t g c c c πωωω*-= 式中*记做卷积，而ωc ＞ωm 。

试确定常数A 的值，以使得
t
t
A t t g t x m c πωωs i n *}c o s )({)(=。