ug函数曲线创建方法
UG NX 10案例教程教学案例空间曲线
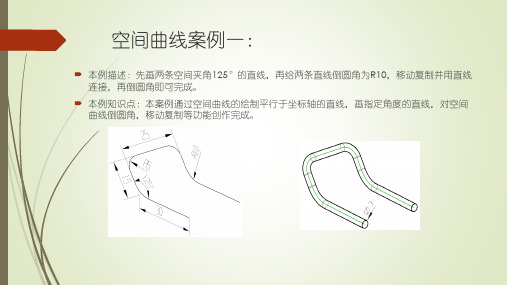
本例描述:先画两条空间夹角125°的直线,再给两条直线倒圆角为R10,移动复制并用直线 连接,再倒圆角即可完成。
本例知识点:本案例通过空间曲线的绘制平行于坐标轴的直线,画指定角度的直线,对空间 曲线倒圆角,移动复制等功能创作完成。
操作步骤:
1. 点击图标 图标,起点为原点,画一条沿着X轴长度30的直线,如图3所示; 2.点击图标 图标,起点为原点,终点选择成一个角度并选择图3画的直线,在指定平面选
操作步骤:
6.选择曲面,点更多-管道 图标如图13所示。最后选择如图14所示。外径为3,内径为0,选 择曲线为画好的空间曲线,最终结果如图15所示。
空间曲线案例二:
本例描述:先画水平平行于y轴80长的直线、平行于x轴180长的直线、平行于y轴-80长的直线,再给 直线之间倒圆角为R20,复制旋转再倒圆角即可完成。 本例知识点:本案例通过空间曲线的绘制平行于坐标轴的直线,画指定角度的直线,对空间曲线倒圆 角,移动复制旋转等功能创作完成。
13.点击图标
图标,选择一条螺旋线和一个上面画的空间直线,如图14所示,这样
螺旋线与直线就是光滑连接。
14.点击
图标,选择直线和桥接线,这样选择对象里面出现(2)个,变换选择角
度,指定矢量选择Z轴正向,角度为180°,结果选择“复制原先的”,“非关联副本数”
为1,其他为默认即可。最后复制结果如图15所示。
小半圆,如图不是小半圆可以通过补弧和关联来调节,如图4所示
操作步骤:
5.点击 图标,圆弧起点为直线的另外一个端点,终点为直线中心,中点旋转半径,半径 值为16,画小半圆,如图不是小半圆可以通过补弧和关联来调节,如图5所示
6.点击 图标,选择一个小半圆弧,在起点位置输入-6,如图6所示。
UG6.0二维曲线绘制

学习情境2:零件曲线—曲线学习目标:1、掌握直线和圆弧命令的使用。
2、掌握基本曲线(直线、圆弧、圆、倒圆角、修剪)命令的使用。
3、掌握典型二维曲线的绘制。
任务一、绘制手柄二维曲线——直线和圆弧手柄二维曲线图如图2一l所示。
图2-l 手柄二维曲线图l、操作步骤(1)选择[插入]/[曲线]/[直线],在起点的点构造器中输入(0,0,0),(默认绘图平面在坐标平XC-YC),在终点选项中选择XC 沿XC,终止限制距离90,单击“应用”。
(2)捕捉左侧端点,在终点选项中选择YC沿YC,终止限制距离10,单击“应用”。
(3)捕捉刚画线段未端,在终点选项中选择XC沿XC,终止限制距离15,单击“应用”。
(4)捕捉刚画线段末端,在终点选项中选择“成一角度”,选择已画的水平线(角度约束线)输入角度90,终止限制距离5,单击“确定”。
(5)选择[插入]/[曲线]/[圆弧/圆],选择类型“从圆心开始的圆弧”,在圆心的点构造器中输入(15,0,0),捕捉刚画线段未端,起点限制角度0,终止限制角度90,单击“应用”。
在圆心的点构造器中输入(80,0,0),捕捉90线段右端,起点限制角度0,终止限制角度90,单击“确定”。
(6)选择[插入]/[曲线]/[线/圆弧]/[线/点/平行],输入点(0,-35,0),选择水平线(平行参考),在合适位置单击左键。
(7)选择[插入]/[曲线]/[圆弧/圆],选择类型“从圆心开始的圆弧”,捕捉Rl0圆弧的圆心,输入半径40,在限制中设置整圆,单击“应用”。
捕捉圆和直线交点,输入半径50,单击“确定”。
(8)选择[插入]/[曲线]/[圆弧/圆],选择类型“三点画圆弧”,选择R15圆弧,选择R50圆弧,输入半径12,单击“确定”。
(9)选择[编辑]/[曲线]/[修剪],选择修剪曲线,选择边界,单击“确定”。
2、直线直线用于绘制两点间或以其他限定方式创建的线段。
选择工具栏图标:曲线工具栏中的直线图标或下拉菜单:[插入]→[曲线]→[直线],弹出如图2-2所示“直线”对话框。
ug规律延伸使用方法

ug规律延伸使用方法
UG软件是一款常用的三维建模软件,在使用UG软件时,我们有时候需要使用UG规律延伸。
UG规律延伸可以在三维模型上非常便捷地生成曲线和曲面,其使用方法如下:
1. 选择绘制曲线或曲面的区域,在菜单栏中点击插入 - 曲线 - 规律延伸,进入规律延伸对话框。
2. 在规律延伸对话框中选择需要使用的曲线或曲面,并设置规律延伸的方式,如沿着一条指定曲线方向延伸,或者沿着一个指定角度方向延伸。
3. 根据需要设置规律延伸的参数,例如延伸的距离、数量、旋转角度等。
4. 点击确定,即可生成对应的曲线或曲面。
需要注意的是,在使用UG规律延伸时,要注意控制曲线和曲面的精度和平滑度。
一般来说,精度越高,曲线和曲面的质量就越好,但同时也会占用更多的计算资源。
因此,在使用UG规律延伸时,需要合理设置精度和平滑度,以满足实际需求。
最全地UG方程曲线及详细表达式

在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x 轴上),虚半轴b为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
UG入门基本操作教程
UG基本操作一、启动UG NX4.01、利用开始菜单2、利用NX图标均可以进入:二、界面介绍1、标题栏2、菜单栏3、工具栏4、资源条5、图形窗口6、提示行7、状态行8、进度条:为了满足自己的意愿,我们通常希望提示行和状态行在窗口下方。
我们可以选择“工具”→“自定义”,布局标签,选择底部,关闭自定义窗口。
如下图所示:界面窗口也发生改变:三、鼠标操作鼠标键动作MB1选择或拖曳对象MB2 在一操作中OK。
在图形窗口中按下与保持_旋转视图。
按下与保持Shift+MB2 平移视图。
按下与保持Ctrl+MB2缩放视图。
MB3 (在图形窗口中) 显示弹出菜单,捷径到各种功能。
也显示由MB1选择对象的动作信息。
旋转鼠标轮在图形窗口中缩放。
在对话框列表框中、对话框选项菜单和信息窗口中滚卷。
光标在图符或对话框中的选项上显示图符或选项标记。
光标在图形窗口中的对象、特征或组件上基于选择工具条设置(如: Select Features)、预先高允对象。
一种利用鼠标操纵视图更方便的方法。
•旋转∶按下和保持M B2并旋转。
•单轴旋转∶1.放光标到视图边缘;2.按下和保持M B2并在你要旋转的方向拖拽。
单轴旋转放光标于光标绕X旋转视图的左侧或右侧绕Y旋转视图的底部绕Z旋转视图的顶部•摇移∶按下和保持<Shift>并利用MB2拖拽。
•缩放∶按下和保持<Ctrl> 并利用MB2拖拽。
四、新建/打开一个prt文件1、新建一个prt文件:选择“文件”→“新建”或1、目标文件夹2、新建文件名3、新建文件类型4、模型单位选择(公制/英制)5、是否主体模型部件2、打开一个prt文件:选择“文件”→“打开”或1、显示prt文件的预览图像2、打开加载选项对话框五、UG NX4.0常用菜单功能1、文件功能菜单文件操作是各种软件的基本操作功能之一,其中的大部分功能属于常规操作。
而仅讲“关闭”、“选项”、“导入”和“导出”作简单介绍。
UG4.0入门基本操作方法.pdf
UG入门基本操作一、 如何启动UG NX4.01、利用开始菜单2、利用NX图标均可以进入:二、 UG4.0界面介绍1、标题栏2、菜单栏3、工具栏4、资源条5、图形窗口6、提示行7、状态行8、进度条:为了满足自己的意愿,我们通常希望提示行和状态行在窗口下方。
我们可以选择“工具”→“自定义”,布局标签,选择底部,关闭自定义窗口。
如下图所示:界面窗口也发生改变:三、 UG4.0鼠标操作鼠标键 动作 M B1选择或拖曳对象M B2 在一操作中O K。
在图形窗口中按下与保持_旋转视图。
按下与保持S hi ft+M B2 平移视图。
按下与保持C t rl+M B2缩放视图。
M B3 (在图形窗口中) 显示弹出菜单,捷径到各种功能。
也显示由M B1选择对象的动作信息。
旋转鼠标轮 在图形窗口中缩放。
在对话框列表框中、对话框选项菜单和信息窗口中滚卷。
光标在图符或对话框中的选项上显示图符或选项标记。
光标在图形窗口中的对象、特征或组件上基于选择工具条设置(如:S elec t F ea t ures)、预先高允对象。
注::: MB2+MB3=“Pan”;MB1+MB2 =“Zoom In/Out”一种利用鼠标操纵视图更方便的方法。
• 旋转∶ 按下和保持 M B2并 旋转 。
• 单轴旋转∶ 1.放光标到视图边缘;2.按下和保持 M B2并在你要旋转的方向拖拽。
单轴旋转 放光标于 光标绕X旋转 视图的左侧或右侧四、 UG4.0新建/打开一个prt文件1、新建一个prt文件:选择“文件”→“新建”或1、目标文件夹2、新建文件名3、新建文件类型4、模型单位选择(公制/英制)5、是否主体模型部件2、打开一个prt文件:选择“文件”→“打开”或1、显示prt文件的预览图像2、打开加载选项对话框五、 UG 4.0常用菜单功能1、文件功能菜单文件操作是各种软件的基本操作功能之一,其中的大部分功能属于常规操作。
而仅讲“关闭”、“选项”、“导入”和“导出”作简单介绍。
最全的UG方程曲线及详细表达式讲解
在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsinθsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1图1 图22.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG 表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图3图3 图44.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
UG-基本曲线用法
第二部分 UG/Curve曲线
一、概述
1、曲线功能(What):用于建立遵循设 计要求的点、直线、圆弧、样条、平面 等几何要素,并可对这些几何要素进行 编辑。 2、应用意义(When&Why):通常按设 计要求建立曲线,所建立的曲线作为构 造3D模型的初始条件,用于生成扫描 特征及构造空间曲面等。 3、应用入口(Where): 建立及编辑: Application—>Modeling—>Toolbox— >Curve 4、主界面:
第二部分 UG/Curve曲线
(八)、点组
操作步骤:
定义生成点组方法——> 定义控制参数——> 定义目标曲线
UG曲线技巧 (第三讲)
全面攻破UG曲线技巧 (第三讲)发布日期:2006-5-16 8:39:09 作者:未知出处:网上转摘∙本期讲述曲线造型中有关曲线操作方面的内容,所谓曲线操作是指对已存在的曲线进行几何运算处理,如曲线偏置、桥接、投影、合并等。
∙∙ Offset Curve曲线偏置【功能】对已存在的二维曲线(如直线、弧、二次曲线、样条线以及实体的边缘线等)进行偏置,从而产生新的曲线。
【操作步骤】1. 调用Offset Curve,弹出图1对话框。
图1Solid Face:选择一个实体的面,该面上所有的边缘线将进行偏置。
Solid Edge:选择一条实体的边缘线,仅对所选边缘线进行偏置。
2. 选择偏移的曲线。
3. 设置相关参数。
图21) Offset by:指定偏移方式。
有3种偏移方式:Distance:在曲线所在的平面内偏移曲线。
需指定偏移的距离和产生偏移曲线的数量。
Draft:拔模方式。
将曲线按指定的拔模角度(Draft Angle)偏移到与曲线所在平面相距拔模高度(Draft Height)的平面上。
拔模高度是原曲线所在平面和偏移后所在平面间的距离。
拔模角度是偏移方向与原曲线所在平面的法线所的夹角。
如图3所示。
图3Law Control:法则控制。
通过定义法则函数定义偏移曲线距离。
2) Distance:偏移距离。
3) Draft Height:拔模高度。
4) Draft Angle:拔模角度5) Trim:修剪方式。
None:不修剪。
Extended Tangents:切线延伸。
Fillet:倒圆角。
图46) Extend Factor(略)7) Group Obiects(略)8) Approx Tolerance:公差。
9) Number of Copies:一次性创建的偏移曲线数。
10) Reverse direction:反方向。
选定曲线后,曲线上将出现一箭头,用于显示偏移方向,如图5所示。
如果方向不对,可单击Reverse direction按钮,即可使该方向相反。
最全的UG方程曲线及详细表达式
图 10-1
图 10-2
11.三尖瓣线
三尖瓣线数学方程:x=r(2cosθ+cos2θ);y=r(2sinθ-sin2θ)若将 2 变为 n 即扩展为 n+1 尖瓣线。若 r=20,即 UG 表达式为: r=20 n=2 theta=t*360 xt=r*(n*cos(theta)+cos(n*theta)) yt=r*(n*sin(theta)-sin(n*theta)) zt=0 效果如图 11
第 5 页 共 49 页
图 11
图 12
12.星形线【四尖瓣线】
星形线的数学方程:x=r*cos3θ;y=r*sin3θ。【由 n+1 尖瓣线通式:x=r(n*cosθ+cos(n*θ)); y=r(n*sinθ-sin(n*θ))当 n=3 时的情况。三角函数公式: sin3θ=3sinθ-4sin3θ;cos3θ=4cos3θ-3cosθ】若 r=20,即 UG 表达式为: r=20 theta=t*360 xt=r*(cos(theta))^3 yt=r*(sin(theta))^3 zt=0 效果如图 12
13.渐开线
渐开线的数学方程:x=r(cosθ+θ*sinθ);y=r(sinθ-θ*cosθ)。假设渐开线的基圆半径 r 为 10,展开角度 θ 为 360*2,即 UG 表达式为: r=10 theta=360*2*t s=r*rad(theta)=r*(2*pi()/360)*theta=2*pi()*r*t*2 xt=r*cos(theta)+s*sin(theta) yt=r*sin(theta)-s*cos(theta) zt=0 效果如图 13
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ug函数曲线创建方法
UF_MODL_dissect_exp_string()
功能:将表达式的名称与数值分离,并得到表达式的标识;
UF_MODL_ask_exp()
功能:根据表达式的名称查找表达式是否存在,并取的表达式的
全名;
UF_MODL_delete_exp()
功能:删除表达式;
UF_MODL_eval_exp()
功能:计算表达式的数值;
UF_MODL_edit_exp()
功能:更新表达式的数值,需与UF_MODL_update()合用;
UF_MODL_rename_exp()
功能:重命名表达式;
UF_MODL_ask_exps_of_feature()
功能:获取特征的所有表达式标识;
UF_MODL_ask_exps_of_part()
功能:获取part的所有表达式标识;
UF_MODL_ask_exp_tag_string()
功能:根据表达式的标识获取表达式的字符串;
UG_表达式详解
看见论坛里有好多人对表达式都不是很了解,这次就来一个详细
的讲解。
先来一个最简单的,圆,
众所周知,圆的方程是x^2+y^2=r^2,
在ug里我们必须把方程都转换为参数方程,参数方程大家在高中
的时候都学过,圆的参数方程不是难事,即;x=r*sint,y=r*cost,因为
ug里的t是永远只从0递增到1,而我们实际要求的t要从0到360,
所以把方程变一下,即;xt=r*sin(360*t),yt=r*cos(360*t),(因为ug
默认x,y变量为xt,yt所以一般把x,y写成xt,yt,当然你写成x,y
也行只要在形成规律曲线时改过来就行了),好,这样就可以用规律
曲线
形成圆了,如果再稍微复杂一点呢?
现在再来讲一个如下图的弹簧的方程。
我的方法是先分析曲线在x,y平面投影的曲线方程,显然该投影曲
线是一个半径不断变化的圆,而半径
的变化规律为常数加上一个正弦曲线,即;r=a+b*sint.如是把圆
的参数方程里的r 替换一下,即
xt=(a+b*sint)*sint
yt=(a+b*sint)*cost
(这里面的t只是代表其为一个变量,真正出表达式的时候要赋予
变量范围的)
x,y平面投影的曲线写好之后再来看z方向上的曲线方程,显然是
一个正弦(或余弦)曲线,但是该曲线
必须与x,y平面的正弦曲线错开一个90度的相位,为什么?(留
给大家去分析,不难想的!)
即;zt=b*cost
好,方程都已经分析完了,现在就要赋予变量不同的变化范围,
例如,螺旋圈数
啊,螺旋半径啊等等,
这也不难,这儿就不讲了。
下面是图示弹簧的方程!
a=360*t
n=20
t=0
R=40
r=10
xt=(R+r*sin(a*n))*sin(a)
yt=(R+r*sin(a*n))*cos(a)
zt=r*cos(a*n)
下面再给几个其他常用的曲线方程。
渐开线方程(用于齿轮)
R=40
a=720*t
t=0
xt=R*(cos(a)+a*sin(a))
yt=R*(sin(a)-a*cos(a))
阿基米德螺线(等进螺线)(用于凸轮)
a=360*t
t=0
xt=a*sin(a)
yt=a*cos(a)
