二次函数图像和性质习题精选(含答案)
二次函数的图象和性质部分练习题(附参考答案)

新华师大版九年级下册数学第26章 二次函数的图象和性质部分练习题姓名____________ 时间: 90分钟 满分:120分 总分____________一、选择题(每小题3分,共30分)1. 抛物线()312--=x y 的对称轴是 【 】(A )y 轴 (B )直线1-=x (C )直线1=x (D )直线3-=x2. 将抛物线2x y =向右平移1个单位,所得的抛物线的关系式是 【 】 (A )12-=x y (B )12+=x y (C )()21-=x y (D )()21+=x y3. 抛物线332-=x y 向右平移3个单位,得到新抛物线的表达式为 【 】 (A )()3332--=x y (B )23x y =(C )()3332-+=x y (D )632-=x y4. 对于函数()22m x y --=的图象,下列说法不正确的是 【 】(A )开口向下 (B )对称轴是直线m x = (C )最大值为0 (D )与y 轴不相交5. 对于二次函数()212+--=x y 的图象与性质,下列说法正确的是 【 】(A )对称轴是直线1=x ,最小值是2 (B )对称轴是直线1=x ,最大值是2 (C )对称轴是直线1-=x ,最小值是2 (D )对称轴是直线1-=x ,最大值是26. 有一抛物线和抛物线22x y -=的形状、开口方向完全相同,顶点坐标是()3,1-,则该抛物线的关系式为 【 】 (A )()3122+--=x y (B )()3122++-=x y(C )()3122++-=x y (D )()3122+--=x y7. 将函数2x y =的图象用下列方法平移后,所得的图象不经过点A (1 , 4)的方法是 【 】 (A )向左平移1个单位 (B )向右平移3个单位(C )向上平移3个单位 (D )向下平移1个单位 8. 若点()1,4y A -,()2,1y B -,()3,1y C 在抛物线()12212-+-=x y 上,则321,,y y y 的大小关系是 【 】 (A )231y y y << (B )312y y y << (C )213y y y << (D )123y y y << 9. 对于抛物线()31212++-=x y ,下列结论:①抛物线的开口向下;②对称轴为直线1=x ;③顶点坐标为()3,1-;④当1>x 时,y 随x 的增大而减小;⑤函数的最大值为 3.其中正确结论的个数为【 】(A )2 (B )3 (C )4 (D )510. 将抛物线152+-=x y 向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为 【 】 (A )()1152-+-=x y (B )()1152---=x y(C )()3152++-=x y (D )()3152+--=x y二、填空题(每小题3分,共30分)11. 抛物线()223+-=x y 的对称轴为直线_________.12. 抛物线()3122-+=x y 的顶点坐标为_________.13. 若抛物线()512-+--=m x y 的最大值为3,则=m _________.14. 若二次函数22x y =的图象向左平移2个单位后,得到函数()22h x y +=的图象,则=h _________.15. 将抛物线231x y =向右平移3个单位,再向下平移2个单位,所得的抛物线的关系式为________________.16. 已知函数()21--=x y 图象上两点()1,2y A ,()2,y a B ,其中2>a ,则1y 与2y 的大小关系是_________.17. 已知二次函数图象的顶点坐标为(2 , 0),直线1+=x y 与二次函数图象交于A 、B 两点,其中点A 在y 轴上,则二次函数的解析式为____________.18. 若抛物线()()12++-=m m x y 的顶点在第一象限,则m 的取值范围是____________.19. 已知抛物线()2132+-=x y ,当x _________时,y 随x 的增大而减小.20. 点()1,2y A ,()2,3y B 是二次函数122+-=x x y 的图象上两点,则1y 与2y 的大小关系是_________.三、解答题(共60分)21.(8分)已知二次函数()23-=x y .(1)写出它的图象的开口方向、对称轴、顶点坐标和最值;(2)若点()11,y x A ,()22,y x B 位于对称轴右侧的抛物线上,且21x x <,试比较1y 与2y 的大小; (3)抛物线()27+=x y 可以由抛物线()23-=x y 平移得到吗?如果可以,请写出平移的方法;如果不可以,请说明理由.22.(8分)对于函数()2231+=x y ,请回答下列问题: (1)把抛物线231x y =怎样移动得到抛物线()2231+=x y ?(2)写出图象的对称轴和顶点坐标; (3)试讨论函数()2231+=x y 的增减性及最值问题.23.(8分)用配方法把函数10632+--=x x y 化为()k h x a y +-=2的形式,并写出抛物线的开口方向、对称轴、顶点坐标和最值.24.(8分)已知二次函数图象的对称轴为直线2=x ,函数的最小值为3,且图象经过点()5,1-,求这个二次函数的表达式.25.(8分)如图,已知二次函数的图象顶点坐标为(2 , 0),直线1+=x y 与二次函数的图象交于A 、B 两点,其中点A 在y 轴上.(1)二次函数的关系式为________________;(2)证明点()12,--m m 不在(1)中所求的二次函数的图象上.yxA BO26.(10分)如图所示,抛物线()412+-=x a y 与x 轴交于点A 、B ,与y 轴交于点C ,过点C 作x CD //轴,交抛物线的对称轴于点D ,连结BD ,已知点A 的坐标为()0,1-.(1)求该抛物线的解析式; (2)求梯形COBD 的面积.yxBDCA O27.(10分)如图所示,二次函数()212++=x a y 的图象与x 轴交于A 、B 两点,已知()0,3-A ,根据图象回答下列问题:(1)求a 的值和点B 的坐标;(2)设抛物线的顶点是P ,试求△P AB 的面积;(3)在抛物线上是否存在点M ,使得△MAB 的面积是△P AB 的面积的2倍?若存在,求出点M 的坐标.新华师大版九年级下册数学第26章 二次函数的图象和性质部分练习题参考答案一、选择题(每小题3分,共30分)二、填空题(每小题3分,共30分)11. 2-=x 12. ()3,1-- 13. 8 14. 2 15. ()23312--=x y 16. 21y y > 17. ()2241-=x y 18. 0>m 19. 1< 20. 21y y < 三、解答题(共60分)21.(8分)已知二次函数()23-=x y .(1)写出它的图象的开口方向、对称轴、顶点坐标和最值;(2)若点()11,y x A ,()22,y x B 位于对称轴右侧的抛物线上,且21x x <,试比较1y 与2y 的大小;(3)抛物线()27+=x y 可以由抛物线()23-=x y 平移得到吗?如果可以,请写出平移的方法;如果不可以,请说明理由.解:(1)开口向上,对称轴为直线3=x ,顶点为(3 , 0),最小值为0;……………………………………………4分 (2)在对称轴直线3=x 的右侧,y 随x 的增大而增大∵213x x << ∴21y y <;……………………………………………6分 (3)可以.将抛物线()23-=x y 向左平移10个单位即可得到抛物线()27+=x y .……………………………………………8分 22.(8分)对于函数()2231+=x y ,请回答下列问题:(1)把抛物线231x y =怎样移动得到抛物线()2231+=x y ? (2)写出图象的对称轴和顶点坐标; (3)试讨论函数()2231+=x y 的增减性及最值问题.解:(1)把抛物线231x y =向左平移2个单位即可得到抛物线()2231+=x y ; ……………………………………………2分 (2)图象的对称轴为直线2-=x ,得到坐标为()0,2-;……………………………………………4分 (3)当2-<x 时,y 随x 的增大而减小; 当2->x 时,y 随x 的增大而增大;……………………………………………6分当2-=x 时,函数()2231+=x y 取得最小值,最小值为0.……………………………………………8分 23.(8分)用配方法把函数10632+--=x x y 化为()k h x a y +-=2的形式,并写出抛物线的开口方向、对称轴、顶点坐标和最值. 解:()10232++-=x x y()()131310112322++-=+-++-=x y x x y……………………………………………4分 抛物线的开口向下,对称轴为直线1-=x ,顶点坐标为()13,1-,函数的最大值为13=y . ……………………………………………8分 (每个结果1分)24.(8分)已知二次函数图象的对称轴为直线2=x ,函数的最小值为3,且图象经过点()5,1-,求这个二次函数的表达式.解:由题意可设该二次函数的表达式为()k h x a y +-=2∵其对称轴为直线2=x ,函数的最小值为3 ∴3,2==k h ∴()322+-=x a y……………………………………………5分 ∵其图象经过点()5,1- ∴()53212=+--⨯a解之得:92=a ……………………………………………8分 ∴这个二次函数的表达式为()32922+-=x y . 25.(8分)如图,已知二次函数的图象顶点坐标为(2 , 0),直线1+=x y 与二次函数的图象交于A 、B 两点,其中点A 在y 轴上. (1)二次函数的关系式为________________;(2)证明点()12,--m m 不在(1)中所求的二次函数的图象上.yxA BO解:(1)()2241-=x y ; ……………………………………………3分(2)证明:当m x -=时()1214124122-≠++=--=m m m m y ……………………………………………7分 ∴点()12,--m m 不在(1)中所求的二次函数的图象上.……………………………………………8分 26.(10分)如图所示,抛物线()412+-=x a y 与x 轴交于点A 、B ,与y 轴交于点C ,过点C 作x CD //轴,交抛物线的对称轴于点D ,连结BD ,已知点A 的坐标为()0,1-. (1)求该抛物线的解析式; (2)求梯形COBD 的面积.yxBDCA O解:(1)把()0,1-代入()412+-=x a y 得:()04112=+--⨯a解之得:1-=a……………………………………………3分 ∴该抛物线的解析式为()412+--=x y ;……………………………………………4分 (2)∵该抛物线的对称轴为直线()0,1,1-=A x∴()0,3B……………………………………………5分 ∴3=OB当0=x 时,()341012=+-⨯-=y∴C (0 , 3) ∴3=OC……………………………………………6分 ∵x CD //轴 ∴D (1 , 3) ∴1=CD……………………………………………7分∴()OB CD OC S COBD +⋅=21图象 ()631321=+⨯⨯= …………………………………………10分 27.(10分)如图所示,二次函数()212++=x a y 的图象与x 轴交于A 、B 两点,已知()0,3-A ,根据图象回答下列问题:(1)求a 的值和点B 的坐标;(2)设抛物线的顶点是P ,试求△P AB 的面积;(3)在抛物线上是否存在点M ,使得△MAB 的面积是△P AB 的面积的2倍?若存在,求出点M 的坐标.解:(1)把()0,3-A 代入()212++=x a y 得:()02132=++-⨯a解之得:21-=a ……………………………………………2分 ∴()21212++-=x y ∵抛物线的对称轴为直线1-=x ,()0,3-A 、B 两点关于对称轴对称 ∴()0,1B ;……………………………………………3分 (2)∵()21212++-=x y ∴抛物线的顶点坐标为P ()2,1-……………………………………………4分 ∵()0,3-A ,()0,1B ∴()431=--=AB ∴42421=⨯⨯=∆PABS ; ……………………………………………6分 (3)存在.理由如下:设点M 的纵坐标为m ,则有842221=⨯==⋅=∆∆PAB MAB S m AB S ∴8421=⨯⨯m ,4=m ∴4±=m当4=m 时,()421212=++-=x y ,无解; 当4-=m 时,()421212-=++-=x y解之得:321,32121--=+-=x x ∴点M 的坐标为()4,321-+-或()4,321---.…………………………………………10分 关于求抛物线的解析式:在求抛物线的解析式时,要先根据题目的意思或结合图象设出抛物线的解析式,然后再求字母的值.设抛物线的解析式时,有以下几种情况: (1)若抛物线的顶点是坐标原点,则抛物线的解析式应设为2ax y =;(2)若抛物线的顶点在y 轴上(不是原点),则抛物线的解析式应设为k ax y +=2; (3)若抛物线的顶点在x 轴上(不是原点),则抛物线的解析式应设为()2h x a y -=;(4)若抛物线的顶点在象限内,则抛物线的解析式应设为()k h x a y +-=2.如果知道的是抛物线的对称轴和最值,则抛物线的解析式应设为()2h x a y -=或()k h x a y +-=2,视具体情况而定.。
初中数学二次函数图像性质练习题(附答案)

初中数学二次函数图像性质练习题一、单选题1.二次函数2y ax bx c =++的部分图象如图所示.有以下结论:①30a b -=;②240b ac ->;③520a b c -+>;④430b c +>.其中错误结论的个数是( )A.1B.2C.3D.42.将二次函数24y x x a =-+的图象向左平移1个单位,再向上平移1个单位.若得到的函数图象与直线2y =有两个交点,则a 的取值范围是( )A.3a >B.3a <C.5a >D.5a <3.在同一平面直角坐标系中,若抛物线2(21)24y x m x m =+-+-与2(3)y x m n x n =-++关于y 轴对称,则符合条件的m ,n 的值为( ) A.518,77m n ==- B.5,6m n ==- C.1,6m n =-= D.1,2m n ==- 4.二次函数2y x ax b =-+的图象如图所示,对称轴为直线2x =,下列结论不正确的是( )A.4a =B.当4b =-时,顶点的坐标为(2,8)-C.5b >-D.当3x >时,y 随x 的增大而增大 5.对于函数()223y x =--,下列说法不正确的是( )A.开口向下B.对称轴是直线3x =C.最大值为0D.与y 轴不相交6.二次函数2y ax bx c =++的图象如图所示,则下列结论正确的是( )A.0,0,0,0a b c >>>∆<B.0,0,0,0a b c <><∆>C.0,0,0,0a b c ><<∆>D.0,0,0,0a b c <<>∆<二、填空题7.如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为8m ,两侧距地面4m 高处各有一盏灯,两灯间的水平距离为6m ,则这个门洞的高度为_________m .8.抛物线2y ax bx c =++经过(3,0),(4,0)A B -两点,则关于x 的一元二次方程2(1)a x c b bx -+=-的解是__________.9.如图,抛物线的顶点为(2,2)P -,与y 轴交于点(0,3)A ,若平移该抛物线使其点P 沿过原点的直线移动到点(2,2)P '-,点A 的对应点为A ',则抛物线上PA 段扫过区域的面积为___________. 10.把二次函数22y x =的图象向左平移1个单位长度,再向下平移3个单位长度.平移后抛物线的解析式是_________.11.如图,抛物线2y ax =与直线y bx c =+的两个交点坐标分别为()()2,4,1,1A B -.则方程2ax bx c =+的解是 .参考答案1.答案:A解析:由题图,知0,0a c <>,对称轴为直线32x =-,3,322b b a a ∴-=-∴=,故①正确.函数图象与x 轴有两个不同的交点,240b ac ∴∆=->,故②正确.当1x =-时,0a b c -+>,当3x =-时,930,()(93)0a b c a b c a b c -+>∴-++-+>,即10420a b c -+>,520a b c ∴-+>,故③正确.由抛物线的对称性,可知1x =时对应的y 值与4x =-时对应的y 值相等,∴当1x =时,0.3a b c b a ++<=,43333333()0,430b c b b c b a c a b c b c ∴+=++=++=++<∴+<,故④错误.故选A.2.答案:D解析:224(2)4,y x x a x a =-+=--+∴将二次函数24y x x a =-+的图象向左平移1个单位,再向上平移1个单位,得到2(21)41y x a =-+-++,即222y x x a =-+-的图象.将2y =代入222y x x a =-+-,得2222x x a =-+-,即2240x x a -+-=,由题意,得44(4)0a ∆=-->,解得5a <.故选D.3.答案:D解析:抛物线2(21)24y x m x m =+-+-与2(3)y x m n x n =-++关于y 轴对称,213,24,m m n m n -=+⎧∴⎨-=⎩解得1,2.m n =⎧⎨=-⎩故选D. 4.答案:C解析:对称轴为直线2x =,2,42a a ∴=∴=,故A 正确.当4b =-时,2244(2)8,y x x x =--=--∴顶点的坐标为 (2, 8)-,故B 正确.由题图,知当1x =-时,0,140y b <∴++<,5b ∴<-,故C 错误.对称轴为直线2x =,且图象开口向上,∴当3x >时,3x >的增大而增大,故D 正确.故选C.5.答案:D 解析:由题意可得,二次函数的图象开口方向向下,对称轴是直线3x =,顶点坐标为(3)0,,函数的最大值为0,故A 、B 、C 说法正确;当0x =时,18y =-,∴函数()223y x =--与y 轴相交,∴D 说法错误6.答案:B 解析:抛物线开口向下,0a ∴<,又0,02b b a->∴>.抛物线与y 轴交于负半轴,0c ∴<.抛物线与x 轴有两个交点,0∴∆>.故选B.7.答案:647解析:建立如图所示的平面直角坐标系.由题意,知(4,0),(4,0)A B -,(3,4)D -.设抛物线的解析式为2(0)y ax c a =+≠,把(4,0),(3,4)B D -代入,得160,94,a c a c +=⎧⎨+=⎩解得4,764,7a c ⎧=-⎪⎪⎨⎪=⎪⎩所以抛物线的解析式为246477y x =-+,令0x =,解得647y =,所以点C 的坐标为640,7⎛⎫ ⎪⎝⎭,所以这个门洞的高度为64m 7. 8.答案:122,5x x =-=解析:一元二次方程2(1)a x c b bx -+=-可变形为2(1)(1)0a x b x c -+-+=.把抛物线2y ax bx c =++向右平移1个单位长度得2(1)(1)y a x b x c =-+-+.因为抛物线2y ax bx c =++经过点(3,0),(4,0)A B -,所以抛物线2(1)( 1) y a x b x c =-+-+与x 轴的交点坐标为(2,0),(5,0)-,所以一元二次方程2(1)(1)0a x b x c -+-+=的解为122,5x x =-=.9.答案:12解析:如图,连接,PA P A '',过点A 作AH PP '⊥于点H .顶点为(2,2)P -的抛物线平移到顶点为(2,2)P '-的抛物线的位置,∴抛物线上PA 段扫过区域的面积等于平行四边形APP A ''的面积.点P 的坐标为(2,2)-,点P '的坐标为(2,2)-,OP ∴==PP '==1132,22APO S OP AH AH ∴=⨯=⨯⨯∴==∴平行四边形APP A ''的面积为12PP AH'⋅==,即抛物线上PA段扫过区域的面积为12.10.答案:()2212y x=+-解析:由抛物线平移的规律“左加右减自变量,上加下减常数项”可得平移后抛物线的解析式为()2212y x=+-.11.答案:122,1x x=-=解析:抛物线2y ax=与直线y bx c=+的两个交点坐标分别为()()2,4,1,1A B-,∴方程组2y axy bx c⎧=⎨=+⎩的解为1124xy=-⎧⎨=⎩或2211xy=⎧⎨=⎩,即关于x的方程20ax bx c--=的解为122,1x x=-=.。
二次函数的图像与性质经典练习题(11套)附带详细答案之欧阳索引创编

欧阳索引创编 2021.02.02 欧阳索引创编 2021.02.02 练习一
欧阳家百(2021.03.07) 1.二次函数的图像开口向____,对称轴是____,顶点坐标是____,图像有最___点,x___时,y随x的增大而增大,x___时,y随x的增大而减小。 2.关于,,的图像,下列说法中不正确的是( ) A.顶点相同 B.对称轴相同 C.图像形状相同 D.最低点相同
3.两条抛物线与在同一坐标系内,下列说法中不正确的是( ) A.顶点相同 B.对称轴相同 C.开口方向相反 D.都有最小值
4.在抛物线上,当y<0时,x的取值范围应为( ) A.x>0 B.x<0 C.x≠0 D.x≥0 5.对于抛物线与下列命题中错误的是( ) A.两条抛物线关于轴对称 B.两条抛物线关于原欧阳索引创编 2021.02.02 欧阳索引创编 2021.02.02 点对称
C.两条抛物线各自关于轴对称 D.两条抛物线没有公共点 6.抛物线y=-b+3的对称轴是___,顶点是___。 7.抛物线y=--4的开口向___,顶点坐标___,对称轴___,x___时,y随x的增大而增大,x___时,y随x的增大而减小。
8.抛物线的顶点坐标是( ) A.(1,3) B.(1,3) C.(1,3) D.(1,3)
9.已知抛物线的顶点为(1,2),且通过(1,10),则这条抛物线的表达式为( ) A.y=3-2 B.y=3+2 C.y=3-2 D.y=-3-2 10.二次函数的图像向左平移2个单位,向下平移3个单位,所得新函数表达式为( ) A.y=a+3 B.y=a-??
C.y??a+????????????????D.y??a-??
.抛物线的顶点坐标是(??????????) 欧阳索引创编 2021.02.02 欧阳索引创编 2021.02.02 A.( , )??????????B.( , )????????????C.( ,??)??????????????D.( ,??)
二次函数的图像与性质经典练习题附带详细答案

练习一1.二次函数y ax 2的图像开口向____,对称轴是____,顶点坐标是____,图像有最___点,x___时,y 随x 的增大而增大,x___时,y 随 x的增大而减小。
2.关于y 1x2,y x2,y3x2的图像,下列说法中不正确的是()3A.顶点相同B.对称轴相同C.图像形状相同D.最低点相同3.两条抛物线y x2与y x2在同一坐标系内,下列说法中不正确的是()A.顶点相同B.对称轴相同C.开口方向相反D.都有最小值4.在抛物线y x2上,当y< 0 时, x 的取值范围应为()A. x>0B. x< 0C. x≠ 0D. x≥ 05.对于抛物线y x2与y x2下列命题中错误的是()A.两条抛物线关于x轴对称B.两条抛物线关于原点对称C.两条抛物线各自关于y 轴对称D.两条抛物线没有公共点6.抛物线y=-b x2+ 3 的对称轴是___,顶点是___。
7.抛物线y=-1(x2) 2-4的开口向___,顶点坐标___,对称轴___,x_2__时,y 随x 的增大而增大,x___时,y 随x 的增大而减小。
8.抛物线y2(x1)23的顶点坐标是()A.( 1, 3)B.(1, 3) C .(1,3)D.(1,3)9.已知抛物线的顶点为(1,2),且通过( 1,10),则这条抛物线的表达式为()A. y=3( x1)2-2B. y=3(x1)2+2C. y=3( x1)2-2D. y=- 3( x1)2-210.二次函数y ax2的图像向左平移 2 个单位,向下平移 3 个单位,所得新函数表达式为()A. y=a C. y=a ( x 2)2+3B.y=a( x 2) 2+3D.y=a( x2)2-3( x2)2-311.抛物线y x24x 4 的顶点坐标是()A.( 2, 0) B .( 2,-2 ) C .(2,-8 )D.(-2,-8)12.对抛物线 y= 2(x2) 2-3与y=- 2( x2)2+4的说法不正确的是()A.抛物线的形状相同B.抛物线的顶点相同C.抛物线对称轴相同D.抛物线的开口方向相反13.函数 y=a x2+ c 与 y=ax + c(a ≠ 0) 在同一坐标系内的图像是图中的()14.化y x24x3为 y= x24x 3为y a ( x h)2k 的形式是____,图像的开口向____,顶点是____,对称轴是____。
初中数学二次函数解析式图像性质练习题(附答案)
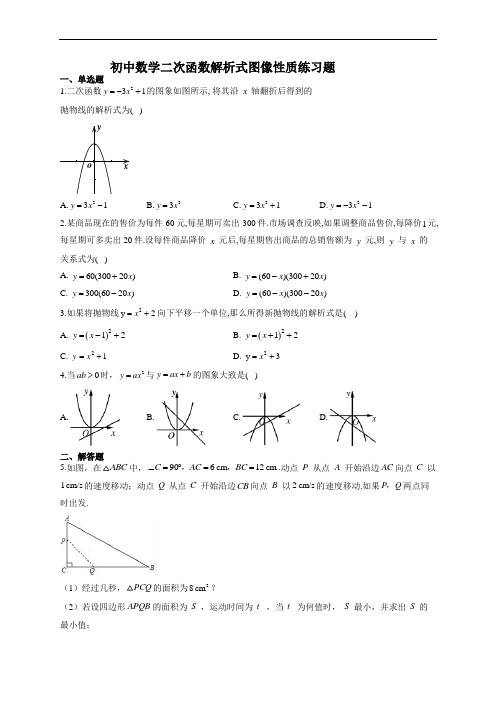
初中数学二次函数解析式图像性质练习题一、单选题1.二次函数231y x =-+的图象如图所示, 将其沿x 轴翻折后得到的抛物线的解析式为( )A.231y x =-B.23y x =C.231y x =+D.231y x =--2.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x 元后,每星期售出商品的总销售额为y 元,则y 与x 的关系式为( )A. 60(30020)y x =+B. (60)(30020)y x x =-+C. 300(6020)y x =-D. (60)(30020)y x x =--3.如果将抛物线2y 2x =+向下平移一个单位,那么所得新抛物线的解析式是( )A. ()212y x =-+B. ()212y x =++ C. 2 1y x =+ D. 2y 3x =+ 4.当0ab >时,2y ax =与y ax b =+的图象大致是( )A. B. C. D.二、解答题5.如图,在ABC 中,906cm 12cm C AC BC ∠=︒==,,.动点P 从点A 开始沿边AC 向点C 以1cm/s 的速度移动;动点Q 从点C 开始沿边CB 向点B 以2cm/s 的速度移动.如果P Q ,两点同时出发.(1)经过几秒,PCQ 的面积为28cm ?(2)若设四边形APQB 的面积为S ,运动时间为t ,当t 为何值时,S 最小,并求出S 的最小值;6.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x 米.(1)若苗圃园的面积为72平方米,求x 的值;(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;(3)当这个苗圃园的面积不小于100平方米时,直接写出x 的取值范围.三、填空题7.请写出一个开口向上,并且与y 轴交于点(01),的抛物线的解析式__________.8.抛物线214y x =+的开口向 ,对称轴是 ,顶点坐标是 . 9.若()2221m y m x mx -=+++是关于自变量x 的二次函数,则m = 。
二次函数的图像与性质练习题及答案

二次函数的图像和性质练习题一、选择题1.下列函数是二次函数的有( )12)5(;)4();3()3(;2)2(;1)1(222+=++=-==-=x y c bx ax y x x y xy x y (6) y=2(x+3)2-2x 2A 、1个;B 、2个;C 、3个;D 、4个 2.关于213y x =,2y x =,23y x =的图像,下列说法中不正确的是( ) A .顶点相同 B .对称轴相同 C .图像形状相同 D .最低点相同 3.抛物线()12212++=x y 的顶点坐标是( ) A .(2,1) B .(-2,1) C .(2,-1) D .(-2,-1)4.已知二次函数)2(2-++=m m x mx y 的图象经过原点,则m 的值为 ( )A . 0或2B . 0C . 2D .无法确定5.已知二次函数213x y -=、2231x y -=、2323x y =,它们的图像开口由小到大的顺序是( )A 、321y y y <<B 、123y y y <<C 、231y y y <<D 、132y y y <<6.两条抛物线2y x =与2y x =-在同一坐标系内,下列说法中不正确的是( )A .顶点相同B .对称轴相同C .开口方向相反D .都有最小值7.已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列结论:①0abc >;②a+b+c>0③a-b+c<0;;其中正确的结论有( ) A .1个B .2个C .3个D .4个8.已知抛物线的顶点为(-1,-2),且通过(1,10), 则这条抛物线的表达式为( )A .y=32(1)x --2 B .y=32(1)x ++2 C .y=32(1)x +-2 D .y=-32)1(-x +29.抛物线23y x =向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )A .23(1)2y x =-- B.23(1)2y x =+- C.23(1)2y x =++ D.23(1)2y x =-+ -1 O x =1y x10.抛物线244y x x =--的顶点坐标是( )A .(2,0)B .(2,-2)C .(2,-8)D .(-2,-8)11.与抛物线y=-12x 2+3x -5的形状、开口方向都相同,只有位置不同的抛物线是( )A. y = x 2+3x -5 B. y=-12x 2+2xC. y =12x 2+3x -5D. y=12x 212.对抛物线y=22(2)x --3与y=-22(2)x -+4的说法不正确的是( )A .抛物线的形状相同B .抛物线的顶点相同C .抛物线对称轴相同D .抛物线的开口方向相反13.对于抛物线21(5)33y x =--+,下列说法正确的是( )A .开口向下,顶点坐标(53),B .开口向上,顶点坐标(53),C .开口向下,顶点坐标(53)-,D .开口向上,顶点坐标(53)-,14.抛物线y=222x mx m -++的顶点在第三象限,试确定m 的取值范围是( )A .m <-1或m >2B .m <0或m >-1C .-1<m <0D .m <-1 15.在同一直角坐标系中,函数y mx m =+和222y mx x =-++(m 是常数,且0m ≠)的图象可能..是( )16.函数y=12-2x +2x -5的图像的对称轴是( ) A .直线x=2 B .直线a=-2 C .直线y=2 D .直线x=4 17.二次函数y=221x x --+图像的顶点在( )A .第一象限B .第二象限C .第三象限D .第四象限 18.如果抛物线y=26x x c ++的顶点在x 轴上,那么c 的值为( )A .0B .6C .3D .9xyOAxyO BxyO CxyO D19.已知二次函数2y ax bx c =++,如果a >0,b <0,c <0,那么这个函数图像的顶点必在( )A .第一象限B .第二象限C .第三象限D .第四象限 20.已知正比例函数kx y =的图像如右图所示,则二次函数222k x kx y +-=的图像大致为( )21.如图所示,满足a >0,b <0的函数y=2ax bx +的图像是( )22.若A (-4,y 1),B (-3,y 2),C (1,y 3)为二次函数y=x 2+4x-5的图象上的三点,则y 1,y 2,y 3的大小关系是( )A 、y 1<y 2<y 3B 、y 2<y 1<y 3C 、y 3<y 1<y 2D 、y 1<y 3<y 2二、填空题:23.二次函数2y ax =(0<a )的图像开口向____,对称轴是____,顶点坐标是____,图像有最___点,x ___时,y 随x 的增大而增大,x ___时,y 随x 的增大而减小。
二次函数的图象和性质练习题(附参考答案和评分标准)
新华师大版九年级下册数学第26章 二次函数的图象和性质练习题姓名____________ 时间: 90分钟 满分:120分 总分____________一、选择题(每小题10分,共30分)1. 下列函数中,是二次函数的为 【 】 (A )54+-=x y (B )()32-=x x y (C )()224x x y -+= (D )21x y =2. 对于函数25x y =,下列结论正确的是 【 】 (A )y 随x 的增大而增大 (B )图象的开口向下(C )图象关于y 轴对称 (D )无论x 取何值,y 的值总是正的 3. 抛物线222,,21x y x y x y -===的共同性质如下: ①都开口向上; ②都以点(0 , 0)为顶点; ③都以y 轴为对称轴; ④都关于x 轴对称.其中正确的个数为 【 】 (A )1 (B )2 (C )3 (D )44. 对于函数12+=x y ,下列结论正确的是 【 】 (A )图象的开口向下 (B )y 随x 的增大而增大 (C )图象关于y 轴对称 (D )最大值是05. 已知二次函数()223-=x y ,则 【 】(A )当2->x 时,y 随x 的增大而减小 (B )当2->x 时,y 随x 的增大而增大 (C )当2>x 时,y 随x 的增大而减小 (D )当2>x 时,y 随x 的增大而增大6. 关于二次函数()212++-=x y 的图象,下列判断正确的是 【 】(A )图象的开口向上 (B )图象的对称轴是直线1=x (C )图象有最低点 (D )图象的顶点坐标为()2,1-7. 将函数2x y =的图象用下列方法平移后,所得的图象不经过点A (1 , 4),的方法是 【 】 (A )向左平移1个单位 (B )向右平移3个单位(C )向上平移3个单位 (D )向下平移1个单位8. 若抛物线()12++-=m m x y 的顶点在第一象限,则实数m 的取值范围是 【 】(A )1>m (B )0>m (C )1->m (D )01<<-m9. 如图所示,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,则下列关系不正确的是 【 】 (A )n k = (B )m h = (C )n k < (D )0,0<<k h第 9 题图x h ) 2 + k y =1yx第 10 题图C BAO10. 如图所示,点A 是抛物线()k x a y +-=23与y 轴的交点,x AB //轴交抛物线于另一点B ,点C 为该抛物线的顶点,若△ABC 为等边三角形,则a 的值为 【 】 (A )21(B )23 (C )33 (D )1二、填空题(每小题3分,共30分)11. 二次函数342-+=x x y ,当1-=x 时,y 的值是_________. 12. 若()23222-++=-x x m y m是二次函数,则m 的值是_________.13. 如果点()a A ,2-在抛物线25x y -=上,则点A 关于y 轴对称的点的坐标是_________. 14. 若抛物线()22x m y -=的开口向下,则m 的取值范围是__________. 15. 已知二次函数221x y =的图象如图所示,x AB //轴,交抛物线于A 、B 两点,且点A 的横坐标为2,则AB 的长度为_________.第 15 题图yx第 18 题图BACDO16. 已知二次函数2x y -=,当0<x 时,y 随x 的增大而_________.17. 将抛物线322+-=x x y 向左平移1个单位,再向下平移3个单位,则抛物线的解析式应为________________.18. 如图所示,抛物线42-=ax y 和42+-=ax y 都经过x 轴上的A 、B 两点,两条抛物线的顶点分别为C 、D .当四边形ACBD 的面积为40时,a 的值为_________.19. 如图,正方形ABCD 的边长为4,E 、F 分别是BC 、CD 上的两个动点,且EF AE ⊥,则AF 的最小值是_________.第 19 题图yx第 20 题图O20. 已知函数21x y =与函数3212+-=x y 的图象如图所示.若21y y >,则自变量x 的取值范围是____________.三、解答题(共60分) 21.(10分)已知函数()422-++=n n x n y 是关于x 的二次函数.(1)求n 的值;(2)当n 为何值时,二次函数的图象有最低点?求出这个最低点,并直接写出x 为何值时,y 随x 的增大而增大;(3)当n 为何值时,函数有最大值?最大值是多少? x 为何值时,y 随x 的增大而减小?22.(10分)如图所示,矩形OABC 的顶点B (2 , 1),在抛物线)0(2>=a ax y 上. (1)求抛物线2ax y =的函数关系式;(2)试写出(1)中的抛物线绕顶点O 旋转︒180后得到的抛物线的函数关系式.yxAC BO23.(10分)写出二次函数322--=x x y 的图象的顶点坐标和对称轴,求出它的最大值或最小值,并在图中画出它的图象.24.(10分)如图所示,直线l 经过点A (3 , 0)、B (0 , 3)两点,且与二次函数12+=x y 的图象在第一象限内相交于点C . (1)求△AOC 的面积;(2)二次函数图象的顶点为D ,求△ABD 的面积.25.(10分)如图所示,抛物线c ax y +=21与x 轴交于A 、B 两点,与y 轴交于点C ,点P 在抛物线上,过()3,1-P ,B (4 , 0)两点作直线b kx y +=2. (1)求抛物线的解析式;(2)根据图象直接写出21y y >时,x 的取值范围.yxPCBA O26.(10分)如图所示,点P 为抛物线241x y =上一动点. (1)若抛物线241x y =是由抛物线()12412-+=x y 通过平移得到的,请写出平移的过程;(2)已知直线l 经过y 轴上一点N ,点N 的坐标为()1,0-,过点P 作l PM ⊥于M .①问题探究:如图1,在y 轴上是否存在一定点F ,使得PF PM =恒成立?若存在,求出点F 的坐标;若不存在,请说明理由.②问题解决:如图2,若点Q 的坐标为(1 , 5),求PF PQ +的最小值.图 1图 2Q新华师大版九年级下册数学第26章 二次函数的图象和性质练习题参考答案一、选择题(每小题3分,共30分)二、填空题(每小题3分,共30分)11. 6- 12. 2 13. ()20,2- 14. 2<m 15. 4 16. 增大 17. 12-=x y 18. 254 19. 5 20. 2-<x 或23>x 三、解答题(共60分) 21.(10分)已知函数()422-++=n n x n y 是关于x 的二次函数. (1)求n 的值;(2)当n 为何值时,二次函数的图象有最低点?求出这个最低点,并直接写出x 为何值时,y 随x 的增大而增大;(3)当n 为何值时,函数有最大值?最大值是多少? x 为何值时,y 随x 的增大而减小? 解:(1)∵函数()422-++=n n x n y 是关于x 的二次函数∴⎩⎨⎧=-+≠+24022n n n……………………………………………2分 解之得:2,321=-=n n ;……………………………………………4分(2)当3-=n 时,2x y -=;当2=n 时,24x y =∴当2=n 时,二次函数的图象有最低点 ……………………………………………5分 最低点为(0 , 0)……………………………………………6分 当0>x 时,y 随x 的增大而增大;……………………………………………7分 (3)由(2)可知,当3-=n 时,函数有最大值……………………………………………8分 最大值为0=y……………………………………………9分 当0>x 时,y 随x 的增大而减小.…………………………………………10分22.(10分)如图所示,矩形OABC 的顶点B (2 , 1),在抛物线)0(2>=a ax y 上. (1)求抛物线2ax y =的函数关系式; (2)试写出(1)中的抛物线绕顶点O 旋转︒180后得到的抛物线的函数关系式.yxA C BO解:(1)把B (2 , 1)代入2ax y =得:122=⨯a解之得:41=a……………………………………………4分 ∴该抛物线的解析式为241x y =; ……………………………………………5分 (2)∵抛物线241x y =的顶点O 为(0 , 0)……………………………………………7分∴抛物线241x y =绕顶点O 旋转︒180后得到的抛物线的函数关系式为:241x y -=.…………………………………………10分 23.(10分)写出二次函数322--=x x y 的图象的顶点坐标和对称轴,求出它的最大值或最小值,并在图中画出它的图象.解:∵322--=x x y ∴()412--=x y……………………………………………3分∴其图象的顶点坐标为()4,1-……………………………………………4分 对称轴为直线1=x……………………………………………5分 ∵01>=a∴函数有最小值,最小值为4-=y ;……………………………………………6分 其图象如图所示.…………………………………………10分24.(10分)如图所示,直线l 经过点A (3 , 0)、B (0 , 3)两点,且与二次函数12+=x y 的图象在第一象限内相交于点C . (1)求△AOC 的面积;(2)二次函数图象的顶点为D ,求△ABD 的面积.解:(1)设直线l 的解析式为b kx y += 把A (3 , 0)、B (0 , 3)分别代入b kx y +=得:⎩⎨⎧==+303b b k 解之得:⎩⎨⎧=-=31b k∴直线l 的解析式为3+-=x y……………………………………………2分解方程组⎩⎨⎧+=+-=132x y x y 得: ⎩⎨⎧==⎩⎨⎧=-=21,522211y x y x ∵点C 在第一象限 ∴C (1 , 2)……………………………………………5分 ∵A (3 , 0)∴3=OA ∴32321=⨯⨯=∆AOC S ; ……………………………………………6分 (2)∵二次函数图象的顶点为D ∴D (0 , 1)……………………………………………7分 ∴1=OD ∵B (0 , 3)∴3=OB∴213=-=-=OD OB BD ∴3322121=⨯⨯=⋅=∆OA BD S ABD . …………………………………………10分 25.(10分)如图所示,抛物线c ax y +=21与x 轴交于A 、B 两点,与y 轴交于点C ,点P 在抛物线上,过()3,1-P ,B (4 , 0)两点作直线b kx y +=2.(1)求抛物线的解析式;(2)根据图象直接写出21y y >时,x 的取值范围.yxPCBA O解:(1)把()3,1-P ,B (4 , 0)分别代入c ax y +=21得:⎩⎨⎧=+-=+0163c a c a 解之得:⎪⎪⎩⎪⎪⎨⎧-==51651c a∴抛物线的解析式为5165122-=x y ; ……………………………………………6分 (2)1<x 或4>x .…………………………………………10分 (注意:写对一个范围给2分) 26.(10分)如图所示,点P 为抛物线241x y =上一动点.(1)若抛物线241x y =是由抛物线()12412-+=x y 通过平移得到的,请写出平移的过程;(2)已知直线l 经过y 轴上一点N ,点N 的坐标为()1,0-,过点P 作l PM ⊥于M . ①问题探究:如图1,在y 轴上是否存在一定点F ,使得PF PM =恒成立?若存在,求出点F 的坐标;若不存在,请说明理由.②问题解决:如图2,若点Q 的坐标为(1 , 5),求PF PQ +的最小值.解:(1)把抛物线()12412-+=x y 先向右平移2个单位,再向上平移1个单位,得到抛物线241x y =; ……………………………………………3分图 1图 2Q(2)①解:存在一定点F ,使得PF PM =恒成立……………………………………………4分 过点P 作y PH ⊥轴∵点P 在抛物线241x y =上 ∴设点P 为⎪⎭⎫⎝⎛241,m m∴1412+==m PF PM ,m PH =在Rt △PFH 中,由勾股定理得:22222141m m PH PF FH -⎪⎭⎫⎝⎛+=-=1412-=m 分为三种情况:第11页当点H 在点F 的上方时(OF m >241), 1414122-=-=-=m OF m OF OH FH∴1=OF ∴F (0 , 1);当点H 与点F 重合时(OF m =241),1414122=-=-=-=m OF m OF OH FH ∴1=OF ∴F (0 , 1);当点H 在点F 的下方时(OF m <241), 1414122-=-=-=m m OF OH OF FH∴1=OF ∴F (0 , 1).综上所述,存在一定点F (0 , 1),使得PF PM =恒成立;……………………………………………7分 ②由①可知:PF PM =∴PF PQ +的最小值也即PM PQ +的最小值,当P 、Q 、M 三点在同一条直线上时,PM PQ +的值最小∵点Q 的坐标为(1 , 5) ∴PM PQ +的最小值为6 ∴PF PQ +的最小值为6.…………………………………………10分。
二次函数的图像和性质练习题
二次函数的图像和性质练习题二次函数是高中数学中的重要内容之一,在数学学习中起着重要的作用。
理解和掌握二次函数的图像和性质对于解题和解决实际问题至关重要。
本文将为您提供一些关于二次函数图像和性质的练习题,以帮助您更好地理解和掌握相关内容。
1. 下列函数中哪个是二次函数?A. y = 3x + 2B. y = x^2 + 2x - 1C. y = √xD. y = |x|解答:答案是B。
只有函数B是含有二次项的函数,其他函数均不是二次函数。
2. 给定一个二次函数 y = ax^2 + bx + c,若 a > 0,那么这个二次函数的图像是什么样的?解答:当 a > 0 时,二次函数的图像开口向上。
这是因为二次函数的图像开口方向与二次项系数 a 的符号相关,当 a > 0 时,函数的图像开口向上,表示函数的最小值在图像的顶点处。
3. 给定一个二次函数 y = -2x^2 + 4x - 1,那么它的顶点坐标是多少?解答:二次函数的顶点坐标可通过公式 x = -b/2a 和 y = f(x) 计算得出。
对于这个二次函数,a = -2,b = 4,c = -1。
代入公式计算可得:x = -4/(2*(-2)) = -4/(-4) = 1y = -2(1)^2 + 4(1) - 1 = 1因此,这个二次函数的顶点坐标为 (1, 1)。
4. 给定一个二次函数的图像为一个开口向下的抛物线,该二次函数的开口向上对称的点是什么?解答:根据二次函数的性质,开口向下的二次函数的开口向上对称的点为顶点。
因此,开口向下的抛物线的开口向上对称的点即为顶点。
可以通过平移顶点的方法来求得这个点的坐标。
5. 给定一个二次函数 y = x^2 + 3x + 2,那么它的零点是什么?解答:二次函数的零点即为方程 y = 0 的解,也就是函数与 x 轴交点的横坐标。
对于这个二次函数,我们需要求解方程x^2 + 3x + 2 = 0。
(完整版)二次函数图像和性质习题.doc
二次函数图像和性质习题精选一.选择题(共 30 小题)y=ax 与 y=ax 2的图象有可能是(1.已知 a ≠0,在同一直角坐标系中,函数 )A .B .C .D .2.函数y=ax 2+1 与y=(a ≠0)在同一平面直角坐标系中的图象可能是()A .B .C .D .3.已知抛物线 y=ax 2+bx 和直线 y=ax+b 在同一坐标系内的图象如图,其中正确的是 () A . B . C .D .4.已知反比例函数 y= 的图象如图,则二次函数y=2kx 2﹣ 4x+k 2的图象大致为()A .B .C .D .5.二次函数 2y=ax +bx+c ( a , b , c 为常数,且 a ≠0)中的 x 与 y 的部分对应值如下表:X ﹣1 0 1 3y ﹣1 3 5 3下列结论:( 1) ac < 0;( 2)当 x > 1 时, y 的值随 x 值的增大而减小.( 3) 3 是方程 ax 2+(b ﹣ 1) x+c=0 的一个根;( 4)当﹣ 1< x < 3 时, ax 2+( b ﹣ 1) x+c > 0. 其中正确的个数为( ) A .4 个B . 3 个C .2 个D . 1 个6.二次函数 y=ax 2+bx+c ( a ≠0)的大致图象如图, 关于该二次函数, 下列说法错误的是 ( )A .函 数有最小值B.对称轴是直线 x=C . 当 x < , y 随 x 的增大而减小D . 当 ﹣ 1< x < 2 时, y > 07.如图,平面直角坐标系中,点 M 是直线 y=2 与 x 轴之间的一个动点,且点 M 是抛物线y= x 2+bx+c 的顶点,则方程 x 2+bx+c=1 的解的个数是()A .0 或 2B . 0 或 1C .1 或 2D . 0,1 或 28.已知二次函数y=a (x ﹣ h )2+k ( a >0),其图象过点 A ( 0, 2), B ( 8, 3),则 h 的值可 以是( )A .6B . 5C .4D . 39.二次函数 y=ax 2+bx+c 图象上部分点的坐标满足下表:x ⋯ 3 2 1 0 1 ⋯ y ⋯3 23 611⋯函数 象的 点坐 ( )A .( 3, 3)B . ( 2, 2)C .( 1, 3)D . (0, 6)10.已知二次函数 y=ax 2+bx+c ( a ≠0)的 象如 所示,下列 法 的是()A . 象关于直 x=1 称B . 函数 y=ax 2+bx+c ( a ≠0)的最小 是 4C . 1 和 3 是方程 ax 2+bx+c=0 ( a ≠0)的两个根 D .当 x < 1 , y 随 x 的增大而增大 11.如 ,二次函数的 象 ( 2, 1),( 1,1)两点, 下列关于此二次函数的 法正确的是()A .y 的最大 小于 0B . 当 x=0 , y 的 大于 1C . 当 x= 1 , y 的 大于 1D . 当 x= 3 , y 的 小于 012. 二次函数 2, 有 y ≥0,当 1≤x ≤3 , 有 y ≤0,那么 c 的取y=x +bx+c ,当 x ≤1 范 是( )A .c=3B . c ≥3C .1≤c ≤3D . c ≤313.如 ,直角坐 系中,两条抛物 有相同的 称 ,下列关系不正确的是()A .h=m B. k=n C.k> n D . h>0, k> 014.已知二次函数数的图象关于直线的个数是()y=ax2+bx+c ( a≠0)的图象如图所示,给出以下结论:x=1 对称;③当 x= ﹣ 1 或 x=3 时,函数y 的值都等于① a> 0;②该函0.其中正确结论A .3 B. 2 C.1 D . 0 15.二次函数y=ax 2+bx+c ( a≠0)的图象如图所示,下列结论正确的是()A .ac< 0B .当 x=1 时, y> 0C.方程 ax 2+bx+c=0 ( a≠0)有两个大于 1 的实数根D .存在一个大于 1 的实数 x0,使得当x<x0时, y 随 x 的增大而减小;当x> x0时, y 随 x 的增大而增大16.如图,抛物线y=ax 2+bx+c( a> 0)的对称轴是直线x=1 ,且经过点 P( 3,0),则 a﹣ b+c的值为()A .0B.﹣ 1C.1 D . 2 17.下列图中阴影部分的面积相等的是()A .① ②B . ② ③C .③ ④D . ① ④18.已知抛物线y=ax 2+bx+c ( a < 0)的部分图象如图所示, 当y > 0 时,x的取值范围是()A .﹣ 2< x < 2B .﹣ 4<x < 2C .x <﹣ 2 或 x > 2D . x <﹣ 4 或 x > 219.已知:二次函数y=x 2﹣ 4x ﹣ a ,下列说法错误的是( )A .当 x < 1 时, y 随 x 的增大而减小B . 若图象与 x 轴有交点,则 a ≤4C . 当 a=3 时,不等式 x 2﹣ 4x+a < 0 的解集是 1< x < 3 D .若 将图象向上平移 1 个单位,再向左平移 3 个单位后过点( 1,﹣ 2),则 a=320.下列表格给出的是二次函数 22y=ax +bx+c ( a ≠0)的几组对应值,那么方程 ax +bx+c=0的一个近似解可以是( A ) x 3.3 3.43.5 3.6 y ﹣ 0.06﹣ 0.020.03 0.09A .3.25B . 3.35C .3.45D . 3.5521.已知二次函数2的 y 与 x 的部分对应值如下表: 则下列判断中正确的是 ( )y=ax +bx+cA .抛 物线开口向上B . 抛物线与 y 轴交于负半轴C . 当 x=3 时, y < 0D . 方程 ax 2+bx+c=0 有两个相等实数根1 2222.已知二次函数 y =ax +bx+c ( a ≠0)与一次函数y =kx+m (k ≠0)的图象相交于点 A (﹣ 2,4), B (8, 2)(如图所示),则能使 y 1< y 2 成立的 x 的取值范围是( )A .x > 2B . x < 2C .x > 0D . 2< x < 823.在 3≤x ≤0 范 内, 二次函数 ( a ≠0)的 象如 所示. 在 个范 内,有 :① y 1 有最大 1、没有最小 ;② y 1 有最大 1、最小 3;③ 函数 y 1 随 x 的增大而增大;2④ 方程 ax +bx+c=2 无解; ⑤ 若 y 2=2x+4 , y 1≤y 2. 其中正确的个数是()A .2B . 3C .4D . 524.抛物 y= x 2+bx+c 上部分点的横坐x , 坐 y 的 如下表:x ⋯ 2 1 1 3 4 ⋯ y ⋯ 0464 0 ⋯根据上表判断下列四种 法: ① 抛物 的 称 是 x=1 ; ② x >1 , y 的 随着 x 的增大 而减小: ③ 抛物 有最高点: ④ 抛物 的 点、与x 的两个交点三点 点的三角形的面 36.其中正确 法的个数有( )A .1B . 2C .3D . 425.如 ,已知抛物y=x 2+bx+c 的 称 x=2,点 A ,B 均在抛物 上,且 AB 与 x平行,其中点 A 的坐 ( 0, 3), 点 B 的坐 ( )A .( 2, 3)B.( 3,2)C.( 3, 3) D .(4, 3)26.如图为二次函数 y=ax 2+bx+c 的图象,给出下列说法:① ab< 0;②方程 ax2+bx+c=0 的根为 x1=﹣1,x2=3;③ a+b+c>0;④ 当 x< 1 时,y 随 x 值的增大而增大;⑤当 y> 0 时,x<﹣ 1 或 x> 3.其中,正确的说法有()A .① ②④B.① ②⑤C.① ③⑤ D .② ④⑤27.已知二次函数y=x 2+2( a﹣ 1) x+2 .如果 x≤4 时, y 随 x 增大而减小,则常数 a 的取值范围是()A .a≥﹣ 5B. a≤﹣ 5C.a≥﹣ 3 D . a≤﹣328.如图,平行于y 轴的直线 l 被抛物线y=0.5x 2+1 ,y=0.5x2﹣1 所截,当直线l 向右平移 3个单位时,直线l 被两条抛物线所截得的线段扫过的图形面积为()平方单位.A .3B. 4C.6 D .无法可求29.已知直线经过点A( 0,2),B( 2,0),点 C 在抛物线y=x 2的图象上,则使得S△ABC=2的点有()个.A .4B. 3C.2 D . 130.如图,已知抛物线,直线y2 =3x+3 ,当x 任取一值时,x 对应的函数值分别为 y1, y2.若 y1≠y2,取 y1, y2中的较小值记为M ;若y1=y 2,记 M=y 1=y 2.下列判断:①当 x> 0 时, y1> y2;② 使得 M 大于 3 的 x 值不存在;③当 x< 0 时, x 值越大, M 值越小;④ 使得M=1 的 x 值是或.其中正确的是()A .① ③B.② ④C.① ④ D .② ③。
初中数学二次函数图像性质练习题(附答案)
初中数学二次函数图像性质练习题一、单选题1.二次函数2y x ax b =-+的图象如图所示,对称轴为直线2x =,下列结论不正确的是( )A.4a =B.当4b =-时,顶点的坐标为(2,8)-C.5b >-D.当3x >时,y 随x 的增大而增大2.已知一次函数b y x c a=+的图象如图,则二次函数2y ax bx c =++在平面直角坐标系中的图象可能是( )A. B. C. D.3.如图,一条抛物线与x 轴相交于()()12,0,,0A x B x 两点(点B 在点A 的右侧),其顶点P 在线段MN 上移动,M ,N 的坐标分别为(1, 2) ,(1,2)-,1x 的最小值为3-,则2x 的最大值为( )A.1-B.1C.3D.5 4.若函数22y x x b =+-的图象与坐标轴有三个交点,则b 的取值范围是( ) A.1b >-且0b ≠ B.1b <且0b ≠ C.1b 且0b ≠ D.1b -且0b ≠ 5.二次函数2y ax bx c =++的图象如图所示,则下列结论正确的是( )A.0,0,0,0a b c >>>∆<B.0,0,0,0a b c <><∆>C.0,0,0,0a b c ><<∆>D.0,0,0,0a b c <<>∆<6.用一条长为40cm 的绳子围成一个面积为2cm S 的长方形,S 的值不可能为( ) A.20 B.40 C.100 D.1207.二次函数2y ax bx c =++的图象如图所示,若点()()122.2,, 3.2,A y B y --是图象上的两点,则1y 与2y 的大小关系是( )A.12y y <B.12y y =C.12y y >D.不能确定8.将抛物线265y x x =-+向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )A.2(4)6y x =--B.2(1)3y x =--C.2(2)2y x =--D.2(4)2y x =-- 9.函数2(2)21m m y m x x +=+++是二次函数,则m 的值为( ) A.2- B.0 C.2-或1 D.110.已知抛物线过点(1,0)A -和点(3,0)B ,与y 轴交于点C ,且BC =,则这条抛物线的解析式为( )A.223y x x =-++B.223y x x =--C.223y x x =-++或223y x x =--D.223y x x =+-或223y x x =-++ 11.已知二次函数的图象如图,则该函数的解析式是( )A.22y x x =-+B.22y x x =++C.22y x x =--+D.22y x x =-++12.已知二次函数在1x =时,有最大值8,其图象的形状、开口方向均与抛物线22y x =-相同,则这个二次函数的解析式是( ) A.223y x x =--+ B.224y x =-+ C.2248y x x =-++ D.2246y x x =-++ 13.抛物线的顶点为(1,4)-,与y 轴交于点(0,3)-,则该抛物线的解析式为( ) A.223y x x =-- B.223y x x =+- C.223y x x =-+ D.2233y x x =-- 14.已知二次函数的图象经过点(1,5),(0,4)---和(1,1),则该二次函数的解析式为( )A.2634y x x =-++B.2234y x x =-+-C.224y x x =+-D.2234y x x =+-15.将抛物线224y x x c =-+向左平移2个单位长度得到的抛物线经过()()12314,,2,,,2y y y ⎛⎫-- ⎪⎝⎭三点,则123,,y y y 的大小关系是( ) A.231y y y >> B.123y y y >> C.213y y y >> D.132y y y >>16.在平面直角坐标系中,对于二次函数2(2)1y x =-+,下列说法中错误的是( ) A.y 的最小值为1B.图象顶点坐标为(2,1),对称轴为直线2x =C.当2x <时,y 的值随x 值的增大而增大,当2x 时,y 的值随x 值的增大而减小D.它的图象可以由2y x =的图象向右平移2个单位长度,再向上平移1个单位长度得到 17.抛物线22(2)1y x m =+++(m 为常数)的顶点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限18.如图,抛物线()20y ax bx c a =++≠经过点()1,0,-对称轴为: 直线1x =,则下列结论中正确的是:( )A. 0a >B.当1x >时, y 随x 的增大而增大C. 0c <D. 3x =是一元二次方程()200ax bx c a ++=≠的一个根19.对于函数()223y x =--,下列说法不正确的是( ) A.开口向下 B.对称轴是直线3x = C.最大值为0D.与y 轴不相交20.将抛物线216212y x x =-+向左平移2个单位后,得到新抛物线的解析式为( ) A .()221852y x x =-+ B .y=()221452y x x =-+C .()221832y x x =-+ D .()221432y x x =-+ 21.已知二次函数2()y x h =--(h 为常数),当自变量x 的值满足25x ≤≤时,与其对应的函数值y 的最大值为1-,则h 的值为( ) A.3或6B.1或6C.1或3D.4或622.在平面直角坐标系中,二次函数()()20y a x h a =-≠的图象可能是( )A. B. C. D.23.将二次函数24y x x a =-+的图象向左平移1个单位,再向上平移1个单位.若得到的函数图象与直线2y =有两个交点,则a 的取值范围是( ) A.3a > B.3a < C.5a > D.5a <24.在同一平面直角坐标系中,若抛物线2(21)24y x m x m =+-+-与2(3)y x m n x n =-++关于y 轴对称,则符合条件的m ,n 的值为( )A.518,77m n ==- B.5,6m n ==- C.1,6m n =-= D.1,2m n ==-25.二次函数2y ax bx c =++的部分图象如图所示.有以下结论:①30a b -=;②240b ac ->;③520a b c -+>;④430b c +>.其中错误结论的个数是( )A.1B.2C.3D.4二、解答题26.如图,抛物线2534y x x =-+与x 轴相交于A ,B 两点(A 在B 的左侧),与y 轴相交于点C ,点D 是直线BC 下方抛物线上一点,过点D 作y 轴的平行线,与直线BC 相交于点E .(1)求直线BC 的解析式;(2)当线段DE 的长度最大时,求点D 的坐标.27.如图,抛物线2y ax bx c =++过点(1,0),(3,0),(0,3)A B C -.(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在一点P ,使得PAC 的周长最小?若存在,请求出点P 的坐标及PAC 的周长;若不存在,请说明理由.(3)在(2)的条件下,在x 轴上方的抛物线上是否存在点M (不与点C 重合),使得PAM PAC S S =?若存在,请求出点M 的坐标;若不存在,请说明理由.28.俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y 本,销售单价为x 元.(1)请直接写出y 与x 之间的函数关系式和自变量x 的取值范围; (2)当每本足球纪念册销售单价是多少元时,商店每天获利2 400元?(3)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w 最大?最大利润是多少?29.已知抛物线2342y ax x =++的对称轴是直线3x =,与x 轴相交于A ,B 两点(点B 在点A 右侧),与y 轴交于点C .(1)求抛物线的解析式和A ,B 两点的坐标;(2)如图1,若点P 是抛物线上B ,C 两点之间的一个动点(不与B ,C 重合),是否存在点P ,使四边形PBOC 的面积最大?若存在,求点P 的坐标及四边形PBOC 面积的最大值;若不存在,请说明理由.(3)如图2,若点M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,当3MN =时,求点M 的坐标.参考答案1.答案:C解析:对称轴为直线2x =,2,42aa ∴=∴=,故A 正确.当4b =-时,2244(2)8,y x x x =--=--∴顶点的坐标为 (2, 8)-,故B 正确.由题图,知当1x =-时,0,140y b <∴++<,5b ∴<-,故C 错误.对称轴为直线2x =,且图象开口向上,∴当3x >时,3x >的增大而增大,故D 正确.故选C. 2.答案:A解析:由题图中一次函数b y x c a =+的图象可知,0ba<,0c >.对于二次函数2y ax bx c =++,0,02bc a>->,∴它的图象与y 轴的交点在x 轴上方,且对称轴在y 轴右侧,故只有选项A中的图象符合题意.故选A. 3.答案:C解析:当抛物线的顶点平移到点M 时,1x 的值最小,设此时抛物线的解析式为2(1)2y a x =++,把(3,0)-代入,得12a =-,所以当抛物线的顶点平移到点N 时,抛物线的解析式为21( 1) 22y x =--+.令0y =,得3x =或1x =-,所以此时抛物线与x 轴的两个交点坐标为(3,0)和(1,0)-,所以2x 的最大值为3.故选C. 4.答案:A解析:根据题意,得函数22y x x b =+-的图象与x 轴有两个交点,与y 轴有一个交点,且与x 轴、y 轴不能交于点(0,0),所以2240b +>且0b ≠,解得1b >-且0b ≠.故选A. 5.答案:B解析:抛物线开口向下,0a ∴<,又0,02bb a->∴>.抛物线与y 轴交于负半轴,0c ∴<.抛物线与x 轴有两个交点,0∴∆>.故选B. 6.答案:D解析:设所围成长方形的长为cm x ,则宽为(20)cm x -.由题意,得2(20)(10)100(020)S x x x x =-=--+<<,∴当10x =时,S 取得最大值100,结合选项,知选D. 7.答案:A解析:由题图,知该函数图象开口向下,对称轴是直线3x =-.因为点()12.2,A y -,()23.2,B y -是图象上的两点,且点A 到对称轴的距离大于点B 到对称轴的距离,所以12y y <.故选A. 8.答案:D解析:因为2265(3)4y x x x =-+=--,所以该函数图象的顶点坐标为(3,4)-,所以将抛物线265y x x =-+向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线的顶点坐标为(4,2)-,所以抛物线的解析式为2(4)2y x =--.故选D.9.答案:D解析:函数2(2)21m my m x x +=+++是二次函数,22,20,1m m m m ∴+=+≠∴=.故选D.10.答案:C解析:因为3BC OB ==,所以点C 的坐标有两种可能:12(0,3),(0,3)C C -.设所求抛物线的解析式为(1)( 3 ) y a x x =+-,将1(0,3)C 代入,得1a =-;将2(0,3)C -代入,得1a =,所以所求抛物线的解析式为223y x x =-++或223y x x =--.故选C. 11.答案:D解析:由题中图象,可知该二次函数图象与x 轴的交点坐标为(1,0),(2,0)-,可设二次函数的解析式为(1)(2)y a x x =+-,因为图象过点(0,2),所以将(0,2)代入,得22a =-,解得1a =-,所以该函数的解析式为2(1)(2)2y x x x x =-+-=-++.故选D. 12.答案:D解析:二次函数在1x =时,有最大值8,∴顶点坐标为 (1, 8 ) ,∴可设该二次函数的解析式为2(1)8y a x =-+,又其图象的形状、开口方向均与抛物线22y x =-相同,2a ∴=-,∴该二次函数的解析式为222(1)8246y x x x =--+=-++.故选D. 13.答案:A解析:根据题意,设抛物线的解析式为2(1)4y a x =--,将(0,3)-代入,得23(01)4a -=--,解得1a =,所以该抛物线的解析式为22(1)423y x x x =--=--.故选A.14.答案:D解析:设所求函数的解析式为2y ax bx c =++,把(1,5),(0,4)---,(1,1)分别代入,得5,4,1,a b c c a b c -+=-⎧⎪=-⎨⎪++=⎩解得2,3,4,a b c =⎧⎪=⎨⎪=-⎩所以所求函数的解析式为2234y x x =+-.故选D. 15.答案:D解析:将224y x x c =-+配方得22(1)2y x c =-+-,∴原抛物线的顶点为(1,2)c -,向左平移2个单位长度后,抛物线的顶点变为(1,2)c --,∴新抛物线对应的函数解析式为22(1)2y x c =++-,对称轴为直线1x =-,∴三个点与对称轴的距离由大到小依次是()()13214,,,,2,2y y y ⎛⎫-- ⎪⎝⎭,又抛物线开口向上,132y y y ∴>>.故选D. 16.答案:C解析:二次函数2(2)1y x =-+的图象开口向上,对称轴为直线2x =,顶点坐标为(2,1),所以y 的最小值是1,当2x 时,y 的值随x 值的增大而增大,当2x <时,y 的值随x 值的增大而减小,故A ,B 正确,C 错误.将2y x =的图象向右平移2个单位长度,再向上平移1个单位长度得到2(2)1y x =-+的图象,故D 正确.故选C. 17.答案:B解析:22(2)1y x m =+++,∴顶点坐标为()22,1m -+,220,10,m -<+>∴顶点在第二象限.故选B.18.答案:D解析:图象开口向下, 0a <,故A 错误;对称轴是1x =,当时, y 随x 的增大而减小,故B 错误;图象与y 轴的交点在y 轴正半轴,则0c >,故C 错误;由图象的对称性可得,图象与x 轴的另一个交点的横坐标是3,则3x =是方程20ax bx c ++=的一个根.故选D. 19.答案:D解析:由题意可得,二次函数的图象开口方向向下,对称轴是直线3x =,顶点坐标为(3)0,,函数的最大值为0,故A 、B 、C 说法正确;当0x =时,18y =-,∴函数()223y x =--与y 轴相交,∴D 说法错误 20.答案:D.图象向左平移方法2:直接运用函数图象左右平移的“左加右减”法则向左平移2个单位,即原来解析式中所有的21.答案:B解析:二次函数2()y x h =--(h 为常数),图象的开口向下,顶点坐标为(,0)h ,函数值的最大值为0,因为当25x ≤≤时,与其对应的函数值y 的最大值为-1,所以h 不能取2~5(含2与5)间的数.当2h <时.点(2,1)-在抛物线上.把(2,1)-代入2()y x h =--,解得1h =或3h =(不合题意,舍去);当5h >时,点(5,1)-在抛物线上,把(5,1)-代入2()y x h =--,解得6h =或4h = (不合题意,舍去).综上可知,h 的值为1或6,故选B. 22.答案:D解析:二次函数()()20y a x h a =-≠的图象的顶点坐标为(,0)h ,由于该点的纵坐标为0,所以该点在x 轴上,符合这一条件的图象只有D.故选D.23.答案:D解析:224(2)4,y x x a x a =-+=--+∴将二次函数24y x x a =-+的图象向左平移1个单位,再向上平移1个单位,得到2(21)41y x a =-+-++,即222y x x a =-+-的图象.将2y =代入222y x x a =-+-,得2222x x a =-+-,即2240x x a -+-=,由题意,得44(4)0a ∆=-->,解得5a <.故选D. 24.答案:D 解析:抛物线2(21)24y x m x m =+-+-与2(3)y x m n x n =-++关于y 轴对称,213,24,m m n m n -=+⎧∴⎨-=⎩解得1,2.m n =⎧⎨=-⎩故选D. 25.答案:A解析:由题图,知0,0a c <>,对称轴为直线32x =-,3,322b b a a ∴-=-∴=,故①正确.函数图象与x 轴有两个不同的交点,240b ac ∴∆=->,故②正确.当1x =-时,0a b c -+>,当3x =-时,930,()(93)0a b c a b c a b c -+>∴-++-+>,即10420a b c -+>,520a b c ∴-+>,故③正确.由抛物线的对称性,可知1x =时对应的y 值与4x =-时对应的y 值相等,∴当1x =时,0.3a b c b a ++<=,43333333()0,430b c b b c b a c a b c b c ∴+=++=++=++<∴+<,故④错误.故选A.26.答案:(1)令0y =,则25304x x -+=,解得121515,,,0,,02222x x A B ⎛⎫⎛⎫==∴ ⎪ ⎪⎝⎭⎝⎭.令0x =,则55,0,44y C ⎛⎫=∴ ⎪⎝⎭.设直线BC 的解析式为(0)y kx b k =+≠,则50,25,4k b b ⎧+=⎪⎪⎨⎪=⎪⎩解得1,25,4k b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线BC 的解析式为1524y x =-+.(2)设点D 的横坐标为502m m ⎛⎫<< ⎪⎝⎭,则点D 的纵坐标为2534m m -+,点E 的纵坐标为1524m -+,22155532442DE m m m m m ⎛⎫∴=-+--+=-+ ⎪⎝⎭2525504162m m ⎛⎫⎛⎫=--+<<⎪ ⎪⎝⎭⎝⎭, ∴当54m =时,线段DE 的长最大,此时点D 的坐标为515,416⎛⎫- ⎪⎝⎭.解析:27.答案:(1)由题意,可设抛物线的解析式为(1)(3)y a x x =+-, 把点(0,3)C 代入,得33,1a a -=∴=-,∴抛物线的解析式为2(1)(3)23y x x x x =-+-=-++.(2)存在.如图1,连接PB BC ,.点P 在抛物线的对称轴直线1x =上,点,A B 关于对称轴直线1x =对称, ,PA PB PAC ∴=∴的周长为AC PC PA AC PC PB ++=++, ∴当C P B ,,三点共线时,PAC 的周长最小.(1,0),(3,0),(0,3)A B C -,10,AC BC ∴==,PAC∴的周长的最小值为AC CB +=设直线BC 的解析式为3y kx =+,把(3,0)B 代入,得330k +=,解得1k =-, ∴直线BC 的解析式为3y x =-+,令1x =,得2y =,∴点P 的坐标为(1,2).(3)存在.,PAM PAC S S =∴当以PA 为底时,两三角形等高, ∴点C 和点M 到直线PA 的距离相等.①当点C ,M 在直线AP 的同侧时,如图2,作直线CM ,则//CM PA , 设直线AP 的解析式为y px d =+, 把(1,2),(1,0)P A -代入, 得0,2,p d p d -+=⎧⎨+=⎩解得1,1,p d =⎧⎨=⎩∴直线AP 的解析式为1y x =+, ∴直线CM 的解析式为3y x =+.由23,23,y x y x x =+⎧⎨=-++⎩解得12120,1,3,4,x x y y ⎧==⎧⎪⎨⎨==⎪⎩⎩点C 的坐标是(0,3), ∴点M 的坐标为(1,4).②当点C ,M 在直线AP 的异侧时,如图3,过点M 作直线//.l AP 结合①得直线l 到PA 的距离等于直线3y x =+到PA 的距离, ∴将直线AP 向下平移2个单位长度得直线l :1y x =-. 由21,23,y x y x x =-⎧⎨=-++⎩解得1212,x x y y ⎧⎧==⎪⎪⎪⎪⎨⎨⎪⎪==⎪⎪⎩⎩点M 在x 轴的上方,0y∴>,∴点M 的坐标为⎝⎭.综上,存在满足题意的点M ,且点M 的坐标为(1,4)或⎝⎭.解析:28.答案:(1)10740(4452)y x x =-+.(2)根据题意,得(40)(10740)2400x x --+=,解得1250,64x x ==(不合题意,舍去).答:当每本足球纪念册销售单价是50元时,商店每天获利2 400元.(3)根据题意,得2(40)(10740)10(57)2890w x x x =--+=--+,当57x <时,w 随x 的增大而增大,因为4452x ,所以当52x =时,w 有最大值,最大值为2 640.答:将足球纪念册销售单价定为52元时,商店每天销售纪念册获得的利润最大,最大利润是2 640元.解析:29.答案:(1)抛物线的对称轴是直线3x =,3232a ∴-=,解得14a =-, ∴抛物线的解析式为213442y x x =-++. 当0y =时,2134042x x -++=,解得122,8x x =-=, ∴点A 的坐标为(2,0)-,点B 的坐标为(8,0).(2)当0x =时,2134442y x x =-++=, ∴点C 的坐标为(0,4).如图,连接BC .设BC 所在直线的解析式为y kx b =+,将(8,0),(0,4)B C 代入,得80,4,k b b +=⎧⎨=⎩解得1,24,k b ⎧=-⎪⎨⎪=⎩ BC ∴所在直线的解析式为142y x =-+. 假设存在点P ,使四边形PBOC 的面积最大,设点P 的坐标为213,442x x x ⎛⎫-++ ⎪⎝⎭,其中x 取值范围为08x <<. 如图,过点P 作//PD y 轴,交BC 于点D , 则点D 的坐标为1,42x x ⎛⎫-+ ⎪⎝⎭, 则2213114424224PD x x x x x ⎛⎫=-++--+=-+ ⎪⎝⎭,1122BOC PBD PCD PBOC S S S S OB OC PD OB ∴=++=⨯⨯+⨯⨯=四边形221118482(4)32224x x x ⎛⎫⨯⨯+⨯⨯-+=--+ ⎪⎝⎭, ∴当4x =时,四边形PBOC 的面积最大,最大值是32. ∴存在点(4,6)P ,使得四边形PBOC 的面积最大.(3)设点M 的坐标为213,442m m m ⎛⎫-++ ⎪⎝⎭, 则点N 的坐标为1,42m m ⎛⎫-+ ⎪⎝⎭, 2213114424224MN m m m m m ⎛⎫∴=-++--+=-+ ⎪⎝⎭∣∣∣∣, 213,234MN m m =∴-+=∣∣, 当08m 时,21234m m -+=,解得122,6m m ==, ∴点M 的坐标为(2,6)或(6,4).当0m <或8m >时,21234m m -+=-,解得1244m m =-=+∴点M 的坐标为(41)-或(41)+.综上,点M 的坐标为(2,6)或(6,4)或(41)-或(41)+. 解析:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数图像和性质习题精选 一.选择题(共30小题) 1.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( ) A. B. C. D.
2.函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是( ) A. B. C. D.
3.已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( ) A. B. C. D.
4.已知反比例函数y=的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为( ) A. B. C. D. 5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表: X ﹣1 0 1 3 y ﹣1 3 5 3 下列结论:(1)ac<0; (2)当x>1时,y的值随x值的增大而减小. (3)3是方程ax2+(b﹣1)x+c=0的一个根; (4)当﹣1<x<3时,ax2+(b﹣1)x+c>0. 其中正确的个数为( ) A. 4个 B. 3个 C. 2个 D. 1个 6.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) A. 函数有最小值 B. 对称轴是直线x=
C. 当x<,y随x的增大而减小 D. 当﹣1<x<2时,y>0
7.如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=x2+bx+c的顶点,则方程x2+bx+c=1的解的个数是( )
A. 0或2 B. 0或1 C. 1或2 D. 0,1或2 8.已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( ) A. 6 B. 5 C. 4 D. 3 9.二次函数y=ax2+bx+c图象上部分点的坐标满足下表: x … ﹣3 ﹣2 ﹣1 0 1 … y … ﹣3 ﹣2 ﹣3 ﹣6 ﹣11 … 则该函数图象的顶点坐标为( ) A. (﹣3,﹣3) B. (﹣2,﹣2) C. (﹣1,﹣3) D. (0,﹣6)
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
A. 图象关于直线x=1对称 B. 函数y=ax2+bx+c(a≠0)的最小值是﹣4
C. ﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D. 当x<1时,y随x的增大而增大 11.如图,二次函数的图象经过(﹣2,﹣1),(1,1)两点,则下列关于此二次函数的说法正确的是( ) A. y的最大值小于0 B. 当x=0时,y的值大于1 C. 当x=﹣1时,y的值大于1 D. 当x=﹣3时,y的值小于0 12.设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是( ) A. c=3 B. c≥3 C. 1≤c≤3 D. c≤3 13.如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是( )
A. h=m B. k=n C. k>n D. h>0,k>0 14.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a>0;②该函数的图象关于直线x=1对称;③当x=﹣1或x=3时,函数y的值都等于0.其中正确结论的个数是( )
A. 3 B. 2 C. 1 D. 0 15.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( )
A. ac<0 B. 当x=1时,y>0 C. 方程ax2+bx+c=0(a≠0)有两个大于1的实数根
D. 存在一个大于1的实数x0,使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大 16.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c的值为( ) A. 0 B. ﹣1 C. 1 D. 2 17.下列图中阴影部分的面积相等的是( )
A. ①② B. ②③ C. ③④ D. ①④ 18.已知抛物线y=ax2+bx+c(a<0)的部分图象如图所示,当y>0时,x的取值范围是( )
A. ﹣2<x<2 B. ﹣4<x<2 C. x<﹣2或x>2 D. x<﹣4或x>2 19.已知:二次函数y=x2﹣4x﹣a,下列说法错误的是( ) A. 当x<1时,y随x的增大而减小 B. 若图象与x轴有交点,则a≤4 C. 当a=3时,不等式x2﹣4x+a<0的解集是1<x<3
D. 若将图象向上平移1个单位,再向左平移3个单位后过点(1,﹣2),则a=3 20.下列表格给出的是二次函数y=ax2+bx+c(a≠0)的几组对应值,那么方程ax2+bx+c=0的一个近似解可以是( ) x y ﹣ ﹣
A. B. C. D. 21.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
A. 抛物线开口向上 B. 抛物线与y轴交于负半轴 C. 当x=3时,y<0 D. 方程ax2+bx+c=0有两个相等实数根
22.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2)(如图所示),则能使y1<y2成立的x的取值范围是( ) A. x>2 B. x<﹣2 C. x>0 D. ﹣2<x<8 23.在﹣3≤x≤0范围内,二次函数(a≠0)的图象如图所示.在这个范围内,有结论:
①y1有最大值1、没有最小值; ②y1有最大值1、最小值﹣3; ③函数值y1随x的增大而增大; ④方程ax2+bx+c=2无解; ⑤若y2=2x+4,则y1≤y2. 其中正确的个数是( )
A. 2 B. 3 C. 4 D. 5 24.抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表: x … ﹣2 ﹣1 1 3 4 … y … 0 4 6 4 0 … 根据上表判断下列四种说法:①抛物线的对称轴是x=1;②x>1时,y的值随着x的增大而减小:③抛物线有最高点:④抛物线的顶点、与x轴的两个交点三点为顶点的三角形的面积为36.其中正确说法的个数有( ) A. 1 B. 2 C. 3 D. 4
25.如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A. (2,3) B. (3,2) C. (3,3) D. (4,3) 26.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<﹣1或x>3.其中,正确的说法有( ) A. ①②④ B. ①②⑤ C. ①③⑤ D. ②④⑤ 27.已知二次函数y=x2+2(a﹣1)x+2.如果x≤4时,y随x增大而减小,则常数a的取值范围是( ) A. a≥﹣5 B. a≤﹣5 C. a≥﹣3 D. a≤﹣3
28.如图,平行于y轴的直线l被抛物线y=+1,y=﹣1所截,当直线l向右平移3个单位时,直线l被两条抛物线所截得的线段扫过的图形面积为( )平方单位.
A. 3 B. 4 C. 6 D. 无法可求 29.已知直线经过点A(0,2),B(2,0),点C在抛物线y=x2的图象上,则使得S△ABC
=2的点有( )个.
A. 4 B. 3 C. 2 D. 1 30.如图,已知抛物线,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,
取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断: ①当x>0时,y1>y2;②使得M大于3的x值不存在;③当x<0时,x值越大,M值越小; ④使得M=1的x
值是或. 其中正确的是( )
A. ①③ B. ②④ C. ①④ D. ②③ 二次函数图像和性质习题精选(含答案) 参考答案与试题解析 一.选择题(共30小题) 1.(2014宁夏)已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( ) A. B. C. D.
考点: 二次函数的图象;正比例函数的图象. 专题: 数形结合. 分析: 本题可先由一次函数y=ax图象得到字母系数的正负,再与二次函数y=ax2的图象相比较看是否一致.(也
可以先固定二次函数y=ax2图象中a的正负,再与一次函数比较.) 解答: 解:A、函数y=ax中,a>0,y=ax2中,a>0,但当x=1时,两函数图象有交点(1,a),故A错误;
B、函数y=ax中,a<0,y=ax2中,a>0,故B错误; C、函数y=ax中,a<0,y=ax2中,a<0,但当x=1时,两函数图象有交点(1,a),故C正确; D、函数y=ax中,a>0,y=ax2中,a<0,故D错误. 故选:C. 点评: 函数中数形结合思想就是:由函数图象确定函数解析式各项系数的性质符号,由函数解析式各项系数的性质符号画出函数图象的大致形状.
2.(2014•北海)函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是( ) A. B. C. D.
考点: 二次函数的图象;反比例函数的图象. 分析: 分a>0和a<0两种情况讨论二次函数和反比例函数图象所在的象限,然后选择答案即可. 解答: 解:a>0时,y=ax2+1开口向上,顶点坐标为(0,1),
y=位于第一、三象限,没有选项图象符合, a<0时,y=ax2+1开口向下,顶点坐标为(0,1), y=位于第二、四象限,B选项图象符合. 故选:B. 点评: 本题考查了二次函数图象与反比例函数图象,熟练掌握系数与函数图象的关系是解题的关键.
3.(2014•遵义)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )
