重力异常与垂线偏差
重力异常
重力异常重力异常(gravity anomaly)由于地球质量分布不规则造成的重力场中各点的重力矢量g和正常重力矢量γ的数量之差。
它是研究地球形状、地球内部结构和重力勘探,以及修正空间飞行器的轨道的重要数据。
重力异常可分为纯重力异常和混合重力异常。
纯重力异常是同一点上地球重力值和正常重力值之差,又称扰动重力。
混合重力异常是一个面上某一点的重力值和另一个面上对应点的正常重力值之差。
例如大地水准面上一点的重力值g0和该点沿平均地球椭球法线在椭球面上的投影点的正常重力值γ0之差,称为大地水准面上的混合重力异常;地面上一点的重力值g和似地球面(见地球形状)上相应点上正常重力值γ之差,称为地面混合重力异常。
【重力异常的求定】纯重力异常不能直接求得,需要通过扰动位间接推求。
混合重力异常可以直接推求。
若求地面混合重力异常,地面上一点的重力可通过实测获得,而似地球面上相应点的正常重力,则先按计算点的纬度用正常重力公式算得平均椭球面上相应点的正常重力,然后再将它归算到似地球面上。
若求大地水准面上混合重力异常,大地水准面上一点的重力是将地面实测重力归算到大地水准面上得到的,平均椭球面上的正常重力则按正常重力公式解算获得。
【重力改正】将地面实测重力值归算到大地水准面上,称为重力改正。
它包含两方面内容:一是清除观测点到大地水准面的高程对重力观测值的影响;二是将大地水准面以外的质量的影响按某种方法完全消去。
改正后得到的是外部没有任何质量的大地水准面上的重力值。
根据所要改正的影响不同,重力观测值中将加上不同的改正。
【空间改正】按地面重力观测点高程考虑正常重力场垂直梯度的改正。
此项改正相当于使地面重力观测点移到大地水准面上,而大地水准面以上的地形质量随观测点平移到大地水准面之下。
【层间改正】消除过观测点的水平面同大地水准面之间的质量层对观测重力的影响而加的改正。
此项改正相当于把高出大地水准面的质量当作一个无限平面厚层全部移掉。
重力勘探—重力异常的数据处理

第四章重力异常的数据处理布格重力异常反映了地壳内部物质密度的不均匀性,即从地表到地下几十公里的地壳深部,只要物质密度横向发生变化,在地下不同的空间和范田内形成剩余质量,就可以引起地表的重力异常。
定性解释侧重于判断引起异常的地质原因,并粗略估计产生异常的地质体的形状、产状及埋深等。
定量解释则是通过理论计算.对地质体的规模、形状、产状及埋深等作出具体解答。
重力异常的推断解释的步骤:①阐明引起异常的地质因素具体地说,就是确定异常是浅部因素还是深部因素引起,是矿体还是构造或其它密度不均匀体(岩性变化、侵入体等)的反映。
——定性解释②划分和处理实测异常重力异常图往往是地表到地球深处所有密度不均匀体产生的异常的叠加图象。
为了获取探测对象产生的异常,需要将它们进行划分。
不同的研究目的提取的异常信息不同,例如,矿产调查要提取队是矿体或没部构造产生的局部异常;而深部重力研究的目标正好相反,需要划分出的是反映地壳深部及上地幔的区域异常。
③确定地质体或地质构造的赋存形态一是根据已知地质体或地质构造的形状、产状及埋深等.研究它们引起的异常的特征,包括异常的形状、幅度、梯度及变化规律等。
二是根据异常的形态及变化规律等,确定地质体或地质构造的形状、产状、埋深及规模等。
前者足由源求场,称为止(演)问题;后者是由场求源,称为反(演)问题。
正问题是反问题的基础,而求解反问题则是定量解择的最终目的。
§4.1 重力异常的主要地质原因一.地壳深部因素莫霍洛维奇面:地壳与上地馒之间存在着一个界西地壳厚度各地不同,大陆平原地区大约20~30km,高山区为40~60km,西藏高原达60km以上,海洋区为10~20km,最薄处仅数公里。
这一界面上下物质密度差达0.3g/cm3以上,界面以上的硅镁层密度为 2.8~3.0g/cm3,硅侣层为2.5~2.7g/cm3,界面以下物质密度为3.3~3.4g/cm3。
该界面的起伏引起地表重力变化的特点是导常分布植围广,幅度变化大。
重力场的基本知识可修改全文

在以上假设下,利用实际观测结果,可以 导出一个近似公式,称为参考椭球面(大 地水准面)上正常重力公式,即
g0 () ge (1 sin 2 1sin 2 2)
式中g0(φ)为正常重力值,其随纬度φ变化;
ge ,gp 分别称为赤道处和两极处重力平均
值;β称为地球重力扁度[ (gp – ge) / ge] ;
历史上使用的是C.G.S.制,它是为了纪念第一个 测定重力加速度值的意大利著名物理学家伽利略 (G.Galieo),取1cm/s2作为重力的一个单位,称作 “伽”(Gal)。
实用中是取它的 千分之一即“毫伽”作常 用单位。
近二十年来随着高精度重力测量,特别是 在水文、工程、 环境勘查中微重力测量的
1m/ s2 =106 g.u.
1Gal = 104 g.u.
1mGal= 10 g.u.
目前,最好的重力仪测量精度可达到微伽 级。
4
重力加速度并不是一个恒量,在空间上和 时间上都存在着一定的变化,只是这种变 化相对重力全值(约9.8m/s2)来说太小了, 因而需要专门设计的仪器—重力仪才能可 靠地测量出这些变化来。
从以上讨论可知,地球表面正常重力场的 基本特征是:
(1)正常重力是人们根据需要而提出来的, 不同的计算公式对应不同参数的地球模型, 反映的是理想化条件下地球表面重力变化 的基本规律,所以它不是客观存在的;
(2)正常重力值只与纬度有关,在赤道上最 小,两极处最大,相差约50000g.u.;
(3)正常重力值随纬度变化的变化率,在纬 度45°处达到最大,而在赤道和两极处为
大地水准面与参考椭球面差异不是均匀分 布的,最大的差异可达 117 m,它与地球表 面地形以及地下物质分布有关。
由于大多数地区大地水准面与参考椭球面 差异不大,因此在很多情况下,可将两者 视为相同,这时,天文纬度近似等于地理 纬度。
布格重力异常图
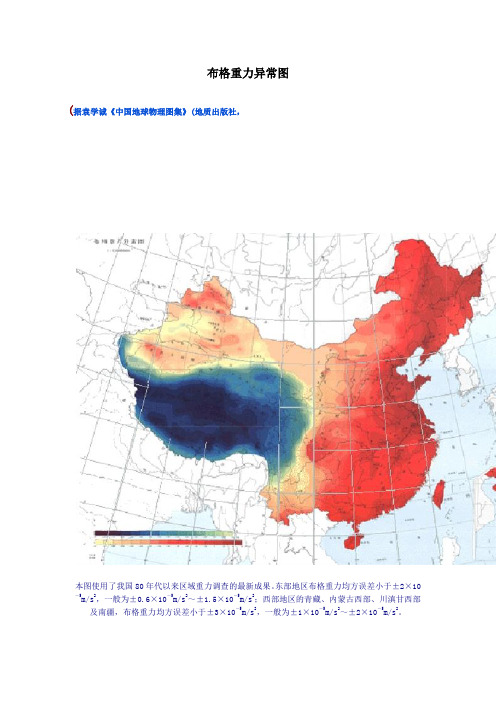
布格重力异常图(据袁学诚《中国地球物理图集》(地质出版社,本图使用了我国80年代以来区域重力调查的最新成果。
东部地区布格重力均方误差小于±2×10-5m/s2,一般为±0.6×10-5m/s2~±1.5×10-5m/s2;西部地区的青藏、内蒙古西部、川滇甘西部及南疆,布格重力均方误差小于±3×10-5m/s2,一般为±1×10-5m/s2~±2×10-5m/s2。
全部资料整理和改算,统一采用波茨坦重力系统;统一采用赫尔默特(1901~1909年)正常重力公式;统一采用重力高度改正系数和中间层密度值(2.67g/cm3)以及统一采用166.7km 的地形改正半径。
我国的布格重力异常是以青藏高原为低值中心(约-550×10-5m/s2),向北向东逐渐升高,形成东高西低、北高南低的总趋势,并被纵、横贯于全国的两大梯级带分割成台阶状的三级区域场,在此背景上叠加有多个形态各异的局部异常和规模较小的梯级带,构成我国复杂而独特的布格重力异常场。
1.重力梯级带(1)大兴安岭-太行山-武陵山大型重力梯级带。
(2)青藏高原周边大型重力梯级带。
2.区域重力场我国大陆区域重力场呈现三级台阶状,由东向西逐次降低,它们被两大梯级带分隔和连接。
1)东部区域重力高,即第一台阶。
2)中部弧形区域重力场,即第二台阶。
3)青藏区域重力低,即第三台阶。
3.局部重力异常1)走向基本为东西向的布格重力异常带。
有天山-阴山-燕山重力低异常带、秦岭-大巴山-大别山重力低异常带,苗岭-南岭-武夷山重力低异常带、唐古拉山重力低异常带及冈底斯重力低异常等。
2)等轴状或团块状布格重力异常。
准噶尔、塔里木、四川等盆地中多出现这类重力高或重力低异常。
3)走向为北东的布格重力异常带。
多呈线状或串珠状出现在东部地区,如长白山重力低、郯-庐-辽-吉重力高异常带等。
【大学考试资料】-大地测量学基础复习重点

《大地测量学基础》1.大地测量学是通过在广大的地面上建立大地控制网,精确测定大地控制网点的坐标,研究测定地球形状、大小和地球重力场的理论、技术与方法的学科。
现代大地测量学包括空间、物理和几何大地测量学2.现代大地测量的三个分支是几何:确定地球的形状和大小及确定地面点的几何位置。
物理:用物理方法(重力测量)确定地球形状及其外部重力场。
空间:以人造地球卫星及格其他空间探测器为代表的空间大地测量的理论、技术与方法。
3.大地测量是测绘学的一个分支。
主要任务是测量和描绘地球并监测其变化,为人类活动提供关于地球的空间信息。
是一门地球信息学科。
是一切测绘科学技术的基础。
4.人类认识地球阶段地球圆球阶段,首次用子午圈弧长测量法来估算地球半径。
这是人类应用弧度测量概念对地球大小的第一次估算。
地球椭球阶段,在这阶段,几何大地测量在验证了牛顿的万有引力定律和证实地球为椭球学说之后,开始走向成熟发展的道路,取得的成绩主要体现在一下几个方面:1)长度单位的建立2)最小二乘法的提出3)椭球大地测量学的形成4)弧度测量大规模展开5)推算了不同的地球椭球参数。
这个阶段为物理大地测量学奠定了基础理论。
大地水准面阶段,几何大地测量学的发展:1)天文大地网的布设有了重大发展,2)因瓦基线尺出现物理大地测量学的发展1)大地测量边值问题理论的提出2)提出了新的椭球参数现代大地测量新时期以地磁波测距、人造地球卫星定位系统及其长基线干涉测量等为代表的新的测量技术的出现,使大地测量定位、确定地球参数及重力场,构筑数字地球等基本测绘任务都以崭新的理论和方法来进行。
由于高精度绝对重力仪和相对重力仪的研究成功和使用,有些国家建立了自己的高精度重力网,大地控制网优化设计理论和最小二乘法的配置法的提出和应用。
5.现代大地测量技术传统方法:几何法和物理法。
随着人造地球卫星的出现,又产生了卫星法。
6.大地测量基本任务是技术任务:精确测定大地控制点的位置及其随时间的变化也就是它的运动速度场,建立精密的大地控制网,作为测图的控制,为国家经济建设和国防建设服务.科学任务:测定地球形状、大小和重力场,提供地球的数学模型,为地球及其相关科学服务。
大地测量学基础习题与思考题及答案含重点及两份武大测绘试题@

《大地测量学基础》习题与思考题一 绪论1.试述您对大地测量学的理解?2.大地测量的定义、作用与基本内容是什么?3.简述大地测量学的发展概况?大地测量学各发展阶段的主要特点有哪些?4.简述全球定位系统(GPS )、激光测卫(SLR )、 甚长基线干涉测量(VIBL )、 惯性测量系统(INS )的基本概念? 二 坐标系统与时间系统1.简述是开普勒三大行星定律? 2.什么是岁差与章动?什么是极移? 3.什么是国际协议原点 CIO?4.时间的计量包含哪两大元素?作为计量时间的方法应该具备什么条件? 5.恒星时、 世界时、 历书时与协调时是如何定义的?其关系如何? 6.什么是大地测量基准?7.什么是天球?天轴、天极、天球赤道、天球赤道面与天球子午面是如何定义的 ? 8.什么是时圈 、黄道与春分点?什么是天球坐标系的基准点与基准面? 9.如何理解大地测量坐标参考框架?10.什么是椭球的定位与定向?椭球的定向一般应该满足那些条件? 11.什么是参考椭球?什么是总地球椭球?12.什么是惯性坐标系?什么协议天球坐标系 、瞬时平天球坐标系、 瞬时真天球坐标系?13.试写出协议天球坐标系与瞬时平天球坐标系之间,瞬时平天球坐标系与瞬时真天球坐标系的转换数学关系式。
14.什么是地固坐标系、地心地固坐标系与参心地固坐标系?15.什么协议地球坐标系与瞬时地球坐标系?如何表达两者之间的关系?16.如何建立协议地球坐标系与协议天球坐标系之间的转换关系,写出其详细的数学关系式。
17.简述一点定与多点定位的基本原理。
18.什么是大地原点?大地起算数据是如何描述的?19.简述1954年北京坐标系、1980年国家大地坐标系、 新北京54坐标系的特点以及它们之间存在相互关系。
20.什么是国际地球自传服务(IERS )、国际地球参考系统(ITRS) 、国际地球参考框架(ITRF)? ITRS 的建立包含了那些大地测量技术,请加以简要说明?21. 站心坐标系如何定义的?试导出站心坐标系与地心坐标系之间的关系?22.试写出不同平面直角坐标换算、不同空间直角坐标换算的关系式?试写出上述两种坐标转换的误差方程式? 23.什么是广义大地坐标微分方程(或广义椭球变换微分方程)?该式有何作用? 三 地球重力场及地球形状的基本理论1.简述地球大气中平流层、对流层与电离层的概念。
1扰动位
1扰动位:某点的扰动位等于该点的重力位与正常重力位之差2重力垂线偏差:指某点的重力方向与该点的正常重力方向之间的夹角,垂线偏差描述了大地水准面的倾斜3、大地水准面:如果在某曲面上重力位处处相等,则此曲面称为重力等位面,又称为水准面。
设想海洋面处于静止状态,则海洋面上的重力必然垂直于海洋面,否则,海水必然会流动。
因此,处于静止状态的海洋面与一个重力等位面重合。
这个假想的静止海洋面向整个地球大陆内部延伸形成的封闭曲面,称为大地水准面。
大地水准面是高程测量中正高系统的起算面4、GPS水准测量:在某点上实施GPS测量获取该点的大地高,同时在该点实施精密水准测量获取该点的正常高或正高(考虑重力场改正),则可以获得该点的大地水准面高或高程异常5重力:(1)狭义定义:地球所有质量对任一质点所产生的引力与该点随地球相对于惯性中心运动而引起的的离心力之合力;(2)广义定义:宇宙间全部物质对任一质点所产生的引力与该点随地球相对于惯性中心运动而引起的的离心力之合力。
6、大地水准面高:大地水准面与平均椭球体表面之间的距离,即大地水准面沿铅垂线方向到平均椭球体表面的距离7、高程异常:似大地水准面与平均椭球体表面之间的距离,即似大地水准面沿正常重力线方向到平均椭球体表面的距离。
8调和函数:如果二元函数f(x,y)在区域Ω内有二阶连续偏导数且满足拉普拉斯方程,则称f 为区域Ω中的调和函数.9.似大地水准面: 从地面点沿正常重力线量取正常高所得端点构成的封闭曲面。
10. 位函数:设有一个标量函数,它对被吸引点各坐标轴的偏导数等于力在相应坐标轴上的分量,这样的函数称为位函数,对引力来说具有引力位函数,简称引力位引力常数11. 物理大地测量学的主要任务是什么?用物理的方法研究和测定地球的形状、地球重力场及其各自随时间的变化。
12为什么要研究和确定地球重力场?地球重力场同其他物理场一样,是客观存在的,不以人的意志为转移,是物质的一种存在形式。
重力异常数据处理
d
g(0, 0, z) V 1 zg( ,) d d
z 2 ( 2 2 z2 )3 2
g(0,0, z) 1
2
g (R, )
zR dRd
2 0 0
(R2 z2 )3 2
• 2.三度体异常的向上延拓 ①等间距近似计算公式
g(0,0,z) 1
2
0
2 0
g
(
R,
)
2
g
(
Ri
)
g(0, 0, z) Ki g(Ri ) i0
g(0, 0, z) Ki g(Ri ) i0
K0
1 2
1
1 2
Ki
1 2
(i
1 1)2
11 2
1 (i 1)2
11 2
i1、2、3
g(0,0,z)
6 i0
Ki g(Ri
)
i7
Ki g(Ri )
g
(R6
)
(R2
zR z
2
)3
2
dRd
1
2
g(R, )d g (R)
2 0
g(0, 0, z) g(R)
zR dR
0
(R2 z2 )3 2
g(0, 0, z) g (Ri ) g (Ri1) Ri1
zR dR
i0
2
Ri (R2 z2 )3 2
i0
g (Ri ) g (Ri1) 2
5
g(2, 1) g(2,1) g(2, 1) g(1, 2) g(1, 2)
g(1, 2) g(1, 2)] ( 27 8)g(2, 2) g(2, 2)
5
g(2, 2) g(2, 2)
25点圆滑公式
加密重力测量规范
中华人民共和国国家标准加密重力测量规范GB/T 17944——2000本标准是在国家测绘局1975年3月发布的《大地重力测量细则》(修订本)和CH/T2003-1999《国家一等重力测量规范》的基础上,结合最新科研和生产成果制定的。
本标准从2000年8月1日起实施。
本标准的附录A和附录B都是标准的附录。
本标准由国家测绘局提出并归口。
本标准由国家测绘局测绘标准化研究所负责起草。
本标准主要起草人:张耀民、戴其潮、杨振岱、王忠良。
1 范围1.1 本标准规定了在陆地上进行加密重力测量的布测原则、精度要求、施测方法等。
1.2 本标准适用于在全国范围内进行加密重力测量,其他区域性的均匀重力测量可参考执行。
2 引用标准GB12897—1991 国家一、二等水准测量规范 GB/T 17942—2000 国家三角测量规范 GB/T 17943—2000 大地天文测量规范 CH 1001—1991 测绘技术总结编写规定 CH 1002—1995 测绘产品检查验收规定 CH 1003—1995 测绘产品质量评定标准 CH/T 1004—1999 测绘技术设计规定CH 2001—1992 全球定位系统(GPS )测量规范 CH/T 2003—1999 国家一等重力测量规范CH 8016—1995 全球定位系统(GPS )测量型接收机检定规程 3 布测原则 3.1 目的与任务3.1.1 加密重力测量是为各种科学目的对有关区域在各级重力控制点的基础上加密一定的重力点所进行的重力测量。
3.1.2 加密重力测量主要用于测定地球重力场的精细结构,为大地测量学、地球物理学、地质学、地震学、海洋学和空间技术等领域所需的重力异常、垂线偏差、高程异常和空间扰动引力场等提供地球重力场数据。
3.1.3 国家加密重力测量得到主要任务是:a )为在全国建立55''⨯的国家基本格网(对于个别大片重力测量空间区域的困难地区可以建立30'30'⨯格网)的数字化平均重力异常模型而进行的全面重力测量;b )为精化大地水准面,采用天文、重力、GPS 水准测量方法确定全国范围的高程异常值而进行的加密重力测量;c )为内插大地点的天文大地垂线偏差而进行的局部加密重力测量;d )为精密水准测量正常高系统改正而进行的局部重力测量。
垂线偏差名词解释
垂线偏差名词解释
垂线偏差是在编码诊断检查中常用的一项测量技术。
它是用来检查几何形状特征以及其与正确定位对抗物体比例维度之间是否存在偏离。
垂线偏差是指外形特征相对于获得正确定位的偏 r 的程度。
它是编码诊断检查
的一种量度指标,用来测量物体的几何特征与正确定位位置之间的相关性。
这个垂线偏差检测结果表明,几何形状和特征的维度的变化可以在一定的比例上被正确地定位。
一般来说,垂线偏差可以被用于指示几何形状是否差异过大,以及影响表面精度的因素给设备带来了多大程度的影响,当被判断在表面形态精度方面存在问题时,可以识别出特征的变化以及错误定位情况,进而从而帮助调节准确度和精度。
垂线偏差测量中用到的项目,如垂直偏差、交叉偏差、垂线偏差等,可以用于检查机构所使用的部件以及部件之间的组装关系过程中的几何特征,从而及时地发现产品的可能缺陷,也可以帮助分析缺陷本身的特征以及缺陷可能会在实际使用中产生的影响。
总而言之,垂线偏差测量技术是一种重要的编码诊断检查技术,它可以在编码诊断检查中得到更精确的结果,从而为改善机构的准确度和精度提供有力的指导作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重力相关资料 1.相关坐标系 地球上任何一个质点都同时受到地心引力和由于地球自转产生的离心力的作用,两个力的合力称为重力。离心力与引力之比约为1:300,所以重力中起主要作用的还是地心引力。重力的作用线称为铅垂线,重力线方向就是铅垂线方向。 1.1 水准面与大地水准面 当液体处于静止状态时,其表面必处处与重力方向正交,否则液体就要流动。这个液体静止的表面就称为水准面。水准面是一个客观存在的、处处与铅垂线正交的面。通过不同高度的点,都有一个水准面,所以水准面有无穷多个。 为了使测量结果有一个共同的基准面,可以选择一个十分接近地球表面又能代表地球形状和大小的水准面作为共同标准。设想海洋处于静止平衡状态,并将它延伸到大陆内部且保持处处与铅垂线正交的水准面,来表示地球的形状是最理想的,这个面称为大地水准面。它是一个光滑的闭合曲面,又称为地球的物理表面。由它包围的形状是地球的真实形体,称为大地体。 地球自然表面的起伏不平、地壳内部物质密度分布不均,使得引力方向产生不规则的变化。因而引力方向除总的变化趋势外,还会出现局部变化,这就引起铅垂线方向发生不规则的变化。由于大地水准面处处与铅垂线正交,所以它是一个略有起伏的不规则的表面。
图1 椭球面与大地水准面 1.2 参考椭球面 从整体上看,大地体接近于一个具有微小扁率的旋转椭球,与大地体吻合的最好的旋转椭球称为总地球椭球,也叫总椭球或平均椭球。要确定总椭球,必须在整个地球表面上布设连成一体的天文大地网和进行全球性的重力测量。 为了大地测量工作的实际需要,各个国家和地区只有根据局部的天文、大地和重力测量资料,研究局部大地水准面的情况,确定一个于总椭球相近的椭球,以表示地球的大小,作为处理大地测量成果的依据。这样的椭球只能较好的接近局部地区的大地水准面,不能反映整个大地体的情况,所以叫做参考椭球面。 1.3大地坐标系与天文坐标系 表1 大地坐标系与天文坐标系的对比 项目 大地坐标系 天文坐标系 基本面线 参考椭球面、法线 大地水准面、垂线 坐标面 起始大地子午面、椭球赤道面 起始天文子午面、地球赤道面
坐标 L:大地子午面间夹角 B:法线与赤道面夹角 H大:沿法线至椭球面距离 :天文子午面间夹角 :垂线与赤道面夹角 H正:沿垂线至大地水准面距离 方位角 A:子午面与包含照准点法截面间的夹角 :子午面与包含照准点垂直面间的夹角
确定方法 在椭球面上推算求得 不能经过推算求得 观测地面点或卫星获得 观测恒星独立获得
特点 依附于椭球面法线 依附于水准面垂线 各点大地坐标相关 各点天文坐标独立 计算求得,定位精度高 观察求得,定位精度低 由于大地水准面起伏,导致同一点的法线和垂线不一致,两者之间的微小夹角称为垂线偏差;导致天地高和海拔高(正高)不一致,两者之间的差距称为大地水准面差距。 设垂线偏差在子午面上的分量(即南北分量)以来表示,在卯酉面上的分量(即东西分量)以来表示,N表示大地水准面差距。考虑垂线偏差和大地水准面差距,大地坐标与天文坐标数学转换公式为
()costanBLANHH正大
(1)
2.重力场 地球重力场的确定就是通过求解某种形式的大地测量边值问题得到一种表达扰动位或其泛函的数学模型,包括解析表达模型和数值模型两种形式。其中,解析表达模型利用斯托克司(Stokes)公式或莫洛金斯基(Molodensky)级数给出积分表达式,或利用球谐函数技术给出谱展开式;数值模型则是重力场参数的一定分辨率的格网数值,包括扰动位、大地水准面、重力异常和垂线偏差等。例如EGM系列地球重力场模型计算软件给出的最终计算结果便是大地水准面差距(geoid undulations),一般用N表示。 研究地球重力场的理论基础即是研究大地测量边值问题的解算,这一边值问题的描述为:在大地水准面或地球自然表面给定边值条件和相应的边值,确定该边界面及其外部的引力位,并满足边值条件,同时在无限空间内是调和函数。位理论自1785年由法国数学家勒让德(Legendre)提出后,经过格林(Green)和高斯(Gauss)等数学家和大地测量学家的进一步研究,不仅解释了表征位场的基本数学关系,同时将引力或重力的3个分力通过引入一个位函数在3个分力方向上的偏导数来表达。同时,引入等位面和大地水准面的概念,从而将地球形状和重力场的研究统一起来,即地球重力场可用地球重力位来表达,地球形状可用大地水准面的形状来代表。由于地球表面形状的不规则和内部质量分布不均匀,通常将地球重力位分为两部分:正常场和扰动场,分别对应于正常位和扰动位。前者可用4个大地测量基本参数确定,是接近真地球位场的一种理想化位场;后者是对应的异常质量分布产生的异常位场。因此,研究地球形状及外部重力场的关键在于确定扰动位。 2.1重力位函数 设有一个标量函数,它对各坐标轴的偏导数等于力在相应坐标轴上的分量,此函数定义为位函数。由此定义可得重力位函数为: WV (2)
其中V为引力产生的位,为地球自转产生的位。若为角速度,X和Y为给定点的地心坐标,则 221()2XY (3)
引力位函数的定义为 max20(,,)1()(cossin)(cos)nnn
nmnmnmnmGMaVrCmSmPrr
(4)
其中,r — 到地球质心的距离 — 地心纬度
— 地心经度
a — 参考椭球长半轴
n,m — 阶次
nmC,nmS — 正常化的地球引力系数
(cos)nmP — 为n阶m次第一类完全正常化缔合Legendre函数
1/20()!(21)(2)(cos)(cos)()!mnmnmnmnPPnm
,1, 0, ijijij (5)
ij
为克罗内克(kroneker)符号,(cos)nmP为蒂合Legendre函数
2/22/221()(1)()(1)(1)2!mnmmmnnmnmnnmddPxxPxxxdxndx
(6)
这些公式对于ra,即在地球表面或近地空间理论上是有效的,公式计算误差比较小,但这些公式不能用于r小于地球半径的情况。 2.2重力加速度和重力梯度 在地球重力场中,重力加速度为 ()TTxyzWWWggradWgggxyz
(7)
重力加速度矢量的空间梯度即是重力位的二阶空间导数,称为重力梯度,可由下述张量表示: 222222222222
xxxxxxyxzyyyyxyyyz
zxzyzzzzz
gggWWWxyzxxyxzgggWWWxyzyxyyzgggWWWxyzzxzyz
(8)
在不考虑地球离心力影响的情况下,地球重力场是一个保守场,重力场的旋度为零,说明重力梯度张量具有对称性;重力场的散度为零,意味着梯度张量的迹为零。因此 ,,0xyyxxzzxyzzyxxyyzz (9)
重力梯度张量中只有五个独立项。 3. WGS84世界大地坐标系与EGM2008
3.1 WGS84坐标系概述及有关常数 WGS84世界大地坐标系是由美国国家影像制图局NIMA和其前身美国国防部测绘局DMA从初始的世界大地坐标系WGS60开始发展,并在随后的WGS66、WGS72基础上不断改进形成的。 WGS84坐标系使用协议地面参考系(CTRS)。这个坐标系根据国际地球自转服务技术注解概要中的标准来定义。这些标准如下: (1)它是一个地心坐标系,地心定义为包括海洋和大气的整个地球的质量中心。 (2)范围局限于地球,即在引力相对论意义下的局部地球框架内。 (3)它的定向由国际时间局(BIH1984.0)给出。 (4)定向的时间演化相对于地壳不产生残余的全球性旋转。 WGS84坐标系是右手地固直角坐标系,坐标原点和坐标轴定义如下: 原点:地球质心。 Z轴:指向国际地球参考系IERS极的方向(IRP)。这个方向与BIH协议地面极的指向(在历元1984.0)相差±0.005″。 X轴:指向国际地球参考系IERS首子午面且垂直于Z轴的方向,这个方向与BIH协议零子午面(在历元1984.0)相差±0.005″。 Y轴与其他两轴构成右手地心地固ECEF(Earth-Centered Earth-Fixed)直角坐标系。 表2 WGS84椭球基本常数
