建筑拓扑学
从拓扑和几何角度领略解构主义大师扎哈的精妙设计

盖达尔·阿利耶夫中心
一方面,曲面复杂的几何为工程施工 带来了巨大的困难,整张曲面无法用 平直的预制板来拟合,须用数目繁多 的三角网格来逼近,且不同的三角形 板材形状彼此不同,无法成批量大规 模制造。
另一方面,从力学角度而言,负曲率 的承重能力远远小于正曲率曲面的承 重能力,增大了冬季雪灾的风险。同 时,穹隆形曲面的内部空间远远大于 负曲率曲面的内部空间。因此,其空 间利用率较低。 尽管造价贵,利用率较低,但具有几 何上的纯粹的美。
曲率突破
• 传统建筑以立方体形状为主,地面墙壁,天花顶棚,泾渭分明。 建筑各个侧面都以欧几里得平面为主,房间表面曲率几乎处处 为零,所有曲率都集中到几个尖角处。穹隆形屋顶也较为常见, 曲率处处为正。
将地面、墙壁和顶棚融合成一张柔和 光滑的巨大曲面,曲面呈流线形状。 整个建筑曲面曲率处处非零,时正时 负。
凸体几何
• 所谓凸体,就是体中任意两点之间的连线仍包含在体之中。 • 石头被江水冲刷,和河床摩擦,每次都是沿着一个平面打磨,石头整 体位于河床平面的一侧。在几何上,如果一个封闭曲面位于它的每个切平 面的一侧,那么该曲面必然是凸曲面,曲率处处为正。 • 给定三维空间中的几个点,包含这几个点的所有凸体之交,或者等价 地,包含这个点的最小凸体,被称为这个点的凸包或凸壳(Convex Hull)。
调和的叶状结构
扎哈设计的游艇,显示了曲面上 的Train Track。
曲面上的Train Track
斯人已逝, 风范长存。
谢谢观赏!
从拓扑和几何角度领略解构主义 大师扎哈的精妙设计
13级建筑学一班 武佳文 130107040010
扎哈穿着她毕生所爱的 叶状结构(foliation), 扎哈的衣服被分解为许 多片“叶子”,这些叶子 层叠联缀成曲面,一如 她设计的建筑。
拓扑学在建筑中的应用——以莫比乌斯住宅与克莱因瓶住宅为例

拓扑学在建筑中的应用——以莫比乌斯住宅与克莱因瓶住宅
为例
李雪玲;卜萍;秦桂明
【期刊名称】《建筑与环境》
【年(卷),期】2009(006)006
【摘要】莫比乌斯与克莱茵瓶是拓扑几何学中典型的特例.拥有一般几何形所不具备的奇异特性,本文便以莫比乌斯住宅和克莱茵瓶住宅为例,介绍了拓扑几何学在建筑设计当中的应用.
【总页数】4页(P135-138)
【作者】李雪玲;卜萍;秦桂明
【作者单位】烟台市建筑设计研究院有限公司;烟台市建筑设计研究院有限公司;烟台市建筑设计研究院有限公司
【正文语种】中文
【中图分类】TU2
【相关文献】
1.浅析传统建筑风格在现代住宅区设计中的应用——以徽派建筑为例 [J], 熊芳;
2.UHPC轻型建筑部品在装配式建筑中的应用探索——以中建低能耗装配式住宅示范楼为例 [J], 邓广; 翁子杰; 张国强; 周泉
3.BIM技术在装配式建筑深化设计中的应用研究
——以宁波某住宅项目为例 [J], 徐健青
4.太阳能在农村住宅建筑节能中的优化应用研究——以安徽省西南部某县为例 [J], 李迎;鲍学芳;吴思敏;黄忠杰
5.数智化技术在住宅建筑施工管理中的深度应用
——以"吉宝静安中心项目"为例 [J], 赵堂君
因版权原因,仅展示原文概要,查看原文内容请购买。
拓扑学课件

拓扑学之旅
Topology
小教4班 郑梦珂 朱桃
简介概要
应用实例
拓扑学
有趣游戏
图片欣赏
拓扑简介
拓扑学(topology)是近代发展起来的一个数 学分支,用来研究各种“空间”在连续性的变 化下不变的性质。在20世纪,拓扑学发展成为 数学中一个非常重要的领域。 有关拓扑学的一些内容早在十八世纪就出现了 。那时候发现一些孤立的问题。后来在拓扑学 的形成中占着重要的地位。譬如哥尼斯堡七桥 问题、多面体的欧拉定理、四色问题等都是拓 扑学发展史的重要问题。除去七桥问题,四色 问题,欧拉定理等,拓扑学中还有很多有趣并 且很基本的问题。例如还有纽结问题,维数概 念,向量场问题,不动点问题。
解答与分析
妮薇先抓住绕在自己手上的绳子的中间部分,然后将绳子穿过诺曼右手 腕A的绳圈,穿越的方向是从手腕的内部顺着手肘的方向到手掌端,随 后将绳子回绕过手掌而伸出到手的外侧。此时妮薇就可和诺曼分开了, 在场的人也会惊讶不已。
他们的手腕仍然绑着,可是两人已经没有被绑在一起了。要注意的是,
如果没有完全依照文中的指示,将会使两条绳子纠缠得更严重。
纽结问题
纽结理论是数学学科代数 拓扑的一个分支,按照数 学上的术语来说,是研究 如何把若干个圆环嵌入到 三维实欧氏空间中去的数 学分支。纽结理论的特别 之处是它研究的对象必须 是三维空间中的曲线。在 两维空间中,由于没有足 够的维数,我们不可能把 让一根曲线自己和自己缠 绕在一起打成结;而在四 维或以上的空间中,由于 维数太多,无论怎么样的 纽结都能够很方便地被解 开成没有结的曲线。
网络应用
图片欣赏
克莱因瓶
趣味游戏
• 在一次聚会中,诺曼和妮薇如图中所示被两条
建筑工程课程拓扑图
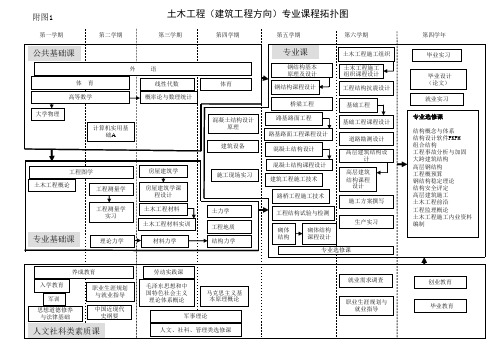
房屋建筑学 房屋建筑学课 程设计 土木工程材料 土木工程材料实训
施工现场实习
建筑工程施工技术 路桥工程施工技术
土力学 工程地质 结构力学
工程结构试验与检测
专业基础课理论力学来自材料力学养成教育 入学教育 军训 思想道德修养 与法律基础 职业生涯规划 与就业指导 中国近现代 史纲要
劳动实践课 毛泽东思想和中 国特色社会主义 理论体系概论
就业需求调查
马克思主义基 本原理概论
创业教育
职业生涯规划与 就业指导
毕业教育
军事理论 人文、社科、管理类选修课
人文社科类素质课
公共基础课
外 体 育 语 线性代数 概率论与数理统计 体育
专业课
钢结构基本 原理及设计
钢结构课程设计 桥梁工程
高等数学 大学物理 计算机实用基 础A
混凝土结构设计 原理 建筑设备
路基路面工程 路基路面工程课程设计 混凝土结构设计 混凝土结构课程设计
工程图学 土木工程概论 工程测量学 工程测量学 实习
附图1
第一学期 第二学期
土木工程(建筑工程方向)专业课程拓扑图
第三学期 第四学期 第五学期 第六学期 土木工程施工组织 土木工程施工 组织课程设计 工程结构抗震设计 基础工程 基础工程课程设计 道路勘测设计 高层建筑结构设 计 高层建筑 结构课程 设计 施工方案撰写 生产实习 砌体 结构 砌体结构 课程设计 专业选修课 第四学年 毕业实习 毕业设计 (论文) 就业实习 专业选修课 结构概念与体系 结构设计软件PKPM 组合结构 工程事故分析与加固 大跨建筑结构 高层钢结构 工程概预算 钢结构稳定理论 结构安全评定 高层建筑施工 土木工程前沿 工程监理概论 土木工程施工内业资料 编制
建筑表皮的拓扑表达

怠 i ,  ̄
图2袁 皮的 内陷 3 . I 表 皮的 内移
资料 来 源 : 资料 来 源 : 李滨 全 , 建 筑表 皮 的拓 扑发 生 , 《 华 中建 .  ̄} 2 0 1 0 年0 6 H 建 筑表 皮 的 内陷可 以分 为 三个 不连续 阶段 ( 图2 ) 。表 皮 腔体 早 期 内陷 完 成后 , 经过 较 为短 暂 的停 留 , 开始 第 二时 期 的变形 。 在此 期 间表 皮腔 体 开始 大 幅度拉 长 , 又 粗又 短 的表皮 腔 体变 成又 细 又长 的 管状 结 构 。有 些管 状 结构 在 拉伸 过程 中 中间 部位发 生 破裂 。 紧接 着 , 表 皮腔 出现第 三个 变形 延 长期 , 表皮 腔体继 续 拓扑 延伸 与另 一 端表 皮腔 接触 之 后连 通 , 从 而 形 成贯 穿整 个 建筑 的 管状 结构 , 表 皮腔 壁 在与 外 表皮 接 触 的位 置 处 最终 形 成 内 陷 口, 内陷 口与表 皮腔 的最 顶端 部 位最 终形 成一 个 连续 相通 的 管状 表皮 形 态 。例 如 : 深 圳 湾体 育 中心— — “ 春茧” 等等 建 筑 。
紧接着表皮腔出现第三个变形延长期表皮腔体继续拓扑延伸与另一端表皮腔接触之后连通从而形成贯穿整个建筑的管状结构表皮腔壁在与外表皮接触的位置处最终形成内陷口内陷口与表皮腔的最顶端部位最终形成一个连续相通的管状表皮形态
建筑理论 与设 计
建筑表皮 的拓扑表达
谷理 唐 晶 郑州
4 5 0 0 0 0 郑 州 大 学 综 合 设 计研 究 院有 限公 司
够用拓扑表皮表达相关理论及发 生方式指导现代建筑表皮形态, 以促进建筑形态学的发展。 关 键字 : 拓扑 学 建 筑 表皮 拓 扑表达 方 式
克莱因瓶建筑 Klein Bottle House

克莱因瓶建筑Klein Bottle House
这个由Rob McBride设计,距离墨尔本一个班小时车程的258平米的度假屋Klein bottle
house顾名思义是受克莱因瓶的启发将拓扑学应用到建筑中的一个例子。
klein bottle(克莱因瓶)内外连贯的面围成的体量。
在介绍这个房子之前先要了解几个概念,一是拓扑学,“简单地说,拓扑就是研究有形的物体在连续变换下,怎样还能保持性质不变。
”(百度百科)
拓扑等价是拓扑学的重要性质,如何理解呢,打个比方,“对于任意形状的闭曲面,只要不把曲面撕裂或割破,他的变换就是拓扑变幻,就存在拓扑等价”。
形态构成上完全打破了传统意义上建筑学中点、线、面的概念(建立在直角坐标系基础上的),设计者借助电脑cad的大力帮助,将拓扑学的结构模型成功运用到建筑设计中,使内外面连贯成一体,材料上,采用了当地主要的建筑材料——混凝土板材结合黑色金属板材.
建筑坐落在沙丘上,旁边就是树林和沙滩运动场地。
最开始的构思是这个度假建筑落在树间,呈复杂的螺旋式,但进一步考虑到家庭功能是,建筑师选择了现在这个方案。
这个颇具实验感的几何体很好的满足了现代居住要求。
屋子中间有一个中央庭院,楼梯就靠着庭院,人们上上下下,感受着丰富的层面和空间变化。
什么是拓扑学及其应用
拓扑学(Topology)是数学的一个重要分支,它研究的是空间中的形状、结构以及它们之间的关系。
拓扑学的研究对象可以是任意维度的空间,而不仅仅是平面或者立体空间。
拓扑学起源于18世纪的欧洲,当时人们对于空间形状和连续性的研究逐渐形成了拓扑学的雏形。
拓扑学的主要研究内容包括拓扑空间、连续映射、同胚等概念。
其中最重要的概念之一是拓扑空间,它是一组元素的集合,配合着一些定义在这些元素上的开集公理,从而定义出拓扑空间中的结构和关系。
而连续映射则是拓扑空间之间的映射,它保持了空间中元素之间的邻近关系。
同胚是指两个拓扑空间之间存在一一对应关系,并且保持了空间中元素之间的邻近关系。
拓扑学具有广泛的应用领域,尤其是在自然科学和工程技术领域中起着重要的作用。
一个典型的应用领域是网络拓扑。
网络拓扑是指将网络中的各个节点和连接关系抽象成数学模型,通过对网络拓扑的分析和优化,可以实现更高效的数据传输和通信。
拓扑学的方法可以帮助网络管理员设计合理的路由算法、降低网络拥塞和延迟等问题。
另一个应用领域是物理学。
在物理学领域中,拓扑学被用来研究凝聚态物质中的拓扑相变和拓扑保护态。
通过研究拓扑相变,人们可以深入了解物质中的微观结构和相互作用规律,也可以寻找新的物质性质和应用。
拓扑保护态则是指在一些量子体系中存在的特殊电子态,它们具有稳定的拓扑性质,对外界扰动具有抗干扰的能力。
这种抗干扰能力使得拓扑保护态在量子计算和量子通信领域有着广阔的前景。
此外,拓扑学还在计算机科学领域具有重要的应用价值。
拓扑学中的图论是计算机科学中的基础模型之一,它研究了图的形状和结构以及它们之间的关系。
图论在算法设计、网络优化、数据挖掘等领域中有着广泛的应用。
拓扑学的其他概念和方法,如同伦理学、群论等,也被应用于计算机图形学、数据库理论等领域。
总而言之,拓扑学是一门研究空间形状和结构的学科,它的应用涵盖了自然科学、工程技术和计算机科学等领域。
通过拓扑学的方法,人们能够深入了解空间中的结构和关系,从而提高数据传输的效率、研究物质中的新性质,并且在计算机科学领域中提供了一些基础模型和方法。
结构拓扑优化在建筑领域的应用综述
结构拓扑优化在建筑领域的应用综述摘要:结构拓扑优化是一种寻找最佳材料分布的方法,以在给定的设计约束下实现某些性能指标的优化。
本综述论文旨在探讨结构拓扑优化在建筑领域的应用及其影响。
首先,我们简要回顾了拓扑优化的基本原理和方法,如梯度下降法、水平集法和SIMP方法等。
接下来,我们深入讨论了拓扑优化在建筑结构设计中的应用,包括建筑物的主体结构、楼梯、墙体和桥梁等。
我们还探讨了拓扑优化如何提高建筑物的耐久性、节能性能和减轻结构重量。
最后,我们展望了结构拓扑优化在建筑领域的未来发展趋势和挑战。
关键词:拓扑优化、建筑结构、设计方法、应用、耐久性、节能0引言本文将对结构拓扑优化在建筑领域的应用进行综述,重点介绍拓扑优化方法及其在建筑物主体结构设计、桥梁结构设计和墙体设计等方面的应用。
同时,探讨结构拓扑优化在建筑领域的未来发展趋势和挑战,以期为相关领域的研究和应用提供参考。
1结构拓扑优化的基本原理和方法1.1 SIMP方法SIMP(Solid Isotropic Material with Penalization)方法是一种广泛应用于结构拓扑优化的方法。
这个方法最早由Ole Sigmund和Klaus Svanberg在1990年代初提出[1]。
SIMP方法是基于材料密度的优化方法,其核心思想是通过对结构中每个元素的材料密度进行优化,以达到目标函数的最优化。
1.2 ESO方法ESO(Evolutionary Structural Optimization)方法是一种直观且有效的结构拓扑优化技术。
这种方法最早是由Michael P. Bendsoe和Niels Olhoff于1991年提出的[2],与SIMP方法相比,ESO方法的基本思路更加简单直接,它是基于结构演化过程的优化思想。
1.3 BESO方法BESO(Bi-directional Evolutionary Structural Optimization)方法是一种结构拓扑优化技术,它综合了ESO(Evolutionary Structural Optimization)方法的优点,并进一步拓展了优化过程。
基于拓扑优化的结构形态设计与分析
基于拓扑优化的结构形态设计与分析在传统的建筑结构设计中,结构形态是建筑物的基本特征之一。
然而,随着科技的发展和计算机技术的进步,基于拓扑优化的结构形态设计与分析成为了一种新的方法和工具。
拓扑优化是一种寻找最优结构形态的方法,它通过传统的结构设计方法无法达到的搜索空间来解决问题。
拓扑优化的基本思想是在给定边界条件和约束条件下,通过改变结构的拓扑形态来寻找最佳结构。
它可以优化结构的性能,降低材料的使用量,提高结构的稳定性和耐久性。
在基于拓扑优化的结构形态设计与分析中,首先需要明确设计目标和约束条件。
设计目标可以是最小化结构重量、最大化结构稳定性、最大化结构刚度等;约束条件可以是结构的荷载条件、位移条件、材料性能要求等。
而后,基于拓扑优化的结构形态设计与分析涉及到的步骤可包括以下几个方面:1. 初始设计:根据建筑需求和功能,进行初始的结构形态设计。
这可以是一个简单的几何形状,作为拓扑优化的起点。
2. 离散化:将初始设计离散化为有限元网格。
离散化是拓扑优化的基础,它将结构形态转化为可以计算的离散单元,以便进行进一步的优化和分析。
3. 设计空间定义:定义结构形态的设计空间,即可调整的区域。
设计空间定义可以通过几何形状或者网格区域来实现,以确定那些部分可以被拓扑优化修改。
4. 材料分配:设置材料的分配规则,即指定各个离散单元所使用的材料。
材料分配可以根据结构形态和设计目标来进行调整,以达到最佳的材料利用效率。
5. 设计变量参数化:参数化是拓扑优化中关键的一步。
通过参数化,可以调整设计变量,即结构形态的拓扑和尺寸参数。
参数化的目的是使结构能够充分表达设计目标,同时又要保证计算的高效性。
6. 拓扑优化:在设计变量参数化的基础上,进行拓扑优化搜索。
拓扑优化可以采用各种优化算法,例如遗传算法、粒子群优化等。
通过迭代优化过程,寻找最佳的结构形态。
7. 结构分析:对拓扑优化得到的结构形态进行结构分析。
结构分析可以包括静力分析、动力分析、热力学分析等。
数学拓扑学基础知识及应用
数学拓扑学基础知识及应用拓扑学是数学的一个分支,主要研究空间之间映射的连续性质,即不依赖于距离的性质。
拓扑学的发展源于19世纪的欧几里得几何,但是拓扑学并不仅仅是几何学的一部分,它独立地研究空间的形状和结构,并逐渐发展出许多重要的分支和应用。
一、拓扑学的基本概念1. 拓扑空间拓扑空间是指一个非空集合X和X上的一个拓扑结构T。
拓扑结构T是指X的子集族,它满足以下三个条件:(1)空集和整个X都是拓扑结构的元素;(2)任意多个拓扑结构的交集仍然是拓扑结构的元素;(3)任意两个拓扑结构的并集仍然是拓扑结构的元素。
2. 连通性如果一个拓扑空间X不能被表示成两个非空开集的并集,那么X就是连通的。
简单来说,就是拓扑空间中不存在任何分离的部分。
3. 路径连通性如果对于拓扑空间中的任意两个点p和q,都存在一条连续的曲线从p到q,那么该空间就是路径连通的。
二、拓扑学的应用1. 图形处理在计算机图形学中,拓扑学提供了一种描述图像的方法,可以通过描述点、线、曲面等基本元素之间的关系,表示图像的形状和结构。
拓扑学被广泛应用于计算机辅助设计、图像处理、计算机动画等领域。
2. 环境规划在城市规划、交通规划等领域,拓扑学可以用于描述空间之间的联系和关系,例如街道和道路之间的连通性、建筑物和公园之间的空间布局等。
3. 量子理论在物理学中,拓扑学可以用于研究拓扑相变和拓扑激发态等现象,为量子计算和量子通讯提供理论基础。
4. 生物学在生物学中,拓扑学可以用于描述蛋白质和DNA的空间结构,并研究细胞之间的联系和生物大分子之间的相互作用。
三、经典拓扑学问题1. 形状不变性拓扑学可以研究形状的变化,而不依赖于它们的度量或坐标。
例如,对于一个球和一个圆环而言,它们虽然形状不同,但它们具有相同的拓扑性质,因为它们可以通过连续变形互相转化。
2. 贝尔定理贝尔定理是拓扑学中的一项经典成果,它说明了在三维空间中不存在一种连续变形,可以将一朵玫瑰变成一个球,而不破坏它的结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建筑拓扑学——探求当代空间的本质草译自 Juan Antonio Cortes, Architectural Topology -— An Inquiry into Nature of ContemporarySpace, EL(), P33—57】1, 空间组织的清晰性“对我们而言,清晰地解释每个项目的内在关系是十分重要的……以最简洁与直接的方式,而非通过图形或者形式来表现概念.评判一个方案是否简洁,概念必须得以清晰阅读。
”(妹岛和世,2004)“通常,体量上的透明与轻巧并非最终目的,我们致力于将各构成部分以一种清晰的方式来组织.”(SANAA,2005)评论家反复地将妹岛和西泽的建筑学冠以简洁、朴素(austerity)、纯粹几何的特征。
话虽如此,我们还是该定义这些特征在他们作品中的含义。
总的来说,热衷简洁的建筑师常被称为极简主义者(minimalist).10多年前,Atan Allen就认为妹岛不应被归类为本质主义者的极简主义(essentialist minimalism),本质主义者们总想着去除作品中不必要的成分(component)以显现理想形式。
实际上,妹岛和西泽都不能被称为极简主义者,如开篇的引言,他们并非像要构筑理想形式,而是要让概念——空间或者构成要素的组织-—明晰。
这两位建筑师的作品也常被冠以“非物质性”(immateriality)、“轻巧"、“透明”。
然而,就前两个特征而言,应该说他们的作品看起来是“非物质的”与“轻巧”的,而非真正的非物质.虽然常使用透明的玻璃,他们总是强调物质上的透明性并非他们设计的最终目的。
“透明性意味着创造各种关系,它并非只是被看穿。
透明性也意味着清晰性,不仅在视觉方面,更指概念方面.”妹岛和西泽在一些访谈与出版物中表达过一些观点,其中,追求清晰的空间组织并清晰地展现出来是最明确的设计目的,这使得他们以简单方案的方式来做项目,只画线条,没有厚度,也没有对物质的期待,线条勾勒出空间轮廓、明确总平面。
在方案中,他们用“最简单与直接的方式”来组织基本的空间关系,从而呈现出关于拓扑学(topological issue)议题的基本组织形式:群集或分区(clustering or compartmentalisation)、集中或分散(concentration or dispersal)、紧凑或分裂(compactness or breakup)、缝隙或封闭(aperture or closure)、室外或室内、限制与联系、连续与断裂。
他们想象的便是这些有关空间限定与关系的几何学基础议题,而非几何本身。
妹岛和西泽作品可被看作是建筑拓扑学的指南手册。
2 群集与分区的非层级性特征“在阿尔梅勒剧院,每一种材料,都给予同等的重视”。
“在日本传统建筑中,每一部分都有着相同的权重”。
“我们努力设计一个没有等级性的平面——从头到尾.我们的平面重视表现出自由的移动……光线散布在每个角落也表示从等级性中释放出来”.对层级性的消除是妹岛、西泽的首要目的,包括建立项目各组成部分的平衡,建立空间属性的均质性.他们的这些原则不仅是表现出“非材料性”或者“透明性",更与现代主义运动有着紧密联系。
风格派运动(De Stijl,现代主义的范例之一)便是基于构成元素的非层级组合,上述原则也被密斯等现代主义建筑师所运用.在风格派和密斯作品中,构图决定了各元素的相对位置与大小;而妹岛、西泽的建筑中则创造出仅仅是重复、或者带有某种程度上的随意、不确定性的构图.除了缺乏如中心、轴线、焦点等层级性元素,他们作品中的等值性,则通过对统一分布的光源以及白颜色,表现为均质性.消除,或者说急剧的减少层级性,这种思想主导了妹岛、西泽的作品。
这类建筑师的职业历程可看作是在消除层级性的方向上不断开拓空间组织的多样可能性。
案例如下:再春馆制药女子公寓(1990/1991)的楼层平面基于宿舍单元的重复而生成,两侧成排的宿舍面对着公共空间。
这种空间组织消灭了走廊并允许多样化的路径与关系在住户间产生。
在歧阜北方町住宅(1994/1998),住房被当做组成公寓的单元,住房不同的组合方式促成多样化的公寓。
这种重复的构图原则与传统的三段式构图(tripartite)相反,随意的构图机制促成潜在的统一秩序。
【再春馆制药女子公寓】【歧阜北方町住宅】阿尔梅勒剧院(1998/2006)有着激进的平面组织,平面由一个矩形被分割成不同尺寸的小矩形而组成,所有矩形等级相同,平面看起来几乎就是几何图案。
作者声称多样化的空间联系就在这单一的平面中展开。
【阿尔梅勒剧院的平面与模型】空间组织的方向是简单地将平面划分成组的矩形,广场藏在其中。
矩形内部使用功能的可交换性促成了建筑的灵活性。
“我们构想这个房子没有层级性,公共性很强,从走道到用房,空间配置原则均相同.”特别是,“总是存在不同大小的用房,一个矩形有可能是一个卧室,另一个则可能为走廊或者庭院,这就是其灵活之处。
”另一个重要项目是金泽21世纪美术馆(1999—2004),西泽曾在一篇文章中提到,该建筑的基本原则之一是“分割用房”(separating the rooms).分割用房,然后再组合的设计方法日后也应用在他们的诸多项目中.用房分配的过程是随意的,唯一的标准在于亲密性或者距离感、集中或者分散,而不依赖于传统的层级方式。
这种非层级性的安排,类似于风格派的构图,然而构图的元素是用房,而没有将造型简化为分离的线或者面的要素化过程(elementarization process)。
西泽解释说,在这座博物馆的设计中,“分割用房"的原则首先是作为平面构思,然后,从平面草图转移到工作模型,当给予用房不同的高度后,他们认识到了将平面三维化的潜力。
设计过程的另一个基本原则是创造走廊,它在平面组织的成型过程中十分关键,在反复试验中,最初的迷宫状的方案被现在重视观者方向感的方案所取代。
当然,将族群的用房环绕一个4.5米高的玻璃封套,高矮不一的盒子从屋顶中立起,从而赋予其与周边环境一个强有力的联系,也是构思的基本点。
这一外围的圆形抹去了建筑的正面与背面的分别。
通过这样的设计,建筑向周边环境平等一致地开放.最后则是包含室内外的景观设计。
【金泽21世纪美术馆的用房“要素化"过程】“分割用房”的方法在日后的一些列项目中得以应用,用房成为独立体量,从包围的外套中解放出来。
在东京森山住宅(2002—2005)中,散布的体块仍保持着平行的安排.并且,建筑师寻求在各独立体量中的可交换的灵活性,“在这个房子中,客户可自由决定哪些房子自住,哪些房子出租……他可以更换自己的居住领域。
想法是设计一个让客户可以享受不同的空间与生活方式,不拘于固定地点的房子"。
在Towada艺术中心(2008-2008)中,各用房体块零散布置,但用一条线性走廊相联系。
“我们设计的平面由分散的展室组成……展室并非简单分离,而是群团式地聚集,它们构成了整体的连续景观"。
【东京森山住宅】【Towada艺术中心】在纽约当代艺术新馆(2003—2007)中,一系列不同尺寸的盒子被偏离中心的堆积起来,从而形成采光天窗和平台。
在丰田Aizuma讲堂(2006-)中,三层体块同样地自由堆积。
三层体块有着起伏的周界,形状各自略有不同,从而产生室外的楼板与天花板—-平台和雨篷.室内外的中介空间使建筑与外部环境发生连接。
在建筑内部,用房墙面基本都是曲线,大小不一、且互不相连,并和外墙也分开。
【纽约当代艺术新馆】【丰田Aizuma讲堂】在阿尔梅勒剧院中,平面只是直角、而非网格状地划分,通过对大房间的分隔而获得成组的小房间。
而在其它项目中,平面是被格网分隔,通过不同的分隔来形成多样尺寸的用房.如在Funabashi住宅(2002-2004)中,这里的另一大特征是缺乏作为中介的交通空间,和阿尔梅勒剧院相似。
在复杂的、不规则的平面中也可见到直角的房间划分,比如在Eda住宅中,不同的格网以平行于周边街道、铁路以及车站广场的不同角度共存.【Eda住宅】【Funabashi住宅】Glass Pavilion at the Toledo Museum of Art(2001-2006)特别有趣。
虽然它始于矩形周界内的网格分隔,最终成型于一个个独立的、连续外墙的用房,相互间偶然性地联系。
如此一来,平面由相互联系的泡泡组合而成,人流追随着形式。
建筑严格维系着网格模式与外在轮廓间的内在秩序。
矩形网格与外在轮廓具有几何的相似性。
【Glass Pavilion at the Toledo Museum of Art】所有的机制—-房间的连续重复、将矩形简单拼贴而成的平面、房间的分隔以及随意的分布、楼层的任意叠合、利用一个或者多个网格划分平面-—都从不同方式生成建筑,然而,他们都具有非等级性的当代空间品质。
3、几何学上的变形—-拓扑等值(topological equivalences)近来,妹岛与西泽的几何形有很大的转变--从简单的圆柱、方体、棱柱(prism)等体型向自由的、通常变形虫式(amoeboid)的几何体所转变。
看起来是建筑师的观念有了急剧的变化,实则不然,他们的几何体仍然维系着在原型与变型之间的所谓“拓扑等值”.虽然加入了新属性,这些变型仍保持着与原型间的“拓扑等值".长野森林别墅(1992—94)呈圆形,这是因为,“考虑到周围自然环境的均质性,圆形能够有效地和周边环境发生关联,而无需考虑方向性。
"他们不是因为完型而考虑使用圆,而是因为其至高的连续性与等向性(isotropic)。
庭院也是圆形,但游离于外环圆心一侧,屋顶倾斜方向与斜坡方向相反,相互抵消圆形本身的等向性。
【森林别墅】阿尔梅勒公园咖啡厅(1999-)的周界也是圆形,内圆如前例,稍稍歪曲(wrap)。
Emona酒店(2005-)由两个封闭的环组成,但内环与外环形式上不完全相同,形成内部空间的宽度变化,这与前例“拓扑等值”,但几何形式不同。
环空间内维持着相同的层高,但在剖面上有起伏,以适应地形。
【阿尔梅勒公园咖啡厅】【Emona酒店】21世纪美术馆则是更大尺度的圆形。
“我们使用圆形是因为基地位于城市中心,人们从各个方向汇集而来”,“圆形能创造一个连续的形式而不存在任何的衔接点(articulation)……当你想在各自为政的环境内制造连续性空间,圆形是一个理想形式".但是,建筑师并不认为圆形的完型是值得保持的重要属性,他们开始尝试其它的“拓扑等值”图形.Alessi 茶具(2002)在拓扑变型方面是具有教示意义的例子:不同的物件像是经过切割后的结果,带有手工不精确性的棱镜体块,但都是没有改变内在属性的初始形式的变型。
