高二数学必修三第三章练习题《古典概型(习题课)》
高中数学 第三章第2节古典概型同步练习难题 文 人教实验B版必修3
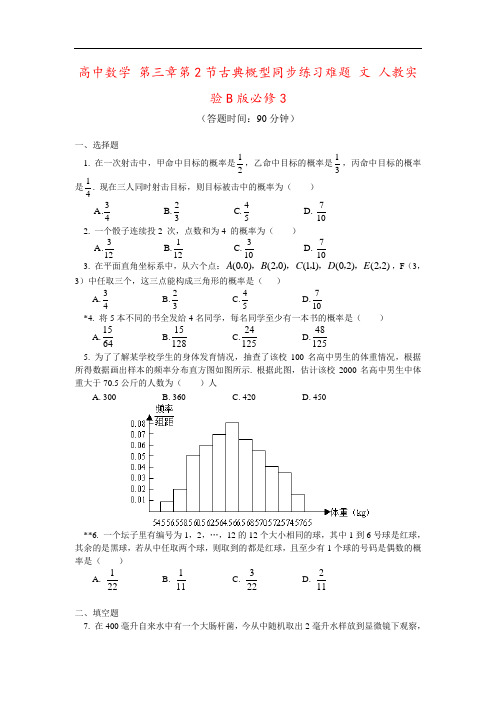
高中数学 第三章第2节古典概型同步练习难题 文 人教实验B 版必修3 (答题时间:90分钟) 一、选择题1. 在一次射击中,甲命中目标的概率是21,乙命中目标的概率是31,丙命中目标的概率是41. 现在三人同时射击目标,则目标被击中的概率为( ) 43A. 32B. 54C. 107D. 2. 一个骰子连续投2 次,点数和为4 的概率为( )123A. 121B. 103C. 107D. 3. 在平面直角坐标系中,从六个点:(00)(20)(11)(02)(22)A B C D E ,,,,,,,,,,F (3,3)中任取三个,这三点能构成三角形的概率是( ) A.43 B.32 C.54 D.107 *4. 将5本不同的书全发给4名同学,每名同学至少有一本书的概率是( ) A.1564 B.15128 C.24125 D.481255. 为了了解某学校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示. 根据此图,估计该校2000名高中男生中体重大于70.5公斤的人数为( )人A. 300B. 360C. 420D. 450**6. 一个坛子里有编号为1,2,…,12的12个大小相同的球,其中1到6号球是红球,其余的是黑球,若从中任取两个球,则取到的都是红球,且至少有1个球的号码是偶数的概率是( )A. 122B. 111C. 322D. 211二、填空题7. 在400毫升自来水中有一个大肠杆菌,今从中随机取出2毫升水样放到显微镜下观察,则发现大肠杆菌的概率为________.*8. 某班有52人,男女各半,男女各自平均分成两组,从这个班中选出4人参加某项活动,这4人恰好来自不同组别的概率是_________.9. 在五个数字12345,,,,中,若随机取出三个数字,则剩下的两个数字都是奇数的概率是(结果用数值表示)三、解答题10. 假设车站每隔10 分钟发一班车,乘客随机地到达车站,问等车时间不超过3 分钟的概率?*11. 甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.6,计算:(1)两人都击中目标的概率;(2)其中恰有一人击中目标的概率;(3)至少有一人击中目标的概率.**12. 盒中装着标有数字1,2,3,4的卡片各2张,从盒中任意抽出3张,每张卡片被抽出的可能性都相等,求:(Ⅰ)抽出的3张卡片上最大的数字是4的概率;(Ⅱ)抽出的3张卡片中有2张卡片上的数字是3的概率;(Ⅲ)抽出的3张卡片上的数字互不相同的概率。
高中数学人教新课标A版必修3 第三章 概率 3.2古典概型(I)卷

高中数学人教新课标A版必修3 第三章概率 3.2古典概型(I)卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分)从三男三女6名学生中任选2名(每名同学被选中的机会相等),则2名都是女同学的概率等于()A .B .C .D .2. (2分) (2016高二下·南城期中) 甲、乙、丙、丁、戊五位同学站成一排照相留念,则在甲乙相邻的条件下,甲丙也相邻的概率为()A . 1B .C .D .3. (2分) 2016年春运期间为查醉酒驾驶,将甲、乙、丙三名交警安排到某商业中心附近的两个不同路口突击检查,每个路口至少一人,则甲、乙两名交警不在同一路口的概率是()A .B .C .D .4. (2分)从正四面体的6条棱中随机选择2条,则这2条棱所在直线互相垂直的概率为().A .B .C .D .5. (2分)一个不透明的盒子里有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.那么甲赢的概率是()A .B .C .D . 以上均不对6. (2分)有编号分别为1,2,3,4,5的5个红球和5个黑球,从中取出4个,则取出的编号互不相同的种数为()A . 5B . 80C . 105D . 2107. (2分)已知集合,在集合M中任取一个元素x ,则“”的概率是()A .B .C .D .8. (2分) (2018高二下·甘肃期末) 已知在10件产品中可能存在次品,从中抽取2件检查,其次品数为,已知,且该产品的次品率不超过,则这10件产品的次品率为()A .B .C .D .二、填空题 (共3题;共3分)9. (1分)(2020·南京模拟) 学校准备从甲、乙、丙三位学生中随机选两位学生参加问卷调查,则甲被选中的概率为________.10. (1分) (2017高一下·伊春期末) 将3个不同的小球放入4个盒子中,有 ________种不同的放法11. (1分) (2016高二下·宁波期末) 掷两颗质地均匀的骰子,在已知它们的点数不同的条件下,有一颗是6点的概率是________.三、解答题 (共3题;共25分)12. (5分)用红、黄、蓝三种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,求3个矩形颜色都不同的概率.13. (10分)在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,将该小球放回箱子中摇匀后,乙再从该箱子中摸出一个小球.(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(数字相同为平局),求甲获胜的概率;(2)规定:两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜,这样规定公平吗?14. (10分) (2018高二下·青铜峡期末) 已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.用X 表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;参考答案一、选择题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共3题;共3分)9-1、10-1、11-1、三、解答题 (共3题;共25分)12-1、13-1、13-2、14-1、14-2、。
高中数学 专题1.11 古典概型练习(含解析)新人教A版必

古典概型1.下列试验中,属于古典概型的是( )A .种下一粒种子,观察它是否发芽B .从规格直径为250 mm ±0.6 mm 的一批合格产品中任意抽一根,测量其直径dC .抛一枚硬币,观察其出现正面或反面D .某人射击中靶或不中靶【答案】 C【解析】 依据古典概型的特点判断,只有C 项满足:①试验中所有可能出现的基本事件只有有限个;②每个基本事件出现的可能性相同.2.一枚硬币连掷3次,有且仅有2次出现正面向上的概率为( )A.38B.23C.13D.143.四条线段的长度分别是1,3,5,7,从这四条线段中任取三条,则所取出的三条线段能构成一个三角形的概率是( )A .14B .13C .12D .25【答案】 A【解析】 从四条长度各异的线段中任取一条,每条被取出的可能性均相等,所以该问题属于古典概型.又所有基本事件包括(1,3,5),(1,3,7),(1,5,7),(3,5,7)四种,而能构成三角形的基本事件只有(3,5,7)一种,所以所取出的三条线段能构成一个三角形的概率是P =14. 4.集合A ={2,3},B ={1,2,3},从A 、B 中各任意取一个数,则这两数之和等于4的概率是( ) A.23 B.12 C.13 D.165.从1,2,3,4,5中任意取出两个不同的数,其和为5的概率是________.6、现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9.若从中一次抽取2根竹竿,则它们的长度恰好相差0.3 m的概率为________.答案1 5解析基本事件共有(2.5,2.6),(2.5,2.7),(2.5,2.8),(2.5,2.9),(2.6,2.7),(2.6,2.8),(2.6,2.9),(2.7,2.8),(2.7,2.9),(2.8,2.9)10种情况.相差0.3 m的共有(2.5,2.8),(2.6,2.9)两种情况,所以P=210=1 5.7.有100张卡片(从1号到100号),从中任取1张,取到的卡号是7的倍数的概率为________.8.在不大于100的自然数中任取一个数.(1)求所取的数为偶数的概率;(2)求所取的数是3的倍数的概率;(3)求所取的数是被3除余1的数的概率.。
高中数学 人教A版 必修三 第三章 3.2 古典概型(1)

四、课堂练习
1、将一枚质地均匀的硬币连掷三次,分别求出现“2 次正面朝上、1次反面朝上”和“1次正面朝上、2次反 面朝上”的概率。
解:将一枚质地均匀的硬币连掷三次会出现以下8种情况: 正正正、正正反、正反正、正反反
反正正、反正反、反反正、反反反
其中“2次正面朝上、 1次反面朝上”出现了3次, “1次正面朝上、2次反面朝上” 也出现了3次, 所以“2次正面朝上、 1次反面朝上”和“1次正面 朝上、2次反面朝上”出现的概率都为3/8。
共36个 其中检测出不合格事件数为:18个 所求概率 P(A)=18/30 =0.6
答:检测出不合格产品的概率为0.6
解二:(不考虑抽取顺序) 可以理解为一次“随机抽取2听”,这样(1,2),
(2,1)作为相同事件, 于是基本事件总数就为:
(1,2),(1,3),(1,4),(1,a),(1,b), (2,3),(2,4),(2,a),(2,b), (3,4),(3,a),(3,b), (4,a),(4,b), (a,b) 而检测出不合格事件数为: 9个 所求概率 P(A)=9/15 =0.6
我们将具有这两个特点的概率模型称为古典概率 模型,简称古典概型。
作业:P134 习题3.2 A组 第4题
四、课堂练习
2、在大小相同的5个球中,2个是红球,3个是白球, 若从中任取2个,则所取的2个球中至少有一个红球的 概率是多少?
五、课时小结 1、基本事件 在一个试验可能发生的所有结果中,那些不能再分 的最简单的随机事件称为基本事件.(其他事件都可由 基本事件来描述)
2、古典概型
(1) 试验中所有可能出现的基本事件只有有限个; (2) 每个基本事件出现的可能性相等。
解:(1)掷一个骰子的结果有6种。同时抛掷两个骰 子的结果如图所示,共有36种。
高中数学必修3《古典概型与几何概型》复习课

(3)几何概型的概率公式:
P(A)=区域的构全成部事结件果A所的构区成域的长区度域(面长积度或(面体积积或) 体积).
1.从长度分别为 2,3,4,5 的四条线段中任意取出三条,则以
这三条线段为边可以构成三角形的概率是( D )
A.14
B.12
C.23
D.34
2.连掷两次骰子得到的点数分别为 m 和 n,记向量 a=(m,
考点 1 古典概型 例 1:先后随机投掷 2 枚正方体骰子,其中 x 表示第 1 枚骰 子出现的点数,y 表示第 2 枚骰子出现的点数. (1)求点 P(x,y)在直线 y=x-1 上的概率; (2)求点 P(x,y)满足 y2<4x 的概率.
解析:(1)每颗骰子出现的点数都有 6 种情况, ∴基本事件总数为 6×6=36(个). 记“点 P(x,y)在直线 y=x-1 上”为事件 A,A 有 5 个基本 事件:A={(2,1),(3,2),(4,3),(5,4),(6,5)},∴P(A)=356. (2)记“点 P(x,y)满足 y2<4x”为事件 B,则 事件 B 有 17 个基本事件: 当 x=1 时,y=1;当 x=2 时,y=1,2; 当 x=3 时,y=1,2,3;当 x=4 时,y=1,2,3; 当 x=5 时,y=1,2,3,4;当 x=6 时,y=1,2,3,4. ∴P(B)=3167.
乙赢的概率为 P(B)=1160=58.
∵P(A)<P(B),∴该游戏不公平.
(2)方法一:设“甲抽出的数字是奇数”为事件 C,则 C 发生
的概率为 P(C)=24=12.
又由(1)知,甲赢的概率即事件 A 发生的概率,
∴P(AC)=P(A)=38.
故由条件概率得此时甲赢的概率为
高中数学古典概型练习 新课标人教A版必修3

古典概型(一)1.概率P(A)的取值范围任意事件A 的概率的范围是:_____________其中不可能事件的概率是________ ,必然事件的概率是_______2.概率的加法公式当事件A 与B 互斥时, A ∪B 发生的概率为_______________特别地,若事件A 与事件B 互为对立事件,则A ∪B 为必然事件_______________3、基本事件我们把上述试验中的随机事件称为基本事件,它是试验的每一个可能结果。
基本事件有如下的两个特点 :(1)(2)4、古典概率概型:例1 、 从字母a 、b 、c 、d 中任意取出两个不同字母的试验中,有哪些基本事件?例2 单选题是标准化考试中常用的题型,一般是从A ,B ,C ,D 四个选项中选择一个正确答案。
如果考生掌握了考察的内容,他可以选择唯一正确的答案。
假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?练习:1.在20瓶饮料中,有2瓶已过了保质期。
从中任取1瓶,取得已过保质期的饮料的概率是多少?2.、同时抛掷1角与1元的两枚硬币,计算:(1)两枚硬币都出现正面的概率是(2)一枚出现正面,一枚出现反面的概率是求古典概型概率的步骤:(1)判断该概率模型是否为古典概型;(2)计算所有基本事件的总数n .(3)计算事件A 所包含的基本事件个数m .(4)计算 nm P (A )例3 同时掷两个骰子,计算:(1)一共有多少种不同的结果?(2)其中向上的点数之和是5的结果有多少种?(3)向上的点数之和是5的概率是多少?练习1.从甲、乙、丙三人中任选两名代表,甲被选中的概率为________.2、作投掷二颗骰子试验,用(x,y)表示结果,其中x表示第一颗骰子出现的点数,y表示第二颗骰子出现的点数,求:(1)求事件“出现点数之和大于8”的概率(2)求事件“出现点数相等”的概率3、(掷骰子问题):将一个骰子先后抛掷2次,观察向上的点数。
问: (1)共有多少种不同的结果? (2)两数之和是3的倍数的结果有多少种?(3)两数之和是3的倍数的概率是多少?变式1:两数之和不低于10的结果有多少种?两数之和不低于10的的概率是多少?变式2:点数之和为质数的概率为多少?变式3:点数之和为多少时,概率最大且概率是多少?例4、假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,……,9十个数字中的任意一个。
高中数学人教A版必修3《古典概型综合练习》PPT
古典概型的概率计算公式:
P(A)
A包含的基本事件的个数m
基本事件的总数 n
在使用古典概型的概率公式时,应该注意: 要判断所用概率模型是不是古典概型(前提)
基本概念 方法探究 典型例题 课堂训练 课堂小结
例2.同时抛掷两枚均匀的硬币,会出现几种结果?列举出来. 出现 “一枚正面向上,一枚反面向上” 的概率是多少?
(3)由于所有36种结果是等可能的,其中向上点数之 和为9的结果(记为事件A)有4种,因此,
P(A)= A所包含的基本事件的个数 = 4 =1
基本事件的总数
36 9
基本概念 方法探究 典型例题 课堂训练 课堂小结
为什么要把两个骰子标上记号?如果不标记号会出
现什么情况?你能解释其中的原因吗? 如果不标上记号,类似于(3,6)和(6,3)的结果将没有 区别。这时,所有可能的结果将是:
所去掉大王和小王,在剩下的52张牌中随意抽出一张牌,
试求以下各个事件的概率: A: 抽到一张Q
41 52 13
思考题
B: 抽到一张“梅花” 13 1
C:抽到一张红桃 K
52 1
4
52
同时抛掷三枚均匀的硬币,会出现几种结果?
出现“一枚正面向上,两枚反面向上”的概率是多少?
3. 一副扑克牌,去掉大王和小王,在剩下的52张牌中随意抽出一张牌,
试求以下各个事件的概率: A: 抽到一张Q B: 抽到一张“梅花” C:抽到一张红桃 K
基本概念 方法探究 典型例题 课堂训练 课堂小结
1. 单选题是标准化考试中常用的题型,一般是从 A 、B 、C 、D 四个
选项中选择一个正确的答案。
树状图
基本概念 方法探究 典型例题 课堂训练 课堂小结
高中数学必修三同步练习题库:古典概型(选择题:较难28,困难29)
古典概型(选择题:较难28,困难29)1、位于坐标原点的一个质点P按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是.质点P 移动5次后位于点的概率为A. B. C. D.2、从名男生和名女生中任选人参加演讲比赛,则所选人中至少有名女生的概率()A. B. C. D.3、某班班会准备从含甲、乙、丙的7名学生中选取4人发言,要求甲、乙两人至少有一个发言,且甲、乙都发言时丙不能发言,则甲、乙两人都发言且发言顺序不相邻的概率为()A. B. C. D.4、某班共有6个数学研究性学习小组,本学期初有其它班的3名同学准备加入到这6个小组中去,则这3名同学恰好有2人安排在同一个小组的概率是()A. B. C. D.5、某初级中学篮球队假期集训,集训前共有个篮球,其中个是新的(即没有用过的球),个是旧的(即至少用过一次的球),毎次训练都从中任意取出个球,用完后放回,则第二次训练时恰好取到个新球的概率为()A. B. C. D.6、五个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自已的硬币,若硬币正面朝上,则这个人站起来;若硬币正面朝下,则这个人继续坐着,那么,没有相邻的两个人站起来的概率为()A. B. C. D.7、对同一目标独立地进行四次射击,已知至少命中一次的概率为,则此射手的命中率为()A. B. C. D.8、某高中数学老师从—张测试卷的道选择题、道填空题、道解答题中任取道题作分析,则在取到选择题时解答题也取到的概率为()A. B.C. D.9、国庆节前夕,甲、乙两同学相约10月1日上午8:00到8:30之间在7路公交赤峰二中站点乘车去红山公园游玩,先到者若等了10分钟还没有等到后到者,则需发短信联系.假设两人的出发时间是独立的,在8:00到8:30之间到达7路公交赤峰二中站点是等可能的,则两人不需要发短信联系就能见面的概率是()A. B. C. D.10、一个射箭运动员在练习时只记射中环和环的成绩,未击中环或环就以环记.该远动员在练习时击中环的概率为,击中环的概率为,既未击中环也未击中环的概率为(,,),如果已知该运动员一次射箭击中环数的期望为环,则当取最小值时,的值为()A. B. C. D.11、端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同,从中任意选取3个,则三种粽子各取到1个的概率是()A. B. C. D.12、高三毕业时,甲、乙、丙、丁四位同学站成一排照相留念,已知甲乙相邻,则甲丙相邻的概率为()A. B. C. D.13、若,则的概率为()A. B. C. D.14、箱子里有5个黑球,4个白球,每次随机取出一个球,若取黑球,则放回箱中,重新取球,若取出白球,则停止取球,那么恰好在第4次取球后停止的概率为A. B. C. D.15、投掷两颗质地均匀的骰子,则向上的点数之积为6的概率等于A. B. C. D.16、从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B ={抽到二等品},事件C ={抽到三等品},且已知P(A)=" 0.65" ,P(B)="0.2" ,P(C)=0.1。
高中数学 第三章第2节古典概型同步练习 理 新人教版必修3
高二数学人教新课标A 版(理)必修3第三章第2节古典概型同步练习(答题时间:35分钟)一、选择题(每题5分,共20分)1、从长度为1,3,5,7,9的五条线段中任取三条能构成三角形的概率是( ) A. 21 B. 103 C. 51 D. 52 2、将骰子掷2次,其中向上的点数之和是5的概率是( ) A. 91 B. 41 C. 361 D. 93、掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是( ) A. 9991 B. 10001 C. 1000999 D. 21 4、从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件次品的概率是( )A. 1B. 21C. 13D. 32二、填空题(每题8分,共48分)5、从一副扑克牌(54张)中抽一张牌,抽到牌“K ”的概率是6、从标有1,2,3,4,5,6,7,8,9的9张纸片中任取2张,那么这2张纸片的数字之积为偶数的概率为7、一个口袋里装有2个白球和2个黑球,这4 个球除颜色外完全相同,从中摸出2个球,则1个是白球,1个是黑球的概率是8、先后掷3枚均匀的硬币,至少出现一次正面的概率为9、一个正方体,它的表面涂满了红色,在它的每个面上切两刀,可得27个小正方体,从中任取一个,则恰有一个面涂有红色的概率是 。
10、从1,2,3,4,5这5个数中任取两个,则这两个数正好相差1的概率是________。
三、解答题11、(共12分)一个口袋内装有5个白球和3个黑球,从中任意取出一个球。
(1)“取出的球是红球”是什么事件,它的概率是多少?(2)“取出的球是黑球”是什么事件,它的概率是多少?(3)“取出的球是白球或黑球”是什么事件,它的概率是多少?12、(共20分)在一次口试中,要从5道题中随机抽出3道进行回答,答对其中的2道题就获得优秀,答对其中的1道题就获得及格,某考生会回答5道题中的2道题,试求:(1)他获得优秀的概率是多少?(2)他获得及格与及格以上的概率有多大?一、选择题1、B2、A3、D4、C二、填空题5、425427= 6、435413298182⨯⨯+=⨯ 7、4263= 8、789、92276= 10、52104=三、解答题11、解:(1)由于袋内只装有黑、白两种颜色的球,故“取出的球是红球”不可能发生,因此,它是不可能事件,其概率为0。
最新人教版高中数学必修3第三章《古典概型》达标训练
更上一层楼 基础·巩固 1.一枚硬币连掷2次,恰好出现一次正面的概率是( )
A.21 B.41 C.43 D.0 思路分析:列举出所有基本事件,找出“只有一次正面”包含的结果;一枚硬币连掷2次,基本事件有(正,正),(正,反),(反,正),(反,反)共4个,而只有一次出现正面的包括
(正,反),(反,正)2个,故其概率为2142. 答案:A 2.在第1、3、4、5、8路公共汽车都要停靠的一个站(假定这个站只能停靠一辆汽车),有一位乘客等候第4路或第8路汽车.假定当时各路汽车首先到站的可能性相等,则首先到站正好是这位乘客所需乘的汽车的概率等于( )
A.21 B.32 C.53 D.52 思路分析:读懂题意,找出什么是基本事件,基本事件总数是多少,所求事件包含哪几个基本事件;基本事件分别是第1、3、4、5、8路公共汽车到站,显然共有5个,而“乘客所需乘的汽车”
包括4路和8路两个,故概率P=52. 答案:D 3.某小组共有10名学生,其中女生3名,现选举2名代表,至少有1名女生当选的概率为( )
A.157 B.158
C.153 D.1 思路分析:这是一个古典概型与互斥事件相结合的问题;设“恰有一名女生当选”为事件A,“恰有两名女生当选”为事件B,显然A、B为互斥事件.从10名同学中任选2人共有10×9÷2=45种选法(即45个基本事件),而事件A包括3×7个基本事件,事件B包括3×2÷2=3
个基本事件,故P=P(A)+P(B)=1584534521. 答案:B 4.某银行储蓄卡上的密码是一种4位数字号码,每位上的数字可在0—9这10个数字中选取,某人未记住密码的最后一位数字,如果随意按下密码的最后一位数字,则正好按对密码的概率是( )
A.4101 B.3101 C.2101 D.101 思路分析:前三位密码已经记住,肯定按对,故概率与前三位密码无关.只考虑最后一位数字即可,从0到9的10个数字中随机选一个,概率为101. 答案:D 5.从标有1,2,3,„,9的9张纸片中任取2张,那么这2张纸片上的数字之积为偶数的概率为( ) A.21 B.187 C.1813 D.1811 思路分析:互斥事件与古典概型共用.记“2张纸片上的数字之积为偶数”为事件A,“两张纸片上的数字一奇一偶”为事件B,“两张纸片上的数字都是偶数”为事件C,则B、C互斥且A=B∪C.基本事件总数为9×8÷2=36,事件B包含5×4=20个基本事件,事件C包含4×
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页/共7页
高二数学必修三第三章练习题《古典概型
(习题课)》
一个试验是否为古典概型,在于这个试验是否具有古典
概型的两个特征有限性和等可能性,只有同时具备这两个特
点的概型才是古典概型。小编准备了高二数学必修三第三章
练习题,具体请看以下内容。
本节是学生们在学习完古典概型的一节习题课,本节的主要
任务是通过处理教材上的习题使学生进一步理解古典概型
的概念及其计算方法,本着新课程的教学理念,为提高课堂
效率,本节课我把讲台让给学生,以学习小组为单位,来进
行本节课的教学。
(必修3、P134,第4题)
A、B、C、D四名学生按任意次序站成一排,试求下列事件
的概率:
①A在边上;②A和B都在边上;③A或B在边上;④A和B都
不在边上
教师:同学们,准备好了吗?现在给大家一分钟的时间看看题,
各小组选好自己的代表。
(稍作停留,给学生准备时间),现在请第一组派代表来讲解
第一小问。
学生1:题目中说4名同学站成一排,那么我们就考虑他们
站队的情况,也就是基本事件个数有24种,用列举法表示
第2页/共7页
出来就是:
ABCDABDCACBDACDBADBCADCB
BACDBADCBCADBCDABDACBDCA
CABDCADBCBADCBDACDABCDBA
DABCDACBDBACDBCADCABDCBA
其中A在边上包括有最左边和最右边两种情况:共12种情
况
所以A在边上的概率
学生2:老师,刚才同学1在计算基本事件的时候用列举法
表示,考虑了四个人的顺序,而这道题在题目中说按任意的
次序站,是没有顺序的,他的做法是不是不对?
老师:(心中一惊,看来学生对基本事件中顺序有无的考虑还
有所欠缺,还需要加以强调):那么同学们考虑考虑刚才这位
同学的担心对不对?
学生3:同学1在刚才考虑的时候,基本事件的24种有顺序,
但是所要求的事件A在边上包括12种基本事件也有了顺序,
两者都考虑了顺序,所以甲的计算是对的,结果就应该是 。
老师:刚才同学3说的很好,在具体问题的考虑过程中,如
果考虑顺序的话,那两者我们都要考虑,否则就都不考虑,
那么看看第一小问能不能都不考虑顺序呢?
【学生们互相讨论】
学生4:前面我们在处理2题的时候,电话号码有8位,但
第3页/共7页
是题目中要求的事件中只看前两位的,当时在讲的时候我们
用的第二种方法是:要求前两位,我们当时看的就是前两位,
这个题能用这种思路吗?
老师(暗自高兴):试试不就知道了吗?请上来把你的思路讲
讲。
学生3:现在要安排4个学生的位置,那也就是说有4个位
置
____________
那么同学A就有4个位置可选择,而要求是A在边上,所以
A就只能选两边,就有2种情况,所以 。
老师(惊讶):对吗?
学生:对!这种方法真简单,比第一种方法好呀。
老师:答案是肯定的!我们在处理问题的时候一定要前后联
系,做个有心人。那么,再看看有没有其他的方法?
学生5:这个题的4个问题都是问的边上的情况,那可不可
以只看两边的情况,就是说4个人里面我只看2个个就可以
了。
由题知道:对角线不能要,不要求顺序那我们就只看对角线
一侧的就可以了,一共有6种结果,现在第一问中,要求A
在边上有3种情况,那么很简单了 ,而且有表格以后后面
的3问也就解决了。
第2问:A、B都在边上,那就只有一种情况,所以
第4页/共7页
第3问:A或B在边上有4种情况,所以
第4问:A、B都不在边上,也就是说出现的两个字母中没
有AB的就一种情况CD了
所以 。
教师(心中窃喜):有没有疑惑需要同学5解释的?
学生6:第3问A或B在边上,我算的是 ,而刚才按他的
方法得到的是 ,我不知道为什么? 我认为或中应该有A和
B同时在边上的情况,而刚才同学5做的时候没有A和B同
时在边上的情况。
学生5:打个比方,我回宿舍或回教室,两者不会同时发生,
所以不应该包括A和B同时在边上的情况。
教师:那到底有没有呢?请同学们互相讨论,查查资料看看到
底包括A和B同时在边上的情况吗?
【学生们互相讨论】
学生7:找到了,前面在集合中有过, 的定义就是由集合
A或集合B中的元素构成的,其中或有三层意思:I、是A
中的元素但不是B中的
II、 是B中的元素但不是A中的
III、是由A、B中的公共元素组成的
所以应该包括A和B同时在边上的情况。
教师(感到欣慰):对呀,我们数学中的或与生活中的或有所
不同。是有三层含义的。前两种是二者居其一,第三种是同
第5页/共7页
时具备。所以应该包括A和B同时在边上的情况,所以 。
【学生8举手】
学生8:我觉得还可以通过确定事件之间的关系,根据公式
可以处理。
第一问:A在边上,他坐左边或者右边不会同时发生,是互
斥关系,而他坐左边和右边的概率都是 ,所以A坐两边就
应该是 。
第三问与第四问之间,两个事件很明显是对立事件,所以在
做第三问的时候直接用公式 就行了。
教师(心里美呀!):同学8说的对吗?
学生:对,没问题。
教师:通过这节课,同学们熟练了古典概型的常规的处理思
路和方法,课后大家好好总结一下,看看收获些什么。
课后反思:
“师”之概念,大体是从先秦时期的“师长、师傅、先生”而来。
其中“师傅”更早则意指春秋时国君的老师。《说文解字》中有
注曰:“师教人以道者之称也”。“师”之含义,现在泛指从事
教育工作或是传授知识技术也或是某方面有特长值得学习
者。“老师”的原意并非由“老”而形容“师”。“老”在旧语义中
也是一种尊称,隐喻年长且学识渊博者。“老”“师”连用最初
见于《史记》,有“荀卿最为老师”之说法。慢慢“老师”之说也
不再有年龄的限制,老少皆可适用。只是司马迁笔下的“老师”
第6页/共7页
当然不是今日意义上的“教师”,其只是“老”和“师”的复合构
词,所表达的含义多指对知识渊博者的一种尊称,虽能从其
身上学以“道”,但其不一定是知识的传播者。今天看来,“教
师”的必要条件不光是拥有知识,更重于传播知识。通过本节
的教学,我深深的感觉到调动学生积极性的重要性,因为数
学课堂的枯燥,学生上课的时候常因听不懂而睡觉,总是觉
得数学课那么的漫长,而这节课当我告诉学生们下课的时
候,学生居然说了一句:怎么没一会就下课了,这么快。这
是我听到的最欣慰的一句话。而且在上课的过程中,没有一
个爬在桌子上睡觉的,都是坐的好好的,在整个教学过程中,
学生们都在努力地思考,积极地研究。把讲台让给学生,让
学生有了自我展现的舞台,可以锻炼学生,可以暴露学生在
做题过程中的疑点、难点,使得教师的教学有的放矢。在教
学的进程中,课堂的生成很多,学生的感悟很多,真正培养
了学生的思维和能力。
单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。让
学生把一周看到或听到的新鲜事记下来,摒弃那些假话套话
空话,写出自己的真情实感,篇幅可长可短,并要求运用积累的
成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读
或展出。这样,即巩固了所学的材料,又锻炼了学生的写作能
力,同时还培养了学生的观察能力、思维能力等等,达到“一石
多鸟”的效果。
第7页/共7页
高中是人生中的关键阶段,大家一定要好好把握高中,编辑
老师为大家整理的高二数学必修三第三章练习题,希望大家
喜欢。
单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。让
学生把一周看到或听到的新鲜事记下来,摒弃那些假话套话
空话,写出自己的真情实感,篇幅可长可短,并要求运用积累的
成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读
或展出。这样,即巩固了所学的材料,又锻炼了学生的写作能
力,同时还培养了学生的观察能力、思维能力等等,达到“一石
多鸟”的效果。
