2017年春季学期新版新人教版九年级数学下学期28.1、锐角三角函数导学案27
九年级数学下册 第28章《锐角三角形》28.1 锐角三角函数(3)学案(新版)新人教版
学习目标
(1)能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数。
(2)能熟练计算含有30°、45°、60°角的三角函数的运算式
重点
熟记30°、45°、60°角的三角函数值,能熟练计算含有30°、45°、60°角的三角函数的运算式。
导学过程
师生活动
一、知识回顾
1. sin45°+2tan60°
2. sin60°·cos30°-
3. -tan45°
三、新知探究
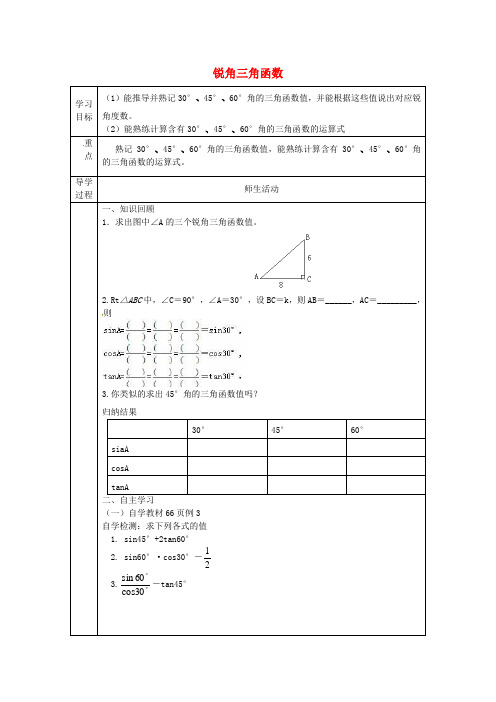
例1(1)如图(1),在Rt△ABC中,∠C=90°,AB= ,BC= ,求∠B的度数和AC的长.
(2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB的 倍,求a.
例2如图,以直角坐标系的原点O为圆心,以1为半径作圆,若P是该圆上第一象限内的点,且OP与x轴正方向组成的角为α,当α为45°时,点P的坐标是__________;当α为60°时,点P的坐标是。
5.在△ABC中,∠A、∠B都是锐角,且sinA= ,
cosB= ,则△ABC的形状是 ()
A .直角三角形B.钝角三 角形C.锐角三角形D.不能确定
6.如图Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tana的值为().
A. B. C. D.
7.当锐角a>60°时,cosa的值().
A.小于 B.大于 C.大于 D.大于1
8.在△ABC中,三边之比为a:b:c=1: :2,则sinA+tanA等于()A
A
二、填空题.
1.设α、β均为锐角,且sinα-cosβ=0,则α+β=_______.
2.. 的值是_______.
人教版九年级数学下册28.1锐角三角函数特殊角的三角函数值优秀教学案例

(一)知识与技能
1.让学生掌握特殊角的三角函数值,包括30°、45°、60°等角的正弦、余弦和正切值。
2.使学生能够运用特殊角的三角函数值进行简化解题,提高问题解决能力。
3.培养学生运用数学知识描述现实生活中的现象,提高数学应用能力。
在教学过程中,我将以生活实例为导入,引导学生主动探究特殊角的三角函数值。通过多媒体课件的展示,让学生直观地理解特殊角的三角函数值,并在实际问题中运用。此外,我将设计具有挑战性的问题,激发学生的思考,培养学生的创新思维和问题解决能力。
3.培养学生勇于挑战、克服困难的勇气,培养他们的自信心和自尊心。
在教学过程中,我将关注学生的情感需求,以鼓励、表扬等方式激励学生,让他们在学习中感受到成功的喜悦。同时,我将引导学生认识到数学在现实生活中的重要性,培养他们的责任感和使命感。
三、教学策略
(一)情景创设
1.生活实例导入:以实际生活中的问题为导入,引发学生对特殊角的三角函数值的兴趣,激发学生的学习动机。
人教版九年级数学下册28.1锐角三角函数特殊角的三角函数值优秀教学案例
一、案例背景
本节课是人教版九年级数学下册28.1锐角三角函数特殊角的三角函数值。在学习了锐角三角函数的基础上,本节课主要让学生掌握特殊角的三角函数值,进一步深化对锐角三角函数的理解和运用。
在案例背景中,学生已经掌握了锐角三角函数的定义和基本性质,具备了一定的数学思维能力和问题解决能力。然而,对于特殊角的三角函数值,学生可能存在一定的困难,需要通过本节课的学习,进一步巩固和提高。
(四)反思与评价
1.自我反思:让学生在学习过程中进行自我反思,发现自己的不足之处,明确改进方向。
2.同伴评价:学生相互评价,给予意见和建议,共同促进彼此的进步。
新人教版九年级数学下册《28章 锐角三角函数 28.1特殊角的三角函数值及用计算器求角的三角函数值》教案_7

28.1 锐角三角函数 第3课时 特殊角的三角函数值学习目标1. 重点:运用三角函数的知识,自主探索,推导出30°、 45°、60°角的三角函数值.2. 难点:熟记三个特殊锐角的三角函数值,并能准确地加以运用.导学过程一、情境导入问题1:一个直角三角形中,一个锐角的正弦、余弦、正切值是怎么定义的? sin ∠A= cos ∠A= tan ∠A= 变式训练:1.说出角B 的三角函数. sin ∠B= cos ∠B= tan ∠B=2. 互余的两角之间的三角函数关系:若∠A +∠B =90°,则sin A cos B ,cos A sin B , tan A · tan B = . 考点小测1.如果把一个直角三角形的各边长都扩大为原来的3 倍,那么它的各锐角的余弦值( ) A .扩大为原来的3倍 B .缩小为原来的 C .不变D .以上都不对2.(2018·孝感)如图,在Rt △ABC 中, ∠C =90°, AB =10,AC =8,则sin A 等于( ) A .35 B .45 C .34 D .433.(2016·广东)如图,在平面 直角坐标系中,点A 的坐标为(4,3),那么cos α的值是( )A .34B .43C .35D .454.(2015·丽水)如图,点A 为∠α边上的任意一点,过点A 作AC ⊥BC 于点C ,过点C 作CD⊥AB 于点D ,下列用线段比表示cos α的值,错误的是( )A .BD BCB .BC ABC .AD AC D .CD AC二、合作探究1.cos 3023322︒(天津中考)的值等于( )A.B. C.1 D.2.(2018.1322︒大庆中考)2cos60等于( )A.1B.C.D.问题2:两块三角尺中有几个不同的锐角?各是多少度?设每个三角尺较短的边长为1,分别求出这几个锐角的正弦值、余弦值和正切值.思考:30°角的三角函数值分别是多少?思考:60°角的三角函数值分别是多少?思考:45°角的三角函数值分别是多少? 归纳结果 30° 45° 60° siaA cosA tanA三、讲授新课例3:求下列各式的值.(1)cos 260°+sin 260°. (2)cos 45sin 45︒︒-tan45°.练习:23.(60cos 60tan 45_____︒+︒-︒=大庆中考)计算:sin4.求下列各式的值:(1)1-2 sin30°cos30°(2)3tan30° - tan45°+2sin60°(3) 三、讲授新课41()906,3,. (2) (2) AO OB AO=3OB .Rt ABC C AB BC A α∆∠=︒=∠例()如图1,在中,,求的度数如图,是圆锥的高,是底面半径,,求的度数()()=︒30sin ()()=︒30cos ()()()()==︒30tan ()()=︒60sin ()()=︒60cos ()()____60tan ==︒()()()()==︒45sin ()()()()==︒45cos ()()____45tan ==︒︒︒︒⨯+60tan )30sin 30(cos 224.(2018.,2tan 1,sin ,ABC A B A B ABC ∆∠∠==∆南关校级一模)在中,都是锐角,对最确切的判断是( )A.等腰三角形 B.等腰直角三角形C.直角三角形 D.锐角三角形2.90721.Rt ABC C BC AC A B ∆∠=︒==∠∠在中,,,,求,的度数 练习:5.(2014·本溪)在△ABC 中,∠B =45°,cos A =12,则∠C 的度数是________.216.sin (tan 1)02________αβαβαβ-+-=+=(酒泉中考)已知,均为锐角,且满足 则度四、强化训练五、知识梳理(1)特殊角的三角函数值:30° 45° 60° sin α 12 22 32 cos α 32 22 12 tan α3313(2)若角α为锐角,则随角α的增大,正弦(sin α) ______, 余弦(cos α) ______,正切(tan α) ______. (3)若角α为锐角,则_____<sin α <______, _____>cos α >_____ , tan α >_____. 重难点突破策略(1)锐角三角函数的基本计算和求锐角大小,准确记忆特殊角的三角函数值是关键.(2)解决与三角函数有关的问题需要有基本图形------直角三角形。
(初三数学教案)人教版初中九年级数学下册第28章锐角三角函数28.1 锐角三角函数第1课时教学设计

28.1 锐角三角函数第1课时一、教学目标【知识与技能】1.理解锐角正弦的概念,掌握正弦的表示方法;2.会根据直角三角形的边长求一个锐角的正弦值,并且能利用正弦求直角三角形的边长。
【过程与方法】1.经历探索直角三角形中的边与角的关系,培养学生由特殊到一般的演绎推理能力。
2.通过学生自我发现培养学生的自我反思能力,通过提出困惑提升学生发现问题的能力。
【情感态度与价值观】1.在主动参与探索概念的过程中,开展学生的合情推理能力和合作交流、探究发现的意识。
2.培养学生独立思考的习惯以及使学生获得成功的体验,建立自信心。
二、课型新授课三、课时第1课时共4课时四、教学重难点【教学重点】理解正弦函数意义,并会求直角三角形中一个锐角的正弦值。
【教学难点】理解当直角三角形的锐角固定时,它的对边与斜边的比值都固定这一事实.五、课前准备教师:课件、三角尺、直尺等.学生:三角尺、铅笔.六、教学过程(一)导入新课(出示课件2)美国人体工程研究学人员调查发现,当高跟鞋的鞋底与地面的夹角为11°左右时,人脚的感觉最舒适,假设某成年人前脚掌到脚后跟长为15厘米,请问鞋跟在几厘米高度为最佳?(二)探索新知为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?(出示课件4)教师问:如右图所示,本题可看作是在三角形ABC 中探求某些问题,你可以把已知条件用数学语言描述出来吗?(学生思考后,找同学回答)学生答:这个问题可以归结为,在Rt △ABC 中,∠C=90°,∠A =30°,BC =35m ,求AB.教师问:可以用学过的什么数学知识来解决这个问题?学生答:根据“直角三角形中,30°角所对的直角边是斜边的一半”来解决.师生一起解答:根据“直角三角形中,30°角所对的直角边是斜边的一半”,即∠A 的对边斜边=BC AB =12,可得AB =2BC =70m ,也就是说,需要准备70m 长的水管.教师问:类比上面的问题,如果使出水口的高度为50 m ,如图所示,那么需要准备多长的水管?(出示课件5)学生讨论后作答:∠A 的对边斜边=B′C′AB′=12,AB ′=2B ′C ′=2×50=100m所以需要准备100m 长的水管.教师问:对于有一个锐角为30°的任意直角三角形,30°角的对边与斜边有怎样的数量关系?可以用一个怎样的式子表示呢?学生回答:30°角的对边是斜边的2倍,∠A 的对边斜边=12。
人教版九年级数学下第28章28.1《锐角三角函数》优秀教学案例

四、教学评价
1.评价学生的知识掌握程度:通过课堂提问、作业批改等方式,了解学生对锐角三角函数知识的掌握情况;
2.评价学生的实践操作能力:通过实际问题解决,评价学生运用锐角三角函数解决实际问题的能力;
3.评价学生的合作交流能力:通过小组讨论、互动交流等方式,评价学生在团队合作中的表现;
3.讲练结合:在课堂中及时进行练习,巩固所学知识,提高学生的实际操作能力;
4.反馈调整:根据学生的学习情况,及时调整教学方法,以提高教学效果。
五、教学过程
1.创设情境,引入新课:通过生活实例,引导学生思考并引入锐角三角函数的概念;
2.自主探究,小组合作:让学生在小组内讨论交流,共同探究锐角三角函数的定义及应用;
(三)情感态度与价值观
1.培养学生对数学学科的兴趣和热爱,激发学生学习数学的内在动力;
2.培养学生合作交流的意识,提高学生团队协作的能力;
3.让学生感受数学与生活的紧密联系,培养学生的应用意识;
4.通过对本节课的学习,使学生树立正确的数学学习观念,相信自己通过努力可以掌握并运用好数学知识。
三、教学重难点
4.评价学生的情感态度与价值观:通过观察学生的学习态度、课堂表现等,评价学生对数学学科的兴趣和热爱。
五、教学拓展
1.利用多媒体技术,展示锐角三角函数在实际生活中的应用,激发学生的学习兴趣;
2.推荐相关的数学读物和网站,让学生课后进行拓展学习,提高学生的数学素养;
3.结合学校或社区的活动,让学生运用所学知识解决实际问题,提高学生的实践能力。
六、教学反思
在教学过程中,教师应不断反思自己的教学方法、教学内容等方面,以确保教学的质量和效果。同时,关注学生的学习反馈,根据学生的需求调整教学策略,以提高教学效果。通过不断的反思和调整,使教学更加符合学生的实际情况,提高学生的数学素养。
教与学 新教案九年级数学下册 28.1 锐角三角函数(第2课时)教学设计 (新版)新人教版-(新版)
锐角三角函数(续表)(续表)(续表)【学习目标】1.掌握余弦、正切的概念;能较正确地用sin A 、cos A 、tan A 表示直角三角形中两边长的比. 2.能够综合运用sin A 、cos A 、tan A 解决简单的实际问题. 【学习重点】理解余弦、正切的概念. 【学习难点】熟练运用锐角三角函数的概念进行有关计算. 一、自学提纲1.我们是怎样定义直角三角形中一个锐角的正弦的?2.在Rt △ABC 中,∠ACB =90°,AC =1,AB =2,那么sin ∠ABC =2. 3.如图28-1-52,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D .已知AC =5,BC =2,那么sin ∠ACD =( A )图28-1-52A .53B .23C .2 55D .524.(1)如图28-1-53,已知AB 是⊙O 的直径,点C 、D 在⊙O 上,且AB =5,BC sin ∠BAC =__35__;sin ∠ADC =__45__;图28-1-53 图28-1-54(2)如图28-1-54,在Rt △ABC 中,∠C =90°,当锐角A 确定时,∠A 的对边与斜边的比是__正切__, 二、合作交流如图28-1-55,Rt △ABC 与Rt △A ′B ′C ′中,∠C =∠C ′=90°,∠B =∠B ′=α,图28-1-55 那么BC AB 与B ′C ′A ′B ′有什么关系?AC AB 与A ′C ′A ′B ′有什么关系?BC AC 与B ′C ′A ′C ′有什么关系?例1 在Rt △ABC 中,∠C =90°,AC =6,BC =8, 求sin A, cos A ,tan B 的值.例2 如图28-1-56,在Rt △ABC 中,∠C =90°,BC =6,sin A =35,求cos A ,tan B 的值.图28-1-56 四、学生展示1.在Rt △ABC 中,∠C =90°,a ,b ,c 分别是∠A 、∠B 、∠C 的对边,a =3,b =4,则cosA =__45__,tanB =__43__.(提高:如把条件中∠C =90°去掉,你会求吗?)2. 在Rt △ABC 中,∠C =90°,如果cos A =45,那么tan B 的值为( D )A .35B .54C .34D .433.如图28-1-57,P 是∠α的边OA 上的一点,且点P 的坐标为(3,4),则cos α= __35__.图28-1-57 课后作业:1.在Rt △ABC 中,∠C =90°,a =2,b =3,则cos A =13,sin B =13,tan B=__32__.2.已知∠α是锐角,tan α=512,则sin α=__513__.3.Rt △ABC 的面积为24 cm 2,直角边AB 为6 cm ,∠A 是锐角,则cos A =__35__.4.等腰三角形底边长10 cm ,周长为36 cm ,则一底角的正切值为__125__.5.在Rt △ABC 中,锐角A 的邻边和斜边同时扩大100倍,则tan A 的值( C )A .扩大100倍B .缩小100倍C .不变D .不能确定6.在Rt △ABC 中,∠C =90°,若tan A =34,则sin A =( C )A .43B .34C .53D .357.如图28-1-58,在△ABC 中,∠C =90°,AC =8 cm ,AB 的垂直平分线MN 交AC 于D ,连接BD .若cos ∠BDC =35,则BC 的长是( A )图28-1-58A .4 cmB .6 cmC .8 cmD .10 cm8.在正方形网格中,△ABC 的位置如图28-1-59所示,则cos B 的值为( B )A .12B .22C .32D .33图28-1-59 标。
人教版九年级下册28.1特殊角的锐角三角函数值优秀教学案例
4.利用多媒体手段,如动画、视频等,形象地展示特殊角的三角函数值的变化规律,增强学生的直观感受。
(二)问题导向
1.设计一系列具有启发性的问题,引导学生思考特殊角三角函数值的意义和作用。
2.引导学生通过实验、观察、讨论等方式,自主探究特殊角三角函数值的规律。
3.提出挑战性的问题,激发学生深入思考,提高学生解决问题的能力。
在实际教学中,我发现许多学生在学习这一部分内容时存在一定的困难,主要是由于对三角函数概念的理解不够深刻,以及对特殊角三角函数值的记忆不牢固。因此,在教学过程中,我需要针对学生的实际情况进行有针对性的教学设计,通过合理的教学方法和手段,帮助学生理解和掌握特殊角的三角函数值,提高他们的学习效果。
二、教学目标
4.采用小组合作学习的方式,培养学生团队合作的精神,提高学生的沟通表达能力。
(三)情感态度与价值观
1.培养学生对数学学科的兴趣,激发学生学习三角函数的内在动机。
2.使学生认识到特殊角三角函数值在实际生活中的应用,提高学生对数学价值的认识。
3.培养学生勇于挑战自我,克服困难的意志,增强学生的自信心。
4.引导学生树立正确的价值观,明白努力学习三角函数的重要性,为今后的学习和生活打下坚实的基础。
4.鼓励学生提出自己的疑问,培养学生敢于质疑、善于思考的良好习惯。
(三)小组合作
1.组织学生进行小组讨论,鼓励学生分享自己的观点和思考,培养学生的团队合作精神。
2.设计小组合作任务,让学生在实践中运用特殊角的三角函数值,提高学生的动手操作能力。
3.采用小组竞赛的方式,激发学生的竞争意识,提高学生的学习积极性。
九年级数学下册28.1锐角三角函数第1课时正弦函数学案无答案新人教版
C B CBC BA 28.1锐角三角函数第1课时 正弦函数目标导航: 【学习目标】⑴经历当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实。
⑵能根据正弦概念正确进行计算 【学习重点】理解正弦(sinA )概念,知道当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实. 【学习难点】当直角三角形的锐角固定时,,它的对边与斜边的比值是固定值的事实。
【导学过程】 一、自学提纲:1、如图在Rt △ABC 中,∠C=90°,∠A=30°,BC=10m ,•求AB2、如图在Rt △ABC 中,∠C=90°,∠A=30°,AB=20m ,•求BC二、合作交流:问题: 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,•在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m ,那么需要准备多长的水管?思考1:如果使出水口的高度为50m ,那么需要准备多长的水管? ; 如果使出水口的高度为a m ,那么需要准备多长的水管? ; 结论:直角三角形中,30°角的对边与斜边的比值 思考2:在Rt △ABC 中,∠C=90°,∠A=45°,∠A 对边与斜边 的比值是一个定值吗?•如果是,是多少?结论:直角三角形中,45°角的对边与斜边的比值 三、教师点拨:从上面这两个问题的结论中可知,•在一个Rt △ABC 中,∠C=90°,当∠A=30°时,∠A的对边与斜边的比都等于12,是一个固定值;•当∠A=45°时,∠A 的对边与斜边的比都等于2,也是一个固定值.这就引发我们产生这样一个疑问:当∠A 取其他一定度数的锐角时,•它的对边与斜边的比是否也是一个固定值?探究:任意画Rt △ABC 和Rt △A ′B ′C ′,使得∠C=∠C ′=90°,斜边c对边abCB(2)1353B A(1)34CBA∠A=∠A ′=a ,那么''''BC B C AB A B 与有什么关系.你能解释一下吗?结论:这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,•∠A 的对边与斜边的比 正弦函数概念:规定:在Rt △BC 中,∠C=90,∠A 的对边记作a ,∠B 的对边记作b ,∠C 的对边记作c .在Rt △BC 中,∠C=90°,我们把锐角A 的对边与斜边的比叫做∠A 的正弦, 记作sinA ,即sinA= =a c . sinA =A aA c∠=∠的对边的斜边 例如,当∠A=30°时,我们有sinA=sin30°=;当∠A=45°时,我们有sinA=sin45°= .四、学生展示:例1 如图,在Rt △ABC 中, ∠C=90°,求sinA 和sinB 的值.随堂练习 (1): 做课本练习.随堂练习 (2):1.三角形在正方形网格纸中的位置如图所示,则sin α的值是﹙ ﹚A .43 B .34 C .53 D .542.如图,在直角△ABC 中,∠C =90o,若AB =5,AC =4,则sinA =( )A .35B .45C .34D .433. 在△ABC 中,∠C=90°,BC=2,sinA=23,则边AC 的长是( )A .13B .3C .43D . 54.如图,已知点P 的坐标是(a ,b ),则sin α等于( )A .ab B .b a CDCB A五、课堂小结:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A•的对边与斜边的比都是.在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A•的,•记作,六、作业设置:课本第68页习题28.1复习巩固第1题、第2题(只做与正弦函数有关的部分).七、自我反思:本节课我的收获: 。
2017年春季学期新版新人教版九年级数学下学期28.1、锐角三角函数教案34
锐角三角函数 28.1 锐角三角函数 第1课时 正弦
素材一 新课导入设计 情景导入 置疑导入 归纳导入 复习导入 类比导入 悬念激趣
情景导入 “神舟十号”载人飞船与“天宫一号”成功实现手控交会对接,对接成功后,将增进人类对太空的了解,解开天宫的神秘面纱.其实,在“神舟十号”发射和对接的过程中,三角函数的测量伴随着航天活动的始终,今天我们就来揭开锐角三角函数的面纱吧!
图28-1-1 [说明与建议] 说明:用学生比较关心的航天活动,吸引学生的注意力,激发他们的好奇心,诱发学生对新知识的渴求. 建议:教师可以根据需要选择航天的精彩图片、对接的某个角度等,配以文字说明,作为情景导入.
置疑导入 如图28-1-2,为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管, 在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35 m,那么需要准备多长的水管?
图28-1-2 思考1:如果使出水口的高度为50 m,那么需要准备多长的水管?__100_m__; 如果使出水口的高度为a m,那么需要准备多长的水管?__2a_m__.
结论:在直角三角形中,30°角的对边与斜边的比值为__12__. 思考2:在Rt△ABC中,∠C=90°,∠A=45°,∠A的对边与斜边的比值是一个定值吗?如果是,是多少?
结论:在直角三角形中,45°角的对边与斜边的比值为__22__. 这就引发我们产生这样一个疑问:当∠A取其他一定度数的锐角时,它的对边与斜边的比值是否也是一个固定值? [说明与建议] 说明:通过对含30°、45°角的直角三角形对边与斜边的比值的探索,激发学生的学习兴趣和探究新知的欲望,引入正弦函数的概念. 建议:教师提出问题后,学生积极思考,让学生回答结果:无论三角形大小如何,30°、45°角的对边与斜边的比值是一个固定的值.学习较好的学生还会想到,以后在这些特殊直角三角形中,只要知道其中一边的长,就可以求出其他未知边的长.
九年级数学下册28.1锐角三角函数第3课时学案新版新人教版06013186【精品教案】
28.1 锐角三角函数(第三课时)【学习目标】1.熟记30°、45°、60°角的各个三角函数值,会计算含有这三个特殊锐角的三角函数值的式子;2.会由一个特殊锐角的三角函数值说出这个角的度数;3.加深学生对锐角三角函数的认识,了解特殊与一般的关系,并对学生进行逆向思维的训练.【重点难点】重点:会计算含有这三个特殊锐角的三角函数值的式子. 难点:会由一个特殊锐角的三角函数值说出这个角的度数. 【新知准备】1.一个直角三角形中,一个锐角正弦是怎么定义的?一个锐角余弦是怎么定义的?一个锐角正切是怎么定义的?2.在Rt △ABC 中,∠C =90°,AC =5,BC =12,求∠B 的锐角三角函数值.【课堂探究】 一、自主探究 探究1请同学们拿出自己的学习工具——一副三角尺,思考并回答下列问题: 1、这两块三角尺各有几个锐角?它们分别等于多少度?2、每块三角尺的三边之间有怎样的特殊关系?如果设每块三角尺较短的边长为1,请 你说出未知边的长度。
探究2二、尝试应用1、求下列各式的值:(1)22cos 60sin 60+; (2) cos 45tan 45sin 45-2:(1)如图(1),在Rt △ABC 中,∠C =90°,ABBCA 的度数. (2)如图(2),已知圆锥的高AO 等于圆锥的底面半径)OBa .三、补偿提高1.在Rt △ABC 中,∠C =90°,BC =7,AC =21,求∠A 、∠B2.求适合下列各式的锐角α.121cos 2)3(;01sin 2)2(;3tan 3)1(=+=-=a a a3..tan )(03cos 2的值,求为锐角已知a a a =-4.如图,△ABC 中,∠C =900,BD 平分∠ABC ,BC =12,BD = 38 ,求∠A 的度数及AD 的长.【学后反思】1.通过本节课的学习你有那些收获?2. 你还有哪些疑惑?ABCDc a A A =∠=斜边的对边sin c b A A =∠=斜边的邻边cos b aA A A =∠∠=的邻边的对边tan ,2263sin ===AB BC A 解.45︒=∠∴A ,33t an ===OB OBOB AO α 解.60︒=∴α28.1 锐角三角函数(第三课时)【新知准备】1、2、125tan ,1312cos ,135sin ===B B B 【课堂探究】二、尝试应用 1.(1)1,(2)0;2.(1)(2)三、补偿提高1. 60,30=∠=∠B A ;2. 60)3(45)2(301===a a a )(;3.33tan =a ; 4.38,30==∠AD A .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角函数
学习 目标: 理解直角三角形中的边角关系
重点: 掌握正弦的定义
难点: 求锐角的正弦
1.理解直角三角形中的边角关系
当直角三角形的一个锐角的大小已确定时,它们 与 的比是一个固定值.
2.掌握正弦的定义
如图,在Rt△ABC中,∠C=90°,我们把锐角A的 与 的比叫
做∠A的正弦,记作sin A,即sin A= = .
重点一:求锐角的正弦
(1)锐角的正弦值是一个比值,没有单位,这个比值只与锐角的大小有关,与边的长短无关.
(2)正弦的定义是在直角三角形中给出的,不能在非直角三角形中随便套用,如果题目给出的角不是在直角
三角形中,应先构造直角三角形再求解.
1.(2013温州)如图,在△ABC中,∠C=90°,AB=5,BC=3,则sin A的值是( )
(A) (B) (C) (D)
2.在平面直角坐标系中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
(A) (B) (C) (D)
3.已知△ABC中,AB=AC=13,BC=10,求∠A、∠B的正弦值.
重点二:正弦的综合运用
锐角的正弦在直角三角形中的应用
(1)已知锐角的正弦及角的对边或斜边时,直接根据定义求斜边或对边,再根据勾股定理求另一边.
(2)若已知锐角的正弦及邻边时,可根据正弦的定义确定另外两边的比值,结合勾股定理列方程求解.
4.(2013杭州)在Rt△ABC中,∠C=90°,若AB=4,sin A=,则斜边上的高等于( )
(A) (B) (C) (D)
5.在Rt△ABC中,∠C=90°,AB=10,sin A=,则S△ABC= .
6.如图,在Rt△ABC中,∠C=90°,sin A=,AB=15,求△ABC的周长.
7.已知BC是☉O的直径,AD⊥BC,若sin∠ACD=,BD=6,求AB.
A层(基础) 1.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( ) (A)不变 (B)缩小为原来的 (C)扩大为原来的3倍 (D)不能确定 2.在Rt△ABC中,∠C=90°,BC=2,sin A=,则边AC的长是( ) (A) (B)3(C) (D) 3.(2013宜宾)如图,已知☉O的半径为1,锐角△ABC内接于☉O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( ) (A)OM的长 (B)2OM的长(C)CD的长 (D)2CD的长 4.如图所示,AB是☉O的弦,半径OA=2,sin A=,则弦AB的长为( ) (A) (B)(C)4 (D) 5.(2013深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点
分别在这三条平行直线上,
则sin α的值是( )
(A) (B) (C) (D)
6.(2013广东)在Rt△ABC中,∠
ABC=90°,AB=3,BC=4,则sin A= .
7.如图所示,△ABC的顶点都在方格纸的格点上,则
sin A= .
8.
(2013南通)如图,在Rt△ABC中,CD是斜边AB上的
中线,已知CD=2,AC=3,则sin B的值是 .
9.在△ABC中,∠C=90°,sin A=,△ABC的周长为
24 cm,求△ABC各边的长.
10.(2013曲靖)如图,点E在正
方形ABCD的边AB上,连接DE,
过点C作CF⊥DE于F,过点A作
AG∥CF交DE于点G.
(1)求证:△DCF≌△ADG;
(2)若点E是AB的中点,设∠DCF=α,求sin α的
值.
