【高一数学学习精品课件】高一人教A版数学必修一课件:2.2.3 对数函数及其性质(一)
高中数学 2.2.1.1对数课件 新人教A版必修1

提示:①a<0,N取某些值时,logaN不存在,如根据指数的运算性质可知,不存在实数x使(-12)x=2成
立,所以log(-
1 2
)2不存在,所以a不能小于0.②a=0,N≠0时,不存在实数x使ax=N,无法定义logaN;N
=0时,任意非零实数x,有ax=N成立,logaN不确定.③a=1,N≠1时,logaN不存在;N=1,loga1有无 数个值,不能确定.
1
30
思考 1 对数恒等式 a logaN=N 成立的条件是什么? 提示:成立的条件是a>0,a≠1且N>0.
思考 2 用 a logaN (a>0 且 a≠1,N>0)化简求值的关键是什么?
提示:用 a logaN (a>0 且 a≠1,N>0)化简求值的关键是凑准公式的结构,尤其是对数的底数和幂底数 要一致,为此要灵活应用幂的运算性质.
思考 根据对数的定义以及对数与指数的关系,你能求出loga1=?logaa=?
提示: ∵对任意a>0且a≠1,都有a0=1, ∴化成对数式为loga1=0; ∵a1=a,∴化成对数式为logaa=1.
1
24
[典例示法] 例3 求下列各式中x的值. (1)logx27=32;(2)log2x=-23; (3)x=log2719;(4)log3(lgx)=1.
题目(1)(2)中的对数式化为指数式是怎样的?题目(3)(4)呢?
3
提示:(1)化为指数式x2
=27,(2)化为指数式2-23
=x,(3)化为指数式27x=19,(4)化为指数式31=lgx.
1
25
[解]
(1)由logx27=32可得x32 =27,
2
对数的运算 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册

=-1.
10
解:
11
2. 用lnx , lny , lnz 表示下列各式:
解:(1) lg(xyz)
=lgx+lgy+lgz.
(2)
=lgx+lgy2–lgz
=lgx+2lgy–lgz.
(1) lg(xyz);
= lg(xy2)–lgz
12
(1)利用计算工具求ln2, ln3的近似值;(2)由对数的定义,你能利用ln2, ln3的值求log23的值吗?(3)根据对数的定义, 你能用logca, logcb表示logab(a>0, 且a≠1; b>0, c>0, 且c≠1)吗?
ax =N logaN = x
5
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
设M=am , N=an,
因为aman=am+n, 所以MN=am+n.
根据指数与对数间的关系可得
logaM=m, logaN=n, loga(MN)=m+n.
3
复习回顾
1. 实数指数幂的运算性质
x = logaN ,
其中a叫做对数的底数,N叫做真数 .
2. 对数的定义
3. 两种特殊的对数
(1) 以10为底的对数叫常用对数, 并把
log10N记作lgN .
(2) 以无理数 e (e=2.71828…)为底的对数叫自然对数, 并把
logeN记作lnN .
(1) aras =ar+s (a>0 , r , s∈R);
解:设里氏9.0级和8.0级地震的能量分别为E1和E2.
由lgE=4.8+1.5M, 可得
对数函数的图像和性质(1)课件高一上学期数学人教A版(完整版)4

点(x, y)与点(x, y)关于x轴对称
y log2 x图像上任意一点 P(x, y)
关于x轴的对称点P1( x, y)都在
函数y log 1 x的图像上,反之亦然.
2
P1(x, -y)
结论:底数互为倒数的两个对数函数的图象关于x轴对称.
根据这种对称性,就可以利用一个函数的图像画出另一个函数的图像.
当0<a<1时 函数y=logax是减函数; 由得
loga5.1 > loga
反思1 根据以上经验,请你说说如何比较比较两个同底对数的大小?
(1)根据底数a的范围判断对应函数y=logax的单调性; (2)比较真数值的大析
例3 比较下列各组中,两个值的大小:
(4) log0.1 3, log0.2 3
解:(1) ∵函数y=log 2 x的底数2大于1
log2
∴y=log 2 x是增函数.
log2
又∵
y
(3)loga5.1, loga5.9.
y log2 x
∴ log23.4< log2
O 1 3.4 8.5 x
(2)∵函数y=log 0.3 x底数0.3<1 ∴y=log 0.3 x 是减函数; 又∵
∴ log 0.3 1.8> log 0.3 2.7
y
1 1.8 2.7
o
x
log
log
y log0.3 x
典例解析
例3 比较下列各组中,两个值的大小:
(1)log23.4, log28.5; (2) log 0.3 1.8, log 0.3 2.7; (3)loga5.1, loga5.9.
解: (3)当a>1时, 函数y=logax是增函数; 由5.1<5.9 得 ∴ loga5.1 < loga5.9
【课件】对数函数的图象和性质(第二课时)课件高一上学期数学人教A版(2019)必修第一册

2
∵函数 y=log0.3t 是减函数,且函数 t=3-2x 是减函数,
3
∞
- ,
∴函数 y=log0.3(3-2x)在
2 上是增函数,
3
-∞,
即函数 y=log0.3(3-2x)的单调递增区间是
2 ,没有单调递减区间.
求复合函数单调性的具体步骤:
(1)求定义域;
(2)拆分函数;
(3)分别求 y=f(u),u=φ(x)的单调性;
0<a<1时,在(0,+∞)是减函数
新知探究
探究一:反函数的含义
新知讲解
问题3 在同一个坐标系中画出指数函数 = 与对数函数 =
的图象,观察它们有什么联系?
概念生成
一般地,指数函数 = ( > 0, 且 ≠ 1)与对数函数 = ( > 0,
3
5
3
5
例题讲解
(3)取中间值 1,
因为 log23>log22=1=log55>log54,
所以 log23>log54.
(4)当 a>1 时,函数 y=logax 在(0,+∞)上是增函数,
又 3.1<5.2,所以 loga3.1<loga5.2;
当 0<a<1 时,函数 y=logax 在(0,+∞)上是减函数,
1
y=log12(2x-1)的减区间为2,+∞.
再思考:
提示:先求 y=f(x)的值域,注意 f(x)>0,在此基础上,分 a>1 和 0<a<1
两种情况,借助 y=logax 的单调性求函数 y=logaf(x)的值域.
高一数学课件:2.4 对数函数及其性质(新人教版必修1)

3
返回
学点三 对数函数的图像 已知a> 且 的图像只能是( 已知 >0且a≠1,函数 ,函数y=ax与y=loga(-x)的图像只能是( ) 的图像只能是 【分析】应先由函数定义域判断图像的位置,再对底 分析】应先由函数定义域判断图像的位置, 进行讨论, 数a进行讨论,最后选出正确选项 进行讨论 最后选出正确选项. 【解析】解法一:首先 曲线 首先,曲线 解析】解法一 首先 曲线y=ax 只可能在上半平面,y=loga(-x)只 只可能在上半平面 只 可能在左半平面上,从而排除 从而排除A,C. 可能在左半平面上 从而排除 其次,从单调性着眼 其次 从单调性着眼,y=ax与 从单调性着眼 y=loga(-x)的增减性正好相反 又 的增减性正好相反,又 的增减性正好相反 可排除D. 可排除 故应选B. 故应选
单调性
当0<x<1时,y∈(0,+∞) 时 ∈ 函数值的 当 x=1 时,y=0; 变化规律 当 x>1 时, y<0.
当x=1时, y=0 ; 时 当x>1时, y>0 . 时
返回
学点一 比较大小 比较大小: 比较大小:
4 6 log 1 ,log 1 ; (1) ) 2 5 2 7
2) (2) 1 3, log 1 5 ; log
) (2) y = log 2 2 ) . - x + 2x + 2 (1)∵x2-4x+6=(x-2)2+2≥2,又∵y=log2x在(0,+∞)上是增 ∵ 又 在 上是增 函数, 函数
(x2-4x+6);
∴log2(x2-4x+6)≥log22=1. ∴函数的值域是[1,+∞). 函数的值域是[ (2) ∵-x2+2x+2=-(x-1)2+3≤3, 1 1 ∴ - x 2 + 2x + 2 <0或 - x 2 + 2x + 2 ≥ 1 . 或 1 3 1 ≥ log 2 ∴ 2 log - x + 2x + 2 1 3 ∴函数的值域是 log 2 ,+∞ ,
高中数学 第二章 指数函数、对数函数和幂函数 2.2.3 对数函数的图象和性质 第1课时 反函数及对
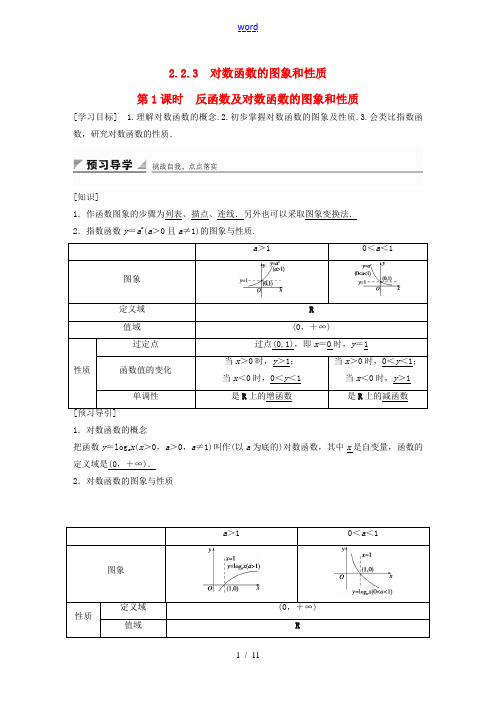
2.2.3 对数函数的图象和性质第1课时反函数及对数函数的图象和性质[学习目标] 1.理解对数函数的概念.2.初步掌握对数函数的图象及性质.3.会类比指数函数,研究对数函数的性质.[知识]1.作函数图象的步骤为列表、描点、连线.另外也可以采取图象变换法.2.指数函数y=a x(a>0且a≠1)的图象与性质.a>10<a<1 图象定义域R值域(0,+∞)性质过定点过点(0,1),即x=0时,y=1函数值的变化当x>0时,y>1;当x<0时,0<y<1当x>0时,0<y<1;当x<0时,y>1 单调性是R上的增函数是R上的减函数[预习导引]1.对数函数的概念把函数y=log a x(x>0,a>0,a≠1)叫作(以a为底的)对数函数,其中x是自变量,函数的定义域是(0,+∞).2.对数函数的图象与性质a>10<a<1 图象性质定义域(0,+∞)值域R过点过点(1,0),即x=1时,y=0函数值的变化当0<x<1时,y<0;当x>1时,y>0当0<x<1时,y>0;当x>1时,y<0单调性是(0,+∞)上的增函数是(0,+∞)上的减函数3.反函数(1)对数函数y=log a x(a>0且a≠1)与指数函数y=a x(a>0,且a≠1)互为反函数.(2)要寻找函数y=f(x)的反函数,可以先把x和y换位,写成x=f(y),再把y解出来,表示成y=g(x)的形式,如果这种形式是唯一确定的,就得到f(x)的反函数g(x).要点一对数函数的概念例1 指出下列函数哪些是对数函数?(1)y=3log2x;(2)y=log6x;(3)y=log x3;(4)y=log2x+1.解(1)log2x的系数是3,不是1,不是对数函数.(2)符合对数函数的结构形式,是对数函数.(3)自变量在底数位置上,不是对数函数.(4)对数式log2x后又加1,不是对数函数.规律方法判断一个函数是对数函数必须是形如y=log a x(a>0且a≠1)的形式,即必须满足以下条件(1)系数为1.(2)底数为大于0且不等于1的常数.(3)对数的真数仅有自变量x.跟踪演练1 若某对数函数的图象过点(4,2),则该对数函数的解析式为( )A.y=log2x B.y=2log4xC.y=log2x或y=2log4x D.不确定答案 A解析设对数函数的解析式为y=log a x(a>0且a≠1),由题意可知log a4=2,∴a2=4,∴a =2,∴该对数函数的解析式为y=log2x.要点二对数函数的图象例2 如图所示,曲线是对数函数y =log a x 的图象,已知a 取3,43,35、110,则相应于c 1、c 2、c 3、c 4的a 值依次为( )A.3、43、35、110B.3、43、110、35C.43、3、35、110D.43、3、110、35 答案 A解析 方法一 先排c 1、c 2底的顺序,底都大于1,当x >1时图低的底大,c 1、c 2对应的a 分别为3、43.然后考虑c 3、c 4底的顺序,底都小于1,当x <1时底大的图高,c 3、c 4对应的a 分别为35、110.综合以上分析,可得c 1、c 2、c 3、c 4的a 值依次为3、43、35、110.故选A.方法二 作直线y =1与四条曲线交于四点,由y =log a x =1,得x =a (即交点的横坐标等于底数),所以横坐标小的底数小,所以c 1、c 2、c 3、c 4对应的a 值分别为3、43、35、110,故选A.规律方法 函数y =log a x (a >0且a ≠1)的底数变化对图象位置的影响.观察图象,注意变化规律:(1)上下比较:在直线x =1的右侧,a >1时,a 越大,图象向右越靠近x 轴,0<a <1时a越小,图象向右越靠近x 轴.(2)左右比较:比较图象与y =1的交点,交点的横坐标越大,对应的对数函数的底数越大. 跟踪演练2 (1)函数y =log a (x +2)+1的图象过定点( ) A .(1,2) B .(2,1) C .(-2,1) D .(-1,1)(2)如图,若C 1,C 2分别为函数y =log a x 和y =log b x 的图象,则( )A .0<a <b <1B .0<b <a <1C .a >b >1D .b >a >1 答案 (1)D (2)B解析 (1)令x +2=1,即x =-1, 得y =log a 1+1=1,故函数y =log a (x +2)+1的图象过定点(-1,1).(2)作直线y =1,则直线与C 1,C 2的交点的横坐标分别为a ,b ,易知0<b <a <1. 要点三 对数函数的定义域例3 (1)函数f (x )=11-x +lg(1+x )的定义域是( )A .(-∞,-1)B .(1,+∞)C .(-1,1)∪(1,+∞) D.(-∞,+∞) (2)若f (x )=121log (21)x +,则f (x )的定义域为( )A.⎝ ⎛⎭⎪⎫-12,0B.⎝ ⎛⎭⎪⎫-12,+∞ C.⎝ ⎛⎭⎪⎫-12,0∪(0,+∞) D.⎝ ⎛⎭⎪⎫-12,2 答案 (1)C (2)C解析 (1)由题意知⎩⎪⎨⎪⎧1+x >0,1-x ≠0,解得x >-1且x ≠1.(2)由题意有⎩⎪⎨⎪⎧2x +1>0,2x +1≠1,解得x >-12且x ≠0.规律方法 求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数;三是按底数的取值应用单调性,有针对性地解不等式. 跟踪演练3 (1)函数y =x ln(1-x )的定义域为( ) A .(0,1) B .[0,1) C .(0,1] D .[0,1] (2)函数y =lgx +1x -1的定义域是( )A .(-1,+∞) B.[-1,+∞)C .(-1,1)∪(1,+∞) D.[-1,1)∪(1,+∞) 答案 (1)B (2)C解析 (1)因为y =x ln(1-x ),所以⎩⎪⎨⎪⎧x ≥0,1-x >0,解得0≤x <1.(2)要使函数有意义,需⎩⎪⎨⎪⎧x +1>0,x -1≠0,解得x >-1且x ≠1,故函数的定义域为(-1,1)∪(1,+∞),故选C. 要点四 反函数例4 求下列函数的反函数:(1)y =2x -5;(2)y =x1-x ;(3)y =1+e 2x . 解 (1)从x =2y -5中解得y =x +52,即为所求;(2)从x =y 1-y 中解得y =xx +1,即为所求;(3)从x =1+e 2y 移项得x -1=e 2y .两端取自然对数得到ln(x -1)=y2,解得y =2ln(x -1),即为所求.规律方法 要找寻函数y =f (x )的反函数,可以先把x 和y 换位,写成x =f (y ),再把y 解出来,表示成y =g (x )的形式.如果这种形式是唯一确定的,就得到了f (x )的反函数g (x ).既然y =g (x )是从x =f (y )解出来的,必有f (g (x ))=x ,这个等式也可以作为反函数的定义. 跟踪演练4 y =ln x 的反函数是________. 答案 y =e x解析 由y =ln x ,得x =e y ,所以反函数为y =e x.1.下列函数是对数函数的是( ) A .y =log a (2x ) B .y =log 22xC .y =log 2x +1D .y =lg x 答案 D解析 选项A 、B 、C 中的函数都不具有“y =log a x (a >0且a ≠1)”的形式,只有D 选项符合. 2.函数f (x )=11-x +lg(3x +1)的定义域是( )A .(-13,+∞) B.(-∞,-13)C .(-13,13)D .(-13,1)答案 D解析 由⎩⎪⎨⎪⎧1-x >0,3x +1>0,可得-13<x <1.3.函数y =a x与y =-log a x (a >0,且a ≠1)在同一坐标系中的图象形状可能是( )答案 A解析 函数y =-log a x 恒过定点(1,0),排除B 项; 当a >1时,y =a x是增函数,y =-log a x 是减函数,排除C 项,当0<a <1时,y =a x是减函数,y =-log a x 是增函数,排除D 项,A 项正确.4.若a >0且a ≠1,则函数y =log a (x -1)+1的图象恒过定点________. 答案 (2,1)解析 函数图象过定点,则与a 无关, 故log a (x -1)=0,所以x -1=1,x =2,y =1, 所以y =log a (x -1)+1过定点(2,1). 5.函数y =lg x 的反函数是________. 答案 y =10x解析 由反函数的定义知x =10y,故反函数为y =10x.1.判断一个函数是不是对数函数关键是分析所给函数是否具有y =log a x (a >0且a ≠1)这种形式.2.在对数函数y =log a x 中,底数a 对其图象直接产生影响,学会以分类的观点认识和掌握对数函数的图象和性质.3.涉及对数函数定义域的问题,常从真数和底数两个角度分析.一、基础达标1.函数y =log a x 的图象如图所示,则a 的值可以是( )A .0.5B .2C .eD .π 答案 A解析 ∵函数y =log a x 的图象单调递减,∴0<a <1,只有选项A 符合题意. 2.函数f (x )=lg(x -1)+4-x 的定义域为( ) A .(1,4] B .(1,4) C .[1,4] D .[1,4) 答案 A解析 由⎩⎪⎨⎪⎧x -1>0,4-x ≥0,解得1<x ≤4.3.在同一坐标系中,函数y =log 3x 与y =13log x 的图象之间的关系是( )A .关于y 轴对称B .关于x 轴对称C .关于原点对称D .关于直线y =x 对称 答案 B解析 ∵y =13log x =-log 3x ,∴函数y =log 3x 与y =13log x 的图象关于x 轴对称.4.如图是三个对数函数的图象,则a 、b 、c 的大小关系是( )A .a >b >cB .c >b >aC .c >a >bD .a >c >b 答案 D解析 y =log a x 的图象在(0,+∞)上是上升的,所以底数a >1,函数y =log b x ,y =log c x 的图象在(0,+∞)上都是下降的,因此b ,c ∈(0,1),又易知c >b ,故a >c >b .5.已知函数f (x )=⎩⎪⎨⎪⎧3x, x ≤0,log 2x ,x >0,那么f (f (18))的值为( )A .27 B.127C .-27 D .-127答案 B解析 f (18)=log 218=log 22-3=-3,f (f (18))=f (-3)=3-3=127.6.已知对数函数f (x )的图象过点(8,-3),则f (22)=________. 答案 -32解析 设f (x )=log a x (a >0,且a ≠1), 则-3=log a 8,∴a =12.∴f (x )=log 12x ,f (22)=log 12(22)=-log 2(22)=-32.7.求下列函数的定义域: (1)f (x )=lg(x -2)+1x -3; (2)f (x )=log (x +1)(16-4x ).解 (1)要使函数有意义,需满足⎩⎪⎨⎪⎧x -2>0,x -3≠0,解之得x >2且x ≠3.∴函数定义域为(2,3)∪(3,+∞). (2)要使函数有意义,需满足⎩⎪⎨⎪⎧16-4x >0,x +1>0,x +1≠1,解之得-1<x <0或0<x <4. ∴函数定义域为(-1,0)∪(0,4). 二、能力提升8.设函数f (x )=log 2x 的反函数为y =g (x ),且g (a )=14,则a 等于( )A .2B .-2 C.12 D .-12答案 B解析 ∵函数f (x )=log 2x 的反函数为y =2x,即g (x )=2x. 又∵g (a )=14,∴2a=14,∴a =-2.9.若函数f (x )=log a (x +b )的图象如图,其中a ,b 为常数,则函数g (x )=a x+b 的图象大致是( )答案 D解析 由函数f (x )=log a (x +b )的图象可知,函数f (x )=log a (x +b )在(-b ,+∞)上是减函数.所以0<a <1且0<b <1.所以g (x )=a x+b 在R 上是减函数,故排除A ,B.由g (x )的值域为(b ,+∞).所以g (x )=a x+b 的图象应在直线y =b 的上方,故排除C. 10.若log 2a 1+a21+a<0,则a 的取值X 围是____________.答案 ⎝ ⎛⎭⎪⎫12,1解析 当2a >1时,∵log 2a 1+a21+a <0=log 2a 1,∴1+a 21+a <1.∵1+a >0,∴1+a 2<1+a , ∴a 2-a <0,∴0<a <1,∴12<a <1.当0<2a <1时,∵log 2a 1+a21+a <0=log 2a 1,∴1+a 21+a >1.∵1+a >0,∴1+a 2>1+a , ∴a 2-a >0,∴a <0或a >1,此时不合题意.综上所述,a ∈⎝ ⎛⎭⎪⎫12,1. 11.已知f (x )=log 3x . (1)作出这个函数的图象;(2)若f (a )<f (2),利用图象求a 的取值X 围. 解 (1)作出函数y =log 3x 的图象如图所示.(2)令f (x )=f (2),即log 3x =log 32,解得x =2.由图象知:函数f (x )为单调增函数,当0<a <2时,恒有f (a )<f (2).∴所求a 的取值X 围为(0,2). 三、探究与创新12.求y =(log 12x )2-12log 12x +5在区间[2,4]上的最大值和最小值.解 因为2≤x ≤4,所以log 122≥log 12x ≥log 124,即-1≥log 12x ≥-2.设t =log 12x ,则-2≤t ≤-1,所以y =t 2-12t +5,其图象的对称轴为直线t =14,所以当t =-2时,y max =10;当t =-1时,y min =132.13.若函数f (x )为定义在R 上的奇函数,且x ∈(0,+∞)时,f (x )=lg(x +1),求f (x )的word 11 / 11 表达式,并画出大致图象.解 ∵f (x )为R 上的奇函数,∴f (0)=0. 又当x ∈(-∞,0)时,-x ∈(0,+∞), ∴f (-x )=lg(1-x ).又f (-x )=-f (x ),∴f (x )=-lg(1-x ),∴f (x )的解析式为f (x )=⎩⎪⎨⎪⎧lg x +1,x >0,0,x =0,-lg 1-x ,x <0,∴f (x )的大致图象如图所示:。
高中数学第二章基本初等函数(Ⅰ)2.2对数函数2.2.2对数函数及其性质课件1新人教A必修1
[答案] A [解析] ∵函数y=logax的图象一直上升, ∴函数y=logax为单调增函数,∴a>1,故选A.
3.下列函数中是对数函数的是 ( A.y=log1 x
4 4
)
B.y=log1 (x+1) D.y=log1 x+1
4
C.y=2· log1 x
4
[答案] A
[解析] 形如y=logax(a>0,且a≠1)的函数才是对数函数,
[规律总结] 对于对数概念要注意以下两点:
(1)在函数的定义中,a>0且a≠1. (2)在解析式y=logax中,logax的系数必须为1,真数必须为x, 底数a必须是大于0且不等于1的常数.
跟踪练习
指出下列函数中,哪些是对数函数? ①y=5x;②y=-log3x;③y=log0.5 x;④y=log3 x;⑤y
预习自测
1.下列函数是对数函数的是 ( A.y=2+log3x B.y=loga(2a)(a>0,且 a≠1) C.y=logax2(a>0,且 a≠1) D.y=lnx )
[答案] D
[解析] 判断一个函数是否为对数函数,其关键是看其是
否具有“y=logax”的形式,A,B,C全错,D正确.
2. 函数 y=logax 的图象如图所示, 则实数 a 的可能取值为 ( ) A.5 1 B.5 1 C.e 1 D.2
2.对数函数的图象和性质 一般地,对数函数y=logax(a>0,且a≠1)的图象和性质如下表 所示:
a>1
0<a<1
图象
a> 1
0<a<1
,+∞) 定义域:(0 ______ R 值域:______
性质
(1,0) ,即当 x=1 时,y=0 图象过定点______ 增函数 在(0,+∞)上是______ 减函数 在(0,+∞)上是______
人教A版高中数学必修1《二章 基本初等函数 2.2 对数函数 互为反函数的两个函数图象之间的关系》示范课件_3
的值.
点评:
利用互反函数的图象关于 直线y=x对称.
2019/10/20
作业: P75 习题2.2B组:1,4,5.
2019/10/20
y=x对称.
方法:
结合这个函数的单
在PQ((m函n,,mn数)),y也证=f在明(x函P)的关数图于y调在=象直f性反(上x线数)可函任的y是=以数取图它x的说,一象自对明 且点上己称它 反.. 点存 函
举例:(1)y=x+c,
(2)y=kx-1.
2019/10/20
例3 若点P(1,2)同时在函数y=
图象上任意一点,点Q(n,m)在哪
个函数的图象上?
将点P的坐标代入y=logax得:
n=logam 化成指数式 m=an
所以,点Q(n,m)在函数y=ax的
图像上.
2019/10/20
探究3:点P(m,n)与点Q(n,m)有怎样 的位置关系?由此说明对数函数y=logax
的图象与指数函数y=ax的图象有怎样
2019/10/20
探究(二):反函数的存在性
问题1:在函数y=x2中,若将y作自变量, 那么x与y的对应关系是函数吗?为什 么?
对比: 下列函数哪些存在反函数:
(1)y=x2(x>0);
(2)y=x2(x<-2);
(3)y=x2(x>-2);
2019/10/20
(4)y=x3(x∈R).
探究(二):反函数的存在性 问题2:一个函数在其对应形式上有一 对一和多对一两种,那么在哪种对应 下的函数才存在反函数? 结论:
探究(一):反函数的概念 一般地,由函数y=f(x)解得x=f-1(y), 且x是y的函数(即对于每一个y值,都 有唯一的x与之对应),那么,我们把 函数x=f-1(y)叫做函数y=f(x)的反函数.
对数函数的概念课件-2024-2025学年高一上学期数学人教A版(2019)必修第一册
解析:AC 由题意可知, − 2 ≠ 1, 即 ≠ 3, 因此2<a<5且a≠3.故选A、C.
5 − > 0,
< 5,
目录
7.函数f(x)=(m-1)logax(a>0,且a≠1)是对数函数,且过点(4,2),则f(m)
=
.
解析:由题意m=2.又2=log a 4,故a=2,因此f(x)=log 2 x.所以f(m)=f(2)=
.
解析:因为y=lg(x2+2x+a)的定义域为R,所以x2+2x+a>0恒成立,所以Δ=44a<0,所以a>1.故实数a的取值范围是(1,+∞).
答案:(1,+∞)
目录
14.设函数f(x)=lg
8 +4 +·2
,a∈R,若当x∈(-∞,1)时,f(x)都有意义,求实数a
2
的取值范围.
解:f(x)=lg
− 2 ≠ 1,
≠ 3,
函数的定义域为(2,3)∪(3,5).
答案:(2,3)∪(3,5)
目录
题型三
对数型函数的实际应用
【例3】 某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万
元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超出A万元,则超
出部分按2log5(A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万
4
= .故选D.
3
目录
3.若f(x)=logax+(a2-4a-5)是对数函数,则a=
.
2 − 4 − 5 = 0,
解析:由对数函数的定义可知, > 0,
≠ 1,
解得a=5.
答案:5
目录
4.求下列函数的定义域:
人教A版高中数学必修1.2对数函数及其性质优秀课件
复习
1、指数、对数的互化关系:
ab N log a N b
2、指数函数的图象与性质:
复习
2、指数函数的图象与性质:
a>1
y=ax y
图 a>1
象
1
x
o
性 1、定义域: R
2、值域: (0,)
0<a<1
y=axy
0<a<1
1 x
o
质 3、定点: (0,1)
在R上是增函数 在R上是减函数
1、分组用描点法画出对数函数 的图象。
作图步骤: ①列表, ②描点, ③连接。
(1)作y=log2x图象
列X 表 y=log2x
…1 1
42
… -2 -1
1 0
2 1
4… 2…
y
描2 点
y=log2x
1 11
42
连
0 1 23 4
x
线 -1
-2
(2)作 y log 1 x 的图象
列
x
2
… 1/4 1/2 1
人 教 A 版 高中 数学必 修1 . 2 对数函 数及其 性质优 秀课件
【提升总结】
由具体函数式求定义域,考虑以下几个方面: (1)分母不等于0; (2)偶次方根被开方数非负; (3)零指数幂底数不为0; (4)对数式考虑真数大于0; (5)实际问题要有实际意义.
人 教 A 版 高中 数学必 修1 . 2 对数函 数及其 性质优 秀课件
解 : 由 x2 0 得 x 0
∴函数 y log a x 2 的定义域是 x | x 0
(2) y log a (4 x)
解 : 由 4x 0 得 x4
