线性系统的根轨迹法(1-2)
零度根轨迹非最小相位系统

问题。由于它是一种图解求根的方法,比较直观,避免了求解高阶系统
特征根的麻烦,所以,根轨迹法在工程实践中获得了广泛的应用。 采用根轨迹法分析和设计系统,必须绘制出根轨迹图。用数学解析
法去逐个求出闭环特征方程的根再绘制根轨迹图,十分困难且没有意义。
重要的是找到一些规律,以便根据开环传递函数与闭环传递函数的关系 以及开环传递函数零点和极点的分布,迅速绘出闭环系统的根轨迹。这 种作图方法的基础就是根轨迹方程。
第四章 根轨迹法
二、根轨迹方程
[例] 闭环传递函数为
( s) G(s) 1 G( s) H ( s)
R( s )
G( s) H ( s)
C ( s)
闭环特征方程是 1 G(s) H (s) 0
根轨迹增益
就其实质来说,根轨迹方程就是闭环的特征方程式 系统开环 传递函数 开环传递函数化成如下形式: 零点 m
K ( s z1 )(s z 2 ) ( s z m ) G( s) H ( s) ( s p1 )(s p 2 ) ( s p n )
K (s zi )
i 1
(s p
j 1
n
j
)
系统开环传 递函数极点
第四章 根轨迹法
i 1 j 1
m
n
0
s2 p2
(s 2 p1 ) (s2 p2 ) 180
s2 p1
s2
满足相角条件,所以s2在根轨迹上,即s2是该系统的闭环极 点。
第四章 根轨迹法
根轨迹方程 G(s)H(s) 1
G (s)H(s) K
' i 1 n i 1
(s z )
南京信息工程大学817自动控制原理2020年考研专业课初试大纲

南京信息工程大学硕士研究生招生入学考试考试大纲
考试科目代码:817
考试科目名称:自动控制原理
第一部分大纲内容
一、课程目标
本课程为控制系统提供了数学模型的建立、性能分析和系统设计的基本方法。
要求考生掌握自动控制系统的基本理论知识和基本分析计算方法,强调基础性和综合性。
注重测试考生对相关的基本概念、理论和分析方法的理解,以及运用基本概念、基本原理,灵活分析和解决实际问题的能力。
二、基本要求
考试内容包括经典控制理论和现代控制理论。
要求理解、掌握:控制系统传递函数和信号流图等数学模型的建立;系统稳定性、动态性能、稳态性能的时域分析;根轨迹法;频域法;系统串联校正的设计方法;线性离散系统的分析;系统状态空间建模及其求解;系统可控性和可观测性;线性定常系统状态反馈及观测器设计;李雅普诺夫稳定性理论。
三、课程内容与考核目标
(1)自动控制的一般概念
1.掌握基本控制方式:开环、闭环(反馈)控制;
2.熟悉自动控制的性能要求:稳、快、准;
3.掌握反馈控制原理与动态过程的概念,以及建立原理方块图的方法。
(2)控制系统的数学模型
1.掌握动态方程建立及线性化方法;
2.熟练掌握结构图的等效变换方法;
3.掌握梅逊公式及应用;
4.熟悉典型环节。
(3)线性系统的时域分析法。
自动控制原理 第四章 根轨迹法
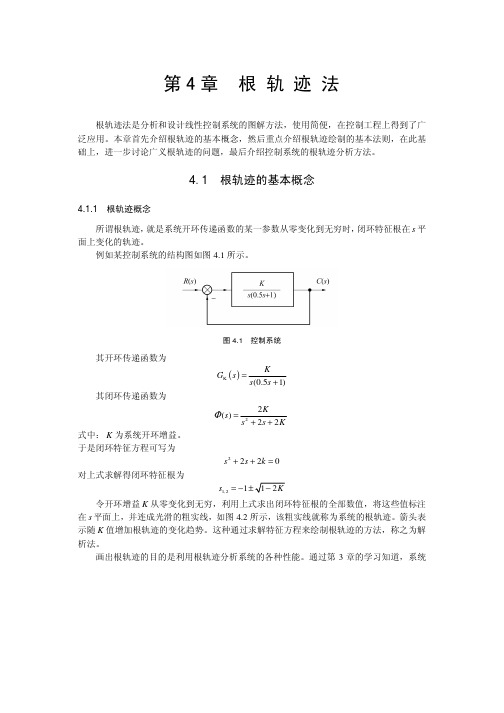
第4章 根 轨 迹 法根轨迹法是分析和设计线性控制系统的图解方法,使用简便,在控制工程上得到了广泛应用。
本章首先介绍根轨迹的基本概念,然后重点介绍根轨迹绘制的基本法则,在此基础上,进一步讨论广义根轨迹的问题,最后介绍控制系统的根轨迹分析方法。
4.1 根轨迹的基本概念4.1.1 根轨迹概念所谓根轨迹,就是系统开环传递函数的某一参数从零变化到无穷时,闭环特征根在s 平面上变化的轨迹。
例如某控制系统的结构图如图4.1所示。
图4.1 控制系统其开环传递函数为()K (0.51)KG s s s =+其闭环传递函数为22()22Ks s s KΦ=++式中:K 为系统开环增益。
于是闭环特征方程可写为2220s s k ++=对上式求解得闭环特征根为1,21s =−令开环增益K 从零变化到无穷,利用上式求出闭环特征根的全部数值,将这些值标注在s 平面上,并连成光滑的粗实线,如图4.2所示,该粗实线就称为系统的根轨迹。
箭头表示随K 值增加根轨迹的变化趋势。
这种通过求解特征方程来绘制根轨迹的方法,称之为解析法。
画出根轨迹的目的是利用根轨迹分析系统的各种性能。
通过第3章的学习知道,系统第4章 根轨迹法·101··101·特征根的分布与系统的稳定性、暂态性能密切相关,而根轨迹正是直观反应了特征根在复平面的位置以及变化情况,所以利用根轨迹很容易了解系统的稳定性和暂态性能。
又因为根轨迹上的任何一点都有与之对应的开环增益值,而开环增益与稳态误差成反比,因而通过根轨迹也可以确定出系统的稳态精度。
可以看出,根轨迹与系统性能之间有着比较密切的联系。
图4.2 控制系统根轨迹4.1.2 根轨迹方程对于高阶系统,求解特征方程是很困难的,因此采用解析法绘制根轨迹只适用于较简单的低阶系统。
而高阶系统根轨迹的绘制是根据已知的开环零、极点位置,采用图解的方法来实现的。
下面给出图解法绘制根轨迹的根轨迹方程。
西南石油大学-硕士研究生招生考试-927_自动控制原理考试大纲

西南石油大学2019年硕士研究生入学考试
《自动控制原理》考试大纲
一、参考书目
胡寿松,《自动控制原理》,科学出版社,第六版
二、考试范围
第一章自动控制的一般概念
(一)基本要求
1、了解反馈控制系统基本组成框图;
2、了解自动控制系统基本控制方式:(1)、反馈控制方式,(2)、开环控制方式,
(3)、复合控制方式等;
3、了解自动控制系统的分类;
4、了解对控制系统的稳定性、准确性(稳态特性)和快速性(动态特性)基本要求。
(二)基本内容
1-1 自动控制的基本原理与方式
1-3 自动控制系统的分类
1-4 对自动控制系统的基本要求
第二章控制系统的数学模型
(一)基本要求
1、掌握运用拉氏变换解微分方程的方法;
1。
第四章 根轨迹法(1)

第四章 根轨迹法
(1)当 K * = 0时,s1 = 0、s2 = -2, 此时闭环极点就是开环极点。 (2)当0< K * <1时, s1 、 s2 均为负 实数,且位于负实轴的(-2,0) 一 段上。 (3)当K * = 1时,s1 = s2 = -1,两 个负实数闭环极点重合在一起。 (4)当1< K * <∞时, s1, 1 1 k * 2 两个闭环极点变为一对共轭复数极点。 s1 、 s2 的实部不随K * 变化,其位于过 (-1,0)点且平行于虚轴的直线上。 (5)当K * =∞时, s1 = -1+ j∞、 s2 = -1-j∞,此时s1、s2将趋于无限 远处。
第四章 根轨迹法
② 位于s1左边的实数零、极 点: (S1 – P4 ) 、(S1 – Z1 ) 、 向量引起的相角为0°
∴ 判断 s1是否落在根轨迹 上,位于s1左边的零、极点不 考虑。
③ 位于s1右边的实数零、极点: 每个零、极点提供180°相 角,其代数和为奇数,则满足相角条件。
第四章 根轨迹法
a
(0) (1 j1) (1 j1) (4) (1) 5 4 1 3
60 180 2k 1 180 2k 1 a 180 nm 3 300
k 0 k 1 k 2
第四章 根轨迹法
五、法则五 根轨迹分离点和分离角
K G( s) H ( S )
* i 1 n j 1
(s z )
i
m
S (s p j )
-1
m个开环零点 n个开环极点 K *根轨迹增益
∴在s平面上凡是满足上式的任意一个点s1、s2、…、 s∞,都 是闭环特征根,即闭环极点。
第四章 根轨迹法
第四章 线性系统的根轨迹法

n
j
s
lim s
s i
nm
nm
sz
i 1
开环传递函数中,若令 s 当 m<n 时, G(s)H(s) =0
称 s ( m<n),是 G(s)H(s) 的无限零点 (n-m个)。
• 法则2. 根轨迹的分支数、对称性和连续性: 根轨迹的分支数与开环有限零点数 m、开环有 限极点数 n 中的大者相等,连续对称于实轴。
d 2.3
4)确定起始角。量测各向量相角,算得起始 角=-71. 6°
5)确定根轨迹与虚袖交点。闭环特征方程式 为:
s 5s 8s 6 s K 0
4 3 2
将s j代入,得实部方程为: 8 K 0
4 2
虚部方程为: 5 6 0
3
解得: 1.1 K 8.16 ,
2
试绘制闭环系统的概略根轨迹。 解 按下述步骤绘制概略根轨迹: 1)确定实轴上的根轨迹。实轴上[0,-3]区域必 为根轨迹。 2)确定根轨迹的渐近线。由于n-m=4,故有四条 根轨迹渐近线,其: a 1.25
a 45 ,135
3)确定分离点。
1 d 1 d 3 1 d 1 j 1 d 1 j 0
三、n-m条渐近线;
四、根轨迹的出射角、入射角; 五、根轨迹与虚轴的交点; 六、根轨迹的分离点、会合点; 结合根轨迹的连续性、对称性、根轨迹的 支数、起始点和终点,闭环极点与闭环极点之 和及之积等性质画出根轨迹。
例4—4 设系统开环传递函数为设系统开 环传递函数为: K
G( s) s( s 3)( s 2s 2)
d 3.414 ,d 0.586(舍去)
自动控制原理
L(s)的相角
单位反馈系统的 开环传递函数 一个开环极点 负实轴上点 s1 s2=-1-j
G (s) =
K s
P1=0
∑ ∠( s − z ) −∑ ∠(s − p ) | = −∠s
i =1 i i =1 i
m
n
1
− p1 = −180o
负实轴上都是根轨迹上的点!
∑ ∠( s − z ) −∑ ∠( s − p ) | = −∠s
3.
根轨迹法
一种求取闭环系统的特征根的图解法(1948年 一种求取闭环系统的特征根的图解法(1948年, 由 W. R. Evans在 “ 控制系统的图解分析 ” 一文 Evans 在 控制系统的图解分析” 中提出) 中提出)。 已知开环零极点分布, 已知开环零极点分布,研究一个或几个参数变化 对闭环极点位置的影响, 对闭环极点位置的影响,从而进一步分析系统的 性能(如稳定性、动态性能、稳态性能等) 性能(如稳定性、动态性能、稳态性能等)。 以前控制系统根轨迹绘制很麻烦,现在使用 MATLAB非常方便。 MATLAB非常方便。
根 轨 迹
K : 开环增益 K*: 根轨迹增益
C ( s) K* Φ( s ) = = 2 R( s ) s + 2 s + K *
D( s ) = s 2 + 2 s + K * = 0
λ1, 2 = −1 ± 1 − K *
(4).闭环系统极点与标准化参数之间的关系可由图4-2 闭环系统极点与标准化参数之间的关系可由图4 表示
1 + G (s) H (s) = 0
G (s)H (s) = −1
将上式改写成
G ( s) H (s) e
j ∠G ( s ) H ( s )
根轨迹法的基本概念
K*
s1,2 1
1 K*
令K*(由0到∞ )变动,s1、s2在s平面的移动轨 迹即为根轨迹。
K* 0, s1 0, s2 2 K* 1, s1 1, s2 1 K* 2, s1 1 j, s2 1 j K* 5, s1 1 2 j, s2 1 2 j
特征方程的根 运动模态 性、系统性能)
1
1
1 ,d 4
m
(s zi )
1 G(s)H(s) 0
G(s)H(s) K*
i1 n
m
(s pj )
(s zi )
j 1
K * i1 n
1
(s pj )
j 1
m
n
模值条件: (s zi ) (s pj ) (2k 1)
i1
j1
n
s pj
相角条件: K *
j 1 m
s zi
i 1
相角条件是确定根轨迹的充分必要条件。相角条件满足(2k 1) 称为180º根轨迹。
4-2 绘制根轨迹的基本法则
一、基本法则
1、 根轨迹的起点和终点:
根轨迹起始于开环极点,终止于开环零点;如果开环零点个数少于 开环极点个数,则有(n-m)条根轨迹终止于无穷远处。
起点: K* 0 s pi
K* s p1 s z1
i 1, 2, n
s pn s zm
终点: K* s zi j 1, 2, m
例题:单位反馈系统的开环传递函数为:G(s)H (s) K *(s 1)
s(s 2)(s 3)
试绘制闭环系统的根轨迹
解: 1、开环零点z1=-1,开环极点p1=0,p2=-2,p3=-3, 根轨迹分支数为3条,有两个无穷远的零点。
根轨迹法(自动控制原理)
i1
l 1
nm
规则4:实轴上的根轨迹
➢ 实轴上的开环零点和开环极点将实轴分为若干段,对其中任一段,如果其右
边实轴上的开环零、极点总数是奇数,那么该段就一定是根轨迹的一部分。
❖ 该规则用相角条件可以证明,设实轴上有一试验点s0。 ➢ 任一对共轭开环零点或共轭极点(如p2,p3),与其对应的相角(如θ2,θ3)
第四章 根轨迹法
4.1 根轨迹的基本概念 4.2 绘制典型根轨迹 4.3 特殊根轨迹图 4.4 用MATLAB绘制根轨迹图 4.5 控制系统的根轨迹分析
内容提要
➢ 根轨迹法是一种图解法,它是根据系统的开环零 极点分布,用作图的方法简便地确定闭环系统的 特征根与系统参数的关系,进而对系统的特性进 行定性分析和定量计算。
规则3:渐近线
❖ 当n>m时,根轨迹一定有n-m支趋向无穷远;当n<m时,根轨迹一定有m-n支 来自无穷远。可以证明:
➢ 当n≠m时,根轨迹存在|n-m|支渐近线,且渐近线与实轴的夹角为:
所有渐近线交于k实轴上(2的k一n点1,)m1其8坐00标,为 k 0,1,2,,| n m | 1
n
m
pi zl
之和均为360°,也就是说任一对共轭开环零、极点不影响实轴上试验点s0的相 角条件。
➢ 对于在试验点s0左边实轴上的任一开环零、极点,与其对应的相角(如θ4,φ3) 均为0。
➢ 而试验点s0右边实轴上任一开环零、极点,与其对应的相角(如θ1,φ1,φ2) 均为180°。
所以要满足相角条件,s0右边实轴上的开环零、极点总数必须是奇数。
❖ 1948年伊凡思(W.R.Evans)提出了根轨迹法,它不 直接求解特征方程,而用图解法来确定系统的闭环 特征根。
根轨迹的基本概念
m
n
上述两式称为满足根轨迹方程(kg>=0)的幅值条件和相角条件。
当根轨迹增益kg<0时:
根轨迹方程可写为:
| kg | s z j
j 1
m
s p
i 1
m j 1
n
e
n m j ( s z j ) ( s pi ) i 1 j 1
的旁边。
根轨迹的两种类型:
180o等相角根轨迹:复平面上所有满足相角条件式(kg>=0)
的点连成的曲线,称为180o等相角根轨迹,简称根轨迹。 0o等相角根轨迹:复平面上所有满足相角条件式(kg<0)的 点连成的曲线,称为0o等相角根轨迹。
这样,当根轨迹增益从kg=0到kg=±∞变化时,根据根轨
称 Gk (s) 1 或 k ×
g
(s z ) (s p )
j1
j
m
i1 n
i
1
为负反馈系统根轨迹方程
4.1.2
根轨迹的幅值和相角条件
当根轨迹增益kg>=0时: 根轨迹方程可写为:kg s Nhomakorabea z j
j 1
m
kg
1
(s z )
i
m
s p
i 1
不满足相角条件,所以点B不是根轨迹上 的点。
Im
B A
A2
p2
s2
s
A1
p1
Re
利用幅值条件在根轨迹上确定特定点的根轨迹增益kg
上例中,若A点的坐标是-1+j1,则根据幅值条件:
kg s( s 2) s 1 j1
1 , kg 2
