线性系统的根轨迹分析
夏德钤《自动控制原理》（第4版）章节题库-第4章线性系统的根轨迹分析【圣才出品】
夏德钤《⾃动控制原理》（第4版）章节题库-第4章线性系统的根轨迹分析【圣才出品】第4章 线性系统的根轨迹分析1．系统的开环传递函数试证明：点在根轨迹上，并求出相应的和系统开环增益K。
证明：根据系统的开环传递函数可知，系统的开环极点为由闭环根轨迹的相⾓条件可得：当时，故点在根轨迹上。
由闭环根轨迹的幅值条件可知，此时即相应的根轨迹增益和系统开环增益仿真曲线如图4-1所⽰。
MATLAB程序：exe402.m２．设单位反馈控制系统的开环传递函数为试⽤解析法绘出K*从零变到⽆穷时的闭环根轨迹图，并判断下列点是否在根轨迹上：（﹣2＋j0），（0＋j1），（﹣3＋j2）解：闭环传递函数为则闭环特征⽅程为闭环特征根为当。
可逐个描点得闭环根轨迹如图4-2所⽰，从图4-2中明显可见，只有（－2，j0）在根轨迹上。
图4-2３．设单位反馈控制系统的开环传递函数如下，试概略绘制闭环根轨迹图。
解：（1）系统的开环传递函数令为根轨迹增益。
①实轴上的根轨迹：[0，－2]，[－5，－∞）。
②根轨迹的渐近线：③根轨迹的分离点：根轨迹的分离点坐标满⾜解得④根轨迹与虚轴的交点：由系统的开环传递函数可知系统的闭环特征⽅程令s＝jω，将其代⼊上式可得即由于ω≠0，故可解得则根轨迹与虚轴的交点为±j3.16。
根据以上⼏点，可以画出概略根轨迹如图4-3所⽰。
图4-3 系统（1）概略根轨迹图（2）系统的开环传递函数①实轴上的根轨迹[0，－2]，[－3，－5]。
③根轨迹的分离点：根轨迹的分离点坐标满⾜通过试凑可得d＝－0.89。
根据以上⼏点，可以画出概略根轨迹如图4-4所⽰。
图4-4 系统（2）概略根轨迹图（3）系统的开环传递函数①实轴上的根轨迹：[－1，－3]，[－10，－5]。
②根轨迹的渐近线：③根轨迹的分离点：根轨迹的分离点坐标满⾜通过试凑可得d＝－7.27。
根据以上⼏点，可以画出概略根轨迹如图4-5所⽰。
图4-5 系统（3）概略根轨迹图（4）系统的开环传递函数实轴上的根轨迹为[－2，－1]，系统概略根轨迹如图4-6所⽰。
自动控制原理第第四章 线性系统的根轨迹法
2
自动控制原理
§4.1 根轨迹的基本概念
例：开环传递函数
Gs
k1
ss
a
开环系统两个极点为：P1 0, P2 a R(s)
闭环传递函数为:
GB s
s2
k1 as
k1
-
k1
C(s)
ss a
闭环特征方程： s2 as k1 0
闭环特征根：s1,2
a 2
a 2
2
k1
（闭环极点）
3
自动控制原理
在p5附近取一实验点sd， 则∠sd-p5可以认为是p5点的出射角 Sd Z Sd P1 Sd P2 Sd P3 Sd P4 Sd P5 1800
近似为 P5 Z P5 P1 P5 P2 P5 P3 P5 P4 p 1800
p Sd P5 1800
法则4 实轴上存在根轨迹的条件——
这些段右边开环零极点个数之和为奇
数。
m
n
证明：根据相角条件 S Z j S Pi 18002q 1
j 1
i 1
p4
j s平面
例：sd为实验点
p3
z2 sd
p2 z1 p1
p5
① 实验点sd右侧实 轴上零极点提供 1800相角
③ 共轭复零点，复极点提供的相角和为 3600。
2
s1=-1.172，s2＝-6.828
33
自动控制原理
法则6 开环复数极点处根轨迹出射角为
p 1800
开环复数零点处根轨迹入射角为：
Z 1800
其中 z p（不包括本点）
34
自动控制原理
j p5
p5
p3 p3
p2
自动控制原理-线性系统的根轨迹实验报告
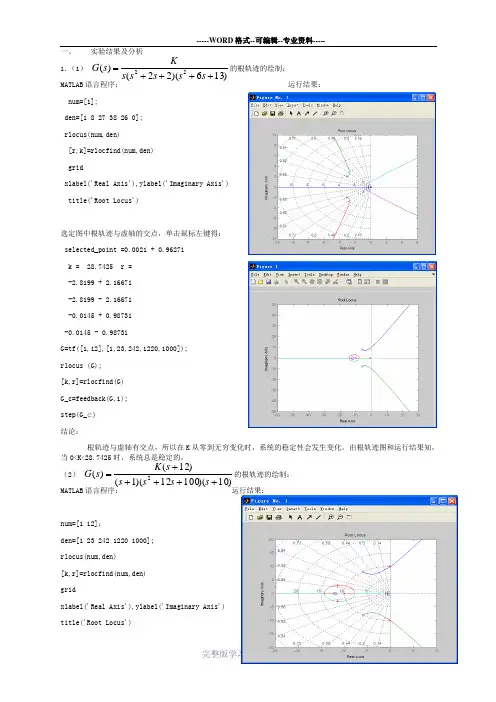
一、 实验结果及分析1.（1） )136)(22()(22++++=s s s s s K s G 的根轨迹的绘制： MATLAB 语言程序： 运行结果：num=[1];den=[1 8 27 38 26 0];rlocus(num,den)[r,k]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis')title('Root Locus')选定图中根轨迹与虚轴的交点，单击鼠标左键得：selected_point =0.0021 + 0.9627ik = 28.7425 r =-2.8199 + 2.1667i-2.8199 - 2.1667i-0.0145 + 0.9873i-0.0145 - 0.9873iG=tf([1,12],[1,23,242,1220,1000]);rlocus (G);[k,r]=rlocfind(G)G_c=feedback(G,1);step(G_c)结论：根轨迹与虚轴有交点，所以在K 从零到无穷变化时，系统的稳定性会发生变化。
由根轨迹图和运行结果知，当0<K<28.7425时，系统总是稳定的。
（2） )10)(10012)(1()12()(2+++++=s s s s s K s G 的根轨迹的绘制： MATLAB 语言程序： 运行结果：num=[1 12]；den=[1 23 242 1220 1000];rlocus(num,den)[k,r]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis')title('Root Locus')选定图中根轨迹与虚轴的交点，单击鼠标左键得：selected_point =0.0059 + 9.8758ik =1.0652e+003 r=-11.4165 + 2.9641i -11.4165 - 2.9641i -0.0835 + 9.9528i -0.0835 - 9.9528i 结论：根轨迹与虚轴有交点，所以在K 从零到无穷变化时，系统的稳定性会发生变化。
线性系统的根轨迹-自动控制原理实验报告
自动控制原理实验报告实验题目：线性系统的根轨迹班级：学号：姓名：指导老师：实验时间：一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、实验内容同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围。
2．1绘制下面系统的根轨迹曲线)136)(22()(22++++=s s s s s Ks G程序：G=tf([1],[1 8 27 38 26 0]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统 step(G_c) %绘制闭环系统的阶跃响应曲线-12-10-8-6-4-20246-10-8-6-4-20246810Root LocusReal AxisI m a g i n a r y A x i s0204060801001201400.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围：K>28.74252．2绘制下面系统的根轨迹曲线)10)(10012)(1()12()(2+++++=s s s s s K s G 程序：G=tf([1 12],[1 23 242 1220 1000]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统 step(G_c) %绘制闭环系统的阶跃响应曲线-60-50-40-30-20-100102030-50-40-30-20-1001020304050Root LocusReal AxisI m a g i n a r y A x i s01234560.0020.0040.0060.0080.010.012Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围： K>1.1202e+032．3绘制下面系统的根轨迹曲线)11.0012.0)(10714.0()105.0()(2++++=s s s s s K s G 程序：G=tf([5 100],[0.08568 1.914 17.14 100 0]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统step(G_c) %绘制闭环系统的阶跃响应曲线-60-50-40-30-20-10010203040-60-40-200204060Root LocusReal AxisI m a g i n a r y A x i s012345670.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围：K> 7.8321根据实验结果分析根轨迹的绘制规则：⑴绘制根轨迹的相角条件与系统开环根轨迹增益 值的大小无关。
《自动控制原理》第4章 线性系统的根轨迹法
68
4.5 广义根轨迹
根轨迹部分是个半圆,半径是 k *
证明：根轨迹上一点S满足相角条件
s (s j2) (s j2)
代入s j
( j) ( j( 2)) ( j( 2))
arctan arctan 2 arctan 2
K* G(s)
s(s 2)(s 1)
26
法则五：根轨迹的分离点与分离角
分离点：几条根轨迹在[s]某一点相遇后又分开 的点。
说明有重根
27
实轴上的分离点（常见）
如果根轨迹位于实轴上相邻的两个开环极点之间， 其中一个可以是无限极点，则在这两个极点之间至 少存在一个分离点；
如果根轨迹位于实轴上相邻的两个开环零点之间， 其中一个可以是无限零点，则在这两个零点之间至 少存在一个分离点；
开环极点：
p1 0 p2 0 p3 2 p4 5
（2）实轴上的根轨迹 （3）根轨迹分支数
4
59
G0 ( s)
s2(s
k* 2)(s
5)
（4）渐近线
4条
渐近线与实轴的夹角
a
4
3
4
3
4
4
渐近线与实轴的交点（σa ， 0）
4
pi
a
i 1
4
1.75
60
G0 ( s)
s2(s
k* 2)(s
法则二：根轨迹的分支数，对称性和 连续性
• 根轨迹的分支数与开环有限零点数m和有限 极点数n中的大者相等，它们是连续的并且 对称于实轴。
22
法则三：根轨迹的渐近线(n>m)
• 当开环有限零点数m小于有限极点数n时， 有n-m条根轨迹分支沿着与实轴交点 ，
第4章 线性系统的根轨迹法(《自动控制原理》课件)
如果用试凑的方法由相角条件来绘制根轨迹, 如果用试凑的方法由相角条件来绘制根轨迹 将会非常不方 人们利用前面介绍的几个式子, 便. 人们利用前面介绍的几个式子 导出一些绘制根轨迹的法则 利用导出的法则, 可方便地绘制出根轨迹的大至形状, 利用导出的法则 可方便地绘制出根轨迹的大至形状 叫概略根 轨迹, 轨迹 这在利用根轨迹对系统进行初步分析和设计时已基本可用 了.
(2) 当0<K<=0.25时, 一个根的绝对值随 的增大而增大 另 的增大而增大, 时 一个根的绝对值随K的增大而增大 一个根的绝对值随K的增大而减小 两根的变化轨迹如下图所示: 的增大而减小, 一个根的绝对值随 的增大而减小 两根的变化轨迹如下图所示 jω ω σ -2 -1.5 -1 0
当K=0.25时, 两根相等 均为 时 两根相等, 均为-1.5 (3) 0.25<K<+∞ 时, 两根为共軛复根 且其实部均为 两根为共軛复根, 且其实部均为-1.5 , 而 +∞ 虚部的绝对值随K的增大而增大 两根的变化轨迹如下图所示: 的增大而增大, 虚部的绝对值随 的增大而增大 两根的变化轨迹如下图所示 jω ω σ
4-2 根轨迹绘制的基本法则
本节通过一个例子, 介绍绘制根轨迹的七条法则, 本节通过一个例子 介绍绘制根轨迹的七条法则 但对法则 不予推导和证明. 不予推导和证明 需指出的是, 需指出的是 绘制根轨迹的前提是必须已知闭环系统的开环 传递函数的零点和极点的具体数值, 一般以K’为参变量 为参变量. 传递函数的零点和极点的具体数值 一般以 为参变量 某闭环系统的开环传递函数为: 例: 某闭环系统的开环传递函数为
阶数. 阶数 K叫开环系统的增益 K’叫开环系统的根轨迹增益 叫开环系统的增益, 叫开环系统的根轨迹增益, 叫开环系统的增益 叫开环系统的根轨迹增益 K与K’的本质相同 仅它们间的值有一系数关系, 即: 与 的本质相同, 仅它们间的值有一系数关系 的本质相同
4第四章__根轨迹法(2)
2
1
Imag Axis
0
-1
-2
-3 -2
-1.5
-1
-0.5 Real Axis
0
0.5
1
第四章 线性系统的根轨迹分析
2)确定内环的闭环极点 要求内环的反馈系数 内环的特征方程 3.2<Kf<3.5
( s 0.6)(s2 2s 4) K f 0
在实轴上选取试验点进行试探，P1=-1.6时，Kf =3.36 可求得内环的另外两个闭环极点为 p2 0.5 j1.83 p3 0.5 j1.83 3)绘制外环的根轨迹图 外环的开环传递函数
（2）根轨迹的起点 （3）实轴上的根轨迹
0，-1，-3
终点 均为∞
[0 , ] [3 , 1]
第四章 线性系统的根轨迹分析
（4）根轨迹的渐近线
a
n
2k 180 0 ,120 nm
m j i 1 i
k 0、 1
a＝
( p ) ( z )
i 1 j与虚轴的交点 (相同) （9）闭环极点的和 (相同)
第四章 线性系统的根轨迹分析
例：控制系统方框图如下所示
R(s )
Kc s2
K0 s( s 1)
C (s )
1 s3
系统的内环为正反馈，绘制内环根轨迹图。 解： （1）内环的开环传递函数
G1 ( s ) H1 ( s ) K0 s( s 1)(s 3)
第四章 线性系统的根轨迹分析
4-3
广义根轨迹
其它种类的根轨迹: 1.参数根轨迹
2.多回路系统的根轨迹 3.正反馈回路和零度根轨迹
第四章线性系统的根轨迹法
4 分离角不变
1-G(S)H(S)=0 G(K)=1 例题：开环传递函数：
绘制系统的根轨迹。
解：①n=3.所以根轨迹有三条。 ②极点： ③渐近线： 5 分离点：
令 1． 闭环零极点由前向通道的零点和反馈通道的极点构成，对于单 位负反馈系统的闭环零点就是开环零点。 2． 闭环极点与开环极点，开环零极点及根轨迹都有关系。
4）.根轨迹方程：
幅值条件： 相角条件： ①满足相角条件的点肯定是根轨迹上的点，相角条件是确定根轨迹 的充要条件。 ②幅值条件是用来确定根轨迹上的点所对应的根轨迹增益。 5）.绘制更轨迹的法则： ①根轨迹的连续性：根轨迹是连续变化的直线或曲线。 ②根轨迹的对称性：根轨迹位于幅平面的实轴上或对称的实轴上。 ③根轨迹的条数;等于系统的阶次。即：闭环特征根最高次幂。 ④根轨迹的起点和终点：起源于n个开环极点，终止于m个开环零点。 以及n-m个无穷远零点。
闭环极点。
解 （1）系统的开环极点为，，是根轨迹各分支的起点。由于 系统没有有限开环零点，三条根轨迹分支均趋向于无穷远处。 （2）系统的根轨迹有条渐进线
渐进线的倾斜角为 取式中的K=0，1，2，得=π/3，π，5π/3。
渐进线与实轴的交点为
三条渐近线如图的虚线所示。 （3）实轴上的根轨迹位于原点与－1点之间以及－2点的左边，如图中 的粗实线所示。 （4）确定分离点：系统的特征方程式为 即
所以 即： ②分离点： 证明：
②除以①式
无零点 分离点重根 ③分离角：指根轨迹进入分离点的切线方向与离开分离点的切线方向之 间的夹角。当l条根轨迹进入并立即离开分离点时 8）根轨迹的出射角和入射角： 出射角：起始于开环极点的根轨迹在起点处，切线方向与正实轴的夹 角。 入射角：终止于开环零点的根轨迹在终点处切线方向与正实轴的夹角。
自动控制原理-胡寿松-第四章-线性系统的根轨迹法.详解
系统的信号流图见图4-28，从信号流图中看出，系统中含有一个积分环节， 因此为1型系统，因此系统对阶跃输入信号的稳态误差为0。
K m 变化时系统的根轨迹， 2）为了绘制电动机传递系数（含放大器附加增益） 可将有关参数代入传递函数中，并将系统的特征方程进行整理，等价根轨迹增 益方程为：
1 K* P( s ) ( s 6.93 j 6.93)( s 6.93 j 6.93) 1 K * Q( s ) s 2 ( s 13.86)
当所有根轨迹分支都在左半平面时，系统稳定。 2) 稳态性能：
回忆：稳态性能主要取决于系统的开环增益和积分环节个数。
由根轨迹图不仅可以方便的确定开环增益和积分环节个数，而且可以根据给定系统 的稳态误差要求, 确定闭环极点位置的容许范围。
3)动态性能： 回忆：动态性能形态主要取决于系统的——闭环极点。 从根轨迹图上，可以直观地看到特征根随着参数的变化情况，从而，可以方便地 确定动态性能随着参数的变化情况。
K * lim
s
j 1 i 1 m
n
s pi s zj
lim s
s
nm
, 0 ,
nm nm
（无穷零点）
（无穷极点）
(n m 1)
（续）
且均为实数开环零、极点。
（续）
（续）
小结论： 由两个极点（实数极点或者复数极点）和一个有限零点组成的开环系 统，只要有限零点没有位于两个实数极点之间，当 K * 从零变化到无穷时， 闭环根轨迹的复数部分，是以有限零点为圆心，以有限零点到重根点的距 离为半径的一个圆，或圆的一部分。这在数学上是可以严格证明的。
例如，在上列程序之后增加语句： [k,p]=rlocfind(num,den)
第4章 线性系统的根轨迹分析
３．暂态性能 （１） 当０<Ｋ< ０.25时， 闭环特征根为实根，系统是过 阻尼状态，阶跃响应为非周期 过程。
∞ K K=0 × -1 K
jω
K=0.25 K=0 ×
σ
（２） 当Ｋ＝０.25时，两 特征根重合，均为－0.5，系 统处于临界阻尼状态。
∞
（３） 当Ｋ＞０.25时，两特征根变为共轭 复根，系统处于欠阻尼状态，阶跃响应为衰 减振荡过程。
§４－２绘制根轨迹的基本规则 续例４－２，将 s j 代入特征方程。
j ( j 1)( j 2) K 1 0 j ( 2 j 3 2) K 1 0 j 3 3 2 j 2 K 1 0
jω
j 2
K1=6
实部 虚部
K 13 2 0 2 3 0
i 1
n
q 0,1,2,
…
（＊＊）
三．根据相角条件确定根轨迹上的点
设某一系统的开环零极点如图， 在Ｓ平面中的任意一点 s 0 ，用 相角条件可以判断 s 0 是不是根 轨迹的点。 １．从 s 0 到各零极点连直线 ２．用量角器量(s0 p1 ) ,…等 各个角． ３．将量好的值代入（＊＊） 式，若等式成立，则 s 0 就是根 轨迹上的点．
§４－１根轨迹的基本概念
G H
绘制根轨迹是求解特征方程的根，特征方程可改 写为 G ( S ) H ( S ) 1
G( S ) H ( S ) 是复变量Ｓ的函数，根据上式两边的
幅值和相角分别相等的条件，可以得到
§４－１根轨迹的基本概念
G( S ) H ( S ) 1
G( S ) H ( S ) 180(2q 1),
z1
实验2 线性系统的根轨迹分析
自动控制理论实验报告
实验二 线性系统的根轨迹分析
哈尔滨工业大学
实验二 线性系统的根轨迹分析
一、实验目的
1、掌握使用MATLAB绘制控制系统根轨迹图的方法；
2、掌握根据根轨迹法对控制系统进行性能分析方法。
二、 实验设备
Pc机一台，MATLAB软件。
三、实验内容
A、已知一负反馈系统的开环传递函数为
（1）绘制根迹。
（2）选取根轨迹与虚轴的交点，并确定系统稳定的根轨迹增益K的范围 。
（3）确定分离点的超调量 及开环增益K。
（4）用时域相应曲线验证系统稳定的根轨迹增益K的范围
（5）分析根轨迹的一般规律。
B、. 已知系统的开环传递函数为：
求：1）绘制根轨迹。
2）选择系统当阻尼比 =0.7时系统闭环极点的坐标值及增益K值。
分析系统性能。
四、实验结果与分析
A:1、根轨迹
2、由根轨迹图知，与虚轴交点i=4.46，增益K=12，故K<12时系统稳定
3、由根轨迹图知，分离点超调量Mp=0%，增益K=0.458
4、将不同的K带入时域响应，如下图
由图可知当K=11.9时系统依旧稳定，但当K=12时系统已经开始震荡，进入临界稳定。故与根轨迹结论一致。
超调量越靠近虚轴越大，系统处于欠阻尼状态，其动态响应将出现衰减振荡，而且越靠近虚轴，增益K越大，阻尼越小，振荡频率 越高，振幅衰减越大。
5）当根轨迹与虚轴相交时，闭环根位于虚轴上，闭环极点是一对纯虚根，阻尼 ，超调量最大，系统处于无阻尼状态，其动态响应将出现等幅振荡。此时对应的增益 ，称为临界稳定增益。
5、根轨迹的一般规律
1）根轨迹，随着k值从 变化，趋向无穷远处或者零点。
根轨迹法PPT课件
W.R.EVAOVS(依万斯)于1948年首先提出了求解特征方程 式根的图解法─根轨迹法。
根轨迹简称根迹，它是开环系统某一参数从零变到无穷
时，闭环系统特征方程的根在 s 平面上变化的轨迹。
解： n 3，m 0
① p1 0，p2 1，p3 2 为根轨迹的起点；
开环无零点，故三个分支终点均趋向无穷远。
②
a
(2q 1)
nm
(2q 1)
3
60、180、300
(q 0,1,2)
n
m
a
i 1
pi z j
j 1
nm
3 0 1 3
③ 实轴上根轨迹：
（ ,2]，[1,0]
j
p3 2
第四章 线性系统的根轨迹法
§4-1 根轨迹法的基本概念 §4-2 绘制根轨迹的基本条件和基本规则 §4-3 参数根轨迹 §4-4 正反馈回路和零度根轨迹 §4-5 利用根轨迹法分析系统的暂态响应
§4-1 根轨迹法的基本概念
一、根轨迹的概念
从上一章讨论知道，闭环系统的动态性能与闭环极点在
s 平面上的位置是密切相关的，分析系统性能时往往要求确
对于实轴上0至1线段的实数根而言，其对应的K*值在
b 点为极大值。
可以证明，当l 条根轨迹分支进入并立即离开分离点时，
分离角为 (2k 1) l .
k 0，1， ，l -1
例4-3：求上例中 b 点的坐标。
[规则3] 根轨迹的渐进线
当开环有限极点数 n大于有限零点数时，有 (n m)
条根轨迹分支沿着与实轴交角为 a 、交点为 a的一组
《模块化自控原理》线性系统的根轨迹分析实验
《模块化自控原理》线性系统的根轨迹分析实验模块化自控原理中的线性系统的根轨迹分析实验是探究线性系统的稳定性和动态特性的一种常用方法，通过实验观测和分析系统的根轨迹，可以得到系统的传递函数以及系统的稳定性等重要信息。
下面是对该实验的详细说明和分析。
1.实验目的1.1理解线性系统的根轨迹概念及其重要性；1.2学习使用根轨迹法进行系统的稳定性和动态特性分析；1.3掌握根轨迹分析实验的具体步骤；1.4提高实验操作和数据处理的能力。
2.实验原理2.1根轨迹的概念根轨迹是以参数变化为基础的线性系统稳定性和动态特性的分析方法之一、根轨迹是指在参数变化的范围内，系统传递函数极点的轨迹，可以用来判断系统的稳定性、响应特性和动态响应快慢等重要指标。
2.2根轨迹的画法根轨迹的画法需要先确定系统的开环传递函数，然后通过对传递函数进行拆项和配平，求解极点的位置。
根轨迹的位置可以通过极点的实部和虚部来表示，根据虚轴对称性和极点与零点的关系，可以画出根轨迹的大致形状和方向。
2.3根轨迹分析的应用根据根轨迹的形状、分布和方向可以判断系统的稳定性和动态特性：-根轨迹在左半平面则系统稳定；-根轨迹与虚轴交点奇数个则系统不稳定；-根轨迹的分布越往左上角或右上角，系统的动态特性越好。
3.实验装置和器材3.1实验装置数字控制系统实验台、计算机、示波器、信号发生器、数模转换器等。
3.2实验器材电脑、电源线、连接线、示波器探头等。
4.实验步骤4.1连接实验装置将数字控制系统实验台与计算机、示波器、信号发生器和数模转换器等设备进行连接。
4.2系统参数调整设置合适的实验参数，包括采样频率、控制周期、信号幅值等。
4.3系统根轨迹绘制在计算机上运行相应的根轨迹绘制软件，根据实验所给的开环传递函数和稳定域范围，绘制系统的根轨迹。
4.4根轨迹分析根据根轨迹的形状、位置和分布等信息，分析系统的稳定性和动态特性，并给出相应的结论和解释。
4.5记录实验数据记录实验中所绘制的根轨迹和分析结果，包括根轨迹的形状、交点、分布等重要特征。
第4章线性系统的根轨迹分析
k (s z1)(s z2 )(s zm ) 1 (s p1)(s p2 )(s pn )
(4-2-6)
g(t) c(t) 1 et /
闭环系统特征方程为
f (s) s3 3s2 2s k 0
df (s) 3s2 6s 2 0 ds
s1 0.422, s2 1.578
由前边分析得知，s2 不是根轨迹上的点，故舍 去。s1是根轨迹与实轴分离点坐标。最后画出
根轨迹如图4-2-4所示。
图4-2-4 例4-2-1的跟轨迹图
利用多项式乘法和除法，由式(4-2-6)可得
n
s n ( pi )s n1
k
i 1 m
s m ( z j )s m1
j 1
m
n
s nm ( z j
pi )s nm1
j 1
i 1
将式(4-2-8)代入上式可得
m
n
(s )nm snm ( z j pi )snm1
(n m)
(4-2-1)
式中 s z j ( j 1,2,, m) 为系统的开环零点 s pi (i 1,2,, n) 为系统的开环极点
k称为根轨迹增益或根轨迹放大倍数。设系统为v型， 即有s=0的开环极点，将式(4-2-1)改写为
G(s)H (s)
K (1s 1)( 2s 1)( ms 1)
当1<k<∞时，两个闭环极点变为一对共轭复数极点
明当sk1→、s21、∞ 时s12，位js1于、k(s-121,将,且j趋0s1)、向点s于且2 无平的限行实远于部处虚不。轴随图的k变4直-化1线的，上控说。
实验三 线性系统的根轨迹分析
实验三 线性系统的根轨迹分析09电信 任旭乐 20095042046一、 实验目的1.熟悉Matlab 的基本操作；2.掌握利用Matlab 函数实现系统根轨迹的绘制及设计的方法。
3.能够根据所得结果对系统进行性能分析。
二、 实验内容1、已知单位负反馈系统的开环传递函数为： （1）试画出K=0 →∞时的闭环系统根轨迹； （2）求出临界时的K 值及闭环极点； （3）求出使系统稳定的K 值的区间; （4）利用Matlab 函数将剩余的根求出。
程序： a=[1 0]; b=[0.05 1]; c=[0.05 0.2 1]; d=conv(a,b); e=conv(c,d); G=tf([1],e); figure(1); rlocus(G);[k,pole]=rlocfind(G);解：（1）根轨迹如图所示。
（2）临界时k=4.62；闭环极点p=0.336+4.34j （3）由图可知：0<k<4.62时系统稳定。
Root LocusReal AxisI m a g i n a r y A x i s-80-60-40-200204060-60-40-20204060System: G Gain: 4.62P ole: 0.336 + 4.34i Damping: -0.0772Overshoot (%): 128Frequency (rad/sec): 4.35System: G Gain: 0P ole: 0Damping: -1Overshoot (%): 0Frequency (rad/sec): 0System: GGain: 8.5P ole: -19.5Damping: 1Overshoot (%): 0Frequency (rad/sec): 19.5根轨迹2()(0.051)(0.050.21)KG s s s s s =+++2、已知单位负反馈系统的开环传递函数为：（1）试画出K=0 →∞时的闭环系统根轨迹；（2）找出ζ=0.707附近的点，绘制出其相应的单位阶跃响应曲线。
线性控制系统的根轨迹分析法
PART 01
引言
线性控制系统简介
线性控制系统是由线性微分方程描述 的一类控制系统，其特点是系统的输 出和输入之间存在线性关系。
线性控制系统广泛应用于工程领域， 如航空航天、化工、电力等，用于实 现各种控制目标，如稳定性、快速性 和准确性。
根轨迹分析法的定义和重要性
根轨迹分析法是一种通过分析线性控制系统闭环极点的变化来研究系统性能的方法。
系统校正与改进
通过根轨迹分析，可以找到系统性 能不足的原因，进而对系统进行校 正或改进设计。
PART 04
根轨迹分析法的限制和挑 战
参数变化对根轨迹的影响
01
参数变化可能导致根轨迹的形状和位置发生变化，从而影响 系统的稳定性和性能。
02
参数变化可能使系统从稳定状态变为不稳定状态，或反之。
03
参数变化可能影响系统的动态响应，如调节时间和超调量。
分析系统动态特性
通过根轨迹分析，可以了 解系统在不同参数下的动 态特性，如超调和调节时 间等。
控制系统性能优化
1 2 3
优化系统性能指标
通过调整系统参数，利用根轨迹分析优化控制系 统的性能指标，如减小超调量、缩短调节时间等。
提高系统抗干扰能力
通过根轨迹分析，可以找到提高系统抗干扰能力 的参数设置，使系统在受到扰动时仍能保持良好 的性能。
分支性
当参数变化超过一定阈值 时，根轨迹可能出现分支， 表示系统出现多解或不稳 定。
PART 03
根轨迹分析法的应用
控制系统稳定性分析
判断系统稳定
通过根轨迹分析，可以判 断线性控制系统的稳定性， 即系统在受到扰动后是否 能恢复稳定状态。
确定系统临界状态
根轨迹分析可以确定系统 临界状态，即系统在某一 特定参数下从稳定状态变 为不稳定状态。
线性系统的根轨迹法
i
3）若n>m,另(n-m)条根轨迹的终点？？
由
kg
(s p )
j 1 m j
n
同理，若m>n, (s p ) s 则有 (m-n) 条根轨迹起于无穷远处。 lim lim lim s 当 s 时，
i 1 i
(s z )
s
可知， k
n j 1 m j
Kg= 0 2
Kg=1 1
Kg
Kg= 0 0
当 k g 1 时，闭环两个实极点重合，系统为 临界阻尼系统，单位阶跃响应为非周期过程。
当 k g 1 时，闭环极点为一对共轭复数极点， 系统为欠阻尼系统，单位阶跃响应为阻尼振荡 过程。
3. 根轨迹的条件方程
系统的结构如图所示：
开环传函：
1.根轨迹的定义
当某一参数从0变化时，系统闭环特征 方程的根在s 平面上的变化轨迹，称为根轨 迹。 当闭环系统没有零、极点相消时，闭环特 征根就是闭环传递函数的极点，即闭环极点。
引例：
已知系统的结构图所示，分 析 0 K 时，闭环特征根在 s平面上变化的轨迹。 解：系统的开环传递函数为
pj zi
s-zi
矢量的模：
s zi
s pj
矢量的相角：
（矢量与正实轴的夹角）
( s zi )
( s p j )
Kg
( s z
i 1 n j 1
m
i
) 1 )
——根轨迹的条件方程
( s p
j
• 根轨迹方程可看成一个矢量方程，因此可分 解出以下的模值条件和相角条件方程：
g
时，左边=∞
n
n m
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
出射角/入射角
i
n (s
1
pi
)
m (s
j1
z
j)
(2k
1)π
根轨迹从某个开环极点出发时的切线与实轴方向的夹
角称为出射角，根轨迹进入某个开环零点的切线与实
轴的正方向的夹角称为入射角。
m
l 1
n
pl 180 ( pl zi ) ( pl p j ) ( pl p j )
i 1
l1,2 1 1 K *
§4.1.2 闭环零点与开环零、极点之间的关系
系统结构图如图所示，确定闭环零点
闭环零点=前向通道零点+反馈通道极点 闭环极点与开环零点、开环极点及 K* 均有关
§4.1.3 绘制根轨迹方程—绘制根轨迹的两个条件
根轨迹方程及其含义
K* G(s)
(s) G(s)
s p
系统的闭环特征方程可以表示为：
K* > 0
1 + K* (s - z1 )(s - z2 )....(s - zm ) = 0 (s - p1 )(s - p2 )....(s - pn )
以K*为参变量的根轨迹上的每一点都必须满足该方程，
相应地，我们称之为典型根轨迹方程。
将典型根轨迹方程可以写成幅值条件和相角条件：
注意
只有复数极点或复 数零点才需要计算 出射角/入射角。
出射角/入射角示例
N(s)
dD(s) ds
-
D(s)
dN(s) ds
=
0
d ds
D(s) N(s)
=
0
dK * = 0 ds
n 1
m1
i1 d pi j1 d z j
分离点的必要条件
m
K * (s zi )
n
(s pj)
G(s)H(s)
i 1 n
1 K *
j 1 m
(s pj)
(s zi )
根轨迹在s平面上的分支数等于控制系统特征方程的阶数 n，即根轨迹的分支数与开环极点的数目相同。
特征方程中的参数为实数且连续变化，特征方程的根
要么是实根要么是共轭复根（对称于实轴），同时特
征方程的根连续变化，则根轨迹连续且对称。
基本法则（3）——根轨迹的起点和终点
法则3 根轨迹起始于开环极点，终止于开环零点；如果
s
p j zi
j 1
i 1
K e 1 *nm
j (2k 1) nm
nm
基本法则（5）——实轴上的根轨迹
法则5 实轴上根轨迹是那些在其右侧的开环实极点数 与开环实零点数的总数为奇数的线段。简记为“奇是 偶不是”。
m
n
G(s)H(s) (s zi ) (s pj ) (2k 1)
i 1
j 1
j 1
j l 1
简记“加零去余极”
m
l 1
n
zl 180 (zl pi ) (zl z j ) (zl z j )
i 1
j 1
jl 1
简记为“加极去余零”
出射角/入射角示例
例4 单位反馈系统的开环传递函数为 G(s) K *(s 1.5)( s 2 j) ，绘制根轨迹。 s(s 2.5)( s 0.5 1.5)
开环零点个数少于开环极点个数，则有 n-m 条根轨迹
终止于无穷远处。
K*
s p1 s pn s z1 s zm
snm 1 p1 1 pn
s
s
1 z1 1 zm
0
s
s
s pi
i 1, 2, n
K*
s p1 s pn s z1 s zm
snm 1 p1 1 pn
G(s)H(s) =
K*(s - z1 )
(s - p1 )(s - p2 )(s - p3 )(s - p4 )
基于相角条件，在复平面上选足够多的试验点，对每
一个试验点检查它是否满足相角条件，如果是则该点
在根轨迹上，如果不是则该点不在根轨迹上，最后将
在根轨迹上的试验点连接就得到根轨迹图。
先在复平面上标出开环极点p1, p2, p3, p4和开环零点z 1如图。对试验点s，如果它在根轨迹上，就应当满足
1)
arctan
1
1 1
+
2
=
1
1 1
2 4 4 2 2
( 2)2 2
2
2
定理：若系统有2个开环极点，1个开环零点，且在复平面存在根轨迹， 则复平面的根轨迹一定是以该零点为圆心的圆弧。
基本法则（6）——与虚轴交点
1）系统临界稳定点
法则6 与虚轴交点：
[接例3] G(s)
m
G(s)H(s)
K * s z1 s zm s p1 s p2 s pn
K*
(s zi )
i 1 n
1
(s pj)
j 1
— 模值条件
m
n
G(s)H (s) (s zi ) (s p j ) (2k 1)
i 1
j1
— 相角条件
例:以下列4阶系统为例手工绘制根轨迹图.
2
ReD( j ) 3 2 K * 0
2
ImD( j) 3 2 0
K* 6
基本法则（7）——分离点 d
法则7 分离点 d： dK * = 0 或 ds
（对应重根）
n 1
m1
i1 d pi j1 d z j
当K*从0变到∞时，根轨迹可能出现先会合后分离，这样的点
称分离点。分离点对应重闭环极点。
K*
2）s
=
j
是根的点
Re[1 + G(jω)H(jω)] Im[1 + G(jω)H(jω)]
= =
0 0
s(s 1)( s 2)
D(s) s(s 1)( s 2) K * s3 3s2 2s K * 0
2
解法I ：Routh ：
解法II ：D( j ) j 3 3 2 j2 K * 0
ds
ds
ds
该方程只是必要条件而非充分条件，也就是说它的解不
一定是分离点，是否是分离点还要看是否满足相角条件。
分离点的必要条件
D(s) + K*N(s) = 0 K* = -D(s) / N(s)
dD(s) + K* dN(s) = dD(s) - D(s) dN(s) = 0
ds
ds
ds N(s) ds
实轴上的根轨迹示例
例3 某单位反馈系统的开环传递函数为 ，证明复平面的根轨迹为圆弧。
s = σ + jω
(s 2) s - (s 1)= (2k 1)
( 2 j) ( j) - ( 1 j)= (2k 1)
arctan
2
arctan
-
arctan
1
=
(2k
1)
+
arctan
2
=
(2k
显然，位于实轴上的两个相邻的开环极点之间一定有分离点， 因为任何一条根轨迹不可能开始于一个开环极点终止于另一个 开环极点。同理，位于实轴上的两个相邻的开环零点之间也一 定有分离点。
当然，分离点也可以是复数，两个相邻的开环复极点（或零 点）之间可能有分离点。
复数分离点示例
p3
j
0
p2
p1
p4
分离点的必要条件
§4.1 根轨迹法的基本概念
系统的动态性能主要取决于闭环系统特征方程的 根—闭环极点，所以控制系统的动态设计，关键就 是合理地配置闭环极点。调整开环增益是改变闭环 极点的常用办法。 1948年W.R.Evans提出了根轨迹法，它不直接求解 特征方程，而用图解法来确定系统的闭环特征根。
根轨迹：系统某一参数由0 → ∞变化时，闭环特
G(s)H(s)
(s
K*(s p1 )(s
z1 )(s zm p2 )(s
) pn
)
1
m
G(s)H(s)
K * s z1 s zm s p1 s p2 s pn
K*
(s zi )
i 1 n
1 —
(s pj)
模值条件
j 1
m
n
G(s)H (s) (s zi ) (s p j ) (2k 1)
j 1
i 1
dK * = 0
d
ds
ds
n
(s
pj
)
j 1 m
(s zi )
0
d
ln
ds
n
(s
pj
)
j 1 m
(s zi )
0
i1
i1
d
ds
n j 1
ln(s
pj
)
m i 1
ln(s
zi )
0
n1
m1
i1 d pi j1 d z j
法则8
基本法则（8）——出射角/入射角
pj——(j=1,2,…,n) 为系统的开环极点； zi——(i=1,2,…,m) 为系统的开环零点；
(s) G(s) 1 G(s)H(s)
1 G(s)H(s) 0
G(s)H(s) = K*(s - z1 ) (s - zm ) = 1 — 根轨迹方程 (s - p1 )(s - p2 ) (s - pn )
§4 线性系统的根轨迹分析
§4.1 根轨迹法的基本概念 §4.2 绘制根轨迹的基本条件和基本规 则 §4.3 特殊根轨迹 §4.4 利用根轨迹分析控制系统性能
根轨迹法
根轨迹法: 三大分析校正方法之一
特点:
（1）图解方法，直观、形象。 （2）适用于研究当系统中某一参数变化时，系统