求解不可压缩流动的一种新算法
fluent求解器基于密度和基于压力介绍

Pressure-Based Solver是基于压力法的求解器,使用的是压力修正算法,求解的控制方程是标量形式的,擅长求解不可压缩流动,对于可压流动也可以求解;Fluent 6.3以前的版本求解器,只有Segregated Solver和Coupled Solver,其实也就是Pressure-Based Solver的两种处理方法;Density-Based Solver 应该是Fluent 6.3新发展出来的,它是基于密度法的求解器,求解的控制方程是矢量形式的,主要离散格式有Roe,AUSM+,该方法的初衷是让Fluent具有比较好的求解可压缩流动能力,但目前格式没有添加任何限制器,因此还不太完善;它只有Coupled的算法;对于低速问题,他们是使用Preconditioning方法来处理,使之也能够计算低速问题。
Preconditioning方法应该是以压力、速度、晗值为原始变量,以时间推进方法(TMM)为基础,能够将可压和不可压流场计算方法统一起来。
Segregated方法是基于压力,而coupled求解是基于密度的。
这样就使得segregated求解低速流动较好,而coupled求解音速/超音速问题较好。
不推荐使用coupled求解马赫数低于4的流动。
但是速度越高,需要的网格就越多(因为segregated 趋向于“平滑”波动),所以必须多加注意划分网格。
分离式求解器(Segregated Solver)以前主要用于不可压缩流动和微可压流动,而耦合式求解器用于高速可压流动。
现在,两种求解器都适用于从不可压到高速可压的很大范围的流动,但总的来讲,当计算高速可压流动时,耦合式求解器比分离式求解器更有优势。
分离式求解器是顺序的、逐一的求解各方程(关于u,v,w,p和T 的方程),也就是先在全部网格上解出一个方程(如u动力方程)后,再解另外一个方程(如v动量方程)。
由于控制方程是非线性的,且相互之间是耦合的,因此,在得到收敛街之前,要经过多轮迭代。
第七章 不可压缩流体动力学基础

当液体平衡时: 当液体平衡时:
du x du y du z = = =0 dt dt dt
则可以得到欧拉平衡微分方程。 则可以得到欧拉平衡微分方程。 欧拉平衡微分方程
1 ∂p X= ρ ∂x
1 ∂p Y= ρ ∂y
1 ∂p Z= ρ ∂z
运动方程 应力状态及切应力互等定律
σzz +
τ yz +
∂τ yz ∂y dy
速度环量
通常, 通常,涡通量是利用速度环量这个概念来 计算的。 计算的。 在流场中任取一封闭曲线s则流速沿曲线 在流场中任取一封闭曲线 则流速沿曲线 s的积分称为曲线 上的速度环量。并规定积分 的积分称为曲线s上的速度环量 的积分称为曲线 上的速度环量。 逆时针方向绕行为s的正方向 沿s逆时针方向绕行为 的正方向。 逆时针方向绕行为 的正方向。
y
ρ v y vx
ρ vz vx
x 动量在微元体表面的输入与输出
输入输出微元体的动量流量
∂ ( ρυ x 2 ) ∂ ( ρυ yυ x ) ∂ ( ρυ zυ x ) + dxdydz x方向: ∂x + 方向: 方向 ∂y ∂z ∂ ( ρυ xυ y ) ∂ ( ρυ y 2 ) ∂ ( ρυ zυ y ) + + dxdydz y方向: 方向: 方向 ∂x ∂y ∂z
平移运动、旋转运动、 平移运动、旋转运动、线变形运动 和角变形运动
右图为任意t时刻 右图为任意 时刻 在平面流场中所取的一 个正方形流体微团。 个正方形流体微团。由 于流体微团上各点的运 动速度不一致, 动速度不一致,经过微 小的时间间隔后, 小的时间间隔后,该流 体微团的形状和大小会 发生变化, 发生变化,变成了斜四 边形。 边形。
不可压N-S方程的高效并行直接求解

不可压N-S方程的高效并行直接求解包芸;叶丰;张义招【摘要】对不可压N-S方程的数值计算,当计算规模增大时,不论是采用湍流模型计算还是直接数值模拟(Direct Numerical Simulation,DNS),大规模的并行计算都难以实现.该问题的关键是求解全场联立的压力泊松方程的并行计算技术.利用并行近似解求解方案,创建高效大规模并行计算的不可压N-S方程的直接求解方法.三维窄方腔热对流的DNS计算结果表明,该直接求解并行计算方法具有很好的并行效率,并且计算的三维湍流热对流的特性是合理的.【期刊名称】《计算机辅助工程》【年(卷),期】2016(025)003【总页数】5页(P19-23)【关键词】泊松方程;并行计算;不可压流动;湍流热对流;直接数值模拟【作者】包芸;叶丰;张义招【作者单位】中山大学力学系,广州 510275;中山大学力学系,广州 510275;中山大学力学系,广州 510275【正文语种】中文【中图分类】O357.5在航空航天等高科技工程的推动下,计算流体力学在可压缩流动的数值模拟计算技术领域进步非凡.不可压流动的数值模拟技术也在不断进步.超级计算机硬件技术的快速发展为计算流体力学数值模拟的进一步发展提供技术支持,高效并行计算技术的发展为进一步扩大不可压N-S方程的数值计算规模提供新的平台,并使计算结果数据能更好地反映流体的流动特性.热对流问题广泛存在于自然界和工业界中,研究其对全球气候变化、海洋环流、反应堆设计、工业冷却设计等问题的影响具有重要意义.[1-2]在Boussinesq假设下,湍流热对流的描述方程为不可压N-S方程联立温度对流扩散方程,因此热对流问题也是典型的不可压流动问题.高瑞利数Ra的湍流Rayleigh-Bénard(RB)热对流的直接数值模拟(Direct Numerical Simulation,DNS)面临重大挑战.[3]随着Ra的提高,热对流进入湍流状态,DNS模拟的规模不断增大导致计算所需要的成本巨大,数值计算难以实现.目前,湍流热对流的DNS只达到Ra=1012水平.[4]大规模可并行的高Ra湍流热对流DNS及其海量数据结果分析已成为热对流研究工作者们特别关注的问题.在不可压流动N-S方程的数值模拟计算中,不论采用何种计算模型或是DNS,其压力泊松方程的求解都是大规模并行计算的难题:直接求解方法不易于并行.迭代求解压力泊松方程通常采用局部算法从而较容易实现并行,但迭代计算过程占用大量的计算时间,所以很难实现高效率的大规模计算.这使得不可压流动的大规模数值模拟难以在有效时间内满足需求,因此妨碍大规模不可压流动N-S方程的湍流模型计算或DNS的进一步发展.一种新的泊松方程块三对角近似求解方案[5-6]可解决在超级计算机上的高效并行直接求解问题.这使得建立不可压流动N-S方程模拟的大规模高效并行计算方法成为可能,并可在超级计算机上实现三维高Ra湍流热对流特性研究的DNS.无量纲化后的三维不可压N-S方程为式中:V为速度矢量;p为压力;Re为雷诺数.计算边界条件为无滑移边界.投影法是数值求解不可压N-S方程组的有效方法之一.[7]实际上,不论采用何种湍流模型或DNS,以及采用何种思路求解不可压N-S方程的速度压力法,一般的动量方程都可以采用显式格式连续方程推导出压力泊松方程并进行迭代求解.大规模并行计算的主要困难为压力泊松方程必须全场联立求解.本文主要针对矩形计算域的特定情况,结合有效的泊松方程高效并行的直接求解方案,创建不可压流动DNS的可高效并行求解计算方法.2.1 网格布置和离散格式计算区域取矩形,见图1.网格数为nx×ny×nz.在设计大规模并行计算时,消息传递接口(Message Passing Interface,MPI)的计算区域沿xOy平面对z方向分割,即图中x方向较粗的线.在该面上并行计算需要数据通信;区域内部用OpenMP并行,无须数据通信.由于直接求解压力泊松方程要用到二维快速傅里叶离散余弦变换[8],因此在x和y方向必须采用等距网格且最好网格数是2k,在z方向上可根据计算的需要采用非等距网格.本文采用不可压流动计算时常用的交错网格,时间方向采用一阶精度离散,空间采用二阶精度离散格式.2.2 不可压N-S方程的并行求解方案在不可压N-S方程的数值求解过程中,采用投影法将计算分步骤进行.动量方程中的速度计算采用显式格式,在求解中很容易实现并行.由连续方程推导出的压力泊松方程在求解时需要全场联立,是求解过程中计算工作量最大的部分.同时,联立求解也给并行造成困难,是大规模高效并行计算的难点.高效合理并可大规模并行计算的压力泊松方程求解方案,是解决不可压N-S方程大规模并行计算的关键技术.建立三维泊松方程的直接求解方法.计算方法只用于矩形计算区域,x方向采用等距网格.具体做法为在xOy平面上使用二维快速傅里叶变换将空间3个方向上都要求联立求解的压力泊松方程解耦,使泊松方程变换为只在z方向上的三对角方程.将三对角方程变换为块三角方程,设计高效且可并行计算求解方法,求解后再使用对应的反变换得到原来压力泊松方程的全场解.压力泊松方程为x和y方向使用等距网格,z方向使用变距网格.二阶精度中心差分的压力泊松方程的离散形式为使用二维离散余弦傅里叶变换将全场联立的泊松方程在x和y方向上解耦.余弦傅里叶变换能使压力泊松方程自动满足压力梯度为0的边界条件.变换通过FFTW软件包[8]实现.二维离散余弦傅里叶变换公式为将式(4)代入压力泊松方程,并令展开式两边对应系数相等,可以得到一组只沿z方向联立的三对角方程,使压力泊松方程在x和y方向上解耦,求解过程变简单. 在以往的二维热对流DNS中,利用追赶法求解三对角方程的泊松方程直接解法[9],与采用迭代求解方法在计算机上单线程计算相比有效得多,但三对角方程的追赶法很难进行大规模并行计算.数学和计算机的研究者们尝试建立块三对角方程的大规模高效并行求解方案[5-6],将变换得来的三对角方程写成块三对角的形式为式中为块三对角矩阵,和为M×N阶矩阵;和为M×N维列向量,T.为已知方程的右端项,通过式(4)求在计算得到块三对角方程的解后,通过对应的二维离散余弦傅里叶的反变换公式利用以上高效并行三维压力泊松方程直接求解方法,联合其他方便并行的动量方程等计算,创建三维不可压N-S方程高效并行直接求解计算方法,使得在一些特定情况下,大规模高效并行的不可压流动N-S方程湍流模型计算或者DNS成为可能.3.1 三维湍流热对流方程RB热对流是研究流体对流传热的典型物理模型.在封闭的盒子内,下底板加热而上底板冷却后形成对流传热的研究系统.在Boussinesq假设下,无量纲化后的三维热对流的描述方程为式中:Ra为瑞利数;Pr为普朗特数;θ为相对温度,下底板为加热,θ=0.5,上底板为冷却,θ=-0.5.通过热对流方程组可以看出,整个计算过程实际上就是数值求解不可压N-S方程组联立温度的对流扩散方程.本文对三维湍流热对流进行DNS.3.2 并行计算效率采用本文建立的三维不可压流动的直接求解并行计算方法,在超级计算机“天河二号”上进行加速比测试.每个计算节点包含24个计算物理核心.测试算例的计算网格数和物理计算核心数见表1.不同计算核数时直接求解并行计算方法的加速比见图2,其中加速比以计算节点24核心数为基数.计算中z方向上网格数1 536是24核心数的64倍.可知当使用32节点即32×24=768核心数时,具有约81.7%的计算效率,当使用64节点即64×24=1 536核心数时,具有约67%的计算效率.加速比随计算机核数的进一步增加仍有较好的可增长性.由于采用快速傅里叶变换解耦压力泊松方程的需要, 并行区域只在z方向上划分,由此本文创建的直接求解方法在大规模并行计算时z方向网格数与计算核心数之间有一定关联.总体上讲,本文的不可压流动直接求解方法在大规模并行计算上已得到较好的计算效率,可以进行较大规模的三维湍流热对流的DNS.新的直接求解计算方法与本课题组原有的迭代计算方法相比,节省1/2以上的总计算时间,计算技术的进步为系列三维热对流的DNS及物理特性的研究提供有力工具.3.3 三维湍流热对流计算结果选取窄方腔,宽高比Γ=1/4,Pr=4.3,对不同Ra的三维热对流进行计算.低Ra计算采用512×64×768网格,高Ra计算采用1 024×128×1 200网格.首先计算流动的初场,根据传热特性计算时平均场统计的需要,当热对流中出现较稳定的大尺度环流流动后,继续迭代计算至少100万时间步.根据不同的Ra及流动特性,计算时间的迭代至少达到300万时间步.RB热对流主要探讨由浮力产生的对流运动对流体传热特性的影响.Ra=1010的平均场温度等值面分布见图3,下底板加热为高温,上底板冷却为低温.温度作为热对流中的重要物理量,其平均场的分布反映传热过程中对流流动带动温度运动的情况.图3中方腔的中间部分没有温度的分布,表明中间没有流动也没有传热作用.图3显示由大尺度环流带动的温度分布形态,RB热对流中对流传热的热量主要沿着侧壁和棱边向上传输.RB热对流研究的核心问题之一是对流传热效率,表征传热的物理参数是努塞尔数Nu,表示流体对流传热与热传导传热的比值.Nu与Ra之间存在一定的标度关系[3],因此需要一系列Ra数的不同数值模拟结果进行研究.一组三维方腔热对流的Nu/Ra0.3随Ra的变化见图4.图4中同时也给出计算得到的二维热对流Nu数的变化结果[10],以及KACZOROWSKI等[11]的三维计算结果对比.由此可见,本文的三维湍流热对流的DNS模拟结果是合理的.图4中可以看到,二维和三维热对流的计算Nu随Ra的变化都存在很好的标度率.计算结果与理论预测和大量试验结果得到的结论一致.[3]Γ=1/4三维方腔的Nu总体偏大(向上平移).在试验和计算中也发现同样的Nu平移现象,并且不同的Γ变化会引起不同的Nu向上平移量.[12]在传热Nu对Ra的标度率中,三维和二维流动计算结果产生差异的物理原因,还有待更深入的研究.在三维不可压流动特性的研究过程中,尤其是到湍流阶段,超大规模的数值模拟计算十分必要.依靠超级计算机技术,探索高效并行的计算方法和计算技术,进行大规模的高自由度三维不可压N-S方程的数值计算,对更深入研究不可压流动的物理和流动特性具有很重要的意义.大规模并行数值模拟计算三维不可压N-S方程,最难的计算方法和计算技术问题是压力泊松方程的高效并行求解.利用块三对角方程的大规模高效并行近似解求解方案,创建大规模高效并行计算三维不可压N-S 方程的直接求解方法.DNS是研究高Ra湍流热对流的重要手段之一.热对流问题是典型的不可压流动问题.利用本文创建的高效并行不可压流动的直接求解方法,对高Ra三维湍流热对流进行DNS.通过并行效率的验证计算,证明本文建立的直接求解方法具有较好的并行效率.一系列不同Ra的三维窄方腔热对流计算得到的传热Nu具有合理的标度率. 本文创建的大规模高效并行计算的直接求解方法,为高Ra的湍流热对流大规模高效并行计算和数值模拟研究提供有价值的计算参考.ZHANG W, ZHANG H. Scalable parallel algorithm of block tridiagonal systems for initial boundary value problem[J]. Journal of Shanghai University(Natural Science), 2007, 13(5): 497-503.XU W, BAO Y. An efficient solution for 2D Rayleigh-Bénard convection using FFT[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(4): 1-6. DOI: 10.6052/0459-1879-12-334.。
CFD

Phoenics是英国CHAM公司开发的模拟传热、流动、反应、燃烧过程的通用CFD软件,有30多年的历史。网格系统包括:直角、圆柱、曲面(包括非正交和运动网格,但在其VR环境不可以)、多重网格、精密网格。可以对三维稳态或非稳态的可压缩流或不可压缩流进行模拟,包括非牛顿流、多孔介质中的流动,并且可以考虑粘度、密度、温度变化的影响。在流体模型上面,Phoenics内置了22种适合于各种Re数场合的湍流模型,包括雷诺应力模型、多流体湍流模型和通量模型及k-e模型的各种变异,共计21个湍流模型,8个多相流模型,10多个差分格式。
STAR-cd的强项在于汽车工业,汽车发动机内的流动和传热。
编辑本段GAMBIT
专用的CFD前置处理器,FLUENT系列产品皆采用FLUENT公司自行研发的Gambit前处理软件来建立几何形状及生成网格,是一具有超强组合建构模型能力之前处理器,然后由Fluent进行求解。也可以用ICEM
CFD进行前处理,由TecPlot进行后处理。
编辑本段Fidap
基于有限元方法的通用CFD求解器,为一专门解决科学及工程上有关流体力学传质及传热等问题的分析软件,是全球第一套使用有限元法于CFD领域的软件,其应用的范围有一般流体的流场、自由表面的问题、紊流、非牛顿流流场、热传、化学反应等等。
FIDAP本身含有完整的前后处理系统及流场数值分析系统。对问题整个研究的程序,数据输入与输出的协调及应用均极有效率。
STAR-Cd是Simulation of Turbulent flow in Arbitrary
Region的缩写,CD是computational Dynamics
Ltd。是基于有限容积法的通用流体计算软件,在网格生成方面,采用非结构化网格,单元体可为六面体多面体,还可与CAD、CAE软件接口,如ANSYS,IDEAS,NASTRAN,PATRAN,ICEMCFD,GRIDGEN等,这使STAR-CD在适应复杂区域方面的特别优势。
第8章 不可压缩流体的管道流动

1v12
2g
00
2 2 v2
2g
hw12
(v1 0)
将水头损失代入上式
hw12 h f12 h j12
l (
d
) 2g
2 v2
短管流速方程:
v2 a2
短管流量方程:
1
l
d
2 gH
Q v2 A a2
短管是指沿程水头损失和局部水头损失均不可忽略不计的 管路,一般l/d<1000。短管的水力计算可分为: 1、自由出流 2、淹没出流
二、简单长管的计算
长管是指局部水头损失的总和与沿程水头损失相比很小,计 算时可以忽略不计的管路,一般l/d>1000。短管的水力计算 可分为: 1、按比阻计算 2、按水力坡度计算
l (
d
) 2g
v2
短管流速方程:
v
1
l
d
2 gH
短管流量方程:
Q v A
1
l
d
A 2 gH
3、短管水力计算的问题
① 已知管道长度l,管径d,沿程阻力系数λ ,局部水头损
失的组成和作用水头H,求流量Q。
②已知流量Q,管道长度l,管径d,沿程阻力系数λ ,局部水 头损失的组成,求作用水头H。
一、圆柱形外管嘴恒定出流
二、收缩断面的真空
三、正常使用条件
四、其它类型的管嘴出流
五、管嘴的变水头出流
一、圆柱形外管嘴恒定出流
1、基本公式
列A-A、B-B断面能量方程
zA pA
g
2 a Av A
openfoam自带算例示例

OpenFOAM 自带算例(部分)示例广州超算2015/1/30 # 摩托车求解器:simpleFoam 使用SIMPLE算法稳态求解不可压缩湍流算例:tutorials/incompressible/simpleFoam/motorBike# 法兰冷热交接面求解器:laplacianFoam 求解简单的laplacian方程,如固体的热扩散问题。
算例:tutorials/basic/laplacianFoam/flange (本例计算热扩散)# 圆柱绕流求解器:potentialFoam 简单的势流求解器,用于建立NS方程求解的初始场算例:tutorials/basic/potentialFoam/cylinder求解器:nonNewtonianIcoFoam 瞬态求解不可压缩非牛顿流体层流算例:tutorials/incompressible/nonNewtonianIcoFoam/offsetCylinder#3 PitzDaliy 管道流求解器:scalarTransportFoam 求解因变量传递方程算例:tutorials/basic/scalarTransportFoam/pitzDaily求解器:adjointShapeOptimizationFoam 稳态求解不可压缩的非牛顿流体在变形的管道中受阻湍流流动,计算压力和速度场的变化情况算例:tutorials/incompressible/adjointShapeOptimizationFoam/pitzDaily#4 化学反应计算(GRI-Mech 3.0. CH4 combustion, 53 species, 325 reactions )求解器:chemFoam 化学问题求解,单单元化学求解器,用于比较。
类似CHEMKIN算例:tutorials/basic/chemFoam/gri求解器:LTSReactingParcelFoam 稳态LTS求解可压缩、层流或湍流反应流及非反应流,多相Lagrangian包裹和多孔介质,包括质量、动量、能量显式源项算例:tutorials/lagrangian/LTSReactingParcelFoam/counterFlowFlame2D#5 发动机求解器:engineFoam 内燃机燃烧算例:tutorials/combustion/engineFoam/kivaTest#6 甲烷燃烧求解器:fireFoam算例:tutorials/combustion/fireFoam/les/smallPoolFire2D #7 均质燃烧求解器:XiFoam 求解可压缩预混/部分预混湍流模型的燃烧算例:tutorials/combustion/XiFoam/ras/moriyoshiHomogeneous#9 管道边界层求解器:boundaryFoam 主要用于1维稳态不可压缩湍流模型求解,并生成一个inlet的边界条件用于后续计算算例:tutorials/incompressible/boundaryFoam/boundaryLaunderSharma# 顶盖驱动流求解器:icoFoam 瞬态求解不可压缩牛顿流体层流算例:tutorials/incompressible/icoFoam/cavityHighRe# 搅拌器求解器:pimpleDyMFoam 算法(PISO-SIMPLE合并算法)瞬态求解不可压缩,动网格下的牛顿流体算例:tutorials/incompressible/pimpleDyMFoam/mixerVesselAMI2D求解器:SRFPimpleFoam 算法(PISO-SIMPLE合并算法)瞬态求解不可压缩湍流旋转流算例:tutorials/incompressible/SRFPimpleFoam/rotor2D# 管内流求解器:pimpleFoam 使用PIMPLE算法计算大时间步长瞬态不可压缩流算例:tutorials/incompressible/pimpleFoam/channel395# 混合器求解器:SRFSimpleFoam 稳态求解不可压缩非牛顿湍流旋转流算例:tutorials/incompressible/SRFSimpleFoam/mixer#弯管流动求解器:rhoSimplecFoam 可压缩层流或RANS湍流simplec算法稳态求解器算例:tutorials/compressible/rhoSimplecFoam/squareBend# annular热交换器求解器:rhoPimpleDyMFoam HVAC或相似情况下的层流或湍流可压缩流动瞬态求解器算例:tutorials/compressible/rhoPimpleDyMFoam/annularThermalMixer# 减压柜求解器:sonicLiquidFoam 层流或湍流可压缩跨音速/超音速液体流瞬态求解器算例:tutorials/compressible/sonicLiquidFoam/decompressionTankFine#室内对流换热求解器:buoyantBoussinesqPimpleFoam 瞬态求解浮力,不可压缩流湍流,Boussinesq+Pimple算例:tutorials/heatTransfer/buoyantBoussinesqPimpleFoam/hotRoom附:OpenFOAM 标准求解器(/features/standard-solvers.php)$FOAM_SOLVERS---->Basic---->Incompressible flow---->Compressible flow---->Multiphase flow---->Direct numerical simulation---->Combustion---->Heat transfer and buoyancy-driven flows---->Particle-tracking flows---->Molecular dynamics methods---->Direct simulation Monte Carlo methods---->Electromagnetics---->Stress analysis of Solids---->Finance1. Basic---->laplacianFoam: 求解简单的laplacian方程,如固体的热扩散问题。
divergence detected in AMG solver pressure correction,fluent典型错误

问题:8-31-rke-steady-4-0.8运行至11000迭代步是报错“divergence detected in AMG solver: pressure correction”(补充:每个工况均遇到此类情况,原因尚未找到,暂时解决办法是将压力松弛因子从0.3改为0.1);解答:This error is reported when Fluent is not able to converge the solution。
The residuals are not converged。
This error may come due to various reasons like improper mesh,improper boundary conditions,wrong material and improper solution settings。
It is advisable to re check the entire case when one encounters this error。
以上老外对这个问题的回复,确实很多客户遇到过这样的问题,原因是多方面的,主要原因集中在网格质量差和边界条件的不合理。
对于你的问题,如果之前都没有错误,到一定计算步才出现这样的问题,说明不是边条的问题,问题可能出在局部的网格上面,你将压力松弛因子调小,增加跌代次数,减小了误差,是解决问题的方法之一。
如果想彻底回避这样的问题出现,建议在网格上还需要下点工夫!附:老外对类似问题的回复,你可以参考一下。
I try to study the turbulence inside a vertical cylinder. In a first time, I take the case of steady flow. The air is introduced axially from below, deflected by means of a small conical deflector and thanks to the geometry of the chamber the air goes up into the cylinder. I take the ideal gas law, k-epsilon model, inlet and outlet pressure for boundary conditions. My problem is that I have directly the message "divergence detected in AMG solver : k when I want to iterate. I try a lot of solutions I have find in this forum without any result. Could anyone help me? Thanksin advance Check your hardware, especially RAM sockets. I have experience, that this could be initiated by some bad memory address sectors.I had a similar problem, but with pressure correction. I found that I had some highly skewed cells. Once I corrected the highly skewed cells by adapting theiso-values of cell skewness my case began to iterate.Perhaps this may be your problem. First initialize the solution and then go to contours grid and select equiangle skew and click compute to get you min and maxs. Having skewed cells of 0.9 or higher isn';t good, as in my case.Hope this helps I have check the skewed cells but it appears that in my case, this number is lower than 0.4 Is it too high?Hi. I have a simulation of a supersonic-valve running but the program shows me this message: divergence detected in AMG solver: temperature I tried to rise the limits for temperature and other solution limits but nothing has helped so far Does anyone what to do thanksTry to use more conservative Under-relaxation factor. I had the same problem with a wing in a transonic flight. According to me the segregated solver is not suitable for the conditions with high compressibility. Let me know if you succeed in using the segregated and how...I suggest using the coupled solver,Your problem will vanish... Hope to hear good news from you soon.Luca this will be something wrong with the either boundary condition or with model selection, generally if things are right fluent just converges fine without any warning or problem.in my opinion these are the signs that you are doing something wrong in setting up the case, look closelyHi, I have the same problem, and couldn't solve it by using the coupled solver. Is there any other possible way. I am simulating office room problem. It seems very simple but on every stage it is creating problems for me. I am going to try to change the underrelaxation. lets see what comes up.Thanks long ago, one of my friend was doing CFD analysis of a kitchen,, using coupled solver, and he faced the same problem, for some time he d idn’t get the converged results. Finally when I looked at his mesh. It seemed the problem is with the mesh not with the solver settings. I suggested him to make mesh more finer, and viola it gave results in one run, without any problem. so moral of the story check your mesh.My mesh is quite fine, but I will try more finer mesh. Thanks then it shall converge ..anyway have you tried using segregated solver, how the results with that Error: Divergence detected in AMG solver? Posted By: frank Date: Sun, 16 Jan 2005, 3:58 p.m. What does mean and how do i fix it? I am runing a rosseland radiation model and it wont run past 1 iteration.Frank you are using the segregated solver, so you must reduce the under relaxation factor as you can. You could have a grid issue concerning high skewness. This can be checked by going to contours grid cell equiangle skew and select compute and check the min and max. You should be below 0.9. If over then this could be your problem. It has happened to me a couple of times. thanks a million i will try this...frank AMG solver: k divergence? Posted By: Robert Date: Sun, 9 Mar 2003,11:23 a.m. How do I remedy a divergence with this message. This is for scramjet combustion in 2D with injectors on both the top and bottom. Is there any way to look up error messages?reduce underalaxtion factor.I have tried reducing the underelaxation factors but the divergence persists. Any other suggestions? Perhaps in the AMG solver Menu? It looks like a problem with your boundary conditions, be sure they're compatible with each other and consistent with the physics of what you';re trying to simulate, I think you'd better don't touch anything in the AMG menu, unless you know exactly what you're doing, It is my opinion, if this could help.请求高手指点:循环流化床中非稳态气固两相流计算,使用欧拉双流体模型,K-E湍流模型,网格质量<0.55。
工程流体力学ch4-不可压缩流体的有旋流动和二维无旋流动
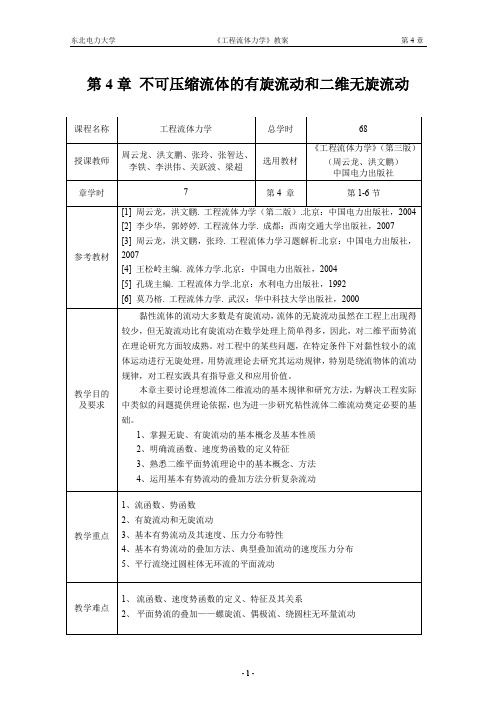
第4章不可压缩流体的有旋流动和二维无旋流动主要教学内容4.1 流体微团运动分析本节教学目的:1、熟悉:流体微团的运动可以分解为移动、转动和变形运动三部分。
2、掌握:移动、转动和变形的速度表达式。
移动(move ) —— 线速度 V x 、V y 、V z 转动 (rotation) —— 角速度ωx 、ωy 、ωz 变形(reform ) —— 线变形、角变形知识点 移动、转动和变形一、流体微团运动的分解1、平移运动如图5-2(a)所示,平移表现为A 点到A '点的位移,即x 方向和y 方向分别移动了u d t 、v d t 距离,形状不变。
流体微团的平移速度为,,u v w2、线变形运动图5-2(b)表示流体微团的平面线变形。
定义单位时间内单位长度流体线段的伸长(或缩短)量为流体微团的线变形速率。
三个方向的线变形速率分别用xx ε、yy ε、zz ε表示,则3、角变形运动图5-2(c)表示流体微团的角变形运动。
角变形速度:两正交微元流体边的夹角在单位时间内的变化量。
剪切变形速率:该夹角变化的平均值在单位时间内的变化量(角变形速度的平均值)。
过流体微团任一点A 的三个正交微元流体面上的剪切变形速率分别为4、旋转运动如图5-2(d)所示。
流体微团在发生角变形的同时,还要发生旋转运动。
若αd =βd , 则流体微团只发生角变形;若αd =-βd ,即y u x v ∂-∂=∂∂,则流体微团只发生旋转,不发生角变形旋转角速度:过流体微团上A 点的任两条正交微元流体边在其所在平面内旋转角速度的平均值,称作A 点流体微团的旋转角速度在垂直该平面方向的分量。
用符号ω表示222z y x ωωωω++=写成矢量形式为(a) (b)(c)(d)图5-2 流体微团平面运动的分解二、表示流体微团运动特征的速度表达式 在一般情况下,流体微团的运动总是可以分解成:平移运动、旋 转 运动、线变形运动及角变形运动,与此相对应的是平移速度、旋转角速度、线变形速率和剪切变形速率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求解不可压缩流动的一种新算法张常贤;高歌;闫文辉【摘要】Based on Jameson finite-volume method, a new numerical method simulating incompressible flow is created. Non-linear momentum equation is solved using four steps Runge-Kutta time stepping scheme. Good convergence of Non-linear quality has been full used. The pressure equation that solves coupled program of pressure and velocity is deducted from the continuity equation. Finally,this method is used to calculate 2-D laminar boundary layer, 2-D lid-driven cavity flow and 2-D diffuser turbulent flows using B-L turbulence model based on body fitted coordinate and appositional grids. Numerical simulation is compared and analyzed with the theoretical value, benchmark and experiment data. The results show that this numerical simulation method has strong capability to compute incompressible flow and advantage to program easily and compute efficiently.%在Jameson有限体积法的基础上发展了一种模拟不可压流动的数值方法.该算法用四步Runge-Kutta时间推进法直接求解非线性的动量方程,充分利用了良好的非线性收敛特性,并从连续方程出发推导了求解压力的方程,解决了压力与速度的耦合问题.最后用该方法在同位网格上,对二维平板边界层流、二维顶盖驱动方腔层流及二维扩压器管道湍流进行了数值模拟.计算结果与理论值、标准解及试验数据进行了比较分析,从而证实了该方法对模拟不可压流动的适用性,并显示出了编程简单、易于推广、计算效率高等优点.【期刊名称】《科学技术与工程》【年(卷),期】2011(011)031【总页数】7页(P7594-7600)【关键词】数值模拟;不可压缩流动;顶盖驱动方腔流;扩压管道流动【作者】张常贤;高歌;闫文辉【作者单位】北京航空航天大学能源与动力工程学院航空发动机气动热力国家级重点实验室,北京100191;北京航空航天大学能源与动力工程学院航空发动机气动热力国家级重点实验室,北京100191;中国航空研究院,北京100012【正文语种】中文【中图分类】O357.5求解不可压流动问题时,压力没有独立的方程,工程上常用的是Simple系列算法,该方法每一步都能满足连续方程。
在同位网格上使用这种方法时,为了解决压力的非物理振荡,须采用动量插值的办法来求解压力[1]。
但这种方法对网格质量要求高,而且把非线性动量方程线性化并迭代求解,线化后的动量方程收敛性不好,编程比较复杂,计算量大;而广泛用于求解可压流的Jameson方法,直接用Runge-Kutta时间推进法显式求解非线性动量方程,非线性的收敛性好,而且程序简单,计算量小。
本文结合了Simpler方法和Jameson方法两者的优点,发展出了一种模拟不可压流的数值方法。
从连续方程直接推导出了求解压力的方程[2],解决了压力的非物理震荡问题。
采用这种方法对二维平板层流、顶盖驱动方腔层流、扩压管道内湍流进行了数值模拟,对流项的计算采用了QUICK格式,扩散项采用二阶中心差分。
为了提高显式求解的收敛速度,文中采用了当地时间步长法。
计算结果表明:这种方法很好地模拟了各种流动的真实情况,而且大大的简化了计算,节省了机时。
1 控制方程忽略彻体力的二维、不可压的N-S方程组守恒形式为:计算层流时μ=μl,μl为层流黏性系数,可由Sutherland公式算得[3];计算湍流时,速度、压力都是经过雷诺平均之后的值,雷诺应力用代数模型求解,μ=μl+μt,μt为湍流黏性系数,本文的算例中采用Baldwin-Lomax湍流模型计算得到[4]。
2 数值方法2.1 动量方程离散在控制体上积分方程(1),并应用格林公式可以得到下面的式子:Ω为控制体的面积,Γ为相应控制体的周线。
方程(2)可以半离散化为:式(3) 中Ci,j为对流通量项,Di,j为黏性通量项,Pi,j为压力项,Ωi,j为第(i,j) 个控制体的面积。
Ci,j离散后可以写成式(4)的形式。
下标 k表示控制体的边界代号(1—e,2—n,3—w,4—s)见图1。
FkGk可以由中心格式、一阶迎风或者显式 QUICK格式[1]插值得到。
本文计算中采用QUICK格式。
图1 控制体示意图Dij离散后可以写成下面的形式:因为R,S项中有偏导数,不能简单的取平均。
采用坐标变换法求导数[2]如果对流项采用中心格式计算,为了保证计算稳定,则Dij中还包括自适应人工黏性项,具体做法参考文献[5],对每个节点式(3)相当于常微方程,可以采用Jameson改进的四步Runge-Kutta法求解,即:在保证计算稳定的前提下,为加快收敛速度,时间步长Δt应尽可能取的大一些,计算中应用了当地时间步长来加速收敛,具体做法是:λ的最大值可以取到10。
计算表明采用当地时间步长的方法可以使收敛速度提高3到4倍。
对流项采用中心格式时,为了减少计算量,人工黏性只在第一步计算,以后各步保持不变。
2.2 压力的求解因为不可压缩流动中没有求解压力的独立方程,而且压力有可能产生很强的振荡,本方法中借鉴了Simpler方法的思想,在连续方程的基础上直接推导出五点格式的求解压力的方程,由于本文算例中物理域简单,生成的网格近似正交,非正交时要做一定的修正[1]。
具体推导如下:由式(3)略去下标可写成:为虚拟速度,式(7)是针对节点上的速度写出的,同理可以得到控制体界面上速度的关系式。
、是用Runge-kutta时间推进法,经过前三步求得的相邻节点上虚拟速度的平均值,把连续方程在控制体上积分可以得到:应用高斯公式进行变换,最终可以得到式(10)中 Ak为控制体边界面积,→—nk为界面单位法向矢量。
把式(8)代入到式(10)中整理,最后可以得到一个关于节点压力的五点格式的方程[2]这样压力就可以求解了。
该算法的具体计算步骤如下:(1)假定初始速度场和压力场;(2)应用Jameson改进的四步Runge-kutta时间推进法,前三步修正速度得到虚拟速度场;(3)确定压力方程系数,在虚拟的速度场上用连续方程确定下一步的压力;(4)Runge-kutta第四步,用所求的压力修正速度,得到下一步的速度;(5) 重复(1) ~(4)步,直到收敛[2]。
图2 平板层流边界层速度剖面3 算例验证3.1 二维平板层流边界层为了校核扩散项计算方法的正确性,以及评估对流项计算格式的数值黏性对解污染的大小,本文首先对平板层流边界层的速度剖面进行了数值计算,并与Blasius解进行了比较。
计算域为1.0×0.1的矩形区域,网格用101×41的双曲正弦函数网格,对流项用QUICK格式,扩散项用中心差分格式。
图2给出了不同截面上相似速度剖面与Blasius解的比较,图3给出了当地摩阻系数Cf与布拉修斯理论值的比较,从计算的结果来看,该数值方法对扩散项和对流项的处理都是成功的。
为后面的算例奠定了基础。
图3 平板层流边界层的当地摩阻系数3.2 二维顶盖驱动方腔层流顶盖驱动方腔流是评估数值方法的经典算例[8,10],本文分别在雷诺数为 100和 1 000 两种情况下计算了方腔内的流动,对速度型、涡量分布、压力分布都进行细致的计算。
图4是在Re=100时计算的方腔竖直中心线上速度U与文献[9]中数据的比较,网格用的是21×21的均匀网格,可以看出本文使用的该算法计算的效果很好。
图5是流场速的矢量图,显示出了涡心的位置。
图6显示了采用当地时间步长技术后,残差加速收敛的情况,残差用了对数坐标表示,可以看到收敛速度提高了近3倍,随着网格数的增加,采用当地时间步长后,收敛速度的提高会更加明显。
图4 垂直中心线上速度U分布(Re=100)图7是在Re=1 000时计算的方腔竖直中心线上速度U与文献[10]中提供的标准解[10]的比较;图8是水平中心线上速度V与文献[10]中提供的标准解[10]的比较,网格分别用了51×51、101 ×101的非均匀网格,边界进行了加密。
从比较的结果可以看出本文应用的方法在比较稀疏的网格上就可以得到与标准解(网格为160×160)很接近的结果。
用SIMPLE方法、QUICK格式则需要高达256×256的网格数才能得到好的结果[11],而且迭代初场的选择,松弛因子的选取对计算都有重要影响。
用本文的方法则避免了以上的诸多不便。
图9是垂直中心线上涡量的分布,图10是水平中心线上涡量的分布,计算值与标准解符合的很好。
图11是流场的速度矢量及流线,图12是流场的压力云图,图13是流场的涡量分布,计算结果表明主涡、二次涡的结构和位置以及光滑分布的压力等值线云图都与文献[10]符合的很好。
图13 流场的涡量分布(Re=1 000)3.3 二维扩压管湍流这也是一个典型流动问题,本文采用的湍流模型是 B-L模型。
扩压管长 3.5 m,进口高 h1=0.412 m,出口高 h2=0.657 m,h2/h1=1.6。
两个实验截面上平均速度的数据是 R.L.Simpson,A.Samuel,P.Joubert[6]做的实验得到的,两个实验截面分别在扩压管下壁面距入口2.87 m和3.4 m处,经无量纲化后位置是在x=0.82和x=0.97处。
计算中使用了75×85的双曲函数网格[7],在壁面处进行了加密。
来流Re数为1.42×106。
对流项和扩散项都用中心格式处理,为使计算稳定加入了自适应人工黏性[5]。
图14、图15分别是第一、二两个试验截面上平均速度u的计算值与试验值的比较。
