六年级~9容斥原理
六年级数学专题详解 容斥原理

容斥原理在一些计数问题中,经常遇到有关集合元素个数的计算。
我们用|A|表示有限集A的元素的个数。
在两个集合的研究中,已经知道,求两个集合并集的元素个数,不能简单地把两个集合的元素个数相加,而要从两根集合的个数之中减去重复计算的元素个数,用式子可以表示成|A∪B|=|A|+|B|–|A∩B|。
我们称这一公式为包含与排除原理,简称为容斥原理。
包含与排除原理|告诉我们,要计算两个集合A、B的并集A∪B的元素个数,可以分一下两步进行:第一步:分别计算集合A、B的元素个数,然后加起来。
即先求|A|+|B|(意思是把A、B的一切元素都“包含”进来,加在一起);第二步“从上面的和中减去交集的元素的个数,即减去|A∩B|(意思是“排除”了重复计算的元素的个数)。
例1.求不超过20的正整数中是2的倍数或3的倍数的数共有多少?解:设I={1、2、3、…、19、20},A={I中2的倍数},B={I中3的倍数}。
显然题目中要求计算并集A∪B的元素个数,即求|A∪B|。
我们知道A ={2、4、6、……、20},所以|A |=10, B ={3、6、9、12、15、18},|B |=6。
A ∩B ={I 中既是2的倍数又是3的倍数}={6、12、18},所以|A ∩B |=3,根据容斥原理有|A ∪B |=|A |+|B |–|A ∩B |=10+6–3=13. 答:所求的数共有13个。
此题可以直观地用图表示如下:例2.某班统计考试成绩,数学得90分以上的有25人,语文得90分以上的有21人,两科中至少有一科在90分以上的有38人,问两科都在90分以上的有多少人?解:设A ={数学在90分以上的学生},B ={语文在90分以上的学生},由题意知|A |=25,|B |=21。
A ∪B ={数学、语文至少一科在90分以上的学生},|A ∪B |=38。
A ∩B ={数学、语文都在90分以上的学生},由容斥原理知|A ∪B |=|A |+|B |–|A ∩B |,所以|A ∩B |=|A |+|B |–|A ∪B |=25+21–38=8。
容斥原理

1、一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?2、五(1)班36个同学在一次测验中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问有几个同学两题都不对?容斥原理(也称包含与排斥原理或逐步淘汰原理或取舍原理) 在计数时,为了既不重复也不遗漏,人们研究出一种新的方法,这种间接的计数方法称为容斥原理。
其基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复。
这个原理直观易懂,思路明确,方法也是程式化,是学习组合数学中计数问题的一个十分重要的基本工具。
1、对于两个有限集合A 、B 的容斥原理,如图: B A B A B A -+=2、对于三个有限集合A 、B 、C 的容斥原理,如图:CB AC B B A B A C B A C B A +---++=容斥原理的灵活运用导入 知识精讲【例1】如图所示: (1)已知:∠AOB=90°,∠COD=80°。
∠COB=30°,求∠AOD 。
(2)已知:∠AOB=100°,∠COD=70°,∠AOD=135°,求∠COB 。
【巩固】1、如图,桌面上放有两本书,A 的面积是56,B 的面积是48,桌面面积是200,书本未覆盖部分面积是116,求两本书重叠部分的面积。
例题精讲B A D BC A O2、如下图,矩形ABCD中,AB=6厘米,BC=4厘米,扇形ABE半径AE=6厘米,扇形CBF的半径CB=4厘米,求阴影部分的面积。
【例2】50 名同学面向老师站成一行.老师先让大家从左至右按1,2,3,…,49,50 依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转。
问:现在面向老师的同学还有多少名?【巩固】1、有100 盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3,…,100,然后将编号为2的倍数的灯线拉一下,再将编号为3 的倍数的灯线拉一下,这时亮着的灯有多少盏?2、有2008 盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3,…,2008,然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?【例3】在一根长的木棍上有三种刻度线,第一种刻度线将木棍分成10等份,第二种将木棍分成12等份,第三种将木棍分成15等份。
小学奥数教程之容斥原理

学习奥数的优点1、激发学生对数学学习的兴趣,更容易让学生体验成功,树立自信。
2、训练学生良好的数学思维习惯和思维品质。
要使经过奥数训练的学生,思维更敏捷,考虑问题比别人更深层次。
3、锻炼学生优良的意志品质。
可以培养持之以恒的耐心和克服困难的信心,以及战胜难题的勇气。
可以养成坚韧不拔的毅力4、获得扎实的数学基本功,发挥创新精神和创造力的最大空间。
容斥原理学生姓名授课日期教师姓名授课时长知识定位容斥原理中的知识点比较简单,是计数问题中比较浅的一支。
这个知识点经常和数论知识结合出综合型题目。
这个原理本身并不是很难理解,不过经常和数论知识结合出题,所以对学生的理解层次要求较高,学生必须充分理解、吃透。
1.充分理解和掌握容斥原理的基本概念2.利用图形分析解决容斥原理问题知识梳理授课批注:本讲的知识点必须让学生充分理解、吃透,这个原理本身并不是很难理解,不过经常和数论知识结合出题所以对学生的理解层次要求较高。
一. 容斥原理的概念定义在一些计数问题中,经常遇到有关集合元素个数的计算。
我们用|A|表示有限集A 的元素个数。
求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:|A∪B| = |A| + |B| - |A∩B|,我们称这一公式为包含与排除原理,简称容斥原理。
图示如右:A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:A∩B,即阴影面积。
用法:包含与排除原理告诉我们,要计算两个集合A、B的并集A∪B的元素的个数,可分以下两步进行:第一步:分别计算集合A、B的元素个数,然后加起来,即先求|A|+|B|(意思是把A、B的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C=|A∩B|(意思是“排除”了重复计算的元素个数)二.竞赛考点1.容斥原理的基本概念2.与数论相结合的综合型题目例题精讲【试题来源】【题目】在一个炎热的夏日,10个小学生去冷饮店每人都买了冷饮。
六年级下册数学试题-第三节 容斥原理 全国通用(无答案)

第三节容斥原理知识提要:1.容斥原理:当两个(或几个)计数部分有重复时,为了不重复计数,应从它们的和中减去重复部分。
这种解题方法概括为一般的原理即为容斥原理。
2.容斥原理一:如下图所示,如果要计算三部分的总数,直接计算A+B就会算多了,而多算的正好是③的部分,只要把多算的减掉就可以了。
公式:A、B总数=A+B-A、B重叠概括为:单加、双减。
A B①③②3.容斥原理二:如下图所示,在计算A+B+C时,有一些部分被重复计算了:④、⑤、⑥被计算了两次,而⑦被计算了三次。
因此需要把重复计算的去掉。
去掉A、B重叠,B、C 重叠和A、C重叠的部分后,④、⑤、⑥重复计算的一次去掉了,但⑦被去掉了三次,还需要补上一次。
公式:A、B、C的总数=A+B+C-A、B重叠-B、C重叠-C、A重叠+A、B、C重叠概括为:单加、双减、三再加。
A①④⑥⑦B ②⑤③ C4.文氏图是解决容斥问题最重要的方法。
(1)实验小学四年级二班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加.这个班有多少人参加了语文或数学兴趣小组?练习1:(1)智考学校四年级学生中,有56人参加了英语竞赛,有124人参加了数学竞赛,既参加英语竞赛又参加数学竞赛的有22人,那么参加英语竞赛和数学竞赛的共有多少人?(1)对全班同学调查发现,会游泳的有20人,会打篮球的有25人.两项都会的有10人,两项都不会的有9人.这个班一共有多少人?(2)47名学生参加数学和语文考试,其中语文得分95分以上的14人,数学得分95分以上的21人,两门都不在95分以上的有22人.问:两门都在95分以上的有多少人?练习2:(1)有100位旅客,其中有10人既不懂英语又不懂俄语,有75人懂英语,83人懂俄语.问既懂英语又懂俄语的有多少人?(2)四(一)班有48名学生,在一节自习课上,写完语文作业的有30人,写完数学作业的有20人,语文数学都没写完的有6人. 问语文数学都写完的有多少人?数学作业没完成语文作业;一种是语文、数学作业都完成了.已知做完语文作业的有37人;做完数学作业的有42人.这些人中语文、数学作业都完成的有多少人?练习3:四年级科技活动组共有63人.在一次剪贴汽车模型和装配飞机模型的定时科技活动比赛中,老师到时清点发现:剪贴好一辆汽车模型的同学有42人,装配好一架飞机模型的同学有34人.每个同学都至少完成了一项活动.问:同时完成这两项活动的同学有多少人?34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?练习4:卫生部对120种食物是否含有维生素A 、C 、E 进行调查,结果发现:含维生素A 的有62种,含维生素C 的有90种,含维生素E 的有68种,同时含维生素A 和C 的有48种,同时含维生素A 和E 的有36种,同时含维生素C 和E 的有50种,同时含这三种维生素的有25种.请问这三种维生素都不含的食物有多少种?1~100的自然数中,既不能被2整除也不能被3整除的数共有多少个?练习5:1~1000的自然数中,不能被5和7整除的数共有多少个?17人会骑自行车,13人会游泳,8人会滑冰,这三个运动项目没有人全会,至少会这三项运动之一的学生数学成绩都及格了,但又都不是优秀.若全班有6个人数学不及格,那么,(1)数学成绩优秀的有几个学生?(2)有几个人既会游泳,又会滑冰?练习6:五年级一班共有36人,每人参加一个兴趣小组,共有A、B、C、D、E五个小组,若参加A 组的有15人,参加B组的人数仅次于A组,参加C组、D组的人数相同,参加E组的人数最少,只有4人.那么,参加B组的有多少人?有2000盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3, (2000)然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?1、芳草地小学四年级有58人学钢琴,43人学画画,37人既学钢琴又学画画,问只学钢琴和只学画画的分别有多少人?2、科技活动小组有55人.在一次制作飞机模型和制作舰艇模型的定时科技活动比赛中,老师到时清点发现:制作好一架飞机模型的同学有40人,制作好一艘舰艇的同学有32人.每个同学都至少完成了一项制作.问两项制作都完成的同学有多少人?3、光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?4、某校参加数学竞赛圾120名男生,80名女生,参加语文竞赛的有120名女生,80名男生,已知该校总共有260名学生参加竞赛,其中75名男生两科竞赛都参加了,那么参加数学竞赛而没有参加语文竞赛的女生有多少人?5、智考学校有学生1000人,其中500人订阅了《中国少年报》,有350人订阅了《少年文艺》,有250人订阅了《数学报》,至少订阅两种报刊的有400人,订阅了三种报刊的有100人。
小学奥数容斥原理

小学奥数容斥原理
小学奥数中的容斥原理是一种经典的数学方法,它常常用于解决有关组合计数的问题。
容斥原理可以帮助我们计算两个集合的交集、并集以及差集的元素个数。
具体来说,容斥原理告诉我们,要计算两个集合的并集的元素个数,我们可以先计算每个集合的元素个数,然后减去这两个集合的交集的元素个数。
这样可以避免重复计算。
例如,假设我们有两个集合A和B,集合A中有3个元素,集合B中有4个元素。
如果我们想计算这两个集合的并集的元素个数,根据容斥原理,我们应该先计算集合A的元素个数,再计算集合B的元素个数,然后减去集合A和集合B的交集的元素个数。
另外,容斥原理也可以用于计算三个集合的并集、四个集合的并集,以及更多集合的并集,只需要依次计算每个集合的元素个数,并根据公式依次加减交集的元素个数。
需要注意的是,在应用容斥原理时,我们需要确保计算交集和并集时没有重复计算的情况发生。
这需要我们对问题进行仔细分析和思考,以保证计算结果的正确性。
总之,容斥原理是一种解决组合计数问题的有力工具,在小学奥数中有着重要的应用,通过灵活运用容斥原理,我们可以更快、更准确地解决各类问题。
容斥原理(二)(含答案)-
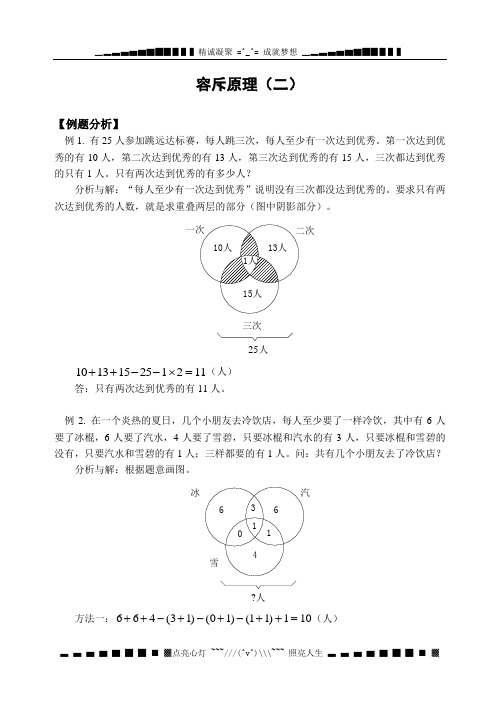
容斥原理(二)【例题分析】例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的++---⨯=(人)方法二:664311210答:共有10个小朋友去了冷饮店。
例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?30人参的有3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参7。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多多少人?最少多少人?满分的人数,即x x ≤≤78,且x ≤9,由此我们得到x ≤7。
另一方面x 最小可能是0,即没有三科都得满分的。
当x 取最大值7时,全班有()39746+=人,当x 取最小值0时,全班有()390+=39人。
答:这个班最多有46人,最少有39人。
【模拟试题】(答题时间:30分钟)1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有12的人订《数学报》,两种刊物都订的有多少人?2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两家他们住的一套房子共有多少平方米?3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
[第3讲]容斥原理
![[第3讲]容斥原理](https://img.taocdn.com/s3/m/1d0365dac1c708a1284a4477.png)
则根据公式
那么两次考试都及格的人数是 人。
3.【分析】
(法 )在 人中懂英语或俄语的有: (人)。
又因为有 人懂英语,所以只懂俄语的有: (人)。
从 位懂俄语的旅客中除去只懂俄语的人,剩下的 人就是既懂英语又懂俄语的旅
客。
(法 )在 人中懂英语或俄语的有: (人)学会把公式进行适当得变换,由包含与排除
原理,得: (人)
4.【分析】
每隔 厘米做一个记号,记号有 (个),每隔 厘米做一个记号,记号有
(个),因为 ,所以其中重合的记号有 (个),
绳子上共有 (个)记号,绳子被剪成 (段)。
5.【分析】
二年级一班共 名同学,这个班男生 人,这个班女生 人,女生中有 人不是少先队
员,女生中有 人是少先队员,男生中有 人是少先队员。
(个),乙单独看的故事有 (个),要使三人共同读过的故事最少,则丙应该尽
量读甲或乙单独看的故事,所以三人共同看过的故事最少有 (个)。
图示如下:
A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:A∩B,即阴影面积。
1.先包含——A+B
重叠部分A∩B计算了2次,多加了1次;
2.再排除——A+B-A∩B
把多加了1次的重叠部分A∩B减去。
A类、B类与C元素个数的总和=A类元素的个数+B类元素个数+C类元素个数-既是A类又是B类的元素个数-既是B类又是C类的元素个数-既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数。
三个纸片共同重叠的面积是8平方厘米三个纸片盖住桌面的总面积是3名学生参加三项课外活动其中24人参加了绘画小组2人参加了合唱小组参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的3倍又是三项活动都参加人数的7倍既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍既参加绘画小组又参加合唱小组的有1人求参加朗诵小组的人数
容斥原理(试题)六年级上册数学人教版

容斥原理容斥原理,也称为重叠原理或包含与排除原理。
原理一:两个集合A,B 相交合并成一个集合C,C 的元素个数等于A ,B 的个数和减去A 、B 的公共元素的个数,如下图所示:即:C=A+B-AB 或 AB=A+B-C原理二:三个集合A.B,C 两两都交合并点一个集合D.D 的元素个数等于A,B.C 的个数减去A.B.C 两两公共元素加上A.B.C 公共元素的个数。
如下图所示:即D=A+B+C-AB-BC-AC+ABC 或ABC=D+AB+BC+AC-A-B-C 。
1. 某校五年级举行语文和数学竞赛,参加人数占全年级人数的25,参加语文占竞赛人数的25,参加数学竞赛的占竞赛人数的34,两项都参加的有12人,全年级共有多少人?2.36名学生参加数学竞赛,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人,两题都没答对的有多少人?3.50名同学面向老师站成一行,老师先让大家从左到右按1,2,3,......依次报数,再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向老师的同学还有多少名?4.有一栋居民楼,每家都订不同的两份报纸,该居民楼共订了三种报纸,其中《楚天都市报》34份,《武汉晚报》30份,《武汉晨报》22份,那么订《武汉晚报》和《武汉晨报》的共有多少家?5、胜一小学六年级课外活动分体育、音乐、书法三个小组,分别有54人,46人.36人同时参加体育.音乐的有4人,同时参加体育书法的有7人.同时参加着乐,书法的有10人。
三个组都参加的有2人,参加课外活动一共多少人?6、桌子上放有甲,乙,西三个正方形;甲、丙重叠部分占甲正方面积的14,乙丙重叠都分占乙正方形面积的25,丙正方形与甲.乙正方形重叠部分占丙正方形面积的19,甲正方形和乙正方形面积的和是丙正方形面积的13,求甲正方形与乙正方形面积的最简整数比?7、某校五年级共有110人,参加语文、数学、英语三科活动小组,每人至少参加一组,已知参加语文小组的有52人,只参加语文小组的有16人;参加英语小组的有61人,只参加英语小组的有15人,参加数学小组的有63人,只参加数学小组的有21人.那么三组都参加的有多少人?8、一次数学竞赛,小王做对的题目占题目总数的23.小李做错5题,两人都做错的题数占题目总数的14,小王做对了多少题?9、某班有60人,其中42人会游泳,46人会骑车,50人会溜冰,55人会打乒乓球,可以肯定至少有多少人这四项都会?10、40名同学在做3道数学题时,有25人做对第一题,有28人做对第二题,有31人做对第三题,那么至少有多少人做对了三道题?11.某班有50名学生,在一次测验中有26人满分,在第二次测验中有21人满分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(一) 容斥原理
包含与排除问题也叫重叠问题,它实际上是一种集合方面的问题。
解答这类问题的主要根据是容斥原理
1.容斥原理一:
设A 、B 是两类有重叠部分的量(如图). 如果A 对应的量为a , B 对应的量为b , A 与B 重叠部分对应的量为ab,那么这两类量 的总量可以用下面的公式计算:总量=a +b —ab.
2.容斥原理二:
设A,B,C 是三类有重叠的部分的量,
如果A 对应的量为a ,B 对应的量为b ,C 对应的量为c , A 与B 重叠部分对应的量为ab. B 与C 重叠部分对应的置为bc,C 与A 重叠部分对应的量为ca,A 、B 、C 三部分重叠部分对应的量为abc,那么,这三类量的总量可以用下面的公式计算:总量=a + b + c —ab-bc-ca+abc
例1:在1到500的全部自然数中,不是7的倍数,也不是9的倍数的 数共有多少个?
例2:六年级一班有45名同学,每人都参加体育训练班,其中足球班报25人,篮球班报20人,游泳班报30人,足球、篮球都报者有10人,足球、游泳都报者有10人,游泳、篮球都报者有12人。
问三项都报者有多少人?
例3:某校六年级二班有49人参加数学、英语、语文学习小组,其中数学有30人参加,英语有20人参加;语文小组有10人参加,老师告诉同学既参加数学小组又参加语文小组 的有3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参加的只有1人,求既参加英语又参加数学小组的人数。
例4某班同学参加升学考试.得满分人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多是多少人?最少是多少人?
例5:向50名同学调查春游去颐和园还是去动物园的态度,赞成去颐和园的人数是全体的5
3,其余不赞成;赞成去动物园的比赞成去颐和园的学生多3人,其余的不赞成,另外 对去两处都不赞成的学生数比对去两处都赞成的学生数的3
1多1人,同时去颐和园和去动物园都赞成和都不赞成的学生各有多少人?
例6 李老师出了两道数学题,全班40人中,第一题有30人做对, 第二题有12人未做对,两题都做对的有20人。
(1)第2题对第1题不对有几个人?
(2)两题都不対的有几人?
【练习】
1.全班有46名同学,仅会打乒乓球的有18人,会打乒乓球又会打羽 毛球的有7人。
不会打乒乓球又不会打羽毛球的有6人。
问,仅会打羽毛球 的有多少人?
2.电视台向100人调查昨天收看电视情况,有62人看过2个频道,有34个人看过8个频道,11人两个频道都看过。
问:两个频道都没有看过的有多少人?
3. —次数学小测验只有两道题.结果全班有10人全对,第一题有25 人作对.第二题有18人做错,那么两题都做错的有多少人?
4.育才学校参加数学竞赛有120名男生,80名女生,参加语文竞赛的有120名女生,80名男生,已知该校总共有260名学生参加竞赛,其中75名男生两科竞赛都參加了,那么只参加数学竞赛而没有参加语文竞赛的有多少人?
5.在从1到1998的自然数中,能被2整除,但不能被3或7整除的数有多少个?z
6.六一儿童节那天,全班45人到颐和园去玩,有33人划了船,20人爬了山,5名同学因身体不好,他们既没有划船也没有爬山,他们游览了长廊。
问:既爬山又划船的同学有多少人?
应用经验归纳法
有些数学竞赛题直接解答有困难,我们可以从该竞赛的几个简单而特殊的情况入手去分析、归纳出一般规律、
并在这一规律的指导下解决问题。
这种解题方法叫经验归纳法。
例1:在操场上划50条直线,他们最多会有多少个交点?
例2:求两个多位数99……9×99……9乘积的各位数字之和。
1994个9 1994个9
练习
1.111…1×999…..9上面这个算式的乘积里有多少个奇数?
20个1 20个9
2.甲、乙、丙三个杯子中各装了一些水,乙杯中的水量等于甲、丙杯中的水量的平均数。
如果给丙杯中增加15毫升的水,那么,甲杯中的水量等于乙、丙两杯中的平均数。
问:甲、乙两杯中的水量哪一个多呢?多多少毫升呢?。
