2017高考试题分类汇编之函数导数(精校版)
历年高考理科数学真题汇编+答案解析(2):函数与导数(2017-2020年)

x
1 (0,1] ,则
f
(x)
2
f
(x
1)
2( x
1)( x
2)
,
f
(x) [
1 ,0] 2
∴当 x (2,3] 时, x 2 (0,1],则 f (x) 22 f (x 2) 4(x 2)(x 3) , f (x) [ 1,0]
函数 f (x) 的图像如图所示.
对任意 x (, m] ,都有 f (x) 8 ,因此 m (2,3] 9
2
2
当 x ( 1 ,1) 时, f (x) 0 , f (x) 在 (, 1) 单调递增.
22
2
当 x (1 , ) 时, f (x) 0 , f (x) 在 (, 1) 单调递减.
2
2
【答案】D
4.(2020 全国 III 卷理 12)已知 55 84 ,134 85 ,设 a log5 3, b log8 5 , c log13 8 ,则
的切线方程为
A. y 2x
B. y x
C. y 2x
D. y x
【解析】∵ f(x)为奇函数,∴ f x f x ,∴ a 1,故 f x x3 x ,因此 f x 3x 2 1 .
故曲线 y f x 在点 (0,0) 处的切线斜率 k f (0) 1 ,∴切线方程为 y x .
当直线 y x a 的截距 a 1 ,即 a 1 时,两个函数的图象有2个交点,即函数g(x)存在2个零
点,故a的取值范围是[–1,+∞) .
【答案】C 【考点】必修 1 指数函数、对数函数
16.(2018 全国 II 卷理 3)函数
f
x
ex
ex x2
福建省各地2017届高三最新考试数学理试题分类汇编:导数及其应用

福建省各地2017届高三最新考试数学理试题分类汇编导数及其应用2017.03一、选择、填空题1、(莆田市2017届高三3月教学质量检查)定义在R 上的函数()f x 的导函数为()f x ',()00f =若对任意x R ∈,都有()()1f x f x '>+,则使得()1x f x e +<成立的x 的取值范围为A .(0,)+∞B .(,0)-∞C .(1,)-+∞D .(,1)-∞2、(福建省“永安、连城、华安、漳平一中等”四地六校2017届高三第二次(12月)月考)若函数()ln f x t x =与函数2()1g x x =-在点(1 , 0)处有共同的切线l ,则t 的值是( )A . 12t =B. 1t =C. 2t =D. 3t = 3、(福建省八县(市)一中联考2017届高三上学期期中)设函数()f x 在R 上存在导数()f x ',x R ∀∈,有2()()f x f x x -+=,在(0,)+∞上()f x x '<,若(4)()84f m f m m --≥-.则实数m 的取值范围为( ) A.[2,2]- B.[2,)+∞C.[0,)+∞D.(,2][2,)-∞-+∞U4、(福州市第八中学2017届高三第六次质量检查)设曲线()1*n y x x N +=∈在点()1,1处的切线与x 轴的交点横坐标为n x ,则20151201522015320152014log log log log x x x x +++⋅⋅⋅+的值为______.5、(晋江市季延中学等四校2017届高三第二次联考)已知函数()e (e )x x f x x a =-有两个极值点,则实数a 的取值范围是________.6、(福建省师大附中2017届高三上学期期中考试)定义在R 上的函数)(x f 满足:)(1)(x f x f ->',6)0(=f ,)(x f '是)(x f 的导函数,则不等式5)(+>x x e x f e (其中e为自然对数的底数)的解集为 (A )),0(+∞ (B )),3(+∞(C )),1()0,(+∞-∞Y(D )),3()0,(+∞-∞Y7、(福建省霞浦第一中学2017届高三上学期期中考试)设函数()sin cos f x x x x =+的图象在点(,())t f t 处切线的斜率为k ,则函数()k g t =的部分图象为二、解答题1、(福建省2017年普通高中毕业班单科质量检查模拟)已知函数()1ln +--=b ax x x f 有两个零点.(Ⅰ)求()1-b a 的取值范围;(Ⅱ)设1x ,2x 是()x f 的两个相异零点,证明:2211ax x a e b <<.2、(莆田市2017届高三3月教学质量检查) 已知函数()()32231,1ln f x x x g x kx x =-+=+-.(1)若过点(,4)P a -恰有两条直线与曲线()y f x =相切,求a 的值;(2)用min{,}p q 表示,p q 中的最小值,设函数()()()min{,}(0)h x f x g x x =>,若()h x 恰有三个零点,求实数k 的取值范围.3、(漳州市八校2017届高三上学期期末联考)已知函数2()ln f x x ax =+,1()g x x b x =++,且直线12y =-是函数()f x 的一条切线. (Ⅰ)求a 的值;(Ⅱ)对任意的1[1e]x ∈,都存在2[1,4]x ∈,使得12()()f x g x =,求b 的取值范围;4、(漳州市八校2017届高三下学期2月联考)已知函数2()3f x x ax =+-,ln ()k xg x x=,当2a =时,()f x 与()g x 的图象在1x =处的切线相同. (1)求k 的值;(2)令()()()F x f x g x =-,若()F x 存在零点,求实数a 的取值范围.5、(漳州市第二片区2017届高三上学期第一次联考)设函数f (x )=e x -12x 2-x -1,函数f '(x )为f (x )的导函数.(I )求函数f '(x )的单调区间和极值;(II )已知函数y =g (x )的图象与函数y =f (x )的图象关于原点对称,证明:当x >0时,f (x )>g (x );(Ⅲ)如果x 1≠x 2,且f (x 1)+f (x 2)=0,证明:x 1+x 2<0.6、(福建省“永安、连城、华安、漳平一中等”四地六校2017届高三第二次(12月)月考) 设函数()2x f x e x ax =-3--.(Ⅰ)当0a =时,求()f x 的单调区间;(Ⅱ)当0x ≥时,()2f x ≥-,求实数a 的取值范围.7、(福建省八县(市)一中联考2017届高三上学期期中)已知函数2()(23)xf x x x e =-⋅ (Ⅰ)求函数()f x 的单调递减区间; (Ⅱ)若方程(23)xax e x-⋅=有且仅有一个实根,求实数a 的取值范围.8、(福州市第八中学2017届高三第六次质量检查)已知函数x x x f -=ln )(.(1)求函数)(x f 的单调区间;(2)若方程m x f =)()2(-<m 有两个相异实根1x ,2x ,且21x x <,证明:2221<x x .9、(福州外国语学校2017届高三适应性考试(九))已知函数()()()222ln 13x f x ax x ax a R =++--∈,()2ln x x cx bx ϕ=--.(Ⅰ)若()y f x =在[)2 +∞,上为增函数,求实数a 的取值范围.(Ⅱ)当2a ≥时,设()()()()322ln 1303x g x x ax ax f x x ⎡⎤=++-->⎣⎦的两个极值点为()1212 x x x x <,,且()()12x x ϕϕ=,求()1212'2x x y x x ϕ+⎛⎫=- ⎪⎝⎭的最小值.10、(晋江市季延中学等四校2017届高三第二次联考)已知R a ∈,函数()ln()f x x a x =+-,曲线()y f x =与x 轴相切.(Ⅰ)求()f x 的单调区间; (Ⅱ)是否存在实数m 使得)e 1()(x m xx f ->恒成立?若存在,求实数m 的值;若不存在,说明理由11、(厦门第一中学2017届高三上学期期中考试)已知函数()()2ln ,01,x f x a x x a b b R a a e =+--∈>≠且是自然对数的底数.(1)讨论函数()f x 在()0,+∞上的单调性;(2)当1a >时,若存在[]12,1,1x x ∈-,使得()()121f x f x e -≥-,求实数a 的取值范围.(参考公式:()ln xxa aa '=)12、(福建省师大附中2017届高三上学期期中考试) 已知a 为常数,R ∈a ,函数x ax x x f ln )(2-+=,x x g e )(=.(其中e 是自然对数的底数)(Ⅰ)过坐标原点O 作曲线)(x f y =的切线,设切点为),(00y x P ,求证:10=x ; (Ⅱ)令)()()(x g x f x F =,若函数)(x F 在区间]1,0(上是单调函数,求a 的取值范围.13、(福建省霞浦第一中学2017届高三上学期期中考试)已知函数2()(1)ln 2af x x a x x =-+-+.(Ⅰ)若1a >-,求函数()f x 的单调区间; (Ⅱ)若1a >,求证:3(21)()3e a a f x --<. 参考答案 一、选择、填空题1、A2、C3、B4、-15、⎪⎭⎫ ⎝⎛21,0 6、A 7、B二、解答题1、(Ⅰ)因为()()1ln ---=b ax x x f ,则()a xx f -=1' 当0≤a 时,()0'>x f 恒成立,此时()x f 至多有一个零点,与题意不符,因此0>a此时令()0'>x f 有a x 10<<;令()0'<x f 有ax 1> 所以()()11ln 1max --+-=⎪⎭⎫⎝⎛=b a a g x f 又因为()(),lim lim 0-∞==+∞→→+x f x f x x所以要使得()x f 有两个零点,则只要使得01>⎪⎭⎫⎝⎛a f 恒成立, 即a b ln 11-<-, ……………3分 所以()a a a b a ln 1-<-,所以()()max ln 1a a a b a -≤-, ……………4分 设()0,ln >-=x x x x x ϕ,则()x x ln -=ϕ, 令()0'>x ϕ可得10<<x ;令()0'<x ϕ可得1>x 所以()()11max ==ϕϕx所以()11≤-b a ……………6分 (Ⅱ)设()x f 的两个零点分别为<<10x 2x ,则()()⎩⎨⎧-+=-+=.1ln ,1ln 2211b ax x b ax x 构造函数()1,1ln 1>+-=x xx x x φ, 则()02122'1<--=xx x x x φ因此()x φ单调递减,所以()()0111=<φφx 所以1,1ln >-<x xx x 令112>=x x x ,可以得到211212ln ln x x x x x x -<-,即ax x x x x x 1ln ln 121221=--<所以2211ax x <……………8分 同理设()1.1212ln 2>⎪⎭⎫ ⎝⎛+--=x x x x φ,可得1.01212ln >>⎪⎭⎫ ⎝⎛+--x x x 令112>=x x x ,可以得到2ln ln 121212xx x x x x +<-- 注意到()x f 存在极大值01>⎪⎭⎫⎝⎛a f ,因此我们可以确定2110x a x <<<所以⎪⎪⎪⎩⎪⎪⎪⎨⎧+<---+<+-21ln ln 121ln ln 1111222a x x a x a a x ax a x即()()⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫ ⎝⎛->⎪⎭⎫ ⎝⎛++-⎪⎭⎫ ⎝⎛->⎪⎭⎫ ⎝⎛++111222121ln ln 121ln ln x a a x x a a x a x a x两式子相加后可以得到()()()()121212212221ln x x x x a b x x ax ax ->--++-+-所以()21ln 112>-++++a b ax ax 即()()a b b x b x ln 21ln 1ln 22-+>+-++- 即a b x x ln ln 21->即ae x x b >21所以,综上有2211ax x a e b << ……………12分 2、3、解(Ⅰ)设直线12y =-与()f x 相切于点20000(,ln )(0)x x ax x +>, 2121()2ax f x ax x x+'=+=,依题意得200200210,1ln ,2ax x x ax ⎧+=⎪⎪⎨⎪+=-⎪⎩ 解得01,1.2x a =⎧⎪⎨=-⎪⎩所以12a =-, 经检验:12a =-符合题意...............................................5分 (Ⅱ)由(Ⅰ)得21()ln 2f x x x =- 所以2'11()x f x x x x -=-=当x ∈时,'()0f x <,所以()f x在上单调递减,所以当x ∈时,min 1()22e f x f ==- ,max 1()(1)2f x f ==-, 22211()1x g x x x-+'=-+=, 当(1,4]x ∈时,'()0g x >,所以()g x 在[1,4]上单调递增, 所以当(1,4]x ∈时,min ()(1)2g x g b ==+,max 17()(4)4g x g b ==+, 依题意得1e 117[,][2,]2224b b --⊆++,所1e 2,22171,42b b ⎧+≤-⎪⎪⎨⎪+≥-⎪⎩ 解得193e422b -≤≤--.。
福建省各地2017届高三最新考试数学文试题分类汇编:导数及其应用

福建省各地2017届高三最新考试数学文试题分类汇编导数及其应用2017.03一、选择、填空题1、(福建省2017年普通高中毕业班单科质量检查模拟)已知函数⎩⎨⎧≥+<-=0,10,sin )(3x x x x x x f ,则下列结论正确的是(A ))(x f 有极值 (B ))(x f 有零点 (C ))(x f 是奇函数 (D ))(x f 是增函数2、(莆田市2017届高三3月教学质量检查)设函数()f x '是定义(0,2)π在上的函数()f x 的导函数()(2)f x f x π=-,当0x π<<时, 若()()133sin cos 0(),0,()23f x x f x x a f b c f π'-<===-,则 A .a b c << B .b c a << C .c b a << D .c a b <<3、(泉州市2017届高三3月质量检测)函数()()()321201f x ax a x x x =+--+≤≤在1x =处取得最小值,则实数a 的取值范围是( )A . 0a ≤B .305a ≤≤C. 35a ≤ D .1a ≤ 4、(漳州市八校2017届高三下学期2月联考)已知曲线与在x =x 0处切线的斜率的乘积为3,则x 0的值为( ) A.-2 B.2 C. D.15、(福建省“永安、连城、华安、漳平一中等”四地六校2017届高三第二次(12月)月考) 已知函数321()3f x x x ax =++.若1()x g x e =,对存在11[,2]2x ∈,存在21[,2]2x ∈,使函数()f x 导函数1()f x '满足12()()f x g x '≤,则实数a 的取值范围是 A .]45,(--∞e e B .(8]e -∞- C .]451,(2--∞e D .]81,(2--∞e 6、(福州外国语学校2017届高三适应性考试(九))知()()y f x x R =∈的导函数为()'f x ,若()()32f x f x x --=,且当0x ≤时,()23f x x ≤,则不等式()()226128f x f x x x -->-+的解集是( ) A .12x >B .1x > C.32x > D .2x > 7、(晋江市季延中学等四校2017届高三第二次联考)若曲线C 1:2(0)y ax a =>与曲线C 2:x y e =存在公共切线,则a 的取值范围为( )A .2[,)4e +∞B .2(0,]4eC .2[,)8e +∞D .2(0,]8e8、(福建省2017年普通高中毕业班单科质量检查模拟)已知函数()()xf x x a e -=-,曲线()y f x =上存在不同的两点,使得曲线在这两点处的切线都与y 轴垂直,则实数a 的取值范围是(A )2(,)e -+∞ (B )2(,0)e - (C )2(,)e --+∞ (D )2(,0)e --二、解答题1、(福州市2017届高三3月质量检测)已知函数()2ln f x a x x ax =+-(a ∈R ).(Ⅰ)若3x =是()f x 的极值点,求()f x 的单调区间; (Ⅱ)求()()2g x f x x =-在区间[]1,e 的最小值()h a .2、(莆田市2017届高三3月教学质量检查) 已知函数()3231,()1ln f x x x g x kx x =-+=+-.(1)设函数()(),1(),1f x x h xg x x <⎧=⎨≥⎩,当0k <时,讨论()h x 零点的个数;(2)若过点(,4)P a -恰有三条直线与曲线()y f x =相切,求a 的取值范围.3、(泉州市2017届高三3月质量检测)函数()()()()21211,,1x f x f x x n x e g x n R x -⎡⎤=-++=∈⎣⎦+.(1)讨论()f x 的单调性;(2)当()f x 在R 上单调递增时,证明:对任意12,x x R ∈且()()()()21211221,2g x g x g x g x x x x x +-≠>-.4、(漳州市八校2017届高三上学期期末联考)已知函数13()ln 144f x x x x=-+-. (1)求函数()f x 的单调递减区间;(2)设2()24g x x bx =-+-,若对任意1(0,2)x ∈,2[1,2]x ∈,不等式12()()f x g x ≥恒成立,求实数b 的取值范围.5、(漳州市八校2017届高三下学期2月联考)已知函数,m ∈R .(Ⅰ)求函数f (x )的单调递增区间; (Ⅱ)设A (x 1,f (x 1)),B (x 2,f (x 2))为函数f (x )的图象上任意不同两点,若过A ,B 两点的直线l 的斜率恒大于-3,求m 的取值范围.6、(漳州市第二片区2017届高三上学期第一次联考) 已知函数f(x)=ax+xlnx(a ∈R)(1)若函数f(x)在区间[e,+∞)上为增函数,求a 的取值范围;(2)当a=1且k ∈Z 时,不等式k(x-1)<f(x)在x ∈(1,+∞)上恒成立,求k 的最大值.7、(福建省“永安、连城、华安、漳平一中等”四地六校2017届高三第二次(12月)月考) 已知函数()(1)ln ()af x x a x a x=--+∈R . (Ⅰ)当10≤<a 时,求函数)(x f 的单调区间;(Ⅱ)是否存在实数a ,使得至少存在一个0(0,)x ∈+∞,使00()f x x >成立,若存在,求出实数a 的取值范围;若不存在,请说明理由.8、(福建省八县(市)一中联考2017届高三上学期期中)已知函数2ln )(x x a x f += (a为常数) .(1)当2a =-时,求()f x 的单调区间;(2)当(1,]x e ∈时,讨论方程()0=x f 根的个数; (3)若0>a ,且对任意的121211,,2x x x x e ⎡⎤∈≠⎢⎥⎣⎦且,都有()()121211f x f x x x -<-,求实数a 的取值范围.9、(福州市第八中学2017届高三第六次质量检查)已知函数x x a ax x f ln )2()(2++-=.(1)当0>a 时,若)(x f 在区间],1[e 上的最小值为2-,求a 的取值范围;(2)若对任意2121),,0(,x x x x <+∞∈,且22112)(2)(x x f x x f +<+恒成立,求a 的取值范围.10、(福州外国语学校2017届高三适应性考试(九))已知函数()ln xf x x=. (1)求函数()f x 的极值;(2)若()()x a g x xf x e +=-,试证明:当2a ≥-时,()0g x <.11、(晋江市季延中学等四校2017届高三第二次联考)已知函数()(1)xf x e x =- (Ⅰ)判断函数()f x 是否存在斜率为1-的切线; (Ⅱ)若方程21()(0)2f x ax a =≠有两个不等的实根,求a 的取值范围.12、(三明市第一中学2017届高三上学期期中考试)已知函数1()ln ,(0,)f x a x a a R x=+≠∈. (I )若1a =,求()f x 的极值和单调区间;(II )若在区间(0,]e 上至少存在一点0x ,使得0()0f x <成立,求实数a 的取值范围.13、(福建省师大附中2017届高三上学期期中考试)已知函数(),ln x a xe x f x-=,曲线()x f y =在点()()11f ,处的切线平行于x 轴.(Ⅰ)求()x f 的单调区间;(Ⅱ)证明:e b ≤时,()22)(2+-≥x x b x f .参考答案一、选择、填空题 1、答案: D解析:(1) 0<x 时,0cos 1)(≥-='x x f ,当且仅当时-∈=Z k k x ,2π取等号,所以)(x f 单调递增;0≥x 时,03)(2≥='x x f ,当且仅当0=x 时取等号,所以)(x f 单调递增; 所以,)(x f 没有极值.(2)由(1)知,利用单调性,0<x 时0)0()(=<f x f ,)(x f 没有零点; 0≥x 时01)0()(>=≥f x f ,)(x f 没有零点 故)(x f 在R 上没有零点,排除B.(3) 显然,),()(),()(x f x f x f x f ≠--≠-既不是奇函数也不是偶函数,排除C. (4) 由(1)(2)分析可知,)(x f 在R 上是增函数。
2017年北京市各区高三文科数学分类汇编函数与导数(教师版)

1 / 372017年北京市各区高三文科数学分类汇编函数与导数(教师版)(2017年朝阳期末) 5.已知0a ,且1a ,则“函数x y a 在R 上是减函数”是“函数3(2)y a x 在R 上是增函数”的( A )A. 充分而不必要条件 B .必要而不充分条件C. 充分必要条件D.既不充分也不必要条件(2017年东城期末)(14)已知函数1)(||)(a xx x f .当0a 时,函数)(x f 的单调递增区间为(,);若函数a x f x g )()(有3个不同的零点,则a 的取值范围为(222,1) .(2017年海淀期末)3. 下列函数中,既是偶函数又在区间上单调递增的是 ( D )A.21()2y B.2y x C.2log y x D.||1y x (2017年西城期末)2.下列函数中,定义域为R 的奇函数是( D )(A )21y x (B )tan y x (C )2x y (D )sin y x x12.函数4x y x的定义域是__(0,)__;最小值是__4__.14.设函数3,0,()log ,,x x a f x x x a ≤≤其中0a .①若3a ,则[(9)]f f __2__;②若函数()2y f x 有两个零点,则a 的取值范围是__[4,9)__.(2017年丰台期末)8.已知函数()ln()sin f x x a x ,给出下列命题:①当0a 时,(0,e)x ,都有()0f x ;②当e a 时,(0,+)x ,都有()0f x ;③当1a 时,0(2,)x ,使得0()0f x .其中真命题的个数是( B )(A )0(B )1(C )2(D )3(2017年石景山期末)4.下列函数中既是奇函数又在区间(0,)上单调递减的是(D)2 / 37A .x y e B .ln()y x C .3y x D .1y x10.函数2()(3)1xf x x x 的最大值为________3_______.(2017年昌平期末)(4) 下列四个函数中,在其定义域上既是奇函数又是单调递增函数的是( D ) (A )x y e (B )2log y x(C )sin y x (D )3y x (11)12,2,ln 2e e 三个数中最大的数是_____12e ____ . (14) 若函数2,11,()ln ,1.x x f x x x a ①当2a 时,若()1f x ,则x______0_____;②若()f x 的值域为[0,2],则a 的取值范围是____122,e e ____ .(2017年通州期末)4.下列函数中,既是偶函数又在区间0,1内单调递减的是( C ) A .2y x B .2x yC .cos y xD .ln y x8.已知函数20,0,x x f x x x 若函数1g x f x k x 有且只有一个零点,则实数k 的取值范围是( D )A .(1),-B .(0),+C .(10)-,D .(1)0,-(,+)(2017年房山期末)3.下列函数中为奇函数的是( A )A .y=sin 2xB .y=xcosxC .y=D .y=|x| 14.设函数f (x )=是(﹣∞,+∞)上的增函数,那么实数k 的取值范围为(﹣∞,﹣1]∪[1,2] .(2017年朝阳一模)(5)已知函数224,2,()log ,>2x x x f x x a x 有两个不同的零点,则实数a 的取值范围是( C )。
(完整word)(完整word版)2017年高考数学理试题分类汇编:三角函数,推荐文档

2017年高考数学理试题分类汇编:三角函数二填空选择题【答案】【答案】【解析】1. (2017年天津卷文)设函数f(X )2sin( x ),x R ,其中o’ 丨兀若 f(5n )2,f0,且f(x)的 最小正周期大2 n ,则2 3 1 3n12 11 n 24(B ) (D)2 3 1 311 n 72 7n 24【解析】由题意得58 11 82匕k2,其中k i ,k 2所以3(k 22kJ -,又 T —23,所以1,所以2k 1,由|也,故选A .2. (2017年天津卷理 )设函数f(x) 2si n(R ,其中)0,且f (x)的最小正周期大于2 ,则(A )12 (B )12 24(D)24【解析】由题意81182k 1 k2所以 2k 11 12 ,3.( 2017年全国川卷文22,其中 k 1,k 2 Z,所以故选A.ABC 内角 3(k2A, B,C 的对边分别为a,b,c ,已知2kJ ,又T 0■,所以015根据正弦定理有:sin 600sin B2 n已知曲线 C 1: y =cos x ,C 2: y =sin (2x +),则下面结论正确的是3冗A •把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C 2450 A7504.(2017年新课标I ) 9.A.4B.2C.D.B .把C 1上各点的横坐标伸长到原来的 2 倍,纵坐标不变,再把得到的曲线向左平移n 个单位长度,得到曲线12 C 2C . 把C 1上各点的横坐标缩短到原来的1倍, 2纵坐标不变, 再把得到的曲线向右平移n个单位长度,得到曲线6C 2D . 把C 上各点的横坐标缩短到原来的1倍, 2纵坐标不变, 再把得到的曲线向左平移n个单位长度,得到曲线12C2【答案】D6.(2017年浙江卷)14 .已知△ABC , AB = AC =4 , BC =2.点D 为AB 延长线上一点,BD=2,连结CD ,贝U △BDC 的面积是 _____ cos Z BDC = _____ ,8.( 2017年新课标n 文)16.△ ABC 的内角 A,B,C 的对边分别为 a,b,c 若2b cosB= a cosC+c cosA,则B=— 39. ( 2017年新课标n 文)3.函数f x = sin ( 2x+—)的最小正周期为 (C )3【解析】f x 1 cos 2 x , 3cosx3 cos 2x \ 3 cosx -44cosx乜21, x 0,:那么cosx 0,1,当 cosx3时函数取得最大值222【答案】11.【解析】取 BC 中点E , DC 中点F , 由题意:AE BC,BF CD , .15 △ ABE 中,BE 1DBC1DBC 1cos ABCcos一 ,siL 1—AB 44:164SA BCD5. ( 2017年新课标n 卷理)14•函数f x .2sin x 3 cosx 0,2的最大值是-BD BC sin DBC .2 22又 cos DBC 1 2s in DBF1, sin DBF 410 4cos BDC sin DBF综上可得,△ BCD 面积为cos BDC-10 47.(2017年新课标n 文).13函数f x =2cosxsinx 的最大值为10.(2017年浙江卷)11.我国古代数学家刘徽创立的“割圆术”可以估算圆周率 n,理论上能把n 的值计算到任意精度.【解析】本题选择D 选项.4]! tan( -)ta^ 1 丄 4 4 614.(2017年江苏卷 5. tan()若15. (2017年新课标I 文)11 . △ABC 的内角A 、B 、C 的对边分别为 a 、b 、c 。
湖北省各地2017届高三最新考试数学理试题分类汇编函数Word版含答案
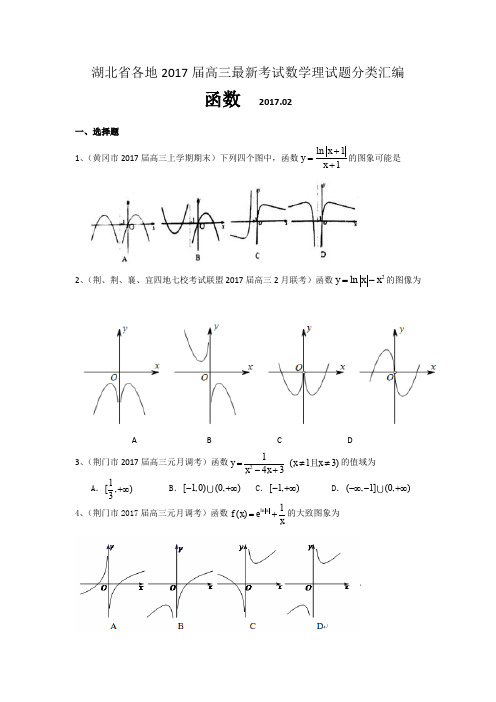
湖北省各地2017届高三最新考试数学理试题分类汇编函数2017.02一、选择题1、(黄冈市2017届高三上学期期末)下列四个图中,函数ln 11x y x +=+的图象可能是2、(荆、荆、襄、宜四地七校考试联盟2017届高三2月联考)函数2ln y x x =-的图像为A B C D3、(荆门市2017届高三元月调考)函数21(13)43y x x x x =≠≠-+且的值域为A .1[,)3+∞ B .[1,0)(0,)-+∞ C .[1,)-+∞ D .(,1](0,)-∞-+∞4、(荆门市2017届高三元月调考)函数ln 1()xf x e x=+的大致图象为5、(天门、仙桃、潜江市2017届高三上学期期末联合考试)定义在R 上的偶函数()f x 满足:对于任意的12,(,0]x x ∈-∞12()x x ≠,有2121()[()()]0x x f x f x -->,则当n *∈N 时,有A .()(1)(1)f n f n f n -<-<+B .(1)()(1)f n f n f n -<-<+C .(1)()(1)f n f n f n +<-<-D .(1)(1)()f n f n f n +<-<-6、(武汉市2017届高三毕业生二月调研考)下列函数既是奇函数,又在[]1,1-上单调递增是是A. ()sin f x x =B.()2ln 2xf x x-=+ C. ()()12x xf x e e -=- D.())ln f x x =-7、(武汉市武昌区2017届高三1月调研)已知函数()23f x ax a =-+,若()01,1x ∃∈-,()00f x =,则实数a 的取值范围是( )A .()(),31,-∞-+∞ B .(),3-∞- C. ()3,1- D .()1,+∞8、(襄阳市2017届高三1月调研)函数()ln 37f x x x =+-的零点所在的区间是 A. ()0,1 B. ()1,2 C. ()2,3 D. ()3,4 9、(襄阳市优质高中2017届高三1月联考)已知函数()2ln xf x x x=-,则函数()y f x =的大致图象为10、(孝感市七校教学联盟2017届高三上学期期末)下列函数中,既是偶函数又在()0,+∞上单调递减的函数是( )A .32y x = B .1y x =+ C .24y x =-+ D .2xy =11、(湖北省部分重点中学2017届高三上学期第二次联考)设()[)[]21,11,1,2x f x x x ∈-=-∈⎪⎩,则()21f x dx -=⎰的值为A.423π+B. 32π+C. 443π+D. 34π+ 12、(荆州中学2017届高三1月质量检测)一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度18()721v t t t=-++ (t 的单位:s ,v 的单位:m/s )行驶至停止,在此期间汽车继续行驶的距离(单位:m )是( )A .48ln2+B .45718ln 42+ C .1018ln6+ D .418ln6+ 13、(天门、仙桃、潜江市2017届高三上学期期末联合考试)已知图甲是函数()y f x =的图象,图乙由图甲变换所得,则图乙中的图象对应的函数可能是A .(||)y f x =B .|()|y f x =C .(||)y f x =-D .(||)y f x =--14、(武汉市武昌区2017届高三1月调研)已知函数()f x 的部分图像如图所示,则()f x 的解析式可以是( )A .()222x f x x -=B .()2cos xf x x = C. ()2cos x f x x =-15、(孝感市七校教学联盟2017届高三上学期期末)下函数xx x f 2)1ln()(-+=的零点所在的大致区间是 ( )A .(3,4)B .(2,e )C .(0,1)D .(1,2)参考答案1、C2、A3、D4、C5、C6、C7、B8、C9、A 10、C 11、A 12、C 13、C 14、D 15、D二、填空、解答题1、(黄冈市2017届高三上学期期末)设函数()2,12,1x x f x x -≥⎧=⎨<⎩,则满足()110xf x -≥的x 取值范围为 .2、(荆州市五县市区2017届高三上学期期末)若函数()()sin x x f x e ae x -=+为奇函数,则a =________.3、(黄冈市2017届高三上学期期末)已知函数()()21, 1.f x x g x a x =-=- (1)若关于x 的方程()()f x g x =只有一个实数解,求实数a 的取值范围; (2)若当x R ∈时,不等式()()f x G X ≥恒成立,求实数a 的取值范围. 参考答案 1、2、13、解:(Ⅰ)方程|f (x )|=g (x ),即|x 2﹣1|=a |x ﹣1|,变形得|x ﹣1|(|x +1|﹣a )=0,显然,x =1已是该方程的根,从而欲使原方程只有一解,即要求方程|x +1|=a 有且仅有一个等于1的解或无解, ∴a <0.…………5分(Ⅱ)当x ∈R 时,不等式f (x )≥g (x )恒成立,即(x 2﹣1)≥a |x ﹣1|(*)对x ∈R 恒成立,①当x =1时,(*)显然成立,此时a ∈R ; ②当x ≠1时,(*)可变形为a≤,令φ(x )==因为当x >1时,φ(x )>2,当x <1时,φ(x )>﹣2,所以φ(x )>﹣2,故此时a ≤﹣2. 综合①②,得所求实数a 的取值范围是a ≤﹣2.…………10分。
《精品》2017-2019三年高考真题数学(理)分项汇编专题03导数及其应用(选择题、填空题)(原卷

专题03导数及其应用(选择题、填空题)1.【2019年高考全国Ⅲ卷理数】已知曲线y a e x x ln x在点(1,a e)处的切线方程为y=2x+b,则A.a e,b1B.a=e,b=1C.a e 1,b 1D.a e 1,b 12.【2018年高考全国Ⅰ卷理数】设函数f(x)x3(a 1)x2ax.若f(x)为奇函数,则曲线y f(x)在点(0,0)处的切线方程为y 2xA.y 2xC.3.【2017年高考全国Ⅱ卷理数】若x2是函数y xB.y xD.f(x)(x2ax 1)e x 1的极值点,则f(x)的极小值为A.1B.2e 3C.5e 3D.14.【2017年高考浙江】函数y=f(x)的导函数y f (x)的图象如图所示,则函数y=f(x)的图象可能是5.【2018年高考全国Ⅱ卷理数】函数f x e xex2x的图像大致为16.【2018 年高考全国Ⅲ卷理数】函数yx 4 x 2 2的图像大致为7.【2019 年高考天津理数】已知 aR ,设函数 f ( x )x 2 2a x 2a , x 1,x a ln x , x 1.若关于 x 的不等式 f ( x ) 0在 R上恒成立,则 a的取值范围为A .C .0,10,eB .D .0,21,e8.【2019 年高考浙江】已知恰有 3 个零点,则 A .a <–1,b<0C .a >–1,b<0x, x 0 a , b R ,函数 f ( x )1 1x 3 (a 1)x 2 ax , x 03 2B .a <–1,b >0D .a >–1,b >0.若函数y f ( x ) ax b9.【2017 年高考全国Ⅲ卷理数】已知函数f ( x ) x22 x a (ex 1ex 1)有唯一零点,则 a =A .12B .1 3C .1 2D .110.【2019 年高考全国Ⅰ卷理数】曲线y 3( x2x )ex在点(0,0) 处的切线方程为____________.211.【2018 年高考全国Ⅱ卷理数】曲线y 2ln( x 1) 在点 (0, 0) 处的切线方程为__________.12.【2018 年高考全国Ⅲ卷理数】曲线yax 1ex在点0,1处的切线的斜率为2,则 a ________.的距离的最小值是 13.【2019 年高考江苏】在平面直角坐标系 xOy 直线 x y 0中,P 是曲线 y x .4 x( x 0)上的一个动点,则点 P 到14.【2018 年高考全国Ⅰ卷理数】已知函数fx 2si n x sin2 x ,则 fx的最小值是_____________.15.【2019 年高考江苏】在平面直角坐标系 xOy中,点 A 在曲线 y =ln x 上,且该曲线在点 A 处的切线经过点(-e ,-1)(e 为自然对数的底数),则点 A 的坐标是.16.【2019 年高考北京理数】设函数fx exa ex(a 为常数).若 f (x )为奇函数,则 a =________; 若 f (x )是 R 上的增函数,则 a 的取值范围是___________.17.【2018 年高考江苏】若函数在内有且只有一个零点,则在上的最大值与最小值的和为.18.【2017 年高考江苏】已知函数f ( x )x 2 x e1e,其中 e 是自然对数的底数.若f (a 1)f (2 a 2) 0 ,则实数 a 的取值范围是.19.【2017 年高考山东理数】若函数e xf ( x ) ( e2.71828是自然对数的底数)在 f ( x )的定义域上单调递增,则称函数 f ( x )具有 M 性质.下列函数中所有具有 M 性质的函数的序号为.①f ( x ) 2x②f ( x ) 3x③f ( x ) x3④f ( x ) x223 xx3。
2017届高三最新考试数学理试题分类汇编:函数含答案

江西省各地2017届高三最新考试数学理试题分类汇编函数2017.02一、选择、填空题 1、(红色七校2017届高三第二次联考)下列函数中,在其定义域内既是增函数又是奇函数的是( ) A .B .y=﹣log 2xC .y=3xD .y=x 3+x 2、(赣吉抚七校2017届高三阶段性教学质量监测考试(二))函数21x x y e+=(其中e 为自然对数的底)的图象大致是( )A .B . C. D .3、(赣中南五校2017届高三下学期第一次联考)设方程有两个不等的实根和,则( ) A .B .C .D .4、(赣州市2017届高三上学期期末考试).函数sin (0)ln ||xy x x =≠的图象大致是( )A .B . C. D .5、(上饶市2017届高三第一次模拟考试)函数2xy x a=+的图象不可能是( )6、(江西省师大附中、临川一中2017届高三1月联考)已知()f x 为奇函数,函数()f x 与()g x 的图像关于直线1y x =+对称,若()14g =,则()3f -=( )A. 2-B. 2C. 1-D. 4 7、(新余市2017高三上学期期末考试)下列四个图中,函数10ln 11x y x +=+的图象可能是( )8、(宜春中学2017届高三2月月考)若a =20.5,b=log 0.25,c=0.52,则a 、b 、c 三个数的大小关系式( ) A .c <a <bB .b <c <aC .c <b <aD .b <a <c9、(江西省重点中学协作体2017届高三下学期第一次联考) 已知函数()y f x =是定义在R 上的偶函数,且在(,0]-∞上是增函数,若不等式)()(x f a f ≥对任意[1,2]x ∈恒成立,则实数a 的取值范围是( )A .]1,(-∞B .]1,1[-C .]2,(-∞D .]2,2[-10、(江西师范大学附属中学2017届高三12月月考)已知函数2(0)()(0)x x x f x e x -->⎧=⎨-≤⎩,若关于x 的方程[()]0f f x m +=恰有两个不等实根1x 、2x ,则12x x +的最小值为 .11、(南昌市八一中学2017届高三2月测试)设函数()f x 是周期为6的偶函数,且当[0,3]x ∈时()3f x x =,则f(2017)=12、(红色七校2017届高三第二次联考)已知函数f (x )=ln ,若f ()+f ()+…+f ()=503(a +b ),则a 2+b 2的最小值为( )A .6B .8C .9D .1213、(赣吉抚七校2017届高三阶段性教学质量监测考试(二))已知函数()10 1 0 0xx x f x e x -≤⎧=⎨>⎩,,(e 为自然对数的底),若函数()()g x f x kx =-恰好有两个零点,则实数k 的取值范围是( )A .()1 e ,B .(] 10e , C.(] 10e , D .()10 +∞, 14、(新余市2017高三上学期期末考试)已知函数()f x 是定义在R 上的奇函数,若22log (1),[0,1)()173,[1,)22x x f x x x x +∈⎧⎪=⎨-+∈+∞⎪⎩,则关于x 的方程()0(01)f x a a +=<<的所有根之和为( )A .11()2a -B .1()12a - C. 12a - D .21a -15、(宜春中学2017届高三2月月考)函数f (x )=+ln|x|的图象大致为( )A .B .C .D .16、(宜春中学2017届高三2月月考)已知f (x )是R 上的奇函数,且当x≥0时,f (x )=﹣x 2+2x ,则当x <0时,f (x )的解析式是( ) A .f (x )=﹣x (x+2) B .f (x )=x (x ﹣2)C .f (x )=﹣x (x ﹣2)D .f (x )=x (x+2)17、(九江市十校2017届高三第一次联考)若)1(,2)]([,21)(-+=-=g x x f g x x f x 则的值为( ).21.-A 6.B 1.C 3.D二、解答题1、(九江市十校2017届高三第一次联考)方便、快捷、实惠的电动车是很多人的出行工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年高考试题分类汇编之函数与导数 一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的) 1(2017北京文)已知函数,则( ) .A是偶函数,且在R上是增函数 .B是奇函数,且在R上是增函数
.C是偶函数,且在R上是减函数 .D是奇函数,且在R上是增函数
2.(2017新课标Ⅱ文)函数2()ln(28)fxxx的单调递增区间是( ) .A(,2) .B (,1) .C(1,) .D (4,)
3.(2017山东文)设,0121,1xxfxxx,若1fafa,则1fa ( )2.A 4.B 6.C 8.D 4.(2017山东文)若函数exfx在fx的定义域上单调递增,则称函数fx具有M性质.下列函数中具有M性质的是( )
xxfA2)(. .B2fxx .C3xfx .D
cosfxx
5.(2017新课标Ⅰ文数)函数sin21cosxyx的部分图像大致为( )
6.(2017新课标Ⅰ文数)已知函数()lnln(2)fxxx,则( )
1()3()3xxfx()fx.A)(xfy在)2,0(单调递增 .B)(xfy在)2,0(单调递减
.C)(xfy的图像关于直线1x对称 .D)(xfy的图像关于点)0,1(对称
7.(2017天津文)已知奇函数()fx在R上是增函数.若 0.822
1(log),(log4.1),(2)5afbfcf,则,,abc的大小关系为( )
.Aabc .Bbac .Ccba .Dcab
8.(2017天津文)已知函数||2,1,()2,1.xxfxxxx设Ra,若关于x的不等式()||2xfxa在R上恒成立,则a的取值范围是( )
.A[2,2] .B[23,2] .C[2,23] .D[23,23] 9.(2017新课标Ⅲ文数)函数2sin1xxxy的部分图像大致为( )
.A .B .C .D 10.(2017新课标Ⅲ文数)已知函数211()2()xxfxxxaee有唯一零点,则a ( ) 21.A .B13 .C12 1.D 11.(2017新课标Ⅲ理数)已知函数211()2()xxfxxxaee有唯一零点,则a ( )21.A 31.B 21.C 1.D 12.(2017新课标Ⅰ理数)函数()fx在(,)单调递减,且为奇函数.若(11)f,则满足21()1xf的x的取值范围是( ) .A[2,2] .B[1,1] .C[0,4] .D[1,3] 13.(2017新课标Ⅱ理)若2x是函数21()(1)exfxxax的极值点,则()fx的极小值为( ) 1.A .B32e .C35e 1.D
14.(2017天津理)已知奇函数()fx在R上是增函数,()()gxxfx.若2(log5.1)ag,0.8(2)bg,(3)cg,则cba,,的大小关系为( )
.Aabc .Bcba .Cbac .Dbca
15.(2017天津理)已知函数23,1,()2,1.xxxfxxxx设Ra,若关于x的不等式()||2xfxa在R上恒成立,则a的取值范围是( ) ]2,1647.[A ]1639,1647.[B ]2,32.[C ]1639,32.[D 16.(2017山东理)已知当0,1x时,函数21ymx的图象与yxm的图象有且只有一个交点,则正实数m的取值范围是( )
.A0,123,U .B0,13,U .C0,223,U.D0,23,U
17.(2017浙江)若函数baxxxf2)(在区间]1,0[上的最大值是M,最小值是m,则mM ( )
.A与a有关,且与b有关 .B与a有关,但与b无关
.C与a无关,且与b无关 .D与a无关,但与b有关
18.(2017浙江)函数)(xfy的导函数的图象如图所示, 则函数)(xfy的图象可能是( ) ()yfx 二、填空题(将正确的答案填在题中横线上) 19.(2017山东文)已知)(xf是定义在R上的偶函数,且)2()4(xfxf.若当[3,0]x时,()6xfx,则)919(f .
20.(2017天津文)已知aR,设函数()lnfxaxx的图象在点))1(,1(f处的切线为l,则l在y轴上的截距为 .
21.(2017新课标Ⅱ文)已知函数()fx是定义在R上的奇函数,当(,0)x时,
32()2fxxx,则
(2)f
.
22.(2017新课标Ⅲ文数)设函数10()20xxxfxx,,,,则满足1()()12fxfx的x的取值范围是__________. 23.(2017新课标Ⅰ文数)曲线21yxx在点)2,1(处的切线方程为_______.
24.(2017新课标Ⅲ理数)设函数10()20xxxfxx,,,,则满足1()()12fxfx的x的取值
范围是_____________. 25.(2017山东理)若函数xefx(2.71828eL是自然对数的底数)在fx的定义域上单调递增,则称函数fx具有M性质.下列函数中所有具有M性质的函数的序号为 . ①2xfx ②3xfx ③3fxx ④22fxx
26.(2017江苏)已知函数.若,则实数的取
值范围是 . 31()2eex
xfxxx2
(1)(2)0fafaa27.(2017江苏).设是定义在R上且周期为1的函数,在区间上,
其中集合,,则方程的解的个数是 . 三、解答题(应写出必要的文字说明、证明过程或演算步骤) 28.(2017北京文)已知函数. (Ⅰ)求曲线在点处的切线方程; (Ⅱ)求函数在区间上的最大值和最小值.
29.(2017新课标Ⅱ文)设函数2()(1)exfxx. (1)讨论()fx的单调性; (2)当0x时,()1fxax,求a的取值范围.
30.(2017天津文))设,abR,||1a.已知32()63(4)fxxxaaxb,()e()xgxfx. (Ⅰ)求()fx的单调区间; (Ⅱ)已知函数()ygx和exy的图象在公共点),(00yx处有相同的切线,
()fx[0,1)2,,(),,xxDfxxxD
1{nDxxn*}nN()lg0fxx
()ecosxfxxx()yfx(0,(0))f
()fxπ[0,]2(i)求证:()fx在0xx处的导数等于0; (ii)若关于x的不等式()exgx在区间00[1,1]xx上恒成立,求b的取值范围.
31.(2017新课标Ⅲ文数)已知函数.)12(ln)(2xaaxxxf (1)讨论()fx的单调性; (2)当0a时,证明3()24fxa. 32.(2017新课标Ⅰ文数)已知函数.)()(2xaaeexfxx (1)讨论()fx的单调性; (2)若()0fx,求a的取值范围.
33.(2017山东文)已知函数3211,32fxxaxaR. (Ⅰ)当2a时,求曲线yfx在点3,3f处的切线方程; (Ⅱ)设函数cossingxfxxaxx,讨论gx的单调性并判断有无极值,有极值时求出极值. 34.(2017新课标Ⅱ理)已知函数2()lnfaxaxxxx,且()0fx. (1)求a; (2)证明:()fx存在唯一的极大值点0x,且220e()2fx. 35.(2017北京理)已知函数.cos)(xxexfx (Ⅰ)求曲线)(xfy在点))0(,0(f处的切线方程; (Ⅱ)求函数)(xf在区间[0,]上的最大值和最小值.
36.(2017浙江)已知函数).21()12()(xexxxfx (Ⅰ)求)(xf的导函数;
π2(Ⅱ)求)(xf在区间上的取值范围.
37.(2017山东理)已知函数22cosfxxx,cossin22xgxexxx. (Ⅰ)求曲线yfx在点,fx处的切线方程; (Ⅱ)令hxgxafxaR,讨论hx单调性并判断有无极值,若有求出极值.
1[+)2,
