简单选择排序的基本过程
C++排序讲义

j j
j
j
ji
ij
ij
ij
i
i
i
二趟排序: 13 4 48 38 27 49 55 65 97 76 Ch8_3.c
希尔排序特点
子序列的构成不是简单的“逐段分割”,而是将相隔某个增 量的记录组成一个子序列 希尔排序可提高排序速度,因为 分组后n值减小,n² 更小,而T(n)=O(n² ),所以T(n)从总体 上看是减小了 关键字较小的记录跳跃式前移,在进行最后一趟增量为1 的插入排序时,序列已基本有序 增量序列取法 无除1以外的公因子 最后一个增量值必须为1
j j j j j j 排序结果:(13 27 38 49 65 76 97)
算法评价
时间复杂度 若待排序记录按关键字从小到大排列(正序) 关键字比较次数: n
1 n 1
i 2
记录移动次数:
2 2(n 1)
i 2
n
若待排序记录按关键字从大到小排列(逆序) n (n 2)(n 1) 关键字比较次数: i
§8.2 交换排序
冒泡排序
排序过程
将第一个记录的关键字与第二个记录的关键字进行比较,若 为逆序r[1].key>r[2].key,则交换;然后比较第二个记录与第 三个记录;依次类推,直至第n-1个记录和第n个记录比较为 止——第一趟冒泡排序,结果关键字最大的记录被安置在最 后一个记录上 对前n-1个记录进行第二趟冒泡排序,结果使关键字次大的记 录被安置在第n-1个记录位置 重复上述过程,直到“在一趟排序过程中没有进行过交换记 录的操作”为止
输出:13 27 38 49 50 65
76 97 50 49 38 65 27 13 输出:13 27 38 49 50 65 97 50
数据结构-第十章-内部排序

0
1
2
3
4
5
6
7
8
i=5
MAXINT 49 2 3
MAXINT 49 6 3 MAXINT 49 6 3 MAXINT 49 6 8
38 1
38 1 38 1 38 1
65 97 5 0
65 5 65 5 65 5 97 0 97 0 97 0
76 4
76 4 76 4 76 4
13
27
49
i=6
最坏情况下,待排记录按关键字非递增有序 排列(逆序)时,第 i 趟时第 i+1 个对象 必须与前面 i 个对象都做排序码比较, 并且 每做1次比较就要做1次数据移动。总比较 次 数 为 (n+2)(n-1)/2 次 , 总 移 动 次 数 为 (n+4)(n-1)/2。 在平均情况下的排序码比较次数和对象移 动次数约为 n2/4。因此,直接插入排序的 时间复杂度为 O(n2)。 直接插入排序是一种稳定的排序方法。
折半插入排序 (Binary Insertsort)
基本思想 既然每个要插入记录之前的纪录 已经按关键字有序排列,在查找插入位 臵时就没有必要逐个关键字比较,可以 使用折半查找来实现。由此进行的插入 排序称之为折半插入排序。
折半插入排序的算法
void BInsertSort (SqList &L){ for (i=2;i<=L.length;++i){ L.r[0]=L.r[i]; low=1;high=i-1; //查找范围由1到i-1 while(low<=high){ m=(low+high)/2; if LT(L.r[0].key,L.r[m].key) high=m-1; else low=m+1; }//while 折半查找 for (j=i-1;j>=high+1;--j) L.r[j+1]=L.r[j]; //折半查找结束后high+1位臵即为插入位臵 L.r[high+1]=L.r[0]; }//for }//BInsertSort
各种排序方法汇总

一.选择排序1. 选择排序法基本思想:每一趟从待排序的数据元素中选出最小<或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
b5E2RGbCAP2. 排序过程:【示例】:初始关键字 [49 38 65 97 76 13 27 49]第一趟排序后 13 [38 65 97 76 49 27 49]第二趟排序后 13 27 [65 97 76 49 38 49]第三趟排序后 13 27 38 [97 76 49 65 49]第四趟排序后 13 27 38 49 [49 97 65 76]第五趟排序后 13 27 38 49 49 [97 97 76]第六趟排序后 13 27 38 49 49 76 [76 97]第七趟排序后 13 27 38 49 49 76 76 [ 97]最后排序结果 13 27 38 49 49 76 76 973.void selectionSort(Type* arr,long len>{long i=0,j=0。
/*iterator value*/long maxPos。
assertF(arr!=NULL,"In InsertSort sort,arr is NULL\n ">。
p1EanqFDPwfor(i=len-1。
i>=1。
i-->{maxPos=i。
for(j=0。
j<I。
J++>< P>if(arr[maxPos]< P>if(maxPos!=i>swapArrData(arr,maxPos, i>。
}}选择排序法的第一层循环从起始元素开始选到倒数第二个元素,主要是在每次进入的第二层循环之前,将外层循环的下标赋值给临时变量,接下来的第二层循环中,如果发现有比这个最小位置处的元素更小的元素,则将那个更小的元素的下标赋给临时变量,最后,在二层循环退出后,如果临时变量改变,则说明,有比当前外层循环位置更小的元素,需要将这两个元素交换.DXDiTa9E3d二.直接插入排序插入排序<Insertion Sort)的基本思想是:每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子文件中的适当位置,直到全部记录插入完成为止。
数字的大小排序

数字的大小排序数字的大小排序在我们的日常生活中经常会用到,不论是在数学领域,还是在实际应用中,都需要对数字按照大小进行排序。
本文将介绍几种常用的数字排序方法,以帮助读者更好地理解和应用数字排序算法。
一、冒泡排序冒泡排序是一种简单直观的排序算法,基本思想是通过比较相邻的两个数字,如果前一个数字大于后一个数字,则交换它们的位置,这样一轮比较下来,最大的数字会“冒泡”到数组的末尾。
重复这个过程,直到所有数字按照从小到大的顺序排列。
举个例子来说明冒泡排序的过程,假设我们有一个包含6个数字的数组:[5, 2, 8, 3, 1, 9]。
经过一轮冒泡比较后,数组变为[2, 5, 3, 1, 8, 9]。
接着再进行一轮冒泡比较,数组变为[2, 3, 1, 5, 8, 9]。
继续进行比较和交换,最终得到按照从小到大排序的数组:[1, 2, 3, 5, 8, 9]。
二、选择排序选择排序是一种简单但不稳定的排序算法,它的基本思想是每次从待排序的数字中选出最小的数字,放到已排序数字的末尾,直到所有数字按照从小到大的顺序排列。
以同样的例子来说明选择排序的过程,假设我们有一个包含6个数字的数组:[5, 2, 8, 3, 1, 9]。
首先,找到数组中最小的数字1,并将其与数组的第一个数字5交换位置,此时数组变为[1, 2, 8, 3, 5, 9]。
接着,在剩下的数字中,找到最小的数字2,并将其与数组的第二个数字8交换位置,此时数组变为[1, 2, 8, 3, 5, 9]。
继续进行比较和交换,最终得到按照从小到大排序的数组:[1, 2, 3, 5, 8, 9]。
三、插入排序插入排序是一种简单且稳定的排序算法,适用于小规模的数字排序。
它的基本思想是从待排序的数字中逐个取出数字,并将其插入到已排序数字的合适位置,直到所有数字按照从小到大的顺序排列。
继续以同样的例子来说明插入排序的过程,假设我们有一个包含6个数字的数组:[5, 2, 8, 3, 1, 9]。
C语言八大排序算法
C语⾔⼋⼤排序算法C语⾔⼋⼤排序算法,附动图和详细代码解释!来源:C语⾔与程序设计、⽵⾬听闲等⼀前⾔如果说各种编程语⾔是程序员的招式,那么数据结构和算法就相当于程序员的内功。
想写出精炼、优秀的代码,不通过不断的锤炼,是很难做到的。
⼆⼋⼤排序算法排序算法作为数据结构的重要部分,系统地学习⼀下是很有必要的。
1、排序的概念排序是计算机内经常进⾏的⼀种操作,其⽬的是将⼀组“⽆序”的记录序列调整为“有序”的记录序列。
排序分为内部排序和外部排序。
若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
反之,若参加排序的记录数量很⼤,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
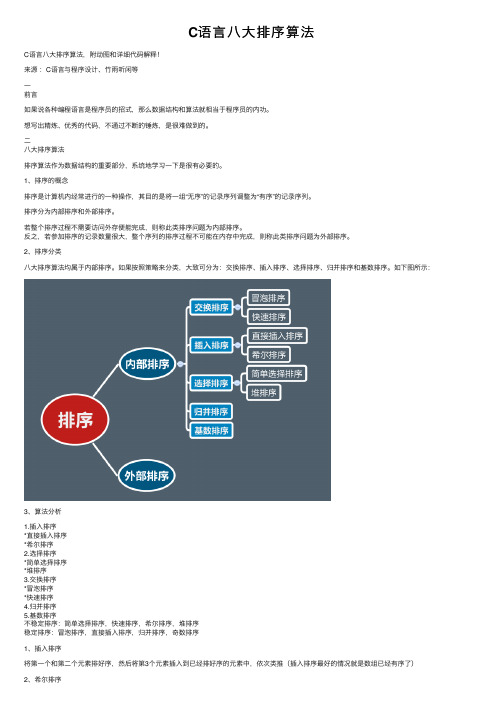
2、排序分类⼋⼤排序算法均属于内部排序。
如果按照策略来分类,⼤致可分为:交换排序、插⼊排序、选择排序、归并排序和基数排序。
如下图所⽰:3、算法分析1.插⼊排序*直接插⼊排序*希尔排序2.选择排序*简单选择排序*堆排序3.交换排序*冒泡排序*快速排序4.归并排序5.基数排序不稳定排序:简单选择排序,快速排序,希尔排序,堆排序稳定排序:冒泡排序,直接插⼊排序,归并排序,奇数排序1、插⼊排序将第⼀个和第⼆个元素排好序,然后将第3个元素插⼊到已经排好序的元素中,依次类推(插⼊排序最好的情况就是数组已经有序了)因为插⼊排序每次只能操作⼀个元素,效率低。
元素个数N,取奇数k=N/2,将下标差值为k的数分为⼀组(⼀组元素个数看总元素个数决定),在组内构成有序序列,再取k=k/2,将下标差值为k的数分为⼀组,构成有序序列,直到k=1,然后再进⾏直接插⼊排序。
3、简单选择排序选出最⼩的数和第⼀个数交换,再在剩余的数中⼜选择最⼩的和第⼆个数交换,依次类推4、堆排序以升序排序为例,利⽤⼩根堆的性质(堆顶元素最⼩)不断输出最⼩元素,直到堆中没有元素1.构建⼩根堆2.输出堆顶元素3.将堆低元素放⼀个到堆顶,再重新构造成⼩根堆,再输出堆顶元素,以此类推5、冒泡排序改进1:如果某次冒泡不存在数据交换,则说明已经排序好了,可以直接退出排序改进2:头尾进⾏冒泡,每次把最⼤的沉底,最⼩的浮上去,两边往中间靠16、快速排序选择⼀个基准元素,⽐基准元素⼩的放基准元素的前⾯,⽐基准元素⼤的放基准元素的后⾯,这种动作叫分区,每次分区都把⼀个数列分成了两部分,每次分区都使得⼀个数字有序,然后将基准元素前⾯部分和后⾯部分继续分区,⼀直分区直到分区的区间中只有⼀个元素的时候,⼀个元素的序列肯定是有序的嘛,所以最后⼀个升序的序列就完成啦。
第十章排序
依次类推,则完成排序。
正序:时间复杂度为O(n) 逆序:时间复杂度为O(n2)
适合于数据较少的情况。
2013-5-13 排序n个记录的文件最多需要n-1趟冒泡排序。 举例:图8-2-5
25
思想:小的 浮起,大的 沉底。
25 56 49 78 11 65 41 36
初 始 关 键 字
25 49 56 11 65 41 36 78
第 一 趟 排 序 后
25 49 11 56 41 36 65
25 11 49 41 36 56
11 25 41 36 49
11 25 36 41
11 25 36
简单选择排序、堆排序。
1、简单选择排序
思想:首先从1~n个元素中选 出关键字最小的记录交换到第 一个位置上。然后再从第2 个 到第n个元素中选出次小的记 录交换到第二个位置上,依次 类推。
时间复杂度为O(n2), 适用于待排序元素较少的情况。
3 j 3 k 3 k 3
互换
9 9 j 9 9
1 1 1 j 1 k 8
插入算法如下:
9
方法:Ki与Ki-1,K i-2,…K1依次比较,直到找到应插入的位置。 void insertSort(RedType L[ ],int n)
{ int i ,j; for(i=2; i<=n; i++) if(L[i].key<L[i-1].key)
{
L[0]=L[i];
L[j+1]=L[j]; L[j+1]=L[0];
数据结构之排序算法
65
865
姓名
学号
成绩
班级 机97.6
李红 9761059 95
3
第二章 数据结构与算法 (续 )
2016/2/25
4
2.8 排
2.8.1 概 述
序
1、排序的功能:将一个数据元素(或记录)的任意 序列,重新排成一个按关键字有序的序列。
2、排序过程的组成步骤:
• 首先比较两个关键字的大小;
• 然后将记录从一个位置移动到另一个位置。
36
n=8, int(n/2)=4开始 25 41 11 65 49 36 11 56
25 41 65
78 (b): 78被筛选后的状态 11 25 49 78 36 56 65 41 49
56 36
78
78
2016/2/25 (d): 56 被筛选后的状态
(c): 49被筛选后的状态
(e): 被筛选之后建成堆
2016/2/25
假设待排序的记录存放在地址连续的 一组存储单元中,那么这种存储方式 下的数据类型可描述为:
5
#define MAX 20 typedef struct { int key; float otherinfo;
0 1 2 3 4
key info
MAX
}RedType;
… … …
2016/2/25
举例,图8-2-2
2016/2/25
2、折半插入排序
11
折半插入排序在寻找插入位置时,不是逐个比较而是利用折半 查找的原理寻找插入位置。待排序元素越多,改进效果越明显。
例:有6个记录,前5 个已排序的基础上,对第6个记录排序。 [ 15 27 36 53 69 ] 42
有五个数从小到大排序的题

有五个数从小到大排序的题全文共四篇示例,供读者参考第一篇示例:有五个数从小到大排序是数学中的一种基本问题,在解题的过程中需要遵循一定的步骤和方法,才能正确地得出答案。
这种问题对于培养学生的逻辑思维能力和数学解题能力都具有很大的帮助。
在本文中,我们将介绍有五个数从小到大排序的题目,探讨其解题方法和意义。
我们来看一个简单的例子:有五个数分别是1,5,3,2,4,请将它们从小到大排序。
要解决这个问题,我们可以采用冒泡排序的方法。
冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来,直到不再需要交换,这样就完成了一次排序。
按照冒泡排序的方法,我们可以先比较1和5,发现它们的顺序正确,然后比较5和3,需要交换它们的位置,然后继续比较5和2,再进行交换,最后再比较5和4,继续进行交换,得到的结果就是1,2,3,4,5,这就是五个数从小到大排序的结果。
除了冒泡排序外,还有很多其他的排序方法,比如快速排序、插入排序、选择排序等等。
每种排序方法都有其独特的优点和适用的场合,要根据具体的情况选择合适的方法。
有五个数从小到大排序的题目,不仅仅是一道简单的排序问题,更是培养学生逻辑思维和解决问题能力的一种有效手段。
通过解决这类问题,学生可以学会如何进行逻辑推理,如何有效地分析和解决问题,从而提高他们的综合素质和解决实际问题的能力。
第二篇示例:有五个数从小到大排序是一道我们在日常生活中经常碰到的题目,排序算法是计算机科学中最基本的算法之一。
虽然看似简单,但是排序问题涉及到了很多计算机科学中的基本概念和技巧。
本文将介绍五个数字从小到大排序的过程,以及几种常见的排序算法。
让我们假设有五个数字分别为5, 3, 1, 4, 2。
我们要将这五个数字从小到大进行排序。
下面将介绍几种不同的排序算法。
冒泡排序是最简单的一种排序算法,它的基本思想是两两比较相邻的元素,如果顺序不对则交换它们的位置,重复这个过程直到整个序列有序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单选择排序的基本过程
简单选择排序是一种基本的排序算法,它的思想是每次从待排序的
元素中选择最小(或最大)的元素,放到已排序序列的末尾。
通过不
断重复这个过程,直到所有元素都排序完成。
1. 初始化
首先,我们需要准备一个待排序的数组。
假设数组的长度为n,我
们将数组的第一个元素作为已排序序列,其余的n-1个元素作为待排序序列。
2. 选择最小元素
从待排序序列中选择最小的元素,将其与待排序序列的第一个元素
交换位置。
这样,已排序序列的长度增加1,待排序序列的长度减少1。
3. 重复选择
重复上述步骤,直到待排序序列中的元素全部被选择完毕。
每次选
择最小元素的过程可以通过遍历待排序序列来实现。
4. 完成排序
当待排序序列中的元素全部被选择完毕后,排序过程结束。
此时,
已排序序列中的元素按照从小到大的顺序排列。
简单选择排序的时间复杂度为O(n^2),其中n为待排序序列的长度。
虽然它的时间复杂度较高,但是它的实现简单,适用于小规模的排序
任务。
下面,我们通过一个具体的例子来演示简单选择排序的基本过程。
假设我们有一个待排序序列:[5, 2, 8, 3, 1, 9, 4, 6, 7]。
首先,我们将数组的第一个元素5作为已排序序列,其余的8个元
素作为待排序序列。
在第一次选择中,我们遍历待排序序列,找到最小的元素1。
然后,将1与待排序序列的第一个元素5交换位置,得到已排序序列[1, 2]和
待排序序列[5, 8, 3, 9, 4, 6, 7]。
在第二次选择中,我们遍历待排序序列,找到最小的元素3。
然后,将3与待排序序列的第一个元素5交换位置,得到已排序序列[1, 2, 3]
和待排序序列[5, 8, 9, 4, 6, 7]。
依次类推,我们可以得到以下的排序过程:
第一次选择:[1, 2, 8, 3, 5, 9, 4, 6, 7]
第二次选择:[1, 2, 3, 8, 5, 9, 4, 6, 7]
第三次选择:[1, 2, 3, 4, 5, 9, 8, 6, 7]
第四次选择:[1, 2, 3, 4, 5, 6, 8, 9, 7]
第五次选择:[1, 2, 3, 4, 5, 6, 7, 9, 8]
第六次选择:[1, 2, 3, 4, 5, 6, 7, 8, 9]
最终,我们得到了一个按照从小到大排列的有序序列。
简单选择排序的基本过程就是这样。
通过每次选择最小的元素,并将其放到已排序序列的末尾,我们可以逐步完成整个排序过程。
虽然简单选择排序的时间复杂度较高,但是它的实现简单直观,适用于小规模的排序任务。
在实际应用中,我们可以根据具体的需求选择合适的排序算法来提高排序效率。
