2019届苏教版(文科数学) 曲线与方程 单元测试
2019届苏教版(文科数学) 圆与方程 单元测试

2019届苏教版(文科数学) 圆与方程 单元测试 一、选择题(共12小题,60分)1.圆与直线的位置关系为( )A.相离B.相切C.相交D.以上都有可能2.已知圆 的弦过点 ,当弦长最短时,该弦所在直线方程为( )A.B.C.D.3.已知动圆 过定点 ,并且在定圆的内部与其相内切,求动圆圆心 的轨迹方程为( ) A.B.C.D.4.已知点A 是圆C :x 2+y 2+ax +4y +10=0上任意一点,点A 关于直线x +2y -1=0的对称点也在圆C 上,则实数a 的值为( ) A.10 B.-10 C.-4 D.45.已知直线l 为圆224x y +=在点处的切线,点P 为直线l 上一动点,点Q 为圆()2211x y ++=上一动点,则PQ 的最小值为 ( )1+ C. 1+ D. 1 6.已知直线x +7y =10把圆x 2+y 2=4分成两段弧,这两段弧长之差的绝对值等于( )A. B. C.π D.2π7.已知圆 与圆 关于直线对称,则圆 的方程为( )A. B.C. D.8.圆 ,圆,M , N 分别是圆,上的动点,P 为x 轴上的动点,则的最小值( )A. B.C. D.9.在空间直角坐标系中,点P(3,4,5)与Q(3,-4,-5)两点的位置关系是( ) A.关于x 轴对称 B.关于xOy 平面对称 C.关于坐标原点对称 D.以上都不对10.若直线 与曲线有两个交点,则实数 的取值范围是( ) A.B.C.D.11.在空间直角坐标系中,与点 ,,等距离的点的个数为( )A.1B.2C.3D.无数12.若直线l :ax +by +1=0始终平分圆M :x 2+y 2+4x +2y +1=0的周长,则(a -2)2+(b -2)2的最小值为 ( ) A.B.5C.2D.10二、填空题(共4小题,20分)13.已知圆M 的圆心坐标为(3,4),且A(-1,1),B(1,0),C(-2,3)三点一个在圆M 内,一个在圆M 上,一个在圆M 外,则圆M 的方程为 .14.在平面直角坐标系中, 分别是 轴和 轴上的动点,若以为直径的圆与直线相切,则圆 .15.与圆22:240C x y x y +-+=外切于原点,且半径为的圆的标准方程为 . 16.过点(3,1)作圆(x -2)2+(y -2)2=4的弦,其中最短弦的长为 . 二、解答题(共6小题,70分)17.已知 为圆 上的动点, 的坐标为, 在线段上,满足.(Ⅰ)求 的轨迹 的方程.(Ⅱ)过点 的直线 与 交于两点,且,求直线 的方程.18.已知直线 过坐标原点 ,圆 的方程为 .(1)当直线 的斜率为时,求 与圆 相交所得的弦长;(2)设直线 与圆 交于两点,且 为的中点,求直线 的方程.19.已知方程22240x y x y m +--+=; (1)若此方程表示圆,求m 的取值范围;(2)若(1)中的圆与直线240x y +-=相交于M 、N 两点且OM ON ⊥ (O 为坐标原点),求m 的值。
2019届苏教版(文科数学) 3.1 导 数 单元测试

五年高考考点一导数的概念及其几何意义1.(2016山东,10,5分)若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是()A.y=sin xB.y=ln xC.y=e xD.y=x3答案A2.(2014课标Ⅱ,8,5分)设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a=()A.0B.1C.2D.3答案D3.(2017课标全国Ⅰ文,14,5分)曲线y=x2+在点(1,2)处的切线方程为.答案x-y+1=04.(2017天津文,10,5分)已知a∈R,设函数f(x)=ax-ln x的图象在点(1,f(1))处的切线为l,则l在y轴上的截距为.答案15.(2016课标全国Ⅲ,15,5分)已知f(x)为偶函数,当x<0时,f(x)=ln(-x)+3x,则曲线y=f(x)在点(1,-3)处的切线方程是.答案y=-2x-16.(2014江苏,11,5分)在平面直角坐标系xOy中,若曲线y=ax2+(a,b为常数)过点P(2,-5),且该曲线在点P处的切线与直线7x+2y+3=0平行,则a+b的值是.答案-37.(2014江西,13,5分)若曲线y=e-x上点P处的切线平行于直线2x+y+1=0,则点P的坐标是.答案(-ln2,2)8.(2016浙江自选,“复数与导数”模块,03(2),5分)求曲线y=2x2-ln x在点(1,2)处的切线方程.解析因为(2x2-ln x)'=4x-,所以曲线在点(1,2)处的切线的斜率为3.因此,曲线在点(1,2)处的切线方程为y=3x-1.9.(2013浙江,22,14分)已知a∈R,函数f(x)=x3-3x2+3ax-3a+3.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)当x∈[0,2]时,求|f(x)|的最大值.解析(1)由题意得f'(x)=3x2-6x+3a,故f'(1)=3a-3.又f(1)=1,所以所求的切线方程为y=(3a-3)x-3a+4.(2)由于f'(x)=3(x-1)2+3(a-1),0≤x≤2.故(i)当a≤0时,有f'(x)≤0,此时f(x)在[0,2]上单调递减,故|f(x)|max=max{|f(0)|,|f(2)|}=3-3a.(ii)当a≥1时,有f'(x)≥0,此时f(x)在[0,2]上单调递增,故|f(x)|max=max{|f(0)|,|f(2)|}=3a-1.(iii)当0<a<1时,设x1=1-2=1+,则0<x1<x2<2,f'(x)=3(x-x1)(x-x2).列表如下:由于f(x1)=1+2(1-a),f(x2)=1-2(1-a)·,故f(x1)+f(x2)=2>0,f(x1)-f(x2)=4(1-a)·>0.从而f(x1)>|f(x2)|.所以|f(x)|max=max{f(0),|f(2)|,f(x1)}.①当0<a<时,f(0)>|f(2)|.又f(x1)-f(0)=2(1-a)-(2-3a)=>0,故|f(x)|max=f(x1)=1+2(1-a)②当≤a<1时,|f(2)|=f(2),且f(2)≥f(0).又f(x1)-|f(2)|=2(1-a)-(3a-2)=-,-所以当≤a<时,f(x1)>|f(2)|.故f(x)max=f(x1)=1+2(1-a)当≤a<1时,f(x1)≤|f(2)|.故f(x)max=|f(2)|=3a-1.综上所述,|f(x)|max=-10.(2013浙江文,21,15分)已知a∈R,函数f(x)=2x3-3(a+1)x2+6ax.(1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;(2)若|a|>1,求f(x)在闭区间[0,2|a|]上的最小值.解析(1)当a=1时,f'(x)=6x2-12x+6,所以f'(2)=6.又因为f(2)=4,所以切线方程为y=6x-8.(2)记g(a)为f(x)在闭区间[0,2|a|]上的最小值.f'(x)=6x2-6(a+1)x+6a=6(x-1)(x-a).令f'(x)=0,得到x1=1,x2=a.当a>1时,比较f(0)=0和f(a)=a2(3-a)的大小可得g(a)=-当a<-1时,得g(a)=3a-1.综上所述,f(x)在闭区间[0,2|a|]上的最小值为-g(a)=-11.(2017北京文,20,13分)已知函数f(x)=e x cos x-x.(1)求曲线y=f(x)在点(0,f(0))处的切线方程;(2)求函数f(x)在区间上的最大值和最小值.解析本题考查导数的几何意义,考查利用导数研究函数的单调性、最值.(1)因为f(x)=e x cos x-x,所以f'(x)=e x(cos x-sin x)-1,f'(0)=0.又因为f(0)=1,所以曲线y=f(x)在点(0,f(0))处的切线方程为y=1.(2)设h(x)=e x(cos x-sin x)-1,则h'(x)=e x(cos x-sin x-sin x-cos x)=-2e x sin x.当x∈时,h'(x)<0,所以h(x)在区间上单调递减.所以对任意x∈有h(x)<h(0)=0,即f'(x)<0.所以函数f(x)在区间上单调递减.因此f(x)在区间上的最大值为f(0)=1,最小值为f=-.12.(2017山东文,20,13分)已知函数f(x)=x3-ax2,a∈R.(1)当a=2时,求曲线y=f(x)在点(3,f(3))处的切线方程;(2)设函数g(x)=f(x)+(x-a)cos x-sin x,讨论g(x)的单调性并判断有无极值,有极值时求出极值.解析本题考查导数的几何意义;用导数研究函数的单调性;用导数求函数的极值、最值. (1)由题意f'(x)=x2-ax,所以当a=2时,f(3)=0,f'(x)=x2-2x,所以f'(3)=3,因此,曲线y=f(x)在点(3,f(3))处的切线方程是y=3(x-3),即3x-y-9=0.(2)因为g(x)=f(x)+(x-a)cos x-sin x,所以g'(x)=f'(x)+cos x-(x-a)sin x-cos x=x(x-a)-(x-a)sin x=(x-a)(x-sin x),令h(x)=x-sin x,则h'(x)=1-cos x≥0,所以h(x)在R上单调递增.因为h(0)=0,所以当x>0时,h(x)>0;当x<0时,h(x)<0.(1)当a<0时,g'(x)=(x-a)(x-sin x),当x∈(-∞,a)时,x-a<0,g'(x)>0,g(x)单调递增;当x∈(a,0)时,x-a>0,g'(x)<0,g(x)单调递减;当x∈(0,+∞)时,x-a>0,g'(x)>0,g(x)单调递增.所以当x=a时g(x)取到极大值,极大值是g(a)=-a3-sin a,当x=0时g(x)取到极小值,极小值是g(0)=-a.(2)当a=0时,g'(x)=x(x-sin x),当x∈(-∞,+∞)时,g'(x)≥0,g(x)单调递增;所以g(x)在(-∞,+∞)上单调递增,g(x)无极大值也无极小值.(3)当a>0时,g'(x)=(x-a)(x-sin x),当x∈(-∞,0)时,x-a<0,g'(x)>0,g(x)单调递增;当x∈(0,a)时,x-a<0,g'(x)<0,g(x)单调递减;当x∈(a,+∞)时,x-a>0,g'(x)>0,g(x)单调递增.所以当x=0时g(x)取到极大值,极大值是g(0)=-a;当x=a时g(x)取到极小值,极小值是g(a)=-a3-sin a.综上所述:当a<0时,函数g(x)在(-∞,a)和(0,+∞)上单调递增,在(a,0)上单调递减,函数既有极大值,又有极小值,极大值是g(a)=-a3-sin a,极小值是g(0)=-a;当a=0时,函数g(x)在(-∞,+∞)上单调递增,无极值;当a>0时,函数g(x)在(-∞,0)和(a,+∞)上单调递增,在(0,a)上单调递减,函数既有极大值,又有极小值,极大值是g(0)=-a,极小值是g(a)=-a3-sin a.教师用书专用(13—19)13.(2015陕西,15,5分)设曲线y=e x在点(0,1)处的切线与曲线y=(x>0)上点P处的切线垂直,则P的坐标为.答案(1,1)14.(2015课标Ⅱ,16,5分)已知曲线y=x+ln x在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=.答案815.(2014广东,10,5分)曲线y=e-5x+2在点(0,3)处的切线方程为.答案5x+y-3=016.(2017山东,20,13分)已知函数f(x)=x2+2cos x,g(x)=e x(cos x-sin x+2x-2),其中e=2.71828…是自然对数的底数.(1)求曲线y=f(x)在点(π,f(π))处的切线方程;(2)令h(x)=g(x)-af(x)(a∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.解析本题考查导数的几何意义和极值.(1)由题意知,f(π)=π2-2,又f'(x)=2x-2sin x,所以f'(π)=2π,因此曲线y=f(x)在点(π,f(π))处的切线方程为y-(π2-2)=2π(x-π),即y=2πx-π2-2.(2)由题意得h(x)=e x(cos x-sin x+2x-2)-a(x2+2cos x),因为h'(x)=e x(cos x-sin x+2x-2)+e x(-sin x-cos x+2)-a(2x-2sin x)=2e x(x-sin x)-2a(x-sin x)=2(e x-a)(x-sin x),令m(x)=x-sin x,则m'(x)=1-cos x≥0,所以m(x)在R上单调递增.因为m(0)=0,所以当x>0时,m(x)>0;当x<0时,m(x)<0.(i)当a≤0时,e x-a>0,当x<0时,h'(x)<0,h(x)单调递减,当x>0时,h'(x)>0,h(x)单调递增,所以当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;(ii)当a>0时,h'(x)=2(e x-e ln a)(x-sin x),由h'(x)=0得x1=ln a,x2=0.①当0<a<1时,ln a<0,当x∈(-∞,ln a)时,e x-e ln a<0,h'(x)>0,h(x)单调递增;当x∈(ln a,0)时,e x-e ln a>0,h'(x)<0,h(x)单调递减;当x∈(0,+∞)时,e x-e ln a>0,h'(x)>0,h(x)单调递增.所以当x=ln a时h(x)取到极大值,极大值为h(ln a)=-a[(ln a)2-2ln a+sin(ln a)+cos(ln a)+2],当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;②当a=1时,ln a=0,所以当x∈(-∞,+∞)时,h'(x)≥0,函数h(x)在(-∞,+∞)上单调递增,无极值;③当a>1时,ln a>0,所以当x∈(-∞,0)时,e x-e ln a<0,h'(x)>0,h(x)单调递增;当x∈(0,ln a)时,e x-e ln a<0,h'(x)<0,h(x)单调递减;当x∈(ln a,+∞)时,e x-e ln a>0,h'(x)>0,h(x)单调递增.所以当x=0时h(x)取到极大值,极大值是h(0)=-2a-1;当x=ln a时h(x)取到极小值,极小值是h(ln a)=-a[(ln a)2-2ln a+sin(ln a)+cos(ln a)+2].综上所述:当a≤0时,h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,函数h(x)有极小值,极小值是h(0)=-2a-1;当0<a<1时,函数h(x)在(-∞,ln a)和(0,+∞)上单调递增,在(ln a,0)上单调递减,函数h(x)有极大值,也有极小值,极大值是h(ln a)=-a[(ln a)2-2ln a+sin(ln a)+cos(ln a)+2],极小值是h(0)=-2a-1;当a=1时,函数h(x)在(-∞,+∞)上单调递增,无极值;当a>1时,函数h(x)在(-∞,0)和(ln a,+∞)上单调递增,在(0,ln a)上单调递减,函数h(x)有极大值,也有极小值,极大值是h(0)=-2a-1,极小值是h(ln a)=-a[(ln a)2-2ln a+sin(ln a)+cos(ln a)+2].17.(2013湖南,22,13分)已知a>0,函数f(x)=-.(1)记f(x)在区间[0,4]上的最大值为g(a),求g(a)的表达式;(2)是否存在a,使函数y=f(x)在区间(0,4)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求a的取值范围;若不存在,请说明理由.解析(1)当0≤x≤a时,f(x)=-;当x>a时,f(x)=-.因此,当x∈(0,a)时,f'(x)=-<0,f(x)在(0,a)上单调递减;当x∈(a,+∞)时,f'(x)=>0,f(x)在(a,+∞)上单调递增.①若a≥4,则f(x)在(0,4)上单调递减,g(a)=f(0)=.②若0<a<4,则f(x)在(0,a)上单调递减,在(a,4)上单调递增.所以g(a)=max{f(0),f(4)}.而f(0)-f(4)=-=-,故当0<a≤1时,g(a)=f(4)=;当1<a<4时,g(a)=f(0)=.综上所述,g(a)=(2)由(1)知,当a≥4时,f(x)在(0,4)上单调递减,故不满足要求.当0<a<4时,f(x)在(0,a)上单调递减,在(a,4)上单调递增.若存在x1,x2∈(0,4)(x1<x2),使曲线y=f(x)在(x1,f(x1)),(x2,f(x2))两点处的切线互相垂直,则x1∈(0,a),x2∈(a,4),且f'(x1)·f'(x2)=-1.即-·=-1.亦即x1+2a=.(*)由x1∈(0,a),x2∈(a,4)得x1+2a∈(2a,3a),∈.故(*)成立等价于集合A={x|2a<x<3a}与集合B=的交集非空.因为<3a,所以当且仅当0<2a<1,即0<a<时,A∩B≠⌀.综上所述,存在a使函数f(x)在区间(0,4)内的图象上存在两点,在该两点处的切线互相垂直,且a的取值范围是.18.(2015安徽,18,12分)设n∈N*,x n是曲线y=x2n+2+1在点(1,2)处的切线与x轴交点的横坐标.(1)求数列{x n}的通项公式;(2)记T n=…-,证明:T n≥.解析(1)y'=(x2n+2+1)'=(2n+2)x2n+1,曲线y=x2n+2+1在点(1,2)处的切线斜率为2n+2.从而切线方程为y-2=(2n+2)(x-1).令y=0,解得切线与x轴交点的横坐标x n=1-=.(2)证明:由题设和(1)中的计算结果知T n=…-=…-.当n=1时,T1=.当n≥2时,因为=-=->---=-=-.所以T n>×××…×-=.综上可得对任意的n∈N*,均有T n≥.19.(2013北京,18,13分)设L为曲线C:y=在点(1,0)处的切线.(1)求L的方程;(2)证明:除切点(1,0)之外,曲线C在直线L的下方.解析(1)设f(x)=,则f'(x)=.所以f'(1)=1.所以L的方程为y=x-1.(2)证明:令g(x)=x-1-f(x),则除切点之外,曲线C在直线L的下方等价于g(x)>0(∀x>0,x≠1).g(x)满足g(1)=0,且g'(x)=1-f'(x)=-.当0<x<1时,x2-1<0,ln x<0,所以g'(x)<0,故g(x)单调递减;当x>1时,x2-1>0,ln x>0,所以g'(x)>0,故g(x)单调递增.所以,g(x)>g(1)=0(∀x>0,x≠1).所以除切点之外,曲线C在直线L的下方.考点二导数的运算1.(2014大纲全国,7,5分)曲线y=xe x-1在点(1,1)处切线的斜率等于()A.2eB.eC.2D.1答案C2.(2013江西,13,5分)设函数f(x)在(0,+∞)内可导,且f(e x)=x+e x,则f'(1)=.答案23.(2017浙江,20,15分)已知函数f(x)=(x--)e-x.(1)求f(x)的导函数;(2)求f(x)在区间上的取值范围.解析本题主要考查函数的最大(小)值,导数的运算及其应用,同时考查分析问题和解决问题的能力.(1)因为(x--)'=1--,(e-x)'=-e-x,所以f'(x)=-e-x-(x--)e-x=-----.(2)由f'(x)=-----=0,解得x=1或x=.因为又f(x)=(--1)2e-x≥0,所以f(x)在区间上的取值范围是-.4.(2016北京,18,13分)设函数f(x)=xe a-x+bx,曲线y=f(x)在点(2,f(2))处的切线方程为y=(e-1)x+4.(1)求a,b的值;(2)求f(x)的单调区间.解析(1)因为f(x)=xe a-x+bx,所以f'(x)=(1-x)e a-x+b.依题设,知-即----解得a=2,b=e.(2)由(1)知f(x)=xe2-x+ex.由f'(x)=e2-x(1-x+e x-1)及e2-x>0知,f'(x)与1-x+e x-1同号.令g(x)=1-x+e x-1,则g'(x)=-1+e x-1.所以,当x∈(-∞,1)时,g'(x)<0,g(x)在区间(-∞,1)上单调递减;当x∈(1,+∞)时,g'(x)>0,g(x)在区间(1,+∞)上单调递增.故g(1)=1是g(x)在区间(-∞,+∞)上的最小值,从而g(x)>0,x∈(-∞,+∞).综上可知,f'(x)>0,x∈(-∞,+∞).故f(x)的单调递增区间为(-∞,+∞).三年模拟A组2016—2018年模拟·基础题组考点一导数的概念及其几何意义1.(2018浙江镇海中学12月测试,2)已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为()A.2B.1C.-1D.-2答案A2.(2017浙江测试卷,4)已知直线y=ax是曲线y=ln x的切线,则实数a=()A. B. C. D.答案C3.(2017浙江衢州质量检测(1月),14)已知函数f(x)=x3+2ax2+1在x=1处的切线的斜率为1,则实数a=,此时函数y=f(x)在[0,1]最小值为.答案-;4.(2017浙江台州质量评估,20)已知函数f(x)=x3+|x-a|(a∈R).(1)当a=1时,求f(x)在(0,f(0))处的切线方程;(2)当a∈(0,1)时,求f(x)在区间[-1,1]上的最小值(用a表示).解析(1)当a=1,x<1时,f(x)=x3+1-x,f'(x)=3x2-1,所以f(0)=1,f'(0)=-1,所以f(x)在(0,f(0))处的切线方程为y=-x+1.(2)当a∈(0,1)时,由已知得f(x)=---≤当a≤x≤1时,由f'(x)=3x2+1>0,知f(x)在(a,1)上是单调递增的.当-1≤x<a时,f'(x)=3x2-1,(i)当a∈时,f(x)在--上递增,在-上递减,在上递增,所以在区间[-1,1]上,f(x)min=min-=min-=a-.(ii)当a∈时,f(x)在--上递增,在-上递减,所以在区间[-1,1]上,f(x)min=min{f(-1),f(a)}=min{a,a3}=a3.综上所述,f(x)min=-∈∈考点二导数的运算5.(2018浙江镇海中学12月测试,1)下列求导结果正确的是()A.(1-x2)'=1-2xB.(cos30°)'=-sin30°C.[ln(2x)]'=D.()'=答案D6.(2017浙江名校(诸暨中学)交流卷四,4)设f1(x)=sin x+cos x,对任意的n∈N*,定义f n+1(x)=f n'(x),则f2017(x)等于()A.sin x-cos xB.sin x+cos xC.-sin x-cos xD.-sin x+cos x答案B7.(2017浙江镇海中学阶段测试(二),13)已知函数f(x)=sin x-f'cos x,若f'=0,则f'=.答案-1B组2016—2018年模拟·提升题组一、选择题1.(2017浙江湖州期末调研,2)函数y=e x(e是自然对数的底数)的图象在点(0,1)处的切线方程是()A.y=x-1B.y=x+1C.y=-x-1D.y=-x+1答案B二、解答题2.(2018浙江重点中学12月联考,20)已知函数f(x)=-ln(x+b)+a(a,b∈R).(1)若y=f(x)的图象在点(2,f(2))处的切线方程为y=-x+3,求a,b的值;(2)当b=0时,f(x)≥--对定义域内的x都成立,求a的取值范围. 解析(1)由f(x)=-ln(x+b)+a,得f'(x)=-,所以--得(6分)(2)当b=0时,f(x)≥--对定义域内的x都成立,即-ln x+a≥--恒成立,所以a≥ln x--恒成立,则a≥(ln x--)max.(9分)令g(x)=ln x--,则g'(x)=--=---.(11分)令m(x)=--x,则m'(x)=--1=--,令m'(x)>0,得x<1,所以m(x)在上单调递增,在(1,+∞)上单调递减,所以m(x)max=m(1)=0,(13分)所以g'(x)≤0,所以g(x)在定义域上单调递减,所以g(x)max=g=ln,所以a≥ln.(15分)3.(2018浙江“七彩阳光”联盟期中,20)已知函数f(x)=+aln x(a>0).(1)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=-x平行,求函数y=f(x)的单调区间;(2)若对任意x∈(0,+∞),都有f(x)>0成立,试求实数a的取值范围;(3)记g(x)=f(x)+2x-b(b∈R),当a=1时,函数g(x)在区间[e-1,e]上有两个零点,求实数b的取值范围.解析(1)直线y=-x的斜率为-1.函数f(x)的定义域为(0,+∞),f'(x)=-+,所以f'(1)=-3+a=-1,解得a=2,(3分)所以f(x)=+2ln x,f'(x)=-.由f'(x)>0,得x>;由f'(x)<0,得0<x<,所以f(x)的单调递减区间为,单调递增区间为.(5分) (2)f'(x)=-+=-(a>0),由f'(x)>0,得x>,由f'(x)<0,得0<x<,所以f(x)的单调递减区间为,单调递增区间为,当x=时,f(x)取极小值,也是最小值,即f(x)min=f,(7分)∵对任意x∈(0,+∞),都有f(x)>0成立,∴f>0,即a+aln>0,(9分)又a>0,∴ln>-1,得0<a<3e.∴实数a的取值范围为(0,3e).(10分)(3)当a=1时,g(x)=+ln x+2x-b(x>0),g'(x)=-=-,由g'(x)>0,得x>1,由g'(x)<0,得0<x<1.所以g(x)的单调递减区间为(0,1),单调递增区间为(1,+∞),则x=1时,g(x)取得极小值g(1).(12分)因为函数g(x)在区间[e-1,e]上有两个零点,所以-≥≥得-∵--=e--2>0,∴5<b≤2e++1.所以b的取值范围是.(15分)4.(2017浙江宁波二模(5月),20)设函数f(x)=x2-ax-ln x,a∈R.(1)若函数f(x)的图象在x=1处的切线斜率为1,求实数a的值;(2)当a≥-1时,记f(x)的极小值为H,求H的最大值.解析(1)f'(x)=--(x>0),由题知,f'(1)=1,解得a=0.(2)令f'(x0)=0,则2-ax0-1=0,解得x0=,且2-1=ax0.可知f(x)在(0,x0)上递减,在(x0,+∞)上递增,则H=f(x)极小值=f(x0)=-ax0-ln x0=-+1-ln x0.记g(a)=(a≥-1),当a≥0时,g(a)为增函数;当-1≤a<0时,g(a)=,g(a)为增函数,故x0≥g(-1)=.设y=-x2+1-ln x.易知,函数y=-x2+1-ln x在上为减函数,所以H的最大值为+ln2.5.(2017浙江高考模拟训练冲刺卷一,20)已知函数f(x)=2aln x+x2-(a+2)x,a∈R.(1)当a=时,求曲线y=f(x)在点M(1,f(1))处的切线方程;(2)求函数f(x)在区间[1,2]上的最大值.解析(1)当a=时,f(x)=ln x+x2-x,所以f(1)=-2.又f'(x)=+x-,所以f'(1)=-.由点斜式得所求切线方程为y=-x-.(2)f'(x)=+x-(a+2)=-=--,因为x∈[1,2],所以有①当a≥2时,函数f(x)在区间[1,2]上为增函数.此时f(x)max=f(2)=2aln2-2a-2.②当1≤a<2时,函数f(x)在区间[1,a]上为增函数,在区间[a,2]上为减函数.此时f(x)max=f(a)=2aln a-a2-2a.③当a<1时,函数f(x)在区间[1,2]上为减函数.此时f(x)max=f(1)=-a-.故函数f(x)在区间[1,2]上的最大值为f(x)max=---≤--6.(2017浙江高考模拟训练冲刺卷四,20)已知函数f(x)=ln x-+1.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)当x∈(0,1)时,函数g(x)=af(x)-x2在x=m处取得极大值,求实数a的取值范围.解析(1)由f'(x)=+,得f'(1)=3.又f(1)=-1,∴曲线y=f(x)在点(1,f(1))处的切线方程为y=3x-4.(2)g(x)=a--x2,∴g'(x)=+-x=---(x>0),∵g(x)在x=m处取得极大值,∴g'(m)=0,∴m3-2am-4a=0,即a=(0<m<1),设h(m)=(0<m<1),则h'(m)==>0.∴h(m)在(0,1)上单调递增,∴0<a<.C组2016—2018年模拟·方法题组方法1导数运算的解题策略1.求下列函数的导数:(1)y=x;(2)y=1+sin cos;(3)y=xsin x+;(4)y=-2x.解析(1)因为y=x+2+,所以y'=1-.(2)因为y=1+sin cos=1+sin x,所以y'=cos x.(3)y'=(xsin x)'+()'=sin x+xcos x+.(4)y'='-(2x)'=-2x ln2=--2x ln2.方法2导数的几何意义的解题策略2.(2017浙江镇海中学模拟卷一,20)已知函数f(x)=x3+3ax2.(1)判断函数f(x)的单调性;(2)若过点(1,0)可作曲线y=f(x)的三条切线,求a的取值范围.解析(1)f'(x)=3x2+6ax=3x(x+2a),所以当a=0时,f'(x)≥0恒成立,因此f(x)在(-∞,+∞)上单调递增;当a<0时,f(x)在(-∞,0)上单调递增,在(0,-2a)上单调递减,在(-2a,+∞)上单调递增;当a>0时,f(x)在(-∞,-2a)上单调递增,在(-2a,0)上单调递减,在(0,+∞)上单调递增.(2)设切点坐标为(t,f(t)),则过该点的切线方程为y-f(t)=f'(t)(x-t).易知该直线经过点(1,0),则有-f(t)=f'(t)(1-t),即t[2t2+(3a-3)t-6a]=0,由题可知,上述方程有三个互不相等的实根,即2t2+(3a-3)t-6a=0有两个互不相等的非零实根,所以有-解得或所以a的取值范围是(-∞,-3)∪-∪(0,+∞).3.(2017浙江镇海中学模拟卷四,20)已知函数f(x)=ax2-ln x(其中a为正常数).(1)当a=时,求曲线y=f(x)在点(2,f(2))处的切线方程;(2)试求函数f(x)在[1,2]上的最小值.解析(1)当a=时,f(x)=x2-ln x,则f'(x)=x-=-,所以f'(2)=,且f(2)=2-ln2,因此曲线y=f(x)在点(2,f(2))处的切线方程为y-(2-ln2)=(x-2),即y=x-(1+ln2).(6分)(2)f'(x)=2ax-=-,其中x>0,因此,f(x)在上单调递减,在上单调递增.(8分)当≤1,即a≥时,f(x)在[1,2]上单调递增,所以f(x)min=f(1)=a;(10分)当≥2,即0<a≤时,f(x)在[1,2]上单调递减,所以f(x)min=f(2)=4a-ln2;(12分)当1<<2,即<a<时,f(x)在上单调递减,在上单调递增,所以f(x)min=f=+ln(2a).(14分)-综上,f(x)min=(15分)。
2019届苏教版(文科数学) 直线与方程 单元测试

1.过点()2,M a -和(),4N a 的直线的斜率为1,则实数a 的值为( ) A .1 B .2 C .1或4 D .1或2 【答案】A 【解析】依题意有41,12aa a -==+. 2.已知直线方程为,3300sin 300cos =+y x则直线的倾斜角为( ) A.60 B.30060或 C.30 D.33030或 【答案】C【解析】由直线方程为,3300sin 300cos =+y x所以直线的斜率为3360sin 60cos )60sin()60cos()60360sin()60360cos(300sin 300cos ==---=---=-= k 因为直线倾斜角的范围)180,0[ 所以倾斜角为 30 故答案为C .3. 坐标平面内有相异两点2(cos ,sin ),(0,1)A B θθ,经过两点的直线的的倾斜角的取值范围是( ) A .,44ππ⎡⎤-⎢⎥⎣⎦ B .30,,44πππ⎛⎤⎡⎫ ⎪⎥⎢⎝⎦⎣⎭ C .30,,44πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭ D .3,44ππ⎡⎤⎢⎥⎣⎦【答案】34παπ≤< 【解析】22sin 1cos cos [1,1]cos cos ABk θθθθθ--===-∈-,且0AB k ≠.设直线的倾斜角为α,当01AB k <≤时,则0tan 1α<≤,所以倾斜角α的范围为04πα≤≤.当10AB k -≤<时,则1tan 0α-≤<,所以倾斜角α的范围为34παπ≤< +- 4. 直线l 过点(4,1)P -,若直线在两坐标轴上的截距相等,求直线l 的方程. 【答案】14y x =-或30x y +-=.5. 已知直线()12:210,:20l ax a y l x ay +++=++=,其中a R ∈,则“3a =-”是“12l l ⊥”的 ( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 【答案】A【解析】直线12l l ⊥的充要条件是()()20300a a a a a a ++=∴+=∴= 或3a =- .故选A. 6.【2018届四川省南充高级中 高三9月检测】已知直线()12:210,:20l ax a y l ax y +++=-+=.若12//l l ,则实数a 的值是( )A. 0或3-B. 2或1-C. 0D. 3- 【答案】A【解析】12//l l ,则()()12a a a ⨯-=+ 即230a a += 03a a ∴==-或 经检验都符合题意故选A.7.已知(2,4),(1,1)A B 两点,直线l 过点(0,2)C 且与线段AB 相交,直线l 的斜率k 的取值范围是 . 【答案】[1,1]-xy l1231234OABC Dxy l1231234OABC D8. 设直线l 的方程为12()()0a x y a a R ∈+++-=. (1)若l 在两坐标轴上截距相等,求l 的方程; (2)若l 不经过第二象限,求实数a 的取值范围.【答案】(1)3x y 0x y 20+=或++=.(2)(1]∞-,-.【解析】 (1)当直线过原点时,该直线在x 轴和y 轴上的截距为零,∴a 2=,方程即为3x y 0+=. 当直线不经过原点时,截距存在且均不为0, ∴21a a -+=a 2-,即a 11.a 0∴+==,方程即为x y 20++=.综上,l 的方程为3x y 0x y 20+=或++=. (2)将l 的方程化为y (a 1)x a 2=-++-,∴()1020a a -+>⎧⎪⎨-≤⎪⎩或()1020a a -+=⎧⎪⎨-≤⎪⎩,a 1.∴≤-综上可知a 的取值范围是(1]∞-,-.点睛:涉及直线在两坐标轴上截距相等问题,要特别注意截距均为0的情况;另外,某些涉及直线问题中,往往要讨论直线的斜率是否存在的情况,也应特别注意. 9.【2018为它们的交点,点.求(1(22的直线方程. 【答案】(1【解析】试题分析:(1)(2)先求两条直线的交点,设出直线方(2当斜率不存在,则方程为. +-10. 已知直线1:30l x y -+=,直线10l x y --=:,若直线1l 关于直线l 的对称直线为2l ,求直线2l 的方程.【答案】50x y --=. 【解析】直线12,l l 关于直线l 对称, 所以1l 与2,l l 与l 间的距离相等.解得5m =-或3m =(舍去), 所以直线2l 的方程为50x y --=.法二:由题意知12//l l ,设直线()2:03,1l x y m m m -+=≠≠-, 在直线1l 上取点()0,3M ,设点M 关于直线l 的对称点为(),M a b ',于是有311031022b aa b -⎧⨯=-⎪⎪⎨++⎪--=⎪⎩,解得41a b =⎧⎨=-⎩,即()4,1M '-.把点()4,1M '-代入2l 的方程,得5m =-, 所以直线2l 的方程为50x y --=.【精选精练】1.【2018届云南省师范大 附属中 高三月考卷(二)】,) A. -2 B. -3 C. -4 D. -52.已知直线1:210l x y -+=与直线2:0l mx y -=平行,则实数m 的值为 ( ) A.12 B .12- C.2 D.2- 【答案】A 【解析】由题意,112m -=-,即12m =,选A. 3.平行于直线012=++y x 且与圆522=+y x 相切的直线的方程是( )A .052=+-y x 或052=--y x B. 052=++y x 或052=-+y x C. 052=+-y x 或052=--y x D. 052=++y x 或052=-+y x 【答案】D .4.已知直线():10,0x yl a b a b+=>>在两坐标轴上的截距之和为4,则该直线与两坐标轴围成的三角形的面积的最大值是 ( )A. 4 C. 6 D. 2 【答案】D 【解析】直线():10,0x yl a b a b+=>>在两坐标轴上的截距之和为4,所以4a b +=,即14422ab ab ≥⇒≤⇒≤ ,则该直线与两坐标轴围成的三角形的面积的最大值是2 .5.若直线20x ay +-=与以()3 1A ,,()1 2B ,为端点的线段没有公共点,则实数a 的取值范围是( ) A .()2 1-, B .()() 2 1 -∞-+∞ ,,C.11 2⎛⎫- ⎪⎝⎭, D .()1 1 2⎛⎫-∞-+∞ ⎪⎝⎭,,【答案】D【解析】直线20x ay +-=过定点()2 0C ,,所以11(,)(2,1)(,1)(,)2CB CA k k a a -∈=-⇒∈-∞-+∞ ,选D.6.直线2:10l mx m y --=经过点()2,1P ,则倾斜角与直线l 的倾斜角互为补角的一条直线方程是( )A .10x y --=B .230x y --=C .30x y +-=D .240x y +-= 【答案】C【解析】将点()2,1P 代入得2210,1m m m --==,直线方程为10x y --=,斜率为1,倾斜角为4π.故和其垂直的直线斜率为1-,故选C.7.点(2,0)A ,(2,4)B -,(5,8)C ,若线段AB 和CD 有相同的垂直平分线,则点D 的坐标是( ) (A )(6,7) (B )(7,6) (C )(5,4)-- (D )(4,5)-- 【答案】A8. 如图所示,已知A(4,0),B(0,4),从点P(2,0)射出的光线经直线AB 反射后再射到直线OB 上,最后经直线OB 反射后又回到P 点,则光线所经过的路程是( )A ..6 C . D . 【答案】A【解析】由题意知点P 关于直线AB 的对称点为D(4,2),关于y 轴的对称点为C(-2,0),则光线所经过的路程为|CD|=A .9.若直线l :1(0,0)x ya b a b+=>>经过点()1,2,则直线l 在x 轴和y 轴的截距之和的最 小值是 .【答案】3+. 【解析】由题意得,∴截距之和为33≥+=+,即时,等号成立,即的最小值为.10.已知两直线1:80l mx y n ++=和210l x my +-=:2.试确定,m n 的值,使 (1)1l 与2l 相交于点(,1)P m -; (2)1l ∥2l ; /(3)1l ⊥2l ,且1l 在y 轴上的截距为-1.【答案】(1)1=m ,7=n ;(2)4=m ,2-≠n 或4-=m ,2≠n ;(3)0=m ,8=n . 【解析】试题分析:(1)将点()1,-m p 代入两直线方程,解出m 和n 的值;(2)由1l ∥2l 得斜率相等,求出m 值,再把直线可能重合的情况排除;(3)先检验斜率不存在的情况,当斜率存在时,看斜率之积是否等于1-,∴42m n =⎧⎨≠-⎩或42m n =-⎧⎨≠⎩即4=m ,2-≠n 时或4-=m ,2≠n 时,21//l l . (3)当且仅当082=⋅+⋅m m ,即0=m 时,21l l ⊥.又18-=-n,∴8=n . 即0=m ,8=n 时,21l l ⊥,且1l 在y 轴上的截距为1-.11.【2018届黑龙江省伊春市第二中 高三上第一次月考】已知直线1l 的方程为34120x y +-=,求2l 的方程,使得:(1)2l 与1l 平行,且过点()1,3-;(2)2l 与1l 垂直,且2l 与两坐标轴围成的三角形面积为4.【答案】(1)3490x y +-=(2)43y =±【解析】试题分析:(1)由2l 与1l 平行可设2:340l x y m ++=,再代点()1,3-得9m =.(2)由2l 与1l 垂直可设2:430l x y n -+=,再得与坐标轴的交点,根据面积公式得1243AOB n nS ∆=⋅,最后解方程得n 试题解析:解:(1)设2:340l x y m ++=, ∵2l 过点()1,3-, ∴9m =.∴2l 方程为3490x y +-=.∴n =±.∴2l 方程为430x y -+=或430x y --=.43y =±12.已知|m |1<,直线12:1,:1l y mx l x my =+=-+, 12l l 与相交于点P ,1l 交y 轴于点A ,2l 交x 轴于点B (1)证明:12l l ⊥;(2)用m 表示四边形OAPB 的面积S ,并求出S 的最大值; (3)设S= f (m), 求1U S S=+的单调区间. 【答案】(1)见解析;(2)1;(3)在(-1,0)上为减函数,在(0,1)上为增函数. 【解析】(1)证明:可把两条直线化为12:10,:10l mx y l x my -+=+-=(3)221111U S m S m =+=+++ , 又11(,1],(,1]22S U ∈ 且在是单调递减的函数, 而11S m =+2在(-1,0)上递增,在(0,1)上递减, 1U S S∴=+在(-1,0)上为减函数,在(0,1)上为增函数。
2019届苏教版(文科数学) 极坐标系 单元测试

(2)极坐标系1、点的直角坐标为(1,,则它的极坐标是( ) A.2,3π⎛⎫⎪⎝⎭ B.42,3π⎛⎫⎪⎝⎭ C.2,3π⎛⎫- ⎪⎝⎭ D.42,3π⎛⎫- ⎪⎝⎭答案:C解析:2,tan ρθ==因为点(1,在第四象限, 故取3πθ=-,所以点的极坐标为2,3π⎛⎫- ⎪⎝⎭.2、在极坐标系中,圆=2cos ρθ的垂直于极轴的两条切线方程分别为()A.0()R θρ=∈和cos 2ρθ=B.()2R πθρ=∈和cos 2ρθ= C.()2R πθρ=∈和D.0()R θρ=∈和答案:B解析:在直角坐标系中,圆的方程为222x y x +=,即22(1)1x y -+=,圆心为,半径为.易得圆的垂直于x 轴的两条切线方程分别为0x =和2x =, 即()2R πθρ=∈和cos 2ρθ=.3、在极坐标系中,直线)sin 2ρθθ-=与圆4sin ρθ=交点的极坐标为( ) A.2,6π⎛⎫⎪⎝⎭ B.2,3π⎛⎫⎪⎝⎭ C.4,6π⎛⎫⎪⎝⎭ D.4,3π⎛⎫⎪⎝⎭答案:A解析:4、极坐标系中,点5(1,),(3,)66A B ππ之间的距离是()答案:C解析:5、点P 的极坐标为,则点P 的直角坐标为( )A.B.C.(2,2)D.(答案:B解析:x=cos sin ρρθ6、点M 的直角坐标为(0,)2π,则点M 的极坐标可以为( ) A.(,0)2πB.(0,)2π C.(,)22ππ D.(,)22ππ- 答案:C解析:∵2πρ==且,2M πθ=∴的极坐标为(,)22ππ7、下列各点与(2,)3π表示极坐标系中同一点的是( ) A.2(2,)3π B.(2,)π C.7(2,)3π D.(2,2)π答案:C 解析:与极坐标(2,)3π相同的点可以表示为(2,2)()3kn k Z π+∈只有7(2,)3π适合 8、下列的点在极轴上方的是( )A.(3,0)B.(73,)6π C.(47,)4π D.(417,)4π 答案:D9、已知圆的极坐标方程为4cos ρθ=, 圆心为C , 点P 的极坐标为4,3π⎛⎫ ⎪⎝⎭,则CP 的值为 .答案:解析:4cos ρθ=,两边同时乘以ρ,化为标准方程。
2019届苏教版(文科数学) 数形结合之——简单线性规划 单元测试
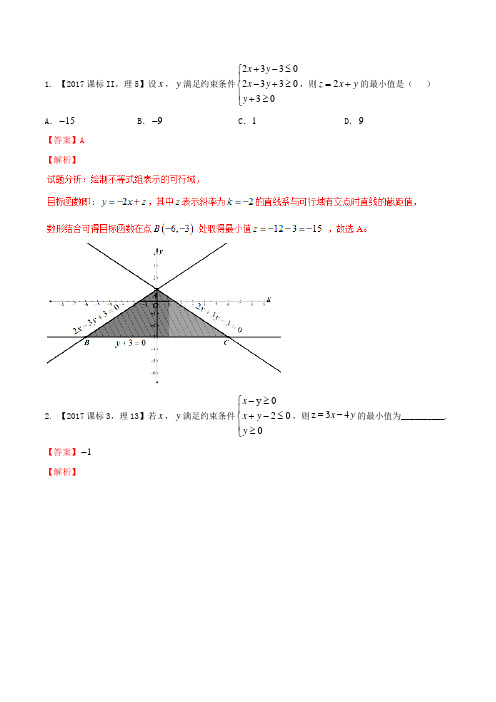
1. 【2017课标II ,理5】设x ,y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩,则2z x y =+的最小值是( )A .15-B .9-C .1D .9 【答案】A 【解析】2. 【2017课标3,理13】若x ,y 满足约束条件y 0200x x y y -≥⎧⎪+-≤⎨⎪≥⎩,则z 34x y =-的最小值为__________.【答案】1- 【解析】【名师点睛】求线性目标函数=ax+by(ab≠0)的最值,当b>0时,直线过可行域且在y轴上截距最大时,值最大,在y轴截距最小时,值最小;当b<0时,直线过可行域且在y轴上截距最大时,值最小,在y轴上截距最小时,值最大.3. 【2018年5月2018届高三第三次全国大联考】已知实数,满足约束条件,则的最小值为()A. B. C. D.【答案】A【解析】作出不等式组表示的平面区域如下图中阴影部分所示,易知表示可行域内的点到点的距离的平方,所以.故选A.4.【2018年5月2018届高三第三次全国大联考】已知实数满足约束条件,则的取值范围为()A. B. C. D.【答案】B5.【2018届宁夏银川市第二中二模】设不等式组所表示的平面区域是Ω1,平面区域Ω2与Ω1关于直线3x-4y-9=0对称.对于Ω1中的任意点A与Ω2中的任意点B,|AB|的最小值等于( )A. B. 4 C. D. 2【答案】B【解析】分析:根据已知的约束条件,画出满足约束条件的可行域Ω1,根据对称的性质,不难得到:当A 点距对称轴的距离最近时,|AB|有最小值.详解:故选B.点睛:本题是常规的线性规划问题,线性规划问题常出现的形式有:①直线型,转化成斜截式比较截距,要注意前面的系数为负时,截距越大,值越小;②分式型,其几何意义是已知点与未知点的斜率;③平方型,其几何意义是距离,尤其要注意的是最终结果应该是距离的平方;④绝对值型,转化后其几何意义是点到直线的距离.6.【2018届云南省曲靖市第一中 4月监测(七)】若不等式,表示的平面区域为三角形且其面积等于,则的最小值为()A. -2B.C. -3D. 1【答案】A【解析】分析:先做出不等式组对应的平面区域,求出三角形的各顶点坐标,利用三角形的面积公式确定值,再利用平移目标函数直线确定最优解.详解:作出不等式组表示的平面区域(如图所示),由图象,得当直线过点时,取得最小值为.故选A.7.【2018届湖南师范大附属中高三月考六】已知满足约束条件若取得最大值的最优解不唯一,则实数的值为( )A. 或-1B. 2或C. -2或1D. 2或-1【答案】C【解析】分析:作出不等式组对应的平面区域,利用目标函数的几何意义,得到直线的斜率的变换,从而求出的值.详解:作出不等式组表示的平面区域,如图所示,则直线与直线平行,此时;综上或,故选C.8.【2018届百校联盟TOP20四月联考】已知,若存在点,使得,则的取值范围为()A. B. C. D.【答案】C【解析】分析:作出不等式组表示的可行域,利用图象的直观性建立的不等式组,即可求出的取值范围. 详解:作出不等式组表示的可行域,如图,要使可行域存在,必有,若可行域存在点,使得,则可行域内含有直线上的点,只需边界点在直线上方,且在直线下方,解不等式,解得故选:C9.【2018届山西省孝义市一模】已知不等式组表示的平面区域为,若函数的图象上存在区域上的点,则实数的取值范围是()A. B. C. D.【答案】C由可解得,即B(2,﹣1)此时有﹣1=|2﹣1|+m,解得m=﹣2;由可解得,即B(1,1)此时有1=|1﹣1|+m,解得m=1;故实数m的取值范围为[﹣2,1 ,故答案为[﹣2,1 .故选C.10.【2018届北京市海淀区二模】两个居民小区的居委会欲组织本小区的中生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同的往返车费及服务老人的人数如下表:小区小区根据安排,去敬老院的往返总车费不能超过37元,且小区参加献爱心活动的同比小区的同至少多1人,则接受服务的老人最多有____人.【答案】【解析】分析:设两区参加活动同的人数分别为,受到服务的老人人数为,找出约束条件与目标函数,准确地描画可行域,平移直线可求得满足题设的最优解.详解:当时,取得最大值为,即接受服务的老人最多有人,故答案为.【精选精练】1.【2018届辽宁省丹东市模拟二】若点满足不等式组,则的取值范围为()A. B.C. D.【答案】A【解析】分析:将不等式组的可行域表示在平面直角坐标系中,进而利用,即,转化为区域内的点和定点连线的斜率即可.详解:故选A.2.【2018届黑龙江省哈尔滨师范大附属中三模】设点满足约束条件,且,则这样的点共有( )个A. 12B. 11C. 10D. 9【答案】A【解析】分析:由约束条件画出可行域,根据可行域,利用,可逐一写出满足条件的点,从而可得结果.详解:画出表示的可行域,由图可知,满足,得,共有,,共个,故选A.3.【2018届陕西省咸阳市三模】已知实数,满足给,中间插入5个数,这7个数构成以为首项,为末项的等差数列,则这7个数和的最大值为()A. B. C. D.【答案】D【解析】分析:实数x,y满足,如图所示,画出可行域△ABC.给x,y中间插入5个数,这7个数构成以x为首项,y为末项的等差数列,则这7个数和=,令x+y=t,则y=﹣x+t.利用线性规划因此这7个数和=的最大值为,故答案为:D4.【2018届相阳教育“黉门云”高考模拟】已知,满足约束条件,若的最小值为1,则=()A. 2B. 1C.D.【答案】C【解析】画出可行域如下图所示,由图可知,目标函数在点处取得最小值,即.故选C.5.【2018届第三次全国大联考】已知不等式组表示的平面区域为,若以原点为圆心的圆与无公共点,则圆的半径的取值范围为()A. B. C. D.【答案】D【解析】作出不等式组表示的平面区域,如图中阴影部分所示,可知当圆的半径小于原点到直线的距离或大于时,圆与无公共点,而原点到直线的距离为,,故圆的半径的取值范围为.6.【2018届浙江省宁波市5月模拟】已知实数,满足不等式组,则的最大值为()A. 0 B. 2 C. 4 D. 8【答案】C|x ﹣y|的几何意义:表示区域内的点到直线x ﹣y=0的距离的倍,由图可知点A(4,0)到直线x-y=0距离最大,所以|x ﹣y|的最大值为故答案为:C .点睛:本题解题的关键是发现|x-y|的几何意义,|x-y|它表示区域内的点到直线x ﹣y=0的距离的倍,利用数形结合分析解答,可以提高解题效率.所以在今后的解题过程中,看到|ax+by|要联想到点到直线的距离公式.7.【2018届广东省佛山市检测二】已知a 0>,设,x y 满足约束条件0{10 3x y a x y x -+≥+-≥≤,且2z x y =-的最小值为-4,则a = ( ) A. 1 B. 2 C. 3 D. 4 【答案】C故选C.8.【2018届安徽省“皖南八校”第三次(4月)联考】已知函数,若满足,则的取值范围是()A. B. C. D.【答案】C【解析】分析:由已知条件可得,函数是定义在上的奇函数,从而将题中的条件转化为关于的二元一次不等式组,画出相应的可行域,之后结合目标函数的几何意义,确定最优解的位置,从而求得范围.最小值,在点处取得最大值,而边界值取不到,故答案是,故选C.9.【2019届高考全程训练】某研究所计划利用“神舟十一号”飞船进行新产品搭载实验,计划搭载新产品,A B,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:则使总预计收益达到最大时,,A B两种产品的搭载件数分别为( )A. 9,4B. 8,5C. 9,5D. 8,4【答案】A由2330{222x yx y+=+=解得9{4xy==,故M(9,4).所以目标函数的最大值为max=80×9+60×4=960,此时搭载产品A有9件,产品B有4件.故选A.10.【2018届第二次全国大联考】若满足不等式组,则目标函数的取值范围是_____.【答案】【解析】,令,并作出不等式组表示的可行域如图中阴影部分所示,11.【2018届辽宁省丹东市测试二】设实数,满足约束条件,则的取值范围为_______.【答案】【解析】分析:画出不等式组表示的可行域,将变形为,然后平移直线确定取最小和最大值时的最优解,进而可得所求范围.详解:画出不等式组表示的可行域(如图阴影部分所示).12.【2018届江西省景德镇市第一中等盟校第二次联考】若实数,满足,则的取值范围是__________.【答案】【解析】分析:画出可行域,设,化为,平移直线,由可行域可得的取值范围,从而可得的取值范围.详解:设,化为,画出,表示的可行域,平移直线,如图,故答案为.。
2019届苏教版(文科数学)简单的线性规划问题单元测试

(十八) 简单的线性规划问题层级一 学业水平达标1.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤2x ,x +y ≤1,y ≥-1,则x +2y 的最大值是________.解析:作出题设约束条件的平面区域如图中阴影部分所示,平移直线l 0:x +2y =0至点A 时,x +2y 取得最大值.由⎩⎪⎨⎪⎧y =2x ,x +y =1⇒⎩⎨⎧x =13,y =23,可得(x +2y )max =13+2×23=53.答案:532.已知a >0,x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥1,x +y ≤3, y ≥a (x -3).若z =2x +y 的最小值为1,则a 等于________.解析:由已知约束条件,作出可行域如图中△ABC 内部及边界部分,由目标函数z =2x +y 的几何意义为直线l :y =-2x +z 在y 轴上的截距,知当直线l 过可行域内的点A (1,-2a )时,目标函数z =2x +y 的最小值为1,则2-2a =1,a =12.答案:123.已知实数x ,y 满足不等式组⎩⎪⎨⎪⎧x -y +2≥0,x +y -4≥0,2x -y -5≤0,若目标函数z =y -ax 取得最大值时的唯一最优解是(1,3),则实数a 的取值范围为________.解析:作出如图可行域,由z =y -ax 得y =ax +z 可知,直线在y 轴上的截距最大时,z 最大,结合图象可知,在A (1,3)处取得最大值,需a >1.答案:(1,+∞)4.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤1,x +y ≥0,x -y -2≤0,则z =x -2y 的最大值为________.解析:如图,画出约束条件表示的可行域,当目标函数z =x -2y 经过x +y =0与x -y -2=0的交点A (1,-1)时,取到最大值3.答案:35.如图所示,点(x ,y )在四边形ABCD 内部和边界上运动,那么2x -y 的最小值为________.解析:由图知,目标函数在点A (1,1)时,2x -y =1; 在点B (3,2)时,2x -y =23-2>1; 在点C (5,1)时,2x -y =25-1>1;在点D (1,0)时,2x -y =2-0=2>1,故最小值为1. 答案:16.已知实数x ,y 满足⎩⎪⎨⎪⎧y ≥0,y -x +1≤0,y -2x +4≥0,若z =y -ax 取得最大值时的最优解(x ,y )有无数个,则a 的值为________.解析:依题意,在坐标平面内画出不等式组表示的平面区域,如图所示.要使z =y -ax 取得最大值时的最优解(x ,y )有无数个,则直线z =y -ax 必平行于直线y -x +1=0,于是有a =1.答案:17.如果实数x ,y 满足条件⎩⎪⎨⎪⎧x -y +1≥0,y +1≥0,x +y +1≤0,那么z =4-x ·2y 的最大值为________.解析:可行域为如图所示的阴影部分,A ,B ,C 三点的坐标分别为(-1,0),(-2,-1),(0,-1),直线y =2x +t 过点B (-2,-1)时,t 取得最大值3,故z =4-x ·2y =2-2x +y的最大值为8.答案:88.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤a ,x +y ≥8,x ≥6,且不等式x +2y ≤14恒成立,则实数a 的取值范围是________.解析:不等式组表示的平面区域如图中阴影部分所示,显然a ≥8,否则可行域无意义.由图可知x +2y 在点(6,a -6)处取得最大值2a -6,由2a -6≤14得,a ≤10.答案:[8,10]9.直线l :x =my +n (n >0)过点A (4,43),若可行域⎩⎪⎨⎪⎧x ≤my +n ,3x -y ≥0,y ≥0的外接圆直径为1433.求实数n 的值. 解:作出可行域如图所示,过原点的直线OA 的倾斜角为60°,由直线l :x =my +n (n >0)过点A (4,43),可得4=43m +n .又由⎩⎨⎧x =my +n ,3x -y =0可解得两直线的交点坐标即为A (4,43), 又点B 坐标为(n,0), ∴AB sin 60°=1433,∴AB =7,∴(4-n )2+(43)2=49, ∴n =3或5.10.已知x ,y 满足条件:⎩⎪⎨⎪⎧7x -5y -23≤0,x +7y -11≤0,4x +y +10≥0,求:(1)4x -3y 的最大值和最小值; (2)x 2+y 2的最大值和最小值. 解:(1)作出不等式组表示的平面区域如图阴影部分所示.其中A (4,1),B (-1,-6),C (-3,2), 设z =4x -3y .直线4x -3y =0经过原点(0,0). 作一组与4x -3y =0平行的直线l :4x -3y =t . 则当l 过C 点时,t 值最小;当l 过B 点时,t 值最大.∴z 最大值=4×(-1)-3×(-6)=14, z 最小值=4×(-3)-3×2=-18.故4x -3y 的最大值为14,最小值为-18.(2)设u =x 2+y 2,则u 为点(x ,y )到原点(0,0)的距离.结合不等式组所表示的区域,不难知道:点B 到原点距离最大;而当(x ,y )在原点时,距离为0.∴u 最大值=(-1)2+(-6)2=37,u 最小值=0, ∴x 2+y 2的最大值为37,最小值为0.层级二 应试能力达标1.设D 为不等式组⎩⎪⎨⎪⎧x ≥0,2x -y ≤0,x +y -3≤0所表示的平面区域,区域D 上的点与点(1,0)之间的距离的最小值为________.解析:作出可行域,如图中阴影部分所示,则根据图形可知,点B (1,0)到直线2x -y =0的距离最小,d =|2×1-0|22+1=255<1,故最小距离为255.答案:2552.若实数x ,y 满足⎩⎪⎨⎪⎧x -y +1≥0,x +y ≥0,x ≤0,则z =3x+2y的最小值是________.解析:由已知不等式组作可行域如图阴影部分所示.令x +2y =k , 则y =-12x +k2,问题由求k 的最小值转化为求直线y =-12x +k 2的纵截距的最小值.显然当直线y =-12x +k2过原点O 时,截距最小,此时k min =0, z =3x+2y的最小值为1.答案:13.已知x ,y 满足不等式组⎩⎪⎨⎪⎧y ≥x ,x +y ≤2,x ≥a ,且z =2x +y 的最大值是最小值的3倍,则a=________.解析:依题意可知a <1.作出可行域如图所示,z =2x +y 在A 点和B 点处分别取得最小值和最大值.由⎩⎪⎨⎪⎧x =a ,y =x ,得A (a ,a ),由⎩⎪⎨⎪⎧x +y =2,y =x ,得B (1,1).∴z max =3,z min =3a . ∴a =13.答案:134.设二元一次不等式组⎩⎪⎨⎪⎧x +2y -19≥0,x -y +8≥0,2x +y -14≤0所表示的平面区域为M ,使函数y =a x (a >0,a ≠1)的图象过区域M 的a 的取值范围是________.解析:作二元一次不等式组的可行域如图所示,由题意得A (1,9),C (3,8).当y =a x 过A (1,9)时,a 取最大值,此时a =9;当y =a x 过C (3,8)时,a 取最小值,此时a =2,∴2≤a ≤9. 答案:[2,9]5.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥1,x +y ≥1,x ≤2,则满足函数y =2x -t 的t 最大值为________.解析:由约束条件作出可行域如图所示,可知(x ,y )是由点A (1,0),B (2,1),C (2,-1)三点组成的三角形区域,令t =2x -y ,即当经过C (2,-1)时,t 有最大值5.答案:56.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤8,x -2y ≥-4,x ≥0,y ≥0,且z =5y -x 的最大值为a ,最小值为b ,则log a (-b )=________.解析:由线性约束条件得可行域为如图所示的阴影部分.由z =5y -x ,得y =x 5+z5.由图知目标函数y =x 5+z5,过点A (8,0)时,z min =5y -x=5×0-8=-8,即b =-8.目标函数y =x 5+z5过点B (4,4)时,z max =5y -x =5×4-4=16,即a =16.所以log a (-b )=log 168=34.答案:347.某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.(1)试用每天生产的卫兵个数x 与骑兵个数y 表示每天的利润ω(元); (2)怎样分配生产任务才能使每天的利润最大,最大利润是多少? 解:(1)依题意每天生产的伞兵个数为100-x -y , 所以利润ω=5x +6y +3(100-x -y )=2x +3y +300. (2)约束条件为⎩⎪⎨⎪⎧5x +7y +4(100-x -y )≤600,100-x -y ≥0,x ≥0,y ≥0,x ,y ∈N.整理得⎩⎪⎨⎪⎧x +3y ≤200,x +y ≤100,x ≥0,y ≥0,x ,y ∈N.目标函数为ω=2x +3y +300, 作出可行域,如图所示,作初始直线l 0:2x +3y =0,平移l 0,当l 0经过点A 时,ω有最大值,由⎩⎪⎨⎪⎧ x +3y =200,x +y =100,得⎩⎪⎨⎪⎧x =50,y =50. ∴最优解为A (50,50),此时ωmax =550元.故每天生产卫兵50个,骑兵50个,伞兵0个时利润最大,且最大利润为550元.8.已知x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥1,x -3y ≤-4,3x +5y ≤30.(1)求目标函数z =2x +y 的最大值和最小值;(2)若目标函数z =ax +y 取得最大值的最优解有无穷多个,求a 的值;(3)求z =y +5x +5的取值范围.解:作可行域如图所示.(1)作直线l :2x +y =0,并平移此直线,当平移直线过可行域内的A 点时,z 取最小值;当平移直线过可行域内的B 点时,z 取得最大值.由⎩⎪⎨⎪⎧x =1,x -3y =-4,得A ⎝⎛⎭⎫1,53. 由⎩⎪⎨⎪⎧x -3y =-4,3x +5y =30,得B (5,3). ∴z max =2×5+3=13,z min =2×1+53=113.(2)一般情况下,当z 取得最大值时,直线所经过的点都是唯一的,但若直线平行于边界直线,即直线z =ax +y 平行于直线3x +5y =30时,线段BC 上的任意一点均使z 取得最大值,此时满足条件的点即最优解有无数个.又k BC =-35,∴-a =-35.∴a =35.(3)z =y +5x +5=y -(-5)x -(-5),可看作区域内的点(x ,y )与点D (-5,-5)连线的斜率, 由图可知,k BD ≤z ≤k CD .由⎩⎪⎨⎪⎧x =1,3x +5y =30,得C ⎝⎛⎭⎫1,275. ∴k BD =3-(-5)5-(-5)=45,k CD =275-(-5)1-(-5)=2615,∴z =y +5x +5的取值范围是⎣⎡⎦⎤45,2615.。
2019届苏教版(文科数学)直线的一般式方程单元测试
一、选择题1.平面直角坐标系中,直线320x y ++=的斜率为A .33B .33-C .3D .3-【答案】B【解析】将直线320x y ++=化为斜截式得32333y x =--,从而可得斜率为33-. 2.经过点A (2,-1),B (-4,5)的直线的一般式方程为 A .x+y+1=0 B .x-y+1=0C .x-y-1=0D .x+y-1=0【答案】D3.若直线x +2ay −1=0与直线(a −1)x −ay +1=0平行,则a 的值为 A .12B .12或0 C .0D .−2【答案】A【解析】解法一:当a =0时,两直线重合,不合题意;当a ≠0时,由112a a a -=-,得12a =, 经检验,当12a =时,两直线平行.解法二:∵直线x +2ay −1=0与直线(a −1)x −ay +1=0平行, ∴1×(−a )−(a −1)×2a =0,即2a 2−a =0,∴a =0或a =12. 经检验,当a =0时,两直线重合.故a =12.4.若直线l 与直线310x y +-=垂直,且它在x 轴上的截距为-2,则直线l 的方程为 A .320x y --= B .320x y -+= C .320x y -+= D .320x y --=【答案】B【解析】因为直线310x y +-=的斜率为-3,所以直线l 的斜率为13.又直线l 在x 轴上的截距为-2,即直线l 与x 轴的交点为(-2,0),所以直线l 的方程为y -0=13(x +2),即x -3y +2=0,故选B. 5.已知直线ax +by +c =0的图象如图,则下列结论正确的是A .若c >0,则a >0,b >0B .若c >0,则a <0,b >0C .若c <0,则a >0,b <0D .若c <0,则a >0,b >0【答案】D6.过点P (1,3),且与x ,y 轴的正半轴围成的三角形的面积等于6的直线l 的一般式方程是 A .3x +y −6=0 B .x +3y −10=0 C .3x −y =0D .x −3y +8=0【答案】A【解析】设所求直线l 的方程为1x y a b +=(a >0,b >0),则有162ab =,且131a b+=.由1221361ab a b a b=⎧=⎧⎪⇒⎨⎨=+=⎩⎪⎩,∴直线l 的方程为126x y +=,即为3x +y −6=0.二、填空题 7.已知直线过定点,且倾斜角为60︒,则直线的一般式方程为________. 【答案】【解析】由题可得,该直线的斜率为,所以该直线的点斜式方程为,其一般式方程为.8.已知直线222()(0)32a x a a y a ++---=在x 轴上的截距为3,则该直线在y 轴上的截距为________. 【答案】415-【解析】把(3,0)代入已知方程,得(a +2)×3−2a =0,∴a =−6,∴直线方程为−4x +45y +12=0. 令x =0,得415y =-. 9.过点(1,2)且垂直于直线的直线的一般式方程为________.【答案】230x y -+=10.已知直线():1210l ax a y a +-+-=不通过第四象限,则a 的取值范围是________. 【答案】]1,21[【解析】因为直线不过第四象限,所以①0,2110,12aa a a ⎧≥⎪⎪-⎨-⎪≥⎪-⎩解得121≤<a ;②1120,2a a -==.综上所述,a 的取值范围是]1,21[. 三、解答题11.把直线的一般式方程化成斜截式,求出直线的斜率以及它在轴与轴上的截距,并画出图形.12.根据下列条件求解直线的一般式方程. (1)直线的斜率为2,且经过点A (1,3); (2)斜率为,且在y 轴上的截距为4;(3)经过两点A (2,-3),B (-1,-5); (4)在x ,y 轴上的截距分别为2,-4.【解析】(1)因为直线的斜率 =2,且经过点A (1,3),由直线的点斜式方程可得y -3=2(x -1), 整理可得直线的一般式方程为2x -y +1=0. (2)由直线的斜率,且在y 轴上的截距为4,得直线的斜截式方程为,整理可得直线的一般式方程为.(3)由直线的两点式方程可得()()325312y x ---=-----,整理得直线的一般式方程为2x -3y -13=0. (4)由直线的截距式方程可得124x y +=-, 整理得直线的一般式方程为2x -y -4=0. 13.已知方程.(1)求该方程表示一条直线的条件;(2)当m 为何实数时,方程表示的直线斜率不存在?求出这时的直线方程; (3)已知方程表示的直线轴上的截距为−3,求实数m 的值; (4)若方程表示的直线倾斜角是,求实数m 的值.(2)由(1)易知,当12m =时,方程表示的直线的斜率不存在, 此时的直线方程为43x =.(3)依题意,有226323m m m -=---,由(1)知当时,,即所求的值为53-.(4)因为直线的倾斜角是45°,所以斜率.故由2223121m m m m ---=+-舍去).所以直线的倾斜角为45°时,43m =. 14.已知直线l 平行于直线,直线l 与两坐标轴围成的三角形的周长是15,求直线l 的方程.∵直线l与两坐标轴围成的三角形周长是15,∴35||||1544b b b++=,∴,∴.∴直线l的方程是453y x=-±,即.。
2019届苏教版圆锥曲线单元测试
圆锥曲线一、选择、填空题1、(2018北京高考)已知椭圆2222:10x yM a ba b,双曲线2222:1x yNm n。
若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的离心率为;双曲线N的离心率为。
2、(2017北京高考)若双曲线221yxm的离心率为3,则实数m=______________3、(2016北京高考)双曲线22221x ya b(0a,0b)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点,若正方形OABC的边长为2,则a_______________.4、(朝阳区2018届高三3月综合练习(一模))若三个点(2,1),(2,3),(2,1)中恰有两个点在双曲线222:1(0)xC y aa上,则双曲线C的渐近线方程为_____________5、(东城区2018届高三5月综合练习(二模))已知双曲线C:x2a2-y2b2=1的一条渐近线的倾斜角为60o,且与椭圆x25+y2=1有相等的焦距,则C的方程为(A)x23-y2=1(B)x29-y23=1(C)x2-y23=1 (D)x23-y29=16、(丰台区2018届高三5月综合练习(二模))已知双曲线2221(0)9x ybb的一条渐近线的倾斜角为π6,则b的值为(A)33(B) 3(C) 233(D) 337、(海淀区2018届高三上学期期末考试)点(2,0)到双曲线2214xy的渐近线的距离是______________8、(石景山区2018届高三3月统一测试(一模))双曲线2212xy的焦距是________,渐近线方程。
2019届苏教版(文科数学) 导函数的基本性质 单元测试
1. (2018苏州(上)末4.)曲线y=x 在x=1处的切线斜率为 .2. (2018苏州(上)末6.)已知函数f (x )=x 3-23x 2+m 在(0,2)上有极值23,则实数m 的值为 .3. (2017苏州(上)末5.)函数y=x 3﹣2x 2+x 的单调递减区间为 .4. (2017苏州(上)末7.)函数y=x 2﹣x ﹣lnx 在区间[1,3]上的最小值等于 .5. (2016苏州(上)末4.)函数y=sinx 的图象在点(π,0)处的切线方程为 .6. (2016苏州(上)末5.)一质点的运动方程为s=t 2+10(位移单位:m ;时间单位:s ),则该质点在t=3时的瞬时速度为 m/s .7. (2016苏州(上)末6.)若函数f(x)=x 3-3x 2+a 在区间[-1,1]上的最大值是2,则实数a 的值为 .8. (2014苏州(上)末4.)已知f (x )=xcosx ,则f′(x )=9. (2014苏州(上)末6.)函数f (x )=x ﹣2e x 的单调减区间是10. (2014苏州(上)末7.)若直线y=﹣3x+b 是曲线y=x 3﹣3x 2+2的一条切线,则实数b 的值是11. (2013苏州(上)末2.)一质点运动的方程为210S t =+(位移单位:m ,时间单位:s ),则该质点在3t =s 的瞬时速度是 m /s .12. (2013苏州(上)末11.)函数22ln y x x =-的单调递增区间是 .13. (2012苏州(上)末3.) 一物体的运动方程为s=1-t+t 2,其中s 的单位是米,t 的单位是秒,那么物体在t=3秒时的瞬时速度为 米/秒。
14. (2011苏州(上)末5.)已知曲线23ln 4x y x =-的一条切线的斜率为21,则切点的横坐标为 .15. (2011苏州(上)末10.)已知[0,π]x ∈,则函数sin cos 2x y x =-的值域为 16. (2011苏州(上)末17.)已知函数(I )若是的极值点,求在上的最小值和最大值;(Ⅱ)若上是增函数,求实数的取值范围.17. (2010苏州(上)末4.)若,13)(2--+=x x e x f x 则=)0('f导函数的基本性质答案:1. 212. 23. (,1).4. 05. x+y-π=06. 67. 28. cosx ﹣xsinx9. (ln ,+∞)10. 311. 612. 1(,)2+∞13. 514. 315. [ . 16. 解:(I )有极大值点,极小值点.此时在上是减函数,在上是增函数.在上的最小值是-18,最大值是-6(Ⅱ)2()3230f x x x '=--≥ 当时恒成立,17. -2。
2019届苏教版(文科数学) 数学文化 单元测试
【2018高三数学各地优质一模试题分项精品】一、选择题1. 【2018江西南昌高三一模】欧拉公式(为虚数单位)是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”。
根据欧拉公式可知,表示的复数位于复平面中的( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】A2. 【2018辽宁朝阳高三一模】《九章算术》是我国古代内容即为丰富的数学名著,书中有如下问题“今有刍凳,下广三丈,袤四丈,上袤二丈,无广,高二丈,问积几何?”其意思为“今有底面为矩形的屋脊状的锲体,下底面宽丈,长丈,上棱长丈,高丈,问它的体积是多少?”已知丈为尺,该锲体的三视图如图所示,在该锲体的体积为()A. 立方尺B. 立方尺C. 立方尺D. 立方尺【答案】A【解析】由题意,将楔体分割为三棱柱与两个四棱锥的组合体,作出几何体的直观图如图所示沿上棱两端向底面作垂面,且使垂面与上棱垂直,则将几何体分成两个四棱锥和1个直三棱柱,则三棱柱的四棱锥的体积由三视图可知两个四棱锥大小相等,立方丈立方尺.故选A.【点睛】本题考查三视图及几何体体积的计算,其中正确还原几何体,利用方格数据分割与计算是解题的关键.3. 【2018辽宁瓦房店高三一模】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题“今有阳马,广五尺,袤七尺,高八尺,问积几何?”其意思为“今有底面为矩形,一侧棱垂直于底面的四棱锥,它的底面长、宽分别为7尺和5尺,高为8尺,问它的体积是多少?”若以上的条件不变,则这个四棱锥的外接球的表面积为()A. 平方尺B. 平方尺C. 平方尺D. 平方尺【答案】B4. 【2018贵州黔东南高三一模】我国古代数学名著《九章算术》在“勾股”一章中有如下数学问题“今有勾八步,股十五步,勾中容圆,问径几何?”.意思是一个直角三角形的两条直角边的长度分别是8步和15步,则其内切圆的直径是多少步?则此问题的答案是()A. 3步 B. 6步 C. 4步 D. 8步【答案】B【解析】由于该直角三角形的两直角边长分别是和,则得其斜边长为,设其内切圆半径为,则有 (等积法),解得,故其直径为(步),故选B.5. 【2018福建南平高三质检一】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面枳,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为()(参考数据,)A. 12B. 24C. 48D. 96【答案】B6. 【2018四川德阳高三二诊】《九章算术》是我国古代一部数学名著,某数学爱好者阅读完其相关章节后编制了如图的程序框图,其中表示除以的余数,例如.若输入的值为8时,则输出的值为()A. 2B. 3C. 4D. 5【答案】B7.【2018北京朝阳区高三一模】庙会是我国古老的传统民俗文化活动,又称“庙市”或“节场”.庙会大多在春节、元宵节等节日举行.庙会上有丰富多彩的文化娱乐活动,如“砸金蛋”(游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”).今年春节期间,某校甲、乙、丙、丁四位同学相约来到某庙会,每人均获得砸一颗金蛋的机会.游戏开始前,甲、乙、丙、丁四位同学对游戏中奖结果进行了预测,预测结果如下甲说“我或乙能中奖”;乙说“丁能中奖”;丙说“我或乙能中奖”;丁说“甲不能中奖”.游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是( )A. 甲B. 乙C. 丙D. 丁【答案】A【解析】由四人的预测可得下表预测结果中奖人甲乙丙丁甲✔✖✖✖乙✔✖✔✔丙✖✖✔✔丁✖✔✖✔1.若甲中奖,仅有甲预测正确,符合题意;2.若乙中奖,甲、丙、丁预测正确,不符合题意;3.若丙中奖,丙、丁预测正确,不符合题意;4.若丁中奖,乙、丁预测正确,不符合题意;故只有当甲中奖时,仅有甲一人预测正确,选.8.【2018广东高三一模】大衍数列,于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,是中华传统文化中隐藏着的世界数学史上第一道数列题.其规律是偶数项是序号平方再除以2,奇数项是序号平方减1再除以2,其前10项依次是0,2,4,8,12,18,24,32,40,50,…,如图所示的程序框图是为了得到大衍数列的前100项而设计的,那么在两个“”中,可以先后填入()A.是偶数,B.是奇数,C.是偶数,D.是奇数,【答案】D9. 【2018山西省高三一模】《九章算术》中对一些特殊的几何体有特定的称谓,例如将底面为直角三角形的直三棱柱称为堑堵.将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均匀直角三角形的四面体).在如图所示的堑堵中,,则阳马的外接球的表面积是()A. B. C. D.【答案】B【解析】以为边,将图形补形为长方体,长方体外接球即阳马的外接球,长方体的对角线为球的直径,即,故球的表面积为.选B.10.【2018安徽芜湖高三一模】“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用形数结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形中较小的锐角,现在向大正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是()A. B. C. D.【答案】D11. 【2018甘肃兰州高三一模】刘徽《九章算术注》记载“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也”.意即把一长方体沿对角面一分为二,这相同的两块叫做堑堵,沿堑堵的一顶点与其相对的面的对角线剖开成两块,大的叫阳马,小的叫鳖臑,两者体积之比为定值,这一结论今称刘徽原理.如图是一个阳马的三视图,则其外接球的体积为()A. B. C. D.【答案】B【解析】【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.12. 【2018山东聊城高三一模】我国三国时期的数学家赵爽为了证明勾股定理创制了一幅“勾股圆方图”,该图是由四个全等的直角三角形组成,它们共同围成了一个如图所示的大正方形和一个小正方形.设直角三角形中一个锐角的正切值为3.在大正方形内随机取一点,则此点取自小正方形内的概率是()A. B. C. D.【答案】D【解析】不妨设两条直角边为,故斜边,即大正方形的边长为,小正方形边长为,故概率为.13. 【2018内蒙古包头高三一模】《九章算术》中的“竹九节”问题现有一根节的竹子,自上而下各节的容积成等差数列,上面节的容积共升,下面节的容积共升,则该竹子最上面一节的容积为()A.升B. 升C. 升D. 升【答案】C【解析】设竹子自上而下各节的容积分别为,且为等差数列,根据题意得,即 ,解得,即最上面一节的容积为升,故选C .14.【2018云南保山高三第二次统测】我国古代数学名著《增删算法统宗》中有如下问题 “有个金球里面空,球高尺二厚三分,一寸自方十六两,试问金球几许金?”意思是 有一个空心金球,它的直径12寸,球壁厚0.3寸,1立方寸金重1斤,试问金球重是多少斤?(注3π≈)( )A. 125.77B. 864C. 123.23D. 369.69 【答案】C15.【2018百校联盟高三3月联考】我国古代数学名著《张丘建算经》中有如下问题 “今有粟二百五十斛委注平地,下周五丈四尺;问高几何?”意思是 有粟米250斛,把它自然地堆放在平地上,自然地成为一个圆锥形的粮堆,其底面周长为54尺,则圆锥形的高约为多少尺?(注 1斛 1.62≈立方尺, 3π≈)若使题目中的圆锥形谷堆内接于一个球状的外罩,则该球的直径为( )A. 5尺B. 9尺C. 10.6尺D. 21.2尺 【答案】D【解析】因为250斛250 1.62=⨯立方尺,设圆锥形的高为h 尺,底面半径为r 尺,则254,9r r π=∴=,因此21250 1.6239,53h h ⨯=⨯⨯⨯⇒=,设球的半径为R ,则()22295R R =+-,可得10.6R =(尺),221.2R ∴=(尺),故选D. 16.【2018江西高三二模】欧阳修的《卖油翁》中写道“(翁)乃取一葫芦置于地,以钱覆盖其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为4cm 的圆面,中间有边长为1cm 的正方形孔.现随机向铜钱上滴一滴油(油滴的大小忽略不计),则油滴落入孔中的概率为( )A.49πB.14πC.19πD.116π【答案】B17.【2018湖南永州高三二模】我国的《洛书》中记载着世界上最古老的一个幻方将1,2,...,9填入33⨯的方格内,使三行、三列、两对角线的三个数之和都等于15 (如图).一般地,将连续的正整数1,2,3,…,2n填入n n⨯的方格内,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方.记n阶幻方的一条对角线上数的和为n N (如在3阶幻方中,315N=),则10N=()A. 1020B. 1010C. 510D. 505 【答案】D【解析】n阶幻方共有2n个数,其和为()222112...,2n nn n++++=阶幻方共有n行,∴每行的和为()()2221122n nn nn++=,即()()2210110101,50522nn nN N+⨯+=∴==,故选D.18.【2018吉林普通高中二调】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(2015浙江文 )如图,斜线段ΑΒ与平面所成的角为60,B为斜足,平面上的动点P满足
30ΡΑΒ
,则点P的轨迹是
A.直线 B.抛物线
C.椭圆 D.双曲线的一支
【答案】C
【解析】由题可知,当P点运动时,在空间中,满足条件的AP绕ΑΒ旋转形成一个圆锥,用一个与圆
锥高成60角的平面截圆锥,所得图形为椭圆.故选C.
2.(2015广东文 )已知过原点的动直线l与圆1:C22650xyx相交于不同的两点Α,Β.
(1)求圆1C的圆心坐标;
(2)求线段ΑΒ的中点Μ的轨迹C的方程;
(3)是否存在实数k,使得直线:L4ykx与曲线C只有一个交点?若存在,求出k的取值范围;
若不存在,说明理由.
【答案】(1)3,0;(2)492322yx335x;(3)存在,752752k或34k.
(3)由题意知直线L表示过定点T(4,0),斜率为k的直线.
结合图形,492322yx335x表示的是一段关于x轴对称,起点为352,35按逆时针
方向运动到352,35的圆弧.根据对称性,只需讨论在x轴对称下方的圆弧.
设P352,35,则752354352PTk,而当直线L与轨迹C相切时, 2314232kkk,解得43k.
在这里暂取43k,因为43752,所以PTkk.
