二次函数中有关线段和角度地问题
2023年九年级数学中考专题训练二次函数与角度问题含答案解析

中考专题训练——二次函数与角度问题1.已知二次函数232y ax bx =+-(0a ≠)的图象经过A (1,0)、B (−3,0)两点,顶点为点C .(1)求二次函数的解析式; (2)如二次函数232y ax bx =+-的图象与y 轴交于点G ,抛物线上是否存在点Q ,使得∠QAB=∠ABG ,若存在求出Q 点坐标,若不存在请说明理由;(3)经过点B 并且与直线AC 平行的直线BD 与二次函数232y ax bx =+-图象的另一交点为D ,DE ∠AC ,垂足为E ,DF y 轴交直线AC 于点F ,点M 是线段BC 之间一动点,FN ∠FM 交直线BD 于点N ,延长MF 与线段DE 的延长线交于点H ,点P 为△NFH 的外心,求点M 从点B 运动到点C 的过程中,P 点经过的路线长. 2.在平面直角坐标系中,抛物线l :()2220y x mx m m =--->与x 轴分别相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,设抛物线l 的对称轴与x 轴相交于点N ,且3OC ON = (1)求m 的值;(2)设点G 是抛物线在第三象限内的动点,若GBC ACO ∠=∠,求点G 的坐标;(3)将抛物线222y x mx m =---向上平移3个单位,得到抛物线l ',设点P 、Q 是抛物线l '上在第一象限内不同的两点,射线PO 、QO 分别交直线=2y -于点P '、Q ',设P '、Q '的横坐标分别为P x '、Q x ',且4P Q x x ''⋅=,求证:直线PQ 经过定点.3.已知二次函数y =x 2十(k ﹣2)x ﹣2k .(1)当此二次函数的图像与x 轴只有一个交点时,求该二次函数的解析式;(2)当k >0时,直线y =kx +2交抛物线于A ,B 两点(点A 在点B 的左侧),点P 在线段AB 上,过点P 做PM 垂直x 轴于点M ,交抛物线于点N . ∠求PN 的最大值(用含k 的代数式表示);∠若抛物线与x 轴交于E ,F 两点,点E 在点F 的左侧.在直线y =kx +2上是否存在唯一一点Q ,使得∠EQO =90°?若存在,请求出此时k 的值;若不存在,请说明理由.4.如图,直线l :33y x =-+与x 轴、y 轴分别相交于A 、B 两点,抛物线223(0)y ax ax a a =--<经过点B .(1)求该抛物线的函数表达式;(2)已知点M 是抛物线上的一个动点,并且点M 在第一象限内,连接AM 、BM ,设点M 的横坐标为m ,ABM 的面积为S ,求S 与m 的函数表达式,并求出S 的最大值;(3)在(2)的条件下,当S 取得最大值时,动点M 相应的位置记为点M ',将直线l 绕点A 按顺时针方向旋转得到直线l ',当直线l '与直线AM '重合时停止旋转,在旋转过程中,直线'l 与线段BM '交于点C ,设点B 、M '到直线l '的距离分别为1d 、2d ,当12d d +最大时,求直线l '旋转的角度(即BAC ∠的度数). 5.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C ,抛物线y =−12x 2+bx +c 经过A 、C 两点,与x 轴的另一交点为点B .(1)求抛物线的函数表达式;(2)点D 为直线AC 上方抛物线上一动点, ∠连接BC 、CD ,设直线BD 交线段AC 于点E ,求DEEB的最大值; ∠过点D 作DF ∠AC ,垂足为点F ,连接CD ,是否存在点D ,使得△CDF 中的∠DCF =2∠BAC ,若存在,求出点D 的坐标;若不存在,请说明理由.6.已知抛物线265y x x =++与x 轴交于点A ,B (点A 在点B 左侧),顶点为D ,且过C (-4,m ). (1)求点A ,B ,C ,D 的坐标;(2)点P 在该抛物线上(与点B ,C 不重合),设点P 的横坐标为t .∠当点P 在直线BC 的下方运动时,求∠PBC 的面积的最大值, ∠连接BD ,当∠PCB =∠CBD 时,求点P 的坐标.7.如图所示,抛物线y =−x 2+bx +3经过点B (3,0),与x 轴交于另一点A ,与y 轴交于点C .(1)求抛物线所对应的函数表达式;(2)如图,设点D 是x 轴正半轴上一个动点,过点D 作直线l ∠x 轴,交直线BC 于点E ,交抛物线于点F ,连接AC 、FC .∠若点F 在第一象限内,当∠BCF =∠BCA 时,求点F 的坐标; ∠若∠ACO +∠FCB =45°,则点F 的横坐标为______.8.已知抛物线2y ax c =+过点()2,0A -和()1,3D -两点,交x 轴于另一点B .(1)求抛物线解析式;(2)如图1,点P 是BD 上方抛物线上一点,连接AD ,BD ,PD ,当BD 平分ADP 时,求P 点坐标; (3)将抛物线图象绕原点O 顺时针旋转90°形成如图2的“心形”图案,其中点M ,N 分别是旋转前后抛物线的顶点,点E 、F 是旋转前后抛物线的交点. ∠直线EF 的解析式是______;∠点G 、H 是“心形”图案上两点且关于EF 对称,则线段GH 的最大值是______.9.如图,在平面直角坐标系中,抛物线()240y ax bx a =++≠经过点()3,4A 和点()1,0B -,连接AB ,过点A 作AD x ⊥轴于点D ,点P 在直线AB 上方的抛物线上,过点P 作PE AD ∥交x 轴于点E ,交线段AB 于点G ,连接PD 交线段AB 于点Q .(1)求抛物线的表达式;(2)当GQ AQ =时,设点P 的横坐标为m ,求m 的值;(3)在(2)的条件下,线段BE 上有一点F ,直线AD 上有一点K ,连接KF 、GF ,当2FKD FGB ∠=∠,且8KF =时,直接写出....点K 的纵坐标.... 10.如图,已知抛物线2y x bx c =++与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点C ,OA =OC =3.(1)求抛物线的函数表达式;(2)若点P 为直线AC 下方抛物线上一点,连接BP 并交AC 于点Q ,若AC 分ABP 的面积为1:2两部分,请求出点P 的坐标;(3)在y 轴上是否存在一点N ,使得45BCO BNO ∠+∠=︒,若存在,请求出点N 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2+2x −3与x 轴交于A 、B 两点,且B (1,0).(1)求抛物线的解析式和点A 的坐标;(2)如图1,点P 是直线y =x 上在x 轴上方的动点,当直线y =x 平分∠APB 时,求点P 的坐标;(3)如图2,已知直线y =23x −49分别与x 轴、y 轴交于C 、F 两点,点Q 是直线CF 下方的抛物线上的一个动点,过点Q 作y 轴的平行线,交直线CF 于点D ,点E 在线段CD 的延长线上,连接QE .问:以QD 为腰的等腰△QDE 的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由. 12.如图,顶点坐标为(3,4)的抛物线2y ax bx c =++交x 轴于A ,B 两点,交y 轴于点()0,5C -.(1)求a ,b 的值;(2)已知点M 在射线CB 上,直线AM 与抛物线2y ax bx c =++的另一公共点是点P .∠抛物线上是否存在点P ,满足:2:1=AM MP ,如果存在,求出点P 的横坐标;如果不存在,请说明理由; ∠连接AC ,当直线AM 与直线BC 的夹角等于ACB ∠的2倍时,请直接写出点M 的坐标.13.如图,抛物线2y x bx c =++与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,若()1,0A -且3OC OA =.(1)求该抛物线的函数表达式;(2)如图1,点D 是该抛物线的顶点,点(),P m n 是第二象限内抛物线上的一个点,分别连接BD 、BC 、BP ,当2PBA CBD ∠=∠时,求m 的值;(3)如图2,BAC ∠的角平分线交y 轴于点M ,过M 点的直线l 与射线AB ,AC 分别交于E ,F ,已知当直线l 绕点M 旋转时,11AE AF+为定值,请直接写出该定值. 14.如图,在平面直角坐标系xOy 中,抛物线1L :2y x bx c =++与x 轴交于(4,0)A -,B 两点,且经过点(1,3)-,点C 是抛物线1L 的顶点,将抛物线1L 向右平移得到抛物线2L ,且点B 在抛物线2L 上.(1)求抛物线1L 的表达式;(2)在抛物线2L 上是否存在一点P ,使得90PAC ∠=︒,若存在,请求出点P 的坐标,若不存在,请说明理由.15.如图,抛物线22y ax bx =++与x 轴相交于A 、B 两点,与y 轴相交于点C ,已知B 点的坐标为()4,0,抛物线的对称轴为直线32x =,点D 是BC 上方抛物线上的一个动点.(1)求抛物线的函数表达式;(2)当BCD △的面积为74时,求点D 的坐标;(3)过点D 作DE BC ⊥,垂足为点E ,是否存在点D ,使得CDE 中的某个角等于ABC ∠的2倍?若存在,请直接写出点D 的横坐标...;若不存在,请说明理由. 16.抛物线2y ax bx c =++的顶点坐标为(1,4),与x 轴交于点,(3,0)A B 两点,与y 轴交于点C ,点M 是抛物线上的动点.(1)求这条抛物线的函数表达式;(2)如图1,若点M 在直线BC 上方抛物线上,连接AM 交BC 于点E ,求MEAE的最大值及此时点M 的坐标;(3)如图2,已知点(0,1)Q ,是否存在点M ,使得1tan 2MBQ ∠=?若存在,求出点M 的坐标;若不存在,请说明理由.17.如图,在平面直角坐标系xOy 中,抛物线2y x bx c =++与y 轴交于点C ,与x 轴交于A 、B 两点,直线4y x =+恰好经过B 、C 两点.(1)求二次函数的表达式;(2)点D 为第三象限抛物线上一点,连接BD ,过点O 作OE BD ⊥,垂足为E ,若2OE BE =,求点D 的坐标;(3)设F 是抛物线上的一个动点,连结AC 、AF ,若2BAF ACB ∠=∠,求点F 的坐标.18.抛物线y 1=x 2+(3-m )x +c 与直线l :y 2=kx +b 分别交于点A (-2,0)和点B (m ,n ),当-2≤x ≤4时,y 1≤y 2.(1)求c 和n 的值(用含m 的式子表示);(2)过点P (1,0)作x 轴的垂线,分别交抛物线和直线l 于M ,N 两点,则∠BMN 的面积是否存在最大值或者最小值,若存在,请求出这个值;若不存在,请说明理由;(3)直线x =m +1交抛物线于点C ,过点C 作x 轴的平行线交直线l 于点D ,交抛物线另一点于E ,连接BE ,求∠DBE 的度数.19.如图,抛物线2323y x x -=-+与x 轴交于点A 和点B ,直线:l y kx b =+与抛物线2323y x x -=-+交于点D和点12F n ⎛⎫⎪⎝⎭,,且与y 轴交与点()02E ,.(1)求直线l 的函数表达式;(2)若P 为抛物线上一点,当POE OED =∠∠时,求点P 的坐标. 20.如图,在平面直角坐标系中,直线122y x =-+与x 轴交于点A ,与y 轴交于点B ,抛物线212y x bx c =-++经过A 、B 两点,且与x 轴的负半轴交于点C .(1)求该抛物线的解析式;(2)若点D 为直线AB 上方抛物线上的一点,2ABD BAC ∠=∠,直接写出点D 的坐标.参考答案1.(1)21322y x x =+- (2)542⎛⎫- ⎪⎝⎭,或322⎛⎫-- ⎪⎝⎭,(3)1【分析】(1)将A (1,0)、B (-3,0)代入232y ax bx =+-,即可求解; (2)先求出BG 的解析式为13y x 22=--,然后再进行分类讨论,分别求得点Q 的坐标即可;(3)可知△DNH 与△FNH 是直角三角形,外心P 在斜边NH 的中点,分别求出直线AC 及直线BD 的函数关系式,再分为当M 运动到C 点时及当点M 运动到B 点时两种情况进行讨论,求解即可.【解析】(1)∠二次函数232y ax bx =+-的图像经过A (1,0)、B (-3,0), ∠30239302a b a b ⎧+-=⎪⎪⎨⎪--=⎪⎩,解得121a b ⎧=⎪⎨⎪=⎩, ∠二次函数的解析式为213y x x 22=+-; (2)由题可知G 点坐标30,2⎛⎫- ⎪⎝⎭,设直线BG 的解析式为y px q =+,得: 30302k b k b -+=⎧⎪⎨+=-⎪⎩,解得:1232k b ⎧=-⎪⎪⎨⎪=-⎪⎩, ∠BG 的解析式为13y x 22=--,∠AQ ∥BG ,直线AQ 的解析式11y x 22=-+,联立直线AQ 与二次函数解析式2112213x 22y x y x ⎧=-+⎪⎪⎨⎪=+-⎪⎩,解得1110x y =⎧⎨=⎩或22452x y =-⎧⎪⎨=⎪⎩此时Q 的坐标为542⎛⎫- ⎪⎝⎭,,∠直线11y x 22=-+与y 轴的交点为K 102⎛⎫⎪⎝⎭,,其关于x 轴的对称点为11K 02⎛⎫- ⎪⎝⎭, 直线1AK 的解析式为:11y x 22=- 与二次函数解析式联立得 2112213x 22y x y x ⎧=-⎪⎪⎨⎪=+-⎪⎩, 解得1110x y =⎧⎨=⎩或22232x y =-⎧⎪⎨=-⎪⎩,此时Q 的坐标为322⎛⎫-- ⎪⎝⎭,, 综上,抛物线上存在点Q 使得∠QAB =∠BAG ,Q 点坐标为542⎛⎫- ⎪⎝⎭,或322⎛⎫-- ⎪⎝⎭,(3)如图,易知△DNH 与△FNH 是直角三角形,外心P 在斜边NH 的中点,∠PD =PF =12NH ,所以点P 是线段DF 的垂直平分线上的动点, ∠直线AC 的解析式为y =x -1,BD ∥AC , ∠直线BD 的解析式为y =x +3, ∠D (3,6),∠当M 运动到C 点时1H 与点E 重合,1FN AC ⊥,则1FN BD ⊥,又因为∠DEF =90°,DE =EF , ∠四边形1DN FE 为正方形, ∠1P 是线段DF 的中点(3,4);∠当点M 运动到B 点时,22FN FH ⊥,∠四边形DN 1FE 是正方形∠122190N FN BFC N N F BCF ∠=∠∠=∠=︒,,∠21N N F BCF ∽, ∠121CF BC N F N N =, ∠四边形DN 1FE 是正方形,∠11,4N (),∠2112BC CF N N N F ==,∠12N N =∠22,5N (), 同理26,3H (), 所以22N H 的中点2P (4,4),∠134P (,), ∠121PP =【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,会用待定系数法求函数的解析式,会求函数的交点坐标,根据点M 的运动情况确定P 点的轨迹是线段是解题的关键.2.(1)1m =(2)点G 的坐标为17,24⎛⎫-- ⎪⎝⎭(3)见解析【分析】(1)由顶点式求得对称轴,由x =0处函数值求得C 点坐标,根据3OC ON =列方程求解即可;(2)连接AC 、BC ,过点C 作CT CB ⊥,设BG 交CT 于点T ,作TH y ⊥轴于点H ,由抛物线解析式求得A 、B 、C 坐标,可得∠OBC 、∠CHT 是等腰直角三角形,由BC 和tan tan GBC ACO ∠=∠可得TC ,进而可得T 点坐标,再由B 点坐标可得直线BC 解析式,然后与二次函数解析式联合求得交点坐标即可解答;(3)设点()2111,2P x x x -,()2222,2Q x x x -,由原点可得直线PO 、QO 的解析式,再由y =-2可得点Q '、P '横坐标,由4P Q x x ''⋅=可得()1212230x x x x -++=;设直线PQ 的解析式为y mx n =+,与l '联立可得()220x m x n -+-=,利用根与系数的关系可得122x x m +=+,12x x n =-,代入()1212230x x x x -++=求得21n m =--,于是直线PQ 为()21y m x =--经过定点2,1;(1)解:依题意得:()222y x m m m =----,∠抛物线的对称轴为直线x m =, ∠ON m m ==,在222y x mx m =---中,令0x =,则2y m =--,∠()0,2C m --, ∠22OC m m =--=+,∠3OC ON =,∠23m m +=,解得1m =;(2)解:如图,连接AC 、BC ,过点C 作CT CB ⊥,设BG 交CT 于点T ,作TH y ⊥轴于点H ,由(1)得1m =,∠抛物线的解析式为2=23y x x --,()0,3C -,3OC =,令0y =,则2230x x --=,解得11x =-,23x =,∠点A 在点B 的左侧,∠()1,0A -,()3,0B ,3OB =,在Rt AOC 中,1tan 3OA ACO OC ∠==, 3OB OC ==,则OBC △是等腰直角三角形,BC =∠OCB =45°,∠TCB =90°,则∠TCH =45°,∠CHT △是等腰直角三角形,∠GBC ACO ∠=∠,∠1tan tan 3GBC ACO ∠=∠=, ∠13CT BC =,1133CT BC ==⨯=∠sin451TH CH ==︒=,∠()1,2T --,由点()1,2T --与点()3,0B ,可求得1322TB y x =-, 联立得2132223y x y x x ⎧=-⎪⎨⎪=--⎩, 解得:1130x y =⎧⎨=⎩,221274x y ⎧=-⎪⎪⎨⎪=-⎪⎩,∠点G 的坐标为17,24⎛⎫-- ⎪⎝⎭;(3)解:如图,将抛物线l 向上平移3个单位后得到抛物线l ':22y x x =-,∠点P 、Q 是抛物线l '上在第一象限内不同的两点,∠设点()2111,2P x x x -,()2222,2Q x x x -,由()2111,2P x x x -,()2222,2Q x x x -分别可求得:()12OP y x x =-,()22OQ y x x =- ∠点P '、Q '在直线=2y -上,∠点12,22P x ⎛⎫--' ⎪-⎝⎭,22,22Q x ⎛⎫--' ⎪-⎝⎭, ∠4P Q x x ''⋅= ∠1222422x x --⋅=--,即()()12221x x --=,整理得()1212230x x x x -++=, 设直线PQ 的解析式为y mx n =+,与l '联立得:22,y x x y mx n⎧=-⎨=+⎩,22x x mx n -=+, 整理得()220x m x n -+-=,由根与系数的关系可得:122x x m +=+,12x x n =-,∠()1212230x x x x -++=,∠()2230n m --++=,∠21n m =--,∠直线PQ 的解析式为21y mx m =--,()21y m x =--,∠当2x =时,1y =-,∠直线PQ 经过定点2,1;【点评】本题考查了一次函数与二次函数的综合,解直角三角形,等腰直角三角形的性质,一元二次方程根与系数的关系;此题综合性较强,正确作出辅助线并掌握函数图象交点坐标的意义是解题关键. 3.(1)244y x x =-+(2)∠32k +,∠存在实数43k =或k =2y kx =+上存在唯一一点Q ,使得90EQO ∠=︒【分析】(1)根据函数图像与x 轴只有一个交点,结合Δ0=求出k 值即可;(2)∠根据题意,求出()2(,2),,(2)2P m mk N m m k m k ++--,利用两点之间距离公式求出PQ ,得出11m ≤∠二次函数综合中的直角三角形分两种情况:当直线2y kx =+与以O 、E 为直径的圆相切时;当圆与直线相交且一个交点为A 时;分情况求解即可.(1)解:二次函数的图像与x 轴只有一个交点,∠22(2)8(2)0k k k ∆=-+=+=,解得2k =-,∠所求抛物线的解析式为244y x x =-+;(2)解:如图所示:∠∠点P 在线段AB 上,且直线AB 解析式为2y kx =+,∠设点M 的横坐标为m ,则()2(,2),,(2)2P m mk N m m k m k ++--,∠22(2)2PN mk m k m k ⎡⎤=+-+--⎣⎦2222m m k =-+++2(1)32m k =--++,把2y kx =+代入2(2)2y x k x k =+--得:2(2)22x k x k kx +--=+,∠222220,(1)2(1)x x k x k ---=-=+,∠0k >,∠2(1)0k +>,∠1x =∠x 的值可以取到1,即11m ≤≤∠m 的值可以取到1,∠当1m =时PN 的最大值为32k +;∠设直线2y kx =+与x 轴、y 轴分别交于点G 、H ,则()22,0,0,2,,2G H OG OH k k ⎛⎫-== ⎪⎝⎭.在Rt GOH 中,由勾股定理得:GH = 令2(2)20y x k x k =+--=,即()(2)0x k x +-=,解得:x k =-或2x =.∠(),0E k -,OE k =.(∠)当直线2y kx =+与以O 、E 为直径的圆相切时,如图∠所示:设直线2y kx =+与以O 、E 为直径的圆相切的切点为Q ,此时90,90GQM EQO ∠∠=︒=︒.设OE 中点为点M ,连接MQ ,如图∠所示,则,0.5MQ GH MQ ME OM k ⊥===.∠22k GM OG OM k =-=-, ∠,90∠=∠∠=∠=︒MGQ HGO MQG HOG , ∠∽MOG HOG , ∠=MQ GM OH GH ,即22222k k k -=, ∠2221618k k k +=-+ ∠2169k =,解得:43k =±, ∠0k >, ∠43k =. (∠)当圆与直线相交且一个交点为A 时,如图∠所示,设另一个交点为Q ,∠OE 是圆的直径,∠90EQO ∠=︒,此时可得:OG OE =, ∠2k k=,解得:k = ∠0k >,∠k =∠存在实数43k =或k =2y kx =+上存在唯一一点Q ,使得90EQO ∠=︒. 【点评】本题考查二次函数综合,涉及到利用判别式求二次函数解析式、二次函数综合中的线段最值问题、二次函数综合中的直角三角形问题,熟练掌握二次函数的图像与性质,并掌握解决相关二次函数综合问题题型的方法技巧是解决问题的关键.4.(1)223y x x =-++ (2)21525()228S m =--+,最大值为258(3)45°【分析】(1)利用直线l 的解析式求出B 点坐标,再把B 点坐标代入二次函数解析式即可求出a 的值;(2)设M 的坐标为(m ,-m 2+2m +3),然后根据面积关系将∠ABM 的面积进行转化;(3)由(2)可知m =52,代入二次函数解析式即可求出纵坐标的值;可将求d 1+d 2最大值转化为求AC 的最小值.(1)解:令x =0代入y =-3x +3,∠y =3,∠B (0,3),把B (0,3)代入223y ax ax a =--,∠3=-3a ,∠a =-1,∠二次函数解析式为:y =-x 2+2x +3;(2)令y =0代入y =-x 2+2x +3,∠0=-x 2+2x +3,∠x =-1或3,∠抛物线与x 轴的交点横坐标为-1和3,∠M 在抛物线上,且在第一象限内,∠0<m <3,令y =0代入y =-3x +3,∠x =1,∠A的坐标为(1,0),由题意知:M的坐标为(m,-m2+2m+3),S=S四边形OAMB-S△AOB=S△OBM+S△OAM-S△AOB=1 2×m×3+12×1×(-m2+2m+3)-12×1×3=-12(m-52)2+258∠当m=52时,S取得最大值258.(3)由(2)可知:M′的坐标为(52,74);过点M′作直线l1∠l′,过点B作BF∠l1于点F,根据题意知:d1+d2=BF,此时只要求出BF的最大值即可,∠∠BFM′=90°,∠点F在以BM′为直径的圆上,设直线AM′与该圆相交于点H,∠点C在线段BM′上,∠F在优弧BM H'上,∠当F与M′重合时,BF可取得最大值,此时BM′∠l1,∠A(1,0),B(0,3),M′(52,74),∠由勾股定理可求得:AB M B M A''===过点M′作M′G∠AB于点G,设BG =x ,∠由勾股定理可得:M ′B 2-BG 2=M ′A 2-AG 2,∠2285125)1616x x -=-,∠,x =cos BG M BG M B ''∠==, ∠l 1∠l ′,∠∠BCA =90°,∠BAC =45°.【点评】本题考查二次函数的综合问题,涉及待定系数求二次函数解析式,求三角形面积,圆的相关性质等知识,内容较为综合,学生需要认真分析题目,化动为静去解决问题.5.(1)213222y x x =--+ (2)∠45;∠存在,D (-2,3)【分析】(1)根据题意得到A (-4,0),C (0,2)代入y =-12x 2+bx +c ,于是得到结论; (2)∠如图1,令y =0,解方程得到x 1=-4,x 2=1,求得B (1,0),过D 作DM ∠x 轴于M ,过B 作BN ∠x 轴交于AC 于N ,根据相似三角形的性质即可得到结论;∠根据勾股定理的逆定理得到△ABC 是以∠ACB 为直角的直角三角形,取AB 的中点P ,求得P (-32,0),得到P A =PC =PB =52,过D 作x 轴的平行线交y 轴于R ,交AC 的延线于G ,解直角三角形即可得到结论.(1)解:对于函数:y =12x +2, 令x =0,则y =2,令y =0,则x =-4,∠A (-4,0),C (0,2),∠抛物线y =-12x 2+bx +c 经过A .C 两点, ∠1016422b c c ⎧=-⨯-+⎪⎨⎪=⎩,∠b =-32,c =2, ∠y =-12x 2-32x +2; (2)解:∠如图,令y =0, ∠213x x 2022--+=, ∠14x =-,21x =,∠B (1,0),过D 作DM ∠x 轴交AC 于点M ,过B 作BN ∠x 轴交于AC 于N ,∠DM BN ∥,∠DME BNE ∽△△, ∠DE DM BE BN=, 设()213,222D a a a --+, ∠1,22M a a ⎛⎫+ ⎪⎝⎭, ∠B (1,0), ∠51,2N ⎛⎫ ⎪⎝⎭, ∠()221214225552a a DE DM a BE BN --===-++, ∠-15<0, ∠当a =-2时,DE BE 的最大值是45; ∠∠A (-4,0),B (1,0),C (0,2),∠AC =BC =AB =5,∠222AC BC AB +=,∠∠ABC 是以∠ACB 为直角的直角三角形,取AB 的中点P , ∠3,02P ⎛⎫- ⎪⎝⎭,∠52PA PC PB ===, ∠∠CPO =2∠BAC ,∠()4tan tan 23CPO BAC ∠=∠=, 过D 作x 轴的平行线交y 轴于R ,交AC 的延长线于G ,如图,∠∠DCF =2∠BAC =∠DGC +∠CDG ,∠∠CDG =∠BAC , ∠1tan tan 2CDG BAC ∠=∠=,即12RC DR =, 令213,222D a a a ⎛⎫--+ ⎪⎝⎭, ∠DR =-a ,21322RC a a =--, ∠2131222a a a --=-,∠10a =(舍去),22a =-,∠2D x =-,3D y =.∠D (-2,3).【点评】本题考查了二次函数综合题,涉及待定系数法求函数的解析式,相似三角形的判定和性质,解直角三角形,直角三角形的性质等知识点,正确的作出辅助线是解题的关键.6.(1)A (-5,0),B (-1,0);C (-4,-3);D (-3,-4) (2)∠278;∠(0,5)或(32-,74-)【分析】(1)把抛物线解析式化为顶点式即可求出点D 的坐标,令y =0,求出x 的值即可得到A 、B 的坐标,把x =-4代入抛物线解析式求出y 即可求出点C 的坐标;(2)∠先求出直线BC 的解析式为1y x =+,过点P 作PE ∠x 轴于E 交BC 于F ,则点P 的坐标为(t ,265t t ++),点F 的坐标为(t ,t +1),254PF t t =---,再根据=PBC PFC PFB S S S +△△△23527228t ⎛⎫=-++ ⎪⎝⎭,进行求解即可;∠分如图1所示,当点P 在直线BC 上方时,如图2所示,当点P 在直线BC 下方时,两种情况讨论求解即可.(1)解:∠抛物线解析式为()226534y x x x =++=+-,∠抛物线顶点D 的坐标为(-3,-4);令y =0,则2650x x ++=,解得=1x -或5x =-,∠抛物线265y x x =++与x 轴交于点A ,B (点A 在点B 左侧),∠点A 的坐标为(-5,0),点B 的坐标为(-1,0);令4x =-,则()()246453y =-+⨯-+=-,∠点C 的坐标为(-4,-3);(2)解:∠设直线BC 的解析式为y kx b =+, ∠043k b k b -+=⎧⎨-+=-⎩, ∠11k b =⎧⎨=⎩, ∠直线BC 的解析式为1y x =+,过点P 作PE ∠x 轴于E 交BC 于F ,∠点P 的横坐标为t ,∠点P 的坐标为(t ,265t t ++),点F 的坐标为(t ,t +1),∠2216554PF t t t t t =+---=---,∠=PBC PFC PFB S S S +△△△()()11=22P C B P PF x x PF x x ⋅-+⋅- ()12B C PF x x =⋅- ()23542t t =-++ 23527228t ⎛⎫=-++ ⎪⎝⎭, ∠当52t =-时,∠PBC 的面积最大,最大为278;∠如图1所示,当点P 在直线BC 上方时,∠∠PCB =∠CBD ,∠PC BD ∥,设直线BD 的解析式为11y k x b =+,∠1111034k b k b -+=⎧⎨-+=-⎩, ∠1122k b =⎧⎨=⎩, ∠直线BD 的解析式为22y x =+,∠可设直线PC 的解析式为22y x b =+,∠()2243b ⨯-+=-,∠25b =,∠直线PC 的解析式为25y x =+,联立22565y x y x x =+⎧⎨=++⎩得240x x +=, 解得0x =或4x =-(舍去),∠5y =,∠点P 的坐标为(0,5);如图2所示,当点P 在直线BC 下方时,设BD 与PC 交于点M ,∠点C 坐标为(-4,-3),点B 坐标为(-1,0),点D 坐标为(-3,-4),∠()()22241318BC =---+-=⎡⎤⎣⎦,()()22231420BD =---+-=⎡⎤⎣⎦,()()22243342CD =---+---=⎡⎤⎡⎤⎣⎦⎣⎦, ∠222BC CD BD +=,∠∠BCD =90°,∠∠BCM +∠DCM =90°,∠CBD +∠CDB =90°,∠∠CBD =∠PCB ,∠MC =MB ,∠MCD =∠MDC ,∠MC =MD ,∠MD =MB ,∠M 为BD 的中点,∠点M 的坐标为(-2,-2),设直线CP 的解析式为23y k x b =+,∠23234322k b k b -+=-⎧⎨-+=-⎩, ∠23121k b ⎧=⎪⎨⎪=-⎩,∠直线CP 的解析式为112y x =-, 联立211265y x y x x ⎧=-⎪⎨⎪=++⎩得2211120x x ++=, 解得32x =-或4x =-(舍去), ∠74y =-, ∠点P 的坐标为(32-,74-); 综上所述,当∠PCB =∠CBD 时,点P 的坐标为(0,5)或(32-,74-);【点评】本题主要考查了二次函数综合,一次函数与几何综合,二次函数的性质,待定系数法求函数解析式,勾股定理的逆定理,等腰三角形的性质与判定等等,正确作出辅助线,利用分类讨论的思想求解是解题的关键.7.(1)y =−x 2+2x +3(2)∠532,39⎛⎫⎪⎝⎭;∠73或5【分析】(1)利用待定系数法即可求解;(2)∠作点A关于直线BC的对称点G,连接CG交抛物线于点F,此时,∠BCF=∠BCA,求得G(3,4),利用待定系数法求得直线CF的解析式为:y=13x+3,联立方程组,即可求解;∠分两种情况讨论,由相似三角形的性质和等腰三角形的性质,可求CF的解析式,联立方程可求解.(1)解:∠B(3,0)在抛物线y=−x2+bx+3上,∠y=−32+3b+3,解得b=2,∠所求函数关系式为y=−x2+2x+3;(2)解:∠作点A关于直线BC的对称点G,AG交BC于点H,过点H作HI∠x轴于点I,连接CG交抛物线于点F,此时,∠BCF=∠BCA,如图:令x=0,y=3;令y=0,−x2+2x+3=0,解得:x=3或x=-1,∠A(-1,0),B(3,0),C(0,3),∠OB=OC,AB=4,∠△OCB是等腰直角三角形,则∠OCB=∠OBC=45°,∠∠HAB=∠OBC=∠AHI=∠BHI=45°,∠HI= AI=BI=12AB=2,∠H(1,2),∠G(3,4),设直线CG的解析式为:y=kx+3,把G(3,4)代入得:4=3k+3,解得:k=13,∠直线CF的解析式为:y=13x+3,∠223133y x xy x⎧=-++⎪⎨=+⎪⎩,解得:53329xy⎧=⎪⎪⎨⎪=⎪⎩,所以F点的坐标为(53,329);∠当点F在x轴上方时,如图,延长CF交x轴于N,∠点B(3,0),点C(0,3),∠OB=OC=3,∠∠CBO=∠BCO=45°,∠点A(-1,0),∠OA=1,∠∠FCE+∠ACO=45°,∠CBO=∠FCE+∠CNO=45°,∠∠ACO=∠CNO,又∠∠COA=∠CON=90°,∠∠CAO∠∠NCO,∠CO NO AO CO=,∠313NO =,∠ON=9,∠点N(9,0),同理可得直线CF解析式为:y=-13x+3,∠-13x+3=-x2+2x+3,∠x1=0(舍去),x2=73,∠点F的横坐标为73;当点F在x轴下方时,如图,设CF与x轴交于点M,∠∠FCE+∠ACO=45°,∠OCM+∠FCE=45°,∠∠ACO=∠OCM,又∠OC=OC,∠AOC=∠COM,∠∠COM∠∠COA(ASA),∠OA=OM=1,∠点M(1,0),同理直线CF解析式为:y=-3x+3,∠-3x+3=-x2+2x+3,∠x1=0(舍去),x2=5,∠点F的横坐标为5,综上所述:点F的横坐标为5或73.【点评】本题是二次函数综合题,考查了二次函数的性质,待定系数法求解析式,相似三角形的判定和性质,全等三角形的判定和性质,两点距离公式,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.8.(1)24y x=-+(2)232,39 P⎛⎫ ⎪⎝⎭(3)∠y x =;∠4【分析】(1)待定系数法求解析式;(2)过点B 作BE x ⊥轴交DP 延长线与点E ,过D 作DF x ⊥轴交x 轴于点F .证明DAB DEB ≌△△,求得点E 的坐标,进而求得直线DE 的解析式为11033y x =+,联立抛物线解析式即可求解; (3)∠根据顺时针旋转90°后点的坐标特征可知对称轴为y x =;∠连接GH ,交EF 于点M ,则2GH GM =,过点G 作x 轴的垂线,交EF 于点N ,当GM 最大时,∠GFE面积最大,设()2,4G m m -+,则(),N m m ,根据()12GFE E F S GN x x =⋅-△以及二次函数的性质求得当12m =-时,∠GFE 面积最大,115,24G ⎛⎫- ⎪⎝⎭,根据∠的方法求得H 的坐标,根据中点公式求得M 的坐标,根据勾股定理求得GH ,由2GH GM =即可求解.(1)∠2y ax c =+过()2,0A -,()1,3D -∠403a c a c +=⎧⎨+=⎩ 解之得14a c =-⎧⎨=⎩∠抛物线解析式为24y x =-+(2)过点B 作BE x ⊥轴交DP 延长线与点E ,过D 作DF x ⊥轴交x 轴于点F .由24y x =-+,令0y =,得122,2x x =-=,则()2,0BD B D y x x =-,即DF BF =,∠45DBF ∠=︒,∠45DBE ∠=︒又∠DB DB =,BD 平分ADP ,∠DAB DEB ≌△△,∠BA BE =,()2,0B∠()2,4E设直线DE 的解析式为y kx b =+,324k b k b -+=⎧⎨+=⎩解得13103k b ⎧=⎪⎪⎨⎪=⎪⎩∠直线DE 的解析式为11033y x =+ 联立2411033y x y x ⎧=-+⎪⎨=+⎪⎩解得213,3329x x y y ⎧=⎪=-⎧⎪⎨⎨=⎩⎪=⎪⎩则232,39P ⎛⎫ ⎪⎝⎭(3)∠直线EF 解析式为y x =.抛物线关于y 轴对称,所以旋转后图形关于x 轴对称, ∠对于抛物线上任意一点(),P a b 关于原点旋转90°后对应点为()1,P b a -在旋转后图形上,()1,P b a -关于x 轴对称的点()2,P b a 在旋转后图形上,∠(),P a b 与()2,P b a 关于y x =对称, ∠图形2关于y x =对称,∠直线EF 解析式为y x =故答案为:y x =∠GH如图,连接GH ,交EF 于点M ,则2GH GM =,过点G 作x 轴的垂线,交EF 于点N ,∠当GM 最大时,∠GFE 面积最大,又∠()12GFE E F S GN x x =⋅-△ 设()2,4G m m -+,则(),N m m ∠22117424G N GN y y m m m ⎛⎫=-=-+-=-++ ⎪⎝⎭ ∠当12m =-时,∠GFE 面积最大,115,24G ⎛⎫- ⎪⎝⎭由∠可知115,24G ⎛⎫- ⎪⎝⎭关于y x =的对称点H 15142⎛⎫ ⎪⎝⎭,- ∴1313,88M ⎛⎫ ⎪⎝⎭8GM ∴=∠GH 的最大值为:2GH GM ==【点评】本题考查了二次函数的性质,旋转的性质,全等三角形的性质与判定,一次函数与二次函数交点问题,掌握以上知识是解题的关键.9.(1)234y x x =-++(2)1m = (3)227或227【分析】(1)直接利用待定系数法求解即可;(2)先求出直线AB 的解析式为1y x =+,然后证明∠PGQ ∠∠DAQ 得到PG =AD =4,再由点P 的坐标为()234m m m ++,-,点G 的坐标为(m ,m +1),得到23414PG m m m =-++--=,由此求解即可;(3)如图所示,过点F 作FH ∠AB 于H ,过点K 作KQ 平分∠FKD 交x 轴于Q ,过点Q 作QM ∠KF 于M ,连接FG ,设2BF t QD s KD k ===,,,则42DF t =-,先证明∠HBF =∠HFB =45°,得到HB HF ==,再由(2)得1m =,求得BG =HG =,tan =2HF t FGH HG t=-∠;根据角平分线的定义和性质得到QM QD s ==,∠FGH =∠QKD ,再由111==222FKD FQK DQK S S S DF DK KF QM DQ DK +⋅=⋅+⋅△△△,推出()428k t s k -=+,则tan tan 2s t QKQ FGH k t ===-∠∠,可以推出()222282168t t t t k t t---+==, 在Rt ∠FKD 中,22264DF DK KF +==,得到()22221684264t t t t ⎛⎫-+-+= ⎪⎝⎭,由此即可求出t 的值即可得到答案.(1) 解:∠抛物线()240y ax bx a =++≠经过点()3,4A 和点()1,0B -,∠934440a b a b ++=⎧⎨-+=⎩, ∠13a b =-⎧⎨=⎩, ∠抛物线解析式为234y x x =-++;(2)解:设直线AB 的解析式为1y kx b =+,∠11034k b k b -+=⎧⎨+=⎩, ∠11k b =⎧⎨=⎩, ∠直线AB 的解析式为1y x =+,∠PE AD ∥,∠∠PGQ =∠DAQ ,∠GPQ =∠ADQ ,又∠AQ =GQ ,∠∠PGQ ∠∠DAQ (AAS ),∠PG =AD =4,∠点P 的横坐标为m ,∠点P 的坐标为()234m m m ++,-,点G 的坐标为(m ,m +1),∠23414PG m m m =-++--=,∠2210m m -+=,解得1m =;(3)解:如图所示,过点F 作FH ∠AB 于H ,过点K 作KQ 平分∠FKD 交x 轴于Q ,过点Q 作QM ∠KF 于M ,连接FG ,设2BF t QD s KD k ===,,,则42DF t =-,∠点B 的坐标为(-1,0),点A 的坐标为(3,4),∠BD =AD =4,∠∠ABD =45°,∠FH ∠AB ,∠∠HBF =∠HFB =45°, ∠HB HF ==,由(2)得1m =,∠点G 的坐标为(1,2),∠BE =GE =2,∠BG = ∠HG BG HB =-=, ∠tan =2HF t FGH HG t=-∠; ∠KQ 平分∠FKD ,QM ∠FK ,QD ∠DK ,∠FKD =2∠FGB ,∠QM QD s ==,∠FGH =∠QKD , ∠111==222FKD FQK DQK S S S DF DK KF QM DQ DK +⋅=⋅+⋅△△△, ∠()111428222k t s sk -=⨯+, ∠()428k t s k-=+, ∠tan tan 2s t QKQ FGH k t ===-∠∠, ∠4282t t k t-=+-, ∠()222282168t t t t k t t---+==, 在Rt ∠FKD 中,22264DF DK KF +==,∠()22221684264t t t t ⎛⎫-+-+= ⎪⎝⎭, ∠43222464288256641616464t t t t t t t -+-+-++=, ∠2344322161644642882566464t t t t t t t t -++-+-+=,∠432880240256640t t t t -+-+=,∠43210243280t t t t -+-+=,∠()()2221016143280t t t t t -++-+=,∠()()()()22827220t t t t t --+--=,∠()()32814420t t t t -+--=,∠()()()28122220t t t t t ⎡⎤-++--=⎣⎦,∠()()()()262220t t t t t --+--=⎡⎤⎣⎦,∠()()226220t t t -+-=, ∠点F 在BE 上,∠22BF t BE =≤=,∠1t ≤,∠2620t t -+=,解得3t =-3t =,∠()22262442168442t t t t t t k t t t -+-+-+-=====,∠2DK =,∠点K 的纵坐标为227或227.【点评】本题主要考查了二次函数综合,一次函数与几何综合,勾股定理,解直角三角形,角平分线的性质,等腰直角三角形的性质与判定,全等三角形的性质与判定等等,熟练掌握二次函数的相关知识是解题的关键.10.(1)223y x x =+-(2)(-2,-3)或(-1,-4)(3)(0,2)或(0,-2)【分析】(1)先求出A 、C 的坐标,然后用待定系数法求解即可;(2)先求出直线AC 的解析为3y x =--,根据AC 把△ABP 的面积分成1:2两部分,得到=12APQ ABQ S S △△::,如图所示,过点P 作PD ∠x 轴于D ,过点Q 作DE ∠x 轴于E , 先求出23EQ PD =,设点P 的坐标为(m ,223m m +-),则点D 的纵坐标为224233m m +-,点D 的坐标为(224133m m ---,224233m m +-),然后求出点B 的坐标,从而求出∠22242411123333BD m BE m m m m ⎛⎫=-=----=++ ⎪⎝⎭,,证明∠BEQ ∠∠BDP ,得到224223313m m m ++=-,据此求解即可; (3)分两种情况当点N 在x 轴上方时,过点N 作NH ∠直线BC 于H ,过点H 作HE ∠y 轴于E ,HF ∠x 轴于F ,求出直线BC 的解析式为33y x =-,证明HN =HF ,四边形EOFH 是矩形,得到∠EHF =90°,OE =HF ,证明∠NEH ∠∠BFH 得到NE =BF ,设H 坐标为(m ,3m -3),则NE =BF =m -1,OE =3m -3ON =EN +OE =4m -4,CE =3m -3+3=3m ,点N 的坐标为(0,4m -4),NC =4m -1在Rt ∠NCH 中,由222NH CH CN +=,得到()()222221941m m m m m +-++=-,由此求解即可;当点N 在x 轴下方时,利用等腰三角形的性质求解即可.(1)解:∠OA =OC =3,∠点A 的坐标为(-3,0),点C 的坐标为(0,-3), ∠9303b c c -+=⎧⎨=-⎩, ∠23b c =⎧⎨=-⎩, ∠抛物线解析式为223y x x =+-;(2)解:设直线AC 的解析式为1y kx b =+,∠11303k b b -+=⎧⎨=-⎩, ∠113k b =-⎧⎨=-⎩, ∠直线AC 的解析为3y x =--,∠AC 把∠ABP 的面积分成1:2两部分,∠=12APQ ABQ S S △△::或=2APQ ABQ S S △△::1(此种情况不符合题意,舍去),如图所示,过点P 作PD ∠x 轴于D ,过点Q 作QE ∠x 轴于E ,∠=32APB ABQ S S △△::,∠132122AB PD AB EQ ⋅=⋅, ∠23EQ PD =, 设点P 的坐标为(m ,223m m +-),则点Q 的纵坐标为224233m m +-, ∠点Q 的坐标为(224133m m ---,224233m m +-), 令y =0,则2230x x +-=,解得1x =或3x =-,∠点B 的坐标为(1,0), ∠22242411123333BD m BE m m m m ⎛⎫=-=----=++ ⎪⎝⎭,, ∠PD ∠x 轴,QE ∠x 轴,∠DP QE ∥,∠∠BEQ ∠∠BDP , ∠23BE QE BD PD ==, ∠224223313m m m ++=-, 解得2m =-或1m =-,∠点P 的坐标为(-2,-3)或(-1,-4);(3)解:如图1所示,当N 在x 轴上方时,过点N 作NH ∠直线BC 于H ,过点H 作HE ∠y 轴于E ,HF ∠x 轴于F , 设直线BC 的解析式为12y k x b =+,∠12203k b b +=⎧⎨=-⎩, ∠1233k b =⎧⎨=-⎩, ∠直线BC 的解析式为33y x =-,∠∠BNO +∠BCO =45°,∠∠NBH =45°,∠∠HNB =45°=∠HBN ,∠HN =HF ,∠EH ∠OE ,FH ∠OF ,OE ∠OF ,∠四边形EOFH 是矩形,∠∠EHF =90°,OE =HF ,∠∠NHE +∠BHE =90°=∠BHF +∠BHE ,∠∠NHE =∠BHF ,又∠∠HEN =∠HFB =90°,∠∠NEH ∠∠BFH (AAS ),∠NE =BF ,设H 坐标为(m ,3m -3),∠NE =BF =m -1,OE =3m -3∠ON =EN +OE =4m -4,CE =3m -3+3=3m ,∠点N 的坐标为(0,4m -4),NC =4m -1在Rt ∠NCH 中,222NH CH CN +=,∠()()222221941m m m m m +-++=-,∠222222191681m m m m m m m +-+++=-+,∠2460m m -=, 解得32m =或0m =(舍去), ∠点N 的坐标为(0,2);如图2所示,当点N 在x 轴下方的1N 点时,由等腰三角形的性质可知当1N B BN =(N 点为图1中的N )时,1BN O BNO =∠∠,∠1OB NN ⊥,∠12ON ON ==,∠点1N 的坐标为(0,-2),综上所述,在y 轴上是否存在一点N (0,2)或(0,-2),使得45BCO BNO ∠+∠=︒.【点评】本题主要考查了二次函数综合,一次函数与几何综合,等腰三角形的性质与判定,全等三角形的性质与判定,三角形外角的性质,相似三角形的性质与判定,勾股定理等等,正确作出辅助线是解题的关键.11.(1)抛物线解析式为y =x 2+2x -3,A 点坐标为(-3,0);(2)P 点坐标为(32,32);(3)以QD 为腰的等腰三角形的面积最大值为5413. 【分析】(1)把B 点坐标代入抛物线解析式可求得a 的值,可求得抛物线解析式,再令y =0,可解得相应方程的根,可求得A 点坐标;(2)当点P 在x 轴上方时,连接AP 交y 轴于点B ′,可证△OBP ∠∠OB ′P ,可求得B ′坐标,利用待定系数法可求得直线AP 的解析式,联立直线y =x ,可求得P 点坐标;(3)过Q 作QH ∠DE 于点H ,由直线CF 的解析式可求得点C 、F 的坐标,结合条件可求得tan∠QDH ,可分别用DQ 表示出QH 和DH 的长,分DQ =DE 和DQ =QE 两种情况,分别用DQ 的长表示出∠QDE 的面积,再设出点Q 的坐标,利用二次函数的性质可求得∠QDE 的面积的最大值.(1)解:把B (1,0)代入y =ax 2+2x -3,可得a +2-3=0,解得a =1,∠抛物线解析式为y =x 2+2x -3,令y =0,可得x 2+2x -3=0,解得x =1或x =-3,∠A 点坐标为(-3,0);(2)解:若y =x 平分∠APB ,则∠APO =∠BPO ,如图1,若P 点在x 轴上方,P A 与y 轴交于点B ′,由于点P 在直线y =x 上,可知∠POB =∠POB ′=45°,在∠BPO 和∠B ′PO 中POB POB OP OP BPO B PO ∠=∠⎧⎪=⎨⎪∠'=∠⎩', ∠∠BPO ∠∠B ′PO (ASA ),∠BO =B ′O =1,设直线AP 解析式为y =kx +b ,把A 、B ′两点坐标代入可得301k b b -+=⎧⎨=⎩,解得131k b ⎧=⎪⎨⎪=⎩, ∠直线AP 解析式为y =13x +1, 联立113y x y x =⎧⎪⎨=+⎪⎩,解得3232x y ⎧=⎪⎪⎨⎪=⎪⎩, ∠P 点坐标为(32,32); (3)解:如图2,作QH ∠CF ,交CF 于点H ,设抛物线交y 轴于点M .∠CF 为y =23x −49, ∠可求得C (23,0),F (0,-49), ∠tan∠OFC =OC OF =32, ∠DQ ∠y 轴,∠∠QDH =∠MFD =∠OFC ,∠tan∠HDQ =32, 不妨设DQ =t ,DH,HQ, ∠∠QDE 是以DQ 为腰的等腰三角形,∠若DQ =DE ,则S △DEQ =12DE •HQ =12×t2,。
2023年九年级数学下册中考数学专题训练:角度问题(二次函数综合)【含答案】

2023年九年级数学下册中考数学专题训练:角度问题(二次函数综合)一、解答题1.如图,直线y =x ﹣3与x 轴、y 轴分别交于B 、C 两点,抛物线y =x 2+bx +c 经过B 、C ,且与x 轴另一交点为49A ,连接AC .(1)求抛物线的解析式;(2)点E 在抛物线上,连接EC ,当∠ECB +∠ACO =45°时,求点E 的横坐标;(3)点M 从点A 出发,沿线段AB 由A 向B 运动,同时点N 从点C 出发沿线段CA 由C 向A 运动,M ,N 的运动速度都是每秒1个单位长度,当N 点到达A 点时,M ,N 同时停止运动,问在坐标平面内是否存在点D ,使M ,N 运动过程中的某些时刻t ,以A ,D ,M ,N 为顶点的四边形为菱形?若存在,直接写出t 的值;若不存在,说明理由.2.已知抛物线y=ax ²+bx +c 经过点A (-6,0)、B (2,0)和C (0,3),点D 是该抛物线在第四象限上的一个点,连接 AD 、AC 、CD ,CD 交x 轴于E .(1)求这个抛物线的解析式;(2)当S △DAE =S △ACD 时,求点 D 的坐标;14(3)在(2)的条件下,抛物线上是否存在点P ,使得△PAD 中的一个角等于2∠BAD ?若存在,直接写出点P 的坐标;若不存在,请说明理由.3.如图1,直线y =ax ²+4ax +c 与x 轴交于点A (-6,0)和点B ,与y 轴交于点C ,且OC =3OB(1)直接写出抛物线的解析式及直线AC 的解析式;(2)抛物线的顶点为D ,F 为抛物线在第四象限的一点,直线AF 解析式为,求∠CAF -∠CAD 的度数.123y x =--(3)如图2,若点P 是抛物线上的一个动点,作PQ ⊥y 轴垂足为点Q ,直线PQ 交直线AC 于E ,再过点E 作x 轴的垂线垂足为R ,线段QR 最短时,点P 的坐标及QR 的最短长度.4.已知顶点为A (2,一1)的抛物线与y 轴交于点B ,与x 轴交于C 、D 两点,点C 坐标(1,O );(1)求这条抛物线的表达式;(2)连接AB 、BD 、DA ,求cos ∠ABD 的大小;(3)点P 在x 轴正半轴上位于点D 的右侧,如果∠APB =45°,求点P 的坐标.5.如图1,抛物线与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,过点C()2102y x bx c c =++<作轴,与抛物线交于另一点D ,直线与相交于点M .CD x ∥BC AD(1)已知点C 的坐标是,点B 的坐标是,求此抛物线的解析式;()04-,()40,(2)若,求证:;112b c =+AD BC ⊥(3)如图2,设第(1)题中抛物线的对称轴与x 轴交于点G ,点P 是抛物线上在对称轴右侧部分的一点,点P 的横坐标为t ,点Q 是直线上一点,是否存在这样的点P ,使得是以点G 为直角顶点的直角三角形,且满足BC PGQ △,若存在,请直接写出t 的值;若不存在,请说明理由.GQP OCA ∠=∠6.抛物线与x 轴相交于A ,B 两点(点A 在点B 的左侧),与y 轴的正半轴相交于点C ,点D 为223y ax ax a =--抛物线的顶点,点O 为坐标原点.(1)若是直角三角形,求抛物线的函数表达式;ABC (2)王亮同学经过探究认为:“若,则”,王亮的说法是否正确?若你认为正确,请加以证明:a<02∠=∠DCB ABC 若是错误的,说明理由;(3)若第一象限的点E 在抛物线上,四边形面积的最大值为,求a 的值.ABEC 2547.如图,抛物线经过,两点,与x 轴交于另一点A ,点D 是抛物线的顶点.22y ax ax c =++(1,0)B (0,3)C(1)求抛物线的解析式及点D 的坐标;(2)如图1,点E 在抛物线上,连接并延长交x 轴于点F ,连接,若是以为底的等腰三角形,求DE BD BDF BD 点E 坐标.(3)如图2,连接、,在抛物线上是否存在点M ,使,若存在,求出M 点的坐标;若不存AC BC ACM BCO ∠=∠在,请说明理由.8.抛物线的顶点坐标为,与x 轴交于点两点,与y 轴交于点C ,点M 是抛物线上的动2y ax bx c =++(1,4),(3,0)A B 点.(1)求这条抛物线的函数表达式;(2)如图1,若点M 在直线BC 上方抛物线上,连接AM 交BC 于点E ,求的最大值及此时点M 的坐标;MEAE (3)如图2,已知点,是否存在点M ,使得?若存在,求出点M 的坐标;若不存在,请说明理(0,1)Q 1tan 2MBQ ∠=由.9.如图,一次函数y =x﹣2的图象与x 轴交于点A ,与y 轴交于点B ,点D 的坐标为(﹣1,0),二次函数12y =ax 2+bx+c (a≠0)的图象经过A ,B ,D 三点.(1)求二次函数的解析式;(2)如图1,已知点G (1,m )在抛物线上,作射线AG ,点H 为线段AB 上一点,过点H 作HE ⊥y 轴于点E ,过点H 作HF ⊥AG 于点F ,过点H 作HM ∥y 轴交AG 于点P ,交抛物线于点M ,当HE•HF 的值最大时,求HM 的长;(3)在(2)的条件下,连接BM ,若点N 为抛物线上一点,且满足∠BMN =∠BAO ,求点N 的坐标.10.已知二次函数.()20y ax bx c a =++>(1)若,,求方程的根的判别式的值;12a =2b c ==-20ax bx c ++=(2)如图所示,该二次函数的图像与x 轴交于点、,且,与y 轴的负半轴交于点C ,()1,0A x ()2,0B x 120x x <<点D 在线段OC 上,连接AC 、BD ,满足 ,.ACO ABD ∠=∠1b c x a -+=①求证:;AOC DOB ≅ ②连接BC ,过点D 作于点E ,点在y 轴的负半轴上,连接AF ,且,DE BC ⊥()120,F x x -ACO CAF CBD ∠=∠+∠求的值.1cx 11.如图,在平面直角坐标系中,已知抛物线的图象与x 轴交于点A ,B 两点,点A 坐标为,243y ax x c =-+()3,0点B 坐标为,与y 轴交于点C .()1,0-(1)求抛物线的函数解析式;(2)若将直线绕点A 顺时针旋转,交抛物线于一点P ,交y 轴于点D ,使,求直线函数解析AC BAP BAC ∠=∠AP 式;(3)在(2)条件下若将线段平移(点A ,C 的对应点M ,N ),若点M 落在抛物线上且点N 落在直线上,求AC AP 点M 的坐标.12.在平面直角坐标系中,抛物线与轴交于点和点(点在点的左侧),与轴交212y x bx c =-++x (2,0)A -B A B y 于点.(0,3)C (1)求抛物线的表达式;的坐标,并直接写出此时直线的表达式.D DC (3)在(2)的条件下,点为轴右侧抛物线上一点,过点作直线的垂线,垂足为,若,E y E DC P ECP DAB ∠=∠请直接写出点的坐标.E 13.已知函数y =(n 为常数).22()1()222x nx n x n n n x x x n ⎧-++≥⎪⎨++<⎪⎩(1)当n =5时,①点P (4,b )在此函数图象上,求b 的值.②求此函数的最大值.(2)当n <0时,作直线x =n 与x 轴交于点P ,与该函数图象交于点Q ,若∠POQ =45°,求n 的值.23(3)若此函数图象上有3个点到直线y =2n 的距离等于2,求n 的取值范围.14.如图,已知抛物线y =ax 2+4(a ≠0)与x 轴交于点A 和点B (2,0),与y 轴交于点C ,点D 是抛物线在第一象限的点.(1)当△ABD 的面积为4时,①求点D 的坐标;②联结OD ,点M 是抛物线上的点,且∠MDO =∠BOD ,求点M 的坐标;(2)直线BD 、AD 分别与y 轴交于点E 、F ,那么OE +OF 的值是否变化,请说明理由.15.如图,已知,抛物线经过A 、B 两点,交y 轴于点C .点P 是第一象限内抛物线(2,0),(3,0)A B -24y ax bx =++上的一点,点P 的横坐标为m .过点P 作轴,垂足为点M ,PM 交BC 于点Q .过点P 作,垂足PM x ⊥PN BC ⊥为点N .(1)求抛物线的函数表达式;(2)请用含m 的代数式表示线段PN 的长,并求出当m 为何值时PN 有最大值,最大值是多少?(3)连接PC ,在第一象限的抛物线上是否存在点P ,使得?若存在,请直接写出m 的值;若290BCO PCN ∠+∠=︒不存在,请说明理由.16.如图1,在平面直角坐标系中.抛物线与x 轴交于和,与y 轴交于点C ,连接22y ax bx =++(4,0)A -(1,0)B .,AC BC(1)求该抛物线的解析式;(2)如图2,点M 为直线上方的抛物线上任意一点,过点M 作y 轴的平行线,交于点N ,过点M 作x 轴的AC AC 平行线,交直线于点Q ,求周长的最大值;AC MNQ △(3)点P 为抛物线上的一动点,且,请直接写出满足条件的点P 的坐标.45ACP BAC ∠=︒-∠17.抛物线经过A (-1,0)、C (0,-3)两点,与x 轴交于另一点B .23y ax bx a =+-(1)求此抛物线的解析式;(2)已知点D 在第四象限的抛物线上,求点D 关于直线BC 对称的点D’的坐标;(m,-m-1)(3)在(2)的条件下,连结BD ,问在x 轴上是否存在点P ,使,若存在,请求出P 点的坐标;PCB CBD ∠=∠若不存在,请说明理由.参考答案:1.(1)y =x 2﹣x ﹣34913(2)或1543916(3)存在,t =或或754415845222.(1);(2);(3)P 点坐标为综上所述:2134y x x =--+(21)D -+-1P,、、、(617-)2P (-5.00.,175)()3 3.47, 3.48P -4(220P -)5P ,.(14.22,33.30)--6(9.74,30.47)P -3.(1)抛物线的解析式为y =-x ²-2x +6,直线BC 的解析式为y =x +612(2)45°(3)点P 的坐标为(,3)或(,3),QR 的最短长度为4.(1)y =x 2﹣4x +3;(23)P (3+,0)5.(1)2142y x x =--(2)11(3)t =t =6.(1)2=y x (2)王亮的说法正确(3)23a =-7.(1)抛物线的解析式为:,223y x x =--+(1,4)D -(2)720(,39E -(3)存在,或()4,5M --57(,)24M -8.(1);223y x x =-++(2);;916315,24⎛⎫ ⎪⎝⎭(3)存在;或(0,3)829,749⎛⎫-- ⎪⎝⎭9.(1)y =x 2﹣x﹣2;(2)2;(3)(1,﹣3)或(﹣,)12325317910.(1) (2)①1;②=2=8∆1c x 11.(1)224233y x x =--(2)223y x =-+(3)或或()3,8-104,3⎛⎫ ⎪⎝⎭102,3⎛⎫- ⎪⎝⎭12.(1);(2)D (2,2),;(3点E 的坐标为(1,3)或211322y x x =-++132y x =-+(,)113179-13.(1)①b =;②此函数的最大值为;92458(2)n 的值是-或-;15232(3)或423n -<<-463n <<-6n =+14.(1)①;②;(2)不变化,值为8)2D ()2M 15.(1)222433y x x =-++(2),当时,有最大值22655PN m m =-+32m =910答案第3页,共3页(3)存在,74m =16.(1)213222y x x =--+(2)6+(3)或()5,3--2375,749⎛⎫- ⎪⎝⎭17.(1)2y x 2x 3=--(2)(0,-1)(3)(1,0)(9,0)答案第4页,共1页。
二次函数综合(5种题型)-2023年新九年级数学核心知识点与常见题型通关讲解练(浙教版)(解析版)

重难点专项突破:二次函数综合(5种题型)【题型细目表】 题型一:线段周长问题题型二:面积问题题型三:角度问题题型四:特殊三角形问题题型五:特殊四边形问题【考点剖析】题型一:线段周长问题一、解答题【答案】(1)()1,0B b +;(2)b =【分析】(1)根据A 、B 两点关于二次函数的对称轴对称,求得点B 的坐标;(2)根据A 的坐标,求出,b c 的关系式,根据平移求出B '的坐标,代入二次函数,求得b 值.【详解】解(1)∵2y x bx c =−++∴对称轴:直线22b b x a =−= ∴2122b AB b ⎛⎫=⨯+=+ ⎪⎝⎭∵A 点横坐标为-1∴()1,0B b +(2)把()1,0A −代入2y x bx c =−++ 得:10b c −−+=,即1c b =+∵平移线段CB ,使C 与D 重合点∴B 平移后得点31,12b B b ⎛⎫+−− ⎪⎝⎭ ∵点B 在抛物线上 ∴233111122b b b b b ⎛⎫⎛⎫−+++++=−− ⎪ ⎪⎝⎭⎝⎭,解得b = ∵0b >∴b =【点睛】涉及到了点的平移变换和一元二次方程,熟练掌握二次函数的有关性质和点的平移规则是解题的关键. 2.(2023·浙江·九年级专题练习)如图,在平面直角坐标系中,抛物线23y ax bx =+−经过点A (-1,0),B (5,0).(1)求抛物线的表达式.(2)过点C (0,m )作直线l x ∥轴交抛物线于点P ,Q (点P 在点Q 的左侧),若3QC PC =,求m 的值.【答案】(1)2312355y x x =−− (2)215. 【分析】(1)把点A (-1,0),B (5,0)代入抛物线表达式进行计算即可解答;(2)根据已知QC=3PC ,可设点P (-n ,m ),点Q (3n ,m ),然后代入(1)中二次函数表达式即可解答.【详解】(1)把点A (-1,0),B (5,0)代入抛物线y=ax2+bx-3中可得:3025530a b a b −−⎧⎨+−⎩==,解得:35125a b ⎧=⎪⎪⎨⎪=−⎪⎩, ∴抛物线的表达式为:2312355y x x =−−;(2)∵PQ ∥x 轴,QC=3PC ,∴设点P (-n ,m ),点Q (3n ,m ),把点P (-n ,m ),点Q (3n ,m )代入2312355y x x =−−中可得:223123552736355n n m n n m ⎧+−=⎪⎪⎨⎪−−=⎪⎩,解得:2215n m =⎧⎪⎨=⎪⎩, ∴m 的值为215.【点睛】本题考查了待定系数法求二次函数解析式,二次函数图象上点的坐标特征,准确熟练地进行计算是解题的关键.(1)求抛物线1P 的对称轴和点(2)求线段AB 和CD 的长度.【答案】(1)对称轴=1x −;点A 的横坐标是-3(2)7AB =;7CD =【分析】(1)根据对称轴公式直接求抛物线P1的对称轴,以及A ,E 关于对称轴x=-1对称和点E 的横坐标直接求出点A 的横坐标;(2)求出P2的对称轴,再求出点B 的坐标,从而求得AB 的长,把1x =分别代入两个函数表达式,求得7m n −=−,从而求得CD 的长.【详解】(1)抛物线1P 的对称轴12b x a =−=−∵点A 与点E 关于直线=1x −对称,且点E 的横坐标是1∴点A 的横坐标是3−(2)抛物线2P 的对称轴522b x a =−= ∵点B 与点E 关于直线52x =对称,且点E 的横坐标是1 ∴点B 的横坐标是4∴()437AB =−−=把1x =分别代入两个函数表达式,得1215m n ++=−+即7m n −=−由题意,当0x =时,D y n =,C y m =.∴7CD n m =−=【点睛】本题考查二次函数的性质,关键是判断点A 与点E 关于对称轴x=-1对称,点B 与点E 关于对称轴52x =对称. 4.(2023·浙江·九年级专题练习)已知二次函数l 1:y =x 2+6x +5k 和l 2:y =kx 2+6kx +5k ,其中k ≠0且k ≠1.(1)分别直接写出关于二次函数l 1和l 2的对称轴及与y 轴的交点坐标;(2)若两条抛物线l 1和l 2相交于点E ,F ,当k 的值发生变化时,判断线段EF 的长度是否发生变化,并说明理由;(3)在(2)中,若二次函数l 1的顶点为M ,二次函数l 2的顶点为N ;①当k 为何值时,点M 与点N 关于直线EF 对称?②是否存在实数k ,使得MN =2EF ?若存在,求出实数k 的值,若不存在,请说明理由.【答案】(1)l1的对称轴为x =﹣3,和y 轴的交点坐标为(0,5k);l2的对称轴为x =﹣3,与y 轴的交点坐标(0,5k)(2)不发生变化,见解析(3)①k 为﹣1;②73或﹣13【分析】(1)二次函数l1的对称轴为x =﹣2ba =﹣621⨯=﹣3,令x =0,则y =5k ,故该抛物线和y 轴的交点坐标为(0,5k );同理可得l2的对称轴为x =﹣3,与y 轴的交点坐标(0,5k );(2)可令y1=y2,求出点E 、F 的横坐标,从而得到点E 、F 的坐标,进行得到EF 的长,就可解决问题;(3)易得点M 、N 的坐标及直线EF 的关系式,然后根据条件建立关于k 的方程,就可解决问题.(1)解:二次函数l1的对称轴为x =﹣2ba =﹣621⨯=﹣3,令x =0,则y =5k ,故该抛物线和y 轴的交点坐标为(0,5k );同理可得:l2的对称轴为x =﹣3,与y 轴的交点坐标(0,5k );(2)解:线段EF 的长度不发生变化,理由:当y1=y2时,x2+6x+5k =kx2+6kx+5k ,整理得:(k ﹣1)(x2+6x )=0.∵k≠1,∴x2+6x =0,解得:x1=0,x2=﹣6.不妨设点E 在点F 的左边,则点E 的坐标为(﹣6,5k ),点F 的坐标为(0,5k ),∴EF =|0﹣(﹣6)|=6,∴线段EF 的长度不发生变化;(3)解:①由y1=x2+6x+5k =(x+3)2+5k ﹣9得M (﹣3,5k ﹣9),由y2=kx2+6kx+5k =k (x+3)2﹣4k 得N (﹣3,﹣4k ).∵直线EF 的关系式为y =5k ,且点M 与N 关于直线EF 对称,∴﹣4k ﹣5k =5k ﹣(5k ﹣9),解得:k =﹣1,∴当k 为﹣1时,点M 与N 关于直线EF 对称;②∵MN =|(5k ﹣9)﹣(﹣4k )|=|9k ﹣9|,MN =2EF =12,∴|9k ﹣9|=12,解得k1=73,k2=﹣13,∴实数k 为73或﹣13.【点睛】本题主要考查了二次函数的性质、解一元二次方程、轴对称的性质、解绝对值方程等知识,需要注意的是当两点横坐标相同时,两点之间的距离应为这两点纵坐标差的绝对值. (1)求抛物线的解析式及顶点(2)判断ABC 的形状,证明你的结论;(3)点M 是抛物线对称轴上的一个动点,当(4)在该抛物线位于第四象限内的部分上是否存在点【答案】(1)抛物线的解析式为:213222y x x =−−;325,28D ⎛⎫− ⎪⎝⎭ (2)ACB △是直角三角形(3)35,24M ⎛⎫− ⎪⎝⎭,ACM △的最小周长为:(4)存在,()2,3P −【分析】(1)根据点()1,0A −在抛物线2122y x bx =+−上,解出b ,得到抛物线的解析式,根据顶点坐标公式,即可求出点D 的坐标;(2)根据(1)得抛物线的解析式,求出点B 的坐标,根据勾股定理的逆定理即可;(3)当点M 在BC 与对称轴的交点上,根据点A ,点B 是对称点,连接AM ,则AM BM =且A ,C ,M 三点在一条直线上,距离最短,设BC 的解析式为:()0y kx b k =+≠,求出BC 的解析式,则得到点M 的坐标,即可;(4)以BC 为底,则12CPB S BC h =,当点P 到BC 的距离最远时,CPB △的面积最大如图所示,作直线l BC ∥,当直线l 与抛物线132222y x x =−−仅有一个交点时,h 最大,交点即为点P .【详解】(1)∵点()1,0A −在抛物线2122y x bx =+−上, ∴1022b =−−, ∴32b =−, ∴抛物线的解析式为:213222y x x =−−; ∵顶点坐标公式为:42,24bac b a a −⎛⎫− ⎪⎝⎭, ∴点325,28D ⎛⎫− ⎪⎝⎭.∴抛物线的解析式为:2122y x =−;325,28D⎛⎫− ⎪⎝⎭.(2)∵抛物线213222y x x =−−与y 轴交于点C ,∴0x =,=2y −,∴2OC =, ∵抛物线213222y x x =−−与x 轴交于点A ,点B , ∴2130222x x =−−,∴=1x −,4x =,∴点()4,0B ,∴1OA =,4OB =,5AB =,∵2225AC OA OC =+=;222222420BC OC OB =+=+=;225AB =,∴222AC BC AB +=,∴ABC 是直角三角形.(3)∵点A ,点B 是对称点,点M 在BC 与对称轴的交点上,∴AM BM =此时A ,C ,M 三点在一条直线上,距离最短,ACM C AC BC =+=设BC 的解析式为:()0y kx b k =+≠,∴042k b b =+⎧⎨−=⎩,解得:122k b ⎧=⎪⎨⎪=−⎩, ∴122y x =− 当32x =时,1352224y =⨯−=−, ∴点35,24M ⎛⎫− ⎪⎝⎭;∴点M 的坐标为35,24M ⎛⎫− ⎪⎝⎭,ACM △的最小周长为:(4)存在,理由如下:∵以BC 为底, ∴12CPB S BC h =⨯,当点P 到BC 的距离最远时,CPB △的面积最大,作直线l BC ∥,且与213222y x x =−−仅有一个交点,设直线l 的解析式为y kx b =+,∵l BC ∥,∴12k =,即12y x b =+,∵直线l 与213222y x x =−−仅有一个交点, ∴21312222x x x b −−=+仅有一个实数根, ∴()144202b −⨯⨯−−=,解得4b =−,∴直线l 的解析式为:1y x 42=−, 由214213222y x y x x ⎧=−⎪⎪⎨⎪=−−⎪⎩,解得23x y =⎧⎨=−⎩, ∴点()2,3P −.【点睛】本题考查二次函数与几何的综合,解题的关键是掌握待定系数法求解析式,勾股定理的逆定理,线段的距离.【答案】(1)证明见详解;(2)交点坐标为(0,a-1)或(-1,-1);(3)证明见详解【分析】(1)先确定出抛物线的顶点坐标,即可得出结论;(2)联立二次函数的解析式与一次函数的解析式,求出方程组的解即可;(3)表示出MN 的长度再利用函数最值求出范围即可得出结论【详解】解:(1)证明:二次函数2221(1)1y ax ax a a x =++−=+−, 顶点坐标为()1,1−−,把()1,1−−代入,1y ax a =+−中左边=-1,右边=-1∴左边=右边,∴二次函数图象的顶点必在一次函数1y ax a =+−的图象上;(2)联立解析式得:2211y ax ax a y ax a ⎧=++−⎨=+−⎩,解得x=0 或x=-1当x=0时,y=a-1 坐标为(0,a-1)当x=-1时,y=-1坐标为(-1,-1)∴交点坐标为(0,a-1)或(-1,-1)(3)证明:由题意可知2(,21)M m am am a ++−,(,1)N m am a +−由(2)可知,当a >0时,-1<x <0有221ax ax a ++−<1ax a +−∴221(21)MN am a am am a am am =+−−++−−−= =21()24a a m −++ 当10m −≤≤时,04a MN ≤≤∵02a <≤ ∴102MN ≤≤ 【点睛】二次函数综合题,主要考查了抛物线的顶点坐标的确定,抛物线与一次函数交点确定,极值的确定,用分类讨论的思想解决问题是解本题的关键. 7.(2023·浙江·九年级专题练习)如图,已知抛物线2:L y x bx c =++经过点(0,5),(5,0)A B −.(1)求,b c 的值;(2)连结AB ,交抛物线L 的对称轴于点M .①求点M 的坐标;②将抛物线L 向左平移(0)m m >个单位得到抛物线1L .过点M 作//MNy 轴,交抛物线1L 于点N .P 是抛物线1L 上一点,横坐标为1−,过点P 作//PE x 轴,交抛物线L 于点E ,点E 在抛物线L 对称轴的右侧.若10PE MN +=,求m 的值.【答案】(1)4,5−−;(2)①(2,3)−;②1或.【分析】(1)直接运用待定系数法求解即可;(2)①求出直线AB 的解析式,抛物线的对称轴方程,代入求解即可;②根据抛物线的平移方式求出抛物线1L 的表达式,再分三种情况进行求解即可.【详解】解:(1)把点(0,5),(5,0)A B −的坐标分别代入2y x bx c =++,得5,2550.c b c =−⎧⎨++=⎩.解得4,5.b c =−⎧⎨=−⎩,b c ∴的值分别为4,5−−.(2)①设AB 所在直线的函数表达式为()0y kx n k =+≠,把(0,5),(5,0)A B −的坐标分别代入表达式,得5,50.n k n =−⎧⎨+=⎩,解得1,5.k n =⎧⎨=−⎩AB ∴所在直线的函数表达式为5y x =−.由(1)得,抛物线L 的对称轴是直线2x =,当2x =时,53y x =−=−.∴点M 的坐标是(2,3)−.②设抛物线1L 的表达式是2(2)9y x m =−+−, //MN y 轴,∴点N 的坐标是()22,9m −.∵点P 的横坐标为1,−∴点P 的坐标是()21,6m m −−,设PE 交抛物线1L 于另一点Q ,∵抛物线1L 的对称轴是直线2,//x m PE x =−轴,∴根据抛物线的轴对称性,点Q 的坐标是()252,6m m m −−.(i )如图1,当点N 在点M 下方,即0m <≤52(1)62PQ m m =−−−=−,()22396MN m m =−−−=−,由平移性质得,QE m =,∴626PE m m m =−+=−10PE MN +=Q ,∴26610m m −+−=,解得12m =−(舍去),21m =.(ii )图2,当点N 在点M 上方,点Q 在点P 右侧,3m ≤时,26,6PE m MN m =−=−,10PE MN +=Q ,26610m m ∴−+−=,解得1m =(舍去),2m =(舍去).(ⅲ)如图3,当点N 在点M 上方,点Q 在点P 左侧,即3m >时,2,6PE m MN m ==−,10PE MN +=Q ,2610m m ∴+−=,解得1m =(舍去),2m =.综上所述,m 的值是1或.【点睛】本题属于二次函数综合题,考查了待定系数法求函数的解析式、抛物线的平移规律和一元二次方程等知识点,数形结合、熟练掌握相关性质是解题的关键. 8.(2023·浙江·九年级专题练习)如图,抛物线2y x bx c =−++经过()()1,0,3,0A B −两点,且与y 轴交于点C .(1)求该抛物线的函数表达式;(2)抛物线上是否存在点P ,使得BCP 是以BC 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,说明理由;(3)点M 为OC 的中点,若有一动点P 自点M 处出发,沿直线运动至x 轴上的某点(设为点E ),再沿直线运动至该抛物线对称轴上的某点(设为点F ),最后又沿直线运动至点C ,则点P 运动的总路程最短为______.(请直接写出答案)【答案】(1)223y x x =−++;(2)存在,点P 的坐标为(1,4)或(-2,-5);(3) 【分析】(1)利用待定系数法求解;(2)分两种情况:①当C 为直角顶点时,过点C 作CP ⊥BC ,交抛物线于点P ,过点P 作PH ⊥y 轴于H ,得到PH=CH ,设P (2,23a a a −++),则2233a a a =−++−,求出a 即可;②当B 为直角顶点时,过点B 作BP ⊥BC ,交抛物线于点P ,交y 轴于R ,过点P 作PG ⊥y 轴于G ,求出OB=OR=3,PG=RG ,设P (2,23a a a −++),则2233a a a −=−−−,求出a 即可;(3)做M 点关于x 轴的对称点M ',做C 点关于对称轴的对称点C ',连接M 'C 交x 轴于E 点,交对称轴于F ,此时点P 运动的总路程最短,由勾股定理求出M C ''=即可求出点P 运动的路径得到答案.【详解】解:(1)将()()1,0,3,0A B −代入2y x bx c =−++,得10930b c b c −−+=⎧⎨−++=⎩,解得23b c =⎧⎨=⎩,∴该抛物线的函数表达式是223y x x =−++;(2)存在.①当C 为直角顶点时,过点C 作CP ⊥BC ,交抛物线于点P ,过点P 作PH ⊥y 轴于H ,∵OB=OC ,∠BOC=90°,∴△BOC 为等腰直角三角形,∠BCO=45°,∴∠PCH=45°,∴△PHC 为等腰直角三角形,即PH=CH ,设P (2,23a a a −++),则2233a a a =−++−,解得121,0a a ==(舍去),此时2234a a −++=,∴P (1,4);②当B 为直角顶点时,过点B 作BP ⊥BC ,交抛物线于点P ,交y 轴于R ,过点P 作PG ⊥y 轴于G , ∵∠CBO=45°,∴∠GPR=∠OBR=45°,∴△PRG 为等腰直角三角形,∴OB=OR=3,PG=RG ,设P (2,23a a a −++),则2233a a a −=−−−,解得122,3a a =−=(舍去),此时2235a a −++=−,∴P (-2,-5);综上,点P 的坐标为(1,4)或(-2,-5);(3)如图3,做M 点关于x 轴的对称点M ',做C 点关于对称轴的对称点C ',连接M 'C 交x 轴于E 点,交对称轴于F∴,ME M E CF C F ='='∵ME EF CF M EF C F M C ++='E++'=''此时点P 运动的总路程最短∵点M 为OC 的中点,C (0,3)∴3(0,)2M ∴3(0,)2M '− ∵2223(1)4y x x x =−++=−−+,∴抛物线的对称轴为直线x=1,∵C (0,3)∴(2,3)C '9 22MC CC ='=∴∴M C ''===, ∴点P运动的路径,故答案为:.【点睛】此题考查了二次函数的综合知识,待定系数法求函数解析式,抛物线的对称轴,直角三角形的性质,勾股定理,等腰直角三角形的性质,最短路径问题,综合掌握各知识点是解题的关键.题型二:面积问题一、解答题1.(2023·浙江衢州·校考一模)如图,抛物线22y ax bx =++经过点()()1040,,,A B −,与y 轴交于点C .【答案】(1)2222y x x =−++(2)存在,点D 的坐标为:(1,3)或(2,3)或(5,-3)(3)【分析】(1)用待定系数法解答;(2)设D (x ,y ),根据题意及利用三角形面积列出方程,求出y 的值后代入抛物线的解析式即可解答(3)由勾股定理解得AC 的长,再根据勾股定理逆定理证明ABC 为直角三角形,设直线AC 与直线BE 交于点F ,过点F 作FM ⊥x 轴于点M ,由平行线分线段成比例解得FM 的长,求得点F 的坐标,最后根据两点间的距离公式解答.【详解】(1)解:把点()()1040,,,A B −代入抛物线22y ax bx =++得2016420a b a b −+=⎧⎨++=⎩,1232a b ⎧=−⎪⎪∴⎨⎪=⎪⎩ ∴213222y x x =−++(2)由题意可知(0,2),(1,0),(4,0)C A B −5,2AB OC ∴==1152522ABC S AB OC ∴=⋅=⨯⨯=23ABC ABD S S =△△ 315522ABD S ∴=⨯= 设D (x ,y ),11155222AB y y ∴⋅=⨯=3y ∴=当y=3时,由2132322x x −++=,解得:1x =或2x =此时点D 的坐标为(1,3)或(2,3);当y=-3时,由2132322x x −++=−,解得:5x =或2x =−(舍去) 此时点D 的坐标为(5,-3);综上所述,点D 的坐标为:(1,3)或(2,3)或(5,-3);(3)1,2,4,5AO OC OB AB ====AC BC ∴===222AC BC AB ∴+=ABC ∴为直角三角形,即BC AC ⊥如图,设直线AC 与直线BE 交于点F ,过点F 作FM ⊥x 轴于点M ,由题意得:45FBC ∠=︒CF BC ∴==OC FMAO AC OM CF ∴=1OM2OC AC OM FM AF ∴==2FM ∴6FM ∴=(2,6),(4,0)F B ∴BF ∴==【点睛】本题考查二次函数的图象上点的特征、待定系数法求二次函数解析式、勾股定理、平行线分线段成比例、两点间的距离公式等,关键是利用面积关系求出点D 的坐标. (1)求抛物线的解析式;(2)当0<x <3时,直接写出y (3)点P 为抛物线上一点,若【答案】(1)2y x 2x 3=−++(2)04y <≤(3)(4,5)−P 或(2,5)P −−【分析】(1)将A 与B 的坐标代入抛物线的解析式即可求出b 与c 的值,(2)根据图象即可求出y 的取值范围,(3)设P (x ,y ),△PAB 的高为|y|,AB=4,由S △PAB=10列出方程即可求出y 的值,从而可求出P 的坐标.【详解】(1)解:将点A (﹣1,0),B (3,0)两点代入y =2x −+bx+c ∴0=1+0=9+3+b c b c −−−⎧⎨⎩,解得=2=3b c ⎧⎨⎩,∴抛物线的解析式为:2y x 2x 3=−++,2y x 2x 3=−++;(2)==−++−−+22y (x 1x 3)x 24,物线的对称轴为=1x ,开口向下,y 的最大值为4,如图,∴0<x <3时,04y <≤;(3)设P (x ,y ),∴△PAB 的高为|y|,A (﹣1,0),B (3,0),4AB ∴=,14102ABP S y ∴=⨯⨯=△,解得5y =±,当=5y 时,2523x x =−++,此时方程无解,当5y =−时,−2523x x =−++,解得124,2x x ==−,(4,5)P ∴−或(2,5)P −−.【点睛】本题考查了二次函数的综合问题,待定系数法求解析式,二次函数图象的性质,掌握二次函数的性质是解题的关键. 3.(2023秋·浙江衢州·九年级校考阶段练习)已知拋物线2()30y ax bx a =++≠与x 轴交于(1,0)A −,(3,0)B 两点,与y 轴交于点C .(1)求抛物线的表达式.(2)连接AC ,BC ,求ABC S .(3)拋物线上是否存在一点E ,使得由.【答案】(1)223y x x =−++(2)6(3)()12,()1,()12−或()12−【分析】(1)把()1,0A −,()3,0B 两点坐标代入解析式即可求解;(2)先求出C 点坐标,即可得到ABC S , (3)根据23ABE ABC S S =△△求出2E y =,代入解析式即可求解.【详解】(1)解:把()1,0A −,()3,0B 两点代入()230y ax bx a =++≠中,得030933a b a b =−+⎧⎨=++⎩,解得12a b =−⎧⎨=⎩,∴抛物线的表达式为223y x x =−++;(2)解:当0x =时,3y =,即()0,3C , ∴3OC =,∵()1,0A −,()3,0B ,∴1OA =,3OB =,∴4AB =,∴1143622ABC S AB OC =⋅⋅=⨯⨯=△,即所求面积为6;(3)解:∵6ABC S =, ∴226433ABE ABC S S ==⨯=△△, ∵142ABE E S AB y =⋅⋅=△, ∴2E y =,把2y =代入抛物线表达式得:2223x x =−++,解得1x =把=2y −代入抛物线表达式得:2223x x −=−++,解得1x =综述所述,点E 的坐标为()12或()1或()12−或()12−.【点睛】此题主要考查二次函数的图象与性质,解题的关键是熟知待定系数法及三角形的面积公式的应用. ,求POA 的面积.【答案】(1)m=3,24y x x =−+ (2)0x <或3x >(3)3【分析】(1)由点A 在一次函数y x =上,可将点A 的坐标代入y x =即可求出m ,然后将求出的点A 坐标代入2y x bx =−+即可求出b 值;(2)观察图象找出二次函数图像在一次函数图像下方部分的自变量取值范围即可;(3)求出点P 的坐标及抛物线与x 轴的另一个交点坐标,先计算由点A 、点P 、点O ,及抛物线与x 轴的另一个交点所构成的四边形面积,然后减去由点A 、点O ,及抛物线与x 轴的另一个交点所构成的三角形面积即可.【详解】(1)解:因为点A 在一次函数y x =上,所以()3m ,满足y x =,即3x =时y m =,可得:3m =;将点A ()33,代入2y x bx =−+得:2333b =−+,解得4b =,故二次函数的表达式为:24y x x =−+, 综上所得,故答案为:m=3,24y x x =−+. (2)解:由图象可知,一次函数与二次函数交于()()0,03,3,两点,观察图象可以看出在0x <或3x >时,2y x bx =−+的图象在y x =图象的下方,所以当0x <或3x >时,2x bx x −+<,故答案为:0x <或3x >.(3)解:方法一:如图1所示,因为点P 为抛物线顶点,所以点P 坐标为:()24,,抛物线与x 轴的另一个交点为点()40B ,,点()33A ,, 则四边形APOB 的面积()11124431139222=⨯⨯+⨯+⨯+⨯⨯=, ABO 的面积14362=⨯⨯=,∴POA 的面积=四边形APOB 的面积−ABO 的面积96=−3=,∴POA 的面积为3,故答案为:3.方法二:如图2所示,过点P 作PC x ⊥轴,垂足为C ,交OA 于点D ,过点A 作AE PC ⊥,垂足为E , 224(2)4y x x x =−+=−−+,∴顶点(2,4)P ,把2x =代入直线方程y x =中得:2y =,2()2D ∴,,422PD ∴=−=, POA 的面积OPD =的面积APD +的面积,111()222PD OC PD AE PD OC AE =⋅+⋅=+ 1232=⨯⨯3=.【点睛】本题考查了二次函数的图像及性质,结合图像求几何图形的面积及解对应的一元二次不等式,关键是解题过程要始终运用数形结合的思想方法.【答案】(1)1a =,3b =,4c =;(2)点E 的坐标为(1,6)时,面积最大;(3)d 最小值为5,此时F 点的坐标为(1,2).【分析】(1)将A 、C 两个点的坐标代入二次函数解析式,即可得出b 、c 的值,将点A (-1,0)代入一次函数中,即可求得a 的值;(2)设点E 的横坐标为m ,则点E 的纵坐标为234m m −++,过点E 作x 轴的垂线l ,交x 轴于点G ,交AD于点H ,则点H 的坐标为(),1m m +.过点D 作l 的垂线,垂足为T ,联立直线方程和二次函数方程,即可得出D 的坐标,再根据ΔΔΔAED AEH HED S S S =+,得出含m 的函数,根据函数图象,可知,当1m =时,面积取得最大值,从而可得出E 的坐标;(3)过A 作y 轴的平行线AS ,过作FG ⊥y 轴交AS 于点M ,过F 作FN ⊥x 轴于N ,根据角平分线的性质可得:FM FN = ,即有11d FE FM FE FN =+−=+−,可知当N 、F 、E 所在直线与x 轴垂直时,d 取得最小值,即可得出点F 的坐标.【详解】解:(1)∵点C (0,4),A (-1,0)在函数的图象上,∴410c b c =⎧⎨−−+=⎩,解得:34b c =⎧⎨=⎩,二次函数解析式为:234y x x =−++, ∵点A (-1,0)在一次一次函数y x a =+上,∴01a =−+,∴1a =,一次函数解析式为:1y x =+;所以1a =,3b =,4c =;(2)设点E 的横坐标为m ,则点E 的纵坐标为234m m −++,过点E 作x 轴的垂线l ,交x 轴于点G ,交AD于点H ,则点H 的坐标为(),1m m +.过点D 作l 的垂线,垂足为T ,将1y x =+与2y 34x x =−++联立组成方程组,解得点D 的坐标为(3,4), 所以ΔΔΔ1122AED AEH HED S S S EH AG EH DT =+=⨯+⨯ ()12EH AG DT =+ ()2134142m m m =−++−−⨯ ()2218m =−−+∵函数图象开口向下,存在最大值,∴AED S ∆有最大值,当1m =时,最大值为8,此时点E 的坐标为(1,6);(3)过A 作y 轴的平行线AS ,过F 作FG ⊥y 轴交AS 于点M ,过F 作FN ⊥x 轴于N ,如图所示:∵点D 的坐标为(3,4),点A 坐标为(-1,0)∴45DAB ∠=︒,∴AD 平分SAB ∠,∴FM FN = ,∴11d FE FM FE FN =+−=+−显然,当N 、F 、E 所在直线与x 轴垂直时,1d FE FN =+−最小,最小值为615d =−=,此时点F 的横坐标为1,代入1y x =+得:F 点的坐标为(1,2).【点睛】题目主要考查二次函数与一次函数的综合问题,二次函数、一次函数解析式的确定,组成面积的最值,角平分线的性质等,理解题意,作出相应辅助线,结合函数的基本性质是解题关键. 6.(2023·浙江·九年级专题练习)如图,已知二次函数y =2x 2﹣8x +6的图象与x 轴交于点A 和点B ,与y 轴交于点C ,顶点为D .求四边形ADBC 的面积.【答案】四边形ADBC 的面积为8.【分析】先把抛物线解析式化成顶点式,求出C 、D 的坐标,然后求出A 、B 的坐标,最后根据=ABC ABD ADBC S S S +△△四边形进行求解即可.【详解】解:∵抛物线解析式为()()22228624446222y x x x x x =−+=−+−+=−−,∴点C 的坐标为(0,6),点D 的坐标为(2,-2),令0y =,则22860x x −+=,∴2430x x −+=,解得1x =或3x =,∴点A 的坐标为(1,0),点B 的坐标为(3,0),∴AB=2,∴=ABC ABD ADBC S S S +△△四边形()11=22C D AB y AB y ⋅+⋅−()11262222=⨯⨯+⨯⨯−8=.【点睛】本题主要考查了求二次函数与坐标轴的交点,二次函数的顶点坐标,四边形面积,解题的关键在于能够熟练掌握二次函数的相关知识.把AOB 的面积分成相等的两部分.个单位,使其顶点落在AOB 的内部(不包括边界)【答案】(1)23b c =⎧⎨=⎩;(2)①3y x =;m <<. 【分析】(1)将(2,3),(1,0)A B −代入2y x bx c =−++中,列方程组求解即可.(2)直线OP 把AOB 的面积分成相等的两部分.则此直线必过AB 中点,求出中点坐标求解即可.(3)因为平移,所以过点D的直线必然与OP 平行,顶点要在三角形内部,画图分析即可.【详解】(1)将(2,3),(1,0)A B −代入2y x bx c =−++,得42310b c b c −++=⎧⎨−−+=⎩,解得:23b c =⎧⎨=⎩.(2)①取AB 的中点C ,∵(2,3),(1,0)A B − ∴13,22C ⎛⎫ ⎪⎝⎭又∵P 是第一象限内抛物线上一点,且直线OP 把AOB 的面积分成相等的两部分.∴直线OP 必过AB 的中点C∴直线OP 的表达式为:3y x =②由(1)可得抛物线的一般式为:223y x x =−++,将一般式转化为顶点式如下:2223(1)4y x x x =−++=−−+∴顶点坐标为()1,4D设过抛物线的顶点(1,4),且与直线OP 平行的直线解析式为:3'y x b =+将顶点()1,4D 代入3'y x b =+,得3'4b +=,解得'1b =∴31y x =+设AB y mx n =+,将(2,3)A ,(1,0)B −代入,得230m n m n +=⎧⎨−+=⎩, 解得11m n =⎧⎨=⎩∴1AB y x =+联立:311y x y x =+⎧⎨=+⎩ ,得:{01x y ==, 设直线31y x =+与直线AB 的交点坐标为点M ,与x 轴的交点坐标为N ,则()0,1M 1,03N ⎛⎫− ⎪⎝⎭ , 抛物线顶点落在AOB 的内部,即顶点在点M ,点N 之间,如图:∴DM ==DN ==m <<【点睛】本题考查的是二次函数的综合,二次函数的解析式求法,两点之间的距离公式,中点坐标公式等相关知识点,根据题意数形结合是解题的关键.【答案】(1)223y x x =+−;(2)存在,638;(3)点M 的坐标为⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭【分析】(1)利用待定系数法求解即可; (2)先求出C 、D 的坐标,设点()2,23(31)H a a a a +−−<<−,即可得到OBH OCHOBHC S S S =+△△四边形21123||22OB a a OC a =⨯+−+⨯,由此求解即可;(3)先求出E 点坐标,利用待定系数法求出直线BD 的解析式,利用PC PE =求出P 点坐标,设设(,0)M d ,则()2,23G d d d +−,()22,23N d d −+−,利用FM MG =建立方程求解即可.【详解】解:(1)∵抛物线2y x bx c =++的图象经过点(1,0)A ,(3,0)B − ∴10930b c b c ++=⎧⎨−+=⎩,∴23b c =⎧⎨=−⎩,∴抛物线的解析式为223y x x =+−;(2)当=1x −时,4y =−,所以点(1,4)D −−,当0x =时3y =−,,所以点(0,3)C − 设点()2,23(31)H a a a a +−−<<−所以OBH OCHOBHC S S S =+△△四边形21123||22OB a a OC a =⨯+−+⨯()2333222a a a =−−−2399222a a =−−+当322b a a =−=−时,638OBHC S =四边形. (3)由(1)知,抛物线的解析式为223y x x =+−;∴(0,3)C −,抛物线的顶点(1,4)D −−,∴(1,0)E −,设直线BD 的解析式为y mx n =+,∴304m n m n −+=⎧⎨−+=−⎩,∴26m n =−⎧⎨=−⎩∴直线BD 的解析式为26y x =−−,设点(,26)P m m −−, ∵(0,3)C −,(1,0)E −,根据勾股定理得,222(1)(26)PE m m =++−−,222(263)PC m m =+−−+,∵PC PE =,∴2222(1)(26)(263)m m m m ++−−=+−−+,∴2m =−,∴2(2)62y =−⨯−−=−,∴(2,2)P −−, 如图,作PF x ⊥轴于F ,∵(2,0)F −,设(,0)M d ,则()2,23G d d d +−,()22,23N d d −+−∴以点F ,N ,G ,M 四点为顶点的四边形为正方形,必有FM MG =,∴2|2|23d d d +=+−∴d =或d =,∴点M的坐标为⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭.【点睛】本题主要考查了二次函数的综合,待定系数法求函数解析式,正方形的性质,两点距离公式等等,【答案】(1)(0,2),(4,0),抛物线的解析式是211242y x x =−++;(2)四边形ABCM 面积最大值为8,此时点M 的坐标为(2,2);(3)34m −≤≤−或32m −≤≤【分析】(1)对直线122y x =−+,分别令x=0,y=0求出相应的y ,x 的值即得点A 、C 的坐标,根据待定系数法即可求出抛物线的解析式,利用抛物线的对称性即可求出点B 的坐标;(2)过点M 作ME ⊥x 轴于点E ,交直线AC 于点F ,如图1所示.设点M 的横坐标为m ,则MF 的长可用含m 的代数式表示,然后根据S 四边形ABCM=S △ABC+S △AMC 即可得出S 四边形ABCM 关于m 的函数关系式,再利用二次函数的性质即可求出四边形ABCM 面积的最大值及点M 的坐标;(3)当m >0时,分旋转后点A '与点O '落在抛物线上时,分别画出图形如图2、图3,分别用m 的代数式表示出点A '与点O '的坐标,然后代入抛物线的解析式即可求出m 的值,进而可得m 的范围;当m <0时,用同样的方法可再求出m 的一个范围,从而可得结果.【详解】解:(1)对直线122y x =−+,当x=0时,y=2,当y=0时,x=4,∴点A 的坐标是(0,2),点C 的坐标是(4,0),把点A 、C 两点的坐标代入抛物线的解析式,得:2214404c b c =⎧⎪⎨−⨯++=⎪⎩,解得:122b c ⎧=⎪⎨⎪=⎩,∴抛物线的解析式为211242y x x =−++, ∵抛物线的对称轴是直线1x =,C (4,0), ∴点B 的坐标为(﹣2,0);故答案为:A (0,2),C (4,0),抛物线的解析式是211242y x x =−++; (2)过点M 作ME ⊥x 轴于点E ,交直线AC 于点F ,如图1所示.设M (m ,211m m 242−++),则F (m ,122m −+),∴221112424122m m m mMF m ⎛⎫⎛⎫=−−+=−++− ⎪ ⎪⎝⎭⎭+⎝,∴S 四边形ABCM=S △ABC+S △AMC =1122BC AO MF OC⋅+⋅2111624224m m ⎛⎫=⨯⨯+⨯−+⨯ ⎪⎝⎭21262m m =−++ ()21282m =−−+,∵0<m <4,∴当m=2时,四边形ABCM 面积最大,最大值为8,此时点M 的坐标为(2,2);(3)若m >0,当旋转后点A '落在抛物线上时,如图2,线段O A ''与抛物线只有一个公共点, ∵点A '的坐标是(m+2,m ),∴()()21122242m m m−++++=,解得:3m =−3m =−;当旋转后点O '落在抛物线上时,如图3,线段O A ''与抛物线只有一个公共点, ∵点O '的坐标是(m ,m ),∴211242m m m−++=,解得:m=2或m=﹣4(舍去);∴当m >0时,若线段O A ''与抛物线只有一个公共点,m 的取值范围是:32m −≤≤;若m <0,当旋转后点O '落在抛物线上时,如图4,线段O A ''与抛物线只有一个公共点, ∵点O '的坐标是(m ,m ),∴211242m m m−++=,解得:m=﹣4或m=2(舍去);当旋转后点A '落在抛物线上时,如图5,线段O A ''与抛物线只有一个公共点, ∵点A '的坐标是(m+2,m ),∴()()21122242m m m−++++=,解得: 3m =−3m =−;∴当m <0时,若线段O A ''与抛物线只有一个公共点,m 的取值范围是:34m −≤≤−;综上,若线段O A ''与抛物线只有一个公共点,m 的取值范围是:34m −≤≤−或32m −≤≤. 【点睛】本题是二次函数的综合题,主要考查了待定系数法求二次函数的解析式、旋转的性质、一元二次方程的解法、二次函数的图象与性质以及抛物线上点的坐标特点等知识,具有较强的综合性,属于中考压轴题,熟练掌握二次函数的图象与性质、灵活应用数形结合的思想是解题的关键.【答案】(1)224y x x =−−+;(2)点M 的坐标为(2,-4);(3)n 的值为9.【分析】(1)直接把点B (-3,1)代入抛物线解析式进行求解即可; (2)由抛物线解析式为()2222y x kx k x x k=−+−=−+−,则当2x =时,4y =−,函数值与k 的取值无关,由此即可得到答案; (3)设直线BM 的解析式为1y k x b=+,直线BM 于y 轴的交点为E ,可求得直线BM 的解析式为2y x =−−,得到E 点坐标为(0,-2),从而求出15ABM S =V ;如图所示,在直线AB 上方作直线1l ∥AB ,且直线1l与抛物线只有一个交点1P ,对应的在直线AB 下方作直线2l ∥AB ,其中直线1l 与直线AB 的距离等于直线2l与直线AB 的距离,则123==ABP ABP ABP S S S △△△(等底等高),根据除去1P ,2P ,3P 这三个位置外,符合21=S nS 的P 点的个数为4个或2个;推出12ABP S nS =△,由此先求出直线AB 的解析式为4y x =+,则可设直线1l的解析式为2y x b =+,联立2224y x b y x x =+⎧⎨=−−+⎩得22340x x b +−+=,求得2254b =,从而求出点1P 的坐标为(32−,194),过点1P作x 轴的垂线交AB 于H ,根据111ABP P BH P AHS S S =+V V V ,求出1ABP S V 即可得到答案.【详解】解:(1)∵抛物线22y x kx k =−+−经过点B (-3,1),∴()21332k k=−−−−,∴2k =−,∴抛物线解析式为224y x x =−−+; (2)∵抛物线解析式为()2222y x kx k x x k=−+−=−+−,当2x =时,4y =−,函数值与k 的取值无关, ∴点M 的坐标为(2,-4);(3)∵抛物线224y x x =−−+与y 轴交于点A ,∴点A 的坐标为(0,4), 设直线BM 的解析式为1y k x b=+,直线BM 于y 轴的交点为E ,∴113124k b k b −+=⎧⎨+=−⎩,∴112k b =−⎧⎨=−⎩,∴直线BM 的解析式为2y x =−−, ∴E 点坐标为(0,-2), ∴()111522ABM ABE AME M B S S S AE x AE x =+=⋅+⋅−=V V V ;如图所示,在直线AB 上方作直线1l ∥AB ,且直线1l 与抛物线只有一个交点1P,对应的在直线AB 下方作直线2l ∥AB ,其中直线1l与直线AB 的距离等于直线2l 与直线AB 的距离, ∴123==ABP ABP ABP S S S △△△(等底等高),∵除去1P ,2P ,3P 这三个位置外,符合21=S nS 的P 点的个数为4个或2个;∴12ABP S nS =△,设直线AB 的解析式为21y k x b =+,∴211314k b b −+=⎧⎨=⎩,∴2114k b =⎧⎨=⎩,∴直线AB 的解析式为4y x =+, ∴可设直线1l 的解析式为2y x b =+,联立2224y x b y x x =+⎧⎨=−−+⎩得22340x x b +−+=, ∴()22344b ∆=+−=0 ,∴2254b =,∴29304x x ++=,解得32x =−,∴点1P 的坐标为(32−,194),过点1P作x 轴的垂线交AB 于H , ∴点H 的横坐标为32−,∴点H 的纵坐标为52,∴194PH =,∴111ABP P BH P AHS S S =+V V V ()()111122H B A H PH x x PH x x =⋅−+⋅−()112A B PH x x =⋅−278=,∴27158n =,∴409n =.【点睛】本题主要考查了二次函数与一次函数综合,平行线间距问题,待定系数法求函数解析式等等,解题的关键在于能够利用数形结合的思想进行求解.【答案】(1)A 点坐标为(2,0),抛物线对称轴为直线x=1;(2)4;(3)(4,﹣8).【分析】(1)在y =﹣x2+2x 中,令y=0,求得x 的值,从而确定A 点坐标,利用对称轴公式2bx a =−求得抛物线对称轴;(2)分别求得B 点和C 点坐标,求得直线OD 的解析式,然后通过求解△OBD 的面积求得平行四边形的面积;(3)结合平行四边形的性质及平移的思想分析点B ,点D 及点C 的坐标,然后仿照(2)中的解题思路分析求解.【详解】解:(1)在y =﹣x2+2x 中,令y=0,可得:﹣x2+2x=0,解得:x1=0,x2=2, ∵抛物线y =﹣x2+2x 与x 轴正半轴交于点A , ∴A 点坐标为(2,0),抛物线y =﹣x2+2x 的对称轴为直线()221x =−⨯−=1,即A 点坐标为(2,0),抛物线对称轴为直线x=1; (2)设OD 与抛物线对称轴交于点E ,连接BD ,∵点B B 的纵坐标是﹣3, ∴B 点坐标为(1,-3),∵点D 在抛物线上,且点D 的横坐标是52,∴点D 的纵坐标为255222⎛⎫−+⨯ ⎪⎝⎭=54−, ∴D 点坐标为55,24⎛⎫− ⎪⎝⎭,设直线OD 的解析式为OD y kx=,将D 点坐标为55,24⎛⎫− ⎪⎝⎭代入,可得5524k =−,解得:12k =−, ∴直线OD 的解析式为12OD y x=−,当x=1时,12y =−,∴E 点坐标为11,2⎛⎫− ⎪⎝⎭, ∴1522BOD S BE =⨯△=()51342⎡⎤⨯−−−⎢⎥⎣⎦=258, ∴S ▱OBCD =2524BOD S =△, 故答案为:254;(3)设OD 与抛物线对称轴交于点E ,连接BD ,设B 点坐标为(1,-b ),D a ,﹣a2+2a ),∵点D 在抛物线上,且在对称轴右侧,且点C 在抛物线上,四边形OBCD 为平行四边形,∴OB=CD ,OB ∥CD ,∵将点O 向右平移1个单位长度,再向下平移b 个单位长度后得到点B ,∴将点D 向右平移1个单位长度,再向下平移b 个单位长度后可得到点C ,∴C 点坐标为(a+1,﹣a2+2a-b ),将C 点坐标代入到y =﹣x2+2x 中,可得:﹣(a+1)2+2(a+1)=﹣a2+2a-b ,整理,可得:b=2a-1,设直线OD 的解析式为1OD y k x =,将D 点坐标(a ,﹣a2+2a ),代入,可得22ka a a =−+,解得:2k a =−+,∴直线OD 的解析式为()2OD y a x =−+,当x=1时,2y a =−+,。
二次函数背景下的倍、半角角度问题(解析版)-2023年中考数学重难点解题大招复习讲义-函数
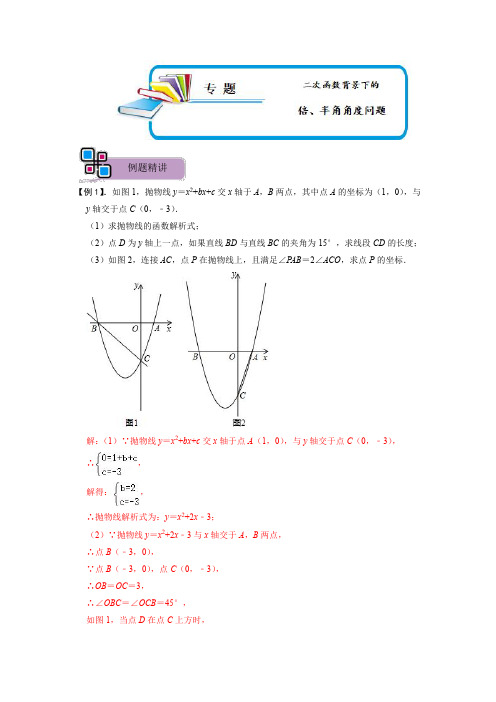
例题精讲【例1】.如图1,抛物线y=x2+bx+c交x轴于A,B两点,其中点A的坐标为(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数解析式;(2)点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;(3)如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.解:(1)∵抛物线y=x2+bx+c交x轴于点A(1,0),与y轴交于点C(0,﹣3),∴,解得:,∴抛物线解析式为:y=x2+2x﹣3;(2)∵抛物线y=x2+2x﹣3与x轴交于A,B两点,∴点B(﹣3,0),∵点B(﹣3,0),点C(0,﹣3),∴OB=OC=3,∴∠OBC=∠OCB=45°,如图1,当点D在点C上方时,∵∠DBC=15°,∴∠OBD=30°,∴tan∠DBO==,∴OD=×3=,∴CD=3﹣;若点D在点C下方时,∵∠DBC=15°,∴∠OBD=60°,∴tan∠DBO==,∴OD=3,∴DC=3﹣3,综上所述:线段CD的长度为3﹣或3﹣3;(3)如图2,在BO上截取OE=OA,连接CE,过点E作EF⊥AC,∵点A(1,0),点C(0,﹣3),∴OA=1,OC=3,∴AC===,∵OE=OA,∠COE=∠COA=90°,OC=OC,∴△OCE≌△OCA(SAS),∴∠ACO=∠ECO,CE=AC=,∴∠ECA=2∠ACO,∵∠PAB=2∠ACO,∴∠PAB=∠ECA,=AE×OC=AC×EF,∵S△AEC∴EF==,∴CF===,∴tan∠ECA==,如图2,当点P在AB的下方时,设AP与y轴交于点N,∵∠PAB=∠ECA,∴tan∠ECA=tan∠PAB==,∴ON=,∴点N(0,﹣),又∵点A(1,0),∴直线AP解析式为:y=x﹣,联立方程组得:,解得:或,∴点P坐标为:(﹣,﹣),当点P在AB的上方时,同理可求直线AP解析式为:y=﹣x+,联立方程组得:,解得:或,∴点P坐标为:(﹣,),综上所述:点P的坐标为(﹣,)或(﹣,﹣).变式训练【变1-1】.如图,在平面直角坐标系中,抛物线y=ax2+x+c交x轴于点A、点B,交y轴于点C.直线y=﹣x+2经过于点C、点B,(1)求抛物线的解析式;(2)点D为第一象限抛物线上一动点,过点D作y轴的平行线交线段BC于点E,交x 轴于点Q,当DE=5EQ时,求点D的坐标;(3)在(2)的条件下,点M为第二象限抛物线上一动点,连接DM,DM交线段OC于点H,点F在线段OB上,连接HF、DF、DC、DB,当HF=,∠CDB=2∠MDF 时,求点M的坐标.解:(1)针对于直线y=﹣x+2,令x=0,则y=2,∴C(0,2),令y=0,则0=﹣x+2,∴x=4,∴B(4,0),将点B,C坐标代入抛物线y=ax2+x+c中,得∴,∴抛物线的解析式为y=﹣x2+x+2;(2)如图1,由(1)知,抛物线的解析式为y=﹣x2+x+2,设点D坐标为(m,﹣m2+m+2),∵DE⊥x轴交BC于E,直线BC的解析式为y=﹣x+2,∴D(m,﹣m+2),∴DE=﹣m2+m+2﹣(﹣m+2)=﹣m2+m,DQ=﹣m+2,∵DE=5EQ,∴﹣m2+m=5(﹣m+2),∴m=3或m=4(点B的横坐标,舍去),∴D(3,3);(3)如图2,由(2)知,D(3,3),由(1)知,B(4,0),C(0,2),∴DB=,DC=,BC=2,∴DC=DB,DB2+DC2=BC2,∴△BDC是等腰直角三角形,∴∠BDC=90°,∵BDC=2∠FDM=90°,∴∠FDM=45°,过点D作DP⊥y轴于P,则DQ=DP,OP=3,∴CP=1=BQ,∴△DPC≌△DQB(SAS),在CP的延长线取一点G,使PG=QF=n,∴OF=3﹣n,OG=3+n,∴△DPG≌△DQF(SAS),∴DG=DF,∠PDG=∠QDF,∴∠FDG=∠PDG+∠PDF=∠QDF+∠PDG=∠PDQ=90°∴∠GDM=90°﹣∠FDM=45°=∠GDM,∵DH=DH,∴△GDH≌△FDH(SAS),∴GH=FH=,∴OH=OG﹣GH=3+n﹣=n+,在Rt△HOF中,根据勾股定理得,(n+)2+(3﹣n)2=,∴n=1或n=(此时,OH=n+=2,所以点H与点C重合,舍去),∴H(0,),∵C(3,3),∴直线CH的解析式为y=x+①,∵抛物线的解析式为y=﹣x2+x+2②,联立①②解得,或(由于点M在第二象限,所以舍去),∴M(﹣,).【例2】.如图,直线y=x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=x2+bx+c 经过点B,C,与x轴的另一个交点为点A.(1)求抛物线的解析式;(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;(3)若点M是抛物线上一点,请直接写出使∠MBC=∠ABC的点M的坐标.解:(1)将点B坐标代入y=x+c并解得:c=﹣3,故抛物线的表达式为:y=x2+bx﹣3,将点B坐标代入上式并解得:b=﹣,故抛物线的表达式为:y=x2﹣x﹣3①;(2)过点P作PH∥y轴交BC于点H,设点P (x ,x 2﹣x ﹣3),则点H (x ,x ﹣3),S 四边形ACPB =S △ABC +S △PCB ,∵S △ABC 是常数,故四边形面积最大,只需要S △PCB 最大即可,S △PCB =×OB ×PH =×4(x ﹣3﹣x 2+x +3)=﹣x 2+6x ,∵﹣<0,∴S △PCB 有最大值,此时,点P (2,﹣);(3)过点B 作∠ABC 的角平分线交y 轴于点G ,交抛物线于M ′,设∠MBC =∠ABC=2α,过点B 在BC 之下作角度数为α的角,交抛物线于点M ,过点G 作GK ⊥BC 交BC 于点K ,延长GK 交BM 于点H ,则GB =BH ,BC 是GH 的中垂线,OB =4,OC =3,则BC =5,设:OG =GK =m ,则CK =CB ﹣HB =5﹣4=1,由勾股定理得:(3﹣m )2=m 2+1,解得:m =,则OG =GK =,GH =2OG =,点G (0,﹣),在Rt △GCK 中,GK =OG =,GC =OC ﹣OG =3﹣=,则cos∠CGK==,sin∠CGK=,则点K(,﹣),点K是点GH的中点,则点H(,﹣),则直线BH的表达式为:y=x﹣…②,同理直线BG的表达式为:y=x﹣…③联立①②并整理得:27x2﹣135x+100=0,解得:x=或4(舍去4),则点M(,﹣);联立①③并解得:x=﹣,故点M′(﹣,﹣);故点M(,﹣)或(﹣,﹣).变式训练【变2-1】.如图,抛物线y=ax2+bx+4交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC.(1)求抛物线的解析式;(2)点P是抛物线上一点,设P点的横坐标为m.①当点P在第一象限时,过点P作PD⊥x轴,交BC于点D,过点D作DE⊥y轴,垂足为E,连接PE,当△PDE和△BOC相似时,求点P的坐标;②请直接写出使∠PBA=∠ABC的点P的坐标.解:(1)∵抛物线y=ax2+bx+4交x轴于A(﹣1,0)、B(3,0)两点,∴,解得,,∴抛物线的解析式为:;(2)令x=0,得=4,∴C(0,4),∴OC=4,∵B(3,0),∴OB=3,设直线BC的解析式为y=kx+n(k≠0),则,解得,∴直线BC的解析式为:y=,设P(m,),则D(m,),∴DP=,DE=m,∴,∵∠BOC=∠PDE=90°,∴当△PDE和△BOC相似时,有两种情况:当△PDE∽△BOC时,则,即=,解得,m=,∴P(,);当△PDE∽△COB时,则,即=,解得,m=2,∴P(2,4).综上,当△PDE和△BOC相似时,点P的坐标(,)或(2,4);②过B作BP平分∠ABC,交抛物线于点P,交OC于点M,过M作MN⊥BC于点N,如图1,则∠PBA=∠ABC,OM=MN,在Rt△BOM和Rt△BNM中,,∴Rt△BOM≌Rt△BNM(HL),∴BN=BO=3,设OM=t,则MN=MO=t,CM=4﹣t,CN=BC﹣BN=﹣3=2,∵MN2+CN2=MC2,∴t2+22=(4﹣t)2,∴t=,∴M(0,),设BM的解析式为:y=mx+(m≠0),代入B(3,0)得,m=,∴直线BM的解析式为:y=﹣,解方程组得,,,∴P(,),取M(0,)关于x轴的对称点,K(0,﹣),连接BK,延长BK,交抛物线于点P',如图2所示,则∠ABP=∠ABC,设直线BK的解析式为y=px(p≠0),代入B(3,0)得,p=,∴直线BK的解析式为:y=,解方程组得,,∴P'(,),综上,使∠PBA=∠ABC的点P的坐标为(,)或(,).【例3】.已知如图,抛物线y=ax2+bx﹣4(a≠0)交x轴于A、B两点(A点在B点的左侧),交y轴于点C.已知OA=OC=2OB.(1)求抛物线的解析式;(2)已知直线y=2x+m,若直线与抛物线有且只有一个交点E,求△ACE的面积;(3)在(2)的条件下,抛物线上是否存在点P,使∠PAB=∠EAC,若存在,请直接写出点P的坐标;若不存在,请说明理由.解:(1)对于抛物线y=ax2+bx﹣4,令x=0,则y=﹣4,∴C(0,﹣4),∴OC=4,∵OA=OC=2OB,∴OA=4,OB=2,∴A(﹣4,0),B(2,0),∵点A,B在抛物线y=ax2+bx﹣4上,∴,∴,∴抛物线的解析式为y=x2+x﹣4;(2)由(1)知,抛物线的解析式为y=x2+x﹣4①,∵直线y=2x+m②与抛物线有且只有一个交点E,联立①②得,,∴x2﹣x﹣(4+m)=0,∴△=1+4×(4+m)=0,∴m=﹣,∴x2﹣x﹣=0,∴x1=x2=1,∴E(1,﹣),∴直线AE的解析式为y=﹣x﹣2如图1,记直线AE与y轴的交点为F,则F(0,﹣2),=CF×|x E﹣x A|=×2×|1﹣(﹣4)|=5;∴S△ACE(3)由(2)知,E(1,﹣),Ⅰ、当点P在x轴上方时,如图2,将线段AE以点E为旋转中心顺时针旋转90°得到线段EG,连接AG,则∠EAG=45°,在Rt△AOC中,OA=OC,∴∠OAC=45°=∠EAG,∴∠CAE=∠OAG,∴点P是AG与抛物线的交点,过点E作MN∥x,过点A作AM⊥MN于M,过点G作GN⊥MN于G,∵A(﹣4,0),E(1,﹣),∴AM=,ME=5,∴∠AME=∠ENG=90°,∴∠MAE+∠AEM=90°,由旋转知,AE=EG,∠AEG=90°,∴∠AEM+∠NEG=90°,∴∠MAE=∠NEG,∴△AME≌△ENG(AAS),∴EN=AM=,GN=ME=5,∴N(,﹣),G(,),∴直线AG的解析式为y=x+③,∵抛物线的解析式为y=x2+x﹣4④,联立③④解得,或,∴P(,),Ⅱ、由Ⅰ知,点G的坐标为G(,),N(,﹣),∴点G与点N关于x轴对称,∴点P是直线AN与抛物线的交点,∵A(﹣4,0),∴直线AN的解析式为y=﹣x﹣⑤,联立④⑤,解得,或,∴P(,﹣),即满足条件的点P的坐标为P(,)或(,﹣).变式训练【变3-1】.如图,已知:抛物线y=a(x+1)(x﹣3)与x轴相交于A、B两点,与y轴的交于点C(0,﹣3).(1)求抛物线的解析式的一般式.(2)若抛物线上有一点P,满足∠ACO=∠PCB,求P点坐标.(3)直线l:y=kx﹣k+2与抛物线交于E、F两点,当点B到直线l的距离最大时,求△BEF的面积.解:(1)把C(0,﹣3)代入y=a(x+1)(x﹣3),得﹣3a=﹣3,解得a=1,所以抛物线解析式为y=(x+1)(x﹣3),即y=x2﹣2x﹣3;(2)当点P在直线BC的下方时,如图1,过点B作BE⊥BC交CP的延长线于点E,过点E作EM⊥x轴于点M,∵y=(x+1)(x﹣3),∴y=0时,x=﹣1或x=3,∴A(﹣1,0),B(3,0),∴,∵OB=OC=3,∴∠ABC=45°,BC=3,∵∠ACO=∠PCB,∴tan,∴BE=,∵∠CBE=90°,∴∠MBE=45°,∴BM=ME=1,∴E(4,﹣1),设直线CE的解析式为y=kx+b,∴,解得:,∴直线CE的解析式为,∴,解得,∴,当点P在直线BC的上方时,过点B作BF⊥BC交CP于点F,如图2,同理求出BF=,FN=BN=1,∴F(2,1),求出直线CF的解析式为y=2x﹣3,∴,解得:x1=0,x2=4,∴P(4,5).综合以上可得点P的坐标为(4,5)或();(3)∵直线l:y=kx﹣k+2,∴y﹣2=k(x﹣1),∴x﹣1=0,y﹣2=0,∴直线y=kx﹣k+2恒过定点H(1,2),如图3,连接BH,当BH⊥直线l时,点B到直线l的距离最大时,求出直线BH的解析式为y=﹣x+3,∴k=1,∴直线l的解析式为y=x+1,∴,解得:,,∴E(﹣1,0),F(4,5),∴=10.1.如图,已知直线AB:y=x﹣3与x、y轴分别交于A、B两点;抛物线y=x2﹣2x﹣m与y 轴交于C点,与线段AB交于D、E两点(D在E左侧)(1)若D、E重合,求m值;(2)连接CD、CE,若∠BCD=∠BEC,求m值;(3)连接OD,若OD=CE,求m值.解:(1)把y=x﹣3代入抛物线y=x2﹣2x﹣m中,得x2﹣3x+3﹣m=0,∵D、E重合,∴△=9﹣4(3﹣m)=4m﹣3=0,∴m=;(2)∵y=x﹣3与x、y轴分别交于A、B两点;抛物线y=x2﹣2x﹣m与y轴交于C点,∴B(0,﹣3),C(0,﹣m),∴BC=3﹣m,解方程组得,,,∴,,∴BD=,BE=,∵∠BCD=∠BEC,∠CBD=∠EBC,∴△BCD∽△BEC,∴,即BC2=BD•BE,∴,解得,m=1或3,当m=3时,B与C重合,不符合题意,舍去,∴m=1;(3)∵OD=CE,∴OD2=CE2,∴+,即,解得,m=0,或m=5,当m=0时,无意义,应舍去,当m=5+时,C点在B点下方,不合题意,舍去,∴m=5﹣,2.如图①,抛物线y=x2﹣(a+1)x+a与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知△ABC的面积为6.(1)求这条抛物线相应的函数表达式;(2)在抛物线上是否存在一点P,使得∠POB=∠CBO,若存在,请求出点P的坐标;若不存在,请说明理由;(3)如图②,M是抛物线上一点,N是射线CA上的一点,且M、N两点均在第二象限内,A、N是位于直线BM同侧的不同两点.若点M到x轴的距离为d,△MNB的面积为2d,且∠MAN=∠ANB,求点N的坐标.解:(1)当y=0时,x2﹣(a+1)x+a=0,解得x1=1,x2=a,∵点A位于点B的左侧,∴点A坐标为(a,0),点B坐标为(1,0),当x=0时,y=a,∴点C坐标为(0,a),∴AB=1﹣a,OC=﹣a,∵△ABC的面积为6,∴,∴a1=﹣3,a2=4,∵a<0,∴y=x2+2x﹣3;(2)设直线BC:y=kx﹣3,则0=k﹣3,∴k=3;①当点P在x轴上方时,直线OP的函数表达式为y=3x,则,∴,,∴点P坐标为;②当点P在x轴下方时,直线OP的函数表达式为y=﹣3x,则∴,,∴点P坐标为,综上可得点P坐标为或;(3)过点A作AE⊥BM于点E,过点N作NF⊥BM于点F,设AM与BN交于点G,延长MN与x轴交于点H;∵AB=4,点M到x轴的距离为d,=×AB×d=×4×d=2d,∴S△AMB=2d,∵S△MNB=S△MNB,∴S△AMB∴,∴AE=NF,∵AE⊥BM,NF⊥BM,∴四边形AEFN是矩形,∵∠MAN=∠ANB,∴GN=GA,∵AN∥BM,∴∠MAN=∠AMB,∠ANB=∠NBM,∴∠AMB=∠NBM,∴GB=GM,∴GN+GB=GA+GM即BN=MA,在△AMB和△NBM中∴△AMB≌△NBM(SAS),∴∠ABM=∠NMB,∵OA=OC=3,∠AOC=90°,∴∠OAC=∠OCA=45°,又∵AN∥BM,∴∠ABM=∠OAC=45°,∴∠NMB=45°,∴∠ABM+∠NMB=90°,∴∠BHM=90°,∴M、N、H三点的横坐标相同,且BH=MH,∵M是抛物线上一点,∴可设点M的坐标为(t,t2+2t﹣3),∴1﹣t=t2+2t﹣3,∴t1=﹣4,t2=1(舍去),∴点N的横坐标为﹣4,可设直线AC:y=kx﹣3,则0=﹣3k﹣3,∴k=﹣1,∴y=﹣x﹣3,当x=﹣4时,y=﹣(﹣4)﹣3=1,∴点N的坐标为(﹣4,1).3.如图1,抛物线C1:y=ax2+c的顶点为A,直线l:y=kx+b与抛物线C1交于A,C两点,=4.与x轴交于点B(1,0),且OA=2OB,S△OAC(1)求直线l的解析式;(2)求抛物线C1与x轴的交点坐标;(3)如图2,将抛物线C1向下平移m(m>0)个单位得到抛物线C,且抛物线C的顶点为P,交x轴负半轴于点M,交射线BC于点N,NQ⊥x轴于点Q,当NP平分∠MNQ 时,求m的值.解:(1)∵B(1,0),∴OB=1,∵OA=2OB,∴OA=2,∴A(0,﹣2),设直线l的解析式为y=kx+b,∴,解得,∴直线l的解析式为y=2x﹣2;=4,(2)∵S△OAC∴,∴x C=4,∴y=8﹣2=6,∴C(4,6),将A(0,﹣2),C(4,6)代入y=ax2+c,∴,解得,∴抛物线C1与的解析式为y=;令y=0,,解得x=±2,∴抛物线C1与x轴的交点坐标为(2,0),(﹣2,0).(3)设抛物线C表达式为:y=x2﹣2﹣m,设点M(n,0),则n2﹣2﹣m=0,抛物线C表达式为:y=x2﹣n2…③,联立②③并解得:x=2﹣n或2+n,则点N(2﹣n,2﹣2n),则NQ=2﹣2n,MQ=2﹣2n,∴△MNQ为等腰直角三角形,则∠MNQ=45°,又点P(0,﹣n2),即点M(n,0),设直线MN与y轴的交点为H,则OH=OM,则点H(0,﹣n),作NK⊥y轴于点K,在△NKH中,NK=KH,则NH=(2﹣n),又HP=OH+OP=n2﹣n,∵PN为角平分线,则∠MNP=∠PNQ=22.5°,故NH=HP,则(2﹣n)=n2﹣n,解得:n=2或﹣2(舍去2),∵n2﹣2﹣m=0,解得:m=2.4.如图,直线y=x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴的另一个交点为C.(1)求抛物线的解析式;(2)点D是直线AB上方抛物线上的一动点,①求D到AB的距离最大值及此时的D点坐标;②若∠DAB=∠BAC,求D点的坐标.解:(1)由y=x+2可得:当x=0时,y=2;当y=0时,x=﹣4,∴A(﹣4,0),B(0,2),把A、B的坐标代入y=﹣x2+bx+c得:,解得:,∴抛物线的解析式为:y=﹣x2﹣x+2;(2)①如图1,过点D作DN⊥AC于N,交AB于F,作DH⊥AB于H,∵A(﹣4,0),B(0,2),∴OA=4,OB=2,∴AB===2,∵∠FAN+∠AFN=90°,∠FDH+∠DFH=90°,∠AFN=∠DFH,∴∠FAN=∠FDH,∴cos∠FAN=cos∠FDH,∴,∴=,∴DH=DF,∴当DF有最大值时,DH有最大值,设点D,F,∴DF==﹣(m+2)2+2,∴当m=﹣2时,DF有最大值为2,∴DH的最大值为,∴当点D(﹣2,3)时,D到AB的距离最大值为;②如图2,延长CB,AD交于点E,∵抛物线y=﹣x2﹣x+2与x轴交于点A,点C,∴点C(1,0),∴OC=1,∵=,∠AOB=∠BOC,∴△AOB∽△BOC,∴∠BAO=∠CBO,∵∠BAO+∠ABO=90°,∴∠ABO+∠CBO=90°,∴∠ABC=90°,∵∠DAB=∠BAC,AB=AB,∠ABC=∠ABE=90°,∴△ABC≌△ABE(ASA),∴BC=BE,∵B(0,2),点C(1,0),∴点E(﹣1,4),∴直线AE的解析式为y=x+,联立方程组:,解得:,,∴点D(﹣,).5.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣2,0)、B(8,0)两点,与y轴交于点C(0,4),连接AC、BC.(1)求抛物线的表达式;(2)D为抛物线上第一象限内一点,求△DCB面积的最大值;(3)点P是抛物线上的一动点,当∠PCB=∠ABC时,求点P的坐标.解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣2,0)、B(8,0)两点,与y 轴交于点C(0,4),∴,解得:,∴抛物线的表达式为y=﹣x2+x+4;(2)如图,过点D作DE∥y轴交BC于点E,交x轴于点F,∵B(8,0),C(0,4),∴直线BC解析式为y=﹣x+4,设D(m,﹣m2+m+4),则E(m,﹣m+4),∵D为抛物线上第一象限内一点,∴DE=DF﹣EF=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+2m,∴△DCB面积=8×DE=4(﹣m2+2m)=﹣m2+8m=﹣(m﹣4)2+16,∴当m=4时,△DCB面积最大,最大值为16;(3)①当点P在BC上方时,如图,∵∠PCB=∠ABC,∴PC∥AB,∴点C,P的纵坐标相等,∴点P的纵坐标为4,令y=4,则﹣x2+x+4=4,解得:x=0或x=6,∴P(6,4);②当点P在BC下方时,如图,设PC交x轴于点H,∵∠PCB=∠ABC,∴HC=HB.设HB=HC=m,∴OH=OB﹣HB=8﹣m,在Rt△COH中,∵OC2+OH2=CH2,∴42+(8﹣m)2=m2,解得:m=5,∴OH=3,∴H(3,0).设直线PC的解析式为y=kx+n,∴,解得:,∴y=﹣x+4,∴,解得:,,∴P(,﹣).综上所述,点P的坐标为(6,4)或(,﹣).6.已知:在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(5,0)、B(﹣3,4),抛物线的对称轴与x轴相交于点D.(1)求抛物线的表达式;(2)联结OB、BD.求∠BDO的余切值;(3)如果点P在线段BO的延长线上,且∠PAO=∠BAO,求点P的坐标.解:(1)将A(5,0),B(﹣3,4)代入y=ax2+bx,得:,解得:,∴所求抛物线的表达式为y=x2﹣x.(2)∵抛物线的表达式为y=x2﹣x,∴抛物线的对称轴为直线x=,∴点D的坐标为(,0).过点B作BC⊥x轴,垂足为点C,如图1所示.∵点B的坐标为(﹣3,4),点D的坐标为(,0),∴BC=4,OC=3,CD=3+=,∴cot∠BDO==.(3)设点P的坐标为(m,n),过点P作PQ⊥x轴,垂足为点Q,如图2所示.则PQ=﹣n,OQ=m,AQ=5﹣m.在Rt△ABC中,∠ACB=90°,∴cot∠BAC===2.∵∠PAO=∠BAO,∴cot∠PAO===2,即m﹣2n=5①.∵BC⊥x轴,PQ⊥x轴,∴∠BCO=∠PQA=90°,∴BC∥PQ,∴=,∴=,即4m=﹣3n②.由①、②得:,解得:,∴点P的坐标为(,﹣).7.抛物线y=x2+bx+c经过点A(﹣3,0)和点B(2,0),与y轴交于点C.(1)求该抛物线的函数表达式;(2)点P是该抛物线上的动点,且位于y轴的左侧.①如图1,过点P作PD⊥x轴于点D,作PE⊥y轴于点E,当PD=2PE时,求PE的长;②如图2,该抛物线上是否存在点P,使得∠ACP=∠OCB?若存在,请求出所有点P的坐标:若不存在,请说明理由.解:(1)∵抛物线y=x2+bx+c经过点A(﹣3,0)和点B(2,0),∴,解得:,∴抛物线解析式为:y=x2+x﹣6;(2)①设点P(a,a2+a﹣6),∵点P位于y轴的左侧,∴a<0,PE=﹣a,∵PD=2PE,∴|a2+a﹣6|=﹣2a,∴a2+a﹣6=﹣2a或a2+a﹣6=2a,解得:a1=,a2=(舍去)或a3=﹣2,a4=3(舍去)∴PE=2或;②存在点P,使得∠ACP=∠OCB,理由如下,∵抛物线y=x2+x﹣6与y轴交于点C,∴点C(0,﹣6),∴OC=6,∵点B(2,0),点A(﹣3,0),∴OB=2,OA=3,∴BC===2,AC===3,如图,过点A作AH⊥CP于H,∵∠AHC=∠BOC=90°,∠ACP=∠BCO,∴△ACH∽△BCO,∴,∴=,∴AH=,HC=,设点H(m,n),∴()2=(m+3)2+n2,()2=m2+(n+6)2,∴或,∴点H(﹣,﹣)或(﹣,),当H(﹣,﹣)时,∵点C(0,﹣6),∴直线HC的解析式为:y=﹣x﹣6,∴x2+x﹣6=﹣x﹣6,解得:x1=﹣2,x2=0(舍去),∴点P的坐标(﹣2,﹣4);当H(﹣,)时,∵点C(0,﹣6),∴直线HC的解析式为:y=﹣7x﹣6,∴x2+x﹣6=﹣7x﹣6,解得:x1=﹣8,x2=0(舍去),∴点P的坐标(﹣8,50);综上所述:点P坐标为(﹣2,﹣4)或(﹣8,50).8.如图1,抛物线y=ax2+c与x轴交于点A、B,与y轴交于点C,P为x轴下方抛物线上一点,若OC=2OA=4.(1)求抛物线解析式;(2)如图2,若∠ABP=∠ACO,求点P的坐标;(3)如图3,点P的横坐标为1,过点P作PE⊥PF,分别交抛物线于点E,F.求点A 到直线EF距离的最大值.解:(1)∵CO=4,故c=﹣4,则抛物线的表达式为y=ax2﹣4,∵OC=2OA=4,故点A(﹣2,0),则0=4a﹣4,解得a=1,故抛物线的表达式为y=x2﹣4;(2)过点A作x轴的垂线交BP的延长线于点Q,在△BAQ和△COA中,,∴△BAQ≌△COA(AAS),∴AQ=OA=2,∴Q(﹣2,﹣2),由点B、Q的坐标得,直线BQ解析式为y=x﹣1,联立,解得x1=2(舍去),x2=,∴P(,);(3)设E(x1,x12﹣4),F(x2,x22﹣4),P(1,﹣3),由点P、E的坐标得,y PE=(x1+1)x﹣4﹣x1,同理可得y PF=(x2+1)x﹣4﹣x2,又∵PE⊥PF,∴(x1+1)(x2+1)=﹣1,∴x1x2+x1+x2+1=﹣1,x1x2=﹣2﹣(x1+x2)(这里可以构造三垂模型如图3,利用相似三角形的性质得到).同理可得EF的解析式为:y EF=(x1+x2)x﹣4﹣x1x2,∴y EF=(x1+x2)x﹣4+2+(x1+x2)=(x1+x2)(x+1)﹣2,∴直线EF恒过定点(﹣1,﹣2),设该点为R,连接点AR,则AR为点A到直线EF距离的最大值,∴AR=.9.如图,已知二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),B(3,0),与y轴交于点C.(1)求抛物线的解析式;(2)M是抛物线上第一象限上的一点,连接AM,正好将△ABC的面积分成相等的两部分,求M点的坐标.(3)抛物线上是否存在点P,使∠PAB=∠ABC,若存在,请求出点P的坐标;若不存在,请说明理由.解:(1)把A(﹣1,0),B(3,0)代入得:,解得,∴抛物线的解析式为y=﹣x2+2x+3;(2)作BC的中点N,连接AN并延长交抛物线于M,如图:∵N为BC中点,∴直线AN将△ABC的面积分成相等的两部分,即M是满足条件的点,在y=﹣x2+2x+3中,令x=0得y=3,∴C(0,3),∵B(3,0),N为BC中点,∴N(,),设直线AN解析式为y=mx+n,将A(﹣1,0),N(,)代入得:,解得,∴直线AN解析式为y=x+,解得或,∴M(,),答:M点的坐标(,);(3)存在点P,使∠PAB=∠ABC,理由如下:过A作AP∥BC交抛物线于P,交y轴于S,作S关于x轴的对称轴点T,作直线AT交抛物线于P',如图:∵AP∥BC,∴∠PAB=∠ABC,P是满足条件的点,∵S关于x轴的对称轴点为T,∴∠P'AB=∠PAB=∠ABC,即P'是满足条件的点,由(2)知C(0,3),设直线BC解析式为y=tx+3,将B(3,0)代入得:3t+3=0,∴t=﹣1,∴直线BC解析式为y=﹣x+3,由AP∥BC设直线AP解析式为y=﹣x+d,将A(﹣1,0)代入得:1+d=0,解得d=﹣1,∴直线AP解析式为y=﹣x﹣1,S(0,﹣1),解得或,∴P(4.﹣5),∵S(0,﹣1),S关于x轴的对称轴点为T,∴T(0,1),设直线AT解析式为y=ex+1,将A(﹣1,0)代入得:﹣e+1=0,解得e=1,∴直线AT解析式为y=x+1,解得或,∴P'(2,3),综上所述,点P的坐标为(4,﹣5)或(2,3).10.如图(1),抛物线y=ax2+(a﹣5)x+3(a为常数,a≠0)与x轴正半轴分别交于A,B(A在B的右边).与y轴的正半轴交于点C.连接BC,tan∠BCO=.(1)直接写出抛物线的解析式;(2)如图(2),设抛物线的顶点为Q,P是第一象限抛物线上的点,连接PQ,AQ,AC,若∠AQP=∠ACB,求点P的坐标;(3)如图(3),D是线段AC上的点,连接BD,满足∠ADB=3∠ACB,求点D的坐标.解:(1)∵抛物线y=ax2+(a﹣5)x+3与y轴的正半轴交于点C,∴C(0,3),∴OC=3,∵tan∠BCO=,∴=,∴OB=1,∴B(1,0),将B(1,0)代入y=ax2+(a﹣5)x+3,得a+a﹣5+3=0,解得:a=1,∴抛物线解析式为:y=x2﹣4x+3;(2)如图(2)设PQ与x轴交于N.∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点Q(2,﹣1),∵A(3,0),B(1,0),C(0,3),∴AB=2,OC=OA=3,∴∠CAO=45°,AC=3,过Q作QH⊥x轴于H,则QH=AH=1,∴∠QAH=45°,AQ=,∴∠CAO=∠QAH=45°,∵∠AQP=∠ACB,∴△CAB∽△QAN,∴=,即=,∴AN=,∴ON=3﹣=,∴N(,0),又Q(2,﹣1),∴直线PQ解析式为:y=3x﹣7,联立方程组,解得:,;∴P(5,8);(3)如图(3)作BM⊥AC于M,当点D在线段CM上时,则∠ADB=3∠ACB,∴∠CBD=2∠ACB,作∠CBD的平分线BE交CD于点E,∴∠CBD=2∠CBE,∴∠ACB=∠CBE,∴BE=CE,∵y=x2﹣4x+3,∴A(3,0),B(1,0),C(0,3),∴直线AC的解析式为y=﹣x+3,∠OAC=∠OCA=45°,设E(a,﹣a+3),则(a﹣1)2+(a﹣3)2=a2+a2,解得:a=,∴E(,),设D(m,﹣m+3),∵∠BCD=∠EBD,∠BDC=∠EDB,∴△BCD∽△EBD,∴BD2=CD•ED,∴(m﹣1)2+(m﹣3)2=(m﹣)•m,解得:m=,∴D(,).11.如图,抛物线y=(x﹣3)(x﹣2a)交x轴于A、B两点(点A在点B的左侧),=.(1)求抛物线的函数表达式;(2)如图①,连接BC,点P在抛物线上,且∠BCO=∠PBA.求点P的坐标;(3)如图②,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点,tan∠AMN=2,点M到x轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.解:(1)把y=0代入抛物线y=(x﹣3)(x﹣2a),得x=3或x=2a,∵点A在点B的左侧,∴A(2a,0),B(3,0),∵∴∴a=﹣1∴抛物线的函数表达式为:y=x2﹣x﹣6;(2)如图①,作线段BC的垂直平分线交y轴于点D,此时DC=DB∵DC=DB,∴∠DCB=∠DBC,∴∠ODB=∠DCB+∠DBC=2∠BCO,∵∠BCO=∠PBA∴∠PBA=2∠BCO,∴∠ODB=∠PBA,∴tan∠ODB=tan∠PBA,设P(m,m2﹣m﹣6),DC=DB=n,∵C(0,﹣6),B(3,0),∴OC=6,OB=3,∴OD=6﹣n,在Rt△BOD中,(6﹣n)2+32=m2,解得,∴,∵tan∠ODB=tan∠PBA∴即,解得,∴∴点P的坐标为;(3)MN的为定值,定值为5∵A(﹣2,0),B(3,0),点M到x轴的距离为2L∴,=5L∵S△AMN=S△AMN∴S△ABM∵△ABM和△AMN同底AM,∴点B、N到直线AM的距离相等,∴AM∥BN,∴∠MAN=∠ANB,∠AMB=∠MBN,∠ABC=∠MAB∴∠ANB=∠MBN∴∠MAN=∠AMB∵tan∠ABC===2,tan∠AMN=2∴△MAB≌△AMN(ASA),∴MN=AB=5∴MN的为定值,定值为5.12.在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D.(1)求抛物线的解析式;(2)点P为直线CD上的一个动点,连接BC;①如图1,是否存在点P,使∠PBC=∠BCO?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由;②如图2,点P在x轴上方,连接PA交抛物线于点N,∠PAB=∠BCO,点M在第三象限抛物线上,连接MN,当∠ANM=45°时,请直接写出点M的坐标.解:(1)y=ax2+bx﹣3=a(x+3)(x﹣1),解得:a=1,故抛物线的表达式为:y=x2+2x﹣3;(2)由抛物线的表达式知,点C、D的坐标分别为(0,﹣3)、(﹣1,﹣4),由点C、D的坐标知,直线CD的表达式为:y=x﹣3①;tan∠BCO=,则cos∠BCO=;①当点P(P′)在点C的右侧时,∵∠P'BC=∠BCO,故P′B∥y轴,则点P′(1,﹣2);当点P在点C的左侧时,设直线PB交y轴于点H,过点H作HN⊥BC于点N,∵∠P'BC=∠BCO,∴△BCH为等腰三角形,则BC=2CH•cos∠BCO=2×CH×=,解得:CH=,则OH=3﹣CH=,故点H(0,﹣),由点B、H的坐标得,直线BH的表达式为:y=x﹣②,联立①②并解得:,故点P的坐标为(﹣5,﹣8);②∵∠PAB=∠BCO,而tan∠BCO=,故设直线AP的表达式为:y=x+s,将点A的坐标代入上式并解得:s=1,故直线AP的表达式为:y=x+1③,联立抛物线与③并解得:,故点N(,);设△AMN的外接圆为圆R,当∠ANM=45°时,则∠ARM=90°,设圆心R的坐标为(m,n),∵∠GRA+∠MRH=90°,∠MRH+∠RMH=90°,∴∠RMH=∠GAR,∵AR=MR,∠AGR=∠RHM=90°,∴△AGR≌△RHM(AAS),∴AG=m+3=RH,RG=﹣n=MH,∴点M(m+n,n﹣m﹣3),将点M的坐标代入抛物线表达式得:n﹣m﹣3=(m+n)2+2(m+n)﹣3④,由题意得:AR=NR,即(m+3)2+n2=(m﹣)2+(﹣n)2⑤,联立④⑤并解得:,故点M(﹣,﹣).13.如图1,抛物线C:y=ax2+bx经过点A(﹣4,0)、B(﹣1,3)两点,G是其顶点,将抛物线C绕点O旋转180°,得到新的抛物线C′.(1)求抛物线C的函数解析式及顶点G的坐标;(2)如图2,直线l:y=kx﹣经过点A,D是抛物线C上的一点,设D点的横坐标为m(m<﹣2),连接DO并延长,交抛物线C′于点E,交直线l于点M,若DE=2EM,求m的值;(3)如图3,在(2)的条件下,连接AG、AB,在直线DE下方的抛物线C上是否存在点P,使得∠DEP=∠GAB?若存在,求出点P的横坐标;若不存在,请说明理由.解:(1)将A(﹣4,0)、B(﹣1,3)代入y=ax2+bx中,得解得∴抛物线C解析式为:y=﹣x2﹣4x,配方,得:y=﹣x2﹣4x=﹣(x+2)2+4,∴顶点为:G(﹣2,4);(2)∵抛物线C绕点O旋转180°,得到新的抛物线C′.∴新抛物线C′的顶点为:G′(2,﹣4),二次项系数为:a′=1∴新抛物线C′的解析式为:y=(x﹣2)2﹣4=x2﹣4x将A(﹣4,0)代入y=kx﹣中,得0=﹣4k﹣,解得k=,∴直线l解析式为y=x﹣,设D(m,﹣m2﹣4m),∵D、E关于原点O对称,∴OD=OE∵DE=2EM∴OM=2OD,过点D作DF⊥x轴于F,过M作MR⊥x轴于R,∴∠OFD=∠ORM,∵∠DOF=∠MOR∴△ODF∽△OMR∴===2∴OR=2OF,RM=2DF∴M(﹣2m,2m2+8m)∴2m2+8m=•(﹣2m)﹣,解得:m1=﹣3,m2=,∵m<﹣2∴m的值为:﹣3;(3)由(2)知:m=﹣3,∴D(﹣3,3),E(3,﹣3),OE=3,如图3,连接BG,在△ABG中,∵AB2=(﹣1+4)2+(3﹣0)2=18,BG2=2,AG2=20∴AB2+BG2=AG2∴△ABG是直角三角形,∠ABG=90°,∴tan∠GAB===,∵∠DEP=∠GAB∴tan∠DEP=tan∠GAB=,在x轴下方过点O作OH⊥OE,在OH上截取OH=OE=,过点E作ET⊥y轴于T,连接EH交抛物线C于点P,点P即为所求的点;∵E(3,﹣3),∴∠EOT=45°∵∠EOH=90°∴∠HOT=45°∴H(﹣1,﹣1),设直线EH解析式为y=px+q,则,解得∴直线EH解析式为y=﹣x,解方程组,∴x=或,∴点P的横坐标为:或.14.已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x 轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.(1)求抛物线的表达式;(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,求tan∠CPA的值;(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB?若存在,求出点E的坐标;若不存在,请说明理由.解:(1)∵抛物线y=ax2+bx+5与x轴交于点A(1,0),B(5,0),∴,解得.∴抛物线的解析式为y=x2﹣6x+5.(2)∵A(1,0),B(5,0),∴OA=1,AB=4.∵AC=AB且点C在点A的左侧,∴AC=4.∴CB=CA+AB=8.。
二次函数综合题--二次函数与线段有关的问题(原卷版)-中考数学重难点题型专题汇总

二次函数综合题-中考数学重难点题型二次函数与线段有关的问题(专题训练)1.小聪设计奖杯,从抛物线形状上获得灵感,在平面直角坐标系中画出截面示意图,如图1,杯体ACB 是抛物线的一部分,抛物线的顶点C 在y 轴上,杯口直径4AB =,且点A ,B 关于y 轴对称,杯脚高4CO =,杯高8DO =,杯底MN 在x 轴上.(1)求杯体ACB 所在抛物线的函数表达式(不必写出x 的取值范围).(2)为使奖杯更加美观,小敏提出了改进方案,如图2,杯体A CB ''所在抛物线形状不变,杯口直径//A B AB '',杯脚高CO 不变,杯深CD '与杯高OD '之比为0.6,求A B ''的长.2.如图1,隧道截面由抛物线的一部分AED 和矩形ABCD 构成,矩形的一边BC 为12米,另一边AB 为2米.以BC 所在的直线为x 轴,线段BC 的垂直平分线为y 轴,建立平面直角坐标系xOy ,规定一个单位长度代表1米.E (0,8)是抛物线的顶点.(1)求此抛物线对应的函数表达式;(2)在隧道截面内(含边界)修建“”型或“”型栅栏,如图2、图3中粗线段所示,点1P ,4P 在x 轴上,MN 与矩形1234PP P P 的一边平行且相等.栅栏总长l 为图中粗线段12PP ,23P P ,34P P ,MN 长度之和.请解决以下问题:(ⅰ)修建一个“”型栅栏,如图2,点2P ,3P 在抛物线AED 上.设点1P的横坐标为()06m m <≤,求栅栏总长l 与m 之间的函数表达式和l 的最大值;(ⅱ)现修建一个总长为18的栅栏,有如图3所示的修建“”型或“”型栅型两种设计方案,请你从中选择一种,求出该方案下矩形1234P P P P 面积的最大值,及取最大值时点1P 的横坐标的取值范围(1P 在4P 右侧).3.在平面直角坐标系xoy 中,已知抛物线y =-x 2+bx +c 经过点A (-1,0)和点B (0,3),顶点为C ,点D 在其对称轴上,且位于点C 下方,将线段DC 绕点D 按顺时针方向旋转90°,点C 落在抛物线上的点P 处.(1)求抛物线的解析式;(2)求点P 的坐标;(3)将抛物线平移,使其顶点落在原点O ,这时点P 落在点E 的位置,在y 轴上是否存在点M ,使得MP +ME 的值最小,若存在,求出点M 的坐标;若不存在,请说明理由.4.如图,在平面直角坐标系中,抛物线223y x x =--与x 轴相交于点A 、B (点A 在点B 的左侧),与y 轴相交于点C ,连接,AC BC .(1)求线段AC 的长;(2)若点Р为该抛物线对称轴上的一个动点,当PA PC =时,求点P 的坐标;(3)若点M 为该抛物线上的一个动点,当BCM 为直角三角形时,求点M 的坐标.5.如图,已知抛物线2:L y x bx c =++经过点(0,5),(5,0)A B -.(1)求,b c 的值;(2)连结AB ,交抛物线L 的对称轴于点M .①求点M 的坐标;②将抛物线L 向左平移(0)m m >个单位得到抛物线1L .过点M 作//MN y 轴,交抛物线1L 于点N .P 是抛物线1L 上一点,横坐标为1-,过点P 作//PE x 轴,交抛物线L 于点E ,点E 在抛物线L 对称轴的右侧.若10PE MN +=,求m 的值.6.如图,在平面直角坐标系中,四边形ABCD 为正方形,点A ,B 在x 轴上,抛物线2y x bx c =++经过点B ,()4,5D -两点,且与直线DC 交于另一点E .(1)求抛物线的解析式;(2)F 为抛物线对称轴上一点,Q 为平面直角坐标系中的一点,是否存在以点Q ,F ,E ,B 为顶点的四边形是以BE 为边的菱形.若存在,请求出点F 的坐标;若不存在,请说明理由;(3)P 为y 轴上一点,过点P 作抛物线对称轴的垂线,垂足为M ,连接ME ,BP .探究EM MP PB ++是否存在最小值.若存在,请求出这个最小值及点M 的坐标;若不存在,请说明理由.7.如图1,在平面直角坐标系xOy 中,抛物线2y ax bx c =++与x 轴分别相交于A 、B 两点,与y 轴相交于点C ,下表给出了这条抛物线上部分点(,)x y 的坐标值:x…1-0123…y …03430…(1)求出这条抛物线的解析式及顶点M 的坐标;(2)PQ 是抛物线对称轴上长为1的一条动线段(点P 在点Q 上方),求AQ QP PC ++的最小值;(3)如图2,点D 是第四象限内抛物线上一动点,过点D 作DF x ⊥轴,垂足为F ,ABD △的外接圆与DF 相交于点E .试问:线段EF 的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.8.已知抛物线23y ax bx =+-与x 轴相交于(1,0)A -,(3,0)B 两点,与y 轴交于点C ,点(,0)N n 是x 轴上的动点.(1)求抛物线的解析式;(2)如图1,若3n <,过点N 作x 轴的垂线交抛物线于点P ,交直线BC 于点G .过点P 作PD BC ⊥于点D ,当n 为何值时,PDG BNG ≌;(3)如图2,将直线BC 绕点B 顺时针旋转,使它恰好经过线段OC 的中点,然后将它向上平移32个单位长度,得到直线1OB .①1tan BOB ∠=______;②当点N 关于直线1OB 的对称点1N 落在抛物线上时,求点N 的坐标.9.如图,在平面直角坐标系xOy 中,抛物线213442y x x =-++与两坐标轴分别相交于A ,B ,C 三点(1)求证:∠ACB=90°(2)点D 是第一象限内该抛物线上的动点,过点D 作x 轴的垂线交BC 于点E ,交x 轴于点F .①求DE+BF 的最大值;②点G 是AC 的中点,若以点C ,D ,E 为顶点的三角形与 AOG 相似,求点D 的坐标.10.如图,抛物线(1)()y x x a =+-(其中1a >)与x 轴交于A 、B 两点,交y 轴于点C .(1)直接写出OCA ∠的度数和线段AB 的长(用a 表示);(2)若点D 为ABC 的外心,且BCD △与ACO △4,求此抛物线的解析式;(3)在(2)的前提下,试探究抛物线(1)()y x x a =+-上是否存在一点P ,使得CAP DBA ∠=∠若存在,求出点P 的坐标;若不存在,请说明理由.11.如图,二次函数y =ax 2+bx+x 的图象过O (0,0)、A (1,0)、B (32,(1)求二次函数的解析式;(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.12.如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,AC,BC.M为线段OB上的一个动点,过点M作PM⊥x轴,交抛物线于点P,交BC于点Q.(2)过点P作PN⊥BC,垂足为点N.设M点的坐标为M(m,0),请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?(3)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.13.在平面直角坐标系xOy中,直线y=−12x+5与x轴、y轴分别交于点A、B(如图).抛物线y=ax2+bx(a≠0)经过点A.(2)如果抛物线y=ax2+bx经过线段AB上的另一点C,且BC=5,求这条抛物线的表达式;(3)如果抛物线y=ax2+bx的顶点D位于△AOB内,求a的取值范围.14,若一次函数y=﹣3x﹣3的图象与x轴,y轴分别交于A,C两点,点B的坐标为(3,0),二次函数y=ax2+bx+c的图象过A,B,C三点,如图(1).(1)求二次函数的表达式;(2)如图(1),过点C作CD∥x轴交抛物线于点D,点E在抛物线上(y轴左侧),若BC 恰好平分∠DBE.求直线BE的表达式;(3)如图(2),若点P在抛物线上(点P在y轴右侧),连接AP交BC于点F,连接BP,S△BFP=mS△BAF.①当m=12时,求点P的坐标;②求m的最大值.15.在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣3,0)、B(1,0),交y 轴于点N,点M为抛物线的顶点,对称轴与x轴交于点C.(1)求抛物线的解析式;(2)如图1,连接AM,点E是线段AM上方抛物线上一动点,EF⊥AM于点F,过点E 作EH⊥x轴于点H,交AM于点D.点P是y轴上一动点,当EF取最大值时:①求PD+PC的最小值;②如图2,Q点为y轴上一动点,请直接写出DQ+14OQ的最小值.16.已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(﹣1,0),交y轴于点C.(1)求抛物线的解析式和顶点坐标;(2)如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴、y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;(3)如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.17.已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,C为抛物线的顶点,抛物线的对称轴交x轴于点D,连结BC,且tan∠CBD=43,如图所示.(1)求抛物线的解析式;(2)设P是抛物线的对称轴上的一个动点.①过点P作x轴的平行线交线段BC于点E,过点E作EF⊥PE交抛物线于点F,连结FB、FC,求△BCF的面积的最大值;②连结PB,求35PC+PB的最小值.。
2020年中考数学压轴解答题10 二次函数与线段关系及最值定值问题(学生版)

备战2020中考数学之解密压轴解答题命题规律专题10 二次函数与线段关系及最值定值问题【类型综述】图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用. 一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【方法揭秘】由勾股定理产生的函数关系,在两种类型的题目中比较常用.类型一,已知“边角边”,至少一边是动态的,求角的对边.如图1,已知点A 的坐标为(3, 4),点B 是x 轴正半轴上的一个动点,设OB =x ,AB =y ,那么我们在直角三角形ABH 中用勾股定理,就可以得到y 关于x 的函数关系式.类型二,图形的翻折.已知矩形OABC 在坐标平面内如图2所示,AB =5,点O 沿直线EF 翻折后,点O 的对应点D 落在AB 边上,设AD =x ,OE =y ,那么在直角三角形AED 中用勾股定理就可以得到y 关于x 的函数关系式.图1 图2【典例分析】【例1】如图①,矩形ABCD 中,2,5,1AB BC BP ===,090MPN ∠=,将MPN ∠绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB (或AD )于点E ,PN 交边AD (或CD )于点F .当PN 旋转至PC 处时,MPN ∠的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D ,此时ABP ∆是否与PCD ∆相似?并说明理由;(2)类比探究:如图③,在旋转过程中,PEPF的值是否为定值?若是,请求出该定值;若不是,请说明理由; (3)拓展延伸:设AE t =时,EPF ∆的面积为S ,试用含t 的代数式表示S ;①在旋转过程中,若1t =时,求对应的EPF ∆的面积; ②在旋转过程中,当EPF ∆的面积为4.2时,求对应的t 的值.【例2】如图1,在矩形ABCD 中,AB =8,AD =10,E 是CD 边上一点,连接AE ,将矩形ABCD 沿AE 折叠,顶点D 恰好落在BC 边上点F 处,延长AE 交BC 的延长线于点G . (1)求线段CE 的长;(2)如图2,M ,N 分别是线段AG ,DG 上的动点(与端点不重合),且∠DMN =∠DAM ,设AM =x ,DN =y . ①写出y 关于x 的函数解析式,并求出y 的最小值;②是否存在这样的点M ,使△DMN 是等腰三角形?若存在,请求出x 的值;若不存在,请说明理由.【例3】抛物线2(0)y ax bx c a =++≠与x 轴交于,A B 两点(点A 在点B 的左侧),与y 轴交于点(0,4)C -.已知(2,0)A -,抛物线的对称轴l 交x 轴于点(1,0)D . (1)求出,,a b c 的值;(2)如图1,连接BC ,点P 是线段BC 下方抛物线上的动点,连接,PB PC .点,M N 分别在y 轴,对称轴l 上,且MN y ⊥轴.连接,AM PN .当PBC ∆的面积最大时,请求出点P 的坐标及此时AM MN NP ++的最小值;(3)如图2,连接AC ,把AOC ∆按照直线y x =对折,对折后的三角形记为A OC ∆'',把A OC ∆''沿着直线BC 的方向平行移动,移动后三角形的记为A O C ∆''''',连接DA '',DC '',在移动过程中,是否存在DA C ∆''''为等腰三角形的情形?若存在,直接写出点C ''的坐标;若不存在,请说明理由.【例4】如图在锐角△ABC 中,BC =6,高AD =4,两动点M 、N 分别在AB 、AC 上滑动(不包含端点),且MN ∥BC,以MN 为边长向下作正方形MPQN,设MN =x,正方形MPQN 与△ABC 公共部分的面积为y . (1)如图(1),当正方形MPQN 的边P 恰好落在BC 边上时,求x 的值;(2)如图(2),当PQ 落△ABC 外部时,求出y 与x 的函数关系式(写出x 的取值范围)并求出x 为何值时y 最大,最大是多少?【例5】如图,抛物线y=12-x2+mx+m(m>0)的顶点为A,交y轴于点C.(1)求出点A的坐标(用含m的式子表示);(2)若直线y=﹣x+n经过点A,与抛物线交于另一点B,证明:AB的长是定值;(3)连接AC,延长AC交x轴于点D,作直线AD关于x轴对称的直线,与抛物线分别交于E、F两点.若∠ECF=90°,求m的值.【例6】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B 点的坐标为(3,0),与y轴交于点C(0,﹣3).(1)求二次函数解析式;(2)若点Q为抛物线上一点,且S△ABQ=12S△ACQ,求点Q的坐标;(3)若直线l:y=mx+n与抛物线有两个交点M,N(M在N的左边),P为抛物线上一动点(不与M,N重合).过P作PH平行于y轴交直线l于点H,若HM HNHP⋅=5,求m的值.【变式训练】1.如图,抛物线y =ax 2+4x +c (a ≠0)与反比例函数y =5x的图象相交于点B ,且点B 的横坐标为5,抛物线与y 轴交于点C (0,6),A 是抛物线的顶点,P 和Q 分别是x 轴和y 轴上的两个动点,则AQ +QP +PB 的最小值为_____.2.如图,在平面直角坐标系中,菱形OABC 的顶点 A 在 x 轴正半轴上,顶点 C 的坐标为(4,3),D 是抛物线 y =﹣x 2+6x 上一点,且在x 轴上方,则△BCD 面积的最大值为__________3.己知抛物线2114y x =+具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x 轴的距离始终相等,如图,点M 的坐标为(3,3),P 是抛物线2114y x =+上一个动点,则△PMF 周长的最小值是__________.4.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =16cm ,AD 为BC 边上的高,动点P 从点A 出发,沿A →D 方向以2/s 的速度向点D 运动,过P 点作PE ∥BC 交AC 于点E ,过E 点作EF ⊥BC 于点F ,设△ABP 的面积为S 1,四边形PDFE 的面积为S 2,则点P 在运动过程中,S 1+S 2的最大值为______.5.在平面直角坐标系中,已知()A 2,4、()P 1,0,B 为y 轴上的动点,以AB 为边构造ABC V ,使点C 在x 轴上,BAC 90.M ∠=o 为BC 的中点,则PM 的最小值为______.6.如图,在平面直角坐标系中,抛物线y=﹣x 2+4x 与x 轴交于点A,点M 是x 轴上方抛物线上一点,过点M 作MP ⊥x 轴于点P,以MP 为对角线作矩形MNPQ,连结NQ,则对角线NQ 的最大值为_________.7.如图,在平面直角坐标系中,过A (-1,0)、B (3,0)两点的抛物线交y 轴于点C,其顶点为点D,设△ACD 的面积为S 1,△ABC 的面积为S 2.小芳经探究发现:S 1︰S 2是一个定值.这个定值为________.8.如图,在平面直角坐标系中,有二次函数23333y x x =--+,顶点为H ,与x 轴交于A 、B 两点(A 在B 左侧),易证点H 、B 关于直线3:33l y x =+对称,且A 在直线l 上.过点B 作直线//BK AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连接HN 、NM 、MK ,则HN NM MK ++的最小值为________9.如图,抛物线2(0)y ax bx c a =++≠与直线1y x =+相交于(1,0)A -,(4,)B m 两点,且抛物线经过点(5,0)C(1)求抛物线的解析式.(2)点P 是抛物线上的一个动点(不与点A 点B 重合),过点P 作直线PD x ⊥轴于点D ,交直线AB 于点E .当2PE ED =时,求P 点坐标;(3)如图所示,设抛物线与y 轴交于点F ,在抛物线的第一象限内,是否存在一点Q ,使得四边形OFQC 的面积最大?若存在,请求出点Q 的坐标;若不存在,说明理由.10.如图,在矩形ABCD 中,AB=18,AD=12,点M 是边AB 的中点,连结DM,DM 与AC 交于点G ,点E,F 分别是CD 与DG 上的点,连结EF,(1)求证:CG=2AG .(2)若DE=6,当以E,F,D 为顶点的三角形与△CDG 相似时,求EF 的长.(3)若点E 从点D 出发,以每秒2个单位的速度向点C 运动,点F 从点G 出发,以每秒1个单位的速度向点D 运动.当一个点到达,另一个随即停止运动.在整个运动过程中,求四边形CEFG 的面积的最小值.11.如图①,抛物线y=a(x 2+2x-3)(a≠0)与x 轴交于点A 和点B,与y 轴交于点C,且OC=OB.(1)直接写出点B 的坐标是( , ),并求抛物线的解析式;(2)设点D 是抛物线的顶点,抛物线的对称轴是直线l,连接BD,线段OC 上的点E 关于直线l 的对称点E'恰好在线段BD 上,求点E 的坐标;(3)若点F 为抛物线第二象限图象上的一个动点,连接BF,CF,当△BCF 的面积是△ABC 面积的一半时,求此时点F 的坐标.12.如图,抛物线y =﹣x 2+mx +2与x 轴交于点A ,B ,与y 轴交于点C ,点A 的坐标为(1,0) (1)求抛物线的解析式(2)在抛物线的对称轴l 上找一点P ,使PA +PC 的值最小,求出点P 的坐标 (3)在第二象限内的抛物线上,是否存在点M ,使△MBC 的面积是△ABC 面积的12?若存在,求出点M 的坐标,若不存在,请说明理由.13.如图,抛物线212y x mx n =++交x 轴于A 、B 两点,直线y=kx+b 经过点A,与这条抛物线的对称轴交于点M (1,2),且点M 与抛物线的顶点N 关于x 轴对称.(1)求抛物线的函数关系式;(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;(3)在(2)的条件下,求△AQC面积的最大值.14.如图,抛物线y=﹣12x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.(1)求抛物线的解析式;(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.15.如图,在平面直角坐标系中,点A在抛物线y=- x2 + 4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB 的长.(2)点P 为线段AB .上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H,点F 为y 轴上一点,当∆PBE 的面积最大时,求PH + HF + 12FO 的最小值. (3)在(2)中,PH+HF+12方FO 取得最小值时,将∆CFH 绕点C 顺时针旋转60°后得到∆CF'H',过点F'作CF'的垂线与直线AB 交于点Q,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.16.已知,二次函数24y x x c =-+的图像与x 轴的一个交点为O(0,0),点P (m,0)是x 轴正半轴上的一个动点.(1)如图1,求二次函数的图像与x 轴另一个交点的坐标; (2)如图2,过点P 作x 轴的垂线交直线33y x =与点C,交二次函数图像于点D, ①当PD=2PC 时,求m 的值;如图3,已知A (3,-3)在二次函数图像上,连结AP,求12AP OP +的最小值;(3如图4,在第(2)小题的基础上,作直线OD,作点C关于直线OD的对称点C’,当C’落在坐标轴上时,请直接写出m的值.17.如图1,已知抛物线y =ax2+bx +c 经过A(-3,0),B (1,0 ),C (0,3 )三点,其顶点为D,对称轴是直线l , l 与x 轴交于点H .(1)求该抛物线的解析式;(2)若点P 是该抛物线对称轴l 上的一个动点,求∆PBC 周长的最小值;(3)如图2,若 E 是线段AD 上的一个动点(E 与A, D 不重合),过 E 点作平行于y 轴的直线交抛物线于点 F ,交x 轴于点G ,设点 E 的横坐标为m ,四边形AODF 的面积为S 。
中考数学总复习《二次函数中的角度问题存在性问题》专题训练-附答案
中考数学总复习《二次函数中的角度问题存在性问题》专题训练-附答案学校:___________班级:___________姓名:___________考号:___________1.如图,抛物线与x 轴相交于原点和点()4,0A ,在第一象限内与直线y x =交于点B ()5,5,抛物线的顶点为C 点.(1)求抛物线的解析式和顶点C 的坐标;(2)点()3,M m 在抛物线上,连接MO MB ,,求MOB △的面积;(3)抛物线上是否存在点D ,使得DOB OBC ∠=∠?若存在,求出所有点D 的坐标;若不存在,请说明理由. 2.综合与探究如图,已知抛物线238y x bx c =-++与x 轴相交于()4,0A -,B 两点(点A 在点B 的左侧),与y 轴相交于点()0,3C ,连接AC .(1)求该抛物线的解析式及对称轴;(2)若过点B 的直线与抛物线相交于另一点D ,当ABD BAC ∠=∠时,求直线的解析式; (3)在(2)的条件下,当点D 在x 轴下方时,连接AD ,此时在y 轴左侧的抛物线上存在点P ,使23BDP ABD S S =△△,请直接写出所有符合条件的点P 的坐标.3.如图,抛物线2y ax bx c =++与x 轴交于点A 、B ,与y 轴交于点()0,2C -,2OC OA =和1tan 2ABC ∠=.直线l :()0y kx n k =+>与抛物线交于M ,N 两点(点M 在点N 的左边).(1)求抛物线的解析式,并写出顶点坐标;(2)当直线l BC ∥时,若MON △的面积被y 轴分成的两个三角形的面积比为1:4时,求n 的值; (3)当0n =时,试在抛物线上找一定点P ,使得90MPN ∠=︒,求P 点坐标以及点P 到MN 的最大距离. 4.如图①,抛物线2y ax bx =+的顶点为()2,4D -.(1)求抛物线的解析式;(2)连接OD ,P 为x 轴上的动点,当AOD ∠与PDO ∠互余时,求点P 的坐标;(3)如图①,点M ,N 都在抛物线上,点M 位于第四象限,点N 位于第二象限,连接MN 分别交x 轴,y 轴于点E ,F ,连接OM ON 、,求证:若NOF MOE ∠=∠,则直线MN 经过一定点.5.如图,在平面直角坐标系中,抛物线2=23y x x --交x 轴于A B 、两点(点A 在点B 的左边),交y 轴于点C .(1)直接写出、、A B C 三点的坐标;(2)若抛物线上有一点,45D ACD ∠=︒,求点D 的坐标.(3)如图2,点P 是第一象限抛物线上一点,过点P 的直线(0)y mx n n =+<与抛物线交于另一点Q ,连接AP AQ 、,分别交y 轴于M N 、两点,若2OM ON ⋅=,探究,m n 之间的数量关系,并说明理由.6.如图,顶点坐标为(3,4)的抛物线2y ax bx c =++交x 轴于A ,B 两点,交y 轴于点()0,5C -.(1)求a ,b 的值;(2)已知点M 在射线CB 上,直线AM 与抛物线2y ax bx c =++的另一公共点是点P .①抛物线上是否存在点P ,满足:2:1=AM MP ,如果存在,求出点P 的横坐标;如果不存在,请说明理由; ①连接AC ,当直线AM 与直线BC 的夹角等于ACB ∠的2倍时,请直接写出点M 的坐标.7.如图,已知(2,0),(3,0)A B -,抛物线24y ax bx =++经过A 、B 两点,交y 轴于点C .点P 是第一象限内抛物线上的一点,点P 的横坐标为m .过点P 作PM x ⊥轴,垂足为点M ,PM 交BC 于点Q .过点P 作PN BC ⊥,垂足为点N .(1)求抛物线的函数表达式;(2)请用含m 的代数式表示线段PN 的长,并求出当m 为何值时PN 有最大值,最大值是多少?(3)连接PC ,在第一象限的抛物线上是否存在点P ,使得290BCO PCN ∠+∠=︒?若存在,请直接写出m 的值;若不存在,请说明理由.8.如图1,已知抛物线233y ax bx =++,与x 轴交于点()2,0A -,点()6,0B 与y 轴交于点C ,抛物线的顶点为M ,其对称轴与x 轴交于Q 点.(1)抛物线解析式为______,顶点M 的坐标为______; (2)判断MAB 的形状,并说明理曲;(3)如图2,点P 是线段MQ 上的一个动点(点P 与点M 、点Q 不重合),连结PA 和PB ,过点B 作BD AP ⊥,射线BD 交射线AP 于点D ,交抛物线于点E ;过点E 作EF AB ⊥,垂足为点F ,EF 交射线BP 于点G . ①当ABD ①EBF 时,请求出此时点P 的坐标; ①当135APB ∠=︒时,请你直接写出BFEG的值. 9.如图1,二次函数y =ax 2+bx +c 的图象交x 轴于点A (﹣1,0),B (3,0),交y 轴于点C (0,﹣3),直线l 经过点B .(1)求二次函数的表达式和顶点D 的坐标; (2)如图2,当直线l 过点D 时,求①BCD 的面积;(3)如图3,直线l 与抛物线有另一个交点E ,且点E 使得①BAC ﹣①CBE >45°,求点E 的横坐标m 的取值范围;(4)如图4,动点F 在直线l 上,作①CFG =45°,FG 与线段AB 交于点G ,连接CG ,当①ABC 与①CFG 相似,且S △CFG 最小时,在直线l 上是否存在一点H ,使得①FHG =45°存在,请求出点H 的坐标;若不存在,请说明理由.10.如图,已知抛物线2y ax bx c =++经过(1,0),(2,0),(0,2)A B C -三点,点D 在该抛物线的对称轴l 上.(1)求抛物线的表达式;(2)若DA DC =,求ADC ∠的度数及点D 的坐标;(3)若在(2)的条件下,点P 在该抛物线上,当PBC DAB ∠=∠时,请直接给出点P 的坐标. 11.如图,抛物线2y ax bx c =++经过()1,0A -,()3,0B 且与y 轴交于点()0,3C -.(1)求抛物线的函数表达式;(2)若点P 是x 轴的正半轴上一点1tan 3APC ∠=,求点P 的坐标;(3)当点P 是抛物线上第一象限上的点1tan 3APC ∠=,直接写出点P 的坐标为______.12.如图,平面直角坐标系中,抛物线24y x nx =-++过点()4,0A -,与y 轴交于点N ,与x 轴正半轴交于点B .直线l 过定点A .(1)求抛物线解析式;(2)连接AN ,BN ,直线l 交抛物线于另一点M ,当①MAN =①BNO 时,求点M 的坐标;(3)过点(),1T t -的任意直线EF (不与y 轴平行)与抛物线交于点E 、F ,直线BE 、BF 分别交y 轴于点P 、Q ,是否存在t 的值使得OP 与OQ 的积为定值?若存在,求t 的值,若不存在,请说明理由.13.抛物线y =ax 2+c (a <0)与x 轴交于A 、B 两点,顶点为C ,点P 在抛物线上,且位于x 轴上方.(1)如图1,若P (1,2),A (-3,0). ①求该抛物线的解析式;①若D 是抛物线上异于点P 一点,满足①DPO =①POB ,求点D 的坐标; (2)如图2,已知直线P A 、PB 与y 轴分别交于E 、F 两点.当点P 运动时,OE OFOC+是否为定值?若是,试求出该定值;若不是,请说明理由.14.如图1,直线y =ax ²+4ax +c 与x 轴交于点A (-6,0)和点B ,与y 轴交于点C ,且OC =3OB(1)直接写出抛物线的解析式及直线AC 的解析式;(2)抛物线的顶点为D ,F 为抛物线在第四象限的一点,直线AF 解析式为123y x =--,求①CAF -①CAD 的度数.(3)如图2,若点P 是抛物线上的一个动点,作PQ ①y 轴垂足为点Q ,直线PQ 交直线AC 于E ,再过点E 作x 轴的垂线垂足为R ,线段QR 最短时,点P 的坐标及QR 的最短长度.15.如图,在平面直角坐标系中,抛物线22y ax bx =++与x 轴交于1,0A ,()4,0B 两点,与y 轴交于点C .直线l :2y kx =+过点C .(1)求抛物线的解析式;(2)当直线l 经过点B 时,取线段BC 的中点M ,作直线l 的平行线,恰好与抛物线有一个交点P 时,判断以点P ,O ,M ,B 为顶点的四边形是什么特殊的平行四边形,并说明理由;(3)在直线l 上是否存在唯一一点Q ,使得90AQB ∠=︒?若存在,请求出此时l 的解析式;若不存在,请说明理由.参考答案:1.(1)24y x x =- ()2,4 (2)15(3)点D 的坐标为(7,21)或1313,39⎛⎫⎪⎝⎭;2.(1)233384y x x =--+,对称轴为直线=1x -(2)3342y x =-+或3342y x =-;(3)322222⎛⎫--- ⎪ ⎪⎝⎭,或12362262⎛⎫+--- ⎪ ⎪⎝⎭, 3.(1)213222y x x =-- (2)149n =(3)()3,2P - 134.(1)24y x x =-(2)()20,或()20-,5.(1)()1,0A -,()3,0B 和()0,3C - (2)()4,5D (3)23n m =-6.(1)-1;6 (2)①存在,5172+或5332+或5332-;①1317,66⎛⎫- ⎪⎝⎭;237,66⎛⎫- ⎪⎝⎭7.(1)222433y x x =-++(2)22655PN m m =-+,当32m =时,有最大值910(3)存在 74m =8.(1)233334y x x =-++和()2,43; (2)①MAB 为等边三角形 (3)①432,3⎛⎫ ⎪ ⎪⎝⎭;①12BF EG =.9.(1)二次函数的表达式为y =x 2﹣2x ﹣3,顶点D 的坐标为(1,﹣4) (2)2(3)﹣23<m <2(4)存在,点H 的坐标为:(65,185)或(95,185)10.(1)22y x x =-++(2)90ADC ∠=︒,点D 的坐标为11,22⎛⎫⎪⎝⎭(3)点P 的坐标为()1,2或15,24⎛⎫- ⎪⎝⎭11.(1)2=23y x x -- (2)点P 的坐标为()9,0 (3)点P 的坐标为()4,512.(1)234y x x =--+ (2)250,39⎛⎫- ⎪⎝⎭或266,525⎛⎫ ⎪⎝⎭(3)存在,4t =-13.(1)①21944y x =-+;①(-1,2)或(133,229-)(2)OE OFOC+是定值,定值为2.14.(1)抛物线的解析式为y =-12x ²-2x +6,直线BC 的解析式为y =x +6 (2)45°(3)点P 的坐标为(-2+10,3)或(-2-10,3),QR 的最短长度为3215.(1)215222y x x =-+;(2)菱形;(3)存在,122y x =-+或53224y x -+=+或53224y x --=+.。
二次函数图像中的几何问题
以抛物线上的三个点为顶点的三角形称为抛物线的内接三角形。已知内接三角形的三个顶点的坐标可以求出抛物线的表达式。
例2、已知抛物线与x轴交于点A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3),抛物线顶点为D,联结AD、AC、CD。
(1)求该抛物线的表达式;
(2)△ACD与△COB是否相似?如果相似,请给予证明;如果不相似,请说明理由。
(1)求A、B两点的坐标;(用m的代数式表示)
(2)如果平行四边行ABCD的顶点D在上述二次函数的图像上,求m的值。
四、综合问题
函数图像中的几何问题已成为历年中考的热门考题,而二次函数的图像与几何图形的结合更是考查的重点,因此,熟悉这类问题的解题思路是必须具备的能力。
下面的例题是抛物线与平行四边、相似三角形的综合。
为。
7、抛物线的顶点为M(2,3),且经过点A(0,-1),若该抛物线上另有点B(m,-1),则m的值为。
8、若抛物线 与x轴交于点A、B,与y轴交于点C,且△ABC是等腰直角三角形,则a、c之间的数量关系是。
9、若抛物线的顶点A在x轴上,且抛物线经过B(0,2),△AOB为等腰三角形,则该抛物线的表达式
(3)若直线AB交y轴于点E,在直线AB上找点F,使△CEF∽△AOM,求点F的坐标。
小结:本题涉及的几何图形是:内接于抛物线与直线之间的平行四边形和相似三角形。解题的关键是:(1)函数 图像上的点的坐标可以表示为P(x,f(x)),即用解析式来代替纵坐标;(2)用垂直于x轴的直线去截函数 和 图像,则截得的线段长PQ=∣f(x)-g(x)∣(其中x为点P或点Q的横坐标)。
精练12+1:
1、若抛物线 与x轴相交于点A、B,顶点为P,则△PAB是()
【最新】数学:二次函数与线段关系问题教案教学设计
【课堂教学备课】唤醒主体 以情激情 以诱达思 启智悟道(生本、生成、生动)九年级(下)数学教案课题:二次函数与线段关系问题主备: 预授时间: 年 月 日 第 周【教学目标】通过本节课的教学,学生能处理二次函数中出现的有关线段的关系问题【教学重点】掌握并会运用线段关系的已知条件解决二次函数有关问题【教学难点】根据线段关系寻求正确的解决方法【教学方法】归纳、探究、引导【教学过程】(一)情景创设,引入新课提问:在解几何题中,往往出现类似AB=CD 这样的已知条件,当看到这样的已知条件时,我们会想到哪些定理或处理方法?(根据这一问题创设一激起想知道的问题情境)(等腰三角形、垂直平分线、中位线等,答对其一均给予表扬)线段关系作为已知条件往往在综合题中呈现有哪些呈现方式呢?面积关系、线段相等关系、线段份数或倍数关系知识联系(结合具体图形,图形教师可随堂画出,问题回答让学生思考教师逐渐补充)面积关系:如S △PAE :S △AEF =2:3 PE :EF=2:3相等关系:AB=CD 中位线等份数或倍数关系:AB=32 CD 线段成比例构平行线,可作为相似对应边成比例的条件根号关系:AB=3CD 可联想到线段的平方关系、可构成特殊三角形 (习惯性地寻找线段关系、特殊角)(二)引入新课例:如图,抛物线y=-x 2-4x+5交坐标轴于A 、B 、C 三点,点P 在抛物线上,PF ⊥x 轴于F 点,交AC 于E 点,若S △PAE :S △AEF =2:3,求P 点坐标分析引导:题目中的主要信息是什么?条件S △PAE :S △AEF =2:3可得出什么结论? PE :EF=2:3这种关系通常怎样处理?P 、E 横坐标相同,纵坐标有关系,如何求P例:如图,抛物线y=x 2-4x+3与y 轴交于点C ,P 在x 轴上,PC 交抛物线于M ,若PM=2CM ,求P 点坐标 y分析引导:根据上面归纳,条件PM=2CM 怎么用?C M如何构成比例关系?O A B P x根据比例关系,可先求哪条线段?这样一来,便可求哪一点坐标?如何求P 点坐标?(学生只需方法,不需解答过程) 例:如图,抛物线y= 21 (x-2)2与x 轴交于点A ,与y 轴交于点C ,直线y=x+n 交抛物线于M 、N ,M 点的横坐标为1,若点F 在MN 上,FP ⊥x 轴于P ,交抛物线于E ,且EF=EP ,求E 点坐标分析引导:题中主要信息除了抛物线这一条件外 y还有哪些信息? C F N M 点横坐标为1可以得出哪些结论?EF=EP 根据归纳可采取什么方式来解决? M E 可得了出E 、F 点坐标中存在几个未知数?可找到几个方程?O A P x六、小结:1、回顾线段关系的处理方法2、如何正确选择方法七、作业练习(2008武汉市四月调考数学试题)在平面直角坐标系中,抛物线y =ax Z +2ax 一b 与x 轴交与A,B 两点,与y 轴正半轴交于C 点,且A (-4,0) ,0C =2OB:(1)求此抛物线的解析式;(2)如图1,作矩形ABCD ,使DE 过点C,点P 是AB 边上的一动点,连接PE,作PH 上PE 交 BD 子点H.设线段PB 的长为x,线段BH 的长为1/2,当P 点运动时,求y 与x 的函数关系式并写出自变量x 的取值范围.在同一直角坐标系中,试函数的图象与(1)DE 的抛物线中Y ≧ 0的部分有何关系?(3)如图2,在(1)的抛物线中,点T 其顶点,L 为抛物线上一动点(不与T 重合),取点N(-1,0),作MN ⊥LN 且MN=2/3LN(点M,N,L 按逆时针顺序)当点L 在抛物线上运动时,直线AM 、TL 是否存在某种确定的位置关系?若存在写出你的证明结论;若不存在,请说明理由.八、教学反思课堂关注情境与问题,阅读与思维,互动与引导,练习与反馈四大要素。
二次函数与特殊角问题(定弦定角类)
二次函数角度问题(定弦定角类)针对所求点为角的顶点我们在隐圆篇讲过一类动点轨迹问题,“定角+定对边”可确定动点轨迹为圆弧。
接下来我们用隐圆来解决二次函数中的一类角度问题。
首先看下面两个小题。
1.点A(﹣5,0),B(1,0),点C在y轴上.若∠ACB=60°,则点C的纵坐标为___________。
分析:AB是定长,∠ACB=60°(定角),所以点C的轨迹为一段弧,又点C在y轴上,所以以AB为底边,∠ADB=120°为顶角作等腰三角形。
再以D为圆心,AD(或BD)为半径作圆,以y轴的交点即为点C。
注意符合题意的点C有两个。
接下来就是如何计算点C的坐标了。
在此提供两种方法:(1)利用垂径定理求解,从点D分别作x轴和y轴的垂线。
角度特殊,计算简单;(2)求半径(AD或BD),设点C(0,y)利用两点距离公式CD=半径求解。
2.如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为.分析:本题的关键在于求解AD。
由于BC定边,∠BAC=45°,满足定角定对边模型。
可用辅助圆求解。
先定圆心,以BC为底边,90°为顶角作等腰三角形BOC。
点O即为辅助圆的圆心。
利用垂径定理可求AD。
总结:以上2题解法不唯一,但辅助圆是一种相对简便的方法。
尤其是前面已经有了隐圆轨迹模型的学习,再用辅助圆来解答,让学生进一步加深对模型的认知。
例1、如图,抛物线y=过点A(3,2),点M为抛物线的顶点,在y轴上是否存在点Q,使∠AQM=45°?若存在,求点Q的坐标;若不存在,请说明理由.分析:先作图再计算。
所求点Q是∠AQM的顶点,可用辅助圆进行求解。
AM为辅助圆的弦,那圆心该如何确定呢?考虑到∠AQM=45°(圆周角),那么弧AM所对的圆心角为90°,过点A作AB⊥直线x=1,垂足为点B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用标准
精彩文档
y
x
EDFQPCB
A
O
(第27题图2)
y
x
EDFQPCB
A
O
(第27题图3)
与线段有关的问题
类型一:已知共线的线段关系-----------------转化为A字型或8字型
1.在平面直角坐标系中,点O为坐标原点,抛物线2()8yaxh(a≠0,a、h为常数)与x轴
交于点A、B(点A在点B的左侧),与y轴的正半轴交于点C,且AB=12,B(9,0).
(1)如图1,求a,h的值;
(2)如图2,点P在第一象限对称轴右侧的抛物线上,PE⊥x轴于点E,交线段BC于点D,点F在线
段BD上,且PD=135PF,FQ⊥BC,交直线PE于点Q,当PQ=8时,求点P的坐标;
(3)如图3,在(2)的条件下,R是线段CD上的一点,过点R作RG平行于x轴,与线段PQ交于点
G,连接OG、OQ,恰好使∠GOQ=45°,延长QR到点H,使QR=RH,连接AH,求线段AH的长,并直接
判断点H是否在此抛物线上?
y
x
C
B
A
O
(第27题图1)
实用标准
精彩文档
xyCBAO
27题图
xyCBAO
27题图
xyCBAO
27题
类型二: 已知不共线的两条线段关系---------利用三角函数解决问题
2.如图,在平面直角坐标系中,抛物线212yxbxc交x轴正半轴于点A、点B,交y轴于
点C, 直线y=-x+6经过点B、点C;
(1)、求抛物线的解析式 ;
(2)、点D在x轴下方的抛物线上,连接DB、DC,点D的横坐标为t,△BCD的面积为S,
求S与t的函数关系式,并直接写出自变量t的取值范围 ;
(3)、在(2)的条件下,点E在x轴上方的抛物线上,过点E作EF⊥x轴,垂足为点F,连
接DE,将射线ED沿直线EF折叠,得到对应射线EG,直线DF交射线EG于点H, 当S=12,
EF=5FH 时,求点E的坐标 .
实用标准
精彩文档
类型三:等腰+直角-----------构造中点直角三角形
3.如图,已知抛物线62212xxy与y轴交于点A,与x轴交于B、C两点,连接AC.
(1)求直线AC的解析式;
(2)点P为直线AC上方抛物线上的一点,过点P作PD⊥AC点D,当线段PD的最长时,求点P的坐标;
(3)在(2)的条件下,连接PB,Q为抛物线上一动点,过点Q做QF⊥PB交直线PB于点F.若Q点的横
坐标为t,抛物线的对称轴与AC交于点E,求t为何值时,EF=QE?
实用标准
精彩文档
类型四:利用已知线段构造可解的三角形
4.如图,在平面直角坐标系中,抛物线的顶点A(-1,0)在x轴上,与y轴交于点B,点C(1,4)为抛物
线上一点,CD∥x轴交抛物线于点D.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴左侧图象上一动点,设点P的横坐标为t,△PBC的面积为S,求S与t的函数
关系式;
(3)在(2)的条件下,延长CP至点Q,使PQ=CP,在线段DB的延长线上取一
点M,使∠DMQ=∠DCB,连接QM交射线CB于点N,当QN=5512时,求t的值.
yxBDACO(第27题图) yxBDACO(第27题备用图) y
x
B
D
ACO
(第27题备用图)
实用标准
精彩文档
与角有关的问题
类型一:与已知直线成定角问题
1.如图,已知抛物线32bxaxy(a≠0)的顶点坐标为Q(2,-1),且与x轴交于A、B两点(点A
在点B的右侧),连接AC.
(1)求该抛物线的函数关系式
(2)点P是抛物线上一个动点,从点C出发沿抛物线向点A运动,过点C作射线CD∥x轴,交抛
物线于点D,直线PC交x轴于点K,将线段CK绕点C逆时针旋转90°得到CK’,过点K’作K’M
∥AC交射线CD于点M,连接MK,求MK长.
(3)在(2)的条件下,设点P的横坐标等于t,连接MA、DA,当t为何值时,∠MAD与∠OBC互
余.
C
AOB
CAOBC
AOB
实用标准
精彩文档
类型二:倍角问题(倍角与半角之间的转化)
2.在平面直角坐标系中,O为坐标原点,抛物线223yaxax与x轴负半轴交于A,与x轴的正半轴交
于点B,与y轴的正半轴交于点C,且AB=4.
(1) 如图1,求a的值.
(2) 如图2,连接AC,BC,点D在第一象限内抛物线上,过D作DE//AC,交线段BC于E,若DE=5EC,求点D
的坐标.
(3) 如图3,在(2)的条件下,连接DC并延长,交x轴于点F,点P在第一象限的抛物线上,连接PF,作CQPF,
交x轴于Q,连接PQ,当2PQCPFQ时,求点P的坐标.
实用标准
精彩文档
类型三:转化为基本图形
3在平面直角坐标系中,点O为坐标原点,抛物线y=ax²+c交x轴于A、B,直线y=43x+49过点A,交y
轴和抛物线分别于D、C的横坐标为23。
(1)求抛物线解析式;
(2)如图2,动点P在抛物线BC段上(不与B、C重合),连接PA交OD于Q,设线段QD的长为d,点P
的横坐标为t,求d与t之间的函数关系式,直接写出t的取值范围;
(3)如图3,在(2)的条件下,直线y=-21x+k交OB、y轴、AP、AC分别于E、T、F、H,连接PE,若
PE=AH,且∠APE+∠AHE=180°,求点P的坐标和DQ的长。
图1
图2
实用标准
精彩文档
类型四:2∠A+3∠B=180°---------转化为等腰的问题
4.如图,在平面直角坐标系中,点O为坐标原点,抛物线1)2(2xay与x轴交于A、B两点,与y
轴交于点C,抛物线的顶点为D,对称轴DE交x轴于点E,OC=3DE.
(1)求a的值;
(2)如图2,点P为点B右侧的抛物线上一点,连接PB、PA,直线PB、PA分别交对称轴于点Q、G,
求证:点D为GQ的中点;
(3)如图3,点P为点B右侧的抛物线上一点,直线PA交y轴于点Q,PF⊥x轴于点F,连接CB,直
线CB交直线PF于点K,点S在线段PK上,当SK=2PS,2∠PQS+3∠QPK=180°时,求点P的横坐标.
yxCDBEAO第27题图1 xy
C
Q
D
B
G
E
A
O
P
第27题图2
y
xQKCDBEF
A
O
P
S
第27题图3
