有理数应用题30题(有答案)

合集下载

有理数应用题

有理数综合应用型
例1 某检修小组从A地出发，在东西方向的马路上检修线路，如果规定向东行驶为正，向
（2）在第次纪录时距A地最远．
（3）若每千米耗油0.3升，每升汽油需7.2元，问检修小组工作一天需汽油费多少元？
例2 李强靠勤工俭学的收入维持上大学的费用．下面是他某一周的收支情况表（收入为
（2）照这样，李强一个月（按30天计算）能有多少节余？
（3）按以上的支出水平，李强一个月（按30天计算）至少有多少收入才能维持正常开支？例3 三溪中学的小卖部最近进了一批计算器，进价是每个8元，今天共卖出20个，实际
（1）这个小卖部的计算器今天卖出的平均价格是多少？
（2）这个小卖部今天卖计算器赚了多少元？
（2）若运进的粮食为购进的，购买价为2000元/吨，运出的粮食为卖出的，卖出价为2300元/吨，则这一周的利润为多少？
（3）若每周平均进出的粮食数量大致相同，问：再过几周粮库存粮食达到200吨？
例5 小王上周五在股市以收盘价每股25元买进某公司股票1000股，在接下来的一周交易日
⑴星期二收盘时，该股票每股多少元？
⑵本周内该股票收盘时的最高价，最低价分别是多少？
⑶已知买入股票与卖出股票均需要支付成交金额的千分之五的交易费，若小王在本
周五以收盘价将全部股票卖出，他的受益情况如何？
例6 下表列出国外几个城市与北京的时差（带符号的表示同一时刻比北京晚的小时数）。

城市纽约巴黎东京
时差（小时） -13 -7 +1
（1）如果现在北京时间是中午12：00，那么东京时间是多少？（2）如果小丽在北京14:00给远在纽约的舅舅打电话，你认为合适吗？(3)如果你在北京时间上午8:00从北京乘飞机去东京,飞机途中需飞2小时,问你到达东京的时间?。

初中有理数运算应用题参考

初中有理数运算应用题参考初中有理数运算应用题参考：1、妈妈买回3千克菜花，她付出5元，找回了0.5元，每千克菜花多少元?2、五一班图书有故事书50本，是艺术类书的2倍还多4本，艺术类的书有多少本?3、一块三角形地，面积是280平方米，底是80米，高是多少米?4、一块梯形的面积是450平方米，高30米，上底是15米，下底是多少米?5、山坡上有羊80只，其中白羊是黑羊的4倍，山坡上黑羊、白羊各多少只?6、商店里卖出两筐柑橘，第一筐重26千克，第二筐重29千克，第二筐比第一筐多卖了9元钱，平均每千克柑橘多少元?7、一块梯形麦田，面积是540平方米，高18米，上底是20米，下底是多少米?8、甲乙两车从相距750千米的两地同时开出，相向而行，5小时相遇，甲车每小时行80千米，乙车每小时行多少千米?9、两辆汽车同时从同地开出，行驶 4.5小时后，甲车落在乙车的后面13.5千米，已知甲车每小时行35千米，乙车每小时行多少千米?10、加工一批零件，甲乙合作5小时完成，甲独做9形式完成。

已知甲每小时比乙多加工2个零件，这批零件共有多少个?11、体育场买来16个篮球和12个足球，共付出760元。

已知篮球与足球的单价比是5：6，体育场买篮球和足球各付出多少元12、某商店购进一批皮凉鞋，每双售出价比购进价多15%。

如果全部卖出，则可获利120元;如果只卖80双，则差64元才够成本。

皮凉鞋的购进价每双多少元?13、张师傅要利用两张铁皮(见下图)做一个圆柱体，选用其中一张剪出两个底面，然后用另一张做侧面。

要求做成的圆柱的体积尽可能大，那么张师傅做成的这个圆柱体的表面积是多少?体积是多少?(不考虑接缝，π取⒊14)14、甲从东城走向西城，每时走5千米，乙从西城走向东城，每时走4千米，如果乙比甲早1时出发，那么两人恰好在两城中间地方相遇，问东西两城的距离是多少千米?15、某经营公司有两个仓库储存彩电，甲乙两仓库储存之比为7∶3，如果从甲仓库调出30台到乙仓库，那么甲、乙两仓库之比为3∶2，问这两个仓库原来储存电视机共多少台?16、一列快车由甲城开到乙城需要10时，一列慢车从乙城开到甲城需要15时，两车同时从两城相对开出，相遇时快车比慢车多行120千米，两城相距多少千米?17、拖拉机5台24天耕地12000亩，问18天耕完54000亩，需增加拖拉机多少台?18、一块边长84米的正方形蕉园，蕉树的株距是2米，行距是8米，如果每棵蕉树收蕉果65千克，每千克0.45元，这个蕉园一年可收入多少元?19、东风牌货车的运输率是拖拉机的'2.5倍，大型集装车的运输率是东风牌货车的3倍，现有一堆货物，用东风车运，要6小时，如果改用拖拉机运一半，再用大型集装车运另一半，一共要用多少小时?20、甲乙两人卖鸡蛋，甲的鸡蛋比乙多10个，可是全部卖出后的收入都是15元，如果甲的鸡蛋按乙的价格出售可卖18元，那么甲、乙各有多少个鸡蛋?。

(完整版)有理数加法应用题

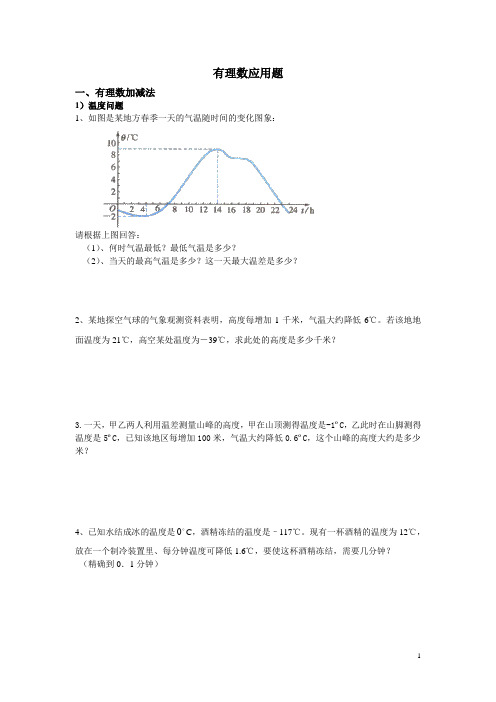
有理数应用题一、有理数加减法1）温度问题1、如图是某地方春季一天的气温随时间的变化图象：请根据上图回答：（1）、何时气温最低？最低气温是多少？（2）、当天的最高气温是多少？这一天最大温差是多少？2、某地探空气球的气象观测资料表明，高度每增加1千米，气温大约降低6℃。

若该地地面温度为21℃，高空某处温度为－39℃，求此处的高度是多少千米？3.一天，甲乙两人利用温差测量山峰的高度，甲在山顶测得温度是-1ºC，乙此时在山脚测得温度是5ºC，已知该地区每增加100米，气温大约降低0.6ºC，这个山峰的高度大约是多少米？4、已知水结成冰的温度是 0C，酒精冻结的温度是–117℃。

现有一杯酒精的温度为12℃，放在一个制冷装置里、每分钟温度可降低1.6℃，要使这杯酒精冻结，需要几分钟？（精确到0．1分钟）2）时差问题1．下表列出了国外几个大城市与北京的时差（带正号的数表示同一时刻比北京时间早的时数）（1）如果现在是北京时间上午8：00，那么东京时间是多少？（2）如果小强在北京时间下午15：00打电话给远在纽约的姑姑，你认为合适吗？试说明你的理由。

3）路程问题1．柳州出租车司机小李，一天下午以白沙客站为出发点，在南北走向的跃进路上营运，如果规定向北为正，向南为负，他这天下午行车里程（单位：千米）如下：+15，－2，+5，－13, +10，－7，－8，+12，+4，－5，+6（1）将最后一名乘客送到目的地时，小李距下午出车时的出发白沙客站多远? 在白沙客站的什么方向？（2）若每千米的价格为3.5元，这天下午小李的营业额是多少？2. 某一出租车一天下午以鼓楼为出发地在东西方向营运，向东为正，向西为负，行车里程（单位：km）依先后次序记录如下：+9、-3、-5、+4、-8、+6、-3、-6、-4、+10。

（1）将最后一名乘客送到目的地，出租车离鼓楼出发点多远？在鼓楼的什么方向？（2）若每千米的价格为2.4元，司机一个下午的营业额是多少？3．李老师在学校西面的南北路上从某点A出发来回检查学生的植树情况，设定向南的路程记为正数．向北的路程记为负数，那么李老师所行路程依次为（单位：百米）：＋12，－l0，＋10，－8，－6，－5，－3．（1）求李老师最后是否回到出发点A？（2）李老师离开出发点A最远时有多少千米? （3）李老师共走了多少千米？4．在一条东西走向的马路旁，有青少年宫、党校、商场、医院四家公共场所．已知青少年宫在学校东300m处，商场在学校西200m处，医院在学校东500m处，若将马路近似地看作一条直线，以学校为原点，向东为正方向，用1个单位长度表示100m．（1）在数轴上表示四家公共场所的位置．（2）列式计算青少年宫与商场之间的距离．5．检修组乘汽车，沿公路检修线路，约定向东为正．向西为负，某天自A出发，到收工时，行走记录为（单位：千米）：＋8、－9、＋4、＋7、－2、－10、＋18、－3、＋7、＋5 回答下列问题：（1）收工时在A地的哪边?距A地多少千米?（2）若每千米耗油0.3升，问从A地出发到收工时，共耗油多少升？6. 某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行-+-++--驶为负，一天中七次行驶纪录如下。

有理数试题及答案

有理数试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是有理数？A. πB. √2C. 0.33333...D. 2/3答案：D2. 有理数a/b（其中a、b为整数，且b≠0）中，b不能等于下列哪个数？A. 1B. 2C. 0D. 3答案：C3. 如果一个有理数的绝对值等于它本身，那么这个数是：A. 正数或零B. 负数或零C. 零D. 正数答案：A4. 下列哪个运算结果不是有理数？A. 3 + 2B. 5 - 4C. 2 × 3D. √9答案：D5. 两个有理数相除，商为有理数的条件是：A. 被除数和除数都是有理数B. 被除数是有理数，除数是无理数C. 被除数和除数都是无理数D. 除数是有理数，被除数是无理数答案：A6. 下列哪个数不是有理数？A. 1/2B. 3.14C. 0.3333...D. √4答案：B7. 有理数的乘法中，两个负数相乘的结果是：A. 正数B. 负数C. 零D. 无理数答案：A8. 有理数的加法中，两个相反数相加的结果是：A. 正数B. 负数C. 零D. 无理数答案：C9. 有理数的减法中，一个数减去它本身等于：A. 正数B. 负数C. 零D. 无理数答案：C10. 有理数的除法中，一个数除以它本身（不为零）的结果是：A. 正数B. 负数C. 1D. 无理数答案：C二、填空题（每题2分，共20分）1. 有理数包括整数和______。

答案：分数2. 一个有理数可以表示为两个整数的比，其中分母不为______。

答案：零3. 有理数的绝对值总是______或正数。

答案：零4. 有理数的乘法中，正数乘以正数的结果是______。

答案：正数5. 有理数的除法中，正数除以正数的结果是______。

答案：正数6. 有理数的加法中，一个正数加上一个负数可以表示为______。

答案：减法7. 有理数的减法中，减去一个数等于加上这个数的______。

答案：相反数8. 有理数的乘法中，任何数乘以______都等于零。

(精品总结)有理数及其运算常考应用题

∵ 每千米的价格为2.42.4元 ∴下午营业额=2.4×60=144元。
5、某铁矿码头将运进铁矿石记为正，运出铁矿石记为负．某天的记录如下：（单位：t） +100，−80，+300，+160，−200， −180，+80，−160 (1)当天铁矿石库存怎样？ (2)码头用载重量为20t的大卡车运送铁矿石，每次运费100元，问这一天共需运费为多少元？
|-25|+|+90|=730（米） ∵ 共5名队员，每人每米消耗氧气0.04升 ∴这段路程共消耗氧气0.04×5×730=146（升）
4、某一出租车一天下午以鼓楼为出发地在东西方向营运，向东为正，向西为负，行车里程（单位：km）依先后次序记录如下：
+9、−3、−5、+4、−8、+6、−3、−6、−4、+12 (1)将最后一名乘客送到目的地，出租车离鼓楼出发点多少km，
1、气象资料表明，高度每增加1km，气温大约降低6℃． (1) 我国著名风景区黄山的天都峰的高度约为1700米，当山下的地面温度约为18℃时，则山顶气温为多少℃？ (2)若某地地面的温度为20℃时，高空某处的气温为−22℃，则此处的高度为多少km？
解：(1)高度每增加1km，气温大约降低6℃ 高度增加1700米=1.7km 则气温降低6×1.7=10.2℃
解：（1）+15-2+5-1+10-3-2+12+4-5=33（千米） ∴在下午出车时的东边，距出发地有33千米远。（2）（15+2+5+1+10+3+2+12+4+5）=59（千米），
共耗油59×0.2=11.8（升） ∴共耗油11.8升（3）小李家距离出车地点的西边35千米处，即-35千米处；由（1）得：小李在下午出车时的东边距出发地33千米；送完最后一名乘客小李还要行驶33-（-35）=68千米． ∴还要行驶68千米才能到家。

专题118有理数的实际应用问题大题专练-2021-2022学年七年级数学上(解析版)【人教版】

2021-2022学年七年级数学上册尖子生同步培优题典【人教版】专题1.18有理数的实际应用问题大题专练（重难点培优）姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷试题共24题，解答24道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、解答题（本大题共24小题．解答时应写出文字说明、证明过程或演算步骤）1．（2020·沭阳县怀文中学七年级期中）课堂上，老师在教室里前后走动，巡视学生的课堂参与情况．如果规定向前黑板方向走为正，向后黑板方向走为负，那么在小组合作时，某老师在教室中间的一条通道上从讲台处出发，巡视行程记录如下（单位：米）：﹣6，﹣3，+8，﹣8，+2，+5，﹣5，+7．（1）请你通过计算说明这位老师最后是否回到讲台处？（2）若老师走动的平均速度是2米/秒，则这位老师此次巡视了多长时间？【答案】（1）回到讲台处；（2）22s【分析】（1）按照有理数加减运算的法则进行计算即可；（2）按照时间=路程÷速度计算即可．【解析】（1）﹣6+（﹣3）+(+8)+(﹣8)+(+2)+(+5)+(﹣5)+(+7)=0，∴可以回到讲台处；（2）（|﹣6|+|﹣3|+|+8|+|﹣8|+|+2|+|+5|+|﹣5|+|+7|）÷2=22(s)答：这位老师此次巡视了22s．2．（2020·江苏常青藤实验中学七年级期中）某检修车从文化宮出发，在东西走向的延陵路上检修线路，如果规定向东行驶为正，向西行驶为负，那么一天中八次行驶记录如下(单位：千米)：6，－13，+11，－8，+12，+7，－10，－5．(1)请你通过计算说明检修车最后是否回到文化宮?(2)若每千米耗油0.4升，则这一天中该检修车共耗油多少升?【答案】（1）能回到文化宫；（2）28.8升【分析】（1）把所有的行驶记录相加，然后根据正负数的意义解答；（2）用所有行驶记录的绝对值的和乘以0.4，计算即可得解．【解析】（1）6+（-13）+（+11）+（-8）+（+12）+（+7）+（-10）+（-5）=0所以，检修车最后能回到文化宫；（2）（6+13+11+8+12+7+10+5）×0.4=28.8升答：这一天中该检修车共耗油28.8升．3．（2020·江苏盐城市·七年级期中）“国庆黄金周”的某天下午，出租车司机小张的客运路线是在南北走向的建军路大街上，如果规定向南为正、向北为负，他这天下午行车里程（单位：千米）如下：++-+--+--+-、、、、、、、、、、．31056431286718（1）求收工时小张距离下午出车时的出发点多远?（2）若汽车耗油量为0.2L/km，这天下午小张共耗油多少升?【答案】（1）6千米；（2）16.4升【分析】（1）把行车记录相加，再根据正、负数的意义解答即可；（2）求出所有行车记录的绝对值的和，再乘以0.2计算即可得解．【解析】（1）3+10-5+6-4-3+12-8-6+7-18=3-3+6-6+10+12+7-5-4-8-18=-6千米．答：距离下午出车时的出发点6千米；（2）3+10+5+6+4+3+12+8+6+7+18=82千米，82×0.2=16.4升．答：这天下午小张共耗油16.4升．4．（2020·江苏南通市·七年级期中）一名快递员骑电动车从饭店出发送外卖，向东走了2千米到达小红家，继续向东走了4千米到达小明家，然后又向西走了8千米到达小刚家，最后回到饭店．现以饭店为原点，以向东的方向为正方向，用一个单位长度表示1千米画数轴，并以点O，A，B，C分别表示饭店，小红家，小明家，小刚家．（1）请画出数轴，并在数轴上标出点O，A，B，C的位置；（2）小刚家距小红家多远？（3）若小红步行到小明家每小时走4千米；小刚骑自行车到小明家每小时骑10千米，若两个人同时分别从自己家出发，问两个人能否同时到达小明家，若不能同时，谁先到达？【答案】（1）见解析；（2）4千米；（3）不能，小刚先到达【分析】（1）画出数轴，根据题意在数轴上表示出点O，A，B，C的位置即可；（2）点A与点C表示的数列式计算即可；（3）根据“时间=路程÷速度”列式计算解答即可．【解析】（1）数轴及点O ，A ，B ，C 的位置如图所示：（2）2－(－2)＝4(千米)，答：小刚家距小红家4千米．（3）小红步行到小明家所需时间为：(6－2)÷4＝1(小时)；小刚骑自行车到小明家所需时间为：[6－(－2)]÷10＝0.8(小时).因为0.8＜1，答：两个人不能同时到达小明家，小刚先到达．5．（2020·浙江七年级期中）某路公交车从起点经过A ，B ，C ，D 站到达终点，各站上下乘客的人数如下（上车为正，下车为负）：起点(20,0),(12,4),(8,9),(6,4),(2,7)A B C D ----，终点()0,____．（1）在横线上填写适当的数，并说明该数的实际意义；（2）行驶在哪两站之间时，车上的乘客最多？（3）若乘坐该车的票价为每人2元，则这一趟公交车能收入多少钱？【答案】（1）−24；（2）公交车行驶在C 站和D 站之间车上的乘客最多；（3）96【分析】（1）根据正负数的意义，利用有理数的加法法则计算即可；（2）根据（1）的计算解答即可；（3）根据各站之间的人数，乘以票价2，然后计算即可得解．【解析】（1）起点到A 站，车上人数：20，A 站到B 站，车上人数：20＋12−4＝28，B 站到C 站，车上人数，28＋8−9＝27，C 站到D 站，车上人数，27＋6−4＝29，D 站到终点，29＋2−7＝24，所以，到终点下车还有24人；故答案为：−24；（2）由（1）的计算可知，公交车行驶在C 站和D 站之间车上的乘客最多，为29人；（3）（20＋12＋8＋6＋2）×2＝96（元）．答：这趟出车能收入96元．6．（2020·浙江宁波市·七年级期中）一位病人早晨8时的体温是39.7℃，下表是该病人一天中的体温变化．（1）这位病人的体温最低是多少摄氏度？（2）若正常体温是37℃，那么从体温看，这位病人的病情是在恶化还是在好转？【答案】（1）体温最低是次日的凌晨5时，是37℃；（2）该病人在逐渐好转【分析】（1）首先利用有理数的加减法计算出每个时刻的体温，然后进行比较即可得出答案；（2）通过分析（1）中的体温，即可得出体温的变化趋势，从而得出答案．【解析】（1）11时的体温是39.7-1.5=38.2（℃）；14时的体温为38.2+1=39.2（℃）；17时的体温是39.2+0.2=39.4（℃）；20时的体温为39.4-1.2=38.2（℃）；23时的体温是38.2-0.5=37.7（℃）；2时的体温是37.7-0.5=37.2（℃）；5时的体温是37.2-0.2=37（℃）；8时的体温是37+0.2=37.2（℃），<<<<<，∵3737.237.738.239.239.4∴体温最低是次日的凌晨5时，是37℃；（2）根据（1）求出的数据分析，该病人在逐渐好转，因为体温与正常体温的差越来越小．7．（2020·浙江宁波市·七年级期中）下面是今年流花河某水文站一周内水位变化情况：（该水文站警戒水位为33.4m．记当日水位上涨为正）（1）上周末水位为32.0m，则本周超过警戒水位的是哪一日？说明理由．（2）本周末比上周末，水位是升高了还是下降了？升或降了多少米？【答案】（1）星期三，理由见解析；（2）下降了0.1米【分析】（1）求得每天的水位，即可作出判断；（2）比较本周末的水位和上周日的水位即可．【解析】（1）星期一：32+0.35=32.35米；星期二：32.35+0.89=33.24米；星期三：33.24+0.26=33.5米；星期四：33.5-0.76=32.74米；星期五：32.74+0.65=33.39米；星期六：33.39-0.94=32.45米；星期日：32.45-0.55=31.9米；∴超过警戒线的是星期三；（2）由（1）可得：本周末的水位是31.9米，32-31.9=0.1米，∴本周末比上周末的水位降低了0.1米．8．（2020·浙江宁波市·）小华某天早晨跑步，他从自己家出发，向东跑了1.5千米到达中心公园，又向西跑了2.3千米到达新华书店，接着又向东跑了1千米到早点铺买了早饭，最后向西跑返回自己家．（1）求新华书店与小华家之间的距离；（2）如果小华跑步的速度是每分钟250米，那么小华跑步一共用了多长时间?【答案】（1）新华书店与小华家之间的距离为0.8千米；（2）小华跑步一共用了20分钟长时间．【分析】（1）计算2.3-1.5即可求出答案；（2）求出每个数的绝对值，相加求出路程，再根据时间=路程÷速度计算即可求解．【解析】（1）2.3-1.5=0.8．故新华书店与小华家之间的距离为0.8千米；-=（千米），（2）10.80.2+++=（千米），1.52.310.255千米=5000米，500025020÷=（分钟）．答：小华跑步一共用了20分钟长时间．9．（2020·浙江七年级期中）某仓库中有一种货物库存为250千克，现规定运入为正，运出为负，一天中七次出入情况如下表：（1）在第_____次记录时库存最多．（2）最终这一天库存增加或减少了多少？（3）若货物装卸费用为每千克0.4元，则这一天需装卸费用多少元？【答案】（1）第四次；（2）增加了24千克；（3）152元【分析】（1）分别计算出每次运输后的库存即可求解；（2）根据表格数据相加计算即可求解；（3）根据总价=单价×数量计算即可求解．【解析】（1）第一次：250-30=220千克，第二次：220+78=298千克，第三次：298-17=281千克，第四次：281+101=382千克，第五次：382-98=284千克，第六次：284+23=307千克，第七次：307-33=274千克，∴在第四次纪录时库存最多；（2）由（1）可得：274-250=24千克，∴最终这一天库存增加了24千克；（3）（30+78+17+101+98+23+33）×0.4=152元，∴这一天需装卸费用152元．10．（2020·舟山市普陀区东港中学七年级期中）目前，我国新冠肺炎疫情防控已进入常态化阶段,截至2020年10月31日24时，据31个省（自治区、直辖市）和新疆生产建设兵团报告，现有确诊病例429例，下表是2020年11月1日至11月7日的当日新增确诊病例和当日新增治愈病例．（统计数据都以当日24时为界）（1）请问到几月几日24时止，现有确诊病例最多？（2）请问到11月7日24时止，现有确诊病例是多少例？（3）若治愈一位新冠肺炎病人需要a 元，那么11月1日0时至11月7日24时治愈的肺炎病人共需要多少元钱？【答案】（1）11月3日；（2）410人；（3）214a 元【分析】（1）算出每日现有确诊病例即可解答；（2）根据（1）的计算解答即可；（3）用治愈病例乘以a 即可；【解析】（1）1日：429+24-20=433人，2日：433+34-30=437人，3日：437++17-16=438人，4日：438+28-30=436人，5日：436+33-36=433人，6日：433+28-37=424人，7日：424+31-45=410人，∴11月3日24时止，现有确诊病例最多；（2）由（1）知，到11月7日24时止，现有确诊病例是410例；（3）(20+30+16+30+36+37+45)a=214a 元．11．（2020·诸暨市浣江初级中学七年级期中）一名足球守门员练习折返跑，从球门线出发，向前跑记作正数，向后跑记作负数，他的练习记录如下（单位：m ）：+5，−3，+10，−8，−6，+13，−10（1）守门员最后是否回到了球门线的位置？（2）守门员在这次练习中共跑了多少米？（3）在练习过程中，守门员离开球门线距离达10m 以上（包括10m ）的次数是多少次？【答案】（1）守门员最后没有回到球门线的位置；（2）55米；（3）2次．【分析】（1）将练习记录的所有数字求和即可得；（2）将练习记录的所有数字的绝对值求和即可得；（3）分别求出每次记录时，守门员离开球门线的距离，由此即可得．【解析】（1）由题意得：()()()()()()5310861310++-+++-+-+++-，5310861310=-+--+-，1=（米），因为10≠，所以守门员最后没有回到球门线的位置；（2）由题意得：5310861310++-+++-+-+++-，5310861310=++++++，55=（米），答：守门员在这次练习中共跑了55米；（3）第1次记录时，守门员离开球门线的距离为55+=米，第2次记录时，守门员离开球门线的距离为()532+-=米，第3次记录时，守门员离开球门线的距离为()21012++=米，第4次记录时，守门员离开球门线的距离为()1284+-=米，第5次记录时，守门员离开球门线的距离为()462+-=米，第6次记录时，守门员离开球门线的距离为()21311-++=米，第7次记录时，守门员离开球门线的距离为()11101+-=米，故守门员离开球门线距离达10m 以上（包括10m ）的次数是2次．12．（2020·宁波滨海国际合作学校）一公路检修班乘沿东西方向检修路线，自O 地出发约定向东为正，向西为负，到收工时，行走记录为(单位：千米)：+20，-35，+40，+25，-25，-45，+15．请根据题意解答下列问题（1）问收工时检修组位于何处？（2）若汽车耗油为0.3升/千米，问从O 地出发到收工时，共耗油多少升？【答案】（1）位于O 地西边5千米处；（2）共耗油61.5升．【分析】（1）根据题意可直接进行列式求解；（2）把每次的行走记录的绝对值相加，然后再进行求解即可．【解析】（1）由题意得：()()()()()()203540252545155++-+++++-+-++=-（千米），答：收工时检修组位于O 地西边5千米处．（2）由题意得：20+35+40+25+25+45+15=205（千米），205×0.3=61.5（升）；答：共耗油61.5升．13．（2021·浙江杭州市·七年级期中）某路公交车从起点经过A，B，C，D站到达终点，一路上下乘客如下表所示．（用正数表示上车的人数，负数表示下车的人数）（1）将表格填写完整；（2）车行驶在哪两站之间车上的乘客最多站和站；（3）若每人乘坐一站需买票0.8元，问该车出车一次能收入多少钱？（列式并计算）【答案】（1）-34；（2）B，C；（3）124元．【分析】（1）根据正负数的意义，上车为正数，下车为负数，求出A、B、C、D站以及终点站的人数，即可得解；（2）根据（1）的计算解答即可；（3）根据各站之间的人数，乘票价0.8元，然后计算即可得解．【解析】（1）根据题意可得：到终点前，车上有18＋15−3＋12−4＋7−10＋8−9＝34，即34人；故到终点下车还有34人，表格应填-34；（2）根据图表：易知B站和C站之间人数最多；（3）根据题意：[18＋（18+15-3）＋（18+15-3+12-4）＋（18+15-3+12-4+7-10）＋34）]×0.8＝124（元）．14．（2020·浙江杭州市·七年级期中）在抗洪抢险中，解放军战士的冲锋舟加满油，沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B地，约定向东为正方向，当天的航行路程记录如下(单位：千米)：+14，−9，+8，−7，+13，−6，+12，−5．（1）请你帮忙确定B地位于A地的什么方向，距离A地多少千米?（2）救灾过程中，冲锋舟离出发点A最远处千米；（3）若冲锋舟每千米耗油0.5升，油箱容量为28升，求冲锋舟当天救灾过程中至少还需补充多少升油?【答案】（1）正东，20千米；（2）25；（3）9升．【分析】（1）将记录的数字求和即可得；（2）分别求出每一次记录时冲锋舟离出发点A 的距离，再比较大小即可得；（3）将记录的数字的绝对值求和可得冲锋舟当天的航行总路程，再乘以0.5，然后减去28即可得．【解析】（1）()()()()()()()()14987136125++-+++-+++-+++-，14987136125=-+-+-+-，20=（千米），答：B 地位于A 地的正东方向，距离A 地20千米；（2）第1次记录时冲锋舟离出发点A 的距离为1414+=千米，第2次记录时冲锋舟离出发点A 的距离为()1495+-=千米，第3次记录时冲锋舟离出发点A 的距离为()5813++=千米，第4次记录时冲锋舟离出发点A 的距离为()1376+-=千米，第5次记录时冲锋舟离出发点A 的距离为()61319++=千米，第6次记录时冲锋舟离出发点A 的距离为()19613+-=千米，第7次记录时冲锋舟离出发点A 的距离为()131225++=千米，第8次记录时冲锋舟离出发点A 的距离为()25520+-=千米，由此可知，救灾过程中，冲锋舟离出发点A 最远处为25千米；（3）冲锋舟当天航行总路程为14987136125++-+++-+++-+++-，14987136125=+++++++，74=（千米），则740.52837289⨯-=-=（升），答：冲锋舟当天救灾过程中至少还需补充9升油．15．（2020·辽宁锦州市·七年级期中）某地饮用水被污染，居民饮水困难．某校师生积极行动起来，各班捐助水的瓶数以100瓶为标准，超过的记为“＋”，不足记为“－”．其中七年级的6个班学生的捐助情况如表所示：班级（1）（2）（3）（4）（5）（6）超过（不足） 10+ 5- 15+ 10- 2-统计员小李统计时不小心将墨水滴到了其中（5）班的数据上．他只记得该校七年级学生共捐助616瓶饮用水，根据以上信息，你用学过的知识还能帮助小李将被覆盖的数据复原出来？如果能，请写出解答过程．不能，请说明理由．【答案】能，8，见解析【分析】由题意可直接进行求解．【解析】由题意得：616100616-⨯=（瓶），()()()()()16105151021688-++-+++-+-=-=⎡⎤⎣⎦（瓶）；答：七（5）班超过标准瓶数8瓶．16．（2020·山东济南市·七年级期中）学校为了备战校园足球联赛，利用体育课让学生进行足球训练，为了训练学生快速抢断转身，体育老师设计了折返跑训练．老师在东西方向的足球场上画了一条直线插上不同的折返旗帜，如果约定向西为正，向东为负，练习一组的行驶记录如下（单位：米）： +40，﹣30，+45，﹣25，+25，﹣35，+15，﹣28，+16，﹣18．（1）学生最后到达的地方在出发点的哪个方向？距出发点多远？（2）学生训练过程中，最远处离出发点多远？（3）学生在一组练习过程中，跑了多少米？【答案】（1）在出发点的正西方向，距出发点5米；（2）最远处离出发点55米；（3）跑了277米【分析】（1）根据加法法则，将正数与正数相加，负数与负数相加，进而得出计算得结果；（2）求出每一段到出发点的距离，即可判断出结果；（3）利用绝对值的性质以及有理数加法法则求出即可．【解析】（1）（+40）+（﹣30）+（+45）+（﹣25）+（+25）+（﹣35）+（+15）+（﹣28）+（+16）+（﹣18）＝+5（米）．答：学生最后到达的地方在出发点的正西方向，距出发点5米；（2）第一段，40米，第二段，40﹣30＝10（米），第三段，10+45＝55（米），第四段，55﹣25＝30（米），第五段，30+25＝55（米），第六段，55﹣35＝20（米），第七段，20+15＝35（米），第八段，35﹣28＝7（米），第九段，7+16＝23（米），第十段，23﹣18＝5（米），故最远处离出发点55米；（3）|+40|+|﹣30|+|+45|+|﹣25|+|+25|+|﹣35|+|+15|+|﹣28|+|+16|+|﹣18|＝277（米）．答：学生在一组练习过程中，跑了277米．17．（2020·河南郑州市第四十七初级中学七年级期中）某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km）：（1）接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？（2）若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？【答案】（1）接送完第5批客人后，该驾驶员在公司南边10千米处；（2）4.8升．【分析】（1）根据有理数加法即可求出答案．（2）根据题意列出算式即可求出答案．【解析】（1）5+2+（﹣4）+（﹣3）+10=10（km）．答：接送完第5批客人后，该驾驶员在公司南边10千米处．（2）（5+2+|﹣4|+|﹣3|+10）×0.2=4.8（升）．答：在这过程中共耗油4.8升．18．（2020·河南郑州市·）新郑大枣来啦！新郑大枣是河南的一大特产，现有30筐新郑大枣，以每筐15千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：（1）这30筐大枣中，最重的一筐比最轻的一筐重多少千克？（2）与标准质量比较，这30筐大枣总计多少千克？（3）若大枣每千克市场售价10元，现在由于要减少库存，厂家搞活动按八折出售，则这30筐大枣全部卖完可卖多少元？【答案】（1）最重的一筐比最轻的一筐重5.5千克；（2）这30筐大枣总计455千克；（3）这30筐大枣全部卖完可卖3640元．【分析】（1）根据有理数的大小，确定最重的和最轻的质量，相减即可；（2）根据图表数据列出算式，然后计算即可得解；（3）求出30筐猕猴桃的总质量，乘以8即可求解；--=（千克）【解析】（1）3( 2.5) 5.5答：最重的一筐比最轻的一筐重5.5千克．-⨯+-⨯+-⨯+⨯+⨯+⨯（2）( 2.5)2(2)5( 1.5)6041538=---++5109524=，5⨯+=（千克）30155455答：这30筐大枣总计455千克．⨯⨯=（元）（3）455100.83640答：这30筐大枣全部卖完可卖3640元．19．（2020·安徽宿州市·七年级期中）光明中学七（1）班学生的平均身高是160cm．（1）下表给出了该班6名学生的身高情况（单位：cm），试完成下表：（2）这6名学生中谁最高？谁最矮？（3）最高与最矮的学生身高相差多少？【答案】（1）162；160；﹣6；163；+5；（2）小刚最高，小亮最矮；（3）11厘米．【分析】（1）根据题意及表格可直接进行求解；（2）由（1）及表格可直接进行求解；（3）由（2）可直接进行列式求解．【解析】（1）小彬的身高为：160+2＝162（cm ）；小丽的身高为：160+0＝160（cm ）；小颖的身高为：160+3＝163（cm ）；小亮的身高与平均身高的差值为：154﹣160＝﹣6；小刚的身高与平均身高的差值为：165﹣160＝+5；故答案为：162；160；﹣6；163；+5；（2）由表格中的数据得：小刚最高，小亮最矮；（3）由（2）及表格可得： 165﹣154＝11（厘米）．答：最高与最矮的学生身高相差11厘米．20．（2020·辽宁沈阳市·七年级期中）一辆流动早餐车从A 站沿着一条笔直的南北方向的马路来回售卖早点，行驶的路程情况如下（向南行驶为正，单位：km ）：2+，5-，6+，5+，3-，3-，6-，3-，3-，9+．（1）当早餐车完成上述行程后共行驶了多少km ？（2）当早餐车完成上述行程后，在A 站的哪侧？距离A 站有多少km ？【答案】（1）45km ；（2）早餐车完成上述行程后在A 站的北面，距离A 站有1千米．【分析】(1)将记录的每一个数字的绝对值相加求和即为所求结果； (2)将记录的所有数字相加求和可得到最终结果．【解析】（1）2565336339++-+++++-+-+-+-+-++256533633945=+++++++++=km ，∴当早餐车完成上述行程后共行驶了45km ．（2）256533633922231-++-----+=-=-km ∴当早餐车完成上述行程后在A 站的北面，距离A 站有1km ．21．（2020·广西南宁市·七年级期中）疫情期间，武汉的出租车司机王师傅在东西走向的公路上免费接送医护人员，如果规定向东为正，向西为负，出租车的行程如下（单位：千米）：+10 -17 +16 -10 -12 +5 -13（1）最后一名医护人员接送完毕，王师傅在出车的什么位置？（2）若出租车耗油量每千米0.4升，王师傅出车前加满油40升，当他送完最后一个老师，问他能否顺利返回？【答案】（1）最后一名医生接送完成，王师傅在出车的西边21千米；（2）不能顺利返回，见解析【分析】（1）根据有理数的加法运算，将所有数据相加即可；（2）根据行车就耗油，可得往返一共耗油量然后跟40比较即可得到结果．【解析】（1）由题意，列式子得：10+（-17）+16+（-10）+（-12）+5+（-13）=﹣21（千米）答：最后一名医生接送完成，王师傅在出车的西边21千米（2）| +10 |+| -17 | +| +16 | +| -10 |+| -12 | + | +5 | +| -13 | =83 （千米）（83+21）× 0.4=41.6 （升）41.6 > 40答：不能顺利返回．22．（2020·湖北宜昌市·七年级期中）今年“十一”期间，某风景区在8天中每天游客的人数变化如下表(正数表示比前一天多的人数，负数表示比前一天少的人数)（1）若9月30日的游客人数记为a，请用含a的代数式表示10月2日的游客人数？（2）请判断八天内游客人数最多的是哪天？请说明理由．（3）此风景区一方面给广大市民提供一个休闲游玩的好去处；另一方面拉动了内需，促进了消费．若9月30日的游客人数为1万人，进园的人每人平均消费60元，问“十一”期间所有游园人员在此风景区的总消费是多少元？（用科学记数法表示）【答案】（1）a+1.4；（2）10月3日游客人数最多为a+1.8；（3）7.92×106元【分析】（1）由题意，10月1日游客人数为a+0.6，则根据表格可求解；（2）根据题意及表格分别得出八天的人数，进而可求解；（3）由题意得a=1万人，则可求出八天总人数，然后问题可求解．【解析】（1）由题意，10月1日游客人数为a+0.6，则10月2日人数为：a+0.6+0.8=a+1.4；（2）由题意可知10月1日至10月8日游客人数分别是：a+0.6，a+1.4，a+1.8，a+1.4，a+0.6，a+0.8，a-0.4，a-1，所以，10月3日游客人数最多为a+1.8；（3）若9月30日人数为1万人，则a=1万人，则10月1日至10月8日游客总人数为：（a+0.6）+（a+1.4）+（a+1.8）+（a+1.4）+（a+0.6）+（a+0.8）+（a-0.4）+（a-1 ）=8a+5.2=8+5.2=13.2（万人），又因为每人平均消费60元，则可得13.2×60=792（万元）=7.92×106（元）；答：“十一”期间所有游园人员在此风景区的总消费是7．92×106（元）．23．（2020·重庆市第一一〇中学校七年级期中）已知某水库上周日的水位是20m，下表是该水库今年某周的水位记录情况．注：正号表示水位比前一天上升，负号表示水位比前一天下降．问：（1）本周星期三的水位是多少米？星期日的水位是多少米？（2）本周哪一天的水位最高，最高水位是多少米，哪一天的水位最低，最低水位是多少米；（3）以上周日水位为0点，用折线统计图表示本周的水位变化情况．【答案】（1）本周星期三的水位是20.25米；星期日的水位是20.30米；（2）本周星期二的水位最高，最高水位是20.45米，星期五的水位最低，最低水位是20.05米；（3）见解析【分析】（1）由有理数的加法运算，即可得到答案；（2）根据已知分别计算出每天的水位，通过计算确定最高和最低水位；（3）根据已知条件，画出折线图即可；++-=；【解析】（1）本周星期三的水位是：200.150.30.220.25++-+-++=；本周星期日的水位是：200.150.30.20.050.250.10.1520.30（2）星期一的水位为：20+0.15=20.15米；星期二的水位为：20.15+0.3=20.45米，星期三的水位为：20.45-0.2=20.25米，星期四的水位为：20.25+0.05=20.30米，星期五的水位为：20.30-0.25=20.05米，星期六的水位为：20.05+0.1=20.15米，星期日的水位为：20.15+0.15=20.30米， ∴星期二的水位最高，最高水位是20.45米；星期五的水位最低，最低水位是20.05米；（3）根据题意，折线图如下图所示：24．（2020·四川成都市·七年级期中）游戏中蜗牛只能沿东西方向直线爬行，规定向东爬行的路程记为正数，向西爬行的路程记为负数．现在，它从O 开始出发，爬过的各段路程依次为（单位：厘米）：6-，12+，10-，5+，3-，10+，8-．（1）通过计算判断蜗牛最后停下来的位置在O 的哪个方向多远处？（2）通过计算判断蜗牛离开出发点O 最远时是多少厘米？（3）将题意画成数轴并标注字母，自我评价第（1）（2）两问的正确性，写下“我对了”或“我错了”只要判断正确，前两问如有错将不扣分（不需要修改前两问的解答）【答案】（1）蜗牛最后回到起点O ．（2）8厘米（3）证明见解析；我对了【分析】（1）把爬过的路程记录相加，即可得解；（2）求出各段距离，然后根据正负数以及借助绝对值的意义进行解答即可；（3）根据题意画数轴即可；-+-+-+-=．【解析】（1）61210531080所以蜗牛最后回到起点O．-=，（2）66-+=，6126-+-=，612104-+-+=，612105161210532-+-+-=，-+-+-+=，6121053108所以蜗牛离开发出点O最远时是8厘米．（3）我对了-------理由：蜗牛爬行路线：O A B C D E F G 由题意画数轴如下：。

有理数专项练习(含答案)

初三复习有理数专项练习1．6-的相反数是2．135-的相反数是________．3．如果收入200元记作＋200元，则-500元表示_______________________．4．如果盈利20元记作+20元，那么亏损30元记作元.5．把向南走8米记作+8米，那么向北走5米可表示为米．6．如果上升3米记作+3米，那么下降3米记作米．7．我国现采用国际通用的公历纪年法，如果我们把公元2013年记作+2013年，那么，处于公元前500年的春秋战国时期可表示为年．8．某商店搞促销活动，店内衣服一律按标价的六折出售，现小明花300元购得一件上衣，则该上衣的标价为元．9．甲、乙、丙三地的海拔高度分别为20米、－5米、和－10米，那么最高的地方比最低的地方高米.10．某天温度最高是12℃，最低是－7℃，这一天温差是 ℃．11．已知，线段AB 在数轴上且它的长度为5，点A 在数轴上对应的数为2-，则点B 在数轴上对应的数为．12．比较大小： 3____2--13．比较大小：23-_____45-． 14．22－（）＝(－2)3．15．π∣= .16．一个数的相反数等于它本身，这个数是_________。

17．倒数等于它本身的数是______________.18．绝对值等于4的所有整数是 .19．我市永丰林生态园区生产的草莓包装纸箱上标明草莓的质量为03.003.05+-千克，如果这箱草莓重4．98千克，那么这箱草莓质量标准．（填“符合”或“不符合”）20．台湾是我国最大的岛屿，总面积约为36000平方千米，这个数据用科学记数法可以表示为平方千米．21．载有239名乘客的MH370飞机失联后，其行踪一度成为世人关注的焦点．小明在百度中搜索“马航最新消息”，找到相关结果约32 800 000个．其中数32 800 000用科学记数法表示为．22．2010年上海世博会的园区规划用地面积约为5 280 0002m ，将5 280 000用科学记数法表示为．23．截至2013年12月31日，余额宝规模已达到1853亿元，这个数据用科学记数法可表示为元．24．有一种病毒的直径为0．000068米，用科学记数法可表示为米．25．用四舍五入法，对0．0070991取近似值，若要求保留三个有效数字，•并用科学记数法表示，则该数的近似值为．用科学记数法表示：．27．近似数51.46010⨯精确到位，有效数字是．28．圆周率π…，取近似值3.142，是精确到__________位。

有理数运算应用题

1．一辆货车从超市出发，向东走了2km，到达小刚家，继续向东走了3km到达小红家，又向西走了9km到达小英家，最后回到超市．（1）请以超市为原点，以向东方向为正方向，用1个单位长度表示1km，画出数轴．并在数轴上表示出小刚家、小红家、小英家的位置；（2）小英家距小刚家有多远？（3）货车一共行驶了多少千米？2．小明靠勤工俭学的收入维持上大学的基本费用，下面是小明一周收支情况表（收入为正，单位：元）（1）一周内小明有多少结余？（2）照这样，一个月（按30天计算）小明能有多少结余？（3）按以上支出，小明一个月（按30天计算），至少要赚多少钱，才能维持正常开支。

3．小花猫从某点O出发在一直线上来回跑动，假定向右跑的路程记为正数，向左跑的路程记为负数，跑动的各段路程依次为（单位：米）：+4，-2，+10，-7，-6，+9，-10，+12．（1）问：小花猫最后在出发点的哪一边？离开出发点O相距多少米？（2）在跑动过程中，如果每跑过10米奖励一条小鱼，则小花猫一共得到多少条小鱼？3.某天一个巡警骑摩托车在一条南北大道上巡逻，他从岗亭出发，在某个时刻停留在A处，以岗亭为原点，向北方向正，这段时间行驶记录如下（单位，千米）+-+-+-+-10,9,1,15,6,14,4,2（1）A在岗亭的哪个方向，距离岗亭多元？（2）如果每10千米耗油0.5升，且巡警最后返回到岗亭，问共耗油多少升？4. “十一”黄金周期间，某风景区在7天中来旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数。

（1）若9月30日来旅游人数记为a，请用a的代数式表示10月2日来旅游的人数。

（2）请判断七天内游客人数最多的是日，最少的是日。

它们相差_________万人？（3）以9月30号游客人数为0点，用折线统计图表示这七天的游客人数变化情况。

5．某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶纪录如下。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

有理数应用题专项练习30题（有答案）

时间2021.03.10 创作：欧阳治 1．某巡警骑摩托车在一条南北大道上来回巡逻，一天早晨，他从岗亭出发，中午停留在A处，规定向北方向为正，当天上午连续行驶情况记录如下（单位：千米）：+5，﹣4，+3，﹣7，+4，﹣8，+2，﹣1．（1）A处在岗亭何方？距离岗亭多远？（2）若摩托车每行驶1千米耗油a升，这一天上午共耗油多少升？ 2．某工厂生产一批零件，根据要求，圆柱体的内径可以有0.03毫米的误差，抽查5个零件，超过规定内径的记作正数，不足的记作负数，检查结果如下：+0.025，﹣0.035，+0.016，﹣0.010，+0.041 （1）指出哪些产品合乎要求？（2）指出合乎要求的产品中哪个质量好一些？ 3．某奶粉每袋的标准质量为454克，在质量检测中，若超出标准质量2克，记作为+2克，若质量低于3欧阳治创编 2021.03.10 欧阳治创编 2021.03.10